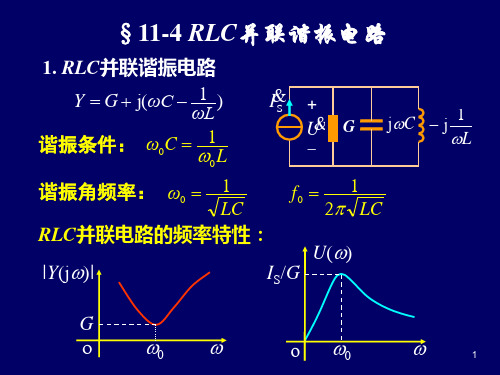
RLC并联谐振电路
RLC并联谐振电路 、 波特图 、 滤波器简介
2. 电感线圈与电容器的并联谐振 实际的电感线圈总是存在电阻，因此电感线圈与 电容器的并联电路如图所示：
R C L
Y jC
1 R jL
L R 2 j C 2 2 2 R (L) R (L)
谐振时：
ω0 L ω0C 2 0 2 R (ω0 L)
2 0
1 当 C2 0 时，发生并联谐振，0 L1
1 L1C2
7
§11-5 波特图
对电路和系统的频率特性进行分析时，为了直观 地观察频率特性随频率变化的趋势和特征，工程上常 采用对数坐标来作频响曲线，这种用对数坐标描绘的 频率响应图就称为频响波特图。
例 画出网络函数的波特图。
200j H ( j ) ( j +2)(j +10)
H ( ) H ( )
1 0 1 2 0 1 0 低通 高通 带通
1 2 带阻
12
典型无源滤波器
1）低通滤波器
2）高通滤波器
13
3）带通滤波器
4）带阻滤波器
14
下次课内容：
• 第十二章 三相电路
• 12.1 三相电路
• 12.2 线电压（电流）与相电压
（电流）的关系
作业：11-6(c,d)，11-10，11-12
15
2
I S
+
U
_
I G
G
I I L C 1 jC j
L
当 Q >>1，IC=IL=QIS >>IS，过电流
3）=cos=1，P=U0IS 达到最大，Q = 0。
2 IS P U 0 IS G
rlc并联谐振电路阻抗的特点
rlc并联谐振电路阻抗的特点【主题介绍】在电路中，RLC并联谐振电路是一种具有特殊频率响应的电路。
它由电感（L）、电阻（R）和电容（C）三个元件组成，能够在特定频率下表现出较低的阻抗。
本文将深入探讨RLC并联谐振电路的阻抗特点，并分享对该电路的观点和理解。
【1. RLC并联谐振电路简介】RLC并联谐振电路由电阻元件、电感元件和电容元件并联连接而成。
在电路中，电感元件储存电能，电容元件储存电荷，而电阻元件对电流产生阻碍。
当电路中的频率等于谐振频率时，电感和电容的阻抗相互抵消，使得电路整体的阻抗具有最小值，这就是并联谐振电路的特点所在。
【2. RL并联谐振电路的阻抗特点】在RLC并联谐振电路中，阻抗以复数形式呈现，由实部和虚部组成。
实部代表电路的有源部分，而虚部则代表电路的无源部分。
2.1 低阻抗：RLC并联谐振电路在谐振频率附近表现出较低的阻抗。
当电路的频率等于谐振频率时，电感和电容的阻抗相互抵消，整个电路的阻抗呈现最小值。
这种低阻抗特点使得电路在谐振频率附近对电流更加敏感，电信号可以更轻松地通过电路，实现有效的能量传输。
2.2 频率选择性：RLC并联谐振电路在谐振频率附近表现出较高的频率选择性。
谐振频率附近，电感和电容的阻抗值会急剧变化，对其他频率的电信号产生较高的阻碍。
这种频率选择性让电路能够选择通过特定频率的信号，抑制其他频率的干扰信号，从而实现滤波的功能。
2.3 相位角特性：RLC并联谐振电路的阻抗特点还表现在相位角上。
在谐振频率附近，电路中的电感和电容的阻抗几乎相等，且互相抵消，导致电路的相位角接近零。
而在谐振频率两侧，相位角逐渐增大，表现出较大的相位差。
这种相位角特性可以用来调节信号的相位，对于某些特定应用具有重要意义。
【3. RLC并联谐振电路的观点和理解】RLC并联谐振电路是一种常用的电路结构，具有诸多特点和应用。
以下是对该电路的观点和理解：3.1 实用性：RLC并联谐振电路的低阻抗特点使其在实际应用中具有广泛用途。
rlc并联谐振电路的谐振频率
RLC并联谐振电路的谐振频率1. 引言RLC并联谐振电路是一种重要的电路结构，它在电子工程和通信领域中广泛应用。
谐振频率是RLC并联谐振电路的一个重要参数，它决定了电路的特性和性能。
本文将围绕任务名称：RLC并联谐振电路的谐振频率，详细介绍RLC并联谐振电路的基本原理、公式推导和计算方法。
2. RLC并联谐振电路RLC并联谐振电路由一个电感器(L)、一个电容器(C)和一个阻抗(R)组成，并且它们是并联连接的。
如图所示：在这个电路中，R代表负载阻抗，L代表电感，C代表电容。
当该电路处于谐振状态时，其频率达到最大值，此时称为谐振频率。
3. 谐振频率公式推导为了推导出RLC并联谐振电路的谐振频率公式，我们需要先分析电路的特性。
3.1 电感器电感器是由线圈或绕组构成的元件，它具有储存和释放电磁能量的能力。
其单位是亨利(H)。
3.2 电容器电容器是由两个导体之间的绝缘介质隔开的元件，它具有储存和释放电荷的能力。
其单位是法拉(F)。
3.3 阻抗阻抗是指在交流电路中对电流流动的阻碍程度，其单位是欧姆(Ω)。
在RLC并联谐振电路中，阻抗可以表示为：Z = R + jX其中，R为阻抗的实部，X为阻抗的虚部。
虚部X可以表示为：X = XL - XCXL为电感器的感抗，XC为电容器的感抗。
感抗可以分别表示为：XL = ωLXC = 1 / (ωC)其中，ω为角频率。
3.4 谐振频率公式当RLC并联谐振电路处于谐振状态时，其阻抗Z达到最小值。
根据以上推导可得：Z = R + j(XL - XC)当XL = XC时，阻抗Z达到最小值。
即：ωL = 1 / (ωC)解方程可得谐振频率：ω = 1 / sqr t(LC)由于谐振频率与角频率之间有关系：ω = 2πf其中，f为谐振频率。
综上所述，RLC并联谐振电路的谐振频率公式为：f = 1 / (2πsqrt(LC))4. 谐振频率计算方法根据上述推导的公式，我们可以计算RLC并联谐振电路的谐振频率。
电路设计--RLC并联谐振电路
电路设计--RLC并联谐振电路
RLC并联谐振电路是一种重要的电路类型，它由电感、电容和电阻元件组成。
当这些
元件被正确地连接在一起时，它们可以形成一个谐振电路，产生一个特定的频率响应。
在RLC并联谐振电路中，电容和电感是并联的，它们共享相同的输入信号，并形成一
个共振电路。
电容和电感的并联使得电路在共振频率下，具有较高的电感和电容值，从而
导致较低的复阻抗。
在这个频率点，电路的耗散功率最小。
如果电路中有电阻元件存在，
那么电路的损耗将会变大，共振频率也会发生变化。
在设计RLC并联谐振电路时，需要确定电容和电感的合适值以确保它们在所需的共振
频率下具有适当的阻抗。
可以通过计算共振频率、品质因数和带宽等参数来确定电路的性能，进而选择合适的元件。
在实际应用中，RLC并联谐振电路被广泛应用于各种领域，如无线电收发器、滤波器、功率放大器、音频放大器、电视机、雷达、天线等。
例如，在收音机中，谐振电路是用来
选择和放大无线电信号的。
总之，RLC并联谐振电路是一种重要的电路类型，它在电子学和通信领域具有广泛的
应用。
设计一个合适的RLC并联谐振电路需要综合考虑电路的参数、元件和应用要求，以
确保电路能够满足实际需求。
RLC并联谐振电路的实验研究
RLC并联谐振电路的实验研究实验所需器材：1.电感器2.电容器3.电阻器4.信号发生器5.示波器6.多用表7.连接线8.电源实验步骤：1.将电感器、电容器和电阻器连接在并联谐振电路中。
2.将信号发生器连接到电路的输入端，用以提供电信号。
3.通过调节信号发生器的频率，使电路处于谐振状态。
4.使用示波器观察并记录电路中电压的变化情况。
5.通过改变电阻器的阻值，观察并记录电路的谐振频率变化情况。
6.测量电路中电感器和电容器的电抗值，使用多用表记录并计算。
7.分析实验结果，得出结论。
实验结果：通过实验观察，我们可以得到以下结果：1.当电路处于谐振状态时，电感器和电容器的电抗相等且相互抵消。
2.在谐振频率的附近，电路中的电压振幅达到最大值。
3.改变电阻器的阻值会影响电路的谐振频率，阻值增大则谐振频率减小，阻值减小则谐振频率增大。
4.电感器和电容器的电抗值可以通过实验测量获得，为电抗值的计算提供了基础。
结论：通过实验研究RLC并联谐振电路，我们可以得出以下结论：1.RLC并联谐振电路的谐振频率与电感器和电容器的电抗相等且相互抵消有关。
2.谐振电路的谐振频率可通过改变电阻器的阻值来调整。
3.通过实验测量可以得到电感器和电容器的电抗值，为电路的分析提供了依据。
进一步的研究：基于RLC并联谐振电路实验研究的结果1.研究在不同频率下电路中电压的变化情况，寻找谐振频率的规律。
2.研究电阻器对电路谐振频率的影响程度，分析电阻器与电路谐振的关系。
3.探索其他外部因素对RLC并联谐振电路的影响，如温度、湿度等。
4.研究RLC并联谐振电路在输入信号频率变化时的响应特性，分析其在通信系统中的应用。
总结：通过实验研究RLC并联谐振电路，我们可以深入了解电路的谐振性质和特点。
研究实验结果可以为电路分析和应用提供参考依据，并为进一步深入研究衍生问题提供基础。
rlc并联谐振电路
rlc并联谐振电路rlc并联谐振电路是一种重要的电路结构，它由电阻（R）、电感（L）和电容（C）三个元件组成，并且这三个元件是并联连接的。
在这篇文章中，我们将详细介绍rlc并联谐振电路的基本原理、特性以及应用。
我们来了解一下rlc并联谐振电路的基本原理。
在电路中，电感元件会产生感抗，电容元件会产生容抗，而电阻元件会产生电阻。
当这三个元件并联连接时，它们共同决定了电路的特性。
当电路中加入交流电源时，rlc并联谐振电路的电阻、电感和电容将产生对电流的不同阻碍。
当频率为特定值时，电路的阻抗将达到最小值，这就是谐振频率。
在谐振频率下，电路中的电感和电容元件将形成一个共振回路，电流将达到最大值。
接下来，我们来讨论一下rlc并联谐振电路的特性。
首先是谐振频率。
谐振频率可以通过以下公式计算得出：f = 1 / (2π√(LC))其中，f为谐振频率，L为电感的值，C为电容的值，π为圆周率。
其次是谐振的带宽。
带宽是指在谐振频率附近，电路的阻抗仍然很小的一段频率范围。
带宽可以通过以下公式计算得出：BW = f2 - f1其中，BW为带宽，f1和f2分别为电路阻抗为谐振阻抗的两个频率。
rlc并联谐振电路还具有选择性增强的特性。
在谐振频率附近，电路对特定频率的信号具有较大增益，而对其他频率的信号则具有较小增益。
这种特性使得rlc并联谐振电路在通信领域中有着重要的应用，例如用于选择性放大特定频率的信号。
除了在通信领域中的应用外，rlc并联谐振电路还广泛应用于许多其他领域。
例如，在音频设备中，它可以用于音频滤波器的设计。
在电力系统中，它可以用于电力因数校正和电力滤波器的设计。
在电子设备中，它可以用于频率选择性放大器的设计。
rlc并联谐振电路是一种重要的电路结构，具有谐振频率、带宽和选择性增强等特性。
它在通信、音频、电力和电子等领域中有着广泛的应用。
通过深入理解rlc并联谐振电路的原理和特性，我们可以更好地应用它，并且为各种应用提供更好的解决方案。
rlc并联谐振电路谐振条件
rlc并联谐振电路谐振条件
（原创实用版）
目录
1.RLC 并联谐振电路的概念
2.RLC 并联谐振电路的谐振条件
3.RLC 并联谐振电路的应用
4.结论
正文
一、RLC 并联谐振电路的概念
RLC 并联谐振电路是由电阻（R）、电感（L）和电容（C）三个元件并联组成的电路。
在这个电路中，当电压与电流的相位角相同时，电路状态达到谐振，这种谐振称为并联谐振或电流谐振。
二、RLC 并联谐振电路的谐振条件
在 RLC 并联电路中，谐振条件为：当电路中的电感（L）、电容（C）和电阻（R）满足一定条件时，电路达到谐振状态。
具体来说，当感纳（B= ωL / ωC）等于电阻（R）时，电路中电流与电压的相位角相同，达到并联谐振状态。
其中，ω表示角频率，B 表示感纳。
三、RLC 并联谐振电路的应用
RLC 并联谐振电路在电子电路中有广泛应用，例如用于测量电缆的交流耐压试验。
通过电感的并联方式，可以提高试验的电流，从而实现试验的目的。
此外，RLC 并联谐振电路在各种具有频率特性的电路网络中也有重要作用。
四、结论
RLC 并联谐振电路是一种特殊的电路，其谐振条件为感纳等于电阻。
这种电路在电子电路和通信领域具有广泛的应用。
rlc并联谐振电路的谐振频率公式
rlc并联谐振电路的谐振频率公式RLC并联谐振电路是电路中常见的一种电路，其在信号处理、滤波等领域中有着广泛的应用。
在进行选型、设计和应用时，了解RLC并联谐振电路的谐振频率公式是非常重要的。
本文将为大家详细介绍RLC 并联谐振电路的谐振频率公式。
RLC并联谐振电路由电源、电感、电容和电阻四部分组成。
其中电感L和电容C串联在一起，构成振荡回路。
在特定的条件下，电路会对输入信号产生共振放大，从而起到滤波器的作用。
RLC并联谐振电路的谐振频率公式如下：
f0=1/2π√(LC)
公式中，f0表示电路的谐振频率，L表示电感的感值，C表示电容器的电容值，π为圆周率，√为平方根符号。
从公式来看，谐振频率与电感和电容的乘积成正比，与它们的平方根的倒数成反比。
换句话说，感值增大电容值减小，均会导致谐振频率变高。
反之则会使谐振频率趋向于降低。
了解RLC并联谐振电路的谐振频率公式，可以帮助我们更好地完成电路的选型和设计。
在实际应用中，根据电路的工作需求以及所需的频率范围，可以选择合适的电感和电容值，从而得到所需的谐振频率。
此外，在使用RLC并联谐振电路时，还需要注意避免电感和电容
的过度共振，以及防止过度放大和损耗。
因此，在电路的设计和应用
过程中，需要根据具体情况合理进行调整和优化，从而达到最佳效果。
总之，了解RLC并联谐振电路的谐振频率公式是电路设计和应用
中必不可少的基础知识。
通过深入理解公式原理，我们可以更好地掌
握电路的特性和工作原理，为电路的选型和设计提供更加有力的支持。
8.7 RLC并联谐振
8.7 RLC并联谐振考纲要求：掌握并联谐振的条件、特点及其应用。
教学目的要求：掌握RLC并联谐振的条件、特点和应用。
教学重点：RLC并联谐振的条件、特点。
教学难点：RLC并联谐振的应用。
课时安排：2节课型：复习教学过程：【知识点回顾】一、RLC并联谐振电路1、条件：。
谐振频率：。
2、特点：（1）阻抗特点：。
（2）相位特点：。
（3）电流特点：。
电阻上的电流。
电感和电容中的电流。
Q为品质因数，Q= 。
（4）能量特点：。
3、应用（1）通频带Δf= 。
（2）频率特性曲线当f<f0时，XL XC，电路呈性；当f>f0时，XL XC，电路呈性；当f=f0时，XL XC，电路呈性。
（3）电流谐振曲线【课前练习】一、判断题1、在R-L-C并联电路中，感抗和容抗的数值越大，电路中的电流就越小，电流与电压的相位差就越大。
( )2、对于RLC并联电路，当电源频率低于谐振频率时，电路呈感性。
( )二、填空题1、如图所示电路中，XL= Xc=R，并已知安培表A1的读数为3A，则A2的读数为 A，A3的读数为 A。
【例题讲解】例1在图所示电路中，u=2202sin314tV,R=25Ω,XL=50Ω，XC=20Ω(1)求电流I及功率因素cosΦ；(2)若R、L、C的值及电压有效值不变，调节电源频率使电路谐振，求谐振电路中电流I0及f0。
例2：正弦交流电路如图所示，已知R 1=50Ω，R 2=100Ω，C=10uF ，电路谐振时的角频率 ω0=103rad/s ，电源电压030100-∠=∙S U V ，试求电感L 和电压∙12U 。
【巩固练习】1、如图所示正弦交流电路中，当开关S 打开时，电路处于谐振状态，则当开关S 闭合时电路的性质为 ( )A ．阻性B ．感性C ．容性D ．纯电感2、在RLC 并联谐振电路中，当电阻R 增大时，其影响是（ ）A 、谐振频率升高B 、电路总电流增大C 、谐振频率降低D 、电路总电流减小【课后练习】一、判断题1、电路发生谐振时，电源与电路之间不存在能量转换。
RLC交流电路的分析(电路的串并联谐振)
在电力系统中，串联谐振可以用于无功补偿和滤波，提高电力系统的 稳定性和可靠性。
03
RLC交流电路的并联谐振
并联谐振的定义
• 并联谐振是指RLC交流电路在特定频率下，电路的阻抗呈现 最小值，即达到最小电阻状态。此时，电流在电路中最大， 电压则呈现最小值。
并联谐振的条件
• 并联谐振的条件是：XL=XC，其中XL是电感L的感抗，XC是 电容C的容抗。当感抗等于容抗时，电路发生并联谐振。
RLC电路的工作原理
01
02
03
当交流电源施加到RLC电 路时，电流和电压的相 位关系会发生变化，产
生不同的响应特性。
在串联谐振状态下，RLC 电路的总阻抗最小，电 流最大；在并联谐振状 态下，RLC电路的总导纳
最大，电流最小。
通过分析RLC电路在不同 频率下的响应特性，可 以了解其工作原理和特
性。
串并联谐振在实际电路中的应用
滤波器设计
利用串联或并联谐振电路的频率选择性，可以设计出不同频段的 滤波器，用于信号的筛选和处理。
信号放大
利用串联或并联谐振电路的增益特性，可以对特定频率的信号进行 放大，用于信号的增强和处理。
测量技术
利用串联或并联谐振电路的测量技术，可以测量电感、电容等元件 的参数，以及电路的频率特性等。
04
05
1. 搭建RLC交流 电路
2. 设定电源和信 号源
3. 测量并记录数 4. 观察和调整 据
5. 分析数据
根据实验箱提供的组件， 搭建RLC交流电路，包括电 阻、电感和电容。
将电源供应器设定为适当 的电压和频率，使用信号 发生器产生正弦波信号输 入到RLC交流电路中。
使用测量工具测量RLC交流 电路的电流、电压等参数 ，记录数据。
R,L,C串并联谐振电路特性分析及应用
R、L、C串/并联谐振电路的特性分析及应用摘要：本文对RLC串联、RLC并联及RL-C并联三种谐振电路的阻抗Z、谐振频率 、及品质因数Q三种特性进行了分析。
其中品质因数Q是电路在谐振状态下最为重要的电路特性，我们从Q的几种定义出发，着重研究了它对三种最基本的谐振电路的几个重要影响。
同时简单介绍了串/并联谐振电路在生活中的具体应用。
关键词：谐振电路；谐振特性；品质因数目录0 引言： (1)1 RLC串联与RLC并联及RL-C并联电路阻抗及谐振频率 (2)1.1 RLC串联电路的阻抗及谐振频率 (2)1.2 RLC并联电路的阻抗及谐振频率 (2)1.3 RL-C并联电路的阻抗及谐振频率 (3)2 R、L、C串/并联电路的品质因数Q (3)2.1 电路的品质因数Q (3)2.2 谐振电路的品质因数Q的几点重要性 (4)2.2.1 Q对回路中能量交换及能量储存的影响 (4)2.2.2 Q值与谐振电路的选择性 (4)2.2.2.1 Q值与串联谐振电路的选择性 (4)2.2.2.2 Q值与RL-C并联谐振电路的选择性 (6)2.2.2.3 RLC并联谐振回路与RL-C并联谐振回路的品质因数的统一性 (8)3 谐振电路在生活中的应用 (11)0 引言：构成各种复杂电路的基础通常是RLC 串/并联谐振电路，本文就简单介绍了其三种连接方式如图，而了解这些基本电路的频率特性对于理解更复杂的电路甚至实用电路是非常有益的,并且对于深入了解其它重要的相关特性是十分有帮助的。
本文简单阐述了下面三种电路图的Z 、ω及Q 以及一些具体实际的应用。
下面是R 、L 、C 串/并联谐振电路的简图，如图1，图2，图3所示。
•R U•L U＋•U•C U图1,串联谐振电路RLC•U— 图2，并联谐振电路RLC图3,并联谐振电路C RL -1 RLC 串联与RLC 并联及RL-C 并联电路阻抗及谐振频率 1.1 RLC 串联电路的阻抗及谐振频率由图1知RLC 串联电路的复阻抗Z 和阻抗z 分别为()()22111CL R z L L j R C jL j R Z ωωωωωω-+=-+=-+=电路中的I 和z 以及U 之间的关系为：()221CL R U zU I ωω-+==(1)由于谐振时01=-C L ωω，故谐振时的电流 R U I I =00为。
rlc并联谐振电路的特点
rlc并联谐振电路的特点RLC并联谐振电路是由电阻器（R）、电感器（L）和电容器（C）三个元件组成的电路。
当电路中的这三个元件处于并联状态时，电路呈现出谐振的现象。
本文将探讨RLC并联谐振电路的特点。
一、谐振频率RLC并联谐振电路的特点之一是其谐振频率。
通常，谐振频率由电感、电容和电阻的值共同决定。
其计算公式为：f = 1 / (2π√LC)其中f表示谐振频率，L表示电感值，C表示电容值，π表示圆周率。
当电路中的电感值或电容值发生变化时，谐振频率也会相应地发生变化。
一般而言，增加电感值或减少电容值会增加谐振频率，而减少电感值或增加电容值会减少谐振频率。
二、阻抗特性另一个RLC并联谐振电路的特点是其阻抗特性。
当电路中的电容器和电感器并联时，电容器会存储电荷并产生电场，电感器则会产生磁场。
在谐振频率下，这两种场的能量将互相转换并保持谐振。
此时电路的总阻抗为最小值，而且只有电阻器对电路的总阻抗有影响。
同时，当电路的阻抗达到最小值时，电路中的电流会达到最大值。
三、质量因数质量因数是一个很重要的参数，用来描述电路在谐振频率下的能量耗散情况。
通常，质量因数的计算公式为：Q = 2πfL / R其中Q表示质量因数，f表示谐振频率，L表示电感器的值，R表示电阻的值。
当电路中的电阻值大于0时，电路的质量因数将小于无阻尼时的质量因数（一个理想的电路，在理想的情况下不存在能量耗散）。
因此，电路的质量因数可以看作是电路中的能量的有限损失程度。
四、带宽特性带宽是指电路在频率范围内的可用功率或信号传输能力。
在RLC并联谐振电路中，可以通过对谐振频率进行调整来控制电路的带宽。
电路的带宽可以通过谐振频率和Q值计算得出。
一般而言，当电路的质量因数越高时，带宽越小，电路的信号传输能力也越强。
五、应用特点RLC并联谐振电路由于其谐振特性，被广泛应用于各种电子设备中，包括通信、放大、滤波等领域。
在通信领域，RLC并联谐振电路可以用于滤波器，以帮助提高信号的传输质量和防止信号干扰。
RLC并联谐振电路 、 波特图 、 滤波器简介.
I L I C QI S I S
6
3.LC串并联电路的谐振
L3 L1
C2
Z jL3
1 jC2 jL1
2
1
L3 1 C2 L3 L1 j 1 C2 L1
L1 L3 L3 当 1 C2 L3 0 时，发生串联谐振，0 L1 L3C2 L1
§11-4 RLC并联谐振电路
1. RLC并联谐振电路 I Y G j(ωC 1 ) + S ωL 1 j C j G U L _ 谐振条件： ω0C 1 0 L 1 谐振角频率： ω0 1 f0 LC 2 LC RLC并联电路的频率特性： U() |Y(j)| I S/G G o
作业：11-6(c,d)，11-10，11-12
15
滤波电路的传递函数定义
Ui
滤波 电路
Uo
U o ( ) H ( ) U i ( )
11
滤波器的分类
①按所处理信号分： 模拟和数字滤波器
②按所用元件分：
③按滤波特性分：
无源和有源滤波器 低通滤波器（LPF） 带通滤波器（BPF） 全通滤波器（APF）
H ( )
H ( )
高通滤波器（HPF） 带阻滤波器（BEF） 理 想 特 0 性
1 ω0 ( R )2 LC L
4
注意 ① 电路发生谐振是有条件的，在电路参数
一定时，满足： 1 R 2 L ( ) 0, 即 R 时, 可以发生谐振 LC L C ② 一般线圈电阻 R<<L，则等效导纳为： Y 2 R 2 j(C 2 L 2 ) R (L) R (L) R R 1 Ge j(C ) 2 2 L ( L ) (L) 0 1 线圈自身 谐振角频率： ω0 LC 品质因数 Ge C L 3 ω0C 0 LC 0 L 品质因数：Q Ge 等效电路 R R
RLC串联和并联谐振电路谐振时的特性
图12－21 并联电路谐振时的能量交换
由于i(t)=iL(t)+iC(t)=0 (相当于虚开路),任何时刻进入电 感和电容得总瞬时功率为零,即pL(t)+pC(t)=0。电感和电容 与电流源和电阻之间没有能量交换。电流源发出得功率全
部被电阻吸收,即pS(t)=pR(t) 。 能量在电感和电容间往复交换(图12－21)，形成了电
IR GU IS
IL
1 U
j0 L
j R
0L
IS
jQIS
IC j0CU j0 RCIS jQIS
(12 43) (12 44) (12 45)
其中
Q
R
0L
R 0 C
R
C L
(12 46)
称为RLC并联谐振电路得品质因数,其量值等于谐振时 感纳或容纳与电导之比。电路谐振时得相量图如图12-20(b) 所示。
L 1 () arctan( C )
R
(12 25) (12 26)
1、 谐振条件
当 ωL ωC1 0 ，即 ω
1 时，()=0,
LC
|Z(j)|=R,电压u(t)与电流i(t)相位相同,电路发生谐振。
也就就是说,RLC串联电路得谐振条件为
0
1 LC
(12 27)
式中 ω 0＝
G j(C 1 ) | Y ( j) | () L
其中
(12 38)
| Y ( j) | G 2 (C 1 )2 L
C 1
() arctan(
L )
G
(12 39) (12 40)
1、谐振条件
当
C
1
L
0 时,
Y(j)=G=1/R，电压u(t)和电流i(t)
RLC串联和并联谐振电路谐振时的特性
全部被电阻吸收，即pS(t)=pR(t) 。
能量在电感和电容间往复交换(图12－21)，形成了电 压和电流的正弦振荡。其情况和 LC并联电路由初始储能 引起的等幅振荡相同，因此振荡角频率也是 ω 串联谐振电路相同。
0
1 LC
，与
图12－21 并联电路谐振时的能量交换
谐振时电感和电容的总能量保持常量，即
令上式虚部为零
1
L C 2 0 2 R (L)
求得
CR 2 1 1 0 1 1 2 L Q LC LC
L C
1 其中 Q R
是RLC串联电路的品质因数。
当Q >>1时,
ω
0
1 LC
代入数值得到
0
1 10 4 10 8
10 8 1 4 rad/s 10 6 rad/s 10
谐振时的阻抗
( 0 L) 2 1 Z ( j 0 ) R R(1 Q 2 ) Y ( j 0 ) R
当0L>>R 时
( ω 0 L) 2 Z ( jω 0 ) (106 104 ) 2 10k R
思考与练习
12-3-l 欲提高串联谐振电路的 Q值，应如何改变 R、L和 C? 12-3-2 欲提高并联谐振电路的 Q值，应如何改变 R、L和 C?
加到4倍，这将造成电压UL=UC增加一倍。若电容 C减少到 l/4( Q增加一倍)，
2 总能量不变，而电压 UL= UC增 W CU C
加一倍。总之， R、L和 C的改变造成 数与UL= UC变化的倍数相同。
Q
1 R
L 变化的倍 C
例12-7 电路如图12-18所示。已知 uS (t ) 10 2 cosωt V 求: (l) 频率为何值时，电路发生谐振。 (2)电路谐振时, UL和UC为何值。
rlc并联谐振电路设计
rlc并联谐振电路设计
要设计一个RLC并联谐振电路，需要遵循以下步骤：
1. 确定谐振频率：根据电路中的电感L、电容C和电阻R，使用
公式f=1/(2π√(LC))计算电路的谐振频率f。
2. 确定电感和电容的值：基于所选的谐振频率，可以使用公式
L=1/(4π²Cf²)和C=1/(4π²Lf²)来计算所需的电感和电容值。
也
可以选择现有的标准值。
3. 选择合适的电阻：并联谐振电路需要一个阻值较大的电阻，
以防止出现过度谐振。
可以选择电阻值为电感和电容串联阻抗的一半，即R=√(L/C)/2。
4. 连接电路：将电感、电容和电阻并联连接到电路中，使其能
够产生谐振。
5. 调整电路：使用频率计和信号发生器来调整电路，并确认它
在预期的谐振频率上工作。
6. 测试电路：连接合适的负载来测试电路的性能，如频率响应
和阻抗匹配。
rlc并联谐振电路的谐振频率
RLC并联谐振电路的谐振频率1. 引言RLC并联谐振电路是一种重要的电路结构，在电子工程和通信领域中得到广泛应用。
它由一个电感器（L）、一个电容器（C）和一个电阻器（R）组成，并在特定频率下表现出谐振现象。
本文将详细介绍RLC并联谐振电路的谐振频率以及相关的计算公式和实际应用。
2. RLC并联谐振电路的基本原理RLC并联谐振电路是由一个电感器、一个电容器和一个电阻器组成的并联结构。
当外加交流信号源与该电路相连时，根据不同频率下元件之间的阻抗大小，会出现不同的响应。
在RLC并联谐振电路中，当外加交流信号源的频率等于或接近某个特定频率时，该谐振频率下的元件阻抗最小，即为共振状态。
这时，通过该电路的电流达到最大值，并且相位差为0。
3. RLC并联谐振电路的谐振频率计算公式RLC并联谐振电路的谐振频率可以通过以下公式计算：其中，f为谐振频率，L为电感器的感值，C为电容器的电容值。
该公式是根据谐振条件下电感器和电容器的阻抗相等推导出来的。
当电感器和电容器的阻抗相等时，谐振频率即可达到最小值。
4. RLC并联谐振电路的实际应用RLC并联谐振电路在实际应用中具有广泛的用途，以下是几个常见的应用场景：4.1 通信系统中的滤波器在通信系统中，需要对输入信号进行滤波处理以去除噪声和干扰。
RLC并联谐振电路可以作为滤波器使用，通过调整其频率来选择需要传递或阻止的特定频段信号。
4.2 音频放大器音频放大器需要对输入信号进行放大，并保持输出信号质量良好。
RLC并联谐振电路可以作为音频放大器中的一部分，在特定频率下实现放大效果，并且提供稳定和清晰的输出声音。
4.3 无线能量传输无线能量传输是一种将能量从一个地方传输到另一个地方的技术。
RLC并联谐振电路可以用于无线能量传输系统中的耦合器，通过调整谐振频率来实现高效的能量传输。
5. 总结本文详细介绍了RLC并联谐振电路的谐振频率及其相关内容。
首先，我们介绍了该电路的基本原理，解释了在特定频率下出现共振状态的机制。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
电路课程设计举例： 以RLC 并联谐振电路
1．电路课程设计目的
（1）验证RLC 并联电路谐振条件及谐振电路的特点； （2）学习使用EWB 仿真软件进行电路模拟。
2．仿真电路设计原理
本次设计的RLC 串联电路图如下图所示。
图1 RLC 并联谐振电路原理图
理论分析与计算：
根据图1所给出的元件参数具体计算过程为
)1(111L
C j R L j C j R Y ωωωω-+=++=
发生谐振时满足L
C ω
ω0
1
=
,则RLC 并联谐振角频率
ω
和谐振频率
f
分别是
LC
LC
f
πω21,
10
0=
=
RLC 并联谐振电路的特点如下。
（1）谐振时Y=G,电路呈电阻性，导纳的模最小
G B G
Y
=+=
2
2
.
（2）若外施电流
I
s
一定，谐振时，电压为最大，G
I U
S
o
=,且与外施电流同相。
（3）电阻中的电流也达到最大，且与外施电流相等，
I
I
S
R
=
.
（4）谐振时
0=+I I
C L
,即电感电流和电容电流大小相等，方向相反。
3．谐振电路设计内容与步骤
（1）电路发生谐振的条件及验证方法 这里有几种方法可以观察电路发生串联谐振： (1)利用电流表测量总电流
I
s
和流经R 的电流
I
R
，两者相等时即为并联谐振。
(2)利用示波器观察总电源与流经R 的电流波形，两者同相即为并联谐振。
例题：已知电感L 为,电容C 为50uf,电阻R 为200Ω。
由LC
f
π210
=
计算得,
Hz f
1.1570
=
按上图进行EWB 的仿真,得到下图。
流经电阻R的电流和总电流I相等为10mA,流进电感L和电容C的总电流为，几乎为零，所以电路达到谐振状态。
总电源与流经R的电流波形同相，所以电路达到并联谐振状态。
4．实验体会和总结
这次实验我学会了运用EWB仿真RLC并联谐振电路，并且运用并联谐振的特点判断达到谐振状态。
尤其是观察总电源与流经R的电流波形，两者同相即为并联谐振。
这种方法我们只能在实验中看到，平时做题试卷上是不可能观察到的。
这加深了我对谐振电路的理解。