三角形中线
三角形的中线与重心

三角形的中线与重心在欧几里得几何学中,三角形是最基本的几何形状之一。
对于一个任意的三角形,我们可以从不同的角度和方法来研究它的性质和特点。
而本文将聚焦于三角形的中线与重心。
一、三角形的中线三角形的中线是指连接三角形的两个顶点与对边中点的线段。
对于一个任意的三角形ABC,我们可以得到三条中线:AA₁,BB₁和CC₁。
这三条中线按照起点的不同,分别与三角形的对边相交于点M、N和P。
简言之,中线就是连接三角形两个顶点和对边中点的线段。
中线的一个重要性质是:三条中线的交点G,称为三角形的重心。
二、重心的性质重心是三角形的一个特殊点,具有许多有趣的性质。
以下是重心的几个重要性质:1. 重心将每条中线划分为两个部分,其中一个部分的长度是另一个部分的两倍。
即AG:GM = BG:GN = CG:GP = 2:1。
2. 重心到三角形的顶点之间的距离满足如下关系式:AG = 2/3 * GM,BG = 2/3 * GN,CG = 2/3 * GP。
换句话说,重心到顶点的距离是重心到中点距离的两倍。
3. 三角形的三条中线交于重心。
这意味着,重心是中线的共同交点,是三角形内部的一个特殊点。
4. 重心到三角形顶点的线段长度相等,即AG = BG = CG。
因此,重心与三角形的顶点等距离。
5. 如果把重心看作是一个质量点,那么三角形的每一条中线将该质量点所受到的力分为两半,即每条中线两边的力矩相等。
三、例题分析让我们通过一个例题来更好地理解中线和重心的性质。
例题:在三角形ABC中,D是BC的中点,E是AC的中点,F是AB的中点。
若AD的中点为M,BE的中点为N,CF的中点为P,则求证:AM,BN和CP交于一点。
解答:首先,连接AD、BE和CF,得到各条中线。
由中线的定义可知,AM是三角形ABC中线AD的一半,BN是三角形ABC中线BE的一半,CP是三角形ABC中线CF的一半。
根据重心的性质,我们知道重心将每条中线划分为两个部分,其中一个部分的长度是另一个部分长度的两倍。
三角形中线的性质
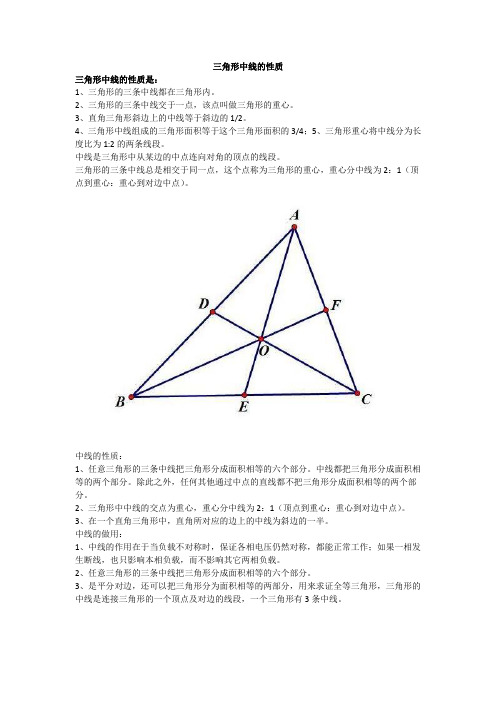
三角形中线的性质
三角形中线的性质是:
1、三角形的三条中线都在三角形内。
2、三角形的三条中线交于一点,该点叫做三角形的重心。
3、直角三角形斜边上的中线等于斜边的1/2。
4、三角形中线组成的三角形面积等于这个三角形面积的3/4;
5、三角形重心将中线分为长度比为1:2的两条线段。
中线是三角形中从某边的中点连向对角的顶点的线段。
三角形的三条中线总是相交于同一点,这个点称为三角形的重心,重心分中线为2:1(顶点到重心:重心到对边中点)。
中线的性质:
1、任意三角形的三条中线把三角形分成面积相等的六个部分。
中线都把三角形分成面积相等的两个部分。
除此之外,任何其他通过中点的直线都不把三角形分成面积相等的两个部分。
2、三角形中中线的交点为重心,重心分中线为2:1(顶点到重心:重心到对边中点)。
3、在一个直角三角形中,直角所对应的边上的中线为斜边的一半。
中线的做用:
1、中线的作用在于当负载不对称时,保证各相电压仍然对称,都能正常工作;如果一相发生断线,也只影响本相负载,而不影响其它两相负载。
2、任意三角形的三条中线把三角形分成面积相等的六个部分。
3、是平分对边,还可以把三角形分为面积相等的两部分,用来求证全等三角形,三角形的中线是连接三角形的一个顶点及对边的线段,一个三角形有3条中线。
三角形的中线高线与角平分线

三角形的中线高线与角平分线三角形的中线、高线与角平分线在几何学中,三角形是最基本的多边形之一。
它由三条线段组成,连接三个非共线点。
三角形中的中线、高线和角平分线是三条重要的直线,在研究三角形的性质和关系时起着重要作用。
一、中线中线是连接三角形的一个角的顶点和所对边中点的线段。
三角形共有三条中线,分别连接各个角的顶点和对边中点。
中线具有以下几个重要性质:1. 中线的长度相等:对于任意一个三角形,它的三条中线的长度相等。
即对于三角形ABC,连接顶点A和对边BC的中线AD,连接顶点B和对边AC的中线BE,连接顶点C和对边AB的中线CF,有AD = BE = CF。
2. 中线的交点称为重心:三条中线的交点被称为三角形的重心,用G表示。
重心是三角形中心的一种,具有重要的几何意义。
3. 重心将中线划分成2:1的比例:重心将每条中线划分成两个线段,其中一个线段的长度是另一个线段的两倍。
二、高线高线是从三角形的一个顶点垂直地引到对边上的线段。
三角形共有三条高线,分别从三个顶点向对边引垂线。
高线具有以下几个重要性质:1. 高线相交于一点:对于任意一个三角形,三条高线相交于一个点,称为垂心。
垂心用H表示。
2. 垂心到顶点的距离相等:垂心到每个顶点的距离相等,即AH = BH = CH。
3. 高线的中点连线平行于底边:连接垂心和对边上垂足的线段平行于底边。
三、角平分线角平分线是指从三角形的一个顶点将角平分成两个相等角的线段。
三角形共有三条角平分线,分别从三个顶点将对角角平分。
角平分线具有以下几个重要性质:1. 角平分线相交于一点:对于任意一个三角形,三条角平分线相交于一个点,称为内心。
内心用I表示。
2. 内心到对边的距离相等:内心到三条对边的距离相等,即AI =BI = CI。
3. 角平分线的交点到边上各顶点的距离相等:内心到三角形的各个顶点的距离都相等,即ID = IE = IF。
通过研究三角形的中线、高线和角平分线,我们可以发现它们之间存在着一种特殊的关系。
三角形中的三种重要线段

03
确定角平分线
中垂线与三角形的一边和 相对的角平分线垂直,因 此可以利用中垂线来确定 三角形的角平分线。
确定高线
中垂线与三角形的一边垂 直,因此可以利用中垂线 来确定三角形的高线。
确定中点
中垂线与三角形的一边平 行,因此可以利用中垂线 来确定三角形的中点。
中垂线的性质
垂直平分线的性质
中垂线是三角形一边的垂直平分线,因此它具有垂直平分线的性质,即中垂线上的点到 三角形的两个端点的距离相等。
三角形中的三种重要线段
contents
目录
• 三角形中的中线 • 三角形中的高线 • 三角形中的角平分线 • 三角形中的中位线 • 三角形中的中垂线
01
三角形中的中线
中线的定义
总结词
三角形中线的定义是连接三角形的一 个顶点与对边中点的线段。
详细描述
在三角形中,中线是连接一个顶点与 对边中点的线段。对于任意一个顶点 ,都可以作出一条中线,且该中线将 对应的底边分为两等分。
中线在三角形中的作用
总结词
中线在三角形中起到稳定结构、简化图形和辅助证明等作用。
详细描述
中线在三角形中具有多重作用。首先,它有助于稳定三角形的结构,因为中线将底边分为两等分,使得三角形的 形状更加稳定。其次,中线可以简化复杂的几何图形,通过将图形划分为更易于处理的部分,有助于问题的解决。 此外,中线还常常作为辅助线用于证明三角形中的一些性质和定理。
中线的性质
要点一
总结词
中线具有平行于第三边、长度为第三边一半等性质。
要点二
详细描述
根据中线的定义和性质,我们可以得出以下几点:首先, 中线平行于三角形的第三边,即中线与对应的底边平行; 其次,中线的长度是第三边长度的一半,即中线的长度等 于$frac{1}{2}$倍的底边长度;最后,中线将对应的底边分 为两等分,即中点是底边的中点。这些性质在几何证明和 解题过程中具有广泛应用。
三角形中线的公式

三角形中线的公式三角形中线是指连接三角形的一个顶点与对边中点的线段。
在三角形ABC中,顶点A与对边BC中点D之间的线段AD就是三角形ABC 的一个中线。
中线有以下几个重要性质:1. 中线的长度三角形中线的长度等于对边的一半。
以三角形ABC为例,设三角形的底边为BC,底边中点为D,则中线AD的长度等于BC的一半。
这可以通过计算底边两个顶点的坐标,然后利用勾股定理得出。
2. 中线的位置三角形的三条中线交于一点,这个点被称为三角形的重心。
重心是三角形的一个重要特征点,它将三角形分成六个小三角形,每个小三角形的面积都相等。
3. 中线的作用中线在三角形中起着重要的作用。
首先,中线可以将三角形分成两个面积相等的小三角形。
其次,中线还可以求解三角形的面积。
通过连接三角形的三个顶点和对边中点,我们可以将三角形分成三个小三角形,然后计算这三个小三角形的面积之和,即可得到整个三角形的面积。
4. 中线的性质除了上述提到的性质外,中线还具有以下几个重要性质:- 三角形的三条中线交于一点,且交点到各顶点的距离满足重心定理,即重心到顶点的距离等于中线长度的两倍。
- 三角形的两条中线所夹角的余弦等于底边上与之对应的角的正弦的两倍。
这一性质可以通过向量的运算得到。
在实际应用中,中线的公式可以用于解决各种几何问题。
比如,可以利用中线的长度和角度关系来求解三角形的面积,或者利用中线的位置和性质来求解三角形的重心坐标等。
三角形中线是三角形的一个重要特征线段,具有多个重要性质和应用。
通过研究和应用中线的公式,我们可以更好地理解和解决与三角形相关的几何问题。
三角形的中线的取值范围

三角形的中线的取值范围1. 中线是什么鬼?好啦,咱们先来聊聊三角形的中线。
说白了,中线就是从三角形的一个顶点,直奔对边的中点。
听起来是不是有点拗口?别急,举个例子。
想象一下你有一个三角形,像个大披萨,上面有三块不同口味的馅料。
你把一块馅料的顶点连到对面的中间,那条线就是中线。
简单吧?这条线就像是你的“爱情线”,在三角形中连接着两个重要的点,起到一个调和的作用。
2. 中线的长度有什么讲究?2.1 长度的计算说到中线的长度,咱们可得认真对待。
中线的长度不是什么任意值,而是有一定的计算公式的。
三角形的中线可以用这个公式来计算:中线长度= √(2a² + 2b² c²) / 4,其中 a、b、c 分别是三角形的三条边。
听起来是不是有点像数学课?别担心,咱们可以把这个公式当成一个大厨的食谱,按照比例加料,最后就能做出美味的“中线”。
2.2 中线长度的取值范围那么,长度的取值范围又是怎样的呢?根据三角形的特性,咱们可以得出一些结论。
中线的长度总是小于等于最大边的一半,也就是说,它不会比最长的那条边要大。
不然的话,三角形就变形了,变成了个不三不四的东西。
换句话说,中线就像是一个“有限制”的角色,永远得在合适的范围内活动。
3. 生活中的中线3.1 生活的比喻好啦,咱们把话题转回生活中。
中线就像是生活中的调和剂,能够让一切看起来更加平衡。
比如,在一段关系中,双方总得有一个“中线”,让彼此的需求能够得到满足。
如果一方总是占据上风,另一方就会觉得不舒服,最终可能导致“关系变形”。
这就和三角形一样,保持平衡才能长久。
3.2 中线的趣味性说到这,咱们还得提提中线的趣味性。
想象一下你和朋友们在一起,三个人围成一个三角形,每个人都有自己的长处和短处。
这时就需要一个“中线”来平衡大家的意见。
比如,A喜欢冒险,B喜欢安静,C则更爱尝试新鲜事。
如果没有中线,这个小团体可能会闹得不可开交。
你看,中线不仅仅是数学上的概念,更是生活中的智慧。
三角形的中线和中位线

三角形的中线和中位线三角形是几何学中最基本的图形之一。
它由三条边和三个顶点组成,具有丰富的性质和特点。
本文将重点介绍三角形的中线和中位线。
一、中线中线是指从一个顶点连到对边中点的线段。
一个三角形有三个顶点,因此它有三条中线。
用示意图表示,如下所示:(插入示意图)中线的特点如下:1. 三角形的三条中线交于一点,这个点叫做三角形的重心。
2. 中线的长度相等,且等于三角形两边的和的一半。
3. 三角形的重心到顶点的距离是中线长度的2/3。
二、中位线中位线是指连接三角形两个顶点的中点的线段。
一个三角形有三个顶点,因此它有三条中位线。
用示意图表示,如下所示:(插入示意图)中位线的特点如下:1. 三角形的三条中位线交于一点,这个点叫做三角形的重心。
2. 中位线的长度相等,且等于三角形两边的和的一半。
3. 重心到中位线的交点的距离是中位线长度的1/3。
三、中线和中位线的关系中线和中位线都是连接顶点和对边中点的线段,它们有一些共同的性质和特点:1. 三角形的三条中位线和三条中线都会交于同一个点,这个点就是三角形的重心。
2. 中线和中位线的长度相等,都等于三角形两边的和的一半。
3. 重心到中线的交点和重心到中位线的交点之间的距离关系为2:1。
4. 中位线的交点将中线一分为二,且分割的线段长度与两条中位线的长度之间的关系为1:2。
四、中线和中位线的应用中线和中位线在几何学中具有广泛的应用,特别是在解决三角形相关问题时:1. 利用中线和中位线的性质可以求解三角形的重心,从而确定三角形的位置和形状。
2. 中线和中位线的长度关系可以用来推导其他三角形边长和角度的关系。
3. 基于中线和中位线的性质,可以证明一些三角形的定理和性质,如垂心定理和松弛定理等。
综上所述,三角形的中线和中位线是三角形的重要属性和特点,它们有着丰富的性质和应用。
通过研究中线和中位线,我们可以更好地理解和分析三角形,深入掌握几何学的知识。
对于几何学的学习和应用来说,中线和中位线是必不可少的重要内容之一。
三角形中线取值范围

三角形中线取值范围1. 三角形的中线定义在三角形中,连接一个顶点与对边中点的线段称为三角形的中线。
一个三角形有三条中线,它们的交点称为三角形的重心。
2. 三角形中线的性质2.1 中线的长度三角形的中线将对边平分,因此三角形的中线的长度等于对边的一半。
设三角形的三边长度分别为a、b、c,对边分别为x、y、z,则三角形的中线分别为m、n、p,有以下关系:m = 1/2 * sqrt(2 * (b^2 + c^2) - a^2) n = 1/2 * sqrt(2 * (c^2 + a^2) -b^2) p = 1/2 * sqrt(2 * (a^2 + b^2) - c^2)2.2 重心的性质三角形的三条中线交于一点,该点称为三角形的重心。
重心到三角形的顶点的距离与重心到对边的距离成比例,比例因子为2:1。
设重心到三角形顶点的距离分别为d1、d2、d3,重心到对边的距离分别为h1、h2、h3,则有以下关系:d1 = (2/3) * h1 d2 = (2/3) * h2 d3 = (2/3) * h32.3 中线的取值范围对于任意给定的三角形,中线的取值范围有一定的限制。
下面将分别讨论各种情况下中线的取值范围。
2.3.1 等边三角形对于等边三角形,三条边的长度相等,设边长为a,则有:m = n = p = a/2重心到顶点的距离与重心到对边的距离相等,即:d1 = d2 = d3 = h1 = h2 = h3 = a/32.3.2 等腰三角形对于等腰三角形,两边的长度相等,设等腰边长为a,底边长为b,则有:m = n = 1/2 * sqrt(2 * (a^2 + b^2/4) - b^2) p = b/2重心到顶点的距离与重心到对边的距离有以下关系:d1 = d2 = (2/3) * sqrt(h1^2 + (b/2)^2) d3 = (2/3) * h3根据三角形不等式,有以下两个条件:a +b > 2 * sqrt(h1^2 + (b/2)^2) b > 2 * h32.3.3 一般三角形对于一般三角形,三边的长度都不相等,设三边长度分别为a、b、c,则有:m = 1/2 * sqrt(2 * (b^2 + c^2) - a^2) n = 1/2 * sqrt(2 * (c^2 + a^2) - b^2) p = 1/2 * sqrt(2 * (a^2 + b^2) - c^2)重心到顶点的距离与重心到对边的距离有以下关系:d1 = (2/3) * sqrt(h1^2 + (b^2 + c^2 - a^2)/4) d2 = (2/3) * sqrt(h2^2 + (c^2 + a^2 - b^2)/4) d3 = (2/3) * sqrt(h3^2 + (a^2 + b^2 - c^2)/4)根据三角形不等式,有以下三个条件:a +b >c b + c > a c + a > b3. 总结与应用三角形中线的取值范围与三角形的形状有关。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形中线
1.三角形中线定义:连结三角形一个顶点和对边中点的线段;
2.三角形中线能将三角形分成面积相等的两部分;
3.三角形的三条中线必交于一点,该交点为三角形重心;
4.重心定理:三角形重心到一个顶点的距离等于它到对边中点距离的2倍;
5.三角形三条中线能将三角形分成面积相等的六部分;
6.解决三角形中线问题,常作的辅助线是倍长中线,塑造全等三角形,或平行四边形;
7.遇到三角形两条中线同时出现时,常需考虑三角形中位线:三角形中位线平行且等于第三边一半;
8.直角三角形斜边上的中线等于斜边的一半;
9.如果三角形一边中线等于这边的一半,那么这个三角形是直角三角形;
10.等边三角形顶角平分线,底边上的高,底边上的中线,互相重合;
重心,是三边上的中线的交点
垂心,是三边上的高线的交点
内心,是三个内角的平分线的交点
外心,是三边的垂直平分线的交点
三角形的五心
三角形的三条中线交于一点,这点到顶点的距离是它到对边距离的2倍,上述交点叫做三角形的重心,上述定理为重心定理。
外心定理三角形的三边的垂直平分线交于一点,这点叫做三角形的外心。
垂心定理三角形的三条高交于一点,这点叫做三角形的垂心。
内心定理三角形的三内角平分线交于一点,这点叫做三角形的内心。
旁心定理三角形的一内角平分线与另外两顶点处的外角平分线交于一点,这点叫做三角形的旁心。
三角形有三个旁心。
可以根据这些“心”的定义,得到很多重要的性质:
(1)重心和三顶点的连线所构成的三个三角形面积相等;
(2)外心扫三顶点的距离相等;
(3)垂心与三顶点这四点中,任一点是其余三点构成的三角形的垂心;
(4)内心、旁心到三边距离相等;
(5)垂心是三垂足构成的三角形的内心,或者说,三角形的内心是它旁心三角形的垂心;(6)外心是中点三角形的垂心;
(7)中心也是中点三角形的重心;
(8)三角形的中点三角形的外心也是其垂足三角形的外心。
(1)三条平分线:
先画一个三角形ABC,再画出任意两个角(设为∠A,∠B)的平分线相交于O点,
自O点作三边的垂线交三边于D,M,N,则OD=OM=ON,连接OC,则OC平分∠C,所以三角形三条角平分线交于一点。
(2)垂直平分线
先作两边的垂直平分线交予一点,连接此点到三个角的顶点,由线段的垂直平分线上的点到这条线段两端点距离相等再过这点向第三边作垂线,根据:到一条线段两端相等的点一定在其垂直平分线上,可知刚做的垂线是第三边的垂直平分线所以三角形的三边垂直平分线一定交于一点
(3)高
先做两条高(角平分线和中线)的交点,连交点和另一顶点.延长交于这个顶点的对边.
角平分线利用的角平分线上的点到角的两边的距离相等.这样三段距离都相等就可以证明第三条是角平分线
没学向量以前中线可以利用面积去算,利用底相等,高相同.然后就可以证明到分开的六块面积都相等。
高的话好象只能用向量积来证明了(高一才学)
(4)中线
设△ABC的两条中线BD、CE交于点G,连结AG并延长交BC于M(我们只要能证明点M是BC的中点即可),作BN‖CE交AM延长线于N,连结CN. 因为E是AB中点,BN‖CE,所以点G是AN中点(平行线等分线段定理),又因为点D是AC的中点,所以GD‖CN(三角形中位线定理),因此四边形BNCG是平行四边形,所以BC、GN互相平分,即点M是BC的中点,AM是BC边上的中线. 由于中线具有唯一性,这就证明了△ABC的三条中线AM、BD、CE交于所设点G.。
