理论力学(大学)课件17.1 求平面图形各点加速度的基点法
合集下载
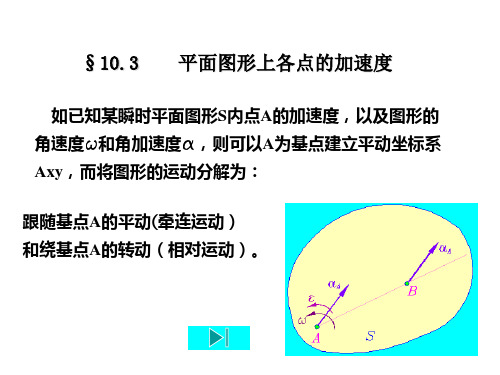
大学理论力学 平面图形上各点的加速度分析
n BE
O
aB
a
n BE
cos45
A ar 由于滑块可沿杆OA滑动，因此 vr 应利用点的合成运动方法求杆OA的 vB aB a e 角速度及角加速度。 ve B ac n 以滑块B为动点。 动系与OA杆固结。 ae 45 va ve vr l
vr 0 ve va vB v
2 2
a 2 a 1 2 1 cot
2
即 a 1 a 2 并由此看出 , AB 作瞬时平动时
aA aB
[例3] 曲柄滚轮机构，滚子半径R=OA=15cm, n=60 rpm，作纯滚 动。 求：当 =60º (OAAB),滚轮的Ｂ，aＢ． 时
分析: 要想求出滚轮的Ｂ, aＢ 先要求出vB, aB
解：轮O作平面运动，P为速度瞬心，
v O / R
（
）
由于
n 以O为基点， P a O a PO a PO a
v O / R 在任何瞬时都成立，且O点作直线运动，故而 d 1 d vO aO a （ ） dt R dt R
2
n a PO R 2 R (
而 1 v A / O1 A ,
(b)
2 vB / O2 B ;
n n aA aB
式中
O1 A O 2 B
τ τ aA aB
1 2
aA aB
a 2 aB / O2 B ;
a 1 a A / O1 A ,
a1 a 2
(b) AB杆作平面运动, 图示瞬时AB杆作瞬时平动, 即 v A vB AB 0
解：OA杆作定轴转动,AB杆和轮B作平面运动
O
aB
a
n BE
cos45
A ar 由于滑块可沿杆OA滑动，因此 vr 应利用点的合成运动方法求杆OA的 vB aB a e 角速度及角加速度。 ve B ac n 以滑块B为动点。 动系与OA杆固结。 ae 45 va ve vr l
vr 0 ve va vB v
2 2
a 2 a 1 2 1 cot
2
即 a 1 a 2 并由此看出 , AB 作瞬时平动时
aA aB
[例3] 曲柄滚轮机构，滚子半径R=OA=15cm, n=60 rpm，作纯滚 动。 求：当 =60º (OAAB),滚轮的Ｂ，aＢ． 时
分析: 要想求出滚轮的Ｂ, aＢ 先要求出vB, aB
解：轮O作平面运动，P为速度瞬心，
v O / R
（
）
由于
n 以O为基点， P a O a PO a PO a
v O / R 在任何瞬时都成立，且O点作直线运动，故而 d 1 d vO aO a （ ） dt R dt R
2
n a PO R 2 R (
而 1 v A / O1 A ,
(b)
2 vB / O2 B ;
n n aA aB
式中
O1 A O 2 B
τ τ aA aB
1 2
aA aB
a 2 aB / O2 B ;
a 1 a A / O1 A ,
a1 a 2
(b) AB杆作平面运动, 图示瞬时AB杆作瞬时平动, 即 v A vB AB 0
解：OA杆作定轴转动,AB杆和轮B作平面运动
理论力学课件 刚体平面运动的加速度分析
aBnA
=
AB
⋅
ω
2 AB
= 4m
s2
加速度矢量式投影到η轴上得
aB cos 45o = aBnA
aB = 5.66 m s2
αAB
an BA
at
y BA
aB aA B
加速度矢量式投影到y轴上得
0
= −a
aBt A
A cos
= 16
45° +
m s2
aBnA
cos
45°
+ aBt A
α AB
sin 45°
•结论：平面图 形角速度不为 零，任一瞬时， 速度瞬心必存在 且唯一。
6-2 刚体平面运动的速度分析
速度瞬心的特点
1、瞬时性：不同的瞬时，有不同的速度瞬心。 2、唯一性：某一瞬时只有一个速度瞬心。 速度瞬心不是一个固定点。理解成“角色”
思考题：杆做什么运动？
vB
ω
vA
定轴转动
车轮在地面上纯滚动
6-2 刚体平面运动的速度分析
6-2 刚体平面运动的速度分析
平移
vvA = vvB
ωAB = 0
avA = avB α AB = 0
瞬时平移
vvA = vvB avA ≠ avB
ωAB = 0 α AB ≠ 0
vA A
ω
O
vB B
牢记！
6-2 刚体平面运动的速度分析
2、确定速度瞬心位置的方法
已知A、B两点的速度方向，
试确定速度瞬心的位置。
例6-5 图示机构，已知曲柄OA的角速度为ω，OA＝AB＝BO1＝ O1C＝r，角α = β = 60º，求滑块C的速度。
解：AB和BC作平面运动，其瞬心分别为P1和P2点，则
理论力学课件《刚体的平面运动》
ABvBA/ABl/l （
）
速度投影法 研究AB, vA l ,
方向OA, vB方向沿BO直线
根据速度投影定理 vBAB vAAB
vAvBcos
vBvA/cos l/cos45 2l() 不能求出 AB
课堂练习．滚子A沿水平面作纯滚动，通过连杆AB带动滑块
理论力学
刚体的平面运动是工程上常见的一种运动， 这是一种较为复杂的运动。对它的研究可以在研 究刚体的平动和定轴转动的基础上，通过运动合 成和分解的方法，将平面运动分解为上述两种基 本运动。然后应用合成运动的理论，推导出平面 运动刚体上一点的速度和加速度的计算公式。
第五章 刚体的平面运动
§5–1 刚体平面运动的研究方法 §5–2 平面图形内各点的速度 §5–3 平面图形内各点的加速度 §5–4 机构运动分析
确定平面图形内任意一条线段的位置．
任意线段AB的位置可 用A点的坐标和AB与x轴夹 角表示．因此图形S 的位
置决定于 xA, yA, 三个
独立的参变量．所以
xA f1(t) 平面运动方程 yA f2(t)
f3(t)
对于每一瞬时 t ，都可以求出对应的xA, yA, ， 图形S
在该瞬时的位置也就确定了。
解：机构中,OA作定轴转动,AB作 平面运动,滑块B作平动。
基点法（合成法）
研究 AB，以 A为基点，
且 vA l ,方向如图示。
根据 vB vA vBA, 在Ｂ点做 速度平行四边形，如图示。
vB vA/cos
l/cos45 2l()
vBAvAtgltg45 l
图中看出：AB A'B'' A''B' ，1 2 于是有
理论力学---第八章_平面运动
且
v A 不平行于 v B
。
vA // vB , 且不垂直于AB vB v A v AB vBA 0 AB 0 vB v A vM
瞬时平移(瞬心在无穷远处)
纯滚动(只滚不滑)约束
找出下列平面运动刚体的速度瞬心。 A ω O1 B O2 O A B
:
:
v F
v GF cos 45 v C cos 45 v r
v F
v GF
cos
45 v C cos 45 v G 'C
vr 0
v GF 2 r
vG
5 r
26 . 6
平面机构如图所示。曲柄AB以匀角速度 绕轴A转动，使杆CG绕E轴转动。已知： AB=BE=EC=r。在图示位置时，ED=r，杆AB 和杆CG均处于水平。试求该瞬时: （1） 滑块D相对于杆CG的速度;
c
c
vB
v BA
绕O轴转动。求在图示瞬间点C的速度。已知
v CB
vc
B
B
ABC
vB
vA
ABC
o1
o
0
A
vA
o1
o
0
A
vA
在图示齿轮齿条机构中，已知：齿轮 半径R，曲柄OA= 2 R，以匀角速度 0 绕O轴作 定轴转动，OO1=L。试求图示位置 =45°时， 齿轮O1的角速度。
分析：
DE
v A r
vC O 1C
1
AB
vA r
v B r
AB
vC
v D v F r 1
922134-理论力学之动力学-2平面运动加速度
x': aBx' aA sin aBnA y': aBy' aA cos aBt A
20
例：求系统在图示位置时，AB杆的角速度和角加速
度。
OA 2R,u R const.
1.求AB杆的角速度
B e
vr vCA R
30 o
uC
O
vA
A
动 点：C 动 系：AB杆 绝 动：直线 相 动：直线 牵 动：平面运动
vA AB CV A 2 3vO
aO OR
7
A
aAt B
y
aA aAn B
aBt O aO
x
B aBnO
aB aO aBt O aBnO
aA aB aAt B aAnB
大小: ?
方向:
4 ABR 4A2BR
aA aO aBt O aBnO aAt B aAnB
x：0
aO
2.加速度瞬心(Instant Center for acceleration)法
定义：某瞬时平面图形上加速度为零的点，称图形在 该瞬时的加速度瞬心C a
定理：当平面图形的角速度与角加速度不同时为零，
必存在唯一的加速度瞬心
问题：过Ca的任一直线上各点的加速度分布有何特点？ —-- 与图形定轴转动时的加速度分布类似
aB
aA
aBt A
a
n BA
AB 0
B
a
n B
aB aA aBt A
aBn
a
t B
aA
aBt A
D y : aBn aA aBt A cos
aBt A 0
10
例：半径为R 的圆盘在水平板A上纯滚动，若该瞬时板的速度 为u，加速度为a，轮心O相对板的速度为vr，相对加速度为ar。 求圆盘的角速度和角加速度以及圆盘最高点B的速度和加速度
20
例：求系统在图示位置时，AB杆的角速度和角加速
度。
OA 2R,u R const.
1.求AB杆的角速度
B e
vr vCA R
30 o
uC
O
vA
A
动 点：C 动 系：AB杆 绝 动：直线 相 动：直线 牵 动：平面运动
vA AB CV A 2 3vO
aO OR
7
A
aAt B
y
aA aAn B
aBt O aO
x
B aBnO
aB aO aBt O aBnO
aA aB aAt B aAnB
大小: ?
方向:
4 ABR 4A2BR
aA aO aBt O aBnO aAt B aAnB
x：0
aO
2.加速度瞬心(Instant Center for acceleration)法
定义：某瞬时平面图形上加速度为零的点，称图形在 该瞬时的加速度瞬心C a
定理：当平面图形的角速度与角加速度不同时为零，
必存在唯一的加速度瞬心
问题：过Ca的任一直线上各点的加速度分布有何特点？ —-- 与图形定轴转动时的加速度分布类似
aB
aA
aBt A
a
n BA
AB 0
B
a
n B
aB aA aBt A
aBn
a
t B
aA
aBt A
D y : aBn aA aBt A cos
aBt A 0
10
例：半径为R 的圆盘在水平板A上纯滚动，若该瞬时板的速度 为u，加速度为a，轮心O相对板的速度为vr，相对加速度为ar。 求圆盘的角速度和角加速度以及圆盘最高点B的速度和加速度
11-1讲 基点法求加速度
O C
§8-4
用基点法求平面图形内各点的加速度
解：⑴ 车轮作平面运动，瞬心为C ⑵ 利用瞬心法求轮的角速度和 角加速度
t aCO
vO OC vO R
dω 1 dvO aO dt R dt R
⑶ 取轮上O点为基点，利用基点法 求瞬心C的加速度
t n aC aO aCO aCO
B
⑶ 取杆AB上的D点为基点,利用 基点法求A点加速度
t n aA aD aAD aAD
AB
D y aD n a AD
O
C
x
A
t a AD
大小 ? 方向 √
√ √
？ √
√ √
aD l 2
n 2 l 2 aAD AD AB
aD
aA
2 n 向y轴投影得 aA cos60 aD cos60 aAD a A l
杆OA作绕O轴转动 行星齿轮Ⅱ作平面运动
vA OA 1 l1 ⑵ 轮Ⅱ的速度瞬心为C,利用瞬 心法求轮Ⅱ（任意时刻）的 角速度 vA CA l1 r 所以角加速度始终为0
⑶ 取A点为基点,利用基点法求 B,D的加速度
大小 ? 方向 ?
t n aD aA aDA aDA
2 1
aA arctan n aBA
1 (l r )
2
a B a ( a ) l
arctan
r l
例8-13 图示机构中,OD=AD=BD=l,曲柄OD以匀角速度ω绕O 轴转动。求当 60 时,尺AB的角加速度和点A的加速度。 解：⑴ 分析各物体的运动 滑块A、B作平移 杆OD绕O 轴转动 杆AB作平面运动 ⑵ 找出杆AB的速度瞬心,利用 瞬心法求杆AB的角速度
103平面图形上各点的加速度理论力学课件
ωII vA / CA (R r)ω0 / r 常量
于是 vMA rωII (R r)ω0
再根据M点的速度平行四边形， 即可求出M点速度的大小和方向：
vM 2(R r)ω0 a （vM，vMA） π / 4
2
由牵连运动为平动时的加速度合成定理可求出点M的加速度。 因
牵连法向加速度沿AO方向
滑块B的相对加速度ar也OA方向。 此瞬时vr=0 ，故ak=0
由aa＝aet ＋ aen＋ar ＋ ak
投影得 aa=aet
ae
aB
2v 2 l
a OA
ae OB
2v 2 l2
aB
2v 2 l
解：BE杆作平面运动，可先 求出点B的速度和加速度。点B连 同滑块在OA杆上滑动，并带动杆 OA转动，可按合成运动方法求解 杆OA的wOA和aOA
BE 2l
2l
BE杆作平面运动，在图中，由vE ＝v及vB方向 可知此瞬时O点为BE杆的速度瞬心，因此
以E为基点，点B的加速度为
式中各矢量方向如图所示。
式中：aB的大小和方向已知；aFra bibliotekn A
的大小为：
aAn
v
2 A
OA
方向由A指向O轴，
aAt ?
方向假设如图所示；
OA＝12cm， AB＝30cm， vB＝2 m/s， aB＝1 m/s2 ， 求AB和aAB
aB = aAt + aAn + aBt A + aBnA (1)
aAn
v
2 A
OA
再由速度合成定理知 vM＝ve＋vr
＝vA＋vMA (1) 式中 M点的相对速度vMA沿M点 的相对轨迹（即轮Ⅱ外缘的 圆周）的切线，如图所示。
于是 vMA rωII (R r)ω0
再根据M点的速度平行四边形， 即可求出M点速度的大小和方向：
vM 2(R r)ω0 a （vM，vMA） π / 4
2
由牵连运动为平动时的加速度合成定理可求出点M的加速度。 因
牵连法向加速度沿AO方向
滑块B的相对加速度ar也OA方向。 此瞬时vr=0 ，故ak=0
由aa＝aet ＋ aen＋ar ＋ ak
投影得 aa=aet
ae
aB
2v 2 l
a OA
ae OB
2v 2 l2
aB
2v 2 l
解：BE杆作平面运动，可先 求出点B的速度和加速度。点B连 同滑块在OA杆上滑动，并带动杆 OA转动，可按合成运动方法求解 杆OA的wOA和aOA
BE 2l
2l
BE杆作平面运动，在图中，由vE ＝v及vB方向 可知此瞬时O点为BE杆的速度瞬心，因此
以E为基点，点B的加速度为
式中各矢量方向如图所示。
式中：aB的大小和方向已知；aFra bibliotekn A
的大小为：
aAn
v
2 A
OA
方向由A指向O轴，
aAt ?
方向假设如图所示；
OA＝12cm， AB＝30cm， vB＝2 m/s， aB＝1 m/s2 ， 求AB和aAB
aB = aAt + aAn + aBt A + aBnA (1)
aAn
v
2 A
OA
再由速度合成定理知 vM＝ve＋vr
＝vA＋vMA (1) 式中 M点的相对速度vMA沿M点 的相对轨迹（即轮Ⅱ外缘的 圆周）的切线，如图所示。
速度基点法和点的合成运动求速度法的比较
速度基点法和点的合成运动求速度法的比较
关于理论力学，用点的合成定理求加速度和用基点法求点的加速度的区别
关于理论力学，用点的合成定理求加速度和用基点法求点的加速度的区别我能不能认为，合成定理（可能存在科氏加速度）适用于2个刚体系统，而基点法只适用于一个刚体计算加速度？
对于刚体的平动,在同一个刚体上的就要用基点法,如果有套筒在一个转动的杆上相对运动这类情况,能够比较明显的判断出相对运动,绝对运动,牵连运动这三种运动,那就是用点的运动合成,多做一些题就可以分清楚了.
理论力学中点的合成理论与基点法求速度是一个方法吗
方法很相似：
速度：都有绝对速度v、相对速度vr、牵连速度ve物理量
加速度：都有绝对加速度a、相对加速度ar、牵连加速度ae物理量
不同的是：
前者动系、动点分别在两个物体上；
基点法求速度是对做刚体平面运动的物体而言的，动系、动点在同一个物体上。
求速度不仅可用基点法，还可用速度瞬心法和速度投影法。
求加速度基本都用基点f法。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
主要内容
1、基点法求平面图形各点加速度
2、基点法求加速度的应用
1、基点法求平面图形各点加速度
基点法求平面图形内各点加速度
平面图形内任一点的加速度等于基点的加速度与该点随图形绕基点转动的切向加速度和法向加速度的矢量和。
基点 ：A 平移坐标系： ''Ax y t BA a AB
a BA ⋅=αt 大小 方向垂直于 ，指向同 AB α
大小 方向由 指向
n BA a n 2BA a AB
ω=⋅B A n r t r e a a a a B ++=n
t BA
BA A B a a a a ++=为什么没有科氏加速度
基点法求平面图形各点加速度
A a t BA a n
BA
a 动点：B 动系： ''Ax y 绝对运动：待求 牵连运动：随同A 点平移 相对运动：B 绕A 的转动。