三角形的格点
小学奥数：格点型面积(毕克定理)
小学奥数：格点型面积（毕克定理）板块一正方形格点问题在一张纸上，先画出一些水平直线和一些竖直直线，并使任意两条相邻的平行线的距离都相等(通常规定是1个单位)，这样在纸上就形成了一个方格网，其中的每个交点就叫做一个格点．在方格网中，以格点为顶点画出的多边形叫做格点多边形，例如，右图中的乡村小屋图形就是一个格点多边形．那么，格点多边形的面积如何计算它与格点数目有没有关系如果有，这两者之间的关系能否用计算公式来表达下面就让我们一起来探讨这些问题吧！用N 表示多边形内部格点，L 表示多边形周界上的格点，S 表示多边形面积，请同学们分析前几个例题的格点数．我们能发现如下规律：12LS N ．这个规律就是毕克定理．【例 1】用9个钉子钉成相互间隔为1厘米的正方阵(如右图)．如果用一根皮筋将适当的三个钉子连结起来就得到一个三角形，这样得到的三角形中，面积等于1平方厘米的三角形的个数有多少面积等于2平方厘米的三角形有多少个【例 2】如图，44的方格纸上放了16枚棋子，以棋子为顶点的正方形有个．【例 3】判断下列图形哪些是格点多边形【例 4】如图，计算各个格点多边形的面积．【巩固】如果两格点之间的距离是2，能利用刚计算的结果说出相应面积么(教师总结：面积数值均扩大4倍．)【例 5】如图(a)，计算这个格点多边形的面积．【例 6】(“新加坡小学数学奥林匹克”竞赛试题)右图是一个方格网，计算阴影部分的面积．【例 7】分别计算图中两个格点多边形的面积．⑴⑵【巩固】求下列各个格点多边形的面积．【例 8】我们开始提到的“乡村小屋”的面积是多少【例 9】右图是一个812面积单位的图形．求矩形内的箭形ABCDEFGH 的面积．【例 10】右图中每个小正方形的面积都是1，那么图中这只“狗”所占的面积是多少【巩固】如图，每一个小方格的面积都是1平方厘米，那么用粗线围成的图形的面积是多少平方厘米【例 11】(“小学数学奥林匹克”竞赛试题)55的方格纸，小方格的面积是1平方厘米，小方格的顶点称为格点．请你在图上选7个格点，要求其中任意3个格点都不在一条直线上，并且使这7个点用直线连接后所围成的面积尽可能大．那么，所围图形的面积是平方厘米．【例 12】(“保良局亚洲区城市小学数学”竞赛试题)第一届保良局亚洲区城市小学数学邀请赛在7月21日开幕，下面的图形中，每一个小方格的面积是1，那么7、2、1三个数字所占的面积之和是多少【例 13】(第六届“从小爱数学”邀请赛试题)两个边长相等的正方形各被分成25个大小相同的小方格．现将这两个正方形的一部分重叠起来，若左上角的阴影部分(块状)面积为25.12cm ，右下角的阴影部分(线状)面积为27.4cm ，求大正方形的面积．【例 14】(第六届“华杯赛”试题)图中正六边形ABCDEF 的面积是54，AP=2PF ，CQ=2BQ ，求阴影四边形CEPQ 的面积．板块二三角形格点问题所谓三角形格点多边形是指：每相邻三点成“∵”或“∴”，所形成的三角形都是等边三角形．规定它的面积为1，以这样的点为顶点画出的多边形为三角形格点多边形．关于三角形格点多边形的面积同样有它的计算公式：如果用S 表示面积，N 表示图形内包含的格点数，L 表示图形周界上的格点数，那么有22S N L ，就是格点多边形面积等于图形内部所包含格点数的2倍与周界上格点数的和减去2．【例 15】如图(a)，有21个点，每相邻三个点成“∵”或“∴”，所形成的三角形都是等边三角形．计算三角形ABC 的面积．【巩固】如图，每相邻三个点所形成的三角形都是面积为1的等边三角形，计算V ABC 的面积．毕克定理若一个格点多边形内部有N 个格点，它的边界上有L 个格点，则它的面积为12LS N ．【例 16】求下列格点多边形的面积(每相邻三个点“∵”或“∴”成面积为1的等边三角形)．【例 17】把大正三角形每边八等分，组成如右图所示的三角形网．如果大三角形的面积是128，求图中粗线所围成的三角形的面积．【例 18】如图，如果每一个小三角形的面积是1平方厘米，那么四边形ABCD的面积是多少平方厘米【例 19】把同一个三角形的三条边分别5等分、7等分(如图1，图2)，然后适当连接这些等分点，便得到了若干个面积相等的小三角形．已知图1中阴影部分面积是294平方分米，那么图2中阴影部分的面积是______平方分米．【例 20】将图中的图形分割成面积相等的三块．【例 21】如图涂阴影部分的小正六角星形面积是16平方厘米，问：大正六角星形面积是多少平方厘米【例 22】(第五届“华杯赛”试题)正六边形ABCDEF的面积是6平方厘米．M是AB中点，N是CD中点，P是EF中点．问：三角形MNP的面积是多少平方厘米【例 23】如果下图中任意相邻的三个点构成的三角形面积都是2平方厘米．那么，三角形ABC的面积是_____平方厘米．。
三角形角格点问题系列：B2-3A
三角形角格点问题系列：B2-3A(图中有:PB=PC,AB+AP=BC,BP平分∠ABC,AB切△BCP的外接圆于B)已知:如图,∠PBA=∠PBC=∠PCB=10°,∠PCA=30°,求∠PAC,∠PCA.解法1:（同一法）作△A＇Ｂ＇Ｄ＇,使Ａ＇Ｂ＇＝Ｂ＇Ｄ＇＝ＡＢ，∠Ａ＇Ｂ＇Ｄ＇＝∠ＡＢＣ＝２０°,在△Ａ＇Ｂ＇Ｄ＇内作正△Ａ＇Ｄ＇Ｐ＇,连Ｂ＇Ｐ＇,延长B＇Ｄ＇到Ｃ＇，使Ｄ＇Ｃ＇＝Ｄ＇Ｐ＇.则∠Ａ＇Ｂ＇Ｐ＇＝∠Ｐ＇Ｂ＇Ｃ＇＝１０°,∠Ｂ＇Ａ＇Ｐ＇＝∠Ｂ＇Ｄ＇Ｐ＇＝２０°，∠Ｐ＇Ａ＇Ｃ＇＝１００°．因为△ＡＢＣ≌△Ａ＇Ｂ＇Ｃ＇，△ＡＢＰ≌△Ａ＇Ｂ＇Ｐ＇．所以ＰＢ＝Ｐ＇Ｂ＇,因为△ＢＰＣ≌△Ｂ＇Ｐ＇Ｃ＇,所以∠ＰＡＢ＝∠Ｐ＇Ａ＇Ｂ＇＝２０°,故∠ＰＡＣ＝∠Ｐ＇Ａ＇Ｃ＇＝１００°,∠ＰＣＡ＝2０°.解法2:如图,作正△DPC,连接DA、DB ,显然D、P关于AC对称.又PB=PC=PD,故P是△DBC的外心,∠PDB=∠PBD=20°,因此∠PBA=∠DBA=10°,则∠APB与∠ADB相等或互补.如果相等，则D、P关于AB 对称,此时△DPB是正三角形.∠BPC=120°,和已知矛盾,因此∠APB与∠ADB互补,D、B、P、A 四点共圆,∠PAB=∠PDB=20°,∠PAC=100°.解法3:（B1-2A）如图,在∠PCA内作∠PCD=20°,交AB于D，连DP，取△DBC的外心为O,连OB、OC、OD、OP.因为∠DCB=30°,所以∠DOB=60°.△DBO是正三角形,故∠OBC=∠OCB=40°,∠BOP=50°,因此∠DOP=∠DBP=10°,所以B、O关于DP对称.得∠BDP=30°=∠PCA,A、D、P、C四点共圆,∠PAC=∠PDC=100°,∠PAB=20°.解法4:（B1-2A）如图,在∠PCA内作∠PCD=20°,交AB于D,连DP,以P为圆心,PB的长为半径作圆,交CD延长线于E,连PE、BE.因为∠ECB=30°，所以∠EPB=60°,故△PBE是正三角形,∠EBA=50°,∠PEC=20°,∠BED=80°，∠BDE=50°,因此BE=ED=EP,E是△PDB的外心，∠PDB=30°=∠PCA,则A、D、P、C四点共圆,∠PAB=∠PCD=20°,∠PAC=100°.解法5:（B1-2A）如图,作正△EBC,连接EB、EC，作∠PCD=20°,交AB于D，连DE、DP.因为∠PBC=∠PCB=10°,故∠BEP=∠CEP=30°,又因为∠BCD=∠ECD=30°,所以∠DEC=∠DBC=20°，则∠DEP=10°=∠DBP，因此E、B、P、D四点共圆.∠BDP=∠BEP=30°=∠ACP,所以A、D、P、C四点共圆,∠PAB=∠PCD=20°,∠PAC=100°.解法6:（B1-2A）如图,在BC上取点D ,使∠PDB=20°,以P为圆心,PD为半径画弧交直线BA于A＇,联结PD、PA＇、DA＇.作∠PCE=20°,交AB于E,连EP,则∠PA＇B=∠PDB=20°=∠PCE,A＇、E、P、C四点共圆,又因为△PDA＇是正三角形,所以DP=DＡ＇=DC,则D是△PA＇C的外心,因此∠PＥB=∠PCＡ＇=30°=∠ＰＣＡ,故A与A＇重合,∠PAB=∠PCE=20°,∠PAC=100°.解法7:如图,作正△DPC,连DA、DB,在BD上截取BE=BP,连AE.由∠ACB=40°,∠ABC=20°,可知∠CAB=120°,由∠PCB=∠PBC=10°.可知PB=PC=PD,有P为△DCB的外心,于是∠DBC=30°,∠CDB=80°,∠PDB=20°.显然∠DBA=10°=∠PBA，可知P、E关于AB对称，有AE=AP，∠APB=∠AEB，由∠PCA=30°,可知CA为DP的中垂线,有AD=AP=AE，于是∠ADB=∠AED.由∠APB+∠ADB=∠AEB+∠AED=180°,可知P、B、D、A四点共圆,有∠PAB=∠PDB=20°.所以∠PAC=∠CAB -∠PAB=100°.解法8:(2B-8)如图,△ABC的外接圆交AP的延长线于D，连接BD、CD.易知∠ADC=20°,∠ADB=40°.△BPC的外接圆交AD的延长线于E,连接BE、CE,易知∠AEC=∠AEB=∠DCE=10°,∠DBE=30°.作E关于BD的对称点F,连接FB、FC、FP、FE,因为∠DBE=30°,所以△BEF是正三角形,∠EDF=80°=∠CDF ,所以C、E关于DF对称,FE=FC=FB,故F是△BCE的外心,因此∠BCE =30°.故∠BCD=20°,∠PAB=20°,∠PAC=100°.解法9:(4B-4)如图,△ABC的外接圆交BP的延长线于D，连接AD、CD.易知∠CAD=10°,∠ADB=40°,∠BDC=120°,∠ACD=10°,∠CPD=20°.以D为圆心,CD长为半径作圆交CP于E,连EA、ED.因为∠ACP=30°,故△ADE是正三角形,所以∠DEC=40°,∠EPD=∠EDP=20°.得到EP=ED=EA,故∠APD=30°,∠PAB=20°,∠PAC=100°..解法10:(27-3)如图,△ABC的外接圆交CP的延长线于D，连接AD、BD.易知∠BAD=10°,∠ADC=20°,∠BDC=20°,∠ABD=30°,∠BPD=20°.作正△ADE,连EB、EP,因为∠ABD=30°,所以E是△ABD的外心,∠BED=20°,∠DBE=80°,∠EBP=∠EDP=40°,所以B、D、P、E四点共圆.所以PD=PE，D、E关于AP对称，所以∠DAP=30°，∠PAB=20°,∠PAC=100°.解法11:(2A-7)如图,如图,△BCP的外接圆交AP的延长线于D，连接BD、CD,易知∠ADC=∠ADB=10°.设△ABC的外接圆交AD于E,连接EB、EC.易知∠DCE=10°,∠DBE=30°.作正△DCF，联结FB，FE.因为∠EBC=∠ECB=10°,故C、D关于EF对称,因此∠DFE=∠CFE=30°,故B、E、D、F四点共圆,∠BFE=10°,∠BFC=20°=∠BDC,因此D、F关于BC 对称,所以∠BCD=30°,∠BCE=20°.故∠PAB=20°,∠PAC=100°.解法12:(B5-5A)如图,如图,△BCP的外接圆交AC的延长线于D，连接BD、DP,易知∠ADP=∠BDP=10°,∠CBD=20°.设E为B关于DP 的对称点，连EB、EP.易知E、A、D三点共线,∠ABE=40°,∠BE=50°,∠AEP=30.作正△PEF,连FA、FD，因为∠AEP=30°,所以P、F关于AE对称.AF=AP,∠APF=∠AFP ,又因为PB=PE=PF,所以P是△BEF的外心,∠EBF=30°,∠PBF=∠PFB=20°,∠ABP=∠ABF=10°,易知∠APB 与∠AFB不等,由正弦定理可得,∠APB与∠AFB互补,所以A、F、B、P 四点共圆.得到∠PAB=20°,∠PAC=100°.解法13:(27-3)如图,如图,△ABP的外接圆交CP的延长线于D，连接BD、AD,易知∠ADC=10°,∠BAD=20°.作正△ADE,连EC、EB,因为∠ACD=30°,所以E是△ACD的外心,∠AEC=20°,∠CDE=80°,∠AEB=∠ACB=40°,所以A、C、E、B四点共圆.所以BA=BE，A、E 关于DB对称，所以∠BDA=30°，∠BDC=20°.得到∠PAB=20°,∠PAC=100°.解法14:(B6-16D)如图,△ABP的外接圆交CA的延长线于D，连接BD、PD,易知∠CDP=10°.作正△DCE,连接EB、EP,显然D、E关于CP对称.得到∠CEP=∠CDP=∠CBP=10°,所以B、E、C、P四点共圆.故∠BEC=∠BCE=20°,BC=BE.得到C、E关于BD对称.∠BDC=30°,∠BDP=20°,所以∠PAB=20°,∠PAC=100°.解法15:(B4-11I)如图,△ABP的外接圆交CB于D，连接AD、PD,易知∠ADP=∠DAP=10°.△ADC的外接圆交CP的延长线于E,连接EA、ED.易知∠DAE=10°,∠ADE=30°,作正△AEF,连FD、FP,因为∠ADE=30°,故F是△ADE的外心,所以FD=FE=FA,又∠DAE=10°，故∠DFE=20°，∠AFD =80°,而PD=PA,故∠PFA=∠PAF=40°,所以A、F 关于CE对称,故∠AEC=30°=∠ADC,得∠PDC=20°.所以∠PAB=20°,∠PAC=100°.解法16:(4A-4)如图,△ACP的外接圆交BP的延长线于D，连接AD、CD,易知∠ADB=30°,∠CAD=20°.作A关于BD对称的对称点E，连接FA、FD。
浅谈格点三角形面积的计算
浅谈格点三角形面积的计算
作者：李云飞
来源：《教育管理与艺术》2014年第04期
在方格图中，我们把每个小正方形的顶点称为“格点”，三个顶点都在格点上的三角形叫做格点三角形。
对格点三角形面积的计算，既有利于学生图形阅读能力和计算能力的提高，又可以培养学生思维的简洁性和严密性。
格点三角形面积的计算方法有哪些呢？我认为最基本的方法有两种——直接法和间接法。
一、直接法
当能够直接从图中看出格点三角形一条底边a的长及这一底上的高h的值时，我们可以直接利用三角形的面积计算公式s=ah进行计算。
如图1，我们容易看出格点三角形ABC的底边BC的长为6、BC边上的高AD为3，所以S△ABC= =BC·AD=×6×3=9。
又如图2中，BC=2，BC边上的高AD是3，所以S△ABC= ×2×3=3。
二、间接法
当格点三角形的底边及其底边上的高不易观察出精确值时，用间接法求其面积较简便。
即用格点三角形所在的矩形面积减去格点三角形四周的小三角形面积，从而求得格点三角形的面积。
如图3，欲求三角形ABC的面积，可用矩形BDEF面积减去三角形ABC四周的三个三角形面积即可。
直接法从细微处着手，具有开门见山、单刀直入、简洁明了的特点，而间接法着眼全局，曲径通幽。
根据图形特点灵活选用不同的方法，自会体会其中的妙处！。
几何第15讲_格点图形公式法(学生版)A4
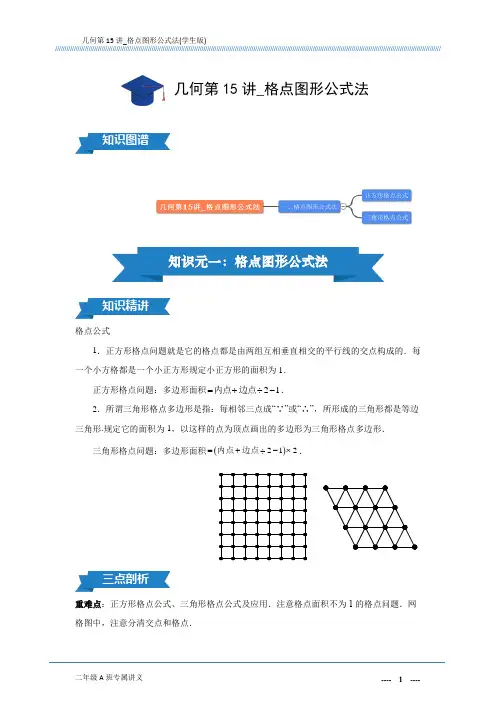
格点公式1．正方形格点问题就是它的格点都是由两组互相垂直相交的平行线的交点构成的．每一个小方格都是一个小正方形规定小正方形的面积为1．正方形格点问题：多边形面积21=+÷-内点边点．2．所谓三角形格点多边形是指：每相邻三点成“∵”或“∴”，所形成的三角形都是等边三角形.规定它的面积为1，以这样的点为顶点画出的多边形为三角形格点多边形．三角形格点问题：多边形面积()212=+÷-⨯内点边点．重难点：正方形格点公式、三角形格点公式及应用．注意格点面积不为1的格点问题．网格图中，注意分清交点和格点．几何第15讲_格点图形公式法题模一：正方形格点公式例1.1.1图中相邻格点围成的最小正方形或正三角形的面积均为1平方厘米．这两个多边形的面积分别是多少平方厘米？例1.1.2如图所示，在58 的方格中，阴影部分的面积为37cm2，则非阴影部分的面积为多少平方厘米？例1.1.3如图，水平方向和竖直方向上相邻两点之间的距离都是m，若四边形ABCD的面积是23，求五边形EFGHI的面积．例1.1.4图中相邻格点围成的最小正方形的面积均为1平方厘米，图中阴影部分的面积为多少平方厘米？例1.1.5图中每个小正方形的面积为2平方厘米，阴影部分的面积是多少平方厘米？题模二：三角形格点公式例1.2.1图中有20个点，其中每相邻的三点“∴”或“∵”所形成的三角形都是面积为1的等边三角形，则三角形ABC 的面积为多少？四边形DEFG 的面积为多少？例 1.2.2（1）左图中每个最小三角形的面积是2平方厘米。
阴影部分面积是多少平方厘米？ （2）右图中每个小正三角形的面积是4平方厘米。
阴影部分的面积是多少平方厘米?例 1.2.3如图，每个最小等边三角形的面积都是1平方厘米．阴影部分的面积是__________________平方厘米．例1.2.4如图，三角形网格的总面积为54，求阴影部分的面积是多少？ABCGDEF例1.2.5如图，每个最小等边三角形的面积都是1平方厘米．阴影部分的面积是多少平方厘米？随练1.1如图，水平相邻和竖直相邻的两个格点间的距离都是1，则图中阴影部分的面积是________．随练1.2如图，相邻两格点间的距离均为1厘米，阴影部分的面积是__________________平方厘米．随练1.3下图是一个三角形点阵，其中能连出的最小等边三角形的面积为5平方厘米．那么阴影图形的面积是______________平方厘米．随练 1.4如图，每个最小等边三角形的面积都是1平方厘米．阴影部分的面积是__________________平方厘米．随练 1.5如图，每个最小等边三角形的面积都是1平方厘米．阴影部分的面积是__________________平方厘米．作业1图中，每一个小正方形的面积都是1平方厘米，阴影部分的面积是__________平方厘米．作业2求下列多边形的面积作业3如图，每一个小正方形的面积都是2，阴影部分的面积是多少？作业4在平面上，用边长为1的单位正方形构成正方形网格，顶点落在单位正方形的顶点（又称为格点）上的简单多边形叫做格点多边形．最简单的格点多边形是格点三角形，二出去三个顶点之外，内部或边上不含格点的格点三角形称为本原格点三角形，如右图所示的三角形MBN．每一个格点多边形都能够很容易的划分为若干个本原格点三角形．那么，右图中的格点多边形BEFGHK可以划分为_________个本原格点三角形．作业5如图，每个最小等边三角形的面积都是1平方厘米，阴影部分的面积是多少平方厘米．作业6如图所示，每个小等边三角形的面积都是1平方厘米，阴影部分的面积是多少平方厘米？作业7如图，每个最小等边三角形的面积都是1平方厘米．阴影部分的面积是多少平方厘米？作业8如图所示，如果每个小等边三角形的面积都是1平方厘米，四边形ABCD 和三角形EFG 的面积分别是多少平方厘米？CBADGFE。
初中数学中的格点问题
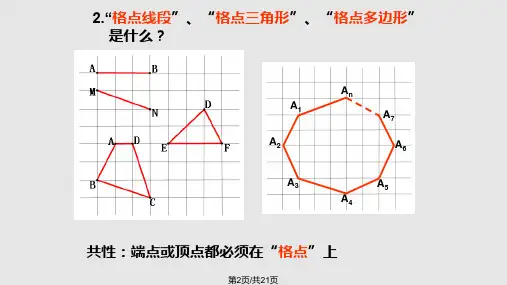
A1 A2
A3
An A7 A6
A5 A4
共性：端点或顶点都必须在“格点”上
第2页/共21页
“格点问题”不但能够加强同学们的基础知识，而且也能提高大家 的基本技能，同时能够逐步培养我们的运算能力、空间想象能力、 力及逻辑推理能力。 它突出了“数形结合”的数学思想方法，考查我们 对图形的观察力和对数学规律的发现探究能力，还考查 我们的创新意识、决策意识和实践能力。
· 13
13
S△ABC=3×3－S1－S2－S3
S△ABC=S1+S2－S3
运用“皮克定理”
(32)23123
2
22
S
1331 2
3.5
3.5
第16页/共21页
练习：如图，在正方形网格（每个小正方形的边长为1）内有一 个格点五边形ABCDE,求五边形ABCDE的面积。
·············
第17页/共21页
例6.如图，A、B为4×5网格中的格点，网格中的每个小正方
形的边长为1. 以A、B、C为顶点的三角形为等腰三角形的所
有格点C的位置有 3
个；并在图中标出。
·C ·C
·C
第12页/共21页
例7.在6×6的正方形网格中，以点D、E为两个顶点作位置不
同的格点三角形，使所作的格点三角形与△ABC全等，这样的
第19页/共21页
第20页/共21页
感谢您的观看！
第21页/共21页
勾股定理
(2) 13
(3)5
第4页/共21页
bc
a
a2b2 c2
∴ c a2 b2
练习.已知网格中的每个小正方形的边长均为1，请画以格点
小升初奥数几何问题之格点与面积知识点
小升初奥数几何问题之格点与面积知识点【篇一】知识点：(一)正方形格点图面积在一张纸上，先画出一些水平直线和一些竖直直线，并使任意两条相邻的平行线的距离都相等(通常规定为1个单位)，这样在纸上就形成了一个方格网，其中的每个交点就叫做一个格点。
多边形的所有顶点都在格点上，在方格网中，像图(a)这样的多边形，以格点为顶点画出的多边形叫做格点多边形。
多边形的顶点至少有一个顶点格点上，比如A点，像图(b)这样的多边形虽然除A点之外所有顶点都是格点，但我们还不能把它称为格点多边形。
(二)三角形格点图的面积三角形格点多边形是指：每相邻三点成“∴”或“∵”，形成的三角形都是等边三角形，规定它的面积为1，以这样的点为顶点画出的多边形为三角形格点多边形。
【篇二】常见解题方法：求格点图面积常见的几种方法：数格子法、分割法、扩展法、毕克定理。
（一）数格子法对于格点图里面的规则图形，我们有时可以直接通过数图形所占的正方形方格或者三角形方格的个数得出规则图形的面积，或者由图形得出规则图形相应的面积公式需要的量，代入公式解出面积即可!【详解】本题所给的图形都是规则图形，它们的面积运用公式直接可求，只要判断出相应的有关数据就行了。
第(1)图是正方形，边长是4，所以面积是4×4=16(面积单位);第(2)图是矩形，长是5，宽是3，所以面积是5×3=15(面积单位);第(3)图是三角形，底是5，高是4，所以面积是5×4÷2=10(面积单位);第(4)图是平行四边形，底是5，高是3，所以面积是5×3=15(面积单位);第(5)图是直角梯形，上底是3，下底是5，高是3，所以面积是(3+5)×3÷2=12(面积单位);第(6)图是梯形，上底是3，下底是6，高是4，所以面积是(3+6)×4÷2=18(面积单位)。
下面几种方法主要针对的是格点图中的不规则图形，这也是本专题的重点!（二）分割法直接将格点图中的不规则图形分成若干个可求面积的规则图形，然后通过计算规则图形的面积来求原图形的面积。
初中数学奥林匹克几何问题-塞瓦定理及应用
初中数学奥林匹克几何问题-塞瓦定理及应用本资料为WoRD文档，请点击下载地址下载全文下载地址第二章塞瓦定理及应用【基础知识】塞瓦定理设，，分别是的三边，，或其延长线上的点，若，，三线平行或共点，则．①证明如图2-1（）、（），若，，交于一点，则过作的平行线，分别交，的延长线于，，得．又由，有．从而．若，，三线平行，可类似证明（略）．注（1）对于图2-1（）、（）也有如下面积证法：由：，即证．（2）点常称为塞瓦点．（3）共点情形的塞瓦定理与梅涅劳斯定理可以互相推证．首先，由梅涅劳斯定理推证共点情形的塞瓦定理．如图2-1（）、（），分别对及截线，对及截线应用梅涅劳斯定理有，．上述两式相乘，得．其次，由共点情形的塞瓦定理推证梅涅劳斯定理．如图2-2，设，，分别为的三边，，所在直线上的点，且，，三点共线．令直线与交于点，直线与交于点，直线与交于点．分别视点，，，，，为塞瓦点，应用塞瓦定理，即对及点（直线，，的交点），有．对及点（直线，，的交点），有．对及点（直线，，的交点），有．对及点（直线，，的交点），有．对及点（直线，，的交点），有．对及点（直线，，的交点），有．上述六式相乘，有．故．塞瓦定理的逆定理设，，分别是的三边，，或其延长线上的点，若，②则，，三直线共点或三直线互相平行．证明若与交于点，设与的交点为，则由塞瓦定理，有，又已知有，由此得，即，亦即，故与重合，从而，，三线共点．若，则．代入已知条件，有，由此知，故．上述两定理可合写为：设，，分别是的，，所在直线上的点，则三直线，，平行或共点的充要条件是．③第一角元形式的塞瓦定理设，，分别是的三边，，所在直线上的点，则三直线，，平行或共点的充要条件是．④证明由，，，三式相乘，再运用塞瓦定理及其逆定理，知结论成立．第二角元形的塞瓦定理设，，分别的三边，，所在直线上的点，是不在的三边所在直线上的点，则，，平行或共点的充要条件是．⑤证明注意到塞瓦定理及其逆定理，有．由此即证得结论．注在上述各定理中，若采用有向线段或有向角，则①、②、③、④、⑤式的右端仍为1．特别要注意的是三边所在直线上的点或者两点在边的延长线上，或者没有点在边的延长线上．④、⑤式中的角也可按①式的对应线段记忆．推论设，，，分别是的外接圆三段弧，，上的点，则，，共点的充要条件是．证明如图2-3，设的外接圆半径为，交于，交于，交于．由，，，，，六点共圆及正弦定理，有．同理，，．三式相乘，并应用第一角元形式的塞瓦定理即证．为了使读者熟练地应用塞瓦定理，针对图2-4中的点、、、、、，将其作为塞瓦点，我们写出如下式子：对及点有，对及点有，对及点有，对及点有，对及点有，对及点有，对及点有，对及点有．【典型例题与基本方法】1．恰当地选择三角形及所在平面上的一点，是应用塞瓦定理的关键例1四边形两组对边延长分别相交，且交点的连线与四边形的一条对角线平行．证明：另一条对角线的延长线平分对边交点连线的线段．（1978年全国高中竞赛题）证明如图2-5，四边形的两组对边延长分别交于，，对角线，的延长线交于．对及点，应用塞瓦定理，有．由，有，代入上式，得，即．命题获证．例2如图2-6，锐角中，是边上的高，是线段内任一点，和的延长线分别交，于，．求证：．（1994年加拿大奥林匹克试题）证法1对及点，应用塞瓦定理，有．①过作，延长，分别交于，，则，且，，从而，．而由①，有，故．由此知为等腰底边上的高，故．证法2对及点应用塞瓦定理，有．即，由锐角性质知．类似地，对及截线或对及截线应用梅涅劳斯定理也可证得有．注将此例中的平角变为钝角，则有如下：例3如图2-7，在四边形中，对角线平分．在上取一点，与相交于，延长交于．求证：．（1999年全国高中联赛题）证明连交于，对及点，应用塞瓦定理，有．平分，由角平分线性质，可得，故．过点作的平行线交的延长线于，过点作的平行线交的延长线于，则．所以．从而，．又，，有．因此，，即有．故．注由此例还可变出一些题目，参见练习题第4、5及19题．例4如图2-8，是的中线，在上，分别延长，交，于，，过作交于，及为正三角形．求证：为正三角形．证明连，对及点应用塞瓦定理，有．而，则．由，由．于是，有，从而，即知四边形为平行四边形，有．又，则．而，，知，有，．于是．故为正三角形．例5如图2-9，在一个中，，为内满足及的一点．求证：是的三等分线．（1994年香港代表队选拔赛题）（其中注意），．证明用表示的度量，令，则，，，对及点，应用第一角元形式的塞瓦定理，有．亦即．于是，即．而，则．因，则．，即．从而．故，即是的三等分线．利用第一角元形式的塞瓦定理可简捷处理20XX年全国高中联赛加试第一题的第1问：例6设、分别为锐角（）的外接圆上弧、的中点．过点作交圆于点，为的内心，联结并延长交圆于点．求证：．证明事实上，易知、、及、、分别三点共线，对及点应用第一角元形式的塞瓦定理，有．①由知，有．于是①式即为．故．2．注意塞瓦定理逆定理的应用以及与梅涅劳斯定理的配合应用例7如图2-10，在中，，为上给定的一点（不是线段的中点）．设为直线上与，都不相同的任意一点，并且直线，交于，直线，交于，直线，交于．试证明交点与在直线上的位置无关．（1990年苏州市高中竞赛题）证明设分线段为定比，分线段为定比．下证由确定，即当，给定后，点的位置由点唯一确定．在中，由，，交于一点，应用塞瓦定理，有，即．对及截线，应用梅涅劳斯定理，得，即．上述两式相加，得．从而，即，故由唯一确定．因此，点与在直线上的位置无关．例8如图2-11，设为内任一点，在形内作射线，，，使得，，．求证：，，三线共点．证法1设交于，交于，交于，则由正弦定理有．同理，,．将上述三式相乘，并应用正弦定理，有．由塞瓦定理的逆定理，知，，共点．证法2设交于，交于，交于，直线交于，直线交于，直线交于．对及点，应用塞瓦定理，有．在和中应用正弦定理，有．同理，，．以上三式相乘，并注意到①式，有．由塞瓦定理的逆定理，知，，共点．证法3设交于，交于，交于，直线交于，直线交于，直线交于．对及点，应用角元形式的塞瓦定理，有．由题设，，，则有，，．于是，对，应用角元形式的塞瓦定理的逆定理，知，，三线共点．例9如图2-12，四边形内接于圆，其边与的延长线交于点，与的延长线交于点，过点作该圆的两条切线，切点分别为和．求证：，，三点共线．（1997年试题）证明连分别交，于，，设与交于．要证，，三点共线，只须证明，，和，，都三点共线，又只须证明，，三线共点．由塞瓦定理的逆定理知只须证明．又直线截，应用梅涅劳斯定理，有，从而只须证明．设圆心为，连交于，连，，，，则由切割线走理和射影定理，有，即知，，，四点共圆，有，此表明为的内角的外角平分线．而，则平分．于是，，结论获证．【解题思维策略分析】1．获得线段比例式的一种手段例10如图2-13，中，，分别为和同方向延长线上的点，与相交于，且．若点满足（为常数），则．证明设交于，对及其形外一点，应用塞瓦定理，有．而，则．不妨设，则，即有，于是，故．此时，点到的距离不小于到的距离，则过作必交延长线于一点，设为．又作的外接圆交于另一点，则四边形为等腰梯形．当时，由，知必在线段上，于是，（同弧上的圆外角小于同弧上的圆周角）．又由，知．故结论获证．2．转化线段比例式的一座桥梁例11设为内任一点，，，分别交，，于，，．求证：．证明如图2-14，记，，．对及点，应用塞瓦定理，有．对及截线，应用梅涅劳斯定理，有，即．由合比定理得，即．同理，，．三式相加，得．例12如图2-15，设为内任意一点，，，的延长线交对边，，于点，，，交于．试证：．证明令，，，对及点，应用塞瓦定理，有．对及截线，应用梅涅劳斯定理，有．注意到，则有，即，故．又对直线截，有．而，则，故．又对及截线，有，即有，故．从而．于是，．其中等号由中等号成立时成立，即当且仅当亦即当且仅当，亦即时取等号．此时，和之间成为如图2-16的双曲线的关系．例13如图2-17，已知直线的三个定点依次为、、，为过、且圆心不在上的圆，分别过、两点且与圆相切的直线交于点，与圆交于点．证明：的平分线与的交点不依赖于圆的选取．（45预选题）证明设的平分线交于点，交圆于点，其中与是不同的两点．由于是等腰三角形，则有．同理，在中，有．在中，视为塞瓦点，由角元形式的塞瓦定理，有．注意到，．则．即，故结论获证．3．求解三角形格点问题的统一方法如果三角形的三个角的度数都是10的整数倍，三角形内一点与三角形的三个顶点分别连结后，得到的所有的角也都具有这个性质，我们称这样的点为三角形的格点．例14如图2-18，在中，，，和分别是和上的点，使得，，是直线和的交点．证明：直线和直线垂直．（1998年加拿大奥林匹克试题）证明设，则，对及点，应用第一角元形式的塞瓦定理，有．从而，即有．．注意到，知，，有，故．延长交于，则．故．注此题也可这样来解：由，有．由于作为的函数在上严格递减，所以．故．因此，．或者过点作于，则，．关于有．所以，、、三线共点，因此点在上，即．例15如图2-19，在内取一点，使得，．设，，求．（1983年前南斯拉夫奥林匹克试题）解设，则．由第一角元形式的塞瓦定理，有．从而．，，．于是．注意到，知，．，故．所以为所求．注此题结果也可直接由①式有且，，求得．另外，此题也可这样来解：由，有．因为作为的函数在（，）上严格递减，所以．故．或者由，令，则．对和点应用第一角元形式的塞瓦定理，有．则．因为作为的函数在上严格递增，所以．例16如图2-20，具有下面性质：存在一个内部的点，使得，，，．证明：是等腰三角形．（1996年美国第25届奥林匹克试题）证明设，则．由第一角元形式的塞瓦定理，有．即有．，．从而且，，故，即，从而．注此题也可这样来求解：由，有．因为作为的函数在（，）上严格递减，所以，即．故．还可对及点应用第一角元形式的塞瓦定理来求．4．论证直线共点的一种工具例17如图2-21，在四边形中，，，过，的交点引，，其中交，于，，交，于，．，分别交于，，则．（1990年cmo选拔试题）证明在，上分别取，，使，，则由对称性可知有下列角相等，即若设，，，，，，则，又，故．又，故，．连交于，在中，．故由塞瓦定理的逆定理，知，，共点，即过点．由对称性知，．例18如图2-22，在锐角中，以点引出的高为直径作圆交，于，，再从作．同样可作出，．试证：三直线，，相交于一点．（第29届预选题）证明设与，分别相交于点，，由，，知，即．同理，设，边上的高，的垂足分别为，，且，分别与，交于，，则有，．由于的三条高相交于垂心，此时应用第一角元形式的塞瓦定理，得，用等角代换上式，有．故由第一角元形式的塞瓦定理，知，，三线共点，即，，相交于一点．例19如图2-23，四边形内接于圆，，的延长线交于，，的延长线交于，为圆上任一点，，分别交圆于，．若对角线与相交于，求证：，，三点共线．证明连，，，，，．由，，有，，此两式相乘，有．①又由，，有，，此两式相乘，有．由①②，得．上式两边同乘以，得．对及截线，应用梅涅劳斯定理，有．于是．此时，应用第一角元形式的塞瓦定理的推论，知，，交于一点．从而，，三点共直线．【模拟实战】习题A1．在中，是上的点，，是中点．与交于，交于，求四边形的面积与的面积的比．2．若通过各顶点的直线，，共点，并且它们在边，，所在直线上的截点，，关于所在边中点的对称点分别为，，，则直线，，也共点．3．一圆交的各边所在直线于两点，设边上的交点为，，边上的交点为，，边上的交点为，．若，，共点，则，，也共点．4．试证：过三角形顶点且平分三角形周长的三条直线共点．5．将各内角三等分，每两个角的相邻三等分线相交得，又，，分别平分，，且它们与，，交于，，．求证：，，三线共点．6．将的各外角三等分，每两个外角的相邻三等分线相交得．又，，分别平分，，且它们与，，交于，，．求证：，，三线共点．7．是的内切圆，，，上的切点各是，，．射线交于，同样可得，．试证：直线，，共点．8．在内部，且从，，各向，，所作的垂线共点，则从，，各向，，所作的垂线也共点．9．在中，，为形内一点，，，求的度数．10．在中，，，为形内一点，且，求的度数．（《数学教学》问题432题）11．在中，，，为形内一点，，求的度数．（《数学教学》问题491题）12．在中，，，为的平分线上一点，使，交于，交于．求证：．（《数学教学》问题531题）13．在中，，，为形内一点，，，求的度数．（《数学通报》问题1023题）14．在中，，，为形内一点，且，，求的度数．（《数学通报》问题1142题）15．在中，，，为形内一点，，，求的度数．（《数学通报》问题1208题）16．中，，，为形内一点，，．求证：．（《数学通报》问题1306题）17．在中，，，为形内两点，，．求证：，，三点共线．（《数学通报》问题1243题）18．中，，，为形内两点，，．求证：．（《数学通报》问题1281题）19．在中，，，为内心，为上一点，满足．试求的度数．（《数学通报》问题1073题）20．，，，，，顺次分别在的三边，，上，且，，，过，，分别作，，的平行线，，．求证：，，三线共点的充要条件是，，三线共点．21．在中，，于，过任作两射线分别交，于点，，交过点的平行线于，，且．求证：，，共点．22．在中，过三边，，边中的中点，，的三条等分三角形周长的直线，，（，，在三角形三边上）分别交，，于，，．求证：，，三线共点．23．的内切圆切，，于，，．是内一点，交内切圆于两点，其中靠近的一点为，类似定义，．试证：，，三线共点．24．在内部，的延长线分别交，于，；的延长线分别交，于，；的延长线分别交，于，，且满足．求证：，，所在直线共点．（《中学数学教学》擂台题（28））25．给定，延长边至，使．的外接圆与以为直径的圆相交于和．设与的延长线分别交和于，．求证：，，共线．（第15届伊朗奥林匹克题）26．在的边上向外作三个正方形，，，是正方形中的边，，对边的中点．求证：直线，，共点．习题B1．是的内切圆，，，，分别是，，上的切点，，，都是的直径．求证：直线，，共点．（《数学通报》问题1396题）2．四边形的内切圆分别与边，，，相切于，，，．求证：，，，四线共点．（《数学通报》问题1370题）3．锐角中，角的平分线与三角形的外接圆交于另一点，点，与此类似．直线与，两角的外角平分线交于，点，与此类似．求证：（Ⅰ）三角形的面积是六边形的二倍；（Ⅱ）三角形的面积至少是三角形面积的四倍．（-30试题）4．设为内一点，使，是线段上的点，直线，分别交边，于，．求证：．5．在凸四边形中，对角线平分，是的延长线上的一点，交于点，延长交的延长线于．试证：．6．在中，，，为内心，为上一点，满足．试求的度数．（《数学通报》问题1073题）7．设是等边三角形，是其内部一点，线段，，依次交三边，，于，，三点．证明：．（-37预选题）8．在一条直线的一侧画一个半圆，，，是上两点，上过和的切线分别交于和，半圆的圆心在线段上，是线段和的交（-35预选题）点，是上的点，．求证：平分．9．设是锐角的内接正方形的中心，其中内接正方形的两个顶点在边上，一个顶点在边上，一个顶点在边上．同样定义两个顶点分别在边和边上的内接正方形的中心分别为，．证明：，，交于一点．（-42预选题）10．以的底边为直径作半圆，分别与，交于点，，分别过点，作的垂线，垂足依次为，，线段和交于点．求证：．（1996年国家队选拔考试题）11．设，是锐角的外接圆的圆心和垂心．证明：存在，，分别在线段，，上，使得，且此时，，三线交于一点．（-41预选题）12．已知是的直径，弦于，点和分别在线段和上，且∶∶，射线，交于，．求证：，，三线共点．13．设是的内心，以为圆心的一个圆分别交于，，交于，，交于，．这六个点在圆上的顺序为，，，，，．设，，为弧，，的中点，直线，相交于，直线，相交于，直线，相交于．求证：直线，，三线共点．14．在的边和上分别向形外作和，使，且．求证：连线，与边上的高三线共点．15．过非等边三角形各顶点作其外接圆的切线，则各切线与其对边的交点共线．16．在内三点，，满足，，则，，三线共点的充要条件是．17．在任意的三边，，上各有点，，，而是内部任一点，直线，，分别交线段，，于，，．求证：直线，，共点的充分必要条件是，，共点，而与点的位置无关．18．设是平面上区域内任一点，，，的延长线交三边于，，．求证：在区域内，存在一个以的某两边为邻边的平行四边形．19．设凸四边形的两组对边所在的直线，分别交于，两点，两对角线的交点为，过点作于．求证：．（2002国家集训队选拔试题）20．在中，和均为锐角．是边上的内点，且平分，过点作垂线于，于，与相交于．求证：．。
8种方法解决一道角格点问题
8种方法解决三角形中的角格点问题
学霸数学
ABC中，ABC ACB 40 0，P为三角形内一点， PAC PCA 200，求PBC 的度数
A
P
B
C
学霸数学
ABC中，ABC ACB 40 0，P为三角形内一点， PAC PCA 200，求PBC 的度数
A
E
B
解法一：
P
C D
在BC上取一点D，使DC AC，CP与AB交于点E
学霸数学
ABC中，ABC ACB 40 0，P为三角形内一点， PAC PCA 200，求PBC 的度数
A
D
B
解法八：
P
E
C
ABC 的平分线交AC于D，直线AP交BC于点E
A、B、E、D四点共圆，有PED 200
D、P、E、C四点共圆，于是PBC 100
PCA PAC 200，DAB 600，由ABC ACB 400
BAD为正三角形，PBC 100
学霸数学
ABC中，ABC ACB 40 0，P为三角形内一点， PAC PCA 200，求PBC 的度数
A
D B
P C
解法三：
以PA为边向内作正PAD，连接BD，得ACP ABD
BD PD，又BDP 1600，故DBP 100，得PBC 100
A
P
B
C
解法五： 以AC为边作正ACD，连接PD、DB，PD为AC的中垂线，于是PDA 300 DPA 1300，得A、B、D、P四点共圆故PBC 100
学霸数学
ABC中，ABC ACB 40 0，P为三角形内一点， PAC PCA 200，求PBC 的度数
A E
D
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
如果三角形的三个角的度数都是１０的整数倍，三角形内一点与三角形的三个顶点分别连结后，得到的所有的角也都具有这个性质，我们称这样的点为三角形中的格点．求解三角形中的格点问题，常可利用对称点．利用对称点求解三角形中的格点问题，方法简单易行，解法简洁巧妙，题面新颖有趣，是学生巩固知识，培养能力，陶冶情操，提高素质的宝贵资料．１证明对称点常用的方法大家知道，把一个图形沿着某一条直线翻折，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线对称．两个图形中的对应点叫做关于这条直线的对称点，这条直线叫做对称轴．Ｑ即可．不过，在证明对称时，只须摆明条件，而不必特别指明两个三角形的全等关系．例１２０°．求∠ＭＡＢ的度数．解：如图１，设∠ＭＢＡ的平分线交ＡＣ于Ｄ，连ＤＭ．图１显然，ＢＭ平分∠ＤＢＣ，而ＣＭ平分∠ＤＣＢ，即Ｍ为△ＤＢＣ的内心．可知∠ＭＤＢ＝∠MDC ＝60°．有∠ＡＤＢ＝６０°＝∠ＭＤＢ．故点Ａ与点Ｍ关于ＢＤ对称．则∠ＭＡＢ＝９０°－∠ＤＢＡ＝７０°．这里证得“点Ａ与点Ｍ关于ＢＤ对称”是根据“角、边、角”．例２在△ＡＢＣ中，∠ＡＢＣ＝∠ＡＣＢ＝４０°，Ｐ为形内一点，∠ＰＣＡ＝∠ＰＡＣ＝２０°．求∠ＰＢＣ的度数．知ＰＡ＝ＰＣ．有点Ａ与点Ｃ关于ＰＤ对称．得∠ＰＤＡ＝21∠ＡＤＣ＝３０°．由∠ＡＣＢ＝∠ＡＢＣ＝４０°，可知ＡＢ＝ＡＣ＝ＡＤ．易知∠ＰＡＤ＝８０°＝∠ＰＡＢ，可知点Ｂ与点Ｄ关于ＰＡ对称．有∠ＰＢＡ＝∠ＰＤＡ＝３０°．则∠ＰＢＣ＝１０°．这里证出“点Ａ与点Ｃ关于ＰＤ对称”是根据“边、边、边”，证出“点Ｂ与点Ｄ关于ＰＡ对称”是根据“边、角、边”．综上可知，证明两个点关于某线段所在直线对称，是一件很容易做的事情．而且熟练以后，更可能节省些笔墨．明确了这一点，我们就要积极、主动地创造条件，注意利用对称点．２在哪些情况下应想到使用对称点三角形中的格点问题，经常会给出或求证角平分线，这是使用对称点的最方便的条件，换言之，在题目给出或求证角平分线时，要想到使用对称点例３在△ＡＢＣ中，∠ＡＢＣ＝４０°，∠ＡＣＢ＝３０°，Ｐ为∠ＡＢＣ的平分线上一点，∠ＰＣＢ＝１０°．求∠ＰＡＢ的度数．解：如图３，在ＢＡ延长线上取一点Ｄ，使ＢＤ＝ＢＣ．连ＤＰ、ＤＣ．图３由ＢＰ平分∠ＡＢＣ，可知点Ｄ与点Ｃ关于ＢＰ对称．有ＰＤ＝ＰＣ．由∠ＤＰＣ＝２（∠ＰＢＣ＋∠ＰＣＢ）＝６０°，可知△ＰＣＤ为正三角形．有ＰＣ＝ＤＣ．在△ＡＣＤ中，由∠ＡＤＣ＝７０°＝∠ＤＡＣ，可知ＡＣ＝ＤＣ．有ＡＣ＝ＰＣ．在△ＰＣＡ中，由∠ＰＣＡ＝２０°，可知∠ＰＡＣ＝８０°．则∠ＰＡＢ＝３０°．这里由ＢＰ平分∠ＡＢＣ，想到在ＢＡ延长线上取一点Ｄ，使ＢＤ＝ＢＣ，则点Ｄ为点Ｃ关于ＢＰ的对称点．这是取对称点的最简单、最基本的方法．例４在△ＡＢＣ中，∠ＡＢＣ＝５０°，∠ＡＣＢ＝３０°，Ｑ为形内一点，∠ＱＢＡ＝∠ＱＣＡ＝２０°．求∠ＱＡＢ的度数．解：如图４，设ＢＱ交ＡＣ于Ｄ，过点Ｄ作ＢＣ的垂线交ＱＣ于Ｅ．连ＢＥ．图４由∠ＱＢＣ＝３０°＝∠ＡＣＢ，可知ＤＥ为ＢＣ的中垂线．由∠ＱＣＢ＝１０°，可知∠ＥＢＣ＝１０°，∠ＱＢＥ＝２０°＝∠ＱＢＡ．由∠ＥＤＢ＝６０°＝∠ＥＤＣ，可知∠ＢＤＡ＝６０°＝∠ＢＤＥ．有点Ａ与点Ｅ关于ＢＤ对称．则∠ＱＡＢ＝∠ＱＥＢ＝∠ＥＢＣ＋∠ＥＣＢ＝２０°．这里注意到ＢＱ是∠ＡＱＣ的平分线，故想到在ＱＣ上取点Ｅ，使∠ＥＢＱ＝∠ＡＢＱ，则点Ｅ为点Ａ关于ＢＱ的对称点．为此想到满足条件的点Ｅ，恰为ＢＣ中垂线与ＱＣ的交点。
又由∠ＱＢＣ＝３０°＝∠ＡＣＢ，想到ＢＱ与ＡＣ的交点Ｄ应为ＢＣ中垂线上的另一点．于是，我们选择了如上的方法找到点Ａ关于ＢＱ的对称点Ｅ．例５在△ＡＢＣ中，∠ＡＢＣ＝５０°，∠ＡＣＢ＝３０°,Ｑ为形内一点，∠ＱＣＡ＝∠ＱＡＢ＝20°．求∠ＱＢＣ的度数．解：如图５，设ＢＣ的中垂线分别交ＢＡ、ＡＣ于Ｄ、Ｅ，Ｆ为垂足．连ＱＥ、ＢＥ、ＤＣ．图５由∠ＡＣＤ＝２０°＝∠ＡＣＱ，∠ＤＡＣ＝８０°＝∠ＱＡＣ，可知点Ｄ与点Ｑ关于ＡＣ对称．有∠ＡＥＱ＝∠ＡＥＤ＝∠ＦＥＣ＝６０°．由∠ＢＥＦ＝∠ＦＥＣ＝６０°，可知∠ＡＥＢ＝６０°＝∠ＡＥＱ．有Ｂ、Ｑ、Ｅ三点共线．则∠ＱＢＣ＝∠ＥＢＣ＝３０°．这里注意到ＡＣ是△ＡＱＢ的∠ＱＡＢ的外角平分线（这一点并不引人注目），在ＢＡ延长线上取一点Ｄ，使ＤＡ＝ＱＡ，则点Ｄ为点Ｑ关于ＡＣ的对称点．为此我们通过ＢＣ的中垂线，把∠ＡＢＣ“翻折”到∠ＤＣＢ的位置，是非常恰当的．例６在△ＡＢＣ中，∠ＣＡＢ＝∠ＣＢＡ＝50°，Ｏ为形内一点，∠ＯＡＢ＝１０°,∠ＯＢＣ＝20°．求∠ＯＣＡ的度数．解：如图６，过点Ｃ作ＡＢ的垂线交ＢＯ延长线于Ｅ．连ＡＥ．图６由∠ＣＡＢ＝∠ＣＢＡ＝５０°，可知点Ａ与点Ｂ关于ＣＥ对称．又由∠ＯＢＣ＝２０°，∠ＥＣＢ＝４０°，有∠ＣＥＡ＝∠ＣＥＢ＝１２０°．于是，∠ＯＥＡ＝１２０°＝∠ＣＥＡ．由∠ＥＡＢ＝∠ＥＢＡ＝３０°，∠ＯＡＢ＝１０°，可知ＡＥ平分∠ＣＡＯ．有点Ｃ与点Ｏ关于ＡＥ对称．则∠ＯＣＡ＝∠ＣＯＡ＝１２（１８０°－∠ＯＡＣ）＝７０°．这里从准确的图形我们能够猜想ＡＯ＝ＡＣ，或说点Ｏ与点Ｃ的对称轴经过点Ａ．由于图中没给出对称轴，我们通过ＡＢ的中垂线，将直线ＢＯ“翻折”到ＡＥ位置，从而解决了∠ＣＡＯ的平分线的问题．处理是巧妙的．综上我们讨论了在图形中出现角平分线时应想到使用对称点．当图形中缺角平分线时，也要设法调整图形，使角平分线及时“出现”，为确定对称关系提供方便．３如何选择对称点的位置恰当地选择对称点，能够使图形出现更多的特殊性，能够使图形具有更多的好性质，能够使求解来得方便，简捷，新颖，巧妙．为此，选择对称点时，应当以能够出现特殊图形为原则．３．１让对称点落在某线段的中垂线上例７０°．求∠ＲＡＢ的度数解：如图７，以ＡＢ为一边在△ＡＢＣ形内一侧作正△ＤＡＢ．连ＤＲ、ＤＣ．图７由∠ＡＣＢ＝３０°，可知点Ｄ为△ＡＢＣ的外心．于是，ＤＢ＝ＤＣ．有∠ＤＣＢ＝∠ＤＢＣ＝１０°，∠ＢＤＣ＝１６０°．由∠ＲＢＣ＝∠RCB ＝20°，可知ＲＢ＝ＲＣ．有ＲＤ为ＢＣ的中垂线，且∠ＲＤＢ＝21∠ＢＤＣ＝80°．由∠ＲＢＡ＝３０°，可知点Ａ与点Ｄ关于ＢＲ对称．有∠ＲＡＢ＝∠ＲＤＢ＝８０°．这里以ＡＢ为一线上，使求解很方便．３．２让对称点落在某三角形的外接圆上例８在△ＡＢＣ中，∠ABC ＝６０°，∠ACB ＝４０°，Ｐ为形内一点，∠PBC ＝２０°，∠PCB ＝10°．求∠ＰＡＢ的度数．解：如图８，设点Ｄ为点Ｂ关于ＰＣ的对称点．连ＤＡ、ＤＢ、ＤＣ、ＤＰ．图８在△ＢＣＤ中，由∠ＤＣＢ＝２０°，可知∠ＢＤＣ＝８０°＝∠ＢＡＣ．有Ａ、Ｄ、Ｂ、Ｃ四点共圆．由ＤＣ平分∠ＡＣＢ，可知ＤＡ＝ＤＢ．易知△ＰＢＤ为正三角形，有故∠ＰＡＢ＝１/２∠ＰＤＢ＝３０°．这里，点Ｂ关于ＰＣ的对称点Ｄ恰好在△ＡＢＣ的外接圆上，使圆内接四边形的性质能在求解中发挥作用．可见在选择对称点时，能使其位于某三角形的外接圆上，也是很理想的．３．３让对称点与另一点的某个对称点重合例９在△ＡＢＣ中，∠ＡＢＣ＝∠ＡＣＢ＝40°，Ｐ为形内一点，∠ＰＡＣ＝２０°，∠ＰＣＢ＝30°．求∠ＰＢＣ的度数．解：如图９，设点Ｄ为点Ｃ关于ＡＰ的对称点．连ＤＡ、ＤＢ、ＤＣ、ＤＰ．图９由∠ＰＡＣ＝２０°，∠ＰＣＡ＝１０°，可知∠ＤＡＣ＝４０°，∠PDA＝∠PCB＝１０°，则△PDC为正三角形．由∠ＡＢＣ＝∠ＡＣＢ＝４０°，可知ＡＣ＝ＡＢ＝ＡＤ．由∠ＢＡＤ＝６０°，可知△ＡＢＤ为正三角形．有∠ＤＢＣ＝６０°－∠ＡＢＣ＝２０°．由∠ＰＣＢ＝３０°，可知点Ｐ与点Ｄ关于ＢＣ对称．故∠ＰＢＣ＝∠ＤＢＣ＝２０°．这里寻到的点Ｄ是点Ｃ关于ＡＰ的对称点，也是点Ｐ关于ＢＣ的对称点．理想的巧合，使解法很漂亮．以上三例分别说明了选择对称点的常见的目标，当然还会有其他的目标．对这些情况的深入研究，能使我们熟悉和喜欢利用对称点解题，即使在较复杂的问题中，也能顺其自然，轻松流畅地寻出理想的解法来．例１０在△ＡＢＣ中，∠ＡＢＣ＝５０°，∠ＡＣＢ＝３０°，Ｒ为形内一点，∠RAC＝∠ＲＣＢ＝20°．求∠ＲＢＣ的度数．解：如图１０，设点Ｅ为点Ｒ关于ＡＣ的对称点，点Ｄ为点Ａ关于ＥＣ的对称点．连ＤＡ、ＤＲ、ＤＥ、ＤＣ、ＥＡ、ＥＣ．图１０易知△EDA∠ＢＡＣ＋∠ＤＡＣ＝１８０°．有Ｂ、Ａ、Ｄ三点共线．得∠ＤＣＢ＝５０°＝∠ＤＢＣ，①且∠ＢＤＣ＝８０°．由∠ＲＡＤ＝１００°，可知∠ＲＤＡ＝∠ＤＲＡ＝４０°＝１２∠ＢＤＣ．②由①、②可知点Ｂ与点Ｃ关于ＤＲ对称．则∠ＲＢＣ＝∠ＲＣＢ＝２０°．这里，先是将△ＲＡＣ沿ＡＣ向上翻，然后又将△ＥＡＣ沿ＥＣ向上翻，这一翻再翻，构造出等腰△DBC 、是奇妙．例１１在△ＡＢＣ中，∠ＡＢＣ＝５０°，∠ＡＣＢ＝２０°，Ｎ为形内一点，∠ＮＡＢ＝４０°，∠ＮＢＣ＝３０°．求∠ＮＣＢ的度数．解：如图１１，过点Ｎ作ＡＣ的垂线交ＢＡ延长线于Ｐ．在ＡＮ延长线上取一点Ｑ，使∠ＱＢＣ＝３０°．连ＰＣ、ＱＣ、ＱＢ、ＰＱ、ＰＮ．图１１由∠ＰＡＣ＝７０°＝∠ＮＡＣ，可知点Ｐ与点Ｎ关于ＡＣ对称．有ＰＣ＝ＮＣ．由∠ＮＡＢ＝４０°，∠ＡＢＣ＝５０°，可知ＡＱ⊥ＢＣ．有点Ｎ与点Ｑ关于ＢＣ对称．得ＱＣ＝ＮＣ．则ＰＣ＝ＱＣ．易知△ＢＱＮ为正三角形，有ＮＢ＝ＮＱ．由∠ＮＰＡ＝９０°－∠ＰＡＣ＝２０°＝∠ＮＢＡ，可知ＮＰ＝ＮＢ．则ＮＰ＝ＮＱ．易知△ＰＮＣ≌△ＱＮＣ．可知∠ＮＣＰ＝∠ＮＣＱ，即２∠ＮＣＡ＝２∠ＮＣＢ．得∠ＮＣＡ＝∠ＮＣＢ．故∠ＮＣＢ＝21∠ＡＣＢ＝１０°．这里，一是将△ＮＡＣ向上翻，二是将△ＮＢＣ向下翻，这上翻下翻构造了正△ＮＢＱ，等腰△ＡＮＰ，以点Ｎ为外心的△ＰＢＱ，两个全等的等腰△ＮＣＰ和△ＮＣＱ．其间，巧用对称，堪称一绝．三角形中的格点问题，为对称点的使用提供了广阔的空间，只要我们潜心研究，科学归纳，总会有新的规律被发掘和利用．练习题题号在△ABC中P为形内一点,求出下面空格中的角的度数答案∠ABC∠ACB∠PBC∠PCB∠PAB1 ４０°３０°２０°１００°10°2 ６０°４０°２０°３０°10°3 ４０°２０°１０°１００°10°4 ６０°２０°４０°１０°30°5 ４０°３０°３０°２０°40°6 ４０°３０°１０°１０°70°7 40°30°30°40°20°8 50°30°10°10°70°9 40°30°10°20°100°10 50°30°20°10°40°11 30°20°10°30°20°12 70°40°30°50°40°13 50°50°10°20°60°14 70°30°20°60°30°15 60°20°10°70°20°。