三角形中的边角关系知识点
第三讲 直角三角形的边角关系讲义
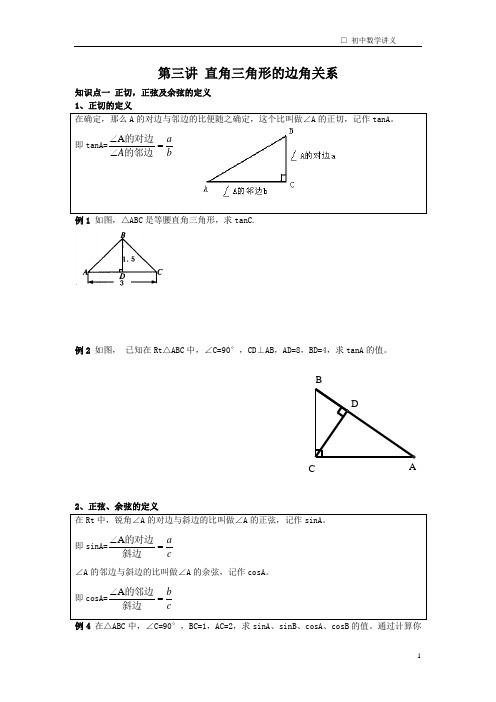
第三讲 直角三角形的边角关系知识点一 正切,正弦及余弦的定义1、正切的定义的对边与邻边的比便随之确定,这个比叫做∠A 的正切,记作例1 如图,△ABC 是等腰直角三角形,求tanC.例2 如图, 已知在Rt △ABC 中,∠C=90°,CD ⊥AB ,AD=8,BD=4,求tanA 的值。
C B A有什么发现?请加以证明。
3、三角函数的定义(重点)能判断谁的木棒更陡吗?说明理由。
同步练习:1、∠C=90°,点D 在BC 上,BD=6,AD=BC ,cos ∠ADC=53,求CD 的长。
2、P 是a 的边OA 上一点,且P 点的坐标为(3,4),求sina 、tana 的值。
3、在△ABC 中,D 是AB 的中点,DC ⊥AC ,且tan ∠BCD=31,求tanA 的值。
4、在Rt △ABC 中,∠C=90°,tanA=125,周长为30,求△ABC 的面积。
5、(2008·浙江中考)在Rt △ABC 中,CD 是斜边AB 上的中线,已知CD=2,AC=3,则sinB 的值是多少?知识点二 30°,45°,60°角的三角函数值例 求下列各式的值。
(1)︒︒-︒60tan 30sin 60sin ;(2)︒-+︒-︒45sin 22460tan 460tan 2。
同步练习:1、 求下列各式的值。
(1)︒+︒+︒45tan 30tan 330sin 2; (2)︒⋅︒+︒30cos 60tan 45cos 2。
(3) 6tan 2 30°-3sin 60°+2tan45°(4)022)30tan 45(sin )60cos (160sin 260sin 60tan 245tan o o o o o oo-+-++----2、 已知a 为锐角,且tana=5,求aa aa sin cos 2cos 3sin +-的值。
直角三角形的边角关系知识点

直角三角形的边角关系知识点一、勾股定理勾股定理是指在直角三角形中,直角边的平方等于两个其他两边平方的和。
即a^2+b^2=c^2,其中c表示直角边,a和b分别表示斜边。
二、正弦定理正弦定理是指在任意三角形中,任意两边的比例等于它们所对的角的正弦值的比例。
在直角三角形中,不包含直角的两个角分别为A和B,直角所对的边为c,则正弦定理可以表示为sinA=a/c,sinB=b/c。
三、余弦定理余弦定理是指在任意三角形中,任意一边的平方等于另外两边的平方和减去它们的两倍乘以它们夹角的余弦。
在直角三角形中,不包含直角的两个角分别为A和B,直角边所对的边为c,则余弦定理可以表示为cosA=b/c,cosB=a/c。
四、正切定理正切定理是指在任意三角形中,两条边的比例等于它们所对的角的正切值的比例。
在直角三角形中,不包含直角的两个角分别为A和B,直角所对的边为c,则正切定理可以表示为tanA=a/b,tanB=b/a。
五、边角关系1.直角三角形中,一个角是90度,另外两个角的和是90度。
2.直角三角形中,直角边所对的角是90度,而另外两边所对的角是锐角。
3.直角三角形中,两个锐角的正弦、余弦、正切值彼此互为倒数。
4.直角三角形中,两个锐角的余弦值等于彼此的正弦值。
5.直角三角形中,一个锐角的正弦值等于另一个锐角的余弦值。
六、特殊三角形1.在直角三角形中,当两个直角边的长度相等时,该直角三角形为等腰直角三角形。
2.在等腰直角三角形中,两个锐角相等,且为45度。
3.在等腰直角三角形中,斜边的长度等于直角边的平方根的两倍。
以上是直角三角形的边角关系的主要知识点。
通过对直角三角形的边长和角度关系的了解,我们可以应用这些关系来解决与直角三角形相关的问题。
同时,直角三角形也是三角学中一个重要的基础概念,为后续学习提供了坚实的基础。
直角三角形的边角关系

编号⒀九年级数学下册《直角三角形的边角关系》复习一班级姓名知识点回顾:1.直角三角形中的边角关系:(如图,在ABC中,∠C为直角)(1)三边之间的关系:(2)锐角之间的关系:(3)边角之间的关系:2.一些特殊角的三角函数值:3.锐角α的三角函数值的符号及变化规律。
(1)锐角α的三角函数值都是正值;(2)若0<α<90° 则sinα,tanα随α的增大而,cosα随α的增大而 . 4.常用到下面几个概念:(1)仰角、俯角:视线与水平线所成的角中,视线在水平线上方的叫做仰角,在水平线下方的叫做俯角.(2)坡度、坡角:坡面的铅直高度h与水平宽度l的比叫做坡度,常用字母i表示,h即i=lh坡面与水平面的夹角叫做坡角,用字母α表示,则tanα=i=l典型例题:1、在Rt△ABC中,如果各边长度都扩大为原来的2倍,那么锐角A的正弦值()A.扩大2倍B.缩小2倍C.扩大4倍D.没有变化2、如图:P是∠α的边OA上一点,且P点的坐标为(3,4),则sin(900 - α)=_____________.3、计算:tan60°·sin60°-cos30°·tan45°=_____________.4、已知0°<α<45° 则sin α,cos α的大小关系为( )A 、sin α>cos αB 、sin α<cos αC 、sin α≥cos αD 、sin α≤cos α. 5、已知在Rt △ABC 中∠C=90° 且tanA =31,则cosB 的值为( ) A 、1013 B 、310 C 、1010 D 10103 6、直角梯形ABCD 中,AD ∥BC ,CD =10,∠B=90°,∠C=30°则AB =( )A 、53B 、5C 、25D 2357、一个三角形的一边长为2,这边上的中线长为1,另两边长之和为1+, 则这个三角形的面积为( )A. 1B.23C. D.43 8、如图,在梯形ABCD 中,AD ∥BC ,∠B=90°,AD=2,BC=5,tanC=34. (1)求点D 到BC 边的距离; (2)求点B 到CD 边的距离.9、外国船只,除特许外,不得进入我国海洋100海里以内的区域。
边角关系知识点总结

边角关系知识点总结1. 任意三角形的边角关系:(1)在任意三角形中,三个内角的和等于180°,即A + B + C = 180°。
(2)三角形的外角等于其不相邻的两个内角的和。
也就是说,三角形的一个内角加上其对边的外角等于180°。
(3)在任意三角形中,任意两边之和大于第三边。
即AB + BC > AC、AC + BC > AB、AB + AC > BC。
2. 直角三角形的边角关系:(1)直角三角形的三个内角中,一个为90°,一个为锐角,一个为钝角。
(2)直角三角形的斜边是其它两条边的平方和的平方根。
即c² = a² + b²。
(3)直角三角形的两个锐角互余,即一个角的余角是另一个角。
3. 等腰三角形的边角关系:(1)等腰三角形的底边相等,顶角相等。
(2)等腰三角形的底角相等,顶角相等。
(3)等腰三角形的底边上的高相等。
4. 等边三角形的边角关系:(1)等边三角形三个内角相等,每个角都是60°。
(2)等边三角形的三条边相等。
(3)等边三角形的高、中线、角平分线、垂径都是同一条线段。
5. 直角三角形、等腰三角形和等边三角形的区别:(1)直角三角形有一个角是90°,等腰三角形和等边三角形没有。
(2)等腰三角形有两条边相等,直角三角形和等边三角形没有。
(3)等边三角形的三条边都相等,直角三角形和等腰三角形没有。
6. 三角形的角平分线:(1)三角形的角平分线是指从三角形的一个角的顶点出发,把这个角平分成两个相等的角的线段。
(2)三角形的三个角都各有一条角平分线。
(3)角平分线和对边的比例关系:AB/BD = AC/CD。
7. 外接角和内切角:(1)外接角:指与三角形的外角相对应的一个角,外接角等于两个不相邻内角的和。
(2)内切角:指与三角形的内角相对应的一个角,内切角等于两个不相邻外角的和。
8. 三角形的全等条件:(1)两个三角形的三边全相等,则这两个三角形全等。
直角三角形的边角关系(精简版)

直角三角形的边角关系知识点1:锐角三角函数一、知识点讲解: 1.锐角三角函数的概念:锐角三角函数包括正弦函数,余弦函数,和正切函数,如图1-1-1,在Rt △ABC 中,∠C =90°,∠A 、∠B 、∠C 的对边分别为a 、b ,c . ∠A 的正弦=A asin A=c∠的对边,即斜边;∠A 的余弦=A b cos A=c∠的邻边,即斜边,∠A 的正切=A a tan=A b∠的对边,即∠的邻边注:三角函数值是一个比值.2.特殊角是指0°,30°,45°,60°,90°的角. 3.特殊角的三角函数值.4.互为余角的三角函数关系.sin (90○-A )=cosA , cos (90○-A )=sin A tan (90○-A )= cotA cot (90○-A )=tanA 5.同角的三角函数关系. ①平方关系:sin 2 A+cos 2A=l ②倒数关系:tanA ×cotA=1③商数关系:sin cos tan ,cot cos sin A AA A A A==④sin cos 12sin cos a a a a +=+ ⑤222tan cot (tan cot )2a a a a +=+- 二、经典例题讲解: 类型一、关于特殊的函数值 例题1、计算:()()013222sin 60-︒-+-+⋅(结果保留根号......)中考典练1: 024cos 458(3)(1)π-+++-分值6分中考典练2:2(tan 301)____-= 中考典练3:13tan 60|2|22-+-+例题2、 2sin60°-cos30°·tan45°的结果为( ) A 、 3 33. .22B C -D .0 例题3、等腰直角三角形一个锐角的余弦为( ) A 、12 32. .22B C D .l 例4、点M(tan60°,-cos60°)关于x 轴的对称点M ′的坐标是( ) 1111.(3,); .(3,); .(3,) .(3,)2222A B C D ----例5、在锐角△ABC 中,如果2sinC=sin90°,则∠C=__。
三角形中的边角关系

三角形中的边角关系知识点梳理一、 边1、根本概念〔三角形、边、 顶点的定义;三角形的符号表示〕2、按边对三角形的分类:≠⎧⎪⎨⎧⎨⎪⎩⎩不等边三角形三角形腰底等腰三角形等边三角形☆3、三边关系:〔1〕任意两边之和大于第三边 〔2〕任意两边之差小于第三边 验证:两条较短边之和与第三边的关系 二、角1、根本概念〔内角、外角〕2、按角对三角形的分类:⎧⎧⎪⎨⎩⎨⎪⎩锐角三角形斜三角形三角形钝角三角形直角三角形3、三角形的内角和〔1〕三角形三个内角和等于180°; 〔2)直角三角形的两个锐角互余; 〔3〕一个三角形最多3个锐角,最多1个钝角,最多1个直角,最少2个锐角。
三、线1、中线(1) 定义 〔2〕 重心 〔3〕中线是线段 〔4〕 表示方法 2、高线〔1〕定义 〔2〕垂心 (3〕高是线段,垂线是直线 〔4〕表示方法 〔5〕钝角三角形高的画法 3、角平分线〔1〕定义 (2)外心 〔3〕画法 〔4〕表示方法 四、方法技能归纳法在规律探索中的应用。
根底练习第1题-〔1〕 第1题-〔2〕 第1题-〔2〕1、〔1〕以AB 为边的三角形有______________;含∠ACB 的三角形有 ;在△BOC 中,OC 的对角是___________;∠OCB 的对边是___________.〔2〕图〔1〕中三角形的个数是____________;★图〔2〕中三角形的个数是____________。
2、三角形按角分类可以分为〔 〕A .锐角三角形、直角三角形、钝角三角形;B .等腰三角形、等边三角形、不等边三角形;C .直角三角形、等边直角三角形;D .以上答案都不正确3、一个等腰三角形的两边长分别是4和9,那么它的周长是___________________________4、假设三角形的三边长分别为3,4,x -1,那么x 的取值范围是_________________________5、有3cm,6cm,8cm,9cm 长的四条线段,任选其中的三条线段组成一个三角形,那么最多能组成_____个三角形6、,,a b c 是ABC 的三条边,且()()0a b c a b ++-=,那么ABC 是__________三角形7、以下说法正确的选项是_____________________〔1〕等边三角形是等腰三角形; 〔2〕三角形的两边之差大于第三边;〔3〕有两边相等的三角形一定是等腰三角形; 〔4〕一个钝角三角形一定不是等腰三角形。
直角三角形三条边的关系公式

直角三角形三条边的关系公式
直角三角形是指其中一个角是90度的三角形。
在直角三角形中,三条边之间有着重要的关系,可以用数学公式来表示。
1. 勾股定理:勾股定理是直角三角形中最基本的关系公式,它表示直角三角形的两条直角边的平方和等于斜边的平方。
即a²+b²=c²,其中a和b分别表示直角三角形的两条直角边,c表示斜边。
2. 正弦定理:正弦定理表示直角三角形中,任意一条边的长度与其对应的角度之间的关系。
即a/sinA=b/sinB=c/sinC,其中a、b、c分别表示直角三角形的三条边,A、B、C分别表示对应的角度。
3. 余弦定理:余弦定理表示直角三角形中,任意一条边的长度与其对应的角度之间的关系。
即a²=b²+c²-2bc*cosA,b²=a²+c²-2ac*cosB,c²=a²+b²-2ab*cosC,其中a、b、c分别表示直角三角形的三条边,A、B、C分别表示对应的角度。
这些公式的应用可以帮助我们解决直角三角形的各种问题,如求解三角形的边长、角度大小等等。
三角形的边角关系.

三角形的三边关系1.三角形的概念不在同一直线上的三条线段首尾顺次相接组成的图形叫做三角形.①三角形有三条边,三个内角,三个顶点.②组成三角形的线段叫做三角形的边;③相邻两边所组成的角叫做三角形的内角简称角;④相邻两边的公共端点是三角形的顶点,⑤三角形ABC 用符号表示为△ ABC ,⑥三角形ABC 的边AB 可用边AB 所对的角C的小写字母 c 表示,AC 可用b表示,BC 可用 a 表示.1:三条线段要不在同一直线上,且首尾顺次相接2:三角形是一个封闭的图形;3:△ ABC 是三角形ABC 的符号标记,单独的△没有意义例例 1 图中三角形的个数是( )A.8 B.9 C.10 D.112.三角形的三边关系三角形的任意两边之和大于第三边; 三角形的任意两边之差小于第三边.1:三边关系的依据是:两点之间线段是短2:判断三条线段能否构成三角形的方法:只要满足较小的两条线段之和大于第三条线段,便可构成三角形; 若不满足,则不能构成三角形.3:三角形第三边的取值范围是: 两边之差<第三边<两边之和例1 :已知四组线段的长分别如下,以各组线段为边,能组成三角形的是( )A.1,2,3 B.2,5,8 C.3,4,5 D.4,5,10例2:下列各组条件中,不能组成三角形的是( )A. a+1、a+2、a+3 (a>3)B. 3cm、8cm、10 cmC. 三条线段之比为1:2:3D. 3a、5a、2a+1 (a>1)例3.△ ABC的三边长分别为4、9、x,⑴ 求x 的取值范围;⑵ 求△ ABC 周长的取值范围;⑶ 当x 为偶数时,求x ;⑷ 当△ ABC 的周长为偶数时,求x ;⑸ 若△ ABC 为等腰三角形,求x .课堂练习1.已知长度为2cm,3cm,4cm,5cm 的四条线段,能组成多少个不等边三角形?2.已知等腰三角形的周长是14 cm ,底边与腰的比为 3 : 2 ,求各边的长.3.在ABC中,AB 9,BC 2,并且AC 为奇数,那么ABC的周长是多少?4.如图, D 是ABC内任意一点,BD 延长线与AC 交于 E 点,连结DC.求证:AB AC BD DC .3.三角形的高、中线、角平分线(1 ) 三角形的高:从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段.注意:①三角形的高是线段;②锐角三角形三条高全在三角形的内部;直角三角形有两条高是直角边,另一条在内部;钝角三角形有两条高在三角形外,另一条在内部。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十四章三角形中的边角关系
一、三角形的分类
1、按边分类:
2、按角分类:
不等边三角形直角三角形三角形三角形锐角三角形等腰三角形(等边三角形是特例)斜三角形钝角三角形
二、三角形的边角性质
1、三角形的三边关系:
三角形中任何两边的和大于第三边;任何两边的差小于第三边。
2、三角形的三角关系:
三角形内角和定理:三角形的三个内角的和等于180°。
三角形外角和定理:三角形的三个外角的和等于360°。
3三角形的外角性质
(1)三角形的一个外角等于与它不相邻的两个内角的和;
(2)三角形的一个外角大于与它不相邻的任何一个内角。
三、三角形的角平分线、中线和高
(说明:三角形的角平分线、中线和高都是线段)
四、命题
1、命题:凡是可以判断出真(正确)、假(错误)的语句叫做命题。
2、命题分类
真命题:正确的命题
命题假命题:错误的命题
3、互逆命题
4、反例:符合命题条件,但不满足命题结论的例子称为反例。
原命题:如果p,那么q;
逆命题:如果q,那么p。
(说明:交换一个命题的条件和结论就是它的逆命题。
)。
