(广西专用)2019年中考数学复习 第四章 图形的认识 4.4 多边形与平行四边形(试卷部分)课件
2019版中考数学总复习 第四章 图形的认识 4.4 多边形与平行四边形课件教学资料

=C
C
E ,CD=4,∴CE=
D
1
2 5
,∴S▱ABCD=2×
1·
2
BD·CE=24.
思路分析 先作出BD边上的高线,构造出Rt△CDE,应用三角函数,再利用平行四边形的面积 公式求出结果.
9.(2018济南,21,6分)如图,在平行四边形ABCD中,连接BD,E,F分别是DA和BC延长线上的点,且 AE=CF,连接EF交BD于点O. 求证:OB=OD.
∴ D E = E F ,∴ 4 = 2 ,
AE EB 12 EB
∴EB=6,∵CF=CB,CG⊥BF,
∴BG= 1 BF=2,
2
在Rt△BCG中,BC=8,BG=2, ∴根据勾股定理得,CG= =BC2=2BG,故2 选8C2. 22 1 5
审题技巧 题目中出现平行线和角平分线时,极易出现等腰三角形.
8.(2017临沂,18,3分)在平行四边形ABCD中,对角线AC,BD相交于点O.若AB=4,BD=10,sin∠BDC
= 3 ,则平行四边形ABCD的面积是
.
5
答案 24 解析 ∵四边形ABCD是平行四边形,∴CD=AB=4.
如图,过点C作CE⊥BD于E,在Rt△CDE中,∵sin∠EDC=
3 5
答案 C 设这个多边形的边数为n,由多边形内角和公式得(n-2)·180°=900°,解得n=7,即这个 多边形为七边形.故选C.
4.(2017青海西宁,13,2分)若正多边形的一个外角是40°,则这个正多边形的边数是
.
答案 9
解析 ∵正多边形的外角和为360°,∴正多边形的边数=360°÷40°=9,∴正多边形的边数为9.
4
∴GH=BD= 1 BC,
中考数学复习《多边形与平行四边形》

证明:∵BD垂直平分AC, ∴AB=BC,AD=DC.
在△ADB与△CDB中,
∴△ADB≌△CDB(SSS). ∴∠BCD=∠BAD. ∵∠BCD=∠ADF,∴∠BAD=∠ADF, ∴AB∥FD. ∵BD⊥AC,AF⊥AC,∴AF∥BD. ∴四边形ABDF是平行四边形.
考题再现
1. (2015广州)下列命题中,真命题的个数有 ( B )
(5)面积:①计算公式:S□=底×高=ah.
②平行四边形的对角线将四边形分成4个面积相等的三角形.
4. 平行四边形的判定 (1)定义法:两组对边分别平行的四边形是平行四边形. (2)两组对角分别相等的四边形是平行四边形. (3)两组对边分别相等的四边形是平行四边形. (4)对角线互相平分的四边形是平行四边形. (5)一组对边平行且相等的四边形是平行四边形. 5. 三角形中位线定理 (1)三角形的中位线:连接三角形两边的中点,所得线段叫 做该三角形的中位线. (2)三角形中位线定理:三角形的中位线平行于第三边并且 等于第三边的一半.
中考考点精讲精练
考点1 多边形的内角和与外角和
考点精讲
【例1】(2016临沂)一个正多边形的内角和为540°,则这
个正多边形的每一个外角等于
()
A. 108°
B. 90°
C. 72° D. 60°
思路点拨:首先设此多边形为n边形,根据题意,得180·
(n-2)=540,即可求得n=5,再由多边形的外角和等于360°,
5. (2016梅州)如图1-4-6-6,平行
四边形ABCD中,BD⊥AD,∠A=45°, E,F分别是AB,CD上的点,且BE=DF, 连接EF交BD于点O. (1)求证:BO=DO; (2)若EF⊥AB,延长EF交AD的延长线于点G,当FG=1时,求 AE的长.
广西南宁2019中考试题-数学(解析版)

广西南宁2019中考试题-数学(解析版)【一】选择题〔共12小题,每题3分,总分值36分〕1、4的倒数是〔D〕A 、4-B 、4C 、14-D 、14【考点】倒数、【专题】计算题、【分析】依照倒数的定义:乘积是1的两个数,即可求解、【解答】解:4的倒数是14、应选D 、【点评】此题要紧考查了倒数的定义,正确理解定义是解题关键、2、如图是由六个小正方体组合而成的一个立体图形,它的主视图是〔B〕A 、B 、C 、D 、【考点】考点:简单组合体的三视图、【专题】【分析】找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中、【解答】解:从正面看易得第一层有3个正方形,第二层中间有2个正方形、应选B 、【点评】此题考查了三视图的知识,主视图是从物体的正面看得到的视图、考查了学生们的空间想象能力、3、芝麻作为食品和药物,均广泛使用、经测算,一粒芝麻约有0.00000201千克,用科学记数法表示为〔A〕A 、2.01×10-6千克B 、0.201×10-5千克C 、20.1×10-7千克D 、2.01×10-7千克【考点】科学记数法—表示较小的数、【专题】【分析】绝对值小于1的正数也能够利用科学记数法表示,一般形式为a ×10-n ,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定、【解答】解:0.00000201=2.01×10-6。
应选A 、【点评】此题考查了用科学记数法表示较小的数,一般形式为a ×10-n ,其中1≤|a|<10,n 为由原数左边起第一个不为零的数字前面的0的个数所决定、4、以下图形中,既是轴对称图形又是中心对称图形的是〔A〕A、B、C、D、【考点】考点:中心对称图形;轴对称图形、【专题】常规题型、【分析】依照中心对称图形的定义:旋转180°后能够与原图形完全重合即是中心对称图形;轴对称图形的定义:假如一个图形沿一条直线折叠,直线两旁的部分能够互相重合,那个图形叫做轴对称图形,这条直线叫做对称轴,即可判断出答案、【解答】解:A、此图形是中心对称图形,也是轴对称图形,故此选项正确;B、此图形不是中心对称图形,也不是轴对称图形,故此选项错误;C、此图形是中心对称图形,不是轴对称图形,故此选项错误;D、此图形不是中心对称图形,是轴对称图形,故此选项错误、应选A、【点评】此题要紧考查了中心对称图形与轴对称的定义,解题关键是找出图形的对称中心与对称轴,属于基础题,比较容易解答、5、以下调查:①调查一批灯泡的使用寿命;②调查全班同学的身高;③调查市场上某种食品的色素含量是否符合国家标准;④企业招聘,对应聘人员进行面试、其中符合用抽样调查的是〔B〕A、①②B、①③C、②④D、②③【考点】全面调查与抽样调查、【专题】【分析】此题需要依照具体情况正确选择普查或抽样调查等方法,并理解有些调查是不适合使用普查方法的、【解答】解:①调查一批灯泡的使用寿命,适合抽样调查;②调查全班同学的身高,适合全面调查;③调查市场上某种食品的色素含量是否符合国家标准,适合抽样调查;④企业招聘,对应聘人员进行面试,适合全面调查;应选B、【点评】此题要紧考查了全面调查和抽样调查,在解题时选择普查依旧抽样调查要依照所要考查的对象的特征灵活选用是此题的关键、6、如图,在平行四边形ABCD中,AB=3cm,BC=5cm,对角线AC,BD相交于点O,那么OA的取值范围是〔C〕A、2cm<OA<5cmB、2cm<OA<8cmC、1cm<OA<4cmD、3cm<OA<8cm【考点】平行四边形的性质;三角形三边关系、【专题】【分析】由在平行四边形ABCD中,AB=3cm,BC=5cm,依照平行四边形对角线互相平分与三AC,2cm<AC<8cm,继而求得OA的取值范围、角形三边关系,即可求得OA=OC=12【解答】解:∵平行四边形ABCD中,AB=3cm,BC=5cm,AC,2cm<AC<8cm,∴OA=OC=12∴1cm<OA<4cm、应选C、【点评】此题考查了平行四边形的性质与三角形三边关系、此题比较简单,注意数形结合思想的应用,注意掌握平行四边形对角线互相平分定理的应用、7、假设点A〔2,4〕在函数y=kx-2的图象上,那么以下各点在此函数图象上的是〔A〕A、〔1,1〕B、〔-1,1〕C、〔-2,-2〕D、〔2,-2〕【考点】一次函数图象上点的坐标特征、【专题】探究型、【分析】将点A〔2,4〕代入函数解析式求出k的值,再把各点的坐标代入解析式,逐一检验即可、【解答】解:∵点A〔2,4〕在函数y=kx-2的图象上,∴2k-2=4,解得k=3,∴此函数的解析式为:y=3x-2,A、∵3×1-2=1,∴此点在函数图象上,故本选项正确;B、∵3×〔-1〕-2=-5≠1,∴此点在不函数图象上,故本选项错误;C、∵3×〔-2〕-2=-7≠-2,∴此点在不函数图象上,故本选项错误;D、∵3×2-2=4≠-2,∴此点在不函数图象上,故本选项错误、应选A、【点评】此题考查的是一次函数图象上点的坐标特点,即一次函数图象上各点的坐标一定适合此函数的解析式、8、以下计算正确的选项是〔C〕A、〔m-n〕2=m2-n2B、〔2ab3〕2=2a2b6C、2xy+3xy=5xyD=2【考点】二次根式的性质与化简;合并同类项;幂的乘方与积的乘方;完全平方公式、【专题】推理填空题、【分析】依照完全平方公式即可判断A;依照积的乘方和幂的乘方,求出式子的结果,即可判断B;依照合并同类项法那么求出后即可判断C;依照二次根式的性质求出后即可判断D、【解答】解:A、〔m-n〕2=m2-2mn+n2,故本选项错误;B、〔2ab3〕2=4a2b6,故本选项错误;C、2xy+3xy=5xy,故本选项正确;D、=应选C、【点评】此题考查了二次根式的性质,合并同类项,幂的乘方和积的乘方,完全平方公式的应用,题目比较典型,然而一道比较容易出错的题目、要紧考查学生的辨析能力和计算能力、9、如图,在平面直角坐标系中,有两条位置确定的抛物线,它们的对称轴相同,那么以下关系不正确的选项是〔A〕A、k=nB、h=mC、k<nD、h<0,k<0【考点】二次函数的性质、【专题】【分析】借助图象找出顶点的位置,判断顶点横坐标、纵坐标大小关系、【解答】解:依照二次函数解析式确定抛物线的顶点坐标分别为〔h ,k 〕,〔m ,n 〕,因为点〔h ,k 〕在点〔m ,n 〕的下方,因此k=n 不正确、应选A 、【点评】此题是抛物线的顶点式定义在图形中的应用、能直截了当依照函数的解析式说出其顶点坐标是解决此题的关键、10、某单位要组织一次篮球联赛,赛制为单循环形式〔每两队之间都赛一场〕,计划安排10场竞赛,那么参加竞赛的球队应有〔C〕A 、7队B 、6队C 、5队D 、4队【考点】一元二次方程的应用、【分析】设邀请x 个球队参加竞赛,那么第一个球队和其他球队打〔x-1〕场球,第二个球队和其他球队打〔x-2〕场,以此类推能够明白共打〔1+2+3+…+x-1〕场球,然后依照计划安排15场竞赛即可列出方程求解、【解答】解:设邀请x 个球队参加竞赛,依题意得1+2+3+…+x-1=10, 即(1)102x x -=,∴x 2-x-20=0,∴x=5或x=-4〔不合题意,舍去〕、应选C 、【点评】此题和实际生活结合比较紧密,准确找到关键描述语,从而依照等量关系准确的列出方程是解决问题的关键、此题还要判断所求的解是否符合题意,舍去不合题意的解、11、如图,在等腰直角三角形ABC 中,AB=AC=8,O 为BC 的中点,以O 为圆心作半圆,使它与AB ,AC 都相切,切点分别为D ,E ,那么⊙O 的半径为〔D〕A 、8B 、6C 、5D 、4【考点】切线的性质;等腰直角三角形、【专题】【分析】首先连接OA ,OD ,由AB ,AC 都与⊙O 相切,依照切线长定理与切线的性质,即可得∠BAO=∠CAO ,OD ⊥AB ,又由在等腰直角三角形ABC 中,AB=AC=8,易得∠B=45°,OA ⊥BC ,继而利用三角函数,即可求得⊙O 的半径、【解答】解:连接OA ,OD ,∵AB ,AC 都与⊙O 相切,∴∠BAO=∠CAO ,OD ⊥AB ,∵在等腰直角三角形ABC 中,AB=AC=8,∴AO ⊥BC ,∴∠B=∠BAO=45°,∴OB=AB •cos ∠B=8×2=∴在Rt △OBD 中,OD=OB •sin ∠B=42=、 应选D 、【点评】此题考查了切线的性质、切线长定理以及等腰直角三角形性质、此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用、12、二次函数y=ax2+bx+1,一次函数y=k 〔x-1〕-k24,假设它们的图象关于任意的非零实数k 都只有一个公共点,那么a ,b 的值分别为〔B〕A 、a=1,b=2B 、a=1,b=-2C 、a=-1,b=2D 、a=-1,b=-2【考点】二次函数的性质;根的判别式、【专题】【分析】依照题意由y=ax 2+bx+c ①,y=k 〔x-1〕-24k ②,组成的方程组只有一组解,消去y ,整理得,ax 2+〔b-k 〕x+1+24k =0,那么△=〔b-k 〕2-4a 〔1+k+24k 〕=0,整理得到〔1-a 〕k 2-2〔2a+b 〕k+b 2-4a=0,由于关于任意的实数k 都成立,因此有1-a=0,2a+b=0,b 2-4a=0,求出a ,b 即可、【解答】解:依照题意得,y=ax 2+bx+1①,y=k 〔x-1〕-24k ②,解由①②组成的方程组,消去y ,整理得,ax 2+〔b-k 〕x+1+k+24k =0, ∵它们的图象关于任意的实数k 都只有一个公共点,那么方程组只有一组解,∴x 有两相等的值,即△=〔b-k 〕2-4a 〔1+k+24k 〕=0, ∴〔1-a 〕k 2-2〔2a+b 〕k+b 2-4a=0,由于关于任意的实数k 都成立,因此有1-a=0,2a+b=0,b 2-4a=0,∴a=1,b=-2,应选B 、【点评】此题考查了用待定系数法求抛物线的解析式、二次函数的一般式:y=ax 2+bx+c 〔a≠0〕;也考查了利用方程组的解的情况确定函数图象交点的问题,而方程组的解的情况转化为一元二次方程根的情况、【二】填空题〔共6小题,每题3分,总分值18分〕13、如下图,用直尺和三角尺作直线AB ,CD ,从图中可知,直线AB 与直线CD 的位置关系为AB ∥CD 、【考点】平行线的判定、【专题】【分析】依照同位角相等,两直线平行判断、【解答】解:依照题意,∠1与∠2是三角尺的同一个角,因此∠1=∠2,因此,AB∥CD〔同位角相等,两直线平行〕、故答案为:AB∥CD、【点评】此题考查了平行线的判定熟练掌握同位角相等,两直线平行,并准确识图是解题的关键、14、在学校艺术节文艺汇演中,甲、乙两个舞蹈队队员的身高的方差分别是S甲2=1.5,S乙2=2.5,那么身高更整齐的是甲队〔填“甲”或“乙”〕、【考点】方差、【专题】【分析】方差是用来衡量一组数据波动大小的量,故由甲乙的方差可作出判断、【解答】解:由于S甲2<S乙2,那么甲队中身高更整齐、∴两队中身高更整齐的是甲队、故答案为:甲、【点评】此题考查方差的意义、方差是用来衡量一组数据波动大小的量,方差越大,说明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,说明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定15、分解因式:ax2-4ax+4a=a〔x-2〕2、【考点】提公因式法与公式法的综合运用、【专题】【分析】先提取公因式a,再利用完全平方公式进行二次分解、【解答】解:ax2-4ax+4a,=a〔x2-4x+4〕,=a〔x-2〕2、【点评】此题考查了提公因式法,公式法分解因式,提取公因式后利用完全平方公式进行二次分解,注意要分解完全、16、如图,点B,A,C,D在⊙O上,OA⊥BC,∠AOB=50°,那么∠ADC=25°、【考点】圆周角定理;垂径定理、【专题】【分析】由OA⊥BC,利用垂径定理,即可求得=AB AC,又由在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半,即可求得答案、【解答】解:∵OA⊥BC,∴=AB AC,∴∠ADC=12∠AOB=12×50°=25°、故答案为:25、【点评】此题考查了圆周角定理与垂径定理、此题难度不大,注意掌握在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半与平分弦的直径平分这条弦,同时平分弦所对的两条弧定理的应用、17、如图,函数y=x-2和y=-2x+1的图象交于点P ,依照图象可得方程组221x y x y -=⎧⎨+=⎩的解是11x y =⎧⎨=-⎩、【考点】一次函数与二元一次方程〔组〕、【专题】推理填空题、【分析】先由图象得出两函数的交点坐标,依照交点坐标即可得出方程组的解、【解答】解:∵由图象可知:函数y=x-2和y=-2x+1的图象的交点P 的坐标是〔1,-1〕,又∵由y=x-2,移项后得出x-y=2,由y=-2x+1,移项后得出2x+y=1,∴方程组221x y x y -=⎧⎨+=⎩的解是11x y =⎧⎨=-⎩, 故答案为:11x y =⎧⎨=-⎩、【点评】此题考查了一次函数与二元一次方程组的应用,要紧考查学生的观看图形的能力和理解能力,题目具有一定的代表性,是一道比较好但又比较容易出错的题目、18、有假设干张边长基本上2的四边形纸片和三角形纸片,从中取一些纸片按如下图的顺序拼接起来〔排在第一位的是四边形〕,能够组成一个大的平行四边形或一个大的梯形、假如所取的四边形与三角形纸片数的和是5时,那么组成的大平行四边形或梯形的周长是20;假如所取的四边形与三角形纸片数的和是n ,那么组成的大平行四边形或梯形的周长是3n+5或3n+4、【考点】规律型:图形的变化类、【专题】【分析】第1张纸片的周长为8,由2张纸片所组成的图形的周长比第1张纸片的周长增加了2、由3张纸片所组成的图形的周长比前2张纸片所组成的图形的周长增加了4,按此规律可知:①纸张张数为1,图片周长为8=3×1+5;纸张张数为3,图片周长为8+2+4=3×3+5;纸张张数为5,图片周长为8+2+4+2+4=3×5+5;…;当n 为奇数时,组成的大平行四边形或梯形的周长为3n+5;②纸张张数为1,图片周长为8+2=3×2+4;纸张张数为4,图片周长为8+2+4+2=3×4+4;纸张张数为6,图片周长为8+2+4+2+4+2=3×6+4;…;当n 为偶数时,组成的大平行四边形或梯形的周长为3n+4、【解答】解:从图形可推断:纸张张数为5,图片周长为8+2+4+2+4=3×5+5=20;当n 为奇数时,组成的大平行四边形或梯形的周长为:8+2+4+…+2+4=3n+5;当n 为偶数时,组成的大平行四边形或梯形的周长为:8+2+…+4+2=3n+4、综上,组成的大平行四边形或梯形的周长为3n+5或3n+4、故答案为:20,3n+5或3n+4、【点评】此题考查了规律型:图形的变化,解题的关键是将纸片的张数分奇偶两种情况进行讨论,得出组成的大平行四边形或梯形的周长、【三】解答题〔共8小题,总分值66分〕19、计算:0201264sin 45(1)-+-、【考点】实数的运算;特别角的三角函数值、【专题】计算题、【分析】分别运算绝对值、二次根式的化简,然后代入sin45°的值,继而合并运算即可、【解答】解:原式64172=+⨯+=、 【点评】此题考查了实数的运算及特别角的三角函数值,属于基础题,特别角的三角函数值是需要我们熟练经历的内容、20、解不等式组2132(1)4x x x x <+⎧⎨--≤⎩,并把解集在数轴上表示出来、【考点】解一元一次不等式组;不等式的性质;在数轴上表示不等式的解集;解一元一次不等式、【专题】计算题、【分析】求出每个不等式的解集,依照找不等式组解集的规律找出即可、【解答】解:2132(1)4x x x x <+⎧⎨--≤⎩①②, ∵解不等式①得:x >-1,解不等式②得:x ≤2,∴不等式组的解集为:-1<x ≤2, 在数轴上表示不等式组的解集为:、【点评】此题考查了不等式的性质,解一元一次不等式〔组〕,在数轴上表示不等式的解集的应用,关键是能依照不等式的解集找出不等式组的解集,题型较好,难度适中、 21、2018年6月5日是“世界环境日”,南宁市某校进行了“绿色家园”演讲竞赛,赛后整理参赛同学的成绩,制作成直方图〔如图〕、〔1〕分数段在85~90范围的人数最多;〔2〕全校共有多少人参加竞赛?〔3〕学校决定选派本次竞赛成绩最好的3人参加南宁市中学生环保演讲决赛,并为参赛选手预备了红、蓝、白颜色的上衣各1件和2条白色、1条蓝色的裤子、请用“列表法”或“树形图法”表示上衣和裤子搭配的所有可能出现的结果,并求出上衣和能搭配成同一种颜色的概率、【考点】频数〔率〕分布直方图;列表法与树状图法、【专题】【分析】〔1〕由条形图可直截了当得出人数最多的分数段;〔2〕把各小组人数相加,得出全校参加竞赛的人数;〔3〕利用“树形图法”,画出搭配方案,由此可求上衣和裤子能搭配成同一种颜色的概率、【解答】解:〔1〕由条形图可知,分数段在85~90范围的人数最多为10人,故答案为:85~90;〔2〕全校参加竞赛的人数=5+10+6+3=24人;〔3〕上衣和裤子搭配的所有可能出现的结果如下图,共有9总搭配方案,其中,上衣和裤子能搭配成同一种颜色的有3种, 上衣和裤子能搭配成同一种颜色的概率为:3193、 【点评】此题考查读频数分布直方图的能力和利用统计图猎取信息的能力;利用统计图猎取信息时,必须认真观看、分析、研究统计图,才能作出正确的判断和解决问题22、如下图,∠BAC=∠ABD=90°,AC=BD ,点O 是AD ,BC 的交点,点E 是AB 的中点、〔1〕图中有哪几对全等三角形?请写出来;〔2〕试判断OE 和AB 的位置关系,并给予证明、【考点】全等三角形的判定与性质、【专题】【分析】〔1〕依照全等三角形的定义能够得到:△ABC ≌△BAD ,△AOE ≌△BOE ,△AOC ≌△BOD ;〔2〕首先证得:△ABC ≌△BAD ,那么OA=OB ,利用等腰三角形中:等边对等角即可证得OE ⊥AB 、【解答】解:〔1〕△ABC ≌△BAD ,△AOE ≌△BOE ,△AOC ≌△BOD ;〔2〕OE ⊥AB 、理由如下:∵在Rt △ABC 和Rt △BAD 中,AC=BD ,∠BAC=∠ABD ,AB=BA ,∴△ABC ≌△BAD ,∴∠DAB=∠CBA ,∴OA=OB ,∵点E 是AB 的中点,∴OE ⊥AB 、【点评】此题考查了全等三角形的判定与性质,以及三线合一定理,正确证明△ABC ≌△BAD是关键、23、如图,山坡上有一棵树AB ,树底部B 点到山脚C 点的距离BC 为为30°、小宁在山脚的平地F 处测量这棵树的高,点C 到测角仪EF 的水平距离CF=1米,从E 处测得树顶部A 的仰角为45°,树底部B 的仰角为20°,求树AB 的高度、〔参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36〕【考点】解直角三角形的应用-仰角俯角问题;解直角三角形的应用-坡度坡角问题、【专题】【分析】首先在直角三角形BDC 中求得DC 的长,然后求得DF 的长,进而求得GF 的长,然后在直角三角形BGF 中即可求得BG 的长,从而求得树高、【解答】解:∵底部B 点到山脚C 点的距离BC 为63米,山坡的坡角为30°、∴DC=BC •cos30°=9==米, ∵CF=1米,∴DC=9+1=10米,∴GE=10米,∵∠AEG=45°,∴AG=EG=10米,在直角三角形BGF 中,BG=GF •tan20°=10×0.36=3.6米,∴AB=AG-BG=10-3.6=6.4米,答:树高约为6.4米、【点评】此题考查了解直角三角形的应用,要求学生借助俯角构造直角三角形,并结合图形利用三角函数解直角三角形、24、南宁市某生态示范村种植基地计划用90亩~120亩的土地种植一批葡萄,原计划总产量要达到36万斤、〔1〕列出原计划种植亩数y 〔亩〕与平均每亩产量x 〔万斤〕之间的函数关系式,并写出自变量x 的取值范围;〔2〕为了满足市场需求,现决定改良葡萄品种、改良后平均每亩产量是原计划的1.5倍,总产量比原计划增加了9万斤,种植亩数减少了20亩,原计划和改良后的平均每亩产量各是多少万斤?【考点】反比例函数的应用、【专题】【分析】〔1〕直截了当依照亩产量、亩数及总产量之间的关系得到函数关系式即可;〔2〕依照题意列出36369201.5x x+-=后求解即可、 【解答】解:〔1〕由题意知:xy=36, 故36y x =〔310≤x ≤25〕 〔2〕依照题意得:36369201.5x x +-= 解得:x=0.3经检验:0.3x =是原方程的根1.5x=0.45答:改良前亩产0.3万斤,改良后亩产0.45万斤、【点评】此题考查了反比例函数的应用,解题的关键是从复杂的实际问题中整理出反比例函数模型,并利用其解决实际问题、25、如图,矩形纸片ABCD ,AD=2,AB=4、将纸片折叠,使顶点A 与边CD 上的点E 重合,折痕FG分别与AB,CD交于点G,F,AE与FG交于点O、〔1〕如图1,求证:A,G,E,F四点围成的四边形是菱形;〔2〕如图2,当△AED的外接圆与BC相切于点N时,求证:点N是线段BC的中点;〔3〕如图2,在〔2〕的条件下,求折痕FG的长、【考点】翻折变换〔折叠问题〕;菱形的判定、【专题】综合题。
2019年中考数学第四章图形的认识4.4多边形与平行四边形(讲解部分)素材

答案 B 思路分析 依据平行四边形的定义或判定定理进行判断. 变式训练 2 (2017 湖北咸宁,18,7 分) 如图,点 B、E、C、F 在一条直线上,AB = DF,AC = DE,BE = FC. (1) 求证:△ABC≌△DFE; (2) 连接 AF、BD,求证:四边形 ABDF 是平行四边形.
边形.多边形相邻两边所组成的角叫做多边形的内角,多边形的
角的一边与另一边的反向延长线所组成的角叫做多边形的外角.
同一顶点处的内角与外角互为① 邻补角 .
2.n 边形的内角和为② (n-2)×180° ,外角和为③ 360° .
3.在平面内,各内角都相等,④
ABCDE 中,AC 与 BE 相交于点 F,则∠AFE 的度数为 .
答案 72°
解析 ∵ 五边形 ABCDE 是正五边形,
∴
∠EAB
= ∠ABC
=
(5-2) ×180° 5
=
108°,
∵ BA = BC,∴ ∠BAC = ∠BCA = 36°,
同理可得∠ABE = 36°,∴ ∠AFE = ∠ABF + ∠BAF = 36° + 36° = 72°.
§ 4.4 多边形与平行四边形
第四章 图形的认识 2 9
98
������������������������������������������������������������������������������������������������������
考点一 多边形
1.在平面内,由一些线段首尾顺次相接组成的图形叫做多
������������������������������������������������������������������������������������������������������������������������������������������������������������������
2019届中考数学复习第四章图形的认识4.4多边形与平行四边形试卷部分课件

6.(2015天津,17,3分)如图,在正六边形ABCDEF中,连接对角线AC,BD,CE,DF,EA,FB,可以得到 一个六角星.记这些对角线的交点分别为H,I,J,K,L,M,则图中等边三角形共有 个.
答案 8 解析 题图中的等边三角形可分为两大类:第一类:分别以B,A,F,E,D,C为顶点的小等边三角
7.(2018湖北黄冈,20,8分)如图,在▱ABCD中,分别以边BC,CD作等腰△BCF,△CDE,使BC=BF, CD=DE,∠CBF=∠CDE,连接AF,AE.
(1)求证:△ABF≌△EDA;
(2)延长AB与CF相交于点G.若AF⊥AE,求证:BF⊥BC.
证明 (1)∵四边形ABCD是平行四边形,∴AB=CD=DE,BF=BC=AD,∠ABC=∠ADC, 又∠CBF=∠CDE,∴∠ABF=∠ADE,
1 2
答案 15
解析 由作图知AQ平分∠DAB,在▱ABCD中,AB∥CD,所以∠DAQ=∠BAQ=∠DQA,所以DQ
=DA=BC=3.因为DQ=2QC,所以DC=4.5,所以平行四边形ABCD的周长为2×(4.5+3)=15.
5.(2017湖北武汉,13,3分)如图,在▱ABCD中,∠D=100°,∠DAB的平分线AE交DC于点E,连接 BE.若AE=AB,则∠EBC的度数为 .
360 30
)
答案 B 由题意得,该正多边形的每个外角均为30°,则该正多边形的边数是 =12.故选B.
4.(2016湖南长沙,4,3分)六边形的内角和是 ( A.540° B.720°
)
C.900°
D.360°
答案 B ∵n边形的内角和是(n-2)· 180°,∴六边形的内角和为(6-2)×180°=720°,故选B.
中考总复习:多边形与平行四边形--知识讲解(基础)
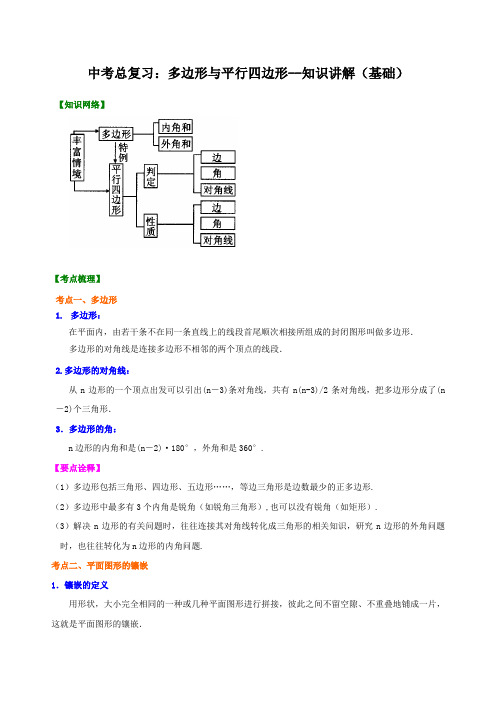
中考总复习:多边形与平行四边形--知识讲解(基础)【知识网络】【考点梳理】考点一、多边形1.多边形:在平面内,由若干条不在同一条直线上的线段首尾顺次相接所组成的封闭图形叫做多边形.多边形的对角线是连接多边形不相邻的两个顶点的线段.2.多边形的对角线:从n边形的一个顶点出发可以引出(n-3)条对角线,共有n(n-3)/2条对角线,把多边形分成了(n -2)个三角形.3.多边形的角:n边形的内角和是(n-2)·180°,外角和是360°.【要点诠释】(1)多边形包括三角形、四边形、五边形……,等边三角形是边数最少的正多边形.(2)多边形中最多有3个内角是锐角(如锐角三角形),也可以没有锐角(如矩形).(3)解决n边形的有关问题时,往往连接其对角线转化成三角形的相关知识,研究n边形的外角问题时,也往往转化为n边形的内角问题.考点二、平面图形的镶嵌1.镶嵌的定义用形状,大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,这就是平面图形的镶嵌.2.平面图形的镶嵌(1)一个多边形镶嵌的图形有:三角形,四边形和正六边形;(2)两个多边形镶嵌的图形有:正三角形和正方形,正三角形和正六边形,正方形和正八边形,正三角形和正十二边形;(3)三个多边形镶嵌的图形一般有:正三角形、正方形和正六边形,正方形、正六边形和正十二边形,正三角形、正方形和正十二边形.【要点诠释】能镶嵌的图形在一个拼接点处的特点:几个图形的内角拼接在一起时,其和等于360°,并使相等的边互相重合.考点三、三角形中位线定理1.连接三角形两边中点的线段叫做三角形的中位线.2.定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.考点四、平行四边形的定义、性质与判定1.定义:两组对边分别平行的四边形是平行四边形.2.性质:(1)平行四边形的对边平行且相等;(2)平行四边形的对角相等,邻角互补;(3)平行四边形的对角线互相平分;(4)平行四边形是中心对称图形,对角线的交点是它的对称中心.3.判定:(1)两组对边分别平行的四边形是平行四边形;(2)两组对边分别相等的四边形是平行四边形;(3)一组对边平行且相等的四边形是平行四边形;(4)两组对角分别相等的四边形是平行四边形;(5)对角线互相平分的四边形是平行四边形.4.两条平行线间的距离:定义:夹在两条平行线间最短的线段的长度叫做两条平行线间的距离.性质:夹在两条平行线间的平行线段相等.【要点诠释】1.平行四边形的面积=底×高;2.同底(等底)同高(等高)的平行四边形面积相等.【典型例题】类型一、多边形与平面图形的镶嵌1.如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP、CP分别平分∠EDC、∠BCD,则∠P的度数是()A.60° B.65° C.55° D.50°【思路点拨】根据五边形的内角和等于540°,由∠A+∠B+∠E=300°,可求∠BCD+∠CDE的度数,再根据角平分线的定义可得∠PDC与∠PCD的角度和,进一步求得∠P的度数.【答案】A【解析】解:∵五边形的内角和等于540°,∠A+∠B+∠E=300°,∴∠BCD+∠CDE=540°﹣300°=240°,∵∠BCD、∠CDE的平分线在五边形内相交于点O,∴∠PDC+∠PCD=(∠BCD+∠CDE)=120°,∴∠P=180°﹣120°=60°.故选:A.【总结升华】本题主要考查了多边形的内角和公式,角平分线的定义,熟记公式是解题的关键.注意整体思想的运用.举一反三:【变式】如图,小林从P点向西直走12米后,向左转,转动的角度为α,再走12米,如此重复,小林共走了108米回到点P,则α=_________.【答案】40°.2.现有边长相同的正三角形、正方形和正六边形纸片若干张,下列拼法中不能镶嵌成一个平面图案的是( )A.正方形和正六边形 B.正三角形和正方形C.正三角形和正六边形 D.正三角形、正方形和正六边形【思路点拨】注意各正多边形的内角度数.【答案】A.【解析】正方形和正六边形的每个内角分别为90°和120°,要镶嵌则需要满足90°m+120°n=360°,但是m、n没有正整数解,故选A.【总结升华】能镶嵌的图形在一个拼接点处的特点:几个图形的内角拼接在一起时,其和等于360°,并使相等的边互相重合.举一反三:【变式】现有四种地面砖,它们的形状分别是:正三角形、正方形、正六边形、正八边形,且它们的边长都相等.同时选择其中两种地面砖密铺地面,选择的方式有( )A.2种 B.3种 C.4种 D.5种【答案】 B.类型二:平行四边形及其他知识的综合运用3.如图,已知在▭ABCD中,对角线AC、BD相交于点O,AE⊥BD,BM⊥AC、DN⊥AC,CF⊥BD垂足分别是E、M、N、F,求证:EN∥MF.【思路点拨】连接ME,FN,由四边形ABCD为平行四边形,得到对角线互相平分,利用AAS得到三角形AOE与三角形COF全等,利用全等三角形对应边相等得到OE=OF,同理得到三角形BOM与三角形DON全等,得到OM=ON,进而确定出四边形MEFN为平行四边形,利用平行四边形的对边平行即可得证.【答案与解析】证明:连接ME,FN,∵四边形ABCD为平行四边形,∴OA=OC,OB=OD,∵AE⊥BD,CF⊥BD,在△AOE和△COF中,,∴△AOE≌△COF(AAS),∴OE=OF,同理△BOM≌△DON,得到OM=ON,∴四边形EMFN为平行四边形,∴EN∥MF.【总结升华】此题考查了平行四边形的判定与性质,熟练掌握平行四边形的判定与性质是解本题的关键.4.如图所示,△ABC中,∠BAC=90°,延长BA到D,使,点E、F分别为边BC、AC 的中点.(1)求证:DF=BE;(2)过点A作AG∥BC,交DF于G,求证:AG=DG.【思路点拨】(1)E、F分别为BC、AC中点,则EF为△ABC的中位线,所以EF∥AB,.而.则EF=AD.从而易证△DAF≌△EFC, 则DF=CE=BE.(2) AG与DG在同一个三角形中,只需证∠D=∠DAG即可.【答案与解析】(1)∵点E、F分别为BC、AC的中点,∴ EF是△ABC的中位线.∴ EF∥AB,.又∵,∴ EF=AD.∵ EF∥AB,∴∠EFC=∠BAC=90°,∵∠BAC=90°,∴∠DAF=90.又∵ F是AC的中点,∴AF=CF,∴△DAF≌△EFC.∴DF=EC=BE.(2)由(1)知∵△DAF≌△EFC,∴∠D=∠FEC.又∵ EF∥AB,∴∠B=∠FEC.又∵ AG∥BC,∴∠DAG=∠B,∴∠ DAG=∠FEC∴∠D=∠DAG.∴AG=DG.【总结升华】三角形中位线定理的作用:位置关系——可以证明两条直线平行;数量关系——可以证明线段的相等或倍分.此外应注意三角形共有三条中位线,并且它们又重新构成一个新的三角形.举一反三:【变式】如图,已知P、R分别是长方形ABCD的边BC、CD上的点,E、F分别是PA、PR的中点,点P在BC上从B向C移动,点R不动,那么下列结论成立的是()A.线段EF的长逐渐增大B.线段EF的长逐渐变小C.线段EF的长不变D.无法确定【答案】C.5.如图:六边形ABCDEF中,AB平行且等于ED,AF平行且等于CD,BC平行且等于FE,对角线FD ⊥BD.已知FD=4cm,BD=3cm.则六边形ABCDEF的面积是_________cm2.【思路点拨】连接AC交BD于G,AE交DF于H.根据一组对边平行且相等的四边形是平行四边形,得平行四边形AEDB和AFDC.易得AC=FD,EH=BG.计算该六边形的面积可以分成3部分计算,即平行四边形AFDC的面积+三角形ABC的面积+三角形EFD的面积.【答案与解析】连接AC交BD于G,AE交DF于H.∵AB平行且等于ED,AF平行且等于CD,∴四边形AEDB是平行四边形,四边形AFDC是平行四边形,∴AE=BD,AC=FD,∵FD⊥BD,∴∠GDH=90°,∴四边形AHDG是矩形,∴AH=DG∵EH=AE-AH,BG=BD-DG∴EH=BG.∴六边形ABCDEF的面积=平行四边形AFDC的面积+三角形ABC的面积+三角形EFD的面积=FD•BD=3×4=12cm2.故答案为:12.【总结升华】注意求不规则图形的面积可以分割成规则图形,根据面积公式进行计算.6 .已知平行四边形ABCD,对角线AC和BD相交于点O,点P在边AD上,过点P作PE⊥AC,PF⊥BD,垂足分别为E、F,PE=PF.(1)如图,若3,EO=1,求∠EPF的度数;(2)若点P是AD的中点,点F是DO的中点,BF=BC+32-4,求BC的长.【思路点拨】(1)连接PO,利用解直角三角形求出∠EPO=30°,再利用“HL”证明△PEO和△PFO全等,根据全等三角形对应角相等可得∠FPO=∠EPO,从而得解;(2)根据三角形中位线定理可得PF∥AO,且PF=12AO,然后根据两直线平行,同位角相等可得∠AOD=∠PFD=90°,再根据同位角相等,两直线平行可得PE∥OD,所以PE也是△AOD的中位线,然后证明四边形ABCD是正方形,根据正方形的对角线与边长的关系列式计算即可得解.【答案与解析】(1)如图,连接PO,∵PE⊥AC,PE=3,EO=1,∴tan∠EPO=3 EOPE=,∴∠EPO=30°,∵PE⊥AC,PF⊥BD,∴∠PEO=∠PFO=90°,在Rt△PEO和Rt△PFO中,PO PO PE PF=⎧⎨=⎩,∴Rt△PEO≌Rt△PFO(HL),∴∠FPO=∠EPO=30°,∴∠EPF=∠FPO+∠EPO=30°+30°=60°;(2)如图,∵点P是AD的中点,点F是DO的中点,∴PF ∥AO ,且PF=12AO , ∵PF ⊥BD ,∴∠PFD=90°, ∴∠AOD=∠PFD=90°,又∵PE ⊥AC ,∴∠AEP=90°,∴∠AOD=∠AEP ,∴PE ∥OD ,∵点P 是AD 的中点,∴PE 是△AOD 的中位线,∴PE=12OD , ∵PE=PF ,∴AO=OD ,且AO ⊥OD ,∴平行四边形ABCD 是正方形,设BC=x ,则x+12x ,∵ -4,∴x , 解得x=4,即BC=4.【总结升华】 本题考查了平行四边形的性质,三角形的中位线定理,正方形的判定与性质,(2)中判定出平行四边形ABCD 是正方形是解题的关键.举一反三:【变式】如图1,已知正比例函数和反比例函数的图象都经过点M (-2,-1),且P (-1,-2)是双曲线上的一点,Q 为坐标平面上的一动点,PA ⊥x 轴,QB ⊥y 轴,垂足分别为A 、B .(1)写出正比例函数和反比例函数的关系式;(2)当点Q 在直线MO 上运动时,是否可以使△OBQ 与△OAP 面积相等?(3)如图2,点Q 在第一象限中的双曲线上运动时,作以OP 、OQ 为邻边的平行四边形OPCQ ,求平行四边形OPCQ周长的最小值.图1 图2【答案】(1)正比例函数解析式为,反比例函数解析式为.(2)当点Q在直线MO上运动时,设点Q的坐标为,,解得.所以点Q的坐标为和.(3)因为P(,),由勾股定理得OP=,平行四边形OPCQ周长=.因为点Q在第一象限中的双曲线上,所以可设点Q的坐标为,由勾股定理可得,通过图形分析可得:OQ有最小值2,即当Q为第一象限中的双曲线与直线的交点时,线段OQ的长度最小.所以平行四边形OPCQ周长的最小值:.。
(广西专用)2019年中考数学复习 第四章 图形的认识 4.2 三角形及其全等(试卷部分)课件

答案 C 由题意知∠ACD=∠A+∠B=60°+40°=100°,因为CE平分∠ACD,所以∠ACE=∠ECD
= 1 ∠ACD= 1 ×100°=50°.
2
2
思路分析 由外角的性质可以求得∠ACD=100°,再由CE平分∠ACD可得∠ECD=50°.
2.(2018百色,5,3分)顶角为30°的等腰三角形三条中线的交点是该三角形的 ( ) A.重心 B.外心 C.内心 D.中心
AB
DE,
BC EF,
∴△ABC≌△DEF.
(2)∵∠A+∠B+∠BCA=180°,∠A=55°,∠B=88°,
∴∠BCA=180°-55°-88°=37°,
∵△ABC≌△DEF,
∴∠F=∠BCA=37°.
评析 本题考查了三角形全等的判定方法、全等三角形的对应角相等以及三角形内角和定 理.
AE∥BC,从而有∠EAC=∠C,故选项A、B、C均正确;因为AB>AC,所以∠ABC≠∠ACB,即∠
DAE≠∠EAC,故选项D错误,故选D.
思路分析 由作图痕迹可知,在三角形ABC的外角∠CAD内画了一个新角∠DAE,且∠DAE= ∠B,由此得到其他相关的结论.
5.(2016河池,4,3分)下列长度的三条线段不能组成三角形的是( ) A.5,5,10 B.4,5,6 C.4,4,4 D.3,4,5 答案 A ∵5+5=10,∴5,5,10不能组成三角形. 方法总结 判断能否组成三角形的简便方法是看较小的两条边长的和是否大于第三条边长.
A.50° B.70° C.75° D.80° 答案 B 因为直线DE是AC的垂直平分线,所以AD=DC,所以∠DAC=∠C=25°,所以∠ADC=1 80°-(25°+25°)=130°.因为∠ADC=∠B+∠BAD,所以∠BAD=∠ADC-∠B=130°-60°=70°,故选B.
2019年中考数学总复习第四章图形的认识4.4多边形与平行四边形(讲解部分)素材

又ȵ BE = DFꎬ
ʑ әGBEɸәHDF. ʑ øGEF = øHFEꎬ ʑ GEʊHFꎬ
ʑ GE = HFꎬøGEB = øHFDꎬ
ʑ 四边形 GEHF 是平行四边形.
㊀ ㊀ 1. 两组对边分别平行的四边形叫做平行四边形. (1) 平行四边形的两组对边分别平行ꎻ
易错清单
㊀ ㊀ 1. 对于平行四边形的判定必须准确掌握ꎬ 一些相关命题的 正确与否要看它是否符合平行四边形的定义ꎬ 是否符合平行四 边形的判定定理. 例㊀ 在四边形 ABCD 中ꎬAC 与 BD 交于点 Oꎬ 如果只给出条 一定是平行四边形. ㊀ ㊀ A.3 个 (6) 如果再加上条件 øDAB = øCBA ꎬ 那么四边形 ABCD 其中正确的说法有 B.4 个 C.5 个 (㊀ ㊀ )
99 数较为方便. 边形是正㊀ ㊀ ㊀ 边形. 例 1㊀ 若一个正多边形的一个内角等于 135ʎ ꎬ 那么这个多 解析㊀ 解法一:设有 n 条边ꎬ
方法一㊀ 确定多边形的相关参数的方法
㊀ ㊀ 求正多边形边数可以从两个角度考虑: 据条件列方程求解ꎻ
(1) 用多边形内角和公式:n 边形内角和 = ( n -2) ������180ʎ ꎬ 根 (2) 若容易求得外角的度数ꎬ则用多边形外角和为 360ʎ 求边
边形是平行四边形) .
ȵ 四边形 ABCD 是平行四边形ꎬʑ OB = ODꎬOA = OC. ʑ 四边形 BEDF 是平行四边形 ( 对角线互相平分的四边形
方法二㊀ 合理选择平行四边形的判定方法
㊀ ㊀ 根据平行四边形的性质可知ꎬ 利用平行四边形的性质是证 明边角相等的有效途径之一ꎬ因此ꎬ 解题时往往先判定一个四边 形是平行四边形ꎬ然后再利用性质解决问题ꎬ 至于使用哪种判定 方法ꎬ应依题目条件灵活确定.
