中考数学复习 第二单元 方程(组)与不等式(组)第7课时 一元二次方程及其应用同步训练
安徽地区中考数学复习第二单元方程组与不等式组第7课时一元二次方程及其应用教案

第二单元方程(组)与不等式(组)第7课时一元二次方程及其应用教学目标【考试目标】1.能够根据具体问题中的数量关系,列出一元二次方程.2.理解配方法,会用因式分解法、公式法、配方法解简单的数字系数的一元二次方程.3.会用一元二次方程根的判别式判别方程根的情况,了解一元二次方程根与系数的关系.【教学重点】1.了解一元二次方程的定义.2.学会一元二次方程的解法.3.熟悉一元二次方程根的判别式与根的关系.4.熟悉一元二次方程根与系数的关系.5.了解一元二次方程的实际应用.教学过程一、知识体系图引入,引发思考二、引入真题,深化理解【例1】(2016年山西)解方程:2(x -3)2=x 2-9.【解析】原方程可变形为2(x -3)2-(x 2-9)=0,即2(x -3)2-(x +3)(x -3)=0.提公因式可得,(x -3)[2(x -3)-(x +3)]=0,即(x -3)(x -9)=0.所以x 1=3,x 2=9.【考点】本题考查了一元二次方程的解法,主要考查了因式分解法的运用.此题的关键是发现公因式,找到公因式后,解决此题会方便很多.【例2】(2016年十堰)已知关于x 的方程(x -3)(x -2)-p 2=0.(1)求证:无论p 取何值时,方程总有两个不相等的实数根.(2)设方程的两根分别为x 1、x 2,且满足x 12+x 22=3x 1x 2,求实数p 的值.【解析】原方程写成一般式为:x 2-5x +6-p 2=0.(1)证明:∆=(-5)2-4×1×(6-p 2)=25-24+4p 2=4p 2+1.∵p 2≥0,∴∆≥1>0.∴无论p 取何值时,方程总有两个不相等的实根.(2)对x 12+x 22=3x 1x 2进行变形,左右两边同时加2x 1x 2得x 12+2x 1x 2+x 22=5x 1x 2,即(x 1+x 2)2=5x 1x 2.由题可知212125,6x x x x p +=⋅=-.代入得,25=30-5p 2.解得p 2=1,∴p = ±1.【考点】此题考查了根的判别式与根之间的关系,以及根与系数的关系、一元二次方程的解法.根与系数的关系、根的判别式与根之间的关系均需要把方程变为一般式.【例3】(2016年包头)一幅长20cm 、宽12cm 的图案,如图,其中有一横两竖的彩条,横竖彩条的宽度比为3:2,设竖彩条的宽度为x cm ,图案中三条彩带所占面积为y cm 2.(1)求y 与x 之间的函数关系式; (2)若图案中三条彩条所占的面积是图案面积的25,求横竖彩条的宽度.【解析】(1)∵横竖彩条的宽度比为3:2,∴横彩条的宽度为1.5x cm.一条竖彩条的面积为12x cm2,一条横彩条的面积为30x cm2.重合部分的面积为2x(1.5x)=3x2∴y=12x×2+30x-3x2.整理得y= -3x2+54x.(2)图案面积为20×12=240(cm2)由题意知y=96. 即-3x2+54x=96.整理得x2-18x+32=0. (x-2)(x-16)=0.∴x1=2,x2=16. 由图可知,x≤8,所以x2=16(舍去),∴x=2.∴横彩条的宽度为2cm.【考点】本题考查了一元二次方程的应用.同时还涉及了解一元二次方程的方法.三、师生互动,总结知识先小组内交流收获和感想,而后以小组为单位派代表进行总结.教师作以补充.课后作业布置作业:同步导练教学反思同学们对本节的内容理解挺到位,但是碰到题目还是很容易出错,希望大家勤加练习,做到熟练.。
中考数学 第一部分 考点研究复习 第二章 方程(组)与不等式(组)第7课时 一元二次方程及其应用真

江苏省2017年中考数学第一部分考点研究复习第二章方程(组)与不等式(组)第7课时一元二次方程及其应用真题精选(含解析)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(江苏省2017年中考数学第一部分考点研究复习第二章方程(组)与不等式(组)第7课时一元二次方程及其应用真题精选(含解析))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为江苏省2017年中考数学第一部分考点研究复习第二章方程(组)与不等式(组)第7课时一元二次方程及其应用真题精选(含解析)的全部内容。
第二章方程(组)与不等式(组)第7课时一元二次方程及其应用江苏近4年中考真题精选(2013~2016)命题点1 一元二次方程及其解法(2015年3次,2014年4次,2013年5次)1. (2016泰州14题3分)方程2x-4=0的解也是关于x的方程x2+mx+2=0的一个解,则m 的值为________.2. (2015徐州20(1)题5分)解方程:x2-2x-3=0。
3。
(2014泰州17(2)题6分)解方程:2x2-4x-1=0.命题点2 一元二次方程根的判别式及根与系数的关系(2016年5次,2015年7次,2014年6次,2013年3次)4。
(2014苏州7题3分)下列关于x的方程有实数根的是( )A。
x2-x+1=0 B. x2+x+1=0C. (x-1)(x+2)=0 D。
(x-1)2+1=05. (2016淮安14题3分)若关于x的一元二次方程x2+6x+k=0有两个相等的实数根,则k=________.6. (2016宿迁12题3分)若一元二次方程x2-2x+k=0有两个不相等的实数根,则k的取值范围是________.7。
人教版九年级数学第二单元《方程(组)与不等式(组)》中考知识点梳理
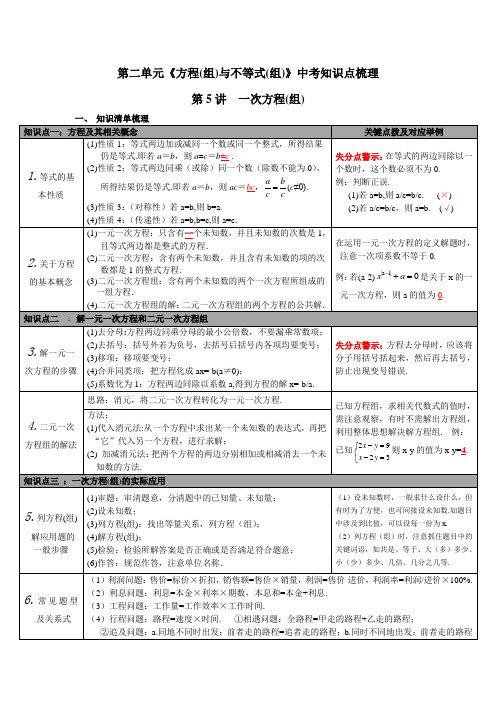
第二单元《方程(组)与不等式(组)》中考知识点梳理第5讲一次方程(组)第6讲一元二次方程第7讲分式方程三、知识清单梳理第8讲一元一次不等式(组)知识点一:不等式及其基本性质关键点拨及对应举例1.不等式的相关概念(1)不等式:用不等号(>,≥,<,≤或≠)表示不等关系的式子.(2)不等式的解:使不等式成立的未知数的值.(3)不等式的解集:使不等式成立的未知数的取值范围.例:“a与b的差不大于1”用不等式表示为a-b≤1.2.不等式的基本性质性质1:若a>b,则a±c>b±c;性质2:若a>b,c>0,则ac>bc,ac>bc;性质3:若a>b,c<0,则ac<bc,ac<bc.牢记不等式性质3,注意变号.如:在不等式-2x>4中,若将不等式两边同时除以-2,可得x<2.知识点二:一元一次不等式3.定义用不等号连接,含有一个未知数,并且含有未知数项的次数都是1的,左右两边为整式的式子叫做一元一次不等式. 例:若230mmx++>是关于x的一元一次不等式,则m的值为-1.4.解法(1)步骤:去分母;去括号;移项;合并同类项;系数化为1.失分点警示系数化为1时,注意系数的正负性,若系数是负数,则不等式改变方向.(2)解集在数轴上表示:x≥a x>a x≤a x<a知识点三:一元一次不等式组的定义及其解法5.定义由几个含有同一个未知数的一元一次不等式合在一起,就组成一个一元一次不等式组.(1)在表示解集时“≥”,“≤”表示含有,要用实心圆点表示;“<”,“>”表示不包含要用空心圆点表示.(2)已知不等式(组)的解集情况,求字母系数时,一般先视字母系数为常数,再逆用不等式(组)解集的定义,反推出含字母的方程,最后求出字母的值.如:已知不等式(a-1)x<1-a 的解集是x>-1,则a的取值范围是a<1.6.解法先分别求出各个不等式的解集,再求出各个解集的公共部分7.不等式组解集的类型假设a<b解集数轴表示口诀x ax b≥⎧⎨≥⎩x≥b大大取大x ax b≤⎧⎨≤⎩x≤a小小取小x ax b≥⎧⎨≤⎩a≤x≤b大小,小大中间找x ax b≤⎧⎨≥⎩无解大大,小小取不了知识点四:列不等式解决简单的实际问题8.列不等式解应用题(1)一般步骤:审题;设未知数;找出不等式关系;列不等式;解不等式;验检是否有意义.(2)应用不等式解决问题的情况:a.关键词:含有“至少(≥)”、“最多(≤)”、“不低于(≥)”、“不高于(≤)”、“不大(小)于”、“超过(>)”、“不足(<)”等;注意:列不等式解决实际问题中,设未知数时,不应带“至少”、“最多”等字眼,与方程中设未知数一致.。
【中考复习】中考数学复习第二单元方程(组)与不等式(组)第7课时一元二次方程及其应用教案

第二单元方程(组)与不等式(组)第7课时一元二次方程及其应用教学目标【考试目标】1。
能够根据具体问题中的数量关系,列出一元二次方程.2.理解配方法,会用因式分解法、公式法、配方法解简单的数字系数的一元二次方程.3。
会用一元二次方程根的判别式判别方程根的情况,了解一元二次方程根与系数的关系。
【教学重点】1.了解一元二次方程的定义。
2.学会一元二次方程的解法.3.熟悉一元二次方程根的判别式与根的关系.4.熟悉一元二次方程根与系数的关系.5.了解一元二次方程的实际应用。
教学过程一、知识体系图引入,引发思考二、引入真题,深化理解【例1】(2016年山西)解方程:2(x —3)2=x 2-9.【解析】原方程可变形为2(x —3)2-(x 2—9)=0,即2(x -3)2—(x +3)(x -3)=0.提公因式可得,(x —3)[2(x —3)-(x +3)]=0,即(x —3)(x -9)=0. 所以x 1=3,x 2=9.【考点】本题考查了一元二次方程的解法,主要考查了因式分解法的运用。
此题的关键是发现公因式,找到公因式后,解决此题会方便很多.【例2】(2016年十堰)已知关于x 的方程(x —3)(x —2)—p 2=0。
(1)求证:无论p 取何值时,方程总有两个不相等的实数根.(2)设方程的两根分别为x 1、x 2,且满足x 12+x 22=3x 1x 2,求实数p 的值.【解析】原方程写成一般式为:x 2-5x +6-p 2=0。
(1)证明:∆=(—5)2-4×1×(6-p 2)=25—24+4p 2=4p 2+1.∵p 2≥0,∴∆≥1>0.∴无论p 取何值时,方程总有两个不相等的实根。
(2)对x 12+x 22=3x 1x 2进行变形,左右两边同时加2x 1x 2得x 12+2x 1x 2+x 22=5x 1x 2,即(x 1+x 2)2=5x 1x 2。
由题可知212125,6x x x x p +=⋅=-.代入得,25=30—5p 2.解得p 2=1,∴p = ±1.【考点】此题考查了根的判别式与根之间的关系,以及根与系数的关系、一元二次方程的解法。
【精选推荐】中考数学复习第二单元方程(组)与不等式(组)(一元二次方程的解法及应用)全新完整版

返回目录
第1部分 第二单元 方程(组)与不等式(组)
2.已知a是方程x2-2x-3=0的一个根,则代数式 a2-2a-1的值为_____2_____.
3.用适当的方法解下列方程: (1)(x+2)2-9=0; (2)x2+5x=0; 解:(1)移项,得(x+2)2=9. 由此可得x+2=±3, x1=1,x2=-5. (2)因式分解,得x(x+5)=0. 于是得x=0,或x+5=0, x1=0,x2=-5.
返回目录
第1部分 第二单元 方程(组)与不等式(组)
五、一元二次方程的应用
步相骤同:,列即一审元、二设次、方列程、解解应、用验题以的及步答骤和列一次方程组解应用题的步骤
应 用
常见类型增利长润率问问题题:总12b利..为增设润增长a为=长率基单后=础件的基量增利量础,量润,量m×则×为销a1平01售0+均%量m增n长=率b ,n为增长次数,
所有一元 二次方程
+c= 0(a≠0,
b2-
4ac≥0)
方程的解
x=± ka-h
-b± b2-4ac x=③_____2_a____
返回目录
第1部分 第二单元 方程(组)与不等式(组)
方法
因式分 解法
方程的形
适用的方程
方程的解
式
容易变形为
(x-a)(x-b) (x-a)(x-
=0形式的 b)=0
x1=a,x2=b
返回目录
第1部分 第二单元 方程(组)与不等式(组)
(3)2x2-4x-1=0; (4)2x2-3x=3.
中考数学 第二单元 方程(组)与不等式(组)第07课时 一元二次方程课件

2021/12/9
第十九页,共三十五页。
高频考向探究
探究(tànjiū)二 一元二次方程根的判别式的应用
例2 关于x的方程mx2+x-m+1=0有以下三个结论:①当m=0时,方程只有一个实数解;②当m≠0时,方程有两个不等的实数解;③
无论m取何值,方程都至少有一个负数(fùshù)解.其中正确的结论是
系:x1+x2=
2021/12/9
-
,x1·x2=
.
第十一页,共三十五页。
课前双基巩固
考点(kǎo diǎn)四
一元二次方程的应用
1.[2017·杭州] 某景点的参观人数逐年增加,据统计,2014 年为
10.8 万人次,2016 年为 16.8 万人次,设参观人次的平均年增长率
为 x,则
(
∴(x1+x2)2-2x1x2=10.
∴(2m-2)2-2(m2-2m)=10.
化简,得m2-2m-3=0,
解得:m1=3,m2=-1.
∴m的值为3或-1.
2021/12/9
第二十三页,共三十五页。
高频考向探究
探究(tànjiū)三 一元二次方程的应用
例3 小丽为校合唱队购买某种服装时,商店(shāngdiàn)经理给出了如下优惠条件:如果一次性购买不超过10件,单价为
[解析] 长方体底面长为(80-2x)cm,宽
掉一个边长为 x cm 的正方形后,剩余的部分刚好能围成一个底面
为(70-2x)cm,由题意可得方程(80-
积为 3000 cm2 的无盖长方体工具箱,根据题意可列方程为
2x)(70-2x)=3000.
2025年湖南中考数学一轮复习考点研析 第二章 方程(组)与不等式(组)一元一次不等式(组)及其应用

(2)不等式②的解集为________;
(3)把不等式组的解集在如图的数轴上表示出来;
解:在数轴上表示不等式组的解集如解图.
1≤x<3
(4)不等式组的解集为____________;
1,2
(5)不等式组的整数解为________.
解图
解
答
变式2-1
是(
C
-+3<5,
(2023·娄底)不等式组ቊ
的单价为380元/个.若学校购买这两种灭火器的总价不超过21 000元,则最多
可购买这种型号的水基灭火器多少个?
解:设可购买这种型号的水基灭火器x个,则购买这种型
号的干粉灭火器(50-x)个.
根据题意,得540x+380(50-x)≤21 000,解得x≤12.5.
∵x为整数,∴x的最大值为12.
∴最多可购买这种型号的水基灭火器12个.
解
1.若a>b,则下列四个选项一定成立的是( A )
A.a+2>b+2
B.-3a>-3b
C. <
4
4
D.a-1<b-1
2.(2022·益阳)若x=2是下列四个选项中的某个不等式组的一个解,则这个不
等式组是( D )
<1,
A.ቊ
<-1
<1,
B.ቊ
> -1
> 1,
C.ቊ
<-1
> 1,
不等式的解集 不等式的解的全体称为不等式的解集
2.不等式的性质
性质
性质1
内容
应用
不等式两边都加上(或减去)同一个数(或式),不等号
b±c
的方向不变,即如果a>b,那么a±c>_______
中考数学总复习 第二单元 方程(组)与不等式(组)第07课时 一元二次方程及其应用课件

[答案] A
是 (
[解析] ∵2- 3是方程 x2-4x+c=0 的
A.1
)
B.3- 3
C.1+ 3
D.2+ 3
一个根,
∴(2- 3)2-4(2- 3)+c=0,∴c=1,故
选 A.
第十五页,共三十一页。
课堂考点探究
探究(tànjiū)二
一元二次方程的解法
解:解法一:移项,得 3x2-2x=2,配方得
A.55(1+x)2=35
B.35(1+x)2=55
C.55(1-x)2=35
D.35(1-x)2=55
4.[九上 P31 练习第 1(3)题改编] 方程(x+3)2-36=0 的解为 x1=3,x2=-9
5.[九上 P48 习题 2.4A 组第 1 题]
-1
(1)设方程 x2-4x-1=0 的两个根为 x1 与 x2,则 x1x2=
x2+(a+b)x+ab=(x+a)(x+b).
所以 x-4=0 或 x+1=0,即 x=4 或 x=-1.
实例分解因式:
x2+5x+6=x2+(2+3)x+2×3=(x+2)(x+3).
(1)尝试分解因式:x2+6x+8=(x+
)(x+
);
(2)应用:请用上述方法解方程:x2-3x-4=0.
第十八页,共三十一页。
UNIT TWO
第二(dì èr)单元 方程(组)与不等式(组)
第 7 课时(kèshí) 一元二次方程及其应用
第一页,共三十一页。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 方程(组)与不等式(组)
第7课时 一元二次方程及其应用
基础导练
一、选择题
1.(2015年重庆)一元二次方程x 2-2x =0的根是 ( )
A .x 1=0,x 2=-2
B .x 1=1,x 2=2
C .x 1=1,x 2=-2
D .x 1=0,x 2=2
2.(2015年兰州)一元二次方程x 2-8x -1=0配方后可变形为 ( )
A .(x +4)2=17
B .(x +4)2=15
C .(x -4)2=17
D .(x -4)2=15
3.(2015·铜仁)已知关于x 的一元二次方程3x 2+4x -5=0,下列说法正确的是
( )
A .方程有两个相等的实数根
B .方程有两个不相等的实数根
C .没有实数根
D .无法确定
二、填空题
1.(2014年眉山)若关于x 的一元二次方程x 2+6x +k =0的两个根分别是x 1,x 2,且
则k 的值为________.
2.(2015年丽水)解一元二次方程x 2
+2x -3=0时,可转化为解两个一元一次方程,请写出其中的一个一元一次方程:__________.
3.(2014年随州)某小区2013年绿化面积为2000平方米,计划2015年绿化面积要达到2880平方米.如果每年绿化面积的增长率相同,那么这个增长率是________.
三、解答题
1.解方程:x 2-3x +2=0;
12
113x x +=
2.(2014·株洲)已知关于x的一元二次方程 (a+c)x2+2bx+(a-c)=0,其中a,b,c 分别为△ABC的三边长.
(1)如果x=-1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;
(3)如果△ABC是等边三角形,试求这个一元二次方程的根.
参考答案.
一、选择题
1.D
2.C
3.B
二、填空题
1. -2
2.(x+3=0)(或x-1=0)
3. 20%
三、解答题
1.解:原方程可变形为(x-2)(x-1)=0.
所以解得x1=1,x2=2.
2.解:(1)当x=-1时,代入方程得a+c-2b+a-c=0.整理得2a-2b=0.∴△ABC为等腰三角形.
(2)如果方程有两个相等的实数根,则∆=(2b)2-4(a+c)(a-c)=4b2-4a2+4c2=0
即c2-b2-a2=0.∴△ABC为直角三角形.
(3)如果三角形为等边三角形,则a=b=c.原方程可写成2ax2+2ax=0.
即x(x+1)=0,∴x1=0,x2=-1.。
