2013届新课标高中数学(理)第一轮总复习第2章 第13讲 指数函数与对数函数
2013届高考数学一轮复习讲义第二章-2.6-指数与指数函数

解
(1)原式=-287
2 3
+5100
- 1 2
51-0 2+1
=-287
2 3
+500
1 2
-10(
5+2)+1
=49+10 5-10 5-20+1=-1697.
(2)原式= 5-2-1- ( 5-2)2
=( 5-2)-1-( 5-2)=-1.
1 21
(a3b2a3b3)2 (3)原式=a2ba1 3b1 3
(2)若函数 y=ax+b-1 (a>0 且 a≠1)的图象经过第二、三、 四象限,则 a、b 的取值范围是__________. (3)方程 2x=2-x 的解的个数是________.
主页
解析
(1) 函 数 定 义 域 为 {x|x∈R , x≠0} , 且
y
=
xax |x|
=
ax,x>0 -ax,x<0
.当 x>0 时,函数是一个指数函数,因为 0<a<1,
所以函数在(0,+∞)上是减函数;当 x<0 时,函数图象与指数
函数 y=ax (x<0,0<a<1)的图象关于 x 轴对称,函数在(-∞,0)
上是增函数,故填④.
(2)函数 y=ax+b-1 的图象经过第二、三、四 象限,大致图象如图.所以函数必为减函数. 故 0<a<1.又当 x=0 时,y<0,即 a0+b-1<0, ∴b<0.
(2)令 a
1 3
=m,b
1 3
=n,则原式=m2m+42-m8nm+n43 n2÷1-2mn·m
=mm2+(m23m-n8+n43)n2·m-m22n=m(3m(m2+-22mnn)(+m24+n22)m(mn-+24nn)2)=m3=a.
2013届高考一轮数学复习理科课件(人教版)第5课时 对数与对数函数

第5课时
高考调研
高三数学(新课标版· 理)
(3)由指数函数的性质: ∵0<0.9<1,而5.1>0, ∴0<0.95.1<1,即0<m<1. 又∵5.1>1,而0.9>0,∴5.10.9>1,即n>1. 由对数函数的性质: ∵0<0.9<1,而5.1>1,∴log0.95.1<0, 即p<0.综上,p<m<n.
图所示,则a,b满足的关系是( A.0<a-1<b<1 B.0<b<a-1<1 C.0<b-1<a<1 D.0<a 1<b 1<1
- -
第二章
第5课时
高考调研
高三数学(新课标版· 理)
【解析】 首先由于函数φ(x)=2x+b-1单调递增, 可得a>1;又-1<f(0)<0,即-1<logab<0,所以a-
【解析】 设f1(x)=(x-1)2,f2(x)=logax,要使当x ∈(1,2)时,不等式(x-1)2<logax恒成立,只需f1(x)=(x- 1)2在(1,2)上的图像在f2(x)=logax的下方即可.(如图所示)
第二章
第5课时
高考调研
高三数学(新课标版· 理)
当0<a<1时,显然不成立. 当a>1时,如图,要使在(1,2)上, f1(x)=(x-1)2的图像在f2(x)=logax的下方,只需 f1(2)≤f2(2), 即(2-1)2≤loga2,loga2≥1,∴1<a≤2.
第二章
第5课时
高考调研
高三数学(新课标版· 理)
2013届高考数学第一轮讲义复习

对数式的化简与求值
例 1 计算下列各式.
(1)lg 25+lg 2·lg 50+(lg 2)2;
(2)
(lg 3)2-lg 9+1·(lg 27+lg 8-lg lg 0.3·lg 1.2
1 000);
(3)(log32+log92)·(log43+log83).
(1)lg 2·lg 50 没有办法直接化简,可考虑提取公因数 lg 2. (2)将根号下配成完全平方的形式,开根号.(3)利用换底公 式,是本题的切入口.
变式训练 1
(1)化简 lg 37+lg 70-lg 3- lg23-lg 9+1; (2)已知 f(3x)=4xlog23+233,求 f(2)+f(4)+f(8)+…+f(28) 的值. 解 (1)原式=lg 37×370- lg23-2lg 3+1 =lg 10- (lg 3-1)2=1-|lg 3-1|=lg 3.
2 5lg 3·6lg
32=54.
探究提高
(1)在对数运算中,先利用幂的运算把底数或真数进行变形,化 成分数指数幂的形式,使幂的底数最简,然后再运用对数运算 法则化简合并,在运算中要注意化同底和指数与对数互化. (2)熟练地运用对数的三个运算性质并配以代数式的恒等变形 是对数计算、化简、证明常用的技巧.
=((1l-g 3l-g 31))·32·((llgg33++22llgg22--11))=-32.
(3)原式=llgg
23+llgg
2 lg 9·lg
43+llgg
3 8
=llgg 32+2llgg23·2llgg32+3llgg32
=32llgg
对数函数的图象与性质
例 2 作出函数 y=log2|x+1|的图象,由图象指出函数的单 调区间,并说明它的图象可由函数 y=log2x 的图象经过怎 样的变换而得到.
高考数学第一轮复习教案-专题2函数概念与基本初等函数

反函数的定义
设函数 y f (x)(x A) 的值域是 C,根据这个函数中 x,y 的关系,用 y 把 x 表
高考数学第一轮复习教案汇总【精华】
专题二 函数概念与基本初等函数
一、考试内容: 映射、函数、函数的单调性、奇偶性. 反函数.互为反函数的函数图像间的关系. 指数概念的扩充.有理指数幂的运算性质.指数函数. 对数.对数的运算性质.对数函数. 函数的应用. 二、考试要求: (1)了解映射的概念,理解函数的概念. (2)了解函数单调性、奇偶性的概念,掌握判断一些简单函数的单调性、奇偶性的方法. (3)了解反函数的概念及互为反函数的函数图像间的关系,会求一些简单函数的反函数. (4)理解分数指数幂的概念,掌握有理指数幂的运算性质,掌握指数函数的概念、图像 和 性质. (5)理解对数的概念,掌握对数的运算性质;掌握对数函数的概念、图像和性质. (6)能够运用函数的性质、指数函数和对数函数的性质解决某些简单的实际问题. 三、命题热点
y f 1(x)
(二)函数的性质 函数的单调性
定义:对于函数 f(x)的定义域 I 内某个区间上的任意两个自变量的值 x1,x2, ⑴若当 x1<x2 时,都有 f(x1)<f(x2),则说 f(x)在这个区间上是增函数; ⑵若当 x1<x2 时,都有 f(x1)>f(x2),则说 f(x) 在这个区间上是减函数.
奇函 数的定 义:如果 对于函 数f(x)的定 义域内 任意一 个x,都有 f(-x)=-f(x),那么 函数f(x)就叫 做奇函 数.
高中数学 第二章 指数函数、对数函数和幂函数 2.2.3 对数函数的图象和性质 第1课时 反函数及对
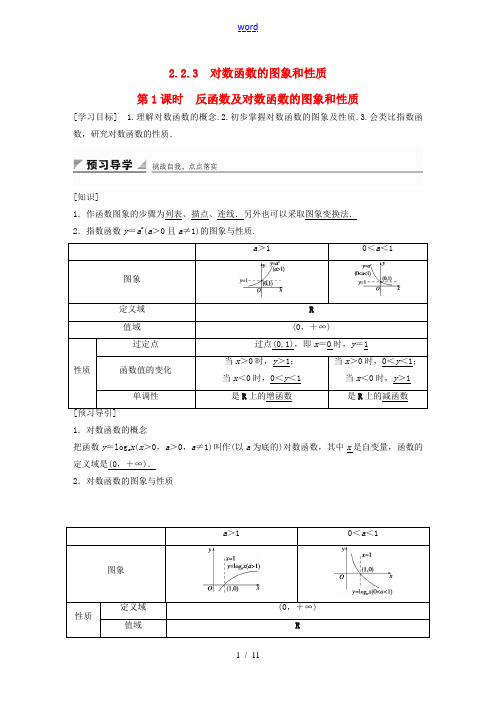
2.2.3 对数函数的图象和性质第1课时反函数及对数函数的图象和性质[学习目标] 1.理解对数函数的概念.2.初步掌握对数函数的图象及性质.3.会类比指数函数,研究对数函数的性质.[知识]1.作函数图象的步骤为列表、描点、连线.另外也可以采取图象变换法.2.指数函数y=a x(a>0且a≠1)的图象与性质.a>10<a<1 图象定义域R值域(0,+∞)性质过定点过点(0,1),即x=0时,y=1函数值的变化当x>0时,y>1;当x<0时,0<y<1当x>0时,0<y<1;当x<0时,y>1 单调性是R上的增函数是R上的减函数[预习导引]1.对数函数的概念把函数y=log a x(x>0,a>0,a≠1)叫作(以a为底的)对数函数,其中x是自变量,函数的定义域是(0,+∞).2.对数函数的图象与性质a>10<a<1 图象性质定义域(0,+∞)值域R过点过点(1,0),即x=1时,y=0函数值的变化当0<x<1时,y<0;当x>1时,y>0当0<x<1时,y>0;当x>1时,y<0单调性是(0,+∞)上的增函数是(0,+∞)上的减函数3.反函数(1)对数函数y=log a x(a>0且a≠1)与指数函数y=a x(a>0,且a≠1)互为反函数.(2)要寻找函数y=f(x)的反函数,可以先把x和y换位,写成x=f(y),再把y解出来,表示成y=g(x)的形式,如果这种形式是唯一确定的,就得到f(x)的反函数g(x).要点一对数函数的概念例1 指出下列函数哪些是对数函数?(1)y=3log2x;(2)y=log6x;(3)y=log x3;(4)y=log2x+1.解(1)log2x的系数是3,不是1,不是对数函数.(2)符合对数函数的结构形式,是对数函数.(3)自变量在底数位置上,不是对数函数.(4)对数式log2x后又加1,不是对数函数.规律方法判断一个函数是对数函数必须是形如y=log a x(a>0且a≠1)的形式,即必须满足以下条件(1)系数为1.(2)底数为大于0且不等于1的常数.(3)对数的真数仅有自变量x.跟踪演练1 若某对数函数的图象过点(4,2),则该对数函数的解析式为( )A.y=log2x B.y=2log4xC.y=log2x或y=2log4x D.不确定答案 A解析设对数函数的解析式为y=log a x(a>0且a≠1),由题意可知log a4=2,∴a2=4,∴a =2,∴该对数函数的解析式为y=log2x.要点二对数函数的图象例2 如图所示,曲线是对数函数y =log a x 的图象,已知a 取3,43,35、110,则相应于c 1、c 2、c 3、c 4的a 值依次为( )A.3、43、35、110B.3、43、110、35C.43、3、35、110D.43、3、110、35 答案 A解析 方法一 先排c 1、c 2底的顺序,底都大于1,当x >1时图低的底大,c 1、c 2对应的a 分别为3、43.然后考虑c 3、c 4底的顺序,底都小于1,当x <1时底大的图高,c 3、c 4对应的a 分别为35、110.综合以上分析,可得c 1、c 2、c 3、c 4的a 值依次为3、43、35、110.故选A.方法二 作直线y =1与四条曲线交于四点,由y =log a x =1,得x =a (即交点的横坐标等于底数),所以横坐标小的底数小,所以c 1、c 2、c 3、c 4对应的a 值分别为3、43、35、110,故选A.规律方法 函数y =log a x (a >0且a ≠1)的底数变化对图象位置的影响.观察图象,注意变化规律:(1)上下比较:在直线x =1的右侧,a >1时,a 越大,图象向右越靠近x 轴,0<a <1时a越小,图象向右越靠近x 轴.(2)左右比较:比较图象与y =1的交点,交点的横坐标越大,对应的对数函数的底数越大. 跟踪演练2 (1)函数y =log a (x +2)+1的图象过定点( ) A .(1,2) B .(2,1) C .(-2,1) D .(-1,1)(2)如图,若C 1,C 2分别为函数y =log a x 和y =log b x 的图象,则( )A .0<a <b <1B .0<b <a <1C .a >b >1D .b >a >1 答案 (1)D (2)B解析 (1)令x +2=1,即x =-1, 得y =log a 1+1=1,故函数y =log a (x +2)+1的图象过定点(-1,1).(2)作直线y =1,则直线与C 1,C 2的交点的横坐标分别为a ,b ,易知0<b <a <1. 要点三 对数函数的定义域例3 (1)函数f (x )=11-x +lg(1+x )的定义域是( )A .(-∞,-1)B .(1,+∞)C .(-1,1)∪(1,+∞) D.(-∞,+∞) (2)若f (x )=121log (21)x +,则f (x )的定义域为( )A.⎝ ⎛⎭⎪⎫-12,0B.⎝ ⎛⎭⎪⎫-12,+∞ C.⎝ ⎛⎭⎪⎫-12,0∪(0,+∞) D.⎝ ⎛⎭⎪⎫-12,2 答案 (1)C (2)C解析 (1)由题意知⎩⎪⎨⎪⎧1+x >0,1-x ≠0,解得x >-1且x ≠1.(2)由题意有⎩⎪⎨⎪⎧2x +1>0,2x +1≠1,解得x >-12且x ≠0.规律方法 求与对数函数有关的函数定义域时,除遵循前面已学习过的求函数定义域的方法外,还要对这种函数自身有如下要求:一是要特别注意真数大于零;二是要注意对数的底数;三是按底数的取值应用单调性,有针对性地解不等式. 跟踪演练3 (1)函数y =x ln(1-x )的定义域为( ) A .(0,1) B .[0,1) C .(0,1] D .[0,1] (2)函数y =lgx +1x -1的定义域是( )A .(-1,+∞) B.[-1,+∞)C .(-1,1)∪(1,+∞) D.[-1,1)∪(1,+∞) 答案 (1)B (2)C解析 (1)因为y =x ln(1-x ),所以⎩⎪⎨⎪⎧x ≥0,1-x >0,解得0≤x <1.(2)要使函数有意义,需⎩⎪⎨⎪⎧x +1>0,x -1≠0,解得x >-1且x ≠1,故函数的定义域为(-1,1)∪(1,+∞),故选C. 要点四 反函数例4 求下列函数的反函数:(1)y =2x -5;(2)y =x1-x ;(3)y =1+e 2x . 解 (1)从x =2y -5中解得y =x +52,即为所求;(2)从x =y 1-y 中解得y =xx +1,即为所求;(3)从x =1+e 2y 移项得x -1=e 2y .两端取自然对数得到ln(x -1)=y2,解得y =2ln(x -1),即为所求.规律方法 要找寻函数y =f (x )的反函数,可以先把x 和y 换位,写成x =f (y ),再把y 解出来,表示成y =g (x )的形式.如果这种形式是唯一确定的,就得到了f (x )的反函数g (x ).既然y =g (x )是从x =f (y )解出来的,必有f (g (x ))=x ,这个等式也可以作为反函数的定义. 跟踪演练4 y =ln x 的反函数是________. 答案 y =e x解析 由y =ln x ,得x =e y ,所以反函数为y =e x.1.下列函数是对数函数的是( ) A .y =log a (2x ) B .y =log 22xC .y =log 2x +1D .y =lg x 答案 D解析 选项A 、B 、C 中的函数都不具有“y =log a x (a >0且a ≠1)”的形式,只有D 选项符合. 2.函数f (x )=11-x +lg(3x +1)的定义域是( )A .(-13,+∞) B.(-∞,-13)C .(-13,13)D .(-13,1)答案 D解析 由⎩⎪⎨⎪⎧1-x >0,3x +1>0,可得-13<x <1.3.函数y =a x与y =-log a x (a >0,且a ≠1)在同一坐标系中的图象形状可能是( )答案 A解析 函数y =-log a x 恒过定点(1,0),排除B 项; 当a >1时,y =a x是增函数,y =-log a x 是减函数,排除C 项,当0<a <1时,y =a x是减函数,y =-log a x 是增函数,排除D 项,A 项正确.4.若a >0且a ≠1,则函数y =log a (x -1)+1的图象恒过定点________. 答案 (2,1)解析 函数图象过定点,则与a 无关, 故log a (x -1)=0,所以x -1=1,x =2,y =1, 所以y =log a (x -1)+1过定点(2,1). 5.函数y =lg x 的反函数是________. 答案 y =10x解析 由反函数的定义知x =10y,故反函数为y =10x.1.判断一个函数是不是对数函数关键是分析所给函数是否具有y =log a x (a >0且a ≠1)这种形式.2.在对数函数y =log a x 中,底数a 对其图象直接产生影响,学会以分类的观点认识和掌握对数函数的图象和性质.3.涉及对数函数定义域的问题,常从真数和底数两个角度分析.一、基础达标1.函数y =log a x 的图象如图所示,则a 的值可以是( )A .0.5B .2C .eD .π 答案 A解析 ∵函数y =log a x 的图象单调递减,∴0<a <1,只有选项A 符合题意. 2.函数f (x )=lg(x -1)+4-x 的定义域为( ) A .(1,4] B .(1,4) C .[1,4] D .[1,4) 答案 A解析 由⎩⎪⎨⎪⎧x -1>0,4-x ≥0,解得1<x ≤4.3.在同一坐标系中,函数y =log 3x 与y =13log x 的图象之间的关系是( )A .关于y 轴对称B .关于x 轴对称C .关于原点对称D .关于直线y =x 对称 答案 B解析 ∵y =13log x =-log 3x ,∴函数y =log 3x 与y =13log x 的图象关于x 轴对称.4.如图是三个对数函数的图象,则a 、b 、c 的大小关系是( )A .a >b >cB .c >b >aC .c >a >bD .a >c >b 答案 D解析 y =log a x 的图象在(0,+∞)上是上升的,所以底数a >1,函数y =log b x ,y =log c x 的图象在(0,+∞)上都是下降的,因此b ,c ∈(0,1),又易知c >b ,故a >c >b .5.已知函数f (x )=⎩⎪⎨⎪⎧3x, x ≤0,log 2x ,x >0,那么f (f (18))的值为( )A .27 B.127C .-27 D .-127答案 B解析 f (18)=log 218=log 22-3=-3,f (f (18))=f (-3)=3-3=127.6.已知对数函数f (x )的图象过点(8,-3),则f (22)=________. 答案 -32解析 设f (x )=log a x (a >0,且a ≠1), 则-3=log a 8,∴a =12.∴f (x )=log 12x ,f (22)=log 12(22)=-log 2(22)=-32.7.求下列函数的定义域: (1)f (x )=lg(x -2)+1x -3; (2)f (x )=log (x +1)(16-4x ).解 (1)要使函数有意义,需满足⎩⎪⎨⎪⎧x -2>0,x -3≠0,解之得x >2且x ≠3.∴函数定义域为(2,3)∪(3,+∞). (2)要使函数有意义,需满足⎩⎪⎨⎪⎧16-4x >0,x +1>0,x +1≠1,解之得-1<x <0或0<x <4. ∴函数定义域为(-1,0)∪(0,4). 二、能力提升8.设函数f (x )=log 2x 的反函数为y =g (x ),且g (a )=14,则a 等于( )A .2B .-2 C.12 D .-12答案 B解析 ∵函数f (x )=log 2x 的反函数为y =2x,即g (x )=2x. 又∵g (a )=14,∴2a=14,∴a =-2.9.若函数f (x )=log a (x +b )的图象如图,其中a ,b 为常数,则函数g (x )=a x+b 的图象大致是( )答案 D解析 由函数f (x )=log a (x +b )的图象可知,函数f (x )=log a (x +b )在(-b ,+∞)上是减函数.所以0<a <1且0<b <1.所以g (x )=a x+b 在R 上是减函数,故排除A ,B.由g (x )的值域为(b ,+∞).所以g (x )=a x+b 的图象应在直线y =b 的上方,故排除C. 10.若log 2a 1+a21+a<0,则a 的取值X 围是____________.答案 ⎝ ⎛⎭⎪⎫12,1解析 当2a >1时,∵log 2a 1+a21+a <0=log 2a 1,∴1+a 21+a <1.∵1+a >0,∴1+a 2<1+a , ∴a 2-a <0,∴0<a <1,∴12<a <1.当0<2a <1时,∵log 2a 1+a21+a <0=log 2a 1,∴1+a 21+a >1.∵1+a >0,∴1+a 2>1+a , ∴a 2-a >0,∴a <0或a >1,此时不合题意.综上所述,a ∈⎝ ⎛⎭⎪⎫12,1. 11.已知f (x )=log 3x . (1)作出这个函数的图象;(2)若f (a )<f (2),利用图象求a 的取值X 围. 解 (1)作出函数y =log 3x 的图象如图所示.(2)令f (x )=f (2),即log 3x =log 32,解得x =2.由图象知:函数f (x )为单调增函数,当0<a <2时,恒有f (a )<f (2).∴所求a 的取值X 围为(0,2). 三、探究与创新12.求y =(log 12x )2-12log 12x +5在区间[2,4]上的最大值和最小值.解 因为2≤x ≤4,所以log 122≥log 12x ≥log 124,即-1≥log 12x ≥-2.设t =log 12x ,则-2≤t ≤-1,所以y =t 2-12t +5,其图象的对称轴为直线t =14,所以当t =-2时,y max =10;当t =-1时,y min =132.13.若函数f (x )为定义在R 上的奇函数,且x ∈(0,+∞)时,f (x )=lg(x +1),求f (x )的word 11 / 11 表达式,并画出大致图象.解 ∵f (x )为R 上的奇函数,∴f (0)=0. 又当x ∈(-∞,0)时,-x ∈(0,+∞), ∴f (-x )=lg(1-x ).又f (-x )=-f (x ),∴f (x )=-lg(1-x ),∴f (x )的解析式为f (x )=⎩⎪⎨⎪⎧lg x +1,x >0,0,x =0,-lg 1-x ,x <0,∴f (x )的大致图象如图所示:。
高中数学竞赛系列讲座:指数函数与对数函数

高中数学竞赛系列讲座:指数函数与对数函数指数、对数以及指数函数与对数函数,是高中代数非常重要的内容。
无论在高考及数学竞赛中,都具有重要地位。
熟练掌握指数对数概念及其运算性质,熟练掌握指数函数与对数函数这一对反函数的性质、图象及其相互关系,对学习好高中函数知识,意义重大。
一、指数概念与对数概念:指数的概念是由乘方概念推广而来的。
相同因数相乘a·a……a(n个)=a n导出乘方,这里的n为正整数。
从初中开始,首先将n推广为全体整数;然后把乘方、开方统一起来,推广为有理指数;最后,在实数范围内建立起指数概念。
欧拉指出:“对数源出于指数”。
一般地,如果a(a>0,a≠1)的b次幂等于N,就是a b=N,那么数b叫做以a为底N的对数,记作:logaN=b其中a叫做对数的底数,N叫做真数。
a b=N与b=logaN是一对等价的式子,这里a是给定的不等于1的正常数。
当给出b求N时,是指数运算,当给出N求b时,是对数运算。
指数运算与对数运算互逆的运算。
二、指数运算与对数运算的性质1.指数运算性质主要有3条:a x·a y=a x+y,(a x)y=a xy,(ab)x=a x·b x(a>0,a≠1,b>0,b≠1)2.对数运算法则(性质)也有3条:(1)loga(MN)=logaM+logaN(2)logaM/N=logaM-logaN(3)logaM n=nloga M(n∈R)(a>0,a≠1,M>0,N>0)3.指数运算与对数运算的关系:X=a logax;m logan=n logam4.负数和零没有对数;1的对数是零,即loga1=0;底的对数是1,即logaa=15.对数换底公式及其推论:换底公式:logaN=logbN/logba推论1:loga m N n=(n/m)logaN推论2:三、指数函数与对数函数函数y=a x(a>0,且a≠1)叫做指数函数。
2013高考数学函数专题三,指数函数

2013高考数学函数专题三:指数函数与对数函数【一】基础知识1.指数的概念及运算性质(1)根据n 次方根的定义,有 (i )0的任何次方根都是0 (ii)());(+∈=N n a a nn(iii )当n 为奇数时,;a a n n =当n 为偶数时,⎩⎨⎧<-≥==0()0(a a a a a a n n(2)正数的分数指数幂的意义).1,,,0(11)1,,,0(>∈>==>∈>=+-+n N n m a aaan N n m a a a nmnm nm n m nm 且且(3)0的正分数指数幂等于0,0的负分数指数幂没有意义。
(4)指数的运算性质:(i ));,,0(Q s r a a a a s r s r ∈>=⋅+ (ii ));.,,0()(Q s r a a a rs s r ∈>= (iii )).,0,0()(Q r b a b a ab r r r ∈>>⋅= 2.指数函数 (1)定义 (2)图象 (3)性质 3. 对数(1)定义(2)常用对数和自然对数 (3)对数的性质(i) 零与负数没有对数; (ii) 01log =a (iii) 1log =a a (4)对数运算法则如果0,0,1,0>>≠>N M a a ,那么 =)(MN Log a =)(NM Log a =n a M Log (5)换底公式 )0,1,,0,(,>≠>=N b a b a bLog NLog N Log a a b 且 (6)几个常见关系式:;log log log c c b a b a =⋅ ;l o g 1l o g ab b a =.l o g l o g b n m b a m a n = 4. 对数函数(1)对数函数的概念:(2) 对数函数的图象(3)对数函数的性质 (i )过定点(1,0);图象在第一,四象限。
【学海导航】2013届高考数学第一轮总复习 2.9指数函数与对数函数(第1课时)课件 理 (广西专版)

第二章 函数 第 9讲
指数函数与对数函数 (第一课时)
1
考 点搜 索
立足教育 开创未来
●指数、对数函数的图象及性质 对照表 ●指数函数、对数函数的复合函 数的性质,求指数函数、对数函 数的复合函数的单调区间、最值 等 ●分类讨论含有字母参数的函数 问题高
2
指数函数、对数函数是高考的 热点问题,高考中,既考查定 义与图象及主要性质,又在数 学思想方法上考查分类讨论的 方法及字符运算能力.有关指数 函数、对数函数的试题每年必 考.既有选择题、填空题,又可 以解答题的形式出现,且对综 合能力要求较高.
立足教育 开创未来
0<a< 1
定义 域
(0,+∞)
值域 R
函数 当x>1时,y>0;
值
当x=1时,y=0;
分布 当0<x<1时,y<0.
(0,+∞)
R 当x>0时,0<y<1; 当x=0时,y=1; 当x<0时,y>1.
单调 在(0,+∞)上是增函数 性
在(0,+∞)上是减函数
7
立足教育 开创未来
立足教育 开创未来
0<a< 1
R (0,+∞) 当x>0时,0<y<1; 当x=0时,y=1; 当x<0时,y>1. R上的减函数
5
立足教育 开创未来
3. 对数函数的概念:一般地,函数 y=logax (a>0,且a≠1)叫做对
数函数,其中x是自变量. 4. 对数函数的图象和性质:
6
a>1 图像
a
31
立足教育 开创未来
1. 比较两个指、对数式的大小,常用作差、 作商或引入中间量来比较;若底数相同,则 可利用指数函数和对数函数的单调性来比较.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对数式的大小比较
【例2】
(1)已知loga5>logb5,比较a、b的大小; (2)设f(x)=loga(1-x),g(x)=loga(1+x)(其
中a>1),在公共定义域下,比较f(x)与g(x)
【变式练习3】
已知函数y=1+2x +a·4x ,当x≤1时,
恒有y>0,求实数a的取值范围.
【解析】由1+2 x+a ( x 1)恒成立.
x
1 2x ,得a - x 4
1 2x 1 2x 1 x 1 x 1 2 1 令f x =- x =-( ) -( ) [( ) ] . 4 2 2 2 2 4 1 设t=( ) x, 2 1 2 1 1 则函数转化为f t =-(t+ ) + ,t [ ,+). 2 4 2 1 3 所以 f t max =f ( )=- . 2 4 3 3 所以a - ,即实数a的取值范围是(- ,+). 4 4
【解析】设t=a ,则函数化为关于t的函数
x
f t =t 2+2t-1=(t+1) 2-2 t 0 . 当a 1时,a-1 t a,ymax=a 2+2a-1=14, 解得a=3或a=-5(舍去); 当0 a 1时,a t a-1,ymax=(a-1 ) 2+2a-1 1 1 -1=14,解得a= 或a=- (舍去). 3 5 1 故所求a的值为3或 . 3
的大小关系.
1 1 【解析】1 当a 1,b 1时, , log 5 a log 5 b 即 log 5 b log 5 a,所以b a 1; 1 1 当0 a 1, 0 b 1时, , log 5 a log 5 b 即 log 5 b log 5 a,所以0 a b 1; 当a 1, 0 b 1时符合题意.
1.函数y=ax-3+2(a>0,且a¹ 1)的图象过定点,
(3,3) 这个定点的坐标是________.
1 1 2.若函数y log ( x ) b的图象不经过 2 2 第一象限,则b的取值范围是 (-∞,-1] .
3.已知函数f(x)=ax+b(a>0)的图象经过点(2,3)
等通过化简后可转化为y=a x的形式的,是指
(2)讨论指数函数问题时,由于a>1与
0<a<1影响了函数的性质,因此在底数不确
定时,应当对底数作分类讨论. (3)指数函数图象的特点,首先它是R 上的单调函数,当底数a>1时,是R上的增 函数;当0<a<1时,是R上的减函数,值域
对数函数的应用
【例4】 x 已知函数f ( x-3)=log a (a 0,且a 1). 6 x 1 判断f x 的奇偶性,写出推理过程;
2 当0 a 1时,求函数f x 的单调区间.
【解析】令u=x-3,得x=u+3, u 3 于是f u =log a (-3 u 3), 3u 3 x 所以f x =log a (-3 x 3). 3 x 3 x 3 x -1 =log a ( ) =-f x , 1因为f (-x)=log a 3 x 3 x 3 x 6 =-1- ,它在(-3,3)上是增函数. 2 令t= 3 x 3 x 当0 a 1时,函数y=log a t是减函数, 3 x 所以函数f x =log a (-3 x 3)是减函数, 3 x 故其单调递减区间是(-3,3).
1.要使g(x)=3x+1+t的图象不经过第二 t≤-3 象限,则t的取值范围为 _______. 【解析】要使g(x)=3x+1+t的图象不经过 第二象限,只要g(0)=31+t≤0,即t≤-3.
2.若函数y=(log 1 a) x是减函数,则a的
1 ( , 1). 取值范围是 ________________ 2
2
【解析】由0 log 1 a 1,得0 -log 2 a 1,
2
1 解得 a 1. 2
2 3.已知函数f x =lg( a)是奇函数, 1 x (-1,0) 则f x 0的解集为 ____________
【解析】由函数f x 在x=0处有意义, 知f 0 =0,得a=-1. 2 1 x 则f x =lg( 1)=lg (-1 x 1). 1 x 1 x 1 x 1 x 由lg 0,得0 1, 1 x 1 x 解得-1 x 0.
xa 4.函数y= 0 a 1的值域是 | x| (-∞,-1)∪(0,1) _____________________
【解析】当x<0时,y=-ax<-a0 = -1;当x>0时,y=ax∈(0,1), 所 以 所 求 函 数 的 值 域 为 ( - ∞ ,- 1)∪(0,1).
x
2 函数f x 与g x 的公共定义域是(-1,1).
1 x 因为f x -g x =log a a 1, 1 x 1 x 所以,当-1 x 0时, 1; 1 x 1 x 1 x 当x=0时, =1;当0 x 1时, 0 1. 1 x 1 x 于是,当x (-1, 0)时,f x g x ; 当x=0时,f x =g x ; 当x 0,1 时,f x g x .
c=log20.8<0,所以c<b<a.
指数式的大小比较
【例1】 比较下列各组实数的大小. 0.9 1 0.8 , ; 0.3 3.1 0.9 2 1.7 , ; 1 -1.5 8 ( 3 4 , , ) . 2
0.9 0.48 1 2 1 3
【解析】1由函数y=x 的单调性得0.8 0.9 ; 由指数函数的单调性得0.9 0.9 , 所以0.8 0.9 . 2 因为1.7 0.3 1, 0.93.1 1,所以1.7 0.3 0.93.1. 1 -1.5 1.5 8 ( 3因为4 =2 , =2 , ) =2 , 2 1 -1.5 0.9 所以由指数函数的单调性得4 ( ) 80.48 . 2
0.9 1.8 0.48 1.44 1 2 1 3 1 2 1 3
1 2
1 2
1 2
(1)(2)两组数据的底数不同,指
数也不同,常见方法是寻找中间 量.(1)题,由数的特点,知0.91/2 是 合适的中间量;(2)题,根据指数函数 的性质,1是最合适的中间量;(3)题,
可转化为同底的指数幂的大小比较,
只需应用指数函数的单调性.
【变式练习1】 (ห้องสมุดไป่ตู้)比较60.7与0.76的大小; (2)若a、b、c都是大于1的正数,且ax<bx<cx , 比较a、b、c的大小. 【解析】(1)因为60.7>1,0.76<1,所以60.7>0.76. (2)设d>1,则y=dx是增函数,对于x>0,当d
增大时,函数值也增大.对于x<0,当d增大
解析: 因为f(2)<f(3),所以f(x)=logax单调递增,
则a∈(1,+∞). 5.若a=log0.40.3,b=log54,c=log20.8,用“<”将a, c<b<a b,c连接起来__________. 解析:
a=log0.40.3>log0.40.4=1,0<b=log54<log55=1,
1.指数函数的概念、图象和性质
1 指数函数y=a x是说明性定义,注意两点:
一是底数范围的规定“ a 0且a 1 , 二是式子a x没有被其他元素复合,如y=2a x, y=a x-1,y=a ,y=a x+1等都不是指数函数. 但要注意:对某些关系式,如y=22x,y=3 数函数.
x 2 1 x
比较对数的大小,有三种具体情况:
①同底数,不同真数,利用对数函数的单调性
进行判断; ②同真数,不同底数,利用对数换底公式转化 为同底的对数; ③不同底数,也不同真数,利用指数、对数互
化或寻找中间量进行判断.(1)中是同真不同底
的两个对数,用对数换底公式比较简便;(2)题 是函数值大小的比较,一般方法是作差,寻找
本题有较强的综合性,首先要通过变
量代换,求出函数f(x)的表达式(防止直接 判断f(x-3)的奇偶性),然后再判断奇偶 性.在研究函数的单调性时,本解答直接 应用了反比例函数的单调性(常见基本函数
的单调性是可以直接应用的),如果一定要
用单调性的定义来解答,也只需讨论 3 x t= (-3 x 3)的单调性即可. 3 x
2 因为0 a 1,故由f x 1,
xa xa 得 log a log a a,则0 a. x x xa 当 0时,得x 0或x a; x xa a 当 a时,得0 x . x 1 a a 又a , 1 a a 所以原不等式的解集为{x | a x }. 1 a
3 和原点,则f(-2)= ____ 4
a2 b 3 a 2 x 解析: ,解得 ,f x 2 1, a0 b 0 b 1 3 所以f 2 2 1 4
2
4.已知函数f(x)=logax(a>0,a¹ 1),若f(2)<f(3), (1,+∞) 则实数a的取值范围是_________.
将复杂的数学问题转化为熟知的数学问题
是数学化归思想的体现.换元法在数学化归思 想中占有重要的地位.本题作换元后,将函数 转化为f(t)=t2 +2t-1(t>0),使题目的结构一下 子变得清晰起来,因为二次函数在闭区间上存
