控制工程基础 第4章 控制系统的频率特性
《控制工程基础》课程作业习题(含解答)
第一章概论本章要求学生了解控制系统的基本概念、研究对象及任务,了解系统的信息传递、反馈和反馈控制的概念及控制系统的分类,开环控制与闭环控制的区别;闭环控制系统的基本原理和组成环节。
学会将简单系统原理图抽象成职能方块图。
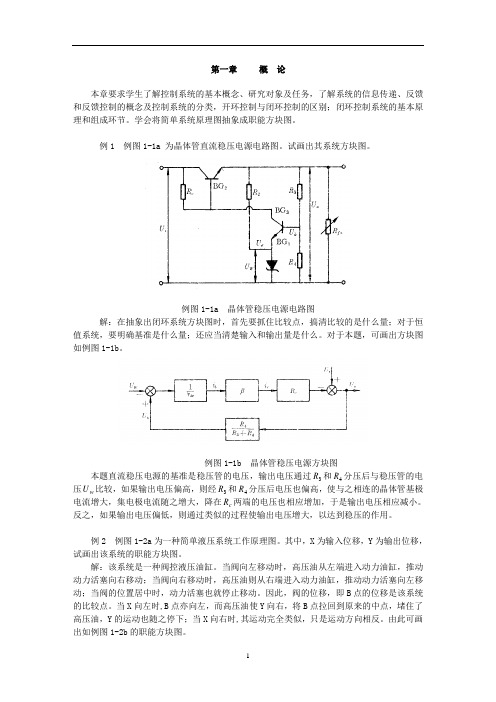
例1 例图1-1a 为晶体管直流稳压电源电路图。
试画出其系统方块图。
例图1-1a 晶体管稳压电源电路图解:在抽象出闭环系统方块图时,首先要抓住比较点,搞清比较的是什么量;对于恒值系统,要明确基准是什么量;还应当清楚输入和输出量是什么。
对于本题,可画出方块图如例图1-1b。
例图1-1b 晶体管稳压电源方块图本题直流稳压电源的基准是稳压管的电压,输出电压通过R和4R分压后与稳压管的电3压U比较,如果输出电压偏高,则经3R和4R分压后电压也偏高,使与之相连的晶体管基极w电流增大,集电极电流随之增大,降在R两端的电压也相应增加,于是输出电压相应减小。
c反之,如果输出电压偏低,则通过类似的过程使输出电压增大,以达到稳压的作用。
例2 例图1-2a为一种简单液压系统工作原理图。
其中,X为输入位移,Y为输出位移,试画出该系统的职能方块图。
解:该系统是一种阀控液压油缸。
当阀向左移动时,高压油从左端进入动力油缸,推动动力活塞向右移动;当阀向右移动时,高压油则从右端进入动力油缸,推动动力活塞向左移动;当阀的位置居中时,动力活塞也就停止移动。
因此,阀的位移,即B点的位移是该系统的比较点。
当X向左时,B点亦向左,而高压油使Y向右,将B点拉回到原来的中点,堵住了高压油,Y的运动也随之停下;当X向右时,其运动完全类似,只是运动方向相反。
由此可画出如例图1-2b的职能方块图。
例图1-2a 简单液压系统例图1-2b 职能方块图1.在给出的几种答案里,选择出正确的答案。
(1)以同等精度元件组成的开环系统和闭环系统,其精度比较为_______ (A )开环高; (B )闭环高; (C )相差不多; (D )一样高。
(2)系统的输出信号对控制作用的影响 (A )开环有; (B )闭环有; (C )都没有; (D )都有。
控制工程基础第四章频域响应法

幅频特性A(): 稳态输出信号的幅值与输入信号的幅值之比: A() Ac G( j) A
相频特性(): 稳态输出信号的相角与输入信号相角之差:
() G( j)
幅相频率特性G(j) : G(j) 的幅值和相位均随输入正弦信
号角频率的变化而变化。 G( j ) A(w)e j ()
在系统闭环传递函数G(s)中,令s= j,即可得到系统的频率 特性。
控制工程基础第四章频 域响应法
2021/7/13
频率响应法是二十世纪三十年代发展起来的一种经典工 程实用方法,是一种利用频率特性进行控制系统分析的图解方 法,可方便地用于控制工程中的系统分析与设计。频率法用于 分析和设计系统有如下优点:
(1)不必求解系统的特征根,采用较为简单的图解方法 就可研究系统的稳定性。由于频率响应法主要通过开环频率特 性的图形对系统进行分析,因而具有形象直观和计算量少的特 点。
对相角进行线性分度;横轴:对频率取以10为底的对数后进行分度)
,合称为伯德图(Bode图)。
对数幅频特性记为
单位为分贝(dB)
对数相频特性记为
单位为弧度(rad)
L(w) (dB) ... 40 20
0
0.01
-20
-4...0
(w)
... 90o
45o
0o 0.01
-45o -9...0o
0. 1
(3)具有相同幅值的两个系统, 由0时, 最小相位系统的相角迟后最小, 而非最小相位系统的相角迟后则较大。
1 : 0 90o Ts 1
1 : 180o 90o Ts 1
Ts 1: 0 90o Ts 1: 180o 270o
(4)非最小相位一般由两种情况产生: 系统内包含有非最小相位元件(如 延迟因子); 内环不稳定。
机械控制工程基础(北京理工)第四章第二节

§4-3开环频率特性
设系统开环传递函数一般形式为:
G (s) H (s) K ( i s 1) s v (T j s 1)
j 1 i 1 n v m
则系统开环频率特性的一般形式为:
G ( j ) H ( j ) K ( j i 1) ( j )
i 1 n v v m
L 时, 20lg T
在高频段,对数幅频曲线近的 为一条斜率为-20dB/dec且与横轴 交与点的直线。
交点处的频率叫惯性环 节的交接频率。
1T
交接频率的地方误差最大
五、一阶微分环节
一阶微分环节的传递函数为
G(s) Ts 1
频率特性为
G( j ) Tj 1
2
1 2
2
2
则
L 20lg 2 40lg 40lg 40lgn L 当 n 时, 0 ,而高频段振 荡环节的对数幅频特性曲线近似为一 条斜率为 40 dB dec 且与横轴相交于 n 点的直线,这条直线就是高频渐近线。 两条渐近线交 n 点处称为振荡环 节的交接频率。
令 则 1 x 2 (T ) 1
2 2
y
2
T
(T ) 1
2
1 (T ) 1 x y x 2 2 2 [(T ) 1] (T ) 1
2 2 2 1 1 1 2 x 2 x y 2 2 2
当 1 时
L() 20lg 2
根据上式可绘制出误差曲线图:
• 工程上,当 0.4 0.7 ,可用渐近线 代替实际曲线,否则须使用上述误
差曲线修正用渐近线表示的对数幅 频曲线。
机械控制工程基础4_控制系统的频率特性(2)

1. Bode 图的特点: ()横坐标对数分度,每 1 10倍频程刻度距离相等, 但标频率的真值。 (2)幅频特性图纵坐标的单位是分贝dB。 分贝的定义:当 20lg G(ji ) 1 时, 表示幅频特性在频率为i 时的值为1分贝。
2. 用Bode图表示频率特性的优点 : 可将串联环节幅值的乘 、除化为幅值的加、减 , 所以可分别做出各个环 节的Bode图,再用叠加法得 出系统的Bode图,因而简化了计算与 做图过程。
0 .1
20
对数幅频特性:
L( ) 20 lg A( ) 20 lg 1
90
G
20 lg
0 90
s1
0 .1
1
10
相频特性、对数相频特性
( ) 900
2018/6/26
积分环节的对数坐标图
4
4.3 典型环节的对数坐标图 L /dB
2018/6/26
2
4.3 典型环节的对数坐标图
(1)比例环节
20lg G dB
20
传递函数
G(s) K G( j) K
幅频特性 G ( j ) K 相频特性G ( j ) 0
20lg K
0
1
s1
100
10
G
10
对数幅频特性 20lg G ( j ) 20 lg K
90 0
G( j) /
s1
1
10
相频特性、对数相频特性
100
1000
( ) 900
2018/6/26
微分环节的对数坐标图
6
4.3 典型环节的对数坐标图
机械控制工程基础-总复习

推论:
d n xt n 0 sx n 2 0 x n 1 0 L n s X s s n 1 x0 s n 2 x dt
零初始条件
0 若:x 0 x x 0 x n 2 0 x n 1 0 0 d n x t n L s X s n dt
一、典型输入信号(掌握)
1. 阶跃函数 2. 斜坡函数 3. 加速度函数 4. 脉冲函数
5. 正弦函数
二、一阶系统的瞬态响应(掌握)
闭环传递函数 输入信号 输出响应
t 1 T e T
ess
0 0
(t )
(t 0)
1 Ts 1
1(t )
1e
t T
(t 0)
t T
t
t
1 2 t 2
t T Te
t 0
T
∞
1 2 2 t Tt T (1 e T ) t 0 2
等价关系: 系统对输入信号导数的响应,就等于系统对该输入信号响应的导数; 系统对输入信号积分的响应,就等于系统对该输入信号响应的积分。
三、二阶系统的瞬态响应
X i s
-
×
n ss 2 n
jV
0 2
G j
K U 0
0 0
jV
[G j ]
nm 3
nm 2
0
U
0 1
n m 1
乃氏图的终点
乃氏图的起点
三、频率响应的对数坐标图—伯德图
1.伯德图的定义(掌握)
由两张图组成。纵坐标分别为
对数幅频特性: L 20lg G j
控制工程基础第4章 控制系统的频率特性

( ) G ( j ) arctanT
As 0, 1) ( gain G ( j ) 1 L( ) 20lg G ( j ) 0
( ) 0
As 1 gain G ( j ) T L( ) 20lg G ( j ) 20 lg(T )
第四章 控制系统的频率特性
4.1 机电系统频率特性的概念及其实验基本方 法 4.2 极坐标图 4.3 对数坐标图 4.4 由频率特性曲线求系统的频率特性 4.5 控制系统的闭环频响
4.1 机电系统频率特性的概念及其实验基本方法
频率响应: 系统对正弦函数输入的问题响应。当输入正弦信号时, 系统的稳态输出也是正弦信号,且其频率与输入信号的 频率相同,其幅值及相角随着输入信号频率的变化而变 化。 当输入为非正弦的周期信号时,可将输入信号利用傅立 叶级数展开成正弦函数叠加的形式,系统的响应也是其 相应正弦函数响应的叠加 输入为非周期信号时也可以将它看作是周期为无穷大的 周期信号
V ( )
相频特性
A( )
( )
U ( )
4.2 极坐标图
Im( )
G ( j n )
Re( )
G ( j 2 )
G ( j1 )
4.2.1 典型环节的乃氏图
k
0
积分环节 比例环节
0
G (s) k G ( j ) k A( ) G ( j ) k
系统开环传递函数为: 100(0.05s+1) G(s)= s(0.1s+1)(0.2s+1) 试绘制其开环对数频率特性图
40 20 1 20lgk 5 10 20
1 -90 -180 -270
5
10
机械控制工程基础第四章习题解答

题目:线性定常系统对正弦信号(谐波输入)的__________________ 称为频率响应。
答案:稳态响应题目:频率响应是系统对_________________ 的稳态响应;频率特性G(j 3 )与传递函数G(s)的关系为_______________ 。
答案:正弦输入、s= j题目:以下关于频率特性、传递函数和单位脉冲响应函数的说法错误的是【】A•G(j ) G(s) s j B•G(s) F (t)C. G(s) L (t)D. G(j ) F (t)分析与提示:令传递函数中s j即得频率特性;单位脉冲响应函数的拉氏变换即得传递函数;单位脉冲响应函数的傅立叶变换即为频率特性。
答案:B题目:以下说法正确的有【】A .时间响应只能分析系统瞬态特性B. 系统的频率特性包括幅频特性和相频特性,它们都是频率3的函数C. 时间响应和频率特性都能揭示系统动态特性D •频率特性没有量纲E.频率特性反映系统或环节对不同频率正弦输入信号的放大倍数和相移分析与提示:时间响应可分析系统瞬态特性和稳态性能;频率特性有量纲也可以没有量纲,其量纲为输出信号和输入信号量纲之比。
答案:B、C、E题目:通常将_______________ 和 ____________ 统称为频率特性。
答案:幅频特性、相频特性题目:系统的频率特性是系统_______________ 响应函数的____________ 变换。
答案:脉冲、傅氏题目:频率响应是系统对_________________ 的稳态响应;频率特性G(j 3 )与传递函数G(s)的关系为_______________ 。
答案:正弦输入、s= j题目:已知系统的单位阶跃响应为x o t 1 1.8e 4t 0.8e 9t, t 0,试求系统的幅频特性和相频特性。
分析与提示:首先由系统的输入输出得到系统传递函数;令s= j即可得到频率特性,进而得到幅频特性和相频特性。
答案:由已知条件有1s ,s 1 1 1 -1.8 0.8 — s s 4 s 9X i X o s传递函数为G s X o s36 X i s s 4 s 9则系统的频率特性为G j36j 4 j 9其中,幅频特性为 ______ 36 16 2 .81相频特性为 题目:系统的传递函数为 arctg 才 arctg § arctg arctg — 3 ,则其频率特性是【0.2 (s) A • G(j 3 s 0.2 G(j 3 0.2 C . G(j _3 ____ 20.04G(j 3— (0.2 j0.04 2 答案:D G(s),在输入 X j (t) 4cos(t30 )作用下的稳态输出是【 】A . X °(t) 4 cos(t 15 )B . X o (t)C . X o (t) 2 2 cos(t 15 )D .Xo(t) 分析与提示: 系统的传递函数为 G(j)- 为A 1.1 2 , j输入信号频率为 题目:一阶系统的传递函数为 1的单频信号, 2 2 cos(t 15 )4 cos(t 15 ) ,幅频特性,相频特性分别1arctg 其稳态输出为同频率的单频信号,输出信号幅值 A 1 1 1 30o arctg 1 15o 答案 题目 答案 题目 答案 题目 答案题目B 频率特性表示了系统对不同频率的正弦信号的 复现能力 频率特性实质上是系统的___________________ 单位脉冲响应函数 频率特性随频率而变化,是因为系统含有 储能元件时间响应分析主要用于分析线性系统过渡过程, 以获得系统的动态特性, 而频率 ,以获得系统的动态特性。
《控制工程基础》第四章习题解题过程和参考答案

《控制工程基础》第四章习题解题过程和参考答案4-1 设单位反馈系统的开环传递函数为:10()1G s s =+。
当系统作用有下列输入信号时:()sin(30)r t t =+︒,试求系统的稳态输出。
解:系统的闭环传递函数为:10()()11()()1()111C s G s s s R s G s Φ===++这是一个一阶系统。
系统增益为:1011K =,时间常数为:111T =其幅频特性为:()A ω=其相频特性为:()arctan T ϕωω=- 当输入为()sin(30)r t t =+︒,即信号幅值为:1A =,信号频率为:1ω=,初始相角为:030ϕ=︒。
代入幅频特性和相频特性,有:1(1)A ====11(1)arctan arctan5.1911T ωϕω==-=-=-︒所以,系统的稳态输出为:[]()(1)sin 30(1)24.81)c t A A t t ϕ=⋅⋅+︒+=+︒4-2 已知系统的单位阶跃响应为:49()1 1.80.8(0)ttc t e e t --=-+≥。
试求系统的幅频特性和相频特性。
解:对输出表达式两边拉氏变换:1 1.80.8361()49(4)(9)(1)(1)49C s s s s s s s s s s =-+==++++++由于()()()C s s R s =Φ,且有1()R s s =(单位阶跃)。
所以系统的闭环传递函数为:1()(1)(1)49s s sΦ=++ 可知,这是由两个一阶环节构成的系统,时间常数分别为:1211,49T T == 系统的幅频特性为二个一阶环节幅频特性之积,相频特性为二个一阶环节相频特性之和:12()()()A A A ωωω===1212()()()arctan arctan arctanarctan49T T ωωϕωϕωϕωωω=+=--=--4-3 已知系统开环传递函数如下,试概略绘出奈氏图。
(1)1()10.01G s s =+ (2)1()(10.1)G s s s =+(3))1008()1(1000)(2+++=s s s s s G (4)250(0.61)()(41)s G s s s +=+ 解:手工绘制奈氏图,只能做到概略绘制,很难做到精确。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
频域法是一种工程上广为采用的分析 和综合系统间接方法。另外,除了电路 与频率特性有着密切关系外,在机械工 程中机械振动与频率特性也有着密切的 关系。机械受到一定频率作用力时产生 强迫振动,由于内反馈还会引起自激振 动。机械振动学中的共振频率、频谱密 度、动刚度、抗振稳定性等概念都可归 结为机械系统在频率域中表现的特性。 频域法能简便而清晰地建立这些概念。
通常,机电系统频率特性分母的阶 次大于分子的阶次,故当ω→∞时,乃 氏图曲线终止于坐标原点处;而当频率 特性分母的阶次等于分子的阶次,当 ω→∞时,乃氏图曲线终止于坐标实轴 上的有限值。 一般在系统频率特性分母上加极点, 使系统相角滞后;而在系统频率特性分 子上加零点,使系统相角超前。
令ω从-∞增长到0,相应得出的乃氏图是 与ω从0增长到十∞得出的乃氏图以实轴对 称的,例如图4-24所示的乃氏图。
为了识别系统的传递函数,我们可以产生一 个近似的单位脉冲信号δ(t)作为系统的输 入,记录系统响应的曲线g(t),则系统的频率 特性为
(4.16) 对于渐近稳定的系统,系统的单位脉冲 响应随时间增长逐渐趋于零。因此,可以对 照式(4.16)对响应g(t)采样足够的点,借 助计算机,用多点求和的方法即可近似求出 系统频率特性,即
K 所以
1
K
1
T1 2 1
2
e
j arctan T1
T1 1 T2 1
2
e
j arctan T1 arctan T2 2
A
K
T1 2 1 T2 2 1
2 arctan T1 arctan T2
频率特性的极坐标图 (乃奎斯特图,或乃氏图)
乃奎斯特(H.Nyquist), 1889~1976,美国Bell实 验室著名科学家 见光盘课件(第四章第二节)
各型乃氏图的低频段
频率特性的物理背景
对于一般线性系统均有类似的性质。系 统对正弦输入的稳态响应称为频率响应。 当输入正弦信号时,线性系统输出稳定后 也是正弦信号,其输出正弦信号的频率与 输入正弦信号的频率相同;输出幅值和输 出相位按照系统传递函数的不同随着输入 正弦信号频率的变化而有规律的变化,如 下图所示。
傅立叶正变换式
1 G j jRC 1
u i t
R
u
C
o
t
K 例:试求 G j 的幅频特 性和相频特性。j T1 j 1T2 j 1 解: 1 1 1 G j K
j T1 j 1 T2 j 1 e
j 2
图4-26 相频特性坐标
见光盘课件(第四章第三、四、 五节)
最小相位系统
I型系统伯德图低频段高度的确定
Ⅱ型系统伯德图低频段高度的确定
频率特性函数求取方法
(1) 如果已知系统的微分方程,可将输入 变量以正弦函数代入,求系统的输出变量 的稳态解,输出变量的稳态解与输入正弦 函数的复数比即为系统的频率特性函数。 (2) 如果已知系统的传递函数,可将系统 传递函数中的s代之以jω,即得到系统的 频率特性函数。 (3) 可以通过实验的手段求出。
频率特性函数实验求取方法
频率特性函数实验求取方法
频率特性函数实验求取方法
频率特性函数实验求取方法
频率特性函数实验求取方法
频率特性函数实验求取方法
由单位脉冲响应求系统的频率特性
已知单位脉冲函数的拉氏变换象函数等 于1,显然,单位脉冲函数的傅氏变换象函数 也等于 1 ,上式说明δ(t)隐含着幅值相等 的各种频率。如果对某系统输入一个单位脉 冲,则相当于用等单位强度的所有频率去激 发系统,系统单位脉冲响应的傅氏变换即为 系统的频率特性。单位脉冲响应简称为脉冲 响应,脉冲响应函数又称为权函数。
第四章 控制系统的频率特性
4.1 机电系统频率特性的概念及其基本实验 方法 4.2 极坐标图(Nyquist图) 4.3 对数坐标图(Bode图) 4.4 由频率特性曲线求系统传递函数 4.5 由单位脉冲响应求系统的频率特性 * 4.6 对数幅相图(Nichols图) 4.7 控制系统的闭环频响 4.8 机械系统动刚度的概念
逆Nyquist图
有时为了将无穷远处的部分表示在原点附 近,可画逆极坐标图,它是在极坐标上画 1 G j H j 图,而不是 图。 F(jω G j H j )的倒数,称为逆频率特性函数,记作
1 F j F j 显然,逆幅频和逆相频特性函数与幅频和相
F ( )
1 f t 2
f (t )e
jt
dt
傅立叶反变换式
F e d
j t
见光盘课件(第四章第一节)
例:如下图所示系统,其传递函数为
1 G s 1 RCs 1 R Cs 1 Cs
将s代之以jω,即得到系统的频率特性函数为
1
频特性函数之间有如下的关系:
1 1 F j F j F 1 j 图象称为逆 Nyquist F 图。 j
频率特性的对数坐标图 (伯德图)
伯德(H.W.Bode), 1905~1982,美国Bell实 验室著名科学家
图4-25 幅频特性坐标 伯德图幅值所用的单位分贝(dB)定义为 n(dB)=201gN 若ω2=10ω1,则称从ω1到ω2为十倍频程,以 “dec.”(decade)表示。
G j g t e
0
jt
dt
G j t
N 1 n 0
g nt e
jnt
t
N 1 n 0
g nt cosnt j sin nt
Re j Im
