相对论性动量与能量共28页
合集下载
大学物理学习课件-§18.4 相对论性动量与能量

Chapter 18. 相对论
§18. 4 相对论性动量与能量
§18.4 相对性动量与能量
·1 ·
Chapter 18. 相对论
§18. 4 相对论性动量与能量
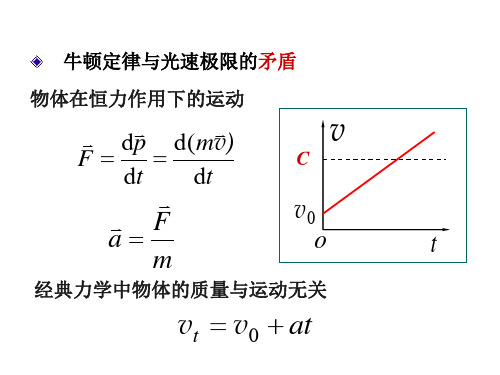
一.动量与质量
经典力学:质量为m的物体的加速度与外力关系为
F ma p mv t v v0 adt
验测得其质量皆大于静止质量。
v 2.7 10 m / s
8
m 2.3mo m 3.9mo
v 2.9 10 m / s
8
m
m0 1 ( vm / c )2
显然,当 vm c 时, m ,说明随着 vm增加, 质点的惯性也增加,作用在物体上的外力永远不能 将质点加速至超过光速的速度。
m0 mA 1 ( vA / c )2
m / m0
7 6 5 4 3 2 1 0.0 0.2 0.4 0.6 0.8 1.0
F1
一般地写成:
m m0 1 ( vm / c )2
vm c时,m m0
质量与速度关系
vm / c
·7 ·
Chapter 18. 相对论
§18. 4 相对论性动量与能量
-1
m / m0
1.661 1011 1.630 1011
1.590 1011 1.511 10
11 11
4
3
2 1
0 0.2 0.4 0.6 0.8 v/ c 1.0
1.283 10
·8 ·
Chapter 18. 相对论
§18. 4 相对论性动量与能量
☻实验测得当质子在加速器中被加速接近光速时,实
S
S
§18. 4 相对论性动量与能量
§18.4 相对性动量与能量
·1 ·
Chapter 18. 相对论
§18. 4 相对论性动量与能量
一.动量与质量
经典力学:质量为m的物体的加速度与外力关系为
F ma p mv t v v0 adt
验测得其质量皆大于静止质量。
v 2.7 10 m / s
8
m 2.3mo m 3.9mo
v 2.9 10 m / s
8
m
m0 1 ( vm / c )2
显然,当 vm c 时, m ,说明随着 vm增加, 质点的惯性也增加,作用在物体上的外力永远不能 将质点加速至超过光速的速度。
m0 mA 1 ( vA / c )2
m / m0
7 6 5 4 3 2 1 0.0 0.2 0.4 0.6 0.8 1.0
F1
一般地写成:
m m0 1 ( vm / c )2
vm c时,m m0
质量与速度关系
vm / c
·7 ·
Chapter 18. 相对论
§18. 4 相对论性动量与能量
-1
m / m0
1.661 1011 1.630 1011
1.590 1011 1.511 10
11 11
4
3
2 1
0 0.2 0.4 0.6 0.8 v/ c 1.0
1.283 10
·8 ·
Chapter 18. 相对论
§18. 4 相对论性动量与能量
☻实验测得当质子在加速器中被加速接近光速时,实
S
S
5-6相对论性动量和能量

27
质量亏损 m 0.22u
原子质量单位 1u 1.6610
2
kg
放出的能量 Q E m c 200 MeV 1g 铀— 235 的原子裂变释放的能量
Q 8.5 10 J
10
14
5-6 相对论性动量和能量
原子弹爆炸(核裂变)
15
5-6 相对论性动量和能量
我国于 1958 年建成的首座重水反应堆
不变
相对论动量守恒定律
6
5-6 相对论性动量和能量
三
质量与能量的关系
设 Ek 0 Fx dx 0
p m0v 1 2
p 0
x x
dp dx dt
p
0
vdp
d( pv ) pdv vdp
v 0
Ek vdp p v
Ek m0 v 2 1 v2 c 2
2 2 E m c ( E m c i i iK i 0 ) 恒量
m
i
恒量
质量守恒定律
在一个孤立系统内,粒子在相互作用过程中相 对论质量保持不变。
质量亏损
E K 1 E K 1 (m01 m02 )c
五 动量与能量的关系
E mc
2
m0c
2
2 2
E
1 v c
pc
p mv
2 2
m0v 1 v2 c 2
2 2 2
E0 m0c 2
E E p c
2 2 0
2 2
2 2
( mc ) ( m0c ) m v c
极端相对论近似 E E0 , E pc
21
5-6 相对论性动量和能量
质量亏损 m 0.22u
原子质量单位 1u 1.6610
2
kg
放出的能量 Q E m c 200 MeV 1g 铀— 235 的原子裂变释放的能量
Q 8.5 10 J
10
14
5-6 相对论性动量和能量
原子弹爆炸(核裂变)
15
5-6 相对论性动量和能量
我国于 1958 年建成的首座重水反应堆
不变
相对论动量守恒定律
6
5-6 相对论性动量和能量
三
质量与能量的关系
设 Ek 0 Fx dx 0
p m0v 1 2
p 0
x x
dp dx dt
p
0
vdp
d( pv ) pdv vdp
v 0
Ek vdp p v
Ek m0 v 2 1 v2 c 2
2 2 E m c ( E m c i i iK i 0 ) 恒量
m
i
恒量
质量守恒定律
在一个孤立系统内,粒子在相互作用过程中相 对论质量保持不变。
质量亏损
E K 1 E K 1 (m01 m02 )c
五 动量与能量的关系
E mc
2
m0c
2
2 2
E
1 v c
pc
p mv
2 2
m0v 1 v2 c 2
2 2 2
E0 m0c 2
E E p c
2 2 0
2 2
2 2
( mc ) ( m0c ) m v c
极端相对论近似 E E0 , E pc
21
5-6 相对论性动量和能量
大学物理-狭义相对论-相对论性动量和能量

我国于 1958 年建成的首座重水反应堆
我国已 建成的岭澳 核电站
我国在 建的单机容 量最大的田 湾核电站
原子弹核裂变
2 轻核聚变
氘核 氦核 质量亏损
释放能量
轻核聚变条件 温度要达到
有
的动能,足以克服两
力.
时,使 具 之间的库仑排斥
1967年6 月17日,中国 第一颗氢弹爆 炸成功
五 动量与能量的关系
而
,所以光速 C 为物体的极限速度 .
当
时
相对论动量守恒定律
当
时
常矢量
若
,则相对论动量守恒 经典动量守恒 .
常矢量
三 质量与能量的关系
相对论质能关系
静能
:物体静止时所具有的能量 .
质能关系预言:物质的质量就是能量的一种储藏 .
爱因斯坦认为(1905)
懒惰性
惯性 ( inertia )
活泼性
物理意义
惯性质量的增加和能量的增加相联系,质量的 大小应标志着能量的大小,这是相对论的又一极其 重要的推论 .
相对论的质能关系为开创原子能时代提供了理 论基础 , 这是一个具有划时代的意义的理论公式 .
质能关系预言:物质的质量就是能量的一种储藏.
例:
现有 100 座楼,每楼 200 套房,每套房用电功率
能量 ( energy )
物体的懒惰性就 是物体活泼性的度量 .
相对论能量和质量守恒是一个统一的物理规律.
一些微观粒子和轻核的静能量
粒子
符号
光子
电子(或正电子) e(或 +e
质子
)p
中子
n
氘
氚
氦( 粒子)
静能量 MeV 0 0.510
相对论的动量和能量
电子的静能 m0c2 8.19 1014 J 0.511MeV
质子的静质量
m0 1.6731027 kg
质子的静能 m0c2 1.5031010 J 938MeV
1千克的物体所包含的静能 9 1016 J
1千克汽油的燃烧值为 4.6 107 焦耳 .
5)相对论能量和质量守恒是一个统一的物理规律。
➢ 锂原子的核反应
E mc 2 m0c2 Ek
7 3
Li11H48
Be42
He42He
α 两 粒子所具有的总动能
1 1
H
Ek 17.3MeV
α 两 粒子质量比静质量增加
4 2
He
3 7
Li
4 2
He
m
Ek c2
3.08 1029 kg
0.01855u
实验测量 mH 1.00783u mLi 7.01601u
质能关系预言:物质的质量就是能量的一种储藏。
例:m0 1kg, E0 m0c2 91016 J
现有 100 座楼,每楼 200 套房,每套房用电功率
10000 W ,总功率 2 108 W ,每天用电 10 小时 ,
年耗电量 2.72 1015 J ,可用约 33 年。 电子的静质量 :m0 0.9111030 kg 电子的静能 :m0c2 8.19 1014 J 0.511MeV
积分后,得 Ek
m0 v 2 1 v2
c2
m0c2
1 v2 c2 m0c2
m m0 Ek mv2 m0c2 1 v2 c2 m0c2
相对论动能 Ek mc2 m0c2 m0c2 (
当 v c 时,
Ek
1 2
m0 v 2
相对论性动量与能量

P.10P. . 10 / 39 .
实验验证
☻1901年,实验物理学家考夫曼从镭辐射测 射线在
电场和磁场中的偏转,发现电子质量随速度变化。
☻1908年,德国物理学家布雪勒用改进了的方法测量
电子的质量,证实了爱因斯坦理论。
v / c e / m实验值(C kg-1)
0.3173 1.661 1011 0.3787 1.630 1011 0.4281 1.590 1011 0.5154 1.511 1011 0.6870 1.283 1011
Chapter 158. 相. 相对对论论
§§51. 48.相2 对洛论沦性兹动变量换与能量
由洛沦兹速度变换得:
P.7.P. 7 / 39 .
vA
vv 1 ( v )v / c2
1
2v v2 /
c
2
v
c2 vA
1
1 ( vA / c )2
S
S
v
代入得:
mA
mB 1 ( vA / c )2
§§51. 48.相2 对洛论沦性兹动变量换与能量
P.13P. . 13 / 39 .
S
S
v
o voA
mA m mB
A
B
代入得: mA
x
vB
x
mB 1 ( vA / c )2
Chapter 158. 相. 相对对论论
§§51. 48.相2 对洛论沦性兹动变量换与能量
P.9.P. 9 / 39 .
可知: mA mB 在S′中,B静止,称 mB为静止质量,常用 m0 表示。 当A静止时,应与B完全一样,其静止质量亦为 m0
P.12P. . 12 / 39 .
相对论的动量和能量

当 v << c 时
Ek
mc2
m0c
m0c2
2( 1
1 v2
/
1
c2
m0c 2 v2 /
1)
c
2
m0c2
m0 c2 (1
v2 2c 2
3v 4 8c 4
1)
1 2
m0v
2
与经典一致
5.实验证明 最早对相对论质量—能量关系提供的实验证明之一,是1932年由考克 罗夫特(J.D.Cockcroft)和瓦尔顿(G.T.S.Walton)提供的.他们利用加速 器加速质子并轰击锂(Li)靶.锂原子核吸收质子形成不稳定的核随即蜕变 为两个粒子,它们以高速沿相反的方向运动.
E2
p2c 2
m02
c4 v2c2 1 v2 / c2
m02c 4
E2 E02 p2c2
对光子 m0=0
E h
p E h h c c
对光子 m0=0
E h p E h h
c c
当 v<<c 时
由E2 E02 p2c2
(E E0 )(E E0 ) p2c2
E E0 2m0c2
u3 vz / 1 2
2.质速关系 质速关系
m m0
1 2
m0为静止质量
光子静止质量为零.
m>m0 已被实验证实. 1901年考夫曼发现电子的
质量是随速度增加而增加的.
m/m0
5 4
3 2 1
v/c
0 0.2 0.4 0.6 0.8 1.0
3.动力学方程
F
dp dt
d dt
(mv)
d dt
(
m0
v)
Ek
mc2
m0c
m0c2
2( 1
1 v2
/
1
c2
m0c 2 v2 /
1)
c
2
m0c2
m0 c2 (1
v2 2c 2
3v 4 8c 4
1)
1 2
m0v
2
与经典一致
5.实验证明 最早对相对论质量—能量关系提供的实验证明之一,是1932年由考克 罗夫特(J.D.Cockcroft)和瓦尔顿(G.T.S.Walton)提供的.他们利用加速 器加速质子并轰击锂(Li)靶.锂原子核吸收质子形成不稳定的核随即蜕变 为两个粒子,它们以高速沿相反的方向运动.
E2
p2c 2
m02
c4 v2c2 1 v2 / c2
m02c 4
E2 E02 p2c2
对光子 m0=0
E h
p E h h c c
对光子 m0=0
E h p E h h
c c
当 v<<c 时
由E2 E02 p2c2
(E E0 )(E E0 ) p2c2
E E0 2m0c2
u3 vz / 1 2
2.质速关系 质速关系
m m0
1 2
m0为静止质量
光子静止质量为零.
m>m0 已被实验证实. 1901年考夫曼发现电子的
质量是随速度增加而增加的.
m/m0
5 4
3 2 1
v/c
0 0.2 0.4 0.6 0.8 1.0
3.动力学方程
F
dp dt
d dt
(mv)
d dt
(
m0
v)
相对论性动量和能量

(4)继续 <加<速c 。时,回c是到速F度 的 极m0限a 。
注:用加速度表示的牛顿第二定律公式在相对论
4
力学中不再成立。
第5页/共27页
三、质量与能量的关系
1. 相对论动能
相对论动力学中,力对粒子做功,使粒子速率由0增
加到v,力所做的功仍和粒子最后的动能相等。
Ek
其中
vdF(mvd)rmvd(ddmvtv)
1.相对论质量
讨论:
m
m0
m0-静止质量
1 v 2 c2 v-物体相对参
考系的速率
(5)对于光子速率 v=c, m又不可能为无限大,由
上式可得光子静止质量 m0=0。
(6) v <<c有时,m≈m0,回到
m
牛顿力学情况,符合“对应原
理”。
m0
o
Cv
1
第2页/共27页
1.相对论质量 2. 相对论动量
m0c2
讨论:
相对论动量能量三角形
(2)低速情况,v≪ c
将 E Ek m0c2 代入上式,得
Ek2 2Ek m0c2 p2c2
∵ Ek m0c2 可略去Ek2项
21
得
Ek
p2 2m0
牛顿力学动能表达式.
第22页/共27页
(3)光子的能量、动量:
光子的静止质量 m0=0;
总质量
m
E c2
与经典物理学相比较,狭义相对论更客观、更真 实地反映了自然的规律。
目前,狭义相对论不但已经被大量的实验事实所证 实,而且已经成为研究宇宙星体、粒子物理以及一系 列工程物理等问题的基础。
当然,随着科学技术的不断发展,一定还会有新的、 目前尚不知道的事实被发现,甚至会有新的理论出现。 然而,以大量实验事实为根据的狭义相对论在科学中 23 的地位是无法否定的。
相对论性动量和能量

15 - 5 相对论性动量和能量
第十八章狭物(义理第学二相教版程)对论
1967年6 月17日,中国 第一颗氢弹爆 炸成功
第十五章 狭义 相对论
15 - 5 相对论性动量和能量
第十八章狭物(义理第学二相教版程)对论
五 动量与能量旳关系
E mc2 m0c2 1 v2 c2
p mv m0v 1 v2 c2
第十八章狭物(义理第学二相教版程)对论
例1 设一质子以速度 v 0.80c 运动. 求其总
能量、动能和动量.
解 质子旳静能 E0 m0c2 938MeV
E mc2
m0c 2 1 v2
c2
938 (1 0.82 )1 2
MeV
1563MeV
Ek E m0c2 625MeV p mv m0v 6.681019 kg m s1
➢ 相对论能量和质量守恒是一种统一旳物理规律.
第十五章 狭义 相对论
15 - 5 相对论性动量和能量
第十八章狭物(义理第学二相教版程)对论
某些微观粒子和轻核旳静能量
粒子 光子 电子(或正电子) 质子 中子 氘 氚
氦( 粒子)
符号
e(或 +e) p
n
2H 3H
4 He
静能量 MeV 0 0.510
m
Ek c2
3.081029 kg
0.01855u
试验测量 mH 1.00783u mLi 7.01601u
mHe 4.00260u
m 0.01864u
理论计算和试验成果相符. 1u 1.66 1027 kg
第十五章 狭义 相对论
第十五章 狭义 相对论
我国在 建旳单机容 量最大旳田 湾核电站
