六逆滤波和维纳滤波-Read
智慧树知到数字图像处理章节测试答案

智慧树知到《数字图像处理》章节测试答案第一章1、表示一幅灰度图像,一般用()?一个常数二维矩阵三维矩阵一个变量答案: 二维矩阵2、彩色图像中,每个像素点用()表示色彩值?一个值二个值三个值四个值答案: 三个值3、不可见光是可以形成图像的对错答案: 对4、数字图像的质量与量化等级有关对错答案: 对5、一幅模拟图像转化为数字图像,要经过()?重拍重拍采样量化变换答案: 采样,量化6、某个像素的邻域,一般有()?4-邻域8-邻域10-邻域对角邻域答案: 4-邻域,8-邻域,对角邻域第二章1、傅里叶变换得到的频谱中,低频系数对应于()?物体边缘噪音变化平缓部分变化剧烈部分答案: 变化平缓部分2、一幅二值图像的傅里叶变换频谱是()?一幅二值图像一幅灰度图像一幅复数图像一幅彩色图像答案: 一幅灰度图像3、傅里叶变换有下列哪些特点()?有频域的概念均方意义下最优有关于复数的运算从变换结果可以完全恢复原始数据答案: 有频域的概念,有关于复数的运算,从变换结果可以完全恢复原始数据4、图像的几何变换改变图像的大小或形状,例如()?平移旋转缩放退化答案: 平移,旋转,缩放5、傅里叶变换得到的频谱中,高频系数对应于图像的边缘部分。
对错答案: 对6、图像平移后,其傅里叶变换的幅度和相位均保持不变。
对错答案: 错第三章1、图像与其灰度直方图间的对应关系是()?一一对应多对一一对多都不对答案:2、下列算法中属于点处理的是()?梯度锐化直方图均衡化傅里叶变换中值滤波答案:3、为了去除图像中某一频率分量,除了用带阻滤波器还可以用()?低通滤波器高通滤波器带通滤波器低通滤波器加高通滤波器答案:4、要对受孤立噪声点影响的图像进行平滑滤波,不能达到效果的滤波器是()?中值滤波器邻域平均滤波器高频增强滤波器线性锐化滤波器答案:5、应用傅里叶变换的可分离性可以把图像的二维变换分解为行和列方向的一维变换。
对错答案:6、基于空域的图像增强方法比基于频域的增强方法的效果要好。
维纳滤波器

w
* 1
m in
w
* 0
w
0
w
1
记 为 w w , w w
* T N 1
( w ) 若 使最 ( w )小 , 须 0 w 即
( w ) ( w ) ( w ) ( w ) , ,, 2 R w 2 p 0 w w w w 0 1 N 1
E dn () 2 w () n E d () n xn () N
2
T
期 望 响 应 的 平 均 功 率
2 d
( n ) 是 w 的 函 数 , 即 ( n ) ( w )
T w () n E xn () xn () w () n N N T
——维纳-霍甫夫(Wiener-Hopf)方程
它反映了相关函数与最佳单位脉冲响应之间的关系。
Wiener-Hopf方程的矩阵形式
R hR s x x x
自相关矩阵 故最佳单位脉冲响应 其中
s () n 与的 x () n互 相 关
h RR s x o p t
R 0, N1 R 1, N1 RN1,N1
xn 观察/测量数据
s n 真实信号
vn 加性噪声/干扰
ˆ s n x n h n h i x n i 线性估计问题 i
ˆ e n s n s n
2
估计误差
n E en m i n h n 最小均方误差(MMSE)估计
得到:
E [] e x 0 i 0 , 1 ,, N 1 i
或
N 1 E h x sx 0 i j j j 0
维纳滤波器

西安电子科技大学统计与自适应信号处理仿真学院:班级:学号:姓名:2013年12月FIR 维纳滤波器1维纳滤波原理概述维纳(Wiener )是用来解决从噪声中提取信号的一种过滤(或滤波)方法。
这种线性滤波问题,可以看做是一种估计问题或一种线性估计问题。
一个线性系统,如果它的单位样本响应为)(n h ,当输入一个随机信号)(n x ,且)()()(n v n s n x += (1) 其中)(n x 表示信号,)(n v )表示噪声,则输出)(n y 为∑-=mm n x m h n y )()()( (2)我们希望)(n x 通过线性系统)(n h 后得到的)(n y 尽量接近于)(n s ,因此称)(n y 为)(n s 的估计值,用^)(n s 表示,即^)()(n s n y = (3) 则维纳滤波器的输入—输出关系可用下面图1表示。
图1 维纳滤波器的输入—输出关系实际上,式(2)所示的卷积形式可以理解为从当前和过去的观察值)(n x ,)1(-n x ,)2(-n x …)(m n x -,…来估计信号的当前值^)(n s 。
因此,用)(n h 进行过滤问题实际上是一种统计估计问题。
一般地,从当前的和过去的观察值)(n x ,)1(-n x ,)2(-n x …估计当前的信号值^)()(n s n y =成为过滤或滤波;从过去的观察值,估计当前的或者将来的信号值)0)(()(^≥+=N N n s n y 称为外推或预测;从过去的观察值,估计过去的信号值)1)(()(^>-=N N n s n y 称为平滑或内插。
因此维纳滤波器又常常被称为最佳线性过滤与预测或线性最优估计。
这里所谓的最佳与最优是以最小均方误差为准则的。
如果我们分别以)(n s 与^)(n s 表示信号的真实值与估计值,而用)(n e 表示他们之间的误差,即)()()(^n s n s n e -= (4)显然)(n e 可能是正值,也可能是负值,并且它是一个随机变量。
维纳滤波

维纳滤波7.2 维纳滤波从连续的(或离散的)输入数据中滤除噪声和干扰以提取有用信息的过程称为滤波,而相应的装置称为滤波器。
根据滤波器的输出是否为输入的线性函数,可将它分为线性滤波器和非线性滤波器两种。
滤波器研究的一个基本课题就是:如何设计和制造最佳的或最优的滤波器。
所谓最佳滤波器是指能够根据某一最佳准则进行滤波的滤波器。
20世纪40年代,维纳奠定了关于最佳滤波器研究的基础。
即假定线性滤波器的输入为有用信号和噪声之和,两者均为广义平稳过程且知它们的二阶统计特性,维纳根据最小均方误差准则(滤波器的输出信号与需要信号之差的均方值最小),求得了最佳线性滤波器的参数,这种滤波器被称为维纳滤波器。
在维纳研究的基础上,人们还根据最大输出信噪比准则、统计检测准则以及其他最佳准则求得的最佳线性滤波器。
实际上,在一定条件下,这些最佳滤波器与维纳滤波器是等价的。
因而,讨论线性滤波器时,一般均以维纳滤波器作为参考。
维纳滤波理论用于解决最小均方误差下的线性滤波问题。
设接收到(或观测到)的信号为随机信号(7-1)其中s(t)是未知的实随机信号,n(t)是噪声。
要设计的线性滤波器,其冲击响应为h(t, τ),输入为x(t),输出为,即(7-2)令为估计误差。
冲击响应h(t, τ)按最小均方误差准则确定,即h(t, τ)必须满足使(7-3)达到最小。
根据最小均方误差估计的正交条件,有以下关系成立(7-4)令(7-5)(7-6)则有(7-7)上述方程通常称为非平稳随机过程条件下的维纳-霍甫(Wiener-Kolmogorov)积分方程。
特别当x(t),s(t)均为广义(或宽)平稳随机信号,而滤波器是线性时不变系统的情况下,x(t)与s(t)必为联合平稳,式(7-7)可写为(7-8)令,,则有(7-9)此处,“*”号表示卷积,对上式两边取Fourier变换,可得(7-10)(7-11)对于因果线性系统,有(7-12)采用完全相同的分析方法,推得因果平稳维纳-霍甫积分方程如下(7-13)(7-14)其中,表示的零、极点位于,表示的零、极点位于。
第八章 维纳滤波
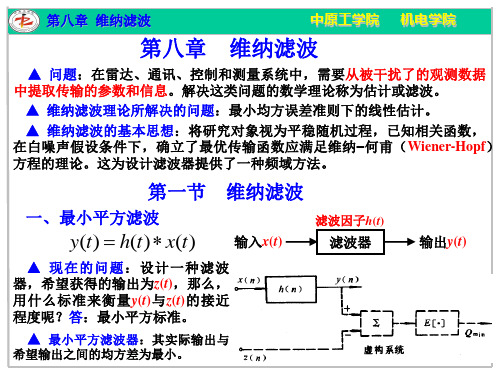
rxx(λ-k)
rzx(λ)
第八章 维纳滤波 维纳-何甫积分方 程式(离散形式):
中原工学院
N xx
机电学院
h(k )r
k 0
N
( k ) rzx ( ) 或 h(k )rxx (k ) rzx ( )
k 0
自相关函数为偶函数
▲ 维纳滤波器 如果已知x(n)与所要求的输出信号z(n),则当x(n)的自相关函 数和z(n)与x(n)的互相关函数为已知时,求解维纳-何甫方程,即可求得满足均 方误差最小的滤波因子h(n)。这就是按照最小平方准则设计的线性滤波系统, 它是一个最佳系统,通常称为维纳滤波器。 这是一个对 称 矩阵 。 卷积形式:
第八章 维纳滤波
中原工学院
机电学院
第二节
反滤波
一、回声鸣震现象及反滤波
问题的提出:在某些情况下(例如,在大礼堂内演讲,由于墙壁多次反射, 而造成回声交混,形成一片轰鸣声,使人们听不清讲话内容)所录取的信号, 可认为是原始信号经过几个物理系统(信号传输的路径或通道)作用的结果, 或者看成是源信号经过几个物理滤波器以串联形式滤波的结果。这时,采用 反滤波方法可以使真正源信号从干扰中恢复出来。
n n n n
期望输出s(n)与输入x(n)的互相关函数为
n n
rsx (k ) s(n k ) x(n) s(n k )[s(n) n(n)] rss (k )
如果以 Rss(ejω) 和 Rnn(ejω) 分别表示 rss(k) 和 rnn(k) 的频谱,即分别为 s(n) 和 n(n) 的功率谱,则在对维纳滤波的时间范围不加限制的情况下,由式H(ejω)=Rzs(ejω)/ Rxx(ejω),可以得到维纳滤波器的频率响应应为:
维纳滤波(最小均方滤波)

(3-10)
其中������������������ (������, ������ )为噪声功率谱,������������������ (������, ������)为图像功率谱。由式(2.5)可以看出, 当没有噪声时,有P u, v = 1/H(u, v),维纳滤波器就可以简化的看成是逆滤波 器。 在有噪声的情况下, 维纳滤波也用信噪功率比作为修正函数对逆滤波器进行 了修正,但它在均方误差最小的意义上提供最佳恢复。 通常将噪声假设为白噪声,即噪声功率谱������������������ (������, ������ )为常数,若������������������ (������, ������)在频 谱空间上高频区下降比������������������ (������, ������ )快得多,这种假设就近似正确。于是可以认为 ������������������ ������, ������ = ������������������ 0,0 = 常数(3-11) 如果噪声时各态历经的,可以用一幅噪声图像进行计算从而求得������������������ 0,0 ,
∞ ������(������ , ������ )������(������ −∞
− ������, ������ − ������ )������������������������(3-6)
式中,������(������, ������)为维纳滤波器的点扩散函数。按照均方误差最小准则,������ ^ x, y 应该满足 ������ 2 = ������ ������ ������, ������ − ������ ^ x, y
∞ ������(������ , ������)������(������ −∞ ∞ ������(������ , ������)������(������ −∞
IIR滤波FIR滤波及维纳滤波简介、程序及仿真结果

IIR 滤波器、FIR 滤波器与维纳滤波器所谓数字滤波器,是指输入、输出均为数字信号,通过一定运算关系改变输入信号所含频率成分的相对比例或者滤除某些频率成分的器件。
数字滤波器从实现的网络结构或者从单位脉冲响应分类,可以分为无限脉冲响应(IIR )滤波器和有限脉冲响应(FIR )滤波器。
它们的系统函数分别为:1.1n N n z n h z H --=∑=10)()( 1.21.1中的H(z)成为N 阶IIR 滤波器,1.2中的H(z)称为(N-1)阶FIR 滤波器函数,这两种类型的设计方法有很大的区别。
IIR 数字滤波器的设计既可以从模拟滤波器的设计入手来进行,也可以直接利用指标参数,通过调用滤波器设计子程序或函数来进行。
可以利用脉冲响应不变法来设计IIR 数字低通滤波器,按照技术要求设计一个模拟低通滤波器,得到模拟低通滤波器的传输函数,再按一定的转换关系将传输函数转换成数字低通滤波器的系统函数H(z)。
设模拟滤波器的传输函数是s H a (),相应的单位冲激响应是)(t h a ,对)(t h a 进行等间隔采样,采样间隔为T ,得到)(nT h a ,将h(n)= )(nT h a 作为数字滤波器的单位取样响应,那么数字滤波器的系统函数便是h(n)的z 变换,因此脉冲响应不变法是一种时域上的转换方法,它使h(n)在采样点上等于)(t h a∑=-=Ni iia s s A s H 1)( 1.3 ∑=--=Ni T s iz eA z H i 111)( 1.4 将s H a ()在s 平面上沿虚轴按照周期2pi/T 延括后,再按标准映射关系sT e z =,映射到z 平面上,就得到了H(z)。
脉冲响应不变法的优点是频率坐标变化时线性的,如果不考虑频率混叠现象,用这种方法设计的数字滤波器会很好的重现模拟滤波器的频率特性。
以下为用matlab 仿真的一个IIR 低通滤波器: % IIR Lowpass Use Butterworth % copyright by Etual clear;fs=20;fpass=4;fstop=5;∑∑=-=--=Nk kk Mk k k z a z b z H 101)(Ap=0.5;As=10;wp=2*pi*fpass/fs;ws=2*pi*fstop/fs;omegap=tan(wp/2);omegas=tan(ws/2);ep=sqrt(10^(Ap/10)-1);es=sqrt(10^(As/10)-1);N=ceil(log(es/ep)/log(omegas/omegap));omega0=omegap/ep^(1/N);K=floor(N/2);for i=1:Ktheta(i)=pi*(N-1+2*i)/(2*N);endfor i=1:KG(i)=omega0^2/(1-2*omega0*cos(theta(i))+omega0^2);endfor i=1:Ka1(i)=2*(omega0^2-1)/(1-2*omega0*cos(theta(i))+omega0^2);endfor i=1:Ka2(i)=(1+2*omega0*cos(theta(i))+omega0^2)/(1-2*omega0*cos(theta(i))+omeg a0^2);endif K<(N/2)G0=omega0/(omega0+1);a0=(omega0-1)/(omega0+1);endw=0:pi/300:pi;Hw2=1./(1+(tan(w/2)/omega0).^(2*N));plot(w/pi,Hw2);grid;图一IIR滤波器频谱图IIR数字滤波器能保留一些典型模拟滤波器优良的幅度特性,但设计中只考虑了幅度特性,没考虑相位特性,所设计的滤波器相位特性一般是非线性的。
python频域逆滤波和维纳滤波

一、概述Python是一种功能强大的编程语言,可以用于各种领域的科学计算和数据处理。
在信号处理领域,频域逆滤波和维纳滤波是两种常用的技术,用于处理受损信号和去噪。
本文将介绍如何使用Python实现频域逆滤波和维纳滤波,并探讨它们在信号处理中的应用。
二、频域逆滤波1. 概念介绍频域逆滤波是一种用于复原受损信号的技术,它利用信号的频谱信息进行处理。
当信号经过损坏或失真后,可以使用频域逆滤波来尝试恢复原始信号。
2. Python实现在Python中,可以使用`numpy`和`scipy`等库来实现频域逆滤波。
需要获取受损信号的频谱信息,然后根据损坏的模型和系统响应函数,进行逆滤波操作。
通过反变换将处理后的频谱信息还原为时域信号。
3. 应用案例频域逆滤波在医学图像处理、通信系统恢复和地震信号处理等领域有广泛的应用。
通过Python实现频域逆滤波,可以方便地应用于各种实际问题的处理和解决。
三、维纳滤波1. 概念介绍维纳滤波是一种统计信号处理方法,用于在有噪声的环境中对信号进行处理。
它结合了信号的频谱信息和噪声的统计特性,可以实现对受噪声干扰的信号进行有效的去噪处理。
2. Python实现在Python中,可以利用`numpy`和`scipy`等库来实现维纳滤波。
需要获取受噪声信号的频谱信息和噪声的统计特性,然后根据维纳滤波器的设计原理进行滤波处理。
通过反变换将处理后的频谱信息还原为时域信号,以实现信号的去噪处理。
3. 应用案例维纳滤波在语音信号处理、图像去噪和雷达信号处理等领域有着广泛的应用。
通过Python实现维纳滤波,可以实现对受噪声干扰的信号进行有效的去噪处理,提高信号的质量和可靠性。
四、总结频域逆滤波和维纳滤波是两种常用的信号处理技术,在处理受损信号和去噪处理中具有重要的应用价值。
通过Python实现这两种滤波方法,可以方便地进行信号处理实验和应用,为信号处理领域的研究和应用提供了新的工具和方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验六 逆滤波和维纳滤波 SC07023017 陆金星一、实验内容1:先由原始图像(任选)产生待恢复的图像;(产生方法如下:冲激函数为240(,)h x y =,将原始图像与冲激函数卷积产生模糊,然后再迭加均值为0,方差为8,16,32的高斯随机噪声而得到一组待恢复的图像;2:分别用逆滤波和维纳滤波恢复上面图像。
实验图像:Cameraman.bmp二、实验原理 【退化模型】 图像恢复需要根据一定的图像退化模型来进行,一个简单的通用图像退化模型如下图所示,在这个模型中,图像退化过程被模型化为1个作用在输入图像(,)f x y 上的系统H ,它与1个加性噪声(,)n x y 的联合作用导致产生退化图像(,)g x y 。
根据这个模型恢复图像也就是要在给定(,)g x y 和H 的基础上得到对(,)f x y 的某个近似的过程(这里假设已知(,)n x y 的统计特性)。
一维情况:设()f x 中x 的取值范围是0,1,,1A -,()h x 中x 的取值范围是0,1,,1B -,为了避免卷积的各周期重叠(设每个采样函数的周期为M ),取1M A B ≥+-,并将函数用零扩展补齐。
用()e f x 和()e h x 表示扩展的函数,它们的卷积为:1()()()()M e e e e m g x f m h x m n x -==-+∑ 0,1,,M-1x =可以用矩阵形式表示为:(0)(0)(1)(1)(0)(0)(1)(1)(0)(2)(1)(1)(1)(1)(2)(0)(1)(1)e e e e e e e e e e e e e e e e e e g h h h M f n g h h h M f n g H f n g M h M h M h f M n M --+⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥-+⎢⎥⎢⎥⎢⎥⎢⎥=+==+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-----⎣⎦⎣⎦⎣⎦⎣⎦(,)f x y(,)g x y(,)n x y根据()e h x 的周期性可知()()e e h x h x M =+,所以上式中的H 可进一步写成:(0)(1)(1)(1)(0)(2)(1)(2)(0)e e e ee e e e e h h h h h h H h M h M h -⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥--⎣⎦二维情况:由一维情况可以推广到二维情况,得到:(,)0 1 01(,)0 1 1e f x y x A y B f x y A x M B y N ≤≤-≤≤-⎧=⎨≤≤-≤≤-⎩和或 (,)0 1 01(,)0 1 1e h x y x C y D h x y C x M D y N ≤≤-≤≤-⎧=⎨≤≤-≤≤-⎩和或 又可以得到:11000,1,,1(,)(,)(,)(,)0,1,,1M N e e e e m n x M g x y f m n h x m y n n x y y N --===-=--+=-∑∑可以用矩阵形式表示为:011102120(0)(0)(1)(1)(1)(1)M e e e e ee M M H H Hf n f n H H Hg H f n f MN n MN H H H ---⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=+=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎢⎥⎣⎦⎣⎦⎣⎦ 其中每个i H 是由扩展函数(,)e h x y 的第i 行而来:i (,0)(,1)(,1)(,1)(,0)(,2)(,1)(,2)(,0)e e e ee e e e e h i h i N h i h i h i h i H h i N h i N h i -⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥--⎣⎦【循环矩阵对角化】直接从g H f n =+的表达式中计算以求解f 的计算量会很大,可以通过对角化H 来简化。
对于一维循环矩阵,可以将H 的M 个本征矢量组成1个M M ⨯的矩阵W ,[(0),(1),,(1)]W w w w M =- 其中22(1)()[1,,,]jk jM kT MMw k eeππ-= 0,1,,1k M =-,这样可以将H 写成1H WDW -=,D 是对角矩阵,元素是H 的本征值。
对于二维块循环矩阵,定义1个MN MN ⨯的矩阵W ,其每个元素为:2(,)jim MN W i m eW π=,,0,1,,1i m M =-,其中N W 为1个N N ⨯的矩阵,其每个元素为:2(,)jkn MN W k n eπ=,,0,1,,1k n N =-,这样可以将H 写成1H W DW -=。
将循环矩阵对角化应用与退化模型计算,可以有n W f DW g W111---+=,令1,,1,0,1,,1,0-=-=N v M u ,则以下各式成立:1100110011001001(,)(,)exp 21(,)(,)exp 21(,)(,)exp 21(,)(,)M N e x y M N e x y M N e x y M N e x y ux vy G u v g x y j MN M N ux vy F u v f x y j MN M N ux vy N u v n x y j MNM N H u v h x y MNπππ--==--==--==--==⎡⎤⎛⎫=-+ ⎪⎢⎥⎝⎭⎣⎦⎡⎤⎛⎫=-+ ⎪⎢⎥⎝⎭⎣⎦⎡⎤⎛⎫=-+ ⎪⎢⎥⎝⎭⎣⎦=∑∑∑∑∑∑∑1exp 2ux vy j M N π⎡⎤⎛⎫-+ ⎪⎢⎥⎝⎭⎣⎦∑而D 的MN 个对角元素可表示为:(),mod , 0 k MN H k N i k D k i N i k ⎧⎛⎫⎢⎥⨯=⎪ ⎪⎢⎥=⎣⎦⎨⎝⎭⎪≠⎩如如,将MN 并入(,)H u v ,得到0,1,,1(,)(,)(,)(,)0,1,,1u M G u v H u v F u v N u v v N =-=+=-上式说明,求解退化模型的大系统方程,只需计算很少几个N M ⨯的傅里叶变换就可以了。
由Hf g n -=,在对n 没有先验知识的情况下,寻找1个f 的估计值∧f ,使n 的模或范数最小:⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛-=-==∧∧∧f H g f H g fH g n n nTT 22,这样可把恢复问题看作是对∧f 求式2∧∧-=⎪⎭⎫ ⎝⎛f H g f L 的最小值,将L 对∧f 求微分并设结果为零,再设N M =和1-H 存在,可得无约束恢复公式:()()g H g H H H g H H H f T T T T 1111----∧===当选取∧f 的1个线性操作符Q (变换矩阵),使得2∧fQ 最小。
设l 为拉格朗日乘数,要找到最小化准则函数()222nHfg l fQ f L --+=⎪⎭⎫⎝⎛∧∧的∧f ,可得到有约束恢复公式(令l s 1=):[]g H QsQ H H f T T T 1-∧+=。
【逆滤波】,逆滤波是一种无恢复约束,设M N =,则将1H WDW-=代入1f Hg ∧-=可以得到,11111()f H g WDW g WD W g ∧-----===,如将上式两边乘以1W -得到:111ˆW f D W g ---=。
式中各个元素能写成形式:(,)(,)(,)G u v F u v H u v ∧=,这种恢复方法称为逆滤波。
将(,)H u v 看作1个滤波函数,则它与(,)F u v 的乘积是退化图像(,)g u v 的傅里叶变换。
用(,)H u v 去除(,)G u v 就是1个逆滤波过程。
将(,)(,)(,)G u v F u v H u v ∧=的结果求反变换就得到恢复后的图像:11(,)ˆ(,)[(,)](,)G u v f x y F F u v F H u v ∧--⎡⎤==⎢⎥⎣⎦, 实际为了减小噪声的影响以及防止(,)H u v 取零或很小的影响,将恢复转移函数(.)M u v 取为 (.)(.)1/(.)k H u v dM u v H u v ≤⎧=⎨⎩如其它,其中k 和d 为小于1的常数,且d 选的较小为好。
【维纳滤波】维纳滤波是一种有约束恢复,是一种最小均方误差滤波器,设f R 和n R 分别是f 和n 的相关矩阵,则1f R WAW -=,1n R WBW -=,其中A 和B 中的元素对应f R 和n R 中的相关元素的变换,代入有约束恢复公式,可以得到:1111111()()T T f n f H H sR R H g WD DW sWA BW WD W g ∧-------=+=*+*也可以写成如下形式:22(,)1ˆ(,)(,)(,)(,)(,)/(,)n f H u v F u v G u v H u v H u v s S u v S u v ⎡⎤⎢⎥=⨯⎡⎤⎢⎥+⎣⎦⎣⎦ 其中,(,)n S u v 和(,)f S u v 分别是(,)e f x y 和(,)e n x y 的功率谱,可通过FFT 变换后模值的平方求得。
上式中,如果1=s ,则方括号中的项就是维纳滤波器;如果s 是变量,就称为参数滤波器;当没有噪声时,(,)n S u v =0,维纳滤波器退化为逆滤波器。
三、实验程序实验程序包含1个.m文件exp_6.m 执行文件,完成图像模糊与图像恢复功能,并给出实验结果具体程序内容在程序内有注释,实验时直接运行exp_6.m即可完成上述实验内容。
四、实验结果与分析【模糊噪声图】【逆滤波恢复结果】【维纳滤波恢复结果】【实验结果分析】(1)在带有噪声干扰的情况下,逆滤波的效果随着噪声的方差值的变大而变小,维纳滤波同样结果,同时恢复结果都带有不同程度的振铃效应。
(2)在带有噪声干扰的情况下,维纳滤波的效果要比逆滤波的效果好,且随着噪声的加强对比效果变得更明显。
