山东省威海市(1)

合集下载

威海介绍

干贝芙蓉
干贝：干贝含有蛋白质、脂肪、碳水化合物、维生素A、钙、钾、铁、镁、硒等营养元素，干贝含丰富的谷氨酸钠，味道极鲜，与新鲜扇贝相比，腥味大减。干贝具有滋阴补肾、和胃调中功能，能治疗头晕目眩、咽干口渴、虚痨咳血、脾胃虚弱等症，常食有助于降血压、降胆固醇、补益健身；据记载，干贝还具有抗癌、软化血管、防止动脉硬化等功效。鸡蛋清：鸡蛋清富含蛋白质和人体必需的8种氨基酸和少量醋酸，可以增强皮肤的润滑作用，保护皮肤的微酸性，以防细菌感染；此外，鸡蛋清还具有清热解毒作用；我国中医还认为，鸡蛋清性微寒而气清，能易经补气，润肺利咽，清热解毒，有助于延缓衰老。牛奶：牛奶中含有丰富蛋白质、维生素及钙、钾、镁等矿物质，可防止皮肤干燥及暗沉，使皮肤白皙，有光泽；也可补充丰富的钙质，适合严重缺钙的人、少儿、老年人、易怒、失眼者以及工作压力大的女性。牛奶味甘，性平、微寒，入心、肺、胃经；具有补虚损，益肺胃，生津润肠之功效。
刘公岛
刘公岛位于威海市区东2.1海里的威海湾中，是中国近代第一支海军的诞生地，是清朝北洋水师全军覆灭的国耻地，也是惨遭英国殖民统治42年的屈辱地。1985年，向游客开放，已成为国家文明风景名胜区和全国著名的爱国主义教育基地。刘公岛上人文景观丰富独特，既有上溯千年的战国遗址，又有汉代刘公、刘母的动人故事；既有清朝北洋海军提督署、水师学堂等大量文物古迹，还有英国殖民统治时期遗留下来的众多欧式建筑。中国甲午战争博物馆累计投资近亿元，重点抢修恢复了海军公所、龙王庙、丁汝昌寓所、东泓炮台、旗顶山炮台、水师学堂等遗迹、遗址。建立了文字、照片记录档案，树立了保护标志，征集文物和资料数千件，其中济远舰前双主炮堪称镇馆之宝。刘公岛博览园通过深入挖掘刘公美德、英租42年、甲午战争等独特的历史文化内涵，向游客展开了一幅幅跌宕起伏、撼人心魄的历史画卷，成为人们感悟悲壮历史、凭吊甲午英烈、接受爱国主义教育的活教材。刘公岛自然风光秀美，素有“海上仙山”和“世外桃源” 的美誉。北部海蚀崖直立陡峭，如刀削斧劈；南部海滩绵延，水清沙洁。听涛崖、板礓石、五花石等地貌奇特。 4000亩森林中，乌桕、龙柏、朴树等70多钟林木、50多钟花草郁郁葱葱，200多头野生梅花鹿以及70多种鸟兽栖息林中，构成一道立体的、流动的风景。

威海地理（1）

初二地理——威海地理内容汇总

走遍四海，还是威海

1.威海地理位置及其优越性：①威海市地处中纬度，属于温带季风气候。因临海，所以与同纬度的内陆地区相比，降水较丰富、气温适宜，适合人类居住，有利于农业的发展；②威海位于胶东半岛最东端，三面临海，东与韩国、朝鲜、日本隔海相望，西与烟台市接壤，海陆交通都很发达。

2.威海市的行政区划：威海市是山东省下辖的一个地级市，由荣成市、文登市、乳山市和环翠区三市一区组成。环翠区是威海市的中心区。

3.威海市2003年获“联合国人居奖”，2006年又获联合国“最适宜人类居住的城市”的荣誉。由此，威海市设立了一年一度的“国际人居节”，有效的促进了威海城市的可持续性发展。

4.人口、民族概况：威海市是山东省第一个进入人口负增长的城市。威海共有46个民族，绝大部分为汉族，少数民族中人口最多的是朝鲜族，其次是满族，第三位是佤族。

5.威海传统特色民居：海草房，就地取材，以石为墙，以海草为顶，屋顶坡度很陡，适应威海夏季高温多雨、冬季寒冷干燥的气候特点，住起来冬暖夏凉。

6.威海最大的岛屿是刘公岛，面临黄海，背接威海湾，是国家森林公园和著名旅游区，岛上有甲午海战纪念馆。幸福门被誉为“威海之门”，成为威海的标志，代表着威海现代化的城市形象。荣成是著名的天鹅之乡。

7.威海市属于温带季风气候，四季变化明显，由于濒临黄海，受海洋的调节作用，威海气候具有：春冷、夏凉、秋暖、冬温的特点。

8.威海气候宜人，空气清洁新鲜。洁净的空气利于人们身体健康，是宜居城市的重要指标，更是生产活动、科学研究的重要条件。“威海星”的发现，正是因为威海空气洁净，能见度高，便于天文观测。

2019-2020学年山东省威海市部编版(五四制)三年级上册期末考试语文试卷(一)(含答案解析)

2019-2020学年山东省威海市部编版（五四制）三年级上册期

末考试语文试卷（一）

学校:___________姓名：___________班级：___________考号：___________

一、填空题

1．看拼音写词语。

lǎ ba chì bǎng là zhú xì jiáo màn yàn

（_____）（_____）（_____）（_____）

líng luàn lí míng chuán cāng mì bú tòu fēng

（_____）（_____）（_____）（_____）

2．根据字的读音组词。

假jià（______）挑tiāo（______）几jī（______）

调diào（______）挣zhèng（______）啦lā（______）

3．比一比组词。

载（______）臂（______）票（______）奏（______）

栽（______）壁（______）飘（______）凑（______）4．括号里要加上合适的标点符号，把下面对话写完整。

小红问我（______）“《安徒生童话》中，你最喜欢哪个故事？为什么？”

“______”我想了想说（______）“________________”

“我也最喜欢这个故事！”小红高兴地说（______）

5．根据背诵积累填空。

1．把下面的名言、诗句补充完整。

（1）有理______，无理寸步难行。

（2）二人同心，______。

（3）______，不贰过。（《论语》）

（4）罔谈彼短，靡恃______。（《千字文》）

（5）______，但爱鲈鱼美。

2023年山东省威海市环翠区中考化学模拟试卷(含解析) (1)

2023年山东省威海市环翠区中考化学模拟试卷

1. 下列物质的用途主要与其化学性质有关的是( )

A. 用活性炭除去水中的色素

B. 用硫酸铜对游泳池池水消毒

C. 汽油洗去金属表面的油污

D. 浓硫酸干燥氧气

2. 取10g混有铁粉、活性炭和食盐三种物质的粉末，加入装有100mL纯水的烧杯中，充分搅拌后依序进行下列实验步骤：①用滤纸过滤杯中液体，收集到无色澄清滤液。②以滴管吸取滤液，滴于蒸发皿上。③加热使蒸发皿的水蒸发，蒸发皿内残留白色固体，检测得知为食盐。下列叙述无法通过以上实验证明的是( )

A. 食盐的沸点比水的沸点高

B. 混合物可尝试用过滤方法分离

C. 此杯无色澄清滤液中含有自由移动的离子

D. 活性炭的溶解度比食盐的溶解度小

3. 化学是创造物质的科学，要创造新物质就要认识物质的微观结构和变化规律。下列关于物质微观结构的说法不正确的是( )

A. 分子很小，但有质量，其质量就是它的相对分子质量

B. 原子能直接构成物质，也可以变成离子、组合成分子间接构成物质

C. 原子得失电子变成离子，其质量几乎不变

D. 原子由更小的微粒构成

4. 含义丰富的化学符号是独特的化学语言。以下符号①2N2②Mg2+③2H④−2O⑤CO2表示含义不正确的是( )

A. ①表示2个氮分子

B. ②④中“2”表示元素化合价

C. ③中“2”表示原子个数

D. ⑤表示二氧化碳这种物质

5. 北斗三号卫星上采用了我国自主研发的高精度铷原子钟。铷原子在元素周期表中的信息及部分原子的结构示意图如下：

下列说法不正确的是( )

A. 铷元素在元素周期表第五周期

威海旅游介绍ppt课件

• 1985年，向游客开放，已成为国家文明风景名胜区和全国著名的爱国主义教育基地。
• 刘公岛上人文景观丰富独特，既有上溯千年的战国遗址，又有汉代刘公、刘母的动人故事；既有清朝北洋海
军提督署、水师学堂等大量文物古迹，还有英国殖民统治时期遗留下来的众多欧式建筑。
甲午海战馆
刘公岛博览园
华夏第一牌楼
骑马
场
三面圣水观音喷泉
Βιβλιοθήκη Baidu
• 养生温泉“天沐温泉”——真山真水真享受。
• “天沐温泉”温泉区包括室外森林养生温泉和室内温泉SPA馆，可同时容纳1500人沐浴温泉，日最高接待量可达上万人。室外温泉区包括“鼋山五福泉”、“鼋水六德汤”、“美芦荟温泉区”、“森林静泡区”、“草本养生谷”、“SPA动感温泉区”、室外无边界游泳池、石板温泉、亲亲温泉鱼疗等，共设有66个室外特色功能温泉浴池，供游客尽情享受。
• 荣成临近黄海、渤海、东海三大渔场，水产资源十分丰富，盛产对虾、鹰爪虾、黄花鱼、牙鲆鱼、扇贝、海带、裙带菜等鱼虾贝藻类海产品100多种，其中海参、鲍鱼、海胆、真鲷、牙鲆、石花菜等海珍品最为著名。
• 主要旅游景区有：成山头风景名胜区：自古成山头就是兵家必争地，三国、隋唐、明清，均有兵事发生。威海荣成赤山风景名胜区：位于山东半岛最东端、被誉为是“佛教圣地”、“森林公园”、“大明圣境”、“海岛民俗”的旅游胜地。拥有两个国家级森林公园一处国家级海洋公园，空气质量优良天数为100%适宜居住和养生。

威海华夏城游玩攻略

华夏城位于山东省威海市环翠区，是一座展示东方古典文化为主的大型文化景区。在华夏城，你可欣赏气势宏大的圣水观音音乐喷泉表演，或在尽显南北古典建筑元素精华的仿古展馆“夏园”中漫步，还可以观看精彩的杂技、马战、武术表演，而晚上的大型山水实景演艺《神游华夏》绝不容错过，定能震撼你的心灵。

旅游攻略：

1、神游海洋世界表演时间：

动感影院：10分钟，9：00、11：30、13：30、15：30

群鱼表演：12分钟，10：00、14：00

欢乐海洋剧场：20分钟，10：30、15：00

2、《神游华夏》演出时间：演出时间19：20 → 20：20

3、华夏城景区表演时间：

圣水观音音乐喷泉：18分钟，3月7日-31日9:30、15:30，3月周六周日9:30、10:30、15:30，4月1日-6月30日9:00、11:00、15:30，5月1日-4日9:00、11:00、14:30、15:30

大转轮杂技表演：10分钟，4月1日-6月30日8:10、13:30，5月1日-4日8:10、13:30

马术表演：10分钟，4月1日-6月30日9:50、14:30，5月1日-4日9:50、14:30

交通指南：

自驾：

济南、淄博方向：济青高速→潍莱高速→同三高速→烟威高速至双岛高速收费站→世昌大道→青岛路→华夏路→华夏城（出收费站后行程约20分钟）

烟台方向：烟威高速至双岛高速收费站→世昌大道→青岛路→华夏路→华夏城（出收费站后行程约20分钟）

青岛方向：青威高速→威海收费站→市区方向至青岛路→华夏路→华夏城（出收费站后行程约10分钟）

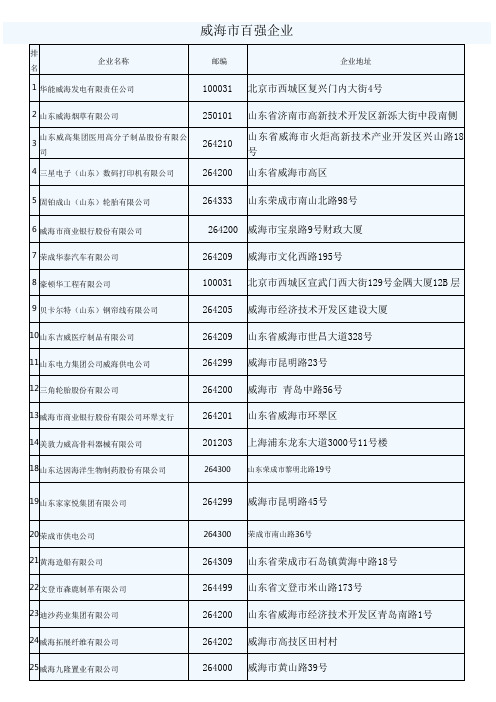
威海市百强企业

264207
·威海市·环翠区·崮山镇九家疃村
28
威海钢铁研究所
264408
威海市高村镇河西村
29
山东威高骨科材料有限公司
264209
山东威海旅游度假区香江街26号
32
金猴集团威海鞋业有限公司
264200
威海市世昌大道３５８号
33
威海魏wk.baidu.com科技工业园有限公司
264203
山东省威海市环翠区张村镇环翠路88号
87
山东威达雷姆机械有限公司
264414
山东省文登市苘山镇中韩路2-4号
88
威海电力燃料有限公司
264200
山东省威海市威海经济技术开发区沟北村北
89
山东威海卫酒业集团威海有限公司
264200
威海市温泉西路98号
90
山东大正医疗器械股份有限公司
264209
威海市大连路65号
91
黄海造船有限公司造船新厂
264205
山东威海经济技术开发区华夏路1号
64
山东黄海船舶配套有限公司
266071
山东省青岛市市南区徐州路１５１号
65
威海味岛食品有限公司
264329
威海市港西镇驻地东侧
66
威海乐扣乐扣塑胶有限公司
264414
威海市苘山镇韩国工业园

威海冬季一日游景点

威海冬季一日游的景点有很多选择，以下是一些推荐：

1、威海刘公岛：这是威海的一处著名景点，可以欣赏到美丽的海景和岛上的风光。

2、威海国际海洋文化博览区：这是一个集海洋文化、娱乐、休闲为一体的综合性景区，可以了解到海洋的奥秘和威海的历史文化。

3、威海华夏城景区：这是一个以展示中国传统文化和历史为主题的景区，可以了解到中国的历史文化。

以上景点都是威海冬季一日游的不错选择，可以根据自己的兴趣和时间安排进行选择。

山东省威海市2020年中考化学真题试题(含答案)(1)

威海市2020年初中学业考试

可能用到的相对原子质量:H—1 C—12 O—16 Na—23 Ba—137

一、选择 (本题包括10小题，每小题2分，共20分。每小题只有一个选项符合题意)

1.物质世界每时每刻都在发生着变化，下列变化属于化学变化的是（）

①电灯通电发光②煤制成焦炭③塑料老化④干冰升华⑤石油分馏⑥海水制镁⑦石块粉碎成石子⑧粮食酿酒

A.②③⑥⑧

B.②⑤⑥⑧

C.①③④⑧

D.①④⑥⑦

2.分类法是化学学习的重要方法之一。下列各组物质按照单质、盐、混合物的顺序排列的是（）

A.生铁、氢氧化铜、冰水混合物

B.液氧、硫酸钡、粗盐

C.天然气纯碱、石油

D.钙片、氯化镁、海水

3.下列实验操作正确的是（）

4.民以食为天，食以安为先。下列做法不会危害人体健康的是（）

A.用甲醛浸泡海产品，延长保鲜时问

B.用二氧化硫熏蒸馒头，使它更白

C.用适量的小苏打做糕点，使它更松软

D.用大量的甜蜜素制作果冻，使它更加可口

5.溶液是一种重要的混合物。下列有关溶液的说法正确的是（）

A.溶液具有均一性和稳定性，因为溶液中的各种粒子保持静止不动

B.饱和溶液是一定温度下不能再溶解该物质的溶液

C.不饱和溶液通过降低温度一定能变成饱和溶液

D.一种物质分散到另一种物质里一定能形成溶液

6.燃烧是一类重要的化学变化，下列关于燃烧的叙述正确的是（）

A.燃烧一定有火焰

B.物质在有限的空间内燃烧，一定会发生爆炸

C.物质跟氧气的反应就是燃烧

D.使可燃物温度降低到着火点以下，可以灭火

7.下列有关化学史的叙述错误的是（）

A.我国化学家侯德榜在工业制烧碱的研究中取得了巨大成就

山东省威海市四年级下学期第一次月考数学试卷(1)

山东省威海市四年级下学期第一次月考数学试卷（1）

姓名:________ 班级:________ 成绩:________

亲爱的小朋友们，这一段时间的学习，你们收获怎么样呢？今天就让我们来检验一下吧！

一、填一填 (共9题；共20分)

1. （1分）写出下面横线上的小数．

地球绕太阳旋转的速度为二十九点八千米/秒．写作：________

【考点】

2. （3分）在66.7％，，0.6，和0.625中，最大数是________，________与________是相等的数。

【考点】

3. （1分） (2019五上·莲湖期中) 一个小数，如果把它的小数点向左移动一位，原数比所得新数大65.52，原数是________.

【考点】

4. （2分） (2019五上·廉江期末) 直角三角形中，两个锐角的度数和是________．如果一个锐角等于26°，另一个锐角是________．

【考点】

5. （2分）把9.675的小数点向右移动一位，得到的新数是________，这个新数中的“5”在________位上．

【考点】

6. （3分） (2019四下·龙华期中) 直角三角形的一个锐角是43°，另一个锐角是________。在一个三角形中，已知∠1=70°，∠2=48°，那么∠3=________，这是一个________三角形。

【考点】

7. （1分） ________是等腰梯形。

【考点】

8. （3分）平行四边形有________条边，________个角，对边________

【考点】

9. （4分） (2020四下·渝中期末)

威海市区旅游景点

威海市区旅游景点有：

1、刘公岛。位于威海湾口，素有“海上仙山”的美誉。

2、定远舰。位于威海港客运码头东侧，与刘公岛隔海相望。

3、国际海水浴场。位于威海市北部环海路，是一个天然海水浴场。

4、塔山公园。位于威海市统一路348号，是集休闲、娱乐、文化于一体的山体公园。

5、仙姑顶风景区。位于威海市区，最高峰海拔375米，是国家AAAA级旅游景区。

6、威海公园。位于威海市市区，公园的画中画（也称大相框）雕塑是威海的地标性景观。

山东省威海市中考语文试题及答案解析 (一)

威海市是山东省的一个美丽的城市，也是中考语文试题较难的考区之一，迎接挑战的考生需要认真准备和复习。接下来，我们将讨论山东

省威海市中考语文试题及答案解析。

试卷结构

山东省威海市中考语文试题分为两部分，试卷共90分。其中，第一部

分为选择题，共40分，包含20道题目，每题2分。第二部分为非选

择题，共50分，包含4个题目，大题分值不等，分别有25分、12分、8分和5分。

知识点分析

在中考语文试卷中，涉及的知识点比较多，主要包括阅读理解、作文、词语运用、语法等。以下是比较常见的知识点：

1. 阅读理解

阅读理解是中考语文试卷重要的部分之一。考生需要认真阅读题目，

理解文章的大意和细节，做到快而准。在阅读时，要注意答题要求的

不同，选择题需要选择正确的答案，而非选择题需要自己进行总结和

归纳。

2. 作文

作文是考察语文能力全面的重要环节。考生需要注意写作的结构和表

达方式，充分考虑文章的整体框架以及段落之间的连贯性。同时，在

用词上也要灵活多变，避免生硬和重复。

3. 词语运用

中考语文试卷中，常涉及词语使用的正确性以及词义的理解。除了通过阅读提升词汇量，考生还需要通过积累归纳，更好地理解并正确使用词语。

4. 语法

语法是中考语文试卷中的重要知识点，包括名词、动词、形容词、副词等。考生也需要了解基本语法知识，如主谓一致、时态等，做到正确地理解和运用。

解析

为了更好地帮助考生提高语文水平和应对考试，下面是一道威海市2019年中考语文试题，及其解析。

例题：在下列句子中，加点的成语使用不当的一项是（）

植物生长素的发现教学设计

感悟科学“线性积累、永无止境”的本质特征

——“植物生长素发现”一节的教学设计

山东省威海市第一中学刘玉凤

一、设计思路

现成的结论容易被人误认为是本来就有的、永恒不变的真理。科学史可以展现科学是永无止境的探究活动的本质特征，使人感受科学发展是一个线性累积、不断壮大的过程，领会“变化”才是科学本身具有的惟一不变特性。

植物生长素的发现过程正是这样一个很好地展现科学在本质上是相对的、可变的、处在不断修正和发展过程中的素材。因此，本节课拟以帮助学生理解科学的本质特征为主要教学目标，按照生长素发现的时间顺序，通过引导学生发现前人通过实验得出的结论正是后人研究的问题，使学生体会科学发现循环往复、步步深入的过程，感悟科学知识并非一经发现、证实之后便永远不会被推翻，而是需要“通过归纳所得并经由观察证实的真命题及其集合的积累”，从而更好地理解科学探究过程中所体现出来的科学的本质特征。

二、教学目标

1.通过生长素的发现过程，领悟科学发现是探究活动线性积累的过程。

2.通过分析实验设计方案，提高做出假设、设计实验、分析实验数据得出结论的能力。

3.通过学习生长素的产生、分布、运输的知识，理解生产生活中许多有关生长素的现象。

4.通过“技能训练”，训练设计实验和得出结论逻辑上的严密性。

三、教学重点

生长素的发现过程。

四、教学难点

1.理解生长素发现过程所包含的科学方法和科学本质特征。

2.理解实验设计的严谨性。

五、教学方法

1.教的方法：按照“发现问题——实验验证——得出结论——再从结论中提出

新的问题……”的线索，引导学生理解在生长素发现过程中探究活动层层深入

2021山东省威海市中考化学试题解析(1)

威海市2021年初中学业考试

化学

温馨提示：

1.本卷共7页，共70分，考试时间80分钟。

2.所有答案必须涂、写在答题卡上，写在试卷中的答案无效。

3.考试结束后，本试卷和答题卡一并交回。

4.可能用到的相对原子质量：H-1 C-12 N-14 O-16 Na-23 C1-3

5.5

亲爱的同学:

化学是中心的科学，认识自然高不开化学；化学是基础的科学，几乎所有的应用科学都以化学为基础；化学是实用的科学，创造有用物质、消除有害物质、获得新型能源都要化学，化学使物质更丰富、生活更美好。在下面的时间里，相信你能用学到的知识、方法和观念交出满意的答卷！

一、选择（本题包括10小题，每小题2分，共20分。每小题只有一个选项符合题意）

1.（2021·威海）下列关于物质组成和构成的认识，不正确的是（）

A.看似庞杂无序的化学物质均统一于种类有限的元素之中

B.“元素论”和“原子-分子论”是物质科学的基石，是科学和哲学的重要思想工具

C.核外电子特别是外层电子，是决定原子间作用方式的重要原因

D.跟卢瑟福原子模型比较，道尔顿原子模型不科学，对科学发展的贡献不大

【答案】D

【解析】科学的发展道路是曲折的，不管成功与失败，对后人都有启示作用；1808年，英国科学家道尔顿提出了原子论；1904年汤姆生提出的葡萄干面包原子模型；1911年卢瑟福提出原子结构行星模型；1913年玻

尔提出轨道式原子模型。

2.（2021·威海）下列关于物质及变化的认识，正确的是（）

A.电子、光子、量子属于化学物质

B.化学变化有可能创造出世界上原来不存在的物质

威海

概况威海位于山东半岛东北端，三面环海一面接陆，东与韩国日本隔海相望，西与烟台接壤，素有“京津的钥匙和门户”之称，全市总面积为5436平方公里，总人口252万，其中市区面积为731平方公里，人口为52万，共辖三市三区，三市分别是荣成，文登，乳山，均是我国的百强县，三区则是环翠区，经济技术开发区，高新技术开发区。

说起威海的历史可以用“悠久”二字来形容，早在7000多年前就有人类在此居住，那是叫做“石落村”元朝则成为“清泉夼”“夼”是上面一个“大”下面一个“川”意味有水洼的地方，清泉就是温泉，从此地名可以看出威海的温泉资源十分丰富，到了明洪武31年（1398年）明政府为了防御海上倭寇的侵扰在此派兵设防，建立卫所，称“威海卫”取威镇海疆之意，从此威海作为地名开始出现，1888年我国第一支海军——北洋舰队成立，并把提督衙门设在威海的刘公岛上，1894年甲午黄海大战，北洋舰队全军覆没，1898年—1930年威海被英国强租了32年，1945年解放，1987年脱离烟台成为山东省17地级市之一。

大家来威海第一是来看海的，另外则是被威海优美的环境和清新的空气吸引而来，威海的噪音指数，水质，空气指标都达到国家一级标准，并且是我国第一个旅游城市，第一个环境城市，第一个绿化城市，第一个卫生城市，而且在03年获得了联合国颁发的人居环境奖，是在获奖的100多个城市中唯一的一个亚洲城市，威海之所以有这么好的环境除了地理位置优越外，还与政府的绿化政策有很大的关系，在绿化方面政府有“三三制”原则，就是一亩地1 /3用来建筑，1/3用来修路，1/3用来绿化，还有个口号：见缝插绿，找缝插绿，造缝插绿。正是由于这个政策的贯彻执行才有了威海今天的优美环境，此外，威海市政府对工业企业也有严格的控制，在威海只有轻工业企业，比较知名的有：金猴皮鞋，环球渔具，威高集团，三角轮胎，山花地毯等都非常的有名，由于良好的投资环境和离韩国很近的地理优势，威海也吸引了韩国的一些企业来此通知，比较有名的有三星电子，大宇企业等，还有一些电子公司和服装公司，韩国企业已占威海经济的47%。我们要参观韩国服装城就是一个韩国商品的集散地，韩国商品在威海一共有三种渠道，1是直接从韩国进口过来的，2是利用韩国的技术在威海加工，3韩国的原材料进口到威海加工而成，所以这里的韩国商品品种齐全价格也很便宜。大家来到威海出了感觉这里的环境好以外，另一个感觉就是威海市个很小的城市，可以用小巧玲珑来形用，原来当地人们用一句顺口溜来形用威海的小：一条马路一盏灯，一个喇

威海地理

（1）多分布在山麓和绿洲上，多沿河流分布。绿洲水源充足，植被较好，人口较多。（2）不合理；新疆的气候干旱，水资源短缺，生态环境脆弱，环境承载量小．如果大量迁入人口，会导致生态环境的恶化；（3）是通向中亚的重要门户，国内外市场广阔；交通便利；自然资源丰富；政策支持。（4）石油开采、食品工业，棉纺，宝石加工等
分析长江中下游沿江地区2016年6月30日以来洪涝灾害产生的人为原因及其对应措施。
（1）以山地丘陵为主，山区面积广大；山地为东北—西南方向；西北高，东南低，起伏较大；（太平洋板块与印度洋）板块相互挤压抬升。（2）北岛（2分）理由：城市数量多；北岛铁路密度更大。（3）特点：终年温和多雨（2分）；
1.威海市位于山东半岛的最东端，南北介于36°41＇N～37°35＇N间，东西介于121°11＇E～122°42＇E间，北、东、南三面濒临黄海，北与辽东半岛相对，东及东南与朝鲜半岛和日本列岛隔海相望，西与烟台市接壤。威海市突出于黄海中部，为渤海锁钥，连南北海防，是东北亚重要的沿海城市。山东半岛东端的成山头(成山角)是中国重要的地理标志地(领海基点) 2.威海市是山东省第一个进入人口负增长的城市，人口负增长带来的影响有：一劳动力不足。二人口的老龄化严重。三社会养老负担加重 3.威海市地理位置的优越性（威海发展经济的有利条件）（1）地处中纬度，暖温带自然条件优越。（1）沿海开放城市，海域面积广大，利于发展海洋经济，海运便利，距离日本韩国最近便于引进日韩的资金和技术与发展外向型经济。 4.日韩和威海的互助合作发展的优势：日韩：资金、技术、人才、管理威海：自然资源丰富、劳动力丰富、土地