几何画板制作深度迭代的方法探究
利用《几何画板》研究问题的思路和方法

李景明
(重庆市云阳县双江中学)
随着时代发展和信息技术的日新月异,现代信息技术和 中学数学教学的整合已经是一个必然趋势。《几何画板》在数 学教学中的作用是显而易见的。《几何画板》为学生架设了数 形结合的桥梁,为解析几何、立体几何、函数等有关概念的 学习、探究提供了绝好的试验工具,使数学实验成为可能。 利用《几何画板》的可操作性,我们能在变化的过程中揭示 恒定不变的规律。在今后的数学教学中,传统的教学模式将被 打破,知识的记忆不再是最重要的教学目的,创新精神和实践 能力的培养将成为教育的核心。本文通过几个具体实例来阐明 利用《几何画板》研究问题的思路,并归纳了几点利用《几何 画板》研究问题的方法,充分体现了《几何画板》的功能。学 生可以在《几何画板》中任意拖动、观察图形,做出猜测并验 证。在观察、探索、发现的过程中增加对各种图形的感性认 识,形成丰富的几何经验背景。
一、利用《几何画板》,变静态为动态来研究问题 几何学是研究物体的形状、大小和相互位置关系的一门学 科。几何图形中的位置关系多是在相对运动的情况下产生的。 许多情况是:概念在运动中形成和定义,规律在运动中发现和 完善,结论在运动中统一和深化。所以,在平面几何教学中, 让点、线、面、图形动起来,这种动态的显示,有利于对知识 发生过程的认识,有利于学生解题思路的开拓,有利于学生思 维品质的培养。要让点、线、面、图形动起来,《几何画板》 就能起到重要的作用。 例如,讲解“三角形高线、中线、角平分线”这一节时, 让学生观察BC边上任一点D在BC上运动的过程,看看哪些角或者 线段会发生变化,在变化过程中有没有特殊的位置。学生通过 操作、演示,发现点D从点B运动到点C的过程中(不包括点B、点 C),有以下事实: (1)∠BDA逐渐减小,而∠ADC逐渐增大,当∠BDA=∠ADC=90°, 这时,AD⊥BC,线段AD称为△ABC的BC边上的高线; (2)∠BAD逐渐增大,而∠DAC逐渐减小,当∠BAD=∠DAC, 这时,线段AD称为△ABC的角平分线; (3)线段BD逐渐增大,线段DC逐渐减小,当BD=DC,这时, 线段AD称为△ABC的BC边上的中线。 这样,学生对三角形的高线、中线、角平分线反映在数量 上的关系就有了更为清晰的认识,增强了学习的直观性、形象 性和生动性。这个实验中,除了教师演示之外,学生也可自己 动手,亲身经历,在操作中体验做数学的过程,并在活动中获 得成功的感受,从而大大激发了学习数学的兴趣和求知欲望。 《几何画板》一个突出的特点在于能动态地保持给定的几何关 系。学生从连续运动变化的图形中能发现恒定不变的几何规 律,从而抓住对象的本质特征,提出问题并论证假设。在教学 中,我们如能充分利用《几何画板》的优势,注意摸索用《几 何画板》展现几何动态效果的教学,那么,既可加深学生对知 识的理解,还可激活学生的想象力、创造力,培养学生的思维 品质。 二、利用《几何画板》,化难为易来研究问题 数学学习中,我们经常会遇到许多不太容易解决的数学 问题,如运动变化的题型。传统的教学只能通过“静态”的描 述加猜想来处理这些问题,无法对解题的结果或过程进行直观 地检验。猜想是在没有现存结论的情况下,根据问题的条件来 推断可能存在的结果的一种直觉思维形式。猜想得出的结论,
几何画板实验报告四

画正n边形
1、画点A,把点A依0°方向移动1cm,得到A’。
2、画射线AA’,在射线上画一点B。
3、先后选中A、A’、B,单击度量/比,得比值AB/AA’。
4、计算trunc(AB/AA’)+3,改标签为n,用来控制正多边形的边数。
5、计算360°/(trunc(AB/AA’)+3),并标记该角。
几何画板实验报告
班别:姓名:学Βιβλιοθήκη :评分:实验题目迭代法作图
实验目的
学习“变换”菜单的“迭代”功能的实现方法,感受迭代的意义
实验环境
WinXP;几何画板5.0
实验过程
1、画线段AB,作AB的垂线段BC,作线段AC。
2、过B作AC的垂线,垂足为D,过D作AB的垂线,垂足为E。作线段BD、DE。
3、选中点B,单击变换/迭代,在迭代对话框中设点E为初象,可以在显示按钮中设置迭代的次数,然后单击迭代按钮。
6、画两点C、D。
7、把点C标记为旋转中心,让点D绕点C旋转标记角度得点D’。
8、画线段DD’。
9、依次选中点D与计算值n,按住Shift键的同时单击变换/深度迭代,然后设置初象为点D’,点击迭代按钮。
10、拖动点B可以改变多边形的边数。
实验结果
实验小结
(完整word)几何画板的深度迭代的用法大全,推荐文档

如何用好几何画板的深度迭代第一章:迭代的概念和操作迭代是几何画板中一个很有趣的功能,它相当于程序设计的递归算法。
通俗的讲就是用自身的结构来描述自身。
最典型的例子就是对阶乘运算可看作一下的定义: 。
递归算法的特点是书写简单,容易理解,!(1)!(1)!(1)(2)!n n n n n n =⨯--=-⨯-但是运算消耗内存较大。
我们先来了解下面这几个最基本的概念。
迭代:按一定的迭代规则,从原象到初象的反复映射过程。
原象:产生迭代序列的初始对象,通常称为“种子”。
初象:原象经过一系列变换操作而得到的象。
与原象是相对概念。
更具体一点,在代数学中,如计算数列1,3,5,7,9......的第n 项。
我们知道,所以迭代的规则就是后一项等于前一项加2。
以1作为原像,12n n a a -=+3作为初像,迭代一次后得到5,再迭代一次得到7,如此下去得到以下数值序列7 , 9,11, 13, 15......如图1.1所示。
图 1.1图 1.2在几何学中,迭代使一组对象产生一组新的对象。
图1.2中A 、B 、C 、D 、E 、F 、G ,各点相距1cm ,那么怎么由A 点和B 点得到其它各点呢?我们可以发现其中的规律就是从左到右,每一个点相当于前面一个点向右平移了1cm 。
所以我们以A 点作为原像,B 点作为初像,迭代一次得到B 点,二次为C 点,以此类推。
所以,迭代像就是迭代操作产生的象的序列,而迭代深度是指迭代的次数。
那么下面我们通过例子来进一步地了解迭代以及相关的概念。
几何画板中迭代的控制方式分为两种,一种是没有参数的迭代,另一种是带参数的迭代,我们称为深度迭代。
两者没有本质的不同,但前者需要手动改变迭代的深度,后者可通过修改参数的值来改变迭代深度。
我们先通过画圆的正n 边形这个例子来看一下它们的区别。
【例1】画圆的内接正7边形。
【分析】由正7边形的特征,我们知道,每一个点都相当于前面的点逆时针旋转,抓住这个规律,我们可以用迭代功能来解决。
几何画板迭代详解之:函数迭代
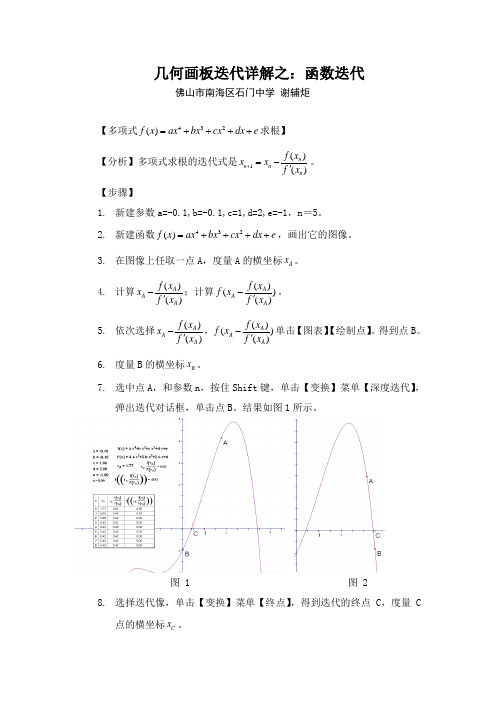
几何画板迭代详解之:函数迭代佛山市南海区石门中学 谢辅炬【多项式432()f x ax bx cx dx e =++++求根】 【分析】多项式求根的迭代式是1()()n n n n f x x x f x +=-'。
【步骤】1. 新建参数a=-0.1,b=-0.1,c=1,d=2,e=-1,n =5。
2. 新建函数432()f x ax bx cx dx e =++++,画出它的图像。
3. 在图像上任取一点A ,度量A 的横坐标A x 。
4. 计算()()A A A f x x f x -';计算()()()A A A f x f x f x -'。
5. 依次选择()()A A A f x x f x -',()()()A A Af x f x f x -'单击【图表】【绘制点】。
得到点B 。
6. 度量B 的横坐标B x 。
7. 选中点A ,和参数n ,按住Shift 键,单击【变换】菜单【深度迭代】,弹出迭代对话框,单击点B 。
结果如图1所示。
图 1图 28. 选择迭代像,单击【变换】菜单【终点】,得到迭代的终点C ,度量C点的横坐标C x 。
9. 观察表格可知,显示方程的一个近似根是0.42。
10. 拖动A 点,改变它的位置。
观察表格可知道方程的另外一个近似根是3.41。
如图2所示。
【MIRA 】【步骤】1. 在平面上取一点A ,度量A 的横坐标A x 和纵坐标A y 。
2. 新建参数a =0.4,b=0,99875。
(b 取得尽量接近1)3. 新建函数22(1)()1a x f x ax x-=++。
4. 计算f(A x )+b A y ,f(f(A x )+b A y )-A x 。
注意这里用的是函数嵌套。
顺次选择这两个结果,单击【图表】【绘制(x ,y )】。
得到点B 。
5. 顺次选择点B 和三个计算结果:f(A x )+bA y ,f(f(A x )+b A y )-A x ,A x 。
从矩形网格的制作谈几何画板的迭代深度与应用技巧

鄞州区钟公庙中学
从理论上讲,矩形网格可按如下方法制作: 在平面上任意画一个自由点 A,按给定的小矩形边长作矩形 ABCD,选定点 A 和参数 n=6,作带参 数迭代,让 A B,添加迭代 A C,再添加迭代 A D,如图 1 所示,制作完成。
注:几何画板版本不同,迭代的深度也各不相同。
4
图 15
3
图 16
上述 3 个 2 次映象,迭代深度可先预设为 n/3,经过测试当 n=7 时迭代深度还欠 1 次,修正为 round((n+1)/3)后,对于 n≤30 时都正确。 如图 16 所示是当 n=30 时图象,可以看出此时线条已十分稠密,再增加边数时图象变化已不十分明 显。 还有一种一劳永逸的方法是,作参数 n=80, 计算 n-1 和3600 /n,象图 10 哪样先不厌其烦地作出一 组对角线(共 79 条),然后再作单次映象的迭代,这样作出的图象对于 n≤80 都正确,但没有什么技术 含量,图 16 是 n=60 时情形,显然线段稠密,没有什么美感。
图 17
图 18
为了不致太稠密,我们把对角线换成一组平行弦,再作带参数的深度迭代 A B,如图 18 所示。可 得如图 19(平行弦间距相等)、图 20(平行弦间距不相等)所示精美图案。
图 19
Байду номын сангаас
图 20
至此,相信读者已经了解几何画板迭代运算随着映象的增加,电脑的运算量将是急剧增加,以致电 脑可能出现半死机状态,所以我们学会一些降低映象深度的方法和技巧是十分必要的,希望此文能对广 大几何画板爱好者有所帮助。
2
同样方法:当 n=48 时,如图 12 所示。
图 11
应用《几何画板》开展数学探究式教学的途径与方法

在应用《几何画板》开展数学探究式教学中,通过改造教材内容使之适合学生在《几何画板》进行实验与探究,通过拓展教材内容以充实丰富画板平台上开展的探究式教学课程,使《几何画板》与数学课程及教学模式得以深度融合,成为教师开展探究示范教学、学生进行探究性学习的有力工具,可以有效培养学生的探究能力,增强学生的创新意识,改变数学课堂教学方式。
摘要关键词几何画板;数学探究式教学;椭圆应用《几何画板》开展数学探究式教学的途径与方法余明芳王钦敏(福建教育学院数学研修部,福建福州350025)《几何画板》(The Geometer's Sketchpad )软件平台可以让操作者精确设定几何对象的位置关系,简易追踪点与直线的运动轨迹,直接观察含参数对象的变化规律,自由地进行构图与动画试验,因而在几何、解析几何与函数等章节的探究式教学中,都有广泛的应用。
教学实践表明,应用《几何画板》开展数学探究式教学,可以有效调动学生学习积极性,让数学变得更有趣味,更易于理解,并且,它也很有利于培养学生的数学探究与发现能力。
应用《几何画板》开展数学探究式教学,需要教师认识《几何画板》软件的各项功能,善于在日常课堂作示范,潜移默化地提高学生的平台操作能力。
同时,还需要教师在课堂上秉持运用信息技术辅助教学的理念,依据教学实情,立足教材,合理地改造与拓展教材内容,[1]使《几何画板》与数学的课程内容和教学方式得以深度融合。
这也是应用《几何画板》开展数学探究式教学的主要途径与方法。
下面以高中数学《椭圆》章节教学为例进行详细说明。
一、改造教材内容,使之适合学生在《几何画板》进行实验与探究适合运用《几何画板》开展探究式教学的教材内数学概念知识,其生成与拓展的过程大多可在画板平台通过顺次构图,顺理地进行多方位的实验与探究,但教材教学内容的编排未必会按同样的次序,也未必都是或比较完整地给出与画板功能相契合的知识内容。
因而,应用《几何画板》开展数学探究式教学,大都需要对教材内容进行较大幅度的改造,使之适合学生在《几何画板》进行实验与探究。
几何画板中的迭代和带参数的迭代实验报告:圆的面积公式转化

几何画板中的迭代和带参数的迭代实验报告一、实验目的1、新建参数以及参数动画按钮的制作2、掌握带参数的迭代思想和操作步骤3、学会通过了解父对象和子对象的关系来逆向分析已有的几何画板课件二、实验原理通过带参数的迭代建立参数与图形之间的关系。
制作参数动画按钮时,参数的变化引起图形个数的变化。
三、实验内容运用几何画板逆向分析圆的面积公式推导课件,并将课件还原制作出来。
四、实验课时:8课时五、实验步骤(略)一、方法:分割拼凑法、划曲为直展开法(等腰三角形)、划曲为直展开法(直角三角形)。
二、实施步骤方法一:分割拼凑法1.新建文件新建页:【文件】-【文档选项】-【增加页】-【空白页面】,命名为:圆的面积推导分割拼凑法。
2.构建参数:【数据】—【新建参数】—构建两个参数:半径r=3厘米,t1=6。
【数据】—【计算参数】—【计算2个数据:分别是2*trunc(t1) 和360度/ 2*trunc(t1) 】。
3.做圆和分割圆:选择【点工具】—在空白处做点A—(保持A为选中状态)+选中r—【构造】—【以圆心和半径作圆】—(保持圆为选中状态)【构造】—【圆上的点】(为点B)。
选中参数360度/ 2*trunc(t1) —鼠标右击—【标记角度】,【双击点A+选中点B】—【变换】—【旋转】—【确定】(得到点B’)。
依次选中点A,点B,点B’—【构造】—【圆上的弧】—(保持弧选中状态)【构造】—【弧内部】—【扇形内部】。
选中点B+选中参数2*trunc(t1)—【按住shift 键】—【变换】—【深度迭代】—【将点B迭代到点B’】—【确定】(得到一个分割好扇形的圆)。
4.做分割后的一个扇形:选中点B+选中点B’—【度量】—【距离】—(保持参数选中状态)鼠标右击【标记距离】。
选择【点工具】—在空白处作点C—【变换】—【平移】(按标记距离平移,得到点C’)。
选中点C和点C’+选中参数r —【构造】—【以圆心和半径作圆】—取两圆上面交点D.。
例析用几何画板深度迭代功能制作数学课件.docx

例析用几何画板深度迭代功能制作数学课件摘要:在教学极限的概念和定积分的定义等涉及图形的无限分割或与操作次数有关的数学内容时,借助几何画板的深度迭代功能,能快速制作出集动态性、交互性、实用性于一体的辅助教学课件,有效突破了教学难点。
关键词:几何画板;深度迭代;数学课件几何画板操作简单、功能强大,是广大数学教师的首选教育软件。
笔者在用几何画板辅助教学的实践中,深感几何画板的深度迭代功能十分强大。
现将有关辅助教学课件的设计思想和制作步骤与大家分享,以期抛砖引玉,共同提高。
•深度迭代功能在数学上,迭代是指把某些数学结构、计算或其他操作的过程重复应用于先前的相同操作的结果。
这些操作必须根据某些输入来定义输出,迭代则是用每一步的输出作为下一步的输入。
几何画板中的迭代是按一定的迭代规则,从原象到初象反复映射的过程。
原象是产生迭代序列的初始对象,通常称为“种子”。
初象是原象经过一定规则变换操作而得到的第一个象。
几何画板中的深度迭代是一种带参数的迭代,通过改变参数的值可改变迭代深度,从而使我们能对某些数学对象反复进行相同操作的工作变得简单易行,可实现人机交互、动态变换。
•课件制作案例1.动态演示圆的内接与外切正多边形(1)设计思想在高中数学极限的概念教学或选修课《数学史选讲》中,一般都会讲到我国古代数学家刘徽的“割圆术",其体现了朴素的极限思想。
在教学中我们若用几何画板动态演示圆的分割过程(如图1),随着分割的份数n的值越来越大,圆的内接和外切正多边形越来越接近于圆,并动态计算圆周率的精确度也越来越高,这有助于提高学生的学习兴趣和对极限概念的理解。
(2)制作步骤①画一个圆,在圆上取一点A,圆心标记为0。
将角度、距离和其他的精确度设为“十万分之一”,新建参数n,参数值为6,计算和的值。
②双击圆心0,将点A按标记角度旋转得点,构造线段、,过作线段的垂线a,将点A按标记角度旋转得点B,构造射线0B,与直线a交于点C。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对应规则:A→A'。
6、选中参数用加减键调整参数,可得到变化的多边形。
7、对参数创建“动画”。
温馨提示:最好在制作之前将精确度精确到个位。
最后制作的效果图:
二、正方形深度迭代
先看最终效果图,如何制作呢?
制作方法:
1、构造正方形、确定原象:
从左至右画线段AB(A、B即为原象);
双击A点→选中AB→变换→旋转→逆时针旋转90°→得C;
双击C点→选中CA→变换→旋转→逆时针旋转90°→得D;
连续BD。
2、构造初象:
在线段AB上任取一点E(其中一个初象),按顺序选中A、B、E→度量→比→标记比;
双击B→将D按标记比进行缩放得另一初象F。
3、新建参数:n=25;
制作方法:
1、构造下图:
构造线段AB→以B为中心将A顺时针旋转90°得点C→以C为中心将B顺时针旋转90°得点D,连结BC、CD、DA得正方形ABCD。
2、以O为中心,分别将E、F、G、H按1:2的缩放比缩放得E’、F’、G’、H’,连结EE’、FF’、GG’、HH’和E’F’G’H’。
3、新建参数n=2
3、构造初象:
选中DC→按ctrl+M得DC的中点E→顺次选定E、C、D→构造→圆上的弧→在弧上构造点
F,连结DF、CF→隐藏弧。
4、新建参数n=3
5、深度迭代:
选中原象A、B和参数→变换→按住shift键→深度迭代;
对应规则:A对D,B对F;(新添映射)A对F,B对C。
6、设置F的“动画”;
7、系列按钮的创建:
4、深度迭代:选定A、B和n,按如下方式进行深度迭代。(注意:在下图显示中一定要选“最终迭代”)
n=2产生的图形如下图:
5、隐藏无关对象即可得最终效果图。
八、正八边形与正方形密铺
最终效果图:
制作方法:
1、先制作下图,A、B为原象。
2、新建参数n=3。
3、深度迭代:选定A、B和n,按如下方式进行深度迭代。
2、新建参数n=2;
3、选中A、B和参数n进行深度迭代,按逆时针方向进行深度迭代。
对应方式:A→B,B→A;A→L,B→K;A→J,B→I;A→G,B→H;A→E,B→F;A→C,B→D。
4、改变n的值再观察。
六、八边形与正方形密铺(外展)
效果ቤተ መጻሕፍቲ ባይዱ:
制作方法:
1、构造下图:
构造线段AB→以B为中心将A顺时针旋转90°得点C→以C为中心将B顺时针旋转90°得点D,连结BC、CD、DA得正方形ABCD。
4、选中参数用加减键调整参数观察效果。
按制作谢宾斯基三角形的方法可制作谢宾斯基四边形(如下图所示)
四、所有正方形都变色的勾股数
效果图:
制作方法:
1、构造原象和正方形:
作线段AB,A、B为主动点;将B以A为旋转中心逆时针旋转90°得D,又以
D为旋转中心,将A逆时针旋转90°得C;连结AD、DC、CB,得正方形ABCD。
4、选中原象A、B和参数n→“变换”→按SHIFT键的同时选“深度迭代”。
对应规则:A→E,B→F。
5、设置动点E的“动画”。
动画演示时,若要改变正方形边的颜色,只要按如下方式处理即可:
选中正方形ABCD的边和参数n→“显示”→“颜色”→“参数”→“参数范围2.0-4.0”;再创建参数n的“动画”;将“E的动画”和“n的动画”选中→编辑→操作类按钮→系列…→系列动作选“同时执行”。
三、多映射制作谢宾斯基三角形
效果图:
制作方法:
1、绘制 ,分别取AB、BC、CA边的中点D、E、F(如图所示);
2、新建参数n=3;
3、选中A、B、C三点和参数n→“变换”→按SHIFT键的同时选“深度迭代”。对应规则:A→A,B→D,C→F;(增添新映射)A→D,B→B,C→E;(增添新映射)A→F,B→E,C→C。
选中“颜色变化”按钮和“动画点”按钮→编辑→操作类按钮→系列→执行动作选“同时执行”
→将系列按钮的标签改为“颜色变化的勾股树”。
8、隐藏无关对象。
五、正十二边形与正三角形密铺
效果图:
制作方法:
1、构造线段AB,以B为中心将A顺时针旋转150°得C,再以C为中心将B顺时针旋转150°得D,
按如此方式一直到点L,连结BC、CD、DE、EF、FG、GH、HI、IJ、JK、KL、LA得正十二边形。
2、设置正方形的动态变化颜色:
选中A、B、C、D→构造→四边形的内部;
任作一条线段MN,并在其上构造O、P、Q三点,度量OA、PB、QD的长度;
选中OA、PB、QD的长度值和正方形ABCD的内部→显示→颜色→参数→确定;
制作O、P、Q三点的“动画”按钮:选中O、P、Q三点→编辑→操作类按钮→动画→确定。
2、以O为中心,分别将E、F、G、H按1:2的缩放比缩放得E’、F’、G’、H’,连结EE’、FF’、GG’、HH’和E’F’G’H’。
3、新建参数n=2
4、深度迭代:选定A、B和n,按如下方式进行深度迭代。
n=2产生的图形如下图:
5、隐藏无关对象即可得如下效果图。
七、八边形与正方形密铺(内敛)
最终效果图:
5、隐藏无关对象即可得最终效果图。
九、蜂状
最终效果图:
制作方法:
1、绘制下图:构造线段AB→以A为旋转中心将B逆时针旋转60°得点C→连结AB、AC并作它们的中点E、F→连结CE、BF交于D→隐藏线段AB、AC、BF、CE→连结AD、BD、CD。
2、新建参数n=3。
3、使用迭代构造蜂窝图形:
(1)选中点A、B和n,选择“变换”→“深度迭代”命令。
2、计算旋转角并标记:“数据”→“计算”→360°/n→标记角度。
3、构造原象和初象:作O,A两点→双击点O→选中点A→“变换”
→“旋转”得到点A'→选中三点→“构造”→“三角形内部”。
4、设置变化颜色:选中参数和“三角形内部”的颜色→“显示”→“颜色”
→“参数”→“参数范围2.0-4.0”。作选段OA,AA',A'O。
几何画板制作深度迭代的方法探究
迭代是几何画板中一个很有趣的功能,它相当于程序设计的递归算法。用几何画板制作迭代或深度迭代,首先必须制作原象对象和初象对象。若原象是点,这点必须是机动的,不能是射线的端点,不能是坐标原点,不是改变数轴或坐标长度的控制点。
一、用深度迭代制作任意正多边形
制作方法:
1、新建参数:n=6,参数属性中的范围设置为3-20。
