几何画板的一些用法.
几何画板对度量结果的各种操作基本内容

【几何画板对度量结果的各种操作基本内容】一、引言在数学中,几何画板是用来测量长度、角度和形状的工具。
它是一种基本的几何工具,用来帮助我们在平面上进行各种几何运算。
在本文中,我们将探讨几何画板对度量结果的各种操作基本内容,包括长度的测量、角度的测量和形状的计算等方面。
二、长度的测量1. 直线段的测量:使用几何画板可以测量直线段的长度,我们可以通过几何画板上的刻度来测量线段的实际长度,这是几何画板最基本的功能之一。
2. 弧长的测量:除了直线段的测量,几何画板还可以用来测量曲线或圆的弧长,我们可以利用几何画板上的刻度来测量圆弧或曲线的长度。
3. 不规则图形的测量:对于不规则的图形,可以利用几何画板的移动功能来测量其周长,通过将几何画板依次沿着不规则图形的边缘移动,从而获得其周长。
三、角度的测量1. 直角的测量:在几何画板上,我们可以利用直角器来测量直角,直角器可以帮助我们准确地确定90°的角度,这对于进行各种几何运算是非常重要的。
2. 锐角和钝角的测量:除了直角的测量,几何画板还可以用来测量各种锐角和钝角,我们可以通过旋转几何画板上的角度尺来测量各种大小的角度。
3. 复杂角度的测量:对于复杂的角度,几何画板还可以使用辅助工具来进行测量,比如通过绘制并测量三角形的各个角度来获得复杂角度的大小。
四、形状的计算1. 面积的计算:在几何画板上,我们可以利用面积尺来测量各种形状的面积,通过将面积尺放置在图形内部来获得图形的面积。
2. 周长的计算:对于各种形状的周长,可以利用几何画板来测量其周长,通过将几何画板依次沿着形状的边缘移动来获得其周长。
3. 体积的计算:在三维几何中,几何画板还可以用来计算立体图形的体积,通过将几何画板置入立体图形中来测量其容积。
五、个人观点和理解几何画板是数学学习中不可或缺的工具,它可以帮助我们更加直观地理解和运用几何知识,通过对度量结果的各种操作,我们可以更加深入地理解几何图形的特性和性质。
几何画板使用技巧
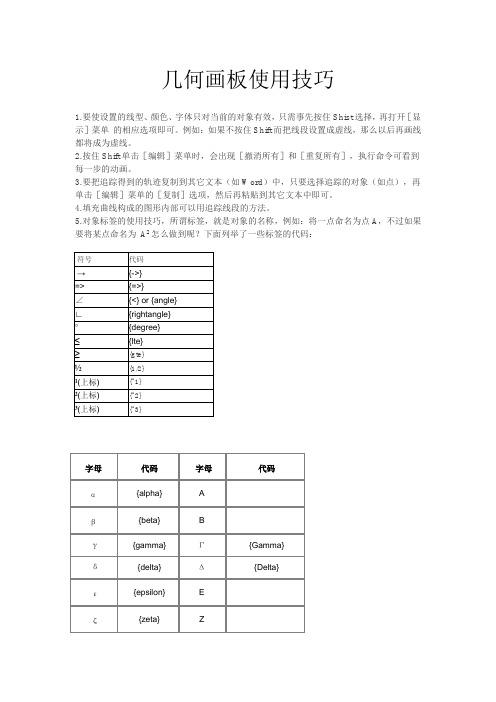
几何画板使用技巧1.要使设置的线型、颜色、字体只对当前的对象有效,只需事先按住Shist选择,再打开[显示]菜单的相应选项即可。
例如:如果不按住Shift而把线段设置成虚线,那么以后再画线都将成为虚线。
2.按住Shift单击[编辑]菜单时,会出现[撤消所有]和[重复所有],执行命令可看到每一步的动画。
3.要把追踪得到的轨迹复制到其它文本(如Word)中,只要选择追踪的对象(如点),再单击[编辑]菜单的[复制]选项,然后再粘贴到其它文本中即可。
4.填充曲线构成的图形内部可以用追踪线段的方法。
5.对象标签的使用技巧,所谓标签,就是对象的名称,例如:将一点命名为点A,不过如果要将某点命名为A2怎么做到呢?下面列举了一些标签的代码:用迭代做正多边形1.新建参数,名称为n,参数属性中的范围设置为3-20。
2.“度量”“计算”用360度除以参数。
标记角度。
3.在画板中作A,B两点,双击点A,选中点B,“变换”“旋转”得到点B’’,选中三点“作图”“三角形内部”。
选中参数和“三角形内部”的颜色,“显示”“颜色”“参数”“参数范围2.0-4.0”。
作选段AB,BB’,B’A。
4.选中点B和参数n,“变换”按SHIFT键的同时“带参数迭代”。
初象为B’。
5.选中参数用加减键调整参数,可得到变化的多边形。
图形之间的互变/gsp/show.asp?id=212运用几何画板的文本输入可以得到以下符号:具体方法:输入小写英文字母abcd...xyz,或者ABCD....XYZ,在字体中选择Wingdings 即可,你可以根据自己的需要输入相应的字母即可得到需要的符号。
(2010年12月20日)能产生正负角的的滚动的圆步骤1“图表”/“定义坐标系”2在x轴上任取一点A3选中点A,“度量”/“横坐标”4选中点g和x轴,“构造”/“垂线”5选中垂线,“构造”/“垂线上的点”B6依次选中A、B,“构造”/“以圆心和圆周上的点画圆”7选中点B,“度量”/“纵坐标”8选中点B和垂线,“构造”/“垂线”9“度量”/“计算”-(180度*A点横坐标)/(pi*abs(B点纵坐标))10选中计算结果,“变换”/“标记角度”11选中点A,“变换”/“标记中心”12选中点B,“变换”/“旋转”,得到点C13依次选中点A点C,“构造”/“线段”,“构造”/“轨迹”14完成。
巧用几何画板 上活数学课堂

巧用几何画板上活数学课堂几何画板是一种用于可视化几何概念和问题的教学工具,可以巧妙地运用在数学课堂上。
下面将介绍几个几何画板的应用示例。
一、直线与角的性质在几何画板上,可以绘制直线、线段和角。
教师可以通过移动线段的端点,让学生观察并找出直线平行、垂直、相交的条件,从而引导学生发现直线的性质。
通过几何画板的实际操作,学生可以更加直观地理解直线的性质和角的性质,提高数学思维和发现问题的能力。
二、图形的变换和对称性几何画板还可以用于图形的变换和对称性的教学。
教师可以绘制一个三角形,要求学生通过平移、旋转和翻转等操作,得到其他形状的图形。
学生可以通过拖动和旋转图形的顶点,观察图形的变换规律,并总结出平移、旋转和翻转的特点和性质。
通过实际操作,学生可以深入理解图形的变换和对称性,掌握相关的概念和方法。
三、空间几何的探索几何画板可以绘制三维图形,用于空间几何的探索和分析。
教师可以绘制一个长方体,要求学生观察它的性质,并找到长方体的面、边和顶点的数量。
四、证明几何定理几何画板还可以用于证明几何定理。
教师可以绘制一个直角三角形,要求学生证明直角三角形的斜边上的高等于直角边上的高和几何平均数的和。
学生可以通过绘制高、勾股定理和相似三角形的证明过程,用几何画板实际操作,展示证明过程的合理性和正确性。
通过几何画板的使用,可以提高学生的证明能力和逻辑思维能力。
几何画板的巧妙运用可以在数学课堂上活化教学内容。
教师可以通过几何画板的实际操作,让学生更加直观地理解几何概念和问题,培养他们的思维能力和创造力。
几何画板的广泛应用有助于提高数学课堂的教学效果和学生的学习兴趣。
几何画板画线段的运用技巧

几何画板画线段的运用技巧
1. 使用直尺:几何画板底面是光滑的,可以通过直尺把线段画得更加精确,尤其是长线段和斜线段。
2. 画勾线图:在画线段前,可以根据需要先画出勾线图,确定线段的长度和方向,以便更加精确地制图。
3. 用分度尺测量:如果需要画一个准确长度的线段,可以使用分度尺进行测量和标记。
4. 画平行线段:可以应用平行线段和垂直线段的特性,来画出一组平行或垂直的线段。
5. 画弧形线段:使用圆规和直尺可以画出圆弧线段。
6. 使用几何板上的比例尺:在需要保持比例的情况下,使用比例尺标记线段的长度。
7. 利用几何变换:可以通过平移、旋转、对称等几何变换来画出有规则的线段。
8. 用剪贴:使用图片、图形等工具进行剪切和合并,使线段的形状更加多样化、美观化。
几何画板基本操作

几何画板基本操作
1.创建几何图形:首先,在几何画板中选择一个几何图形的绘制工具,比如点、线、圆、多边形等。
然后,在绘图区域点击并拖动鼠标,确定几
何图形的位置和尺寸。
最后,松开鼠标按钮,完成几何图形的创建。
3.添加文本:几何画板还支持在绘图区域添加文本。
你可以选择一个
文本工具,在绘图区域点击并拖动鼠标,确定文本的位置和大小。
然后,
输入想要添加的文本内容,并根据需要调整文本的字体、颜色和样式。
4.绘制图表:几何画板通常还提供了一些绘制常见图表的工具,如条
形图、折线图、饼图等。
你可以选择一个适合的图表工具,在绘图区域点
击并拖动鼠标,确定图表的位置和尺寸。
然后,根据数据输入图表的具体
数值,并选择图表的样式和颜色。
最后,完成绘制并呈现出一个漂亮的图表。
6.图层管理:几何画板通常支持图层的创建和管理,用于对绘制的几
何图形进行分组和层次化管理。
你可以创建多个图层,并为每个图层添加
不同的几何图形。
这样可以方便地控制图形的显示和隐藏,或者修改各个
图层中的几何图形而不影响其他图层的内容。
10.自定义设置:几何画板通常提供一些自定义选项,允许用户根据
自己的需求进行个性化设置。
例如,你可以调整绘图区域的背景颜色、网
格线的间距和颜色,或者设置默认文本字体和大小等。
几种常见的几何画板使用教程

几种常见的几何画板使用教程几何画板可以绘制各种基本的几何图形,在作图的时候,有的时候我们需要作一个角等于已知角,有的时候需要绘制一个半圆,有的时候需要绘制一个扇形。
下面我们就来给大家介绍介绍几种常见的几何画板使用教程?给大家做个参考。
一、作一个角等于已知角1.度量已知角的度数。
依次选中已知角的三个顶点,执行“度量”——“角度”命令度量角的度数。
执行“度量”——“角度”度量已知角的度数2.在所需要的地方画一条线段,作为要画的角的一边,然后双击其中一个端点,使其作为标记中心。
作角的一边并双击其中一个端点为标记中心3.选中度量的已知角的度数,执行“变换”——“标记角度”;选中度量的度数对已知角标记角度4.选中所画的角的一边,执行“变换”——“旋转”(在弹出旋转的对话框中,选标记角度),单击“旋转”按钮,即可得到一个等于已知角的角。
选中角的一边执行“变换”——“旋转”得到角二、利用几何画板制作半圆1.打开几何画板,单击“自定义工具”——“三角形”——“直角三角形”,在画布上面单击一下鼠标,然后拖动鼠标就可以画出一个直角三角形。
使用自定义工具绘制直角三角形示例2.用“移动箭头工具”选择直角三角形的三个顶点,单击菜单栏“构造”——过三点的弧,得到如下图所示图形。
选中直角三角形三个顶点构造过三点的弧示例3.分别选中三角形的两直角边,右键选择“隐藏线段”,这样半圆就制作好了,如下图所示。
选中直角三角形两直角边执行隐藏命令三、绘制几何画板扇形步骤一打开几何画板,在左边工具栏选择“自定义工具”——圆工具——扇形(可以选择单弧/双弧)。
在几何画板自定义工具选择绘制扇形工具示例步骤二用鼠标点击画布任意位置拖动鼠标就可以画出扇形(可以画双弧,也可以画单弧)。
几何画板中绘制的扇形图示例以上就是对几种常见的几何画板使用教程的介绍,如果还有什么不清楚的,可以关注几何画板教程。
几何画板的操作

几何画板的操作几何画板是一种帮助学生进行几何图形绘制和操作的工具,可以用来教授和实践各种几何知识。
下面是几何画板的一些基本操作。
1.创建几何图形:几何画板可以用来创建各种几何图形,比如直线、线段、射线、角、三角形、四边形、圆等等。
可以通过点击画板上的对应图形工具,按照提示进行操作,绘制出所需的图形。
3.删除图形:如果不需要一些图形,可以使用几何画板的删除工具来删除它。
点击删除工具,然后点击要删除的图形即可。
有些画板还提供了撤销操作,可以撤销最近进行的操作。
4.存储和载入:几何画板通常可以将绘制的几何图形存储起来,以便以后使用。
可以将它们保存到文件中,然后在需要时重新载入。
这对于教师和学生来说非常有用,可以保存课堂上的示范图形,方便回顾和使用。
5.注释和标记:几何画板通常提供注释和标记工具,可以在图形上添加文字、符号、箭头等。
这可以用来解释图形中的特点、性质和关系,增强学习效果。
6.测量和计算:几何画板通常可以用来进行测量和计算。
可以测量图形的长度、角度、面积等,通过选中所需的图形和使用测量工具来进行操作。
一些画板还提供了计算工具,可以自动计算图形的一些属性,比如周长、面积、相似比等。
7.几何变换:几何画板通常提供几何变换工具,可以对图形进行平移、旋转、翻转等操作。
可以选择所需的图形和变换工具,然后按照提示进行操作。
这对于理解几何变换的概念和性质非常有帮助。
8.几何探索:几何画板不仅可以进行绘制和操作,还可以用来进行几何探索和实验。
可以通过选择几何图形和进行操作,观察其性质和关系,探索几何中的规律和定理。
这对于培养学生的几何思维和发现能力非常有帮助。
总的来说,几何画板是一种非常实用的教学工具,可以帮助学生进行几何图形的绘制、修改、存储和操作,以及进行几何探索和实验。
它能够增加学生对几何知识的理解和掌握,并培养他们的几何思维和发现能力。
几何画板案例

几何画板案例几何画板是一种用来绘制几何图形的工具,它可以帮助学生更好地理解和掌握几何知识。
在教学中,老师可以通过几何画板向学生展示各种几何图形的构造方法,让学生在实际操作中加深对几何知识的理解。
同时,学生也可以利用几何画板进行练习和作业,提高他们的几何图形绘制能力。
下面我们将通过几个实际案例来展示几何画板在教学中的应用。
第一个案例是关于绘制正方形的。
老师可以在几何画板上示范如何利用直尺和圆规绘制一个正方形。
首先,利用直尺在画板上画出一条边,然后利用圆规在这条边的一个端点为圆心,边长为半径画出一个圆弧。
接着,利用圆规在另一个端点为圆心,同样的半径画出另一个圆弧。
最后,连接两个交点即可得到一个完整的正方形。
通过这个案例,学生可以清晰地了解正方形的构造方法,加深对正方形的理解。
第二个案例是关于绘制平行线的。
在几何画板上,老师可以示范如何利用直尺和圆规绘制一组平行线。
首先,在画板上画出一条直线作为基准线,然后利用圆规在这条直线上取一个点。
接着,利用圆规在这个点为圆心,任意半径画出一个圆弧。
然后,在这个圆弧的两个交点处分别利用圆规画出两条弧线。
最后,连接这两条弧线的两个交点即可得到一组平行线。
通过这个案例,学生可以直观地了解平行线的构造方法,掌握绘制平行线的技巧。
第三个案例是关于绘制三角形的。
在几何画板上,老师可以示范如何利用直尺和圆规绘制一个三角形。
首先,在画板上画出一条边作为基准边,然后利用圆规在这条边的一个端点为圆心,任意半径画出一个圆弧。
接着,在另一个端点为圆心,同样的半径画出另一个圆弧。
最后,连接这两个端点和圆弧的交点即可得到一个完整的三角形。
通过这个案例,学生可以学会如何利用直尺和圆规绘制三角形,加深对三角形构造方法的理解。
通过以上几个案例的示范,我们可以看到几何画板在教学中的重要作用。
它不仅可以帮助学生直观地了解几何图形的构造方法,还可以提高学生的绘图能力和几何思维能力。
因此,在教学中,老师可以充分利用几何画板,让学生在实际操作中学习和掌握几何知识,提高他们的学习效果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、几何画板简介
《几何画板》软件是由美国Key Curriculum Press公司制作并出版的优秀教育软件,1996年该公司授权人民教育出版社在中国发行该软件的中文版。
正如其名“21世纪动态几何”,它能够动态地展现出几何对象的位置关系、运行变化规律,是数学与物理教师制作课件的“利剑
1.窗口组成
由题标栏、菜单栏、工具栏、状态栏、绘图窗口和记录窗口等组成。
2.工具栏组成
工具栏依次是选择工具(实现选择,及对象的平移、旋转、缩放功能)、画点工具、画线工具、画圆工具、文本工具和对象信息工具。
在选择工具和画线工具按钮上按住鼠标左键停留片刻,会弹出更多的类型工具;选择对象的方法可以选择点按、按Shift点按或拖动等方式选中对象。
3.对象之间的关系
几何画板中对象之间的关系如同生活中父母与子女关系。
如果改变“父母”的位置或大小,为了保持与父母的几何关系,作为“子女”对象也随之变化。
例如,我们先作出两个点,再作线段,那么作出的线段就是那两个点的“子女”。
又如,先作一个几何对象,再基于这个对象用某种几何关系(平行、垂直等)或变换(旋转、平移等)作出另一个对象,那么后面作出的几何图形就是前面的“子女”。
4.了解对象信息
选择“信息工具”,然后在某个对象上单击或双击,即可显示有关信息或弹出该对象信息对话框。
二、基本操作
1.点的生成与作用
例1 画三角形
先画三个点(可按住Shift键连续画点);然后利用“作图”菜单中的“线段”命令画出三角形。
注:用按住Shift键的方法,最大的好处是三个顶点都被选中。
例2 画多边形
先画多个点(可按住Shift键连续画点);然后利用“作图”菜单中的“线段”命令(或直接按CtrL+L)画出多边形。
注:选取顶点的顺序是十分重要的,不同的顺序会得出不同的多边形。
2.线的作法
“画线工具”有三种线段、直线和射线,选中后在绘图窗口中进行画图即。
例3 制作验证三角形的三边的垂直平分线相交于一点的课件(初步进行作图练习)
3.画圆的方法
画圆有3种方法
用画圆工具作圆;通过两点作圆;用圆心与半径画圆(这种方法作的圆定长不变,除非改变定长时,否则半径不变)
4.画圆弧的方法
画圆弧也有3种方法
按一定顺序选定三点然后作弧(按逆时针方向从起点到终点画弧);选取圆
及圆上2点作弧(从第一点逆时针方向到第二点之间的一段弧);选取圆上三点作弧(与法2相似,只是无需选中圆,作完弧后,可以隐藏原来的圆,可见新作的弧)
5.扇形和弓形
与三角形内部相似(先选中三个顶点),扇形和弓形含有“面”,而不仅仅只有“边界”。
扇形和弓形的画法类似:
用上述方法作圆弧,选择该弧,用“作图”菜单中的“扇形内部”(或“弓形内部”)命令作出扇形或弓形(阴影部分)。
6.度量、计算与制表
[度量] 选中三角形内部后,在“度量”菜单中“面积”和“周长”命令,度量三角形面积与周长。
利用“显示”菜单中“参数选择”命令,可以进行“对象参数”设置。
[计算] “度量”菜单的“计算”命令可以对对象的值进行运算,求得所需要的结果,我们以“相交弦定理”验证为例进行说明。
①画一个圆及两条相交的弦;②度量出四条线段的长度(距离);③分别选择同一直线上的两条线段的距离值,利用“度量”菜单中的计算命令,依次计算出两者之积④拖动动点,观察规律:相交弦定理。
[制表] 在“度量”菜单中“制表”命令。
选择上例中“四条线段的长度”,利用“制表”命令,制出表格。
变化图形,增加表格项的方法有3种:选中表格菜单中“加项”命令;选中表格利用CtrL+E快捷键;双击表格。
7.变换
“变换”包括平移、旋转、缩放、反射等命令。
各标记命令允许指定决定变换的几何对象、几何关系,或度量值。
也可以通过组合平移、旋转、缩放、反射等变换定义自己的变换。
标记中心和标记镜面命令确定了几何变换的类型。
旋转和缩放需要一个中心点,所以在实施这两种变换前要先确定一个中心点。
同样,反射需要一个镜面,在反射前要先确定一个镜面。
8.标签
所谓标签,也就是给作出的点、线、圆、圆弧等几何图形起个名字。
用几何画板作出的几何对象,一般都由系统自动配置好标签。
利用“标签”工具双击标签文本可以进行重命名操作。
