2动力学作业答案
吉大《生物药剂与药物动力学》在线作业二【答案57890】

吉大《生物药剂与药物动力学》在线作业二
红字部分为答案!
一、单选题
1.生物体内进行药物代谢的主要酶系是()
A.肝微粒体代谢酶
B.乙酰胆碱酯酶
C.琥珀胆碱酯酶
D.单胺氧化酶
2.多剂量或重复给药经过几个半衰期体内药物浓度达到稳态是()
A.3
B.10
C.4-5
D.6-7
3.关于药物的分布叙述错误的是
A.药物在体内的分布是不均匀的
B.药效强度取决于分布的影响
C.药物作用的持续时间取决于药物的消除速度
D.药物从血液向组织器官分布的速度取决于药物与组织的亲和力
E.药物在作用部位的浓度与肝脏的代谢无关
4.影响药物分布的因素不包括
A.体内循环的影响
B.血管透过性的影
C.药物与血浆蛋白结合力的影响
D.药物与组织亲和力的影响
E.药物制备工艺的影响
5.对药物动力学含义描述错误的是
A.用动力学和数学方法进行描述
B.最终提出一些数学关系式
C.定性地探讨药物结构与体内过程之间的关系
D.可知道药物结构改造、设计新药
E.制订最佳给药方案
6.溶出度的测定方法中错误的是
A.溶剂需经脱气处理
B.加热使溶剂温度保持在37℃±0.5℃
C.调整转速使其稳定。
D.开始计时,至45min时,在规定取样点吸取溶液适量,
E.经不大于1.0μm微孔滤膜滤过,
7.影响药物代谢的主要因素没有
A.给药途径
B.给药剂量
C.酶的作用
D.生理因素。
动力学基本定律习题答案

动力学基本定律习题答案动力学基本定律习题答案动力学是物理学中研究物体运动的学科,它描述了物体如何受力而运动的规律。
动力学基本定律是研究物体运动的基础,通过习题的形式来理解和应用这些定律是学习动力学的重要环节。
下面将给出一些动力学基本定律习题的答案,并对其中的一些关键点进行解析。
一、牛顿第一定律习题答案1. 问题描述:一个小球在光滑水平面上以匀速运动,它受到的合外力为零吗?答案:是的,根据牛顿第一定律,一个物体如果受到的合外力为零,它将保持静止或匀速直线运动。
二、牛顿第二定律习题答案1. 问题描述:一个质量为2kg的物体受到一个3N的力,求物体的加速度。
答案:根据牛顿第二定律,力等于物体的质量乘以加速度,即F = ma。
代入已知数据,可得3N = 2kg * a,解得a = 1.5 m/s²。
三、牛顿第三定律习题答案1. 问题描述:一个物体受到一个力,它对施力物体的作用力是多大?答案:根据牛顿第三定律,作用力和反作用力大小相等,方向相反。
因此,该物体对施力物体的作用力大小与所受力的大小相等。
四、摩擦力习题答案1. 问题描述:一个物体在水平地面上受到一个10N的水平拉力,摩擦系数为0.2,求物体的摩擦力大小。
答案:摩擦力的大小可以通过乘以摩擦系数和物体的法向力得到。
由于物体受到的水平拉力和摩擦力平衡,所以摩擦力的大小等于10N * 0.2 = 2N。
五、重力习题答案1. 问题描述:一个质量为5kg的物体在重力加速度为10m/s²的情况下,求它所受到的重力大小。
答案:重力的大小可以通过物体的质量乘以重力加速度得到。
所以重力的大小等于5kg * 10m/s² = 50N。
六、弹力习题答案1. 问题描述:一个弹簧的弹性系数为100N/m,它被拉伸2m,求所产生的弹力大小。
答案:弹力的大小可以通过弹性系数乘以弹簧的伸长量得到。
所以弹力的大小等于100N/m * 2m = 200N。
第十二章化学动力学基础(二)练习题及答案

第十二章 化学动力学基础(二)练习题一、 选择题1.以下有关催化剂不正确的说法,是催化剂(A )改变反应物的平衡转化率 (B )改变反应途径(C )改变频率因子 (D )降低活化能 2.催化剂加快反应速率,是由于它能使(A )指前因子增大 (B )几率因子增大 (C )碰撞频率增加 (D )活化分子数增加 3.反应本性、温度、反应途径、浓度与活化能关系正确的是(A )反应途径与活化能无关 (B )反应物浓度与活化能有关(C )反应温度与活化能无关 (D )反应本性与活化能有关 4.气固相催化反应Pt<700K 2CO(g) + O 2(g)2CO 2(g)的速率方程是: r = k p (o 2)/p (co), 其反应级数应为:(A) 一级反应 (B) 二级反应 (C) 对 O 2是一级,对 CO 是负一级 (D) 级数不能确定 5.某反应速率常数与各基元反应速率常数的关系为 12124()2k k k k , 则该反应的表观活化能E a 与各基元反应活化能的关系为:(A) E a =E 2 +12E 1 - E 4 (B) E a = E 2+12(E 1- E 4)(B) E a = E 2+ (E 1- 2E 4)1/2 (D) E a = E 2+ E 1- E 46.在平行反应中要提高活化能较低的反应的产率,应采取的措施为: (A) 升高反应温度 (B) 降低反应温度 (C) 反应温度不变(D) 不能用改变温度的方法。
7.化学反应速率常数的 Arrhenius 关系式能成立的范围是:(A) 对任何反应在任何温度范围内 (B) 对某些反应在任何温度范围内 (C) 对任何反应在一定温度范围内 (D) 对某些反应在一定温度范围内8.一个基元反应,正反应的活化能是逆反应活化能的2倍,反应时吸热120 kJ·mol-1,则正反应的活化能是(kJ·mol-1):(A) 120 (B) 240 (C) 360 (D) 609.物质A 发生两个一级平行反应A B,A C,设两反应的指前因子相近且与温度无关,若E1> E2,则有:(A) k1> k2 (B) k2 > k1 (C) k2= k1 (D) 无法比较k1, k2 的大小10.催化剂能极大地改变反应速率,以下说法不正确的是:(A) 催化剂改变了反应历程(B) 催化剂降低了反应的活化能(C) 催化剂改变了反应的平衡,以致使转化率大大地提高了(D) 催化剂能同时加快正向和逆向反应速率11.下面四种说法中不正确的是:(A)在具有速控步的反应历程中,达到稳态后,速控步后的各个步骤的反应速率都等于速控步的反应速率,速控步前的各步骤均处于平衡状态(B) 根据微观可逆性原理,在反应历程中不可能出现2A → C + 3D 这样的基元反应(C) 在光化学反应中,体系的Gibbs自由能总是在不断地降低(D) 在采用温度跃变的驰豫法来研究溶液中的快速反应时,该反应必须是放热或吸热反应12.除多光子吸收外,一般引起化学反应的光谱,其波长范围应是:(A) 可见光(400 - 800 nm) 及紫外光(150 - 400 nm)(B) X射线(5 - 10-4 nm)(C) 远红外射线(D) 微波及无线电波13.在光的作用下,O2可转变为O3,当1 mol O3生成时,吸收了3.01×1023个光子,则该反应之总量子效率Φ为:(A) Φ=1 (B) Φ=1.5(C) Φ=2 (D) Φ=314.根据微观可逆性原理,反应物分子能量消耗的选择性和产物能量分配的特殊性 有对应关系,因此对正向反应产物主要是平动激发,则对逆向反应更有利于促进反 应进行的能量形式应为:(A)振动能 (B)转动能(C)平动能 (D)能量形式不限,只要足够高 15.对Einstain 光化当量定律的认识下述说法正确的是:(A) 对初级,次级过程均适用 (B) 对任何光源均适用 (C) 对激光光源及长寿命激发态不适用 (D) 对大、小分子都适用 16.在简单碰撞理论中,有效碰撞的定义是:(A) 互撞分子的总动能超过E c (B) 互撞分子的相对总动能超过E c (C)互撞分子联心线上的相对平动能超过E c (D)互撞分子的内部动能超过E c 17.在碰撞理论中校正因子P 小于1的主要因素是:(A) 反应体系是非理想的 (B) 空间的位阻效应 (C) 分子碰撞的激烈程度不够 (D) 分子间的作用力 18.Lindemann 单分子反应机理是假定多原子分子被振动激发后 (A) 立即分解 (B) 有一时滞 (C) 发出辐射 (D) 引发链反应19.同一个反应在相同反应条件下未加催化剂时平衡常数及活化能为k 及E a ,加入正催化剂后则为k '、E a ',则存在下述关系: (A) k '=k , E a =E a ' (B) k '≠k , E a ≠E a ' (C) k '=k , E a >E a ' (D) k '<k , E a '<E a20.过渡态理论的速率常数的公式为()()()k k T h q q q E RT =≠-B AB//exp /∆0,下述说法正确的是(A) q ≠不是过渡态的全配分函数 (B) q A , q B 是任意体积中分子的配分函数 (C) q A , q B , q ≠均是分子在基态时的配分函数(D) ()k T h B /是过渡态M≠中任一个振动自由度配分函数二、 判断题1.关于催化剂特征的不正确描述是在反应前后催化剂的物理性质和化学性质全不改变。
吉大20秋《生物药剂与药物动力学》在线作业二答案

(单选题)1: 影响药物分布的因素不包括
A: 体内循环的影响
B: 血管透过性的影
C: 药物与血浆蛋白结合力的影响
D: 药物与组织亲和力的影响
E: 药物制备工艺的影响
正确答案: E
(单选题)2: 生物体内进行药物代谢的最主要的部位是()。
A: 血液
B: 肾脏
C: 肝脏
D: 唾液
正确答案: C
(单选题)3: 生物药剂学的吸收、分布和排泄的过程没有药物分子结构的改变,被称为()A: 体内过程
B: 转运
C: 转化
D: 处置
正确答案: B
(单选题)4: 生物体内进行药物代谢的主要酶系是()
A: 肝微粒体代谢酶
B: 乙酰胆碱酯酶
C: 琥珀胆碱酯酶
D: 单胺氧化酶
正确答案: A
(单选题)5: 溶出度的测定方法中错误的是
A: 溶剂需经脱气处理
B: 加热使溶剂温度保持在37℃±0.5℃
C: 调整转速使其稳定。
D: 开始计时,至45min时,在规定取样点吸取溶液适量,
E: 经不大于1.0μm微孔滤膜滤过,
正确答案: E
(单选题)6: 药物的排泄途径有()
A: 肾
B: 胆汁
C: 唾液
D: 以上都有可能
正确答案: D。
2021年大学物理习题精选-答案——第2章 质点动力学

质点动力学习题答案欧阳光明(2021.03.07)2-1一个质量为P 的质点,在光滑的固定斜面(倾角为α)上以初速度0v 运动,0v 的方向与斜面底边的水平线AB 平行,如图所示,求这质点的运动轨道.解: 物体置于斜面上受到重力mg ,斜面支持力N .建立坐标:取0v方向为X 轴,平行斜面与X 轴垂直方向为Y 轴.如图2-1.图2-1X 方向: 0=x F t v x 0=① Y 方向: y y ma mg F ==αsin ② 0=t 时 0=y 0=y v由①、②式消去t ,得2-2 质量为m 的物体被竖直上抛,初速度为0v ,物体受到的空气阻力数值为f KV =,K 为常数.求物体升高到最高点时所用时间及上升的最大高度.解:⑴研究对象:m⑵受力分析:m 受两个力,重力P 及空气阻力f ⑶牛顿第二定律:合力:f P F+=y 分量:dtdVm KV mg =-- 即dt mKV mg dV 1-=+mg Ke KV mg K V t m K1)(10-+=⇒-①0=V 时,物体达到了最高点,可有0t 为)1ln(ln 000mgKV K mmg KV mg K m t +=+=② ∵dtdyV =∴Vdt dy =021()1K t m mmg KV e mgt K K-+--⎡⎤=⎢⎥⎣⎦③ 0t t =时,max y y =,2-3 一条质量为m ,长为l 的匀质链条,放在一光滑的水平桌面,链子的一端由极小的一段长度被推出桌子边缘,在重力作用下开始下落,试求链条刚刚离开桌面时的速度. 解:链条在运动过程中,其部分的速度、加速度均相同,沿链条方向,受力为mxg l,根据牛顿定律,有 图2-4通过变量替换有 m dvxg mv l dx =0,0x v ==,积分00l vm xg mvdv l =⎰⎰由上式可得链条刚离开桌面时的速度为v gl =2-5 升降机内有两物体,质量分别为1m 和2m ,且2m =21m .用细绳连接,跨过滑轮,绳子不可伸长,滑轮质量及一切摩擦都忽略不计,当升降机以匀加速a =12g 上升时,求:(1) 1m 和2m 相对升降机的加速度.(2)在地面上观察1m 和2m 的加速度各为多少?解: 分别以1m ,2m 为研究对象,其受力图如图所示.(1)设2m 相对滑轮(即升降机)的加速度为a ',则2m 对地加速度a a a -'=2;因绳不可伸长,故1m 对滑轮的加速度亦为a ',又1m 在水平方向上没有受牵连运动的影响,所以1m 在水平方向对地加速度亦为a ',由牛顿定律,有题2-5图联立,解得g a ='方向向下 (2)2m 对地加速度为22ga a a =-'=方向向上 1m 在水面方向有相对加速度,竖直方向有牵连加速度,即牵相绝a a a+=' ∴g g g a a a 25422221=+=+'=a a '=arctanθo 6.2621arctan ==,左偏上. 2-6 一物体受合力为t F 2=(SI ),做直线运动,试问在第二个5秒内和第一个5秒内物体受冲量之比及动量增量之比各为多少? 解:设物体沿+x 方向运动,25250501===⎰⎰tdt Fdt I N·S (1I 沿i方向)7521051052===⎰⎰tdt Fdt I N·S (2I 沿i方向)∵⎩⎨⎧∆=∆=1122)()(p I p I∴3)()(12=∆∆p p2-7 一弹性球,质量为020.0=m kg ,速率5=v m/s ,与墙壁碰撞后跳回.设跳回时速率不变,碰撞前后的速度方向和墙的法线夹角都为60α︒=,⑴求碰撞过程中小球受到的冲量?=I ⑵设碰撞时间为05.0=∆t s ,求碰撞过程中小球受到的平均冲力?F = 解:i i i mv i I I x10.060cos 5020.02cos 2=⨯⨯⨯===⇒αN·S2-9 一颗子弹由枪口射出时速率为10s m -⋅v ,当子弹在枪筒内被加速时,它所受的合力为 F=(bt a -)N(b a ,为常数),其中t 以秒为单位:(1)假设子弹运行到枪口处合力刚好为零,试计算子弹走完枪筒全长所需时间;(2)求子弹所受的冲量.(3)求子弹的质量.解: (1)由题意,子弹到枪口时,有0)(=-=bt a F ,得ba t =(2)子弹所受的冲量 将ba t =代入,得(3)由动量定理可求得子弹的质量2-10 木块B 静止置于水平台面上,小木块A 放在B 板的一端上,如图所示. 已知0.25A m =kg ,B m =0.75kg ,小木块A 与木块B 之间的摩擦因数1μ=0.5,木板B 与台面间的摩擦因数2μ=0.1. 现在给小木块A 一向右的水平初速度0v =40m/s ,问经过多长时间A 、B 恰好具有相同的速度?(设B 板足够长)它将受解:当小木块A 以初速度0v 向右开始运动时,到木板B 的摩擦阻力的作用,木板B 则在A 给予的摩擦力及台面给予的摩擦力的共同作用下向右运动. 如果将木板B 与小木块A 视为一个系统,A 、B 之间的摩擦力是内力,不改变系统的总动量,只有台面与木板B 之间的摩擦力才是系统所受的外力,改变系统的总动量. 设经过t ∆时间,A 、B 具有相同的速度,根据质点系的动量定理0()k A B A F t m m v m v -∆=+-再对小木块A 单独予以考虑,A 受到B 给予的摩擦阻力'K F ,应用质点的动量定理'0k A B F t m v m v -∆=- 以及'1k A F m g μ= 解得0012121(),A A B v v v m v t m m gμμμμμ-=-∆=+-图2-10代入数据得 2.5v =m/s t ∆=7.65s2-11一粒子弹水平地穿过并排静止放置在光滑水平面上的木块,如图2-11所示. 已知两木块的质量分别为1m 和2m ,子弹穿过两木块的时间各为1t ∆和2t ∆,设子弹在木块中所受的阻力为恒力F ,求子弹穿过后,两木块各以多大速度运动.解:子弹穿过第一木块时,两木块速度相同,均为1v ,初始两木块静止,由动量定理,于是有设子弹穿过第二木块后,第二木块速度变为2v ,对第二块木块,由动量定理有 解以上方程可得2-12一端均匀的软链铅直地挂着,链的下端刚好触到桌面. 如果把链的上端放开,证明在链下落的任一时刻,作用于桌面上的压力三倍于已落到桌面上那部分链条的重量.解:设开始下落时0t =,在任意时刻t 落到桌面上的链长为x ,链未接触桌面的部分下落速度为v ,在dt 时间内又有质量dm dx ρ=(ρ为链的线密度)的链落到桌面上而静止. 根据动量定理,桌面给予dm 的冲量等于dm 的动量增量,即 所以2dxF vv dtρρ== 由自由落体的速度22v gx =得这是t 时刻桌面给予链的冲力. 根据牛顿第三定律,链对桌面的冲力'F F =,'F 方向向下,t 时刻桌面受的总压力等于冲力'F 和t 时刻已落到桌面上的那部分链的重力之和,所以图2-11所以3Nxgρ= 即链条作用于桌面上的压力3倍于落在桌面上那部分链条的重量. 2-13一质量为50kg 的人站在质量为100kg 的停在静水中的小船上,船长为5m ,问当人从船头走到船尾时,船头移动的距离. 解:以人和船为系统,整个系统水平方向上动量守恒 设人的质量为m ,船的质量为M ,应用动量守恒得 其中v ,V 分别为人和小船相对于静水的速度, 可得m -MV =v 人相对于船的速度为'M mM+=-=v v V v 设人在t 时间内走完船长l ,则有在这段时间内,人相对于地面走了0tx vdt =⎰所以Mlx M m=+船头移动的距离为'53ml x l x M m =-==+2-14质量为M 的木块静止在光滑的水平桌面上,质量为m ,速度0v 的子弹水平地射入木块,并陷在木块内与木块一起运动.求: (1)子弹相对木块静止后,木块的速度和动量; (2)子弹相对木块静止后,子弹的动量;(3) 在这个过程中,子弹施于木块的冲量.解:子弹相对木块静止后,其共同速度设为u ,子弹和木块组成系统动量守恒(1)0()mv m M u =+ 所以0mv u m M=+(2)子弹的动量20m m v P mu m M==+(3)针对木块,由动量守恒知,子弹施于木块的冲量为2-15质量均为M 的两辆小车沿着一直线停在光滑的地面上,质量为m的人自一辆车跳入另一辆车,接着又以相同的速率跳回来. 试求两辆车的速率之比.解:质量为m 的人,以相对于地面的速度v 从车A 跳到车B ,此时车A 得到速度1u ,由于车是在光滑的地面上,沿水平方向不受外力,因此,由动量守恒得人到达车B 时,共同得速度为2u ,由动量守恒得人再由车B 以相对于地面的速度v 跳回到车A ,则车B 的速度为'2u ,而车A 与人的共同速度为'1u ,如图所示,由动量守恒得联立方程解得:'22m u v M ='12mu v M m=+ 所以车B 和车A 得速率之比为2-16体重为P 的人拿着重为p 的物体跳远,起跳仰角为ϕ,初速度为0v . 到达最高点时,该人将手中的物体以水平向后的相对速度u抛出,问跳远成绩因此增加多少?解:人和物体组成系统在最高点抛出物体前后沿水平方向动量守恒,注意到对地面这个惯性参考系从最高点到落地,人做平抛运动所需时间0sin v t gϕ= 跳远距离增加为2-17铁路上有一平板车,其质量为M ,设平板车可无摩擦地在水平轨道上运动. 现有N 个人从平板车的后端跳下,每个人的质量均为m ,相对平板车的速度均为u . 问在下述两种情况下,平板车的末速度是多少?(1)N 个人同时跳离;(2)一个人、一个人的跳离. 所得结果是否相同.解:取平板车和N 个人为研究对象,由于在水平方向上无外力作用,故系统在该方向上动量守恒. 取平板车运动方向为坐标轴正方向,设最初平板车静止,则有()0Mv Nm v u +-= 所以N 个人同时跑步跳车时,车速为(2)若一个人、一个人地跳车,情况就不同了. 第一个跳车时,由动量守恒定律可得第二个人跳车时,有以此类推,第N 个人跳车时,有所以1111()2NN n muv mu M m M m M Nm M nm ==++⋅⋅⋅=++++∑因为1112M m M m M Nm>>⋅⋅⋅>+++ 故N v v >2-18质量为kg 10的物体作直线运动,受力与坐标关系如图2-18所示。
专题2 动力学的常见模型

项目 情境2
情境3
图示
关键能力 · 突破
滑块可能的运动情况
续表
①v0>v时,可能一直减速(条件:v≤ v02 2μgl ),也可能先 减速再匀速(条件: v02 2μgl <v<v0); ②v0<v时,可能一直加速(条件:v≥ v02 2μgl ),也可能先 加速再匀速(条件:v0<v< ) v02 2μgl
情境3
关键能力 · 突破
图示
滑块与传送带共速条件
若
v2 2g
≤l,滑块与传送带能共速
若
|
v2 v02 2g
|
≤l,滑块与传送带能共速
若
v02 2g
≤l且v0≥v,滑块与传送带能共速
关键能力 · 突破
例2 (多选)如图所示,水平传送带A、B两端相距x=4 m,以v0=4 m/s的速度(始 终保持不变)顺时针运转。今将一小煤块(可视为质点)无初速度地轻放在A 端,由于煤块与传送带之间有相对滑动,会在传送带上留下划痕。已知煤块与 传送带间的动摩擦因数μ=0.4,重力加速度大小g取10 m/s2。则煤块从A运动 到B的过程中,下列说法正确的是 ( BD ) A.煤块从A运动到B的时间是2.25 s B.煤块从A运动到B的时间是1.5 s C.划痕长度是0.5 m D.划痕长度是2 m
关键能力 · 突破
审题关键 这里只有a球路径属于等时圆模型,b、c球如何跟等时圆模型建 立联系? 提示:b球路径比等时圆弦长要长,c球路径是直径的1/2
关键能力 · 突破
解析 由等时圆模型知,a球运动时间小于b球运动时间,a球运动时间和 沿过CM的直径的下落时间相等,所以从C点自由下落到M点的c球运动时间 最短,故C正确。
(整理)全部动力学答案.
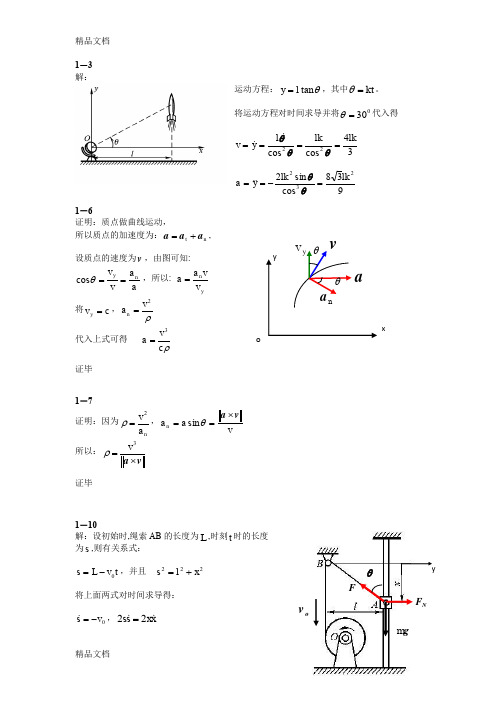
1-3 解:运动方程:θtan l y =,其中kt =θ。
将运动方程对时间求导并将030=θ代入得34cos cos 22lk lk l y v ====θθθ938cos sin 2232lk lk y a =-==θθ1-6证明:质点做曲线运动,所以质点的加速度为:n t a a a +=,设质点的速度为v ,由图可知:aav v yn cos ==θ,所以: y v v a a n =将c v y =,ρ2n va =代入上式可得 ρc v a 3=证毕 1-7证明:因为n 2a v =ρ,v a a v a ⨯==θsin n 所以:va ⨯=3v ρ 证毕1-10解:设初始时,绳索AB 的长度为L ,时刻t 时的长度 为s ,则有关系式:t v L s 0-=,并且 222x l s +=将上面两式对时间求导得:0v s -= ,x x s s 22= ovovF N Fg myθxo由此解得:xsv x 0-= (a ) (a)式可写成:s v x x 0-= ,将该式对时间求导得:2002v v s x x x=-=+ (b)将(a)式代入(b)式可得:3220220xlv x x v x a x -=-== (负号说明滑块A 的加速度向上)取套筒A 为研究对象,受力如图所示,根据质点矢量形式的运动微分方程有:g F F a m m N ++=将该式在y x ,轴上投影可得直角坐标形式的运动微分方程:N F F ym F mg xm +-=-=θθsin cos其中:2222sin ,cos l x l lx x +=+=θθ0,3220=-=y x l v x将其代入直角坐标形式的运动微分方程可得:23220)(1)(x lxl v g m F ++= 1-11解:设B 点是绳子AB 与圆盘的切点,由于绳子相对圆盘无滑动,所以R v B ω=,由于绳子始终处于拉直状态,因此绳子上A 、B 两点的速度在 A 、B 两点连线上的投影相等,即:θcos A B v v = (a ) 因为x R x 22cos -=θ (b )将上式代入(a )式得到A 点速度的大小为:22R x xRv A -=ω (c )由于x v A -=,(c )式可写成:Rx R x x ω=--22 ,将该式两边平方可得:222222)(x R R x xω=-将上式两边对时间求导可得:x x R x x R x xx 2232222)(2ω=--将上式消去x 2后,可求得:22242)(R x xR x--=ω (d)由上式可知滑块A 的加速度方向向左,其大小为 22242)(R x xR a A -=ω取套筒A 为研究对象,受力如图所示,根据质点矢量形式的运动微分方程有:g F F a m m N ++=将该式在y x ,轴上投影可得直角坐标形式的 运动微分方程:mg F F ym F xm N -+=-=θθsin cos其中:x R x xR22cos ,sin -==θθ, 0,)(22242=--=y R x x R x ω将其代入直角坐标形式的运动微分方程可得2525)(,)(225222242R x x R m mg F R x x R m F N --=-=ωω1-13解:动点:套筒A ;动系:OC 杆;定系:机座;运动分析:绝对运动:直线运动;相对运动:直线运动;牵连运动:定轴转动。
机械动力学第二版 石端伟 习题答案

∴ me = a1 2 m1 + m2 a4
简化前后势能相等。
U = 1 k1(a2θ )2 + 1 k 2(a3θ )2 = 1 ke(a4θ )2 ⇒ ke = a2 2 k1 + a3 2 k 2
2
2
2
a4
a4
固有频率: f = 1 ke = 1 a2 2 k1 + a32 k 2
( β 是摆线与 O 之间的夹角)
由几何关系可以得到: R = e (θ 是摆线与水平线之间的夹角) sin β sinθ
当摆角很小时有: sin β = R sinθ ≈ R θ ⇒ meω 2 sin β ≈ mω 2 Rθ
e
e
质量
m
的切向加速度:
l
••
θ+
(R
+
l
)ϕ••
,(
ϕ
是摆线与质量到
O
2π me
2π
a2 1
m1
+
a4
2
m2
( ) 7 解:在临界位置系统的自由振动方程的解为: x = B1 + B2t e−ξωnt 其中
•
B1 = x0, B2 = x 0 + ξωnx0 , n = ωn
∴
x
=
x0
+
•
x
0
+
nx0 te−nt
•
x
=
−n x 0
+
•
x
0
+
nx0 te−nt
+
•
x
2 n=1
••
系统的振动方程为: m x+ kx
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)t 0, B j
(2)t 2 , A i
1 1 1 2 2 2 2 2 (3)W m m0 m ( A B ) 2 2 2
2 3.质量为2kg质点,所受到力为 F 4ti 6t j (SI) 作用,该质点t=0时位于原点并静止,试求:(1) t=2s时物体速度大小;(2)前2s内此力功;(3) t=2s时瞬时功率。
9.一质点受F=3x2i(SI)作用,沿 x 轴正方 向运动,从x=0到x=2m过程中,力F作功为 A.8J B.12J C.16J D.24J 10. 一质点在如图所示的坐标平面内作圆周动, 有一力 F F0 ( x i y j )作用在质点上。在该质点从 坐标原点运动到(0, 2R)位置过程中,力对它所 Y 作的功为
1 ( F mg ) R B. 2 1 C. ( F 3mg) R 2 1 D. ( 2mg F ) R 2
F mg m
2
R
1 A f m 2 mgR 2
13. 一质点在力F=5m(5-2t)(SI)的作用下, t=0时静止开始作直线运动,式中m为质点的质 量,t为时间。当t=5s时,质点速率为 A.25 m·-1 s B.-50 m·-1 s C.0 D.50 m·-1 s
4 T 2 2 (1) : I Fdt F0 1 2 t dt i F0T i 3 T 2 0 0
4 T 2 F F0 [1 2 ( t ) ] i T 2
0 j
T i
I 2 F F0 T 3
质点动力学作业答案
一、选择题 1.牛顿第二定律适用的条件是 A.质点 B.惯性系 C.宏观物体的低速运动 D.上面所有的 2.汽车用不变力制动时,决定其停止下来所 通过的路程的量是 A.速度 B.质量 C.动量 D.动能
1 2 (W FS m ) 2
3.对质点系有以下说法 (1)质点系总动量的改变与内力无关 (2)质点系总动能的改变与内力无关 (3)质点系机械能的改变与保守力无关 以上说法中
t 2
224 ( w )
4.一架质量M=810kg的直升飞机,靠螺旋桨的 转动使S=30平方米面积内的空气以 v0 速度向下 运动,从而使飞机悬停在空中。已知空气密 3 度 0 1.20kg m ,求 v0 的大小,并计算发 动机的最小功率。 解:动量定理,1s内
I Mgt mv0 0 Sv
,这时物体的动量
2.质量为m的汽车,沿 x 轴正方向运动,初始 位置x0=0,从静止开始加速,设其发动机的功 率N维持不变,且不计阻力,则汽车任意时刻速 2 2 Nt ,汽车任意时刻置 2 2 N 3。 率
F N
m
x
d m N dt
3
m
t
N不变
3.在合外力F=3+4t(SI)作用下质量为10kg 物体从静止开始作直线运动。在第3秒末物体加 2 速度为 a 1.5m / s ,速度为 2.7m / s 。 4.下列物理量:质量、动量、冲量、动能、势 能、功中与参照系选取有关的物理量是 是 动量、动能、功 。
2 5. 已知质点质量m=5kg,运动方程 r 2ti t j
则质点在0~2秒内受的冲量I的大小为 20Ns , 在0~2秒内所做的功A= 40J 。
6. 质量为0.25kg 的质点,受力 F ti (SI)的作 用,式中t为时间。t=0 时该质点以 2 j m s 1 的速通过坐标原点,则该质点任意时刻的位置
B. 2
m
A
m
B
C. 2
2 D. 2
m A A mB B A 2 B
EkA A 2 EkB B
12.在半径为R的半球形容器中有一质量为m的 质点从P点由静止下滑,如图所示。质点在最低 点Q时,测得它对容器的压力为F,那么质点从 P点到Q的过程中,摩擦力所做的功为多少? 1 A. ( mg F ) R 2
2 0
v0 Mg 0 S 14.9m / s
1 1 2 3 A mv 0 Sv 0 2 2 A 4 P 5.96 10 W t
5.小滑块A位于光滑水平桌面上,小滑块B处在位于桌 面上的直线型光滑小槽中,两滑块的质量都是m,并用 长为l、不可伸长、无弹性的轻绳连接。开始时,A、B 间的距离为l/2, A、B间的连线与小槽垂直。今给滑块A 一冲击,使之获得水平与槽的速度 ,求滑块B开始运 0 动时的速度。 V’
2 4
所受的平均合外力 3 F i (N ) 。 2
三、计算题
1.质量为m物体在0~T时间内受到一个力作用, 4 T 2 F F0 [1 2 ( t ) ] i T 2 F0和T为常数。物体在t=0时速度是0 j ,t =T 时的速度是T i,求在这段时间内 (1)力 F 的冲量和该力平均值大小; (2)该物体所受合外力的冲量; (3)合外力对该物体所做的功。 T 解: T
m0 m1y m2 l m 0 m1x l sin m1 y l cos 2
设绳拉紧时,A对B的运动是以B为中心的圆 周运动,设相对速度为v’,于是有 1y 2 v' cos 1x v' sin
3 以上各式解得 2 v0 方向沿y方向 7
8. 一个质点同时在几个力作用下产生位移 4 5j 6 ,其中一个力为恒力 r i k (SI), 则此力在该位移过程 F 3i 5 j 9k 中所作的功为 A.67J B.91J C.17J D.-67J
A F r (3 4) (5 5) (6 9) 12 25 54 91
(2)该物体所受合外力的冲量;
(2) : I mT m0 m (i j )
1 1 2 2 ( 3) : W m T m 0 0 2 2
(3)合外力对该物体所做的功。
2.质量m质点在外力作用下,其运动方程为,
r Acos( t ) i B sin( t ) j
8.质量m=1kg的物体,在坐标原点处从静止出发在 水平面内沿x 轴运动,其所受合力方向与运动方向 相同,合力大小为F=3+2x(SI),那么,物体在 开始运动的3m内,合力所作功W= 18J ; 且x=3m时,其速率= 6m/s 。
9. 质量m物体,初速为零,从原点起沿x轴正向 运动,所受外力沿x轴正向,大小为F=kx,物 体从原点运动到坐标为x0的点的过程中所受外力 冲量的大小为 mk x0 。 k d kx m x0 I m dx m 10. 一质量为m=5kg的物体,在0到10秒内,受到 如图所示的变力F的作用,由静止开始沿 x 轴正 向运动,而力的方向始终为x轴的正方向,则10 F (N) 秒内变力F所做的功 4000J 。
矢量 r =
2 3 t i 2tj ( SI ) 3
7. 质量M质点沿x 轴正向运动,该质点通过坐标 为x时的速度大小为kx(k为正常量),则此时作 用于该质点上F= Mk2x ,该质点从 x=x0 点出
1 x1 发运动到 x=x1 处所经历的时间Δt ln k x0 dx d 2 kx Mk x FM dt dt
8t F 20 0t 5 5 t 10
40
1 2 A m 2
20
t (s)
O
5
10
11.一颗子弹在枪筒里前进时所受的合力大小为
4 10 F 400 t 3
5
(SI)
子弹从枪口射出的速率为300。假设子弹离开枪 口时合力刚好为零,则 (1) 子弹走完枪筒全长所用的时间 t = 0.003s , (2) 子弹在枪筒中所受的冲量 I = 0.6Ns , (3) 子弹的质量 m= 2×10-3kg 。
7. 人造卫星绕地球作圆周运动,由于受到空气的 摩擦阻力,人造卫星的速度和轨道半径将如何变 化? A.速度减小,半径增大 B.速度减小,半径减小 C.速度增大,半径增大 D.速度增大,半径减小
人造卫星绕地球作圆周运动,由于受到空气的摩擦阻力, 运行速度要减小,万有引力大于所需要的向心力,万有引 力会使人造卫星向地球运动,人造卫星的轨道半径减小, Mm 2 可知,人造卫星的轨道半径减小,速率 由 G 2 m r r 增大。虽然在此过程中有空气的摩擦阻力,但万有引力做 功大于克服空气的摩擦阻力所做的功,所以人造卫星速率 增大。
12.如图所示,一质量m=1.0kg的质点绕半径为 R=1.0m的圆周作逆时针方向的圆周运动。在t=0 时刻,质点处在A处,质点所经历的路程与时间 π π 的关系为 S ( t t )(m),t 以秒计。则在 4 4 3 i kg m s 1 0~1s时间内,质点的动量变化 p 2 j i 位移 r 。 在这段时间内质点
解:设绳拉紧的瞬时, x A的速度为v1 ,B的速度为v2, 由于在y方向系统不受外力, 动量守恒,有 m0 m1y m2 又,A对B所在位置的角动量守恒,有
l m 0 m1x l sin m1 y l cos 2
B
v1
y
5.一小滑块A位于光滑水平面上,小滑块B处在位于桌面上的直 线型光滑小槽中,两滑块的质量都是m,并用长为 l 、不可伸长、 无弹性的轻绳连接。开始时,A,B间距离为l /2, A,B间的连线与小 槽垂直。今给滑块A一冲击,使之获得平行于槽的速度v0,的 求滑 块B开始运动时的速度。
3 解: I p m t 2 i t j
4 8 80( SI )
2 x 2 y 2 2
1 2 A m 80J 2 2 3 2 P F (4ti 6t j ) (t i t j )
