§14-2 光在球面上的折射解析
1. 4. 光在球面上的反射与折射
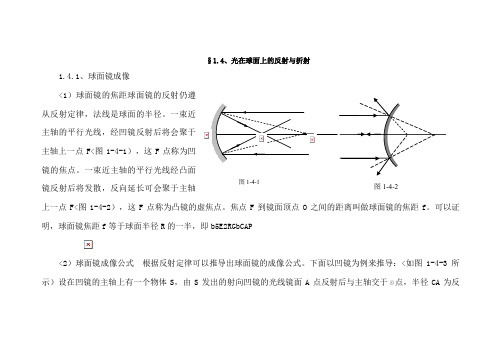
§1.4、光在球面上的反射与折射1.4.1、球面镜成像<1)球面镜的焦距球面镜的反射仍遵从反射定律,法线是球面的半径。
一束近主轴的平行光线,经凹镜反射后将会聚于主轴上一点F<图1-4-1),这F 点称为凹镜的焦点。
一束近主轴的平行光线经凸面镜反射后将发散,反向延长可会聚于主轴上一点F<图1-4-2),这F 点称为凸镜的虚焦点。
焦点F 到镜面顶点O 之间的距离叫做球面镜的焦距f 。
可以证明,球面镜焦距f 等于球面半径R 的一半,即b5E2RGbCAP<2)球面镜成像公式 根据反射定律可以推导出球面镜的成像公式。
下面以凹镜为例来推导:<如图1-4-3所示)设在凹镜的主轴上有一个物体S ,由S 发出的射向凹镜的光线镜面A 点反射后与主轴交于点,半径CA为反图1-4-1图1-4-2射的法线,即S的像。
根据反射定律,,则CA为角A的平分线,根据角平分线的性质有p1EanqFDPw①由为SA为近轴光线,所以,,①式可改写为②②式中OS叫物距u,叫像距v,设凹镜焦距为f,则代入①式化简这个公式同样适用于凸镜。
使用球面镜的成像公式时要注意:凹镜焦距f取正,凸镜焦距f取负;实物u取正,虚物u取负;实像v为正,虚像v为负。
DXDiTa9E3d上式是球面镜成像公式。
它适用于凹面镜成像和凸面镜成像,各量符号遵循“实取正,虚取负”的原则。
凸面镜的焦点是虚的,因此焦距为负值。
在成像中,像长和物长h之比为成像放大率,用m表示,RTCrpUDGiT由成像公式和放大率关系式可以讨论球面镜成像情况,对于凹镜,如表Ⅰ所列;对于凸镜,如表Ⅱ所列。
表Ⅰ 凹镜成像情况~2f表Ⅱ 凸镜成像情况~~2f同侧~<3)球面镜多次成像 球面镜多次成像原则:只要多次运用球面镜成像公式即可,但有时前一个球面镜反射的光线尚未成像便又遇上了后一个球面镜,此时就要引进虚像的概念。
5PCzVD7HxA 如图1-4-4所示,半径为R 的凸镜和凹镜主轴相互重合放置,两镜顶点O1 、 O2 相距2.6R ,现于主轴上距凹镜顶点O1为0.6R 处放一点光源S 。
球面折射

1
n2 n1
---- 临界角(critical angle)
当 i1 > 临界角ic 时,
发生全反射(total internal reflection)
(3) 全反射的应用 —光纤内窥镜(optical fiber)
包裹层 n1
n1 n2
n2
光导纤维(简称光纤),光纤通过光在其内部全反射, 实现远距离传光而损失极小。由于光纤可任意弯曲, 从而使光线拐弯,进而,光纤、光缆的出现使光通讯 得以实现。现已进入社区的宽带网就是基于光通讯。 此外,利用光纤可以弯曲,已做成内窥镜(胃镜) 和激光手术刀。
u1 r1 d
u2
v1
1.0 1.5 1.5 1.0
30 v1
10
解得v1 =90cm , 但实际光线不能到达I1。
对折射面②, I1为其物, 物距u2=d- v1
u2=-50cm, r2=-10cm,
①
②
Q
I2
I1
Thick lens
u1
r1
v2
d
u2
v1
代入单球面折射公式,得
1.5 1.0 1.0 1.5 50 v2 10
i1
i1′
n1
n2
i2 入射面:入射光线与交点处分界面法线构成的平面
定律:1)反射线和折射线 在入射面内;
2)反射角等于入射角 i1=i1′;
3)n1 sin i1 n2 sin i2
;
3.折射定律的讨论:
定义: 光密媒质(denser medium)---折射率大的媒质; 光疏媒质(rarer medium)--- 折射率小的媒质;
tan h / u
tan h / v
光在球面上的反射和折射.ppt

n {s r 2 1 1 } n'{s' r 2 1 1 }
2 s r
2 s' r
Fermat原理
M
等
r
P
O
P’
光 程
n n’ r C
-s
s’
n PM n'MP' n PO n'OP'
n {s r 2 1 1 } n'{s' r 2 1 1 } n (s) n's'
f
'
(nL
1)
1 r1
1 r2
C2
O
证明: I1面: s1, s1’, r1 I2面: s2, s2’, r2
-r2
nL
I1 I2
r1 C1
薄透镜
s = s1, s’ = s2’, s2 = s1’
I 面:nL 1 nL 1
s1' s1
r1
II 面:1 nL 1 nL
s2 ' s2
r2
透镜制造者公式
s1’
解:
-s1
n' n n'n s' s r
n=1.5
O1 R
O2 P’ P1’ s2’ s2
s1’
(1). O1面:s1=-, r1=+R, n1=1, n1’=1.5 O2面:s2=R, r2= -R, n2=1.5, n2’=1
s1’ = 3R O1
C
n n’ r
-s s’
单个折射面成像系统的笛卡尔符号规则
线段
笛卡尔坐标规则补充
纵向线段 以球面顶点O为原点,以入射光线进行 的方向为正方向,建立物空间坐标 s 和像空间坐标 ,
理解几何光学中的球面折射与成像

理解几何光学中的球面折射与成像光学是物理学的一个重要分支,研究光的传播、反射、折射和成像等现象。
在光学中,球面折射与成像是一个重要的概念,它涉及到光线在球面上的传播和折射,以及由此产生的成像效果。
理解球面折射与成像对于我们认识光学现象和应用光学原理具有重要意义。
首先,我们来了解一下球面折射的基本原理。
当光线从一种介质射向另一种介质时,由于介质的折射率不同,光线会发生折射。
而当光线射入球面时,由于球面的曲率,光线会发生弯曲。
这种现象就是球面折射。
球面折射的基本原理可以用斯涅尔定律来描述,即光线在折射时入射角和折射角之间的关系满足sinθ1/sinθ2=n2/n1,其中θ1为入射角,θ2为折射角,n1和n2分别为两种介质的折射率。
在理解了球面折射的基本原理后,我们可以进一步探讨球面折射对成像的影响。
当光线通过球面折射后,会发生折射点的偏移和成像的变化。
具体来说,对于一束平行光线射入球面,经过折射后,光线会集中到球面的一个焦点上。
这个焦点就是球面的主焦点,它是球面折射后光线汇聚的位置。
而对于一个物体,当光线经过球面折射后,会在另一侧的球面上形成一个像。
这个像的位置和形状取决于物体的位置和球面的曲率。
当物体位于球面的主焦点上时,成像会出现在无限远处,形成一个实像。
当物体位于主焦点和球面之间时,成像会出现在球面的另一侧,形成一个放大的虚像。
当物体位于主焦点和球面之外时,成像会出现在球面的同一侧,形成一个缩小的虚像。
除了主焦点外,球面还具有次焦点和次主焦点。
次焦点是光线平行射入球面后汇聚的位置,次主焦点是光线从球面射出后汇聚的位置。
次焦点和次主焦点的位置和主焦点相对应。
当光线从球面射出时,会经过次焦点或次主焦点,然后发散出去。
这种现象在实际应用中有着重要的意义,比如在望远镜和显微镜中,通过调节物镜和目镜之间的距离,可以使光线从球面射出,从而实现放大或缩小的效果。
理解球面折射与成像对于我们认识光学现象和应用光学原理具有重要意义。
光学——球面反射和折射

-u P
C φ
i
i’
-u’ P’ (-s') (-r)
O
sin u
AO s
(-s)
s in ( u ) r(rs 代入 s 中, ) s in ( u')
整理, 即可得到球面反射的近似理想成象公式.
9
球面反射的近似理想成象公式:
化简可得: xx ff ——牛顿公式 也可以用于任何成象过程.
25
[例] 一个折射率为1.6的玻璃哑铃,长20cm,两端的曲率 半径为2cm.若在离哑铃左端5cm处的轴上有一物点,试 求像的位置和性质.
[解]:两次折射成像问题.
1、P为物对球面O1折射成像P1’ 已知:s1=-5cm,r1=2cm n=1,n’=1.6 由折射成像公式: P
n
O1
已 知 :s 5 c m,r c m, 1 1 2 ' n1 ,n 1 .6 P1’ P2’
n n` O2 -s2 -s2’
-s1
s1 ’
n n n n 代入数据,可求得s1’. r1 s1 s1
2、P1’为物对球面O2折射成像
' s 2 0 1 6 4 c m , r 2 c m , n 1 . 6 , n 1 2 2
32
2.说明
P1
n1
P 2'
n2
P1 '
n3
n4
n5
P
4
P
3
① 实物、虚物的判断依据 A、入射光束: 发散——实物;会聚——虚物 B、物所处空间: 物空间——实物;像空间——虚物 ② 虚物处永远没有光线通过(实物不一定,如P1、P2有, P3无) ③ 虚物处像空间,但对应的却是物空间的会聚光束,故折射 率就取物方折射率.(与虚像类似;如上图中P4---物方折 射率为n4) ④ 虚物仍遵从符号法则.(如上图中S4>0)
光在球面上的反射和折射
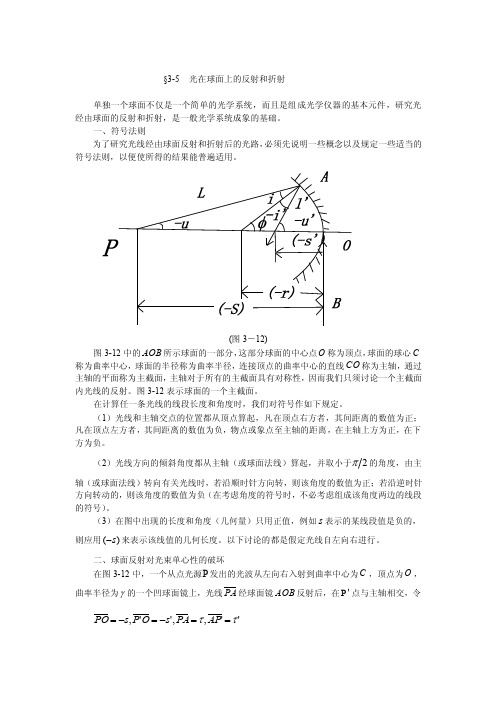
§3-5 光在球面上的反射和折射单独一个球面不仅是一个简单的光学系统,而且是组成光学仪器的基本元件,研究光经由球面的反射和折射,是一般光学系统成象的基础。
一、符号法则为了研究光线经由球面反射和折射后的光路,必须先说明一些概念以及规定一些适当的符号法则,以便使所得的结果能普遍适用。
(图3-12)图3-12中的AOB 所示球面的一部分,这部分球面的中心点O 称为顶点,球面的球心C 称为曲率中心,球面的半径称为曲率半径,连接顶点的曲率中心的直线CO 称为主轴,通过主轴的平面称为主截面,主轴对于所有的主截面具有对称性,因而我们只须讨论一个主截面内光线的反射。
图3-12表示球面的一个主截面。
在计算任一条光线的线段长度和角度时,我们对符号作如下规定。
(1)光线和主轴交点的位置都从顶点算起,凡在顶点右方者,其间距离的数值为正;凡在顶点左方者,其间距离的数值为负,物点或象点至主轴的距离,在主轴上方为正,在下方为负。
(2)光线方向的倾斜角度都从主轴(或球面法线)算起,并取小于2π的角度,由主轴(或球面法线)转向有关光线时,若沿顺时针方向转,则该角度的数值为正;若沿逆时针方向转动的,则该角度的数值为负(在考虑角度的符号时,不必考虑组成该角度两边的线段的符号)。
(3)在图中出现的长度和角度(几何量)只用正值,例如s 表示的某线段值是负的,则应用()s -来表示该线值的几何长度。
以下讨论的都是假定光线自左向右进行。
二、球面反射对光束单心性的破坏在图3-12中,一个从点光源P 发出的光波从左向右入射到曲率中心为C ,顶点为O ,曲率半径为γ的一个凹球面镜上,光线PA 经球面镜AOB 反射后,在'P 点与主轴相交,令 '',,'',ττ==-=-=AP PA s O P s PO半径AC 与主轴的夹角为ϕ,则光线'PAP 的光程为 (')'P A P n n ττ=+ 在PAC ∆和'ACP ∆中应用余弦定理,并注意c o s c o s ()()()'()(')',P C sr r s C P r s s r ϕπϕ=--=---=-=---=- 从而可得()()()()[]2122cos 2ϕs r r s r r l --+-+-=(3-10)以及()()()()[]2122'cos '2'ϕr s r r s r l ----+-= (3-11)因此,光线'PAP 的光程可写成12221222(')()()2()()cos ()(')2()(')cos PAP n r r s r r s n r s r r s r ϕϕ⎡⎤=-+-+--⎣⎦⎡⎤+-+----⎣⎦(3-12)由于当A 点在镜面上移动时,半径r 是常数,而ϕ才是位置的变量,根据费马原理,物象间的光程应取稳定值,为此,把(3-12)式对ϕ求导,并令其等于零,即()()[]()[]0sin '21sin 21''=-+--=ϕϕϕr s r ln s r r l n d PAP d 由此可得 0''=---l rs l s r 或者⎪⎭⎫⎝⎛+=+l s l s r l l ''111'(3-13) 如果发光点P 至O 点的距离s 为已知,从此式即可算出任一反射线和主轴的交点'P 到 O 点的距离's 的值,显然's 的值将随着所取入射线的倾斜角u ,亦即角ϕ的变化而变化,这就是说,从物点发散的单心光束经球面反射后,将不再保持单心(即使平等光束入射时也不例外),关于这一点可说明如下:PC A 1A 2OP 2P'P 3 (图3-13)图3-13中,相应于1PA 及2PA 两入射光线的反射线分别交主轴于1P 和2P 两点,且相交于'P 点,把该图绕主轴PO 转过一个小角度,使三角形12PA A 展成一单心的空间光束,此时'P 点描出一条很短的弧线,它垂直于图面即反射光束的子午象线,而图面中的12PP 则为弧矢象线。
球面折射光线的入射与折射角度

球面折射光线的入射与折射角度折射是光线从一种介质传播到另一种介质时发生的现象。
当光线从一种介质射向另一种介质时,光线的传播速度和方向都会发生改变,而入射角度和折射角度之间存在着一定的关系。
本文将探讨球面折射光线的入射和折射角度之间的关系。
1. 光线的入射角度和折射角度概述入射角度是指光线在从一种介质传播到另一种介质时,与界面法线之间的夹角。
折射角度是指光线从一种介质进入另一种介质后,与界面法线之间的夹角。
根据斯涅尔定律(Snell's Law),光线在界面上的入射角度和折射角度满足以下关系:n1 × sin(入射角度) = n2 × sin(折射角度)其中,n1和n2分别为两种介质的折射率,折射率是介质对光的传播速度的相对性质。
2. 在球面折射中,光线从一种介质射向球形界面,然后折射到另一种介质中。
使用球面坐标系可以更好地描述球面折射情况中的入射与折射角度。
设球心为O,光线从点A入射到球面,入射角度为θ1,光线在球面上经过点B后折射,折射角度为θ2。
根据斯涅尔定律,可以得到以下关系式:n1 × sin(θ1) = n2 × sin(θ2)其中,n1和n2分别为两种介质的折射率。
3. 球面折射光线的入射和折射角度的变化在球面折射光线的入射和折射过程中,光线的入射角度和折射角度会发生变化。
如果入射光线是从一种高折射率介质射入到一个低折射率介质中,即n1 > n2,那么入射角度θ1会小于折射角度θ2。
这是因为光线在从高折射率介质进入低折射率介质时会向法线方向弯曲。
相反地,如果入射光线是从一个低折射率介质射入到一个高折射率介质中,即n1 < n2,那么入射角度θ1会大于折射角度θ2。
光线在从低折射率介质进入高折射率介质时会离开法线。
4. 根据斯涅尔定律计算球面折射光线的入射和折射角度斯涅尔定律可以用来计算球面折射光线的入射和折射角度。
给定两种介质的折射率n1和n2,以及入射角度θ1,可以使用以下公式来计算折射角度θ2:θ2 = arcsin((n1 × sin(θ1)) / n2)其中,arcsin为反正弦函数,用来计算角度的正弦值的反函数。
大学物理下册课件第十四章 光学-几何光学(lou)

即得单球面在近轴条件下的折射公式 n n n n s s r
当入射光为与主光轴平行的平行光时, 像方焦点F′,像方焦距
n f r n n 当像点位于像方无穷远处时,物方焦点F,物方焦距 n f r n n f f 可得高斯公式 1 s s
§14-5 薄透镜
由两个共轴折射曲面构成的光学系统称为透镜 若透镜的厚度比焦距小很多,则称为薄透镜
六种基本透镜类型的主截面
一、薄透镜成像的基本公式 采用逐次成像法进行推导
第一球面O1折射后成像于S" n n1 n n1 s s r1 对于球面O2 物 n2 n n2 n 距 s s r2 n2 n1 n n1 n2 n 两式相加得 s s r1 r2 空气中 n1 = n2 ≈ 1
§14-1 关于光的本性的认识发展简史
17—19世纪 19世纪初
牛顿的微粒说
波动说
获得更多的支持
光是从光源发出的微粒流 杨氏双缝实验显示干涉现象
惠更斯的波动说 光是介质(以太)中的机械波
惠更斯-菲涅耳原理能解 释光直线传播和衍射现象
傅科测出光在水中的速度小 于空气中速度—决定性判据 S2
1850年
波动说
开始占统治地位 M2
傅科旋转镜法测光速
S1 S
M1
L
19世纪 60年代 20世纪初
麦克斯韦电磁波理论 赫兹实验证实了光
是电磁波的预言
波动理论遭遇困难
光电效应、康普顿效应 等不能用波动说解释
光具有波粒二象性
表现为波动 解释传播过程(反射、 折射、干涉、衍射和偏 振)中发生的现象 表现为粒子 解释与实物作用过程 (光的吸收与发射) 中发生的现象
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7
如果要使光线折射后所成的像点处于主光轴上并 落在离开球面无限远处,即l2 = ∞ ,则物点必须放 置在主光轴的F1 点上,而球面顶点C到F1的距离可 以表示为: f 1 l1 n1 R
F1点也是表示折射面性质的点,称为第一主焦点, f2 n2 而f1称为折射面的第一焦距。
点的像距和像的横向放大率。
S1
n1(空气;水)
解:先求放在空气中的情形。
1.50 l2 n1l2 n2l1 1.00 80.0
C
80.0mm
n2(玻璃)
1.50 1.00 20.0 1.00
O
解得l2 = 120 mm
m
1 120 1.50 ( 80.0)
说明像是倒立的实像,位于C点右侧120 mm处。 12
S1O S 2 A sin i n 2 S1 A S 2 O sin r n1
n1
S1
i
θ
A
φ r
n2
S2
n2 n1 n2 n1 l1l 2 n1 Rl 2 n1 l1l 2 n2 Rl1n2 l l1 R 2
近轴光线的球面折射公式。可以看到,对于折射 率为n1和n2的介质以及给定的界面曲率半径R,像点 的位置只依赖于物点的位置。或者说物点和像点之 间存在一一对应的关系。 任何满足近轴光线条件的同心光束在球面上折射 后仍然保持同心性。 5
l1 R l 2 n2 l1 l 2 R n1
C
O
上式对凸状球面和凹状球面都是适用的,只需按
照上面的规定调整球面曲率半径的符号就可以了。
上式也可以用于描述光线在各种球面上的反射,
这时除了应调整球面曲率半径的符号外,还需令
n 2 = -n1 。
还可以用于描述光线在平面上的折射和反射,因 为平面可以认为是曲率半径无限大的球面。 也可以作为研究各种情况下折射和反射成像规 律的基础。
2
二、球面折射公式
根据正弦定理应有:
S1O sin i S1 A sin S1O S 2 A
n1 S1
i
θ
A
φ r
n2 S2
sin i n 2 S1 A S 1 C , S 2 A S 2 C S1 A S 2 O sin r n1 C点是主光轴与球面的交点称为球面的顶点。 S1C是物点到球面顶点的距离称为物距,用l1表示。 S2C是像点到球面顶点的距离称为像距,用l2表示。
13
n1 y1 n2 y2 根据折射定律: l1 l2
y2 n1l2 m y1 n2l1
பைடு நூலகம்11
例题 如图所示一根折射率为1.50的玻璃棒,其一 端被磨成半径为20.0 mm的半球面。若将它先后放 在折射率为1.00的空气中和折射率为1.33的水中,求
在这两种情况下在棒轴上距离顶点80.0 mm处的物
由物点发出的光束,经光学系统后仍为同心光束, 则这个经过光学系统后的光束的心,称为光学系统 对该物点所成的像点。
如果经光学系统后光线本身通过光束心,则该光 束心是物点的实像;如果经光学系统后光线延长线 相交于一点,则该点是物点的虚像。
在近轴光线的情况下,由物点发出的同心光束, 经单球面折射后仍为同心光束,即对应于一个物点 可获得一个像点。
现求放在水中的情形。
这时像距l2应由下式求得:
1.50 l2
横向放大率为:
1.33 80.0
1.50 1.33 20.0
解得l2 = -185 mm ,
m
n1l2 n2l1
1.33 (185 ) 1.50 (80.0)
2.05
表示像是正立的虚像,处于C点左侧185 mm处。
S 2 A sin S 2 O sin r
C
O
线段正负我们规定如下:由折射点或反射点出发到 被考察点所形成的线段的方向,若与入射光的传播 方向相同,则取正值,若相反,则该线段取负值。 3
根据这个规定,我们可以得到:
(1) 物点若为实际物体时,物距一般取负值。 (2) 像距的符号决定于像的位置。像和物若处于折 射面或反射面的同侧,像距取负值;像和物若处于 折射面或反射面的异侧,像距取正值。但是在折射 和反射这两种情况下,对应于同样符号的像距,像 的性质却不同。具体地说,正的像距,在折射的情 况下代表实像,在反射的情况下代表虚像。负的像 距,在折射的情况下代表虚像,在反射的情况下代 表实像。 (3) 曲率半径的符号决定于曲率中心的位置。在凸 状球面的情况下,曲率半径取正值;在凹状球面的 情况下,曲率半径取负值。 4
n 2 n1
折射面的焦距决定于两种介质的折射率和界面的 曲率半径。
焦点有实焦点和虚焦点之分。实焦点是平行光线 经折射后相交的一点;虚焦点是平行光线经折射后 并不相交,而其延长线相交的一点。 8
f1
n1
通过第一主焦点F1所作的垂直于主光轴的平面,称 为第一主焦面;通过第二主焦点F2所作的垂直于主光 轴的平面,称为第二主焦面。如果近轴的平行光线并 不平行于主光轴,则经球面折射后焦点并不处于主焦 点上,但总处于主焦面上。
§14-2 光在球面上的折射
一、介绍几个概念 光线在两种折射率不同的透明介质所形成的球形 分界面上发生一次折射后的规律,这种情形也称为 光在单球面上的折射。物点与球心的连线称为主光 轴,在主光轴附近并与主光轴夹角很小的光线,称 为近轴光线,或傍轴光线。 有一定关系的光线集合称为光束。从一点发出的 光线形成的光束,称为同心光束,或单心光束。 若光束经光学系统反射或折射后,变成会聚于一点 的光束,或者光束本身虽然不会聚于一点,但光线的 延长线相交于一点,这种反射或折射之后的光束也称 同心光束。光线本身不会聚于一点,其延长线也不相 交于一点的光束,称为像散光束。 1
必须条件是物点发出三条光线都必须是近轴光线。
10
五、球面折射的横向放大率
P1
若物体高度为y1,像的 y 2 高度为y2,光学系统 1 S1 F1 QQ 的横向放大率 y
1 3
φ1
Q O φ
2
C
Q’
F2 2
S2
y2
P2
m
2
y1
若像方向与物方向相同称为正像;若方向相反为倒像。
当横向放大率m为正值时,为正像;当横向放大率 m为负值时,为倒像。
n2 n1 n2 n1 用R/(n2 -n1)乘以公式 等号两边,得 l2 l1 R
n2 R n1 R 1 l 2 n2 n1 l1 n2 n1
f1 f2 1 l1 l2
即高斯公式,与近轴光线的球面折射公式完全等效。
9
四、球面折射成像的作图法 如图将一个有限大 小的物体放置在球面 左侧并与主光轴垂直
P1 2 S1 1 3 F1 O 2 F2 S2 P2
物点P1发出的同心光束有三条光线是容易画出: (1) 平行于主光轴的光线折射后通过第二主焦点; (2) 通过第一主焦点的光线折射后平行于主光轴; (3) 通过球面曲率中心的光线沿原路径传播。 三条光线中任意两条的交点就是物点P1的像点P2, 由P2向主光轴作垂线,垂足S2就是S1的像。
6
三、高斯公式
引入焦点焦距,得球面折射的另一种形式:高斯公式。 如果处于主光轴上的物点离开球面的距离为无限大, 即l1 = ∞,那么由它发出而投射到球面上的光线必定 平行于主光轴。这时表示像点位置的像距应为: n2 l2 R n 2 n1 由l2所确定的点表示了折射面的性质,称为第二 主焦点,用F2 表示。 由球面顶点C到F2 的距离,称为折射面的第二焦距, 若用f2 表示,则有:
