1.4.光在球面上的反射与折射
单球面反射和折射

5. 特例
(1)球面反射
n n'
1 1 2 p p' r
平行光线入射,p ,代入物像公式 1 1 2 得 pf'' 2r 2r,f ' 此时对应的像点叫焦点(fpocusp)' r 焦点到顶点的距离— 焦距(focal length)
物像公式为
11 1 p p' f '
(Gauss公式)
1.5 1.0
(8) (1)
1.2
,即成正立、放大的实像。
总的横向放大率
1
2
3
0.5 (
1) 1.2 3
为20cm和15cm,薄透镜折射率为1.5,在凸面 镀银。在球面前方40处的主轴上置一高为1cm 的物,求像的位置和成像的性质。
[解](1)P经凹球面折射成像:
p1=-40cm,n=1.0,n’=1.5,r1=-20cm,代入
n' n n'n p1' p1 r1
1
np1 ' n' p1
1 2
,
1.5 1.0 0.5 p1' 40 20
三、傍轴球面折射的物象关系式
nn'n (u(' u in)) unn('(n'('niu'))') n
p
u
i o
n' h i' c u '
p'
u h p'
r
p
p'
u h p
h
n n nn
p' p r
物像关系式
r
定义 光焦度
Φ n'n r
3-3光在球面介质上的反射、折射

3-3光在球面介质上的反射、折射 光在球面介质上的反射、 光在球面介质上的反射 球面成像的公式
第3章 几何光学 章
n′ n n′ − n − = s′ s r
物、像具有共轭关系,可逆关系. 像具有共轭关系,可逆关系 三 焦点 焦距 焦平面
n′ − n 球面成像的公式; 由球面成像的公式;令:Φ = — 球面光焦度 球面光焦度. r
n r os = f = − n′ − n
且: f ′ /
— 物空间的主焦距 物空间的主焦距 主焦距. (第一主焦距) 第一主焦距)
焦点、焦距是由介质折射率和球面半径决定 焦点、焦距是由介质折射率和球面半径决定.
f = − n′ / n
f ′=
焦距与光焦度关系: 焦距与光焦度关系:
n′ n′ → Φ = Φ f ′ n n f = → Φ = Φ f
像点在像空间无限远处! 像点在像空间无限远处!
— 像空间的主焦距 像空间的主焦距 主焦距. (第二主焦距) 第二主焦距)
n s=− r n′ − n
3-3光在球面介质上的反射、折射 光在球面介质上的反射、 光在球面介质上的反射
第3章 几何光学 章
n s=− r n′ − n
— 物空间的主焦点 (第一主焦点) 物空间的主焦点 第一主焦点) 主焦点.(
第3章 几何光学 章
n s′ s′ − r = (r − s) (− s) n′
此式表明; 只与已知量有关 具有一个像点. 只与已知量有关, 此式表明;s´只与已知量有关,具有一个像点 球面折射成像条件: ) 球面折射成像条件:1)元光束 . 2)光线近轴传播 )光线近轴传播.
s′ n 成像的公式: 成像的公式:由: s ′ − r = (r − s) (− s) n′ s′n′ rn′ rn sn ( s ′ − r ) n′ ( r − s ) n − = − = s′ s′ ( − s ) ( − s ) s′ (− s) n′ n n′ − n ∴ − = s′ s r
光在球面上的反射和折射

1 1 1 s s ( ) l l r l l
考虑近轴光线,进一步得到
它的成像规律与介质无关.
1 1 2 s s r
s:物距
s:像距
'
C
FF
o
令 令
s ,
得 得
s ,
r f f 2
凹面镜
r f ; 2 r f , 2
因此球面镜物方焦点与像方焦点重合 .
P
O n n’
A
P’
r
C
-s
s’
5 近轴光线下球面折射的物像公式
M O n n’
l s, l s
'
'
P
P’
r
C
-s
s’
n' n n'n n'n 定义光焦度(optical power) : s' s r r
r 的单位为米时,光焦度的单位称为屈光度(diopter)
n'n r
P
-u
f
-i’ C
u’
P’
Q
n’
r
s’
-s
单个折射面成像系统的笛卡尔符号规则
笛卡尔坐标规则补充
线段
纵向线段 以球面顶点 O 为原点,以入射光线进行 的方向为正方向,建立物空间坐标 s 和像空间坐标 , 物点坐标为物距,像点坐标为像距 . s 横向线段 以光轴为起点,向上为正向下为负.
n
y
• S
u
O1
R s1 ’
O2
s2 ’ s2
P’
n' n n'n s' s r
(2).
O1面:s1=-2R, r1=+R, n1=1, n1’=1.5
1. 4. 光在球面上的反射与折射
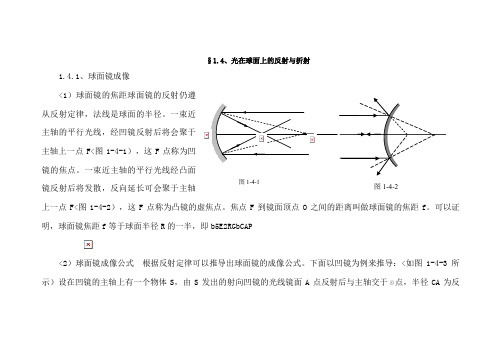
§1.4、光在球面上的反射与折射1.4.1、球面镜成像<1)球面镜的焦距球面镜的反射仍遵从反射定律,法线是球面的半径。
一束近主轴的平行光线,经凹镜反射后将会聚于主轴上一点F<图1-4-1),这F 点称为凹镜的焦点。
一束近主轴的平行光线经凸面镜反射后将发散,反向延长可会聚于主轴上一点F<图1-4-2),这F 点称为凸镜的虚焦点。
焦点F 到镜面顶点O 之间的距离叫做球面镜的焦距f 。
可以证明,球面镜焦距f 等于球面半径R 的一半,即b5E2RGbCAP<2)球面镜成像公式 根据反射定律可以推导出球面镜的成像公式。
下面以凹镜为例来推导:<如图1-4-3所示)设在凹镜的主轴上有一个物体S ,由S 发出的射向凹镜的光线镜面A 点反射后与主轴交于点,半径CA为反图1-4-1图1-4-2射的法线,即S的像。
根据反射定律,,则CA为角A的平分线,根据角平分线的性质有p1EanqFDPw①由为SA为近轴光线,所以,,①式可改写为②②式中OS叫物距u,叫像距v,设凹镜焦距为f,则代入①式化简这个公式同样适用于凸镜。
使用球面镜的成像公式时要注意:凹镜焦距f取正,凸镜焦距f取负;实物u取正,虚物u取负;实像v为正,虚像v为负。
DXDiTa9E3d上式是球面镜成像公式。
它适用于凹面镜成像和凸面镜成像,各量符号遵循“实取正,虚取负”的原则。
凸面镜的焦点是虚的,因此焦距为负值。
在成像中,像长和物长h之比为成像放大率,用m表示,RTCrpUDGiT由成像公式和放大率关系式可以讨论球面镜成像情况,对于凹镜,如表Ⅰ所列;对于凸镜,如表Ⅱ所列。
表Ⅰ 凹镜成像情况~2f表Ⅱ 凸镜成像情况~~2f同侧~<3)球面镜多次成像 球面镜多次成像原则:只要多次运用球面镜成像公式即可,但有时前一个球面镜反射的光线尚未成像便又遇上了后一个球面镜,此时就要引进虚像的概念。
5PCzVD7HxA 如图1-4-4所示,半径为R 的凸镜和凹镜主轴相互重合放置,两镜顶点O1 、 O2 相距2.6R ,现于主轴上距凹镜顶点O1为0.6R 处放一点光源S 。
光的折射与反射

光的折射与反射光是我们日常生活中的常见现象,也是物质的一个重要性质。
在光学中,我们经常涉及到光的两个重要概念,那就是折射和反射。
一、折射折射是指光线从一种介质进入另一种介质时,光线的传播方向发生改变的现象。
常见的折射现象包括:水中的游泳池边沿的失真、光线从玻璃棱角处的偏折等。
为了更好地理解折射现象,我们需要了解折射率这一概念。
简单地说,折射率是指光在某一介质中的传播速度与真空中传播速度的比值。
折射率越大,表示光在该介质中传播的速度越慢。
当光线从一个介质进入另一个折射率较大的介质时,光线会发生向法线(垂直入射面的直线)的方向偏折。
这是因为光在界面处传播速度的改变导致的。
折射定律是描述光在界面处的折射现象的规律,它的数学表达式是n₁sinθ₁=n₂sinθ₂。
其中n₁和n₂分别为两种介质的折射率,θ₁和θ₂分别为入射角和折射角。
根据折射定律,能够计算出光线在不同介质中的折射角。
二、反射反射是指光线在遇到光滑表面时,经过发射回来的现象。
光在反射过程中,保持了入射角和反射角相等的关系。
我们熟悉的镜子便是通过反射现象形成的。
当光线垂直入射在镜子表面时,光线将会直接反射回来。
除了平面镜,我们还经常接触到的是球面镜。
球面镜也能够实现光的反射,但由于镜面不是平的,所以光线的反射方向将会发生改变。
我们常见的凹面镜和凸面镜就是球面镜的两种形式。
凹面镜能够使光线发生发散效果,使物体看起来更小;凸面镜则是使光线聚焦,使物体看起来更大。
三、应用与现象折射和反射现象在生活中有着广泛的应用和实用性。
我们常常利用折射现象来观察物体的失真情况。
例如当我们在游泳池中看自己的身影时,就会发现身体的形状发生了变化。
这是因为水的折射率大于空气,在光线通过不同介质时,折射角度的变化导致了物体形状的改变。
另外,我们还可以利用折射现象来研究光的速度和性质等。
光的反射现象在光学设备和通信技术中也具有重要作用。
典型的例子是反射镜。
反射镜广泛应用于望远镜、显微镜和照相机等光学仪器中。
2023年大学_光学教程第三版(姚启钧著)课后题答案下载

2023年光学教程第三版(姚启钧著)课后题答案下载2023年光学教程第三版(姚启钧著)课后题答案下载本教程以物理光学和应用光学为主体内容。
第1章到第3章为应用光学部分,介绍了几何光学基础知识和光在光学系统中的传播和成像特性,注意介绍了激光系统和红外系统;第4~8章为物理光学部分,讨论了光在各向同性介质、各向异性介质中的传播规律,光的干涉、衍射、偏振特性及光与物质的相互作用,并结合介绍了DWDM、双光子吸收、Raman放大、光学孤子等相关领域的应用和进展。
第9章则专门介绍航天光学遥感、自适应光学、红外与微光成像、瞬态光学、光学信息处理、微光学、单片光电集成等光学新技术。
光学教程第三版(姚启钧著):内容简介绪论0.1 光学的研究内容和方法0.2 光学发展简史第1章光的干涉1.1 波动的独立性、叠加性和相干性1.2 由单色波叠加所形成的干涉图样1.3 分波面双光束干涉1.4 干涉条纹的可见度光波的时间相干性和空间相干性 1.5 菲涅耳公式1.6 分振幅薄膜干涉(一)——等倾干涉1.7 分振幅薄膜干涉(二)——等厚干涉视窗与链接昆虫翅膀上的彩色1.8 迈克耳孙干涉仪1.9 法布里一珀罗干涉仪多光束干涉1.10 光的干涉应用举例牛顿环视窗与链接增透膜与高反射膜附录1.1 振动叠加的三种计算方法附录1.2 简谐波的表达式复振幅附录1.3 菲涅耳公式的推导附录1.4 额外光程差附录1.5 有关法布里一珀罗干涉仪的(1-38)式的推导附录1.6 有同一相位差的多光束叠加习题第2章光的衍射2.1 惠更斯一菲涅耳原理2.2 菲涅耳半波带菲涅耳衍射视窗与链接透镜与波带片的比较2.3 夫琅禾费单缝衍射2.4 夫琅禾费圆孔衍射2.5 平面衍射光栅视窗与链接光碟是一种反射光栅2.6 晶体对X射线的'衍射视窗与链接与X射线衍射有关的诺贝尔奖附录2.1 夫琅禾费单缝衍射公式的推导附录2.2 夫琅禾费圆孔衍射公式的推导附录2.3 平面光栅衍射公式的推导习题第3章几何光学的基本原理3.1 几个基本概念和定律费马原理3.2 光在平面界面上的反射和折射光导纤维视窗与链接光导纤维及其应用3.3 光在球面上的反射和折射3.4 光连续在几个球面界面上的折射虚物的概念 3.5 薄透镜3.6 近轴物近轴光线成像的条件3.7 共轴理想光具组的基点和基面视窗与链接集成光学简介附录3.1 图3-6中P1和JP1点坐标的计算附录3.2 棱镜最小偏向角的计算附录3.3 近轴物在球面反射时物像之间光程的计算附录3.4 空气中的厚透镜物像公式的推导习题第4章光学仪器的基本原理4.1 人的眼睛4.2 助视仪器的放大本领4.3 目镜4.4 显微镜的放大本领4.5 望远镜的放大本领视窗与链接太空实验室——哈勃太空望远镜4.6 光阑光瞳4.7 光度学概要——光能量的传播视窗与链接三原色原理4.8 物镜的聚光本领视窗与链接数码相机4.9 像差概述视窗与链接现代投影装置4.10 助视仪器的像分辨本领视窗与链接扫描隧显微镜4.11 分光仪器的色分辨本领习题第5章光的偏振5.1 自然光与偏振光5.2 线偏振光与部分偏振光视窗与链接人造偏振片与立体电影 5.3 光通过单轴晶体时的双折射现象 5.4 光在晶体中的波面5.5 光在晶体中的传播方向5.6 偏振器件5.7 椭圆偏振光和圆偏振光5.8 偏振态的实验检验5.9 偏振光的干涉5.10 场致双折射现象及其应用视窗与链接液晶的电光效应及其应用5.11 旋光效应5.12 偏振态的矩阵表述琼斯矢量和琼斯矩阵附录5.1 从沃拉斯顿棱镜出射的两束线偏振光夹角公式(5-15)的推导习题第6章光的吸收、散射和色散6.1 电偶极辐射对反射和折射现象的解释6.2 光的吸收6.3 光的散射视窗与链接光的散射与环境污染监测6.4 光的色散6.5 色散的经典理论习题第7章光的量子性7.1 光速“米”的定义视窗与链接光频梳7.2 经典辐射定律7.3 普朗克辐射公式视窗与链接诺贝尔物理学奖7.4 光电效应7.5 爱因斯坦的量子解释视窗与链接双激光束光捕获7.6 康普顿效应7.7 德布罗意波7.8 波粒二象性附录7.1 从普朗克公式推导斯忒藩一玻耳兹曼定律附录7.2 从普朗克公式推导维恩位移定律习题第8章现代光学基础8.1 光与物质相互作用8.2 激光原理8.3 激光的特性8.4 激光器的种类视窗与链接激光产生106T强磁场8.5 非线性光学8.6 信息存储技术8.7 激光在生物学中的应用视窗与链接王淦昌与惯性的束核聚变习题主要参考书目基本物理常量表光学教程第三版(姚启钧著):目录点击此处下载光学教程第三版(姚启钧著)课后题答案。
光在球面上的反射和折射.ppt

n {s r 2 1 1 } n'{s' r 2 1 1 }
2 s r
2 s' r
Fermat原理
M
等
r
P
O
P’
光 程
n n’ r C
-s
s’
n PM n'MP' n PO n'OP'
n {s r 2 1 1 } n'{s' r 2 1 1 } n (s) n's'
f
'
(nL
1)
1 r1
1 r2
C2
O
证明: I1面: s1, s1’, r1 I2面: s2, s2’, r2
-r2
nL
I1 I2
r1 C1
薄透镜
s = s1, s’ = s2’, s2 = s1’
I 面:nL 1 nL 1
s1' s1
r1
II 面:1 nL 1 nL
s2 ' s2
r2
透镜制造者公式
s1’
解:
-s1
n' n n'n s' s r
n=1.5
O1 R
O2 P’ P1’ s2’ s2
s1’
(1). O1面:s1=-, r1=+R, n1=1, n1’=1.5 O2面:s2=R, r2= -R, n2=1.5, n2’=1
s1’ = 3R O1
C
n n’ r
-s s’
单个折射面成像系统的笛卡尔符号规则
线段
笛卡尔坐标规则补充
纵向线段 以球面顶点O为原点,以入射光线进行 的方向为正方向,建立物空间坐标 s 和像空间坐标 ,
大学物理补充内容(几何光学)

会聚透镜成象
•
F1
发出的任一光线PA,与透镜交于A点 (1)从物点 发出的任一光线 ,与透镜交于 点; )从物点P发出的任一光线 作平行于PA的副轴 (2)过透镜中心 作平行于 的副轴 )过透镜中心O作平行于 的副轴OB′,与象 , 方焦平面交于B′点 方焦平面交于 点; 两点, (3)连接 、B′两点,它的延长线就是光的折射 )连接A、 两点 方向, 方向,它与沿主轴的光线交于 P′点,则P′ 点 点即为所求的象点。 点即为所求的象点。
单一球面是组成光学仪器的基本元件和简单的光 学系统,因而是研究光学系统成象问题的基础。 学系统,因而是研究光学系统成象问题的基础。
一、符号规定
1)物距s: 2)像距s’: 实物取正号,虚物取负号。 实像取正号,虚像取负号。
3)曲率半径r:凸球面对着入射光线时取正号; 凹球面对着入射光线时取负号; 平面的曲率半径 r =∞。
解得
s’=12cm
2) 置于水中时:s =8cm ,n1=1.33,n2 =1.5,r =2cm 代入公式得
解得
s’=-18.5cm
【例2】
一条鱼在水面下1米处,水的折射率n=1.33,若在 鱼的正上方观察,其像的位置在哪里? 解:s =1m,n1 = 1.33,n2 = 1,r =∞
解得
s’ =-0.752m
或者说所需的时间)为极值的 ●光总是沿着光程(或者说所需的时间 为极值的 光总是沿着光程 或者说所需的时间 路径传播的,即光沿着光程(亦即所需时间 亦即所需时间)为极 路径传播的,即光沿着光程 亦即所需时间 为极 小、极大或恒定的路径传播 L=极值(极小值、极大值或恒定值) 极值(极小值、极大值或恒定值) 极值 或:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
光源的像只能直接射到凹镜上,问 S 经凹镜和凸镜各反射一次后所成的像在
S
何处?
O1
S2
O2
S1
图 1-4-4
4
u1 0.6R
1
S 在凹镜中成像,
, f1
R 2
111
u1
1 f1
1 12 0.6R 1 R
可解得
1 3R O1O2 2.6R ,
根据题意:所以凹镜反射的光线尚未成像便已又被凸镜反射,此时可将凹镜原来要成像
点。焦点 F 到镜面顶点 O之间的距离叫做球面镜的 焦距 f 。可以证明,球面镜焦距 f 等于球面半径 R
图 1-4-1
的一半,即
R f
2 (2)球面镜成像公式
根据反射定律可以推导出球面镜的成像公式。下面以凹镜为例来推导:
图 1-4-2 (如图 1-4-3 所示)设在凹镜的主
轴上有一个物体 S,由 S 发出的射向凹镜的光线镜面 A 点反射后与主轴交于 S 点,半径 CA为反射的法线, S 即 S 的像。根据反射定律,
镜的厚度为 o o t ,当物点在主轴上的 P 点时,物距 u OP ,现在来计算像点 P 的像距。 S
入射光的折射,这时假定第二个球面 AOB 不存在,并认为球 AOB 右边,都为折射率等于
n 的介质充满,在这种情况下, P 点的像将成在 P 处,其像距
§1.4 、光在球面上的反射与折射
1.4.1 、球面镜成像
(1)球面镜的焦距球面镜的反射仍遵从反射
定律,法线是球Leabharlann 的半径。 一束近主轴的平行光线,经凹镜反射后将会聚于主轴上一点
F(图
1-4-1 ),这 F 点称为凹镜的焦点。 一束近主轴的平 O
行光线经凸面镜反射后将发散, 反向延长可会聚于
F
C
主轴上一点 F(图 1-4-2 ),这 F 点称为凸镜的虚焦
倒
实
2f
同侧 2f
等大
倒
实
2f ~f
同侧 f ~ 2f
放大
倒
实
f
放大
f ~0
异侧 ~
放大
正
虚
0
虚物
异侧 0~f
缩小
正
实
表Ⅱ 凸镜成像情况
3
物的性质 实物
虚 物
物的位置 像的位置 像的大小
f~
同侧 0~f
缩小
~2f 同侧 f ~ 2f
缩小
2f
同侧 2f
等大
f ~2f
同侧 ~
放大
2f
f
像的正倒 正 倒 倒 倒
代入①式
u u 2f 2f
化简
11 1
u
f
这个公式同样适用于凸镜。使用球面镜的成像公式时要注意:凹镜焦距 为正,虚像 v 为负。
11 1
u
f
f 取正,凸镜焦距 f 取负;实物 u 取正,虚物 u 取负;实像 v
2
上式是球面镜成像公式。它适用于凹面镜成像和凸面镜成像,各量符号遵循“实取正,虚取负”的原则。凸面镜的焦点是虚的,
n1 ,
, R R ,即可得到球
11 面镜反射成像公式 u
2
R ,对于凹面镜 R
0 , f1
f2
R
f1
2 ,对于凸面镜 R 0 ,
f2
R 2 ,厚透镜成像。
(C)厚透镜折射成像
设构成厚透镜材料的折射率为 n,物方介质的折射率为 n1 ,像方介质的折射率为 n2 ,前后两边球面的曲率半径依次为 r1和 r2 ,透
SAC S AC ,则 CA为 SAS 角 A 的平分线,根据角平分线的性质有
1
AS CS
AS CS
①
由为 SA为近轴光线,所以 AS S O , AS SO ,①式可改写为
OS CS
OS CS
②
②式中 OS叫物距 u, OS 叫像距 v,设凹镜焦距为 f ,则
CS OS OC u 2 f
CS OC OS 2 f
S n1 和 n2,C 是球心, O 是顶点,球面曲率半径为 R,S 是物点,
是像点,
n1i1 n2i2
A0
A0
A0
i1
, i2
, u , R,
v
联立上式解得
n1 n2 n2 n1
uv
r
这是球面折射的成像公式, 式中 u、υ的符号同样遵循 “实正虚负” 的法则,
对于 R;则当球心 C 在出射光的一个侧,(凸面朝向入射光)时为正,当球心 C
u2 (2.6R 3R)
0.4R , f 2
R 2
111
u2
2 f2
S1 作为凸镜的虚物来处理,
可解得
11 2 0.4R 2 R
2 2R
5
说明凸镜所成的像 S2 和 S 在同一位置上。 1.4.2 、球面折射成像 ( 1)球面折射成像公式 (a)单介质球面折射成像
如图 1-4-5 所示,如果球面左、右方的折射率分别为 1 和 n, S 为 S 的像。因
,这时物距即为
第一焦距 f1,有 f1
n1R ,将 n2 n1
f1 、
f 2 代入成像公式改写成
f1
f2 1
uu
反射定律可以看成折射定律在 n2 n1时的物倒,因此,球面镜的反射成像公式可以从球面镜折射成像公式中得到,由于反射光
的行进方向逆转,像距 υ 和球面半径 R 的正负规定应与折射时相反,在上述公式中令 n2
在入射光的一侧(凹面朝向入射光)时为负。
若引入焦点和焦距概念,则当入射光为平行于主轴的平行光( u=∝)时, 出射光(或其反向延长线)的交点即为第二焦点, (也称像方焦点) ,此时像距
i2 i2
O
图 1-4-6
7
即是第二焦距 f2 ,有 f 2
n2 R 。当出射光为平行光时,入射光(或其延长线)的交点即第一焦点(即物方焦点) n2 n1
因此焦距为负值。在成像中,像长
和物长 h 之比为成像放大率,用 m表示,
mh hu
由成像公式和放大率关系式可以讨论球面镜成像情况,对于凹镜,如表Ⅰ所列;对于凸镜,如表Ⅱ所列。
表Ⅰ 凹镜成像情况
物的性质 物的位置 像的位置 像的大小 像的正倒 像的虚实
实物
同侧 f
缩小
倒
实
~2f 同侧 f ~ 2f
缩小
像的性质 虚 虚 虚 虚
f ~0
异侧 ~
放大
正
实
0
(3)球面镜多次成像 球面镜多次成像原则:只要多次运用球面镜成像公式即可,但有时前一个球面镜反射的光线尚未成像便又
遇上了后一个球面镜,此时就要引进虚像的概念。
如图 1-4-4 所示,半径为 R的凸镜和凹镜主轴相互重合放置,两镜顶点
O1 、 O2 相距 2.6R,现于主轴上距凹镜顶点 O1 为 0.6R 处放一点光源 S。设点
为 i 、 r 均很小,行以
sin i i n
①
sin r r
因为 i
,r
代入①式可有
r n( )
②
对近轴光线来说, α、θ、 β同样很小,所以有
x
x
x
u, R,
代入②式可得
1 n n1
u
R
1i
n
r
SuO
Cv S
图 1-4-5
6
当u
时的 v 是焦距 f ,所以
R
f
n
n1
(b)双介质球面折射成像
如图 1-4-6 所示,球形折射面两侧的介质折射率分别 对于近轴光线
