r 回归参数的标准误差
(完整word)Eviews回归分析输出结果指标解释

Eviews回归分析输出结果指标解释Variable Coefficie Std。
Error t-Statistic Prob.X2。
0288730。
10155819。
977490。
0000回归结果的理解参数解释:1、回归系数(coefficient)注意回归系数的正负要符合理论和实际。
截距项的回归系数无论是否通过T检验都没有实际的经济意义。
2、回归系数的标准误差(Std。
Error)标准误差越大,回归系数的估计值越不可靠,这可以通过T值的计算公式可知3、T检验值(t-Statistic)T值检验回归系数是否等于某一特定值,在回归方程中这一特定值为0,因此T值=回归系数/回归系数的标准误差,因此T值的正负应该与回归系数的正负一致,回归系数的标准误差越大,T值越小,回归系数的估计值越不可靠,越接近于0。
另外,回归系数的绝对值越大,T值的绝对值越大。
4、P值(Prob)P值为理论T值超越样本T值的概率,应该联系显著性水平α相比,α表示原假设成立的前提下,理论T值超过样本T值的概率,当P值<α值,说明这种结果实际出现的概率的概率比在原假设成立的前提下这种结果出现的可能性还小但它偏偏出现了,因此拒绝接受原假设。
5、可决系数(R—squared)都知道可决系数表示解释变量对被解释变量的解释贡献,其实质就是看(y尖-y均)与(y=y均)的一致程度。
y尖为y的估计值,y均为y的总体均值。
6、调整后的可决系数(Adjusted R—squared)即经自由度修正后的可决系数,从计算公式可知调整后的可决系数小于可决系数,并且可决系数可能为负,此时说明模型极不可靠。
7、回归残差的标准误差(S。
E。
of regression)残差的经自由度修正后的标准差,OLS的实质其实就是使得均方差最小化,而均方差与此的区别就是没有经过自由度修正.8、残差平方和(Sum Squared Resid)见上79、对数似然估计函数值(Log likelihood)首先,理解极大似然估计法。
EXCEL回归分析结果分析

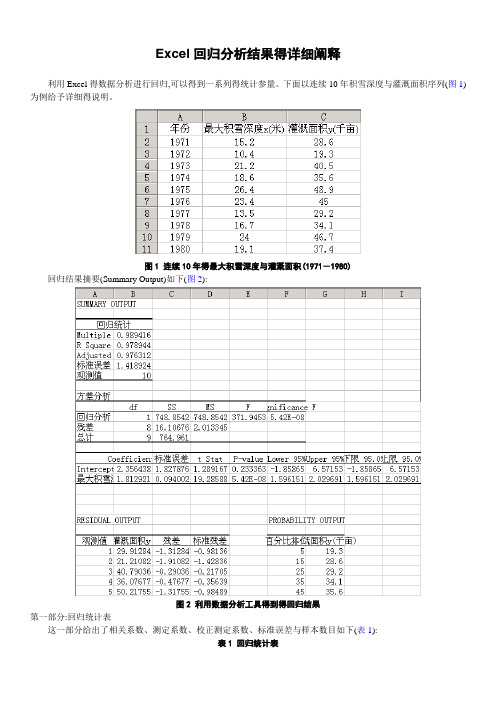
EXCEL回归分析结果分析Excel回归分析结果的详细阐释利用Excel的数据分析进行回归,可以得到一系列的统计参量。
下面以连续10年积雪深度和灌溉面积序列(图1)为例给予详细的说明。
图1 连续10年的最大积雪深度与灌溉面积(1971,1980)回归结果摘要(Summary Output)如下(图2):图2 利用数据分析工具得到的回归结果第一部分:回归统计表这一部分给出了相关系数、测定系数、校正测定系数、标准误差和样本数目如下(表1): 表1 回归统计表逐行说明如下:Multiple对应的数据是相关系数(correlation coefficient),即R=0.989416。
R Square对应的数值为测定系数(determination coefficient),或称拟合优度(goodness of fit),它是相关系数的平方,即有R2=0.9894162=0.978944。
Adjusted对应的是校正测定系数(adjusted determination coefficient),计算公式为式中n为样本数,m为变量数,R2为测定系数。
对于本例,n=10,m=1,R2=0.978944,代入上式得标准误差(standard error)对应的即所谓标准误差,计算公式为这里SSe为剩余平方和,可以从下面的方差分析表中读出,即有SSe=16.10676,代入上式可得最后一行的观测值对应的是样本数目,即有n=10。
第二部分,方差分析表方差分析部分包括自由度、误差平方和、均方差、F值、P值等(表2)。
表2 方差分析表(ANOVA)逐列、分行说明如下:第一列df对应的是自由度(degree of freedom),第一行是回归自由度dfr,等于变量数目,即dfr=m;第二行为残差自由度dfe,等于样本数目减去变量数目再减1,即有dfe=n-m-1;第三行为总自由度dft,等于样本数目减1,即有dft=n-1。
【原创】R语言进行分位数回归数据分析报告论文(附代码数据)

欢迎登陆官网:/datablog用R语言进行分位数回归作者的主要贡献有:(1)整理了分位数回归的一些基本原理和方法;(2)归纳了用R语言处理分位数回归的程序,其中写了两个函数整合估计结果;(3)写了一个分位数分解函数来处理MM2005的分解过程;(4)使用一个数据集进行案例分析,完整地展现了分析过程。
第一节分位数回归介绍(一)为什么需要分位数回归?传统的线性回归模型描述了因变量的条件均值分布受自变量X的影响过程。
其中,最小二乘法是估计回归系数的最基本方法。
如果模型的随机误差项来自均值为零、方差相同的分布,那么回归系数的最小二乘估计为最佳线性无偏估计(BLUE);如果随机误差项是正态分布,那么回归系数的最小二乘估计与极大似然估计一致,均为最小方差无偏估计(MVUL)。
此时它具有无偏性、有效性等优良性质。
但是在实际的经济生活中,这种假设通常不能够满足。
例如当数据中存在严重的异方差,或后尾、尖峰情况时,最小二乘法的估计将不再具有上述优良性质。
为了弥补普通最小二乘法(OLS)在回归分析中的缺陷,1818年Laplace[2]提出了中位数回归(最小绝对偏差估计)。
在此基础上,1978年Koenker 和Bassett[3]把中位数回归推广到了一般的分位数回归(Quantile Regression)上。
分位数回归相对于最小二乘回归,应用条件更加宽松,挖掘的信息更加丰富。
它依据因变量的条件分位数对自变量X进行回归,这样得到了所有分位数下的回归模型。
因此分位数回归相比普通的最小二乘回归,能够更加精确第描述自变量X对因变量Y的变化范围,以及条件分布形状的影响。
(二)一个简单的分位数回归模型[4]假设随机变量的分布函数为(1)Y的分位数的定义为满足的最小值,即(2)回归分析的基本思想就是使样本值与拟合值之间的距离最短,对于Y的一组随机样本,样本均值回归是使误差平方和最小,即(3)样本中位数回归是使误差绝对值之和最小,即(4)样本分位数回归是使加权误差绝对值之和最小,即(5)上式可等价表示为:其中,为检查函数(check function),定义为:欢迎登陆官网:/datablog其中,为指示函数(indicator function),z是条件关系式,当z为真时,;当z为假时,。
回归方程计算过程

回归方程计算过程回归方程是用于预测和建模的统计工具,通过分析自变量和因变量之间的关系,建立一个数学方程来描述这种关系。
在本文中,我们将详细介绍回归方程的计算过程,包括数据收集、数据清洗、模型选择、参数估计和模型评估等步骤。
1.数据收集和数据清洗数据收集是回归分析的第一步,需要收集自变量和因变量的观测数据。
例如,如果我们想要研究体重与身高之间的关系,我们需要收集一组体重和身高的数据。
在数据收集后,需要进行数据清洗,对数据进行整理和处理。
这包括检查和处理缺失值、异常值和重复值等。
确保数据的质量和可用性对于后续的分析非常重要。
2.模型选择在回归分析中,常见的模型包括线性回归模型、多项式回归模型、指数回归模型等。
根据实际问题和数据的特点,选择适当的模型非常重要。
线性回归是最常用的回归模型之一,在处理因变量和自变量之间的线性关系时非常有效。
在线性回归模型中,假设因变量与自变量之间存在一个线性关系,可以用一个线性方程来描述。
3.参数估计通过最小二乘法来估计回归方程中的参数。
最小二乘法是一种常用的参数估计方法,通过最小化预测值与观测值之间的差异来获得最佳拟合结果。
在线性回归模型中,参数估计是求解最小二乘法问题的过程。
通过最小化残差平方和来求解参数的估计值。
残差是观测值与预测值之间的差异,残差平方和是所有观测值的残差的平方之和。
参数估计的结果可以用来建立回归方程,回归方程的形式为:Y=a+bX,其中Y是因变量,X是自变量,a和b是回归方程中的常数。
4.模型评估在获得回归方程后,需要进行模型评估。
模型评估用于评估回归模型的拟合优度和预测能力。
常用的评估指标包括R方值、调整R方值、标准误差等。
R方值是一个常用的模型拟合优度指标,用来评估拟合程度。
R方值的取值范围在0到1之间,越接近1表示模型的拟合效果越好。
调整R方值是对R方值的一种修正,用于解决自变量数量增加导致R方值无法准确评估模型拟合优度的问题。
标准误差是用来评估模型的预测能力的指标。
估计标准误差公式

估计标准误差公式标准误差(Standard Error,SE)是指样本统计量与总体参数之间的差异,它是用来估计样本统计量与总体参数之间的差异的一种测度。
在统计学中,标准误差是对样本统计量的不确定性的一种度量,它可以帮助我们评估样本统计量的精确度和可靠性。
估计标准误差的公式可以根据不同的统计方法和模型来进行推导和计算。
在这篇文档中,我们将介绍一些常见的估计标准误差的公式,并对它们进行简要的说明和比较。
1. 样本均值的标准误差。
样本均值的标准误差是用来衡量样本均值与总体均值之间的差异的一个指标。
当总体标准差未知且样本容量较大(通常大于30)时,可以使用样本标准差来估计总体标准差,此时样本均值的标准误差的计算公式为:\[ SE = \frac{s}{\sqrt{n}} \]其中,s为样本标准差,n为样本容量。
这个公式是在总体标准差未知的情况下,使用样本标准差来估计标准误差的一种常用方法。
2. 回归系数的标准误差。
在回归分析中,回归系数的标准误差是用来衡量回归系数估计值与真实回归系数之间的差异的一个指标。
回归系数的标准误差的计算公式为:\[ SE(\hat{\beta}) = \sqrt{\frac{\hat{\sigma}^2}{\sum_{i=1}^{n}(x_i \bar{x})^2}} \] 其中,\( \hat{\sigma}^2 \)为残差平方和除以自由度的估计值,\( \sum_{i=1}^{n}(x_i \bar{x})^2 \)为自变量的离差平方和。
回归系数的标准误差可以帮助我们评估回归系数的估计值的精确度和可靠性。
3. 样本比例的标准误差。
当我们对一个二项分布进行抽样调查时,我们通常关心的是样本比例的估计值与总体比例之间的差异。
样本比例的标准误差的计算公式为:\[ SE(\hat{p}) = \sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \]其中,\( \hat{p} \)为样本比例的估计值,n为样本容量。
Excel回归分析结果的详细阐释
Excel回归分析结果得详细阐释利用Excel得数据分析进行回归,可以得到一系列得统计参量。
下面以连续10年积雪深度与灌溉面积序列(图1)为例给予详细得说明。
图1 连续10年得最大积雪深度与灌溉面积(1971-1980)回归结果摘要(Summary Output)如下(图2):图2 利用数据分析工具得到得回归结果第一部分:回归统计表这一部分给出了相关系数、测定系数、校正测定系数、标准误差与样本数目如下(表1):表1 回归统计表逐行说明如下:Multiple 对应得数据就是相关系数(correlation coefficient),即R=0、989416。
R Square 对应得数值为测定系数(determination coefficient),或称拟合优度(goodness of fit),它就是相关系数得平方,即有R 2=0、9894162=0、978944。
Adjusted 对应得就是校正测定系数(adjusted determination coefficient),计算公式为1)1)(1(12-----=m n R n R a式中n 为样本数,m 为变量数,R 2为测定系数。
对于本例,n =10,m =1,R 2=0、978944,代入上式得976312.01110)978944.01)(110(1=-----=a R标准误差(standard error)对应得即所谓标准误差,计算公式为SSe 11--=m n s这里SSe 为剩余平方与,可以从下面得方差分析表中读出,即有SSe=16、10676,代入上式可得418924.110676.16*11101=--=s最后一行得观测值对应得就是样本数目,即有n =10。
第二部分,方差分析表方差分析部分包括自由度、误差平方与、均方差、F 值、P 值等(表2)。
表2 方差分析表(ANOVA)逐列、分行说明如下:第一列df 对应得就是自由度(degree of freedom),第一行就是回归自由度dfr,等于变量数目,即dfr=m ;第二行为残差自由度dfe,等于样本数目减去变量数目再减1,即有dfe=n -m -1;第三行为总自由度dft,等于样本数目减1,即有dft=n -1。
Excel 回归分析结果详解

Excel回归分析结果详解利用Excel的数据分析进行回归,可以得到一系列的统计参量。
下面以连续10年积雪深度和灌溉面积序列(图1)为例给予详细的说明。
图1 连续10年的最大积雪深度与灌溉面积(1971-1980)回归结果摘要(Summary Output)如下(图2):图2 利用数据分析工具得到的回归结果第一部分 回归统计表这一部分给出了相关系数、测定系数、校正测定系数、标准误差和样本数目如下(表1):表1 回归统计表逐行说明如下:Multiple 对应的数据是相关系数(correlation coefficient),即R=0.989416。
R Square 对应的数值为测定系数(determination coefficient),或称拟合优度(goodness of fit),它是相关系数的平方,即有R 2=0.9894162=0.978944。
Adjusted 对应的是校正测定系数(adjusted determination coefficient),计算公式为1)1)(1(12-----=m n R n R a式中n 为样本数,m 为变量数,R 2为测定系数。
对于本例,n =10,m =1,R 2=0.978944,代入上式得976312.01110)978944.01)(110(1=-----=a R标准误差(standard error )对应的即所谓标准误差,计算公式为1--=m n SSe s 这里SSe 为剩余平方和,可以从下面的方差分析表中读出,即有SSe=16.10676,代入上式可得418924.11110106761.16=--=s 最后一行的观测值对应的是样本数目,即有n =10。
第二部分 方差分析表方差分析部分包括自由度、误差平方和、均方差、F 值、P 值等(表2)。
表2 方差分析表(ANOV A )逐列、分行说明如下:第一列df 对应的是自由度(degree of freedom ),第一行是回归自由度dfr ,等于变量数目,即dfr=m ;第二行为残差自由度dfe ,等于样本数目减去变量数目再减1,即有dfe=n -m -1;第三行为总自由度dft ,等于样本数目减1,即有dft=n -1。
R语言用于线性回归的稳健方差估计

R语⾔⽤于线性回归的稳健⽅差估计在这篇⽂章中,我们将看看如何在实践中使⽤R 。
为了说明,我们⾸先从线性回归模型中模拟⼀些简单数据,其中残差⽅差随着协变量的增加⽽急剧增加:1. n < - 1002. x < - rnorm(n)3. residual_sd < - exp(x)4. y < - 2 * x + residual_sd * rnorm(n)该代码从给定X的线性回归模型⽣成Y,具有真正的截距0和真实斜率2.然⽽,残差标准差已经⽣成为exp(x),使得残差⽅差随着X的增加⽽增加。
可以直观地看到这个效果:这使模拟Y对X数据的图,其中残差⽅差随着X的增加⽽增加在这个简单的情况下,视觉上清楚的是,对于较⼤的X值,残差⽅差要⼤得多,因此违反了“基于模型”的标准误差所需的关键假设之⼀。
⽆论如何,如果我们像往常⼀样拟合线性回归模型,让我们看看结果是什么:1. > summary(mod)2. lm(formula = y~x)3. 最⼩1Q中位数3Q最⼤值4. -25.9503 -0.8574 -0.1751 0.9809 13.40155. 系数:6. 估计标准。
误差t值Pr(> | t |)7. (截距)-0.08757 0.36229 -0.242 0.8095088. x 1.18069 0.31071 3.800 0.000251 ***9. ---10. Signif。
代码:0'***'0.001'**'0.01'*'0.05'。
' 0.1 '' 111. 残余标准误差:3.605 98上的⾃由度的12. 多R平⽅:0.1284,调整R平⽅:0.119513. F统计:14.44 1和98 DF,p值:0.0002512这表明我们有强有⼒的证据反对Y和X独⽴的零假设。
为了便于⽐较,我们注意到X效果的标准误差是0.311。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
r 回归参数的标准误差
一、引言
回归分析是统计学中常用的一种方法,用于研究两个或多个变量之间的关系。
在回归分析中,参数是用来描述变量之间关系的,而标准误差则是用来评估参数估计可靠性的指标。
本篇文档将介绍如何计算回归参数的标准误差。
二、什么是标准误差?
标准误差是回归参数估计不确定性的度量。
它用于评估参数估计的可靠性,帮助我们了解回归模型的预测能力。
标准误差越小,参数估计的可靠性越高,模型预测的准确性也越高。
三、如何计算标准误差?
1. 打开Excel表格,输入你的回归数据。
包括因变量和自变量,以及对应的观测值。
2. 在数据旁边,输入回归模型的公式。
例如,对于线性回归,公式为:y = b0 + b1 * x1 + b2 * x2。
3. 使用Excel的统计功能,选择“分析”菜单下的“回归”选项,然后选择“描述统计”。
在弹出的对话框中,选择“置信度”和“估计标准误差”。
点击“确定”后,Excel将自动计算回归参数的标准误差。
4. 如果你的数据不适合线性回归,你可以使用非线性回归模型,如多项式回归。
这种情况下,你可以使用Excel的多项式回归功能来计算标准误差。
四、标准误差的应用
标准误差可以用于评估模型的预测能力、比较不同模型的优劣、以及识别模型的异常值。
它可以帮助我们了解模型的预测范围,从而更好地理解和使用模型。
五、结论
回归参数的标准误差是回归分析中非常重要的指标,它可以帮助我们了解参数估计的可靠性,进而评估模型的预测能力。
通过了解标准误差,我们可以更好地使用回归模型,提高预测的准确性。
六、参考文献
在此处添加相关参考文献,例如统计学教材或相关研究论文,以证明上述信息的准确性。
七、致谢
感谢各位读者阅读本篇文档,希望能够对回归分析和标准误差有更深入的了解和认识。
如有任何疑问或建议,请随时联系我们。
