五年级奥数第2讲
五年级奥数题解第二讲《不规则图形面积的计算(二)》[1]
![五年级奥数题解第二讲《不规则图形面积的计算(二)》[1]](https://img.taocdn.com/s3/m/a6f6887aa26925c52cc5bf54.png)
第二讲不规则图形面积的计算(二)不规则图形的另外一种情况,就是由圆、扇形、弓形与三角形、正方形、长方形等规则图形组合而成的,这是一类更为复杂的不规则图形,为了计算它的面积,常常要变动图形的位置或对图形进行适当的分割、拼补、旋转等手段使之转化为规则图形的和、差关系,同时还常要和“容斥原理”合并使用才能解决。
例1:如下图(1),在一个正方形内,以正方形的三条边为直径向内作三个半圆,求阴影部分的面积。
(1)(2)解法一:把上图靠下边的半圆换成(面积与它相等)右边的半圆,得到图(2)。
这时,右图中阴影部分与不含阴影部分的大小形状完全一样,因此它们的面积相等。
所以上图中阴影部分的面积等于正方形面积的一半。
解法二:将上半个“弧边三角形”从中间切开,分别补贴在下半圆的上侧边上,如图(3)所示。
阴影部分的面积是正方形面积的一半。
(3)(4)解法三:将下面的半圆从中间切开,分别贴补在上面弧边三角形的两侧,如图(4)所示。
阴影部分的面积是正方形的一半。
例2:如下图,正方形ABCD的边长为4厘米,分别以B、D为圆心以4厘米为半径在正方形内画圆,求阴影部分面积。
解:由容斥原理,S阴影=S扇形ACB+S扇形ACD-S正方形ABCD=4π×AB2×2-AB2=4π×42×2-42=16×(2π-1)≈16×2214.3-=9.12(平方厘米)。
例3:如下图,矩形ABCD中,AB=6厘米,BC=4厘米,扇形ABE半径AE=6厘米,扇形CBF的半径CB=4厘米。
求阴影部分的面积。
EB解:S阴景=S扇形ABE+S扇形CBF-S矩形ABCD=41×π×62+41×π×42-6×4=41×π(36+16)-24=13π-24=15(平方厘米)(取π=3)例4:如下图,直角三角形ABC中,AB是圆的直径,且AB=20厘米,如果阴影(1)的面积比阴影(2)的面积大7平方厘米,求BC长。
五年级上册奥数第二讲 长方形、正方形的面积教案
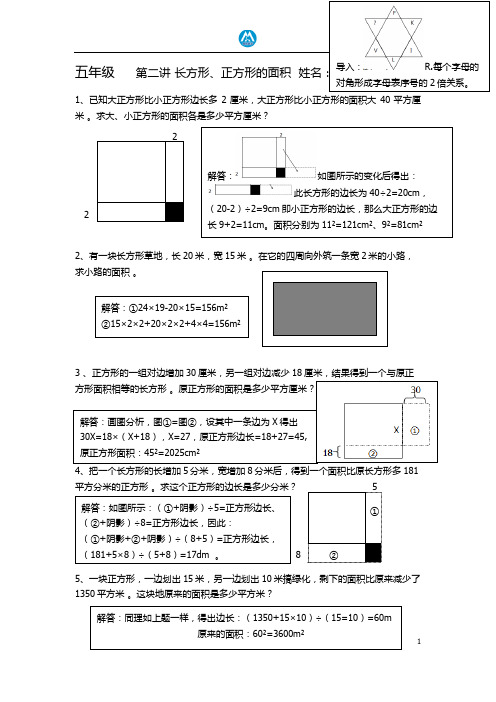
姓名: 1、已知大正方形比小正方形边长多2厘米,大正方形比小正方形的面积大40平方厘米 。
求大、小正方形的面积各是多少平方厘米?2、有一块长方形草地,长20米,宽15米 。
在它的四周向外筑一条宽2米的小路,求小路的面积 。
3 、正方形的一组对边增加30厘米,另一组对边减少18厘米,结果得到一个与原正4、把一个长方形的长增加5分米,宽增加8分米后,得到一个面积比原长方形多181平方分米的正方形 。
求这个正方形的边长是多少分米?5、一块正方形,一边划出15米,另一边划出10米搞绿化,剩下的面积比原来减少了1350平方米 。
这块地原来的面积是多少平方米?导入:R.每个字母的对角形成字母表序号的2倍关系。
解答:如图所示的变化后得出:此长方形的边长为40÷2=20cm ,(20-2)÷2=9cm 即小正方形的边长,那么大正方形的边长9+2=11cm 。
面积分别为11²=121cm ²、9²=81cm ²6、把20分米长的线段分成两段,并且在每一段上作一正方形,已知两个正方形的面积相差40平方分米,大正方形的面积是多少平方分米?7、一个正方形,如果它的边长增加5厘米,那么,面积就比原来增加95平方厘米 。
8、有一个正方形草坪,沿草坪四周向外修建一米宽的小路,路面面积是80平方米 。
求草坪的面积 。
9、已知长方形的长是宽的7倍,长方形的周长是304厘米,求长方形的面积是多少?10、一个矩形被分成8个小矩形,其中有5个小矩形的面积如下图所示,则这个大矩 解答:知识点补充: ①×④=②×③ 交叉相乘相等,让学生用直尺作图具体的数据来证明此公式的正确性后,教师用字母代入证明1234。
最新小学五年级奥数第二讲--定义新运算及作业

第二讲定义新运算一、a、b是自然数,规定a※b=(a+b)÷2,求:3※(4※6)的值。
二、对于任意两个自然数a、b,定义一种新运算“*”:a*b=ab+a÷b,求75*5=?,12*4=?三、定义运算符“◎”:a◎b=3a+4b-5,求6◎9=?9◎6=?四、定义两种运算“○+”和“○×”,对于任意两个整数a、b规定:a○+b=a+b-1,a○×b=a×b-1,那么8○× [(6○+10)○+(5○×3)]等于多少?五、定义运算“○+”=(a+b)÷3,那么(3○+6)○+12与3○+(6○+12)哪一个大?大的比小的大多少?六、a、b是自然数,规定a⊙b= ab-a-b-10,求8⊙8=?七、如果1*2=1+2,2*3=2+3+4,3*4=3+4+5+6,……,请按照此规则计算3*7=?八、规定运算a@b=(a+b)÷2,且3@(x@2)=2,求x=?九、十、规定a△b=ab+2a, a▽b=2b-a,求(8△3)▽(9△5)的值。
第二讲定义新运算作业十一、定义新运算“*”:a*b=3a+4b-2,求(1)10*11;(2)11*10。
十二、定义新运算“△”:a△b= a÷b×3,求(1)24△6;(2)36△9。
十三、规定a○+b,表示自然数a到b的各个数之和,例如:3 ○+10=3+4+5+6+7+8+9+10=52,求1○+200的值。
十四、十五、定义新运算“○×”,a○×b=10a+20b,求(3○×7)+(4○×8)。
十六、定义新运算“△”:a△b=6a+3b+7,那么5△6和6△5哪个大?大的比小的大多少?十七、十八、规定a*b=(a+b)÷2,求[(1*9)*9]*3的值。
十九、规定a☆b=3a-2b,如果x☆(4☆1)=7,求x的值。
五年级奥数第二讲数的整除

第二讲 数的整除知识点:﹤1﹥整除概念: 表示:﹤2﹥整除的性质:﹤3﹥整除的特征:(1)解法:○1 ○2 我要上名校示例﹤1﹥有一个四位数b a 62,它能同时被2、3、5整除,这样的四位数有多少个?练一练:有一个四位数Ο2Ο2,它能同时被2、3、5整除,这样的四位数有多少个?示例﹤2﹥有一个六位数b a 4273,它能被72整除,则a 、b 分别为多少?练一练:若四位数b a 89能被15整除,则a 、b 分别为多少?示例﹤3﹥有一个十位数59911995xy 能被99整除,则χ、y 分别为多少?练一练:有一个六位数Ο2004Ο,能被99整除,则○中分别填多少?示例﹤4﹥六位数ΟΟ1992能被95整除,这个六位数是多少?练一练 能被4、5、6整除的最大的三位数是多少?示例﹤5﹥1~200中,有多少个数能被2或5整除?练一练:1~300中,有多少个数不能被3或5整除?示例﹤6﹥一个整数乘17,积的末三位是999,这个数最小是多少?练一练:一个整数乘19,积的末三位是321,这样的整数中最小是多少?示例﹤7﹥五年级有72名学生,乘车春游,共交车费Ο7.52Ο元(○为污损数字,看不清)平均每个学生交了多少元钱?练一练:一本老账本上记着:老王买了72只桶,共用去Ο9.67Ο元,其中○处是被虫蛀掉的数字,请把这笔账补上。
示例﹤8﹥ 一个两位数能被2整除,且两个数位上的数字之和是8,这样的两位数有多少个?练一练:能被11整除,并且各个数位上数字之和等于43的五位数一共有多少个?示例﹤9﹥在28的前面连续写上若干个1993,得到一个多位数 1993199319931993若干个28如果这个多位数能被11整除,那么它最少是多少位?练一练:如果 2005200520052005个n 01能被11整除,那么n 的最小值是多少?示例﹤10﹥ 商店里有六箱货物,分别重15、16、18、19、20、31千克,两个顾客买走其中的五箱,已知一个顾客买的货物是另一个顾客的2倍,那么商店剩下的一箱货物有多重?练一练:五年级同学分成四个小组集邮,第一组集了127张,第二组集了149张,第三组集了238张,第四小组只集了95张。
A五年级奥数—【第二讲】质数、合数、分解质因数

【例题 2】24 有多少个因数?这些因数的和是多少?
【例题 3】新河村民用几只船分三次运送 315 袋化肥。已知每只船载的化肥袋数 相等且至少载 7 袋。问:每次应有多少只船,每只船载多少袋化肥?
【例题 11】要使 145×32×20×□的积的末五位数都是 0,□里填入的自然数的 最小值是多少?
【例题 12】陈虎是个中学生,他说:“这次考试(百分制),我的名次乘我的年 龄再乘我的考试分数,结果是 2910.”你能算出陈虎的名次、年龄与他这次考试 的分数吗?
【例题 13】用 216 元去买一种钢笔,正好将钱用完。若每支钢笔便宜 1 元,则 可以多买 3 支钢笔,钱也正好用完。共买了多少支钢笔?
【变式训练】船夫用几只船分 3 次把 90 名同学渡过河去,已知每只船载的人数 都相等,并且至少载 2 人,问:每次应有多少只船,每只船载多少人?
【变式训练】某自然数是 3 和 4 的倍数,这个数包括 1 和本身在内共有 10 个因 数,这个自然数是多少?
【变式训练】把 111222 颗棋子摆成一个长方形阵,每一横行的棋子颗数比每一 竖行的棋子颗数多 1,这个长方形阵每一横行有多少颗棋子?
【变式训练】四个连续自然数的积是 1680,则这四个自然数中,最小的是几?
【变式训练】用 1、2、3、4、5、6、7、8、9 这九个数字组成质数,如果每个数 字都要用到,并且只能用一次,那么这九个数字最多能组成多少个质数?
【变式训练】要使四个数的积 175×72×225×□的结果的最后六位数都是零, 问□中的数最小填几。
【变式训练】360 共有多少个因数?240 共有多少个因数?
五年级奥数专题讲义(基础卷+提高卷)-第2讲 等差数列 通用版(含答案)

第 2 讲等差数列基础卷1.计算 1+2+3+ (2012)1+2012=20132+2011=2013以此类推:原式=(1+2012)×2012÷2=20250782.计算 2+3+4+5+ (2588)=(2+2588)×2587÷2=33501653.求首项为 5,公差是 3 的等差数列的前 2000 项的和。
a n=a1+(n-1)d= 5 + 1999 ×3= 6002s n=(a1+a n)×n÷2= (5+6002) ×2000÷2= 60070004.求首项为 10,公差为 5 的等差数列的前 5000 项的和。
首项为10,公差为5的a1=10 d=5等差数列的前5000项的和S n=na1+d×n(n-1)÷2S5000=5000×10+5×5000(5000-1) ÷2=50000+62487500=625375005.计算 11+13+15+ (97)解这是等差数列求和首项为11,末项为97,公差为2即项数11+(n-1)×2=97即n=44即11+13+15+……+97=44(11+97)÷2=23766. 92+90+88+ (2)=2×﹙46+44+43+……+3+2+1)=2×(46+1)×46÷2=2162提高卷1.计算 2012-2010+2008-2006+......+4-2。
将两个数字看成一组2012-2010+2008-2006+……+4-2=(2012-2010)+(2008-2006)+……+(4-2)2是这个式子的第(2012-2)÷2 +1=1006项则一共可以配成503组=503×2=10062.计算 9000-8997+8994-8991+......+6-3。
五年级奥数第2讲 奇偶分析

五年级第二讲奇数和偶数我与知识手拉手★知识提要★自然数按能否被2整除,可分为奇数和偶数两大类,它是自然数的一种分类方法。
灵活地应用奇数、偶数的特征、特质,可以巧妙地解决许多实际生活中的问题。
★知识点★例1在内蒙古大草原上,流传过这样一道数学:三十六只羊,七天来宰光,宰单不宰双,每天各宰几只羊?你能帮着找出答案吗?例2 1+2+3+4+…+3001的和是奇数还是偶数?例3一个班的同学上阅读课时,每人手中都拿着一本书,如果其中拿连环画的比拿故事书的人多3人,而拿故事书的人又比拿科技书的人多1人,如果拿科技书的人是奇数,那么这个班的同学人数是奇数还是偶数?例4桌上有7只茶杯,全部是杯底朝上,你每次翻转4只茶杯,称为一次翻动,经过多少次翻动,能使这7只茶杯的杯口全部朝上?例5、130人排成一列,自1起往下报数,报奇数的人出列,留下的再重新报数,这样继续下去则在报了多少次后只留下一个人,他在第一次报数时报的数是多少?1、三个连续偶数的和,比其中最大的偶数大18,这三个连续偶数分别是多少?2、九个连续的偶数,最大的数是最小数的3倍,求这九个连续的偶数分别是多少?3、有七个连续的奇数,从小到大排列,第二个数与第六个数的和是38,求这七个连续的奇数。
4、101个连续的自然数相加,其和是奇数还是偶数。
5、某校毕业班的同学在离校前,相互之间交换照片,以做留念。
“无论人数是多少,那么用来交换的照片总数一定是偶数。
”这句话对吗?为什么?★★★★ 四星擂台1、有11名同学面向黑板站成一排,听到口令后只能有4个向后转,问经过若干次口令后能否使这11位同学都背向黑板?2、一个数分别与另外两个相邻的两个奇数相乘,所得的两个积的差为160,这个数是多少?3、一次数学竞赛共有20道题,规定答对一题得2分,答错扣1分,未答的题不得分也不扣分,小明得了23分。
已知他未答的题目是偶数,他答错了几道题?4、现在桌子上放了8只杯子,杯子的口都朝下,每次只许同时翻动7只杯子,那么最少要翻动多少次才能使所有杯子的杯口都向上?你是好样的。
五年级下册奥数讲义-第二讲 长方体和正方体的表面积

第二讲长方体和正方体的表面积在数学竞赛中,有许多问题涉及到长方体和正方体表面积的计算。
这些知识不仅有趣而且具有一定的实用性和思考价值。
解答长方体和正方体表面积的问题时,需要同学们具备较强的观察能力、作图能力以及空间想像能力,另外还要掌握一些解题的思路和技巧。
例题选讲例1:一个长方体,前面和上面的面积之和是88平方厘米,这个长方体的长、宽、高是以厘米为单位的数,且都是质数,求这个长方体的表面积。
【分析与解答】要求长方体的表面积,就要求长方体的长、宽、高。
根据题意,前面与上面的面积之和是88平方厘米,也就是长×高+长x宽=88,即长×(高+宽)=88因为长、宽、高都是质数,我们把88分解质因数得88=1l×2×2×2,依题意,11不能分成两个质数和,经试验,有两种情况符合条件,(1)ll×(3+5):88 (2)2×(41+3)一88,因此长方体的表面积可以有两种情况。
解:88—11×2X2×2,2×2×2:3+5,11×2×2—41+3。
长方体的表面积:(1)(11×3+1l×5+5×3)×2=206(平方厘米)(2)(2×3+2x4l+41×3)×2—422(平方厘米)例2:如图,将3个表面积都是24平方米的正方体木块粘成一个长方体,求这个长方体的表面积。
【分析与解答】仔细观察图形,不难看出3个正方体块粘成1个长方体,共有2个粘接处,每一处都有2个面粘在一起,两处共粘去4个面,因此粘成的长方体的表面积等于(6×3—4)个面的面积,即24÷6×(6 x3—4)=56(平方厘米)。
例3:如图所示的是用19个棱长为1厘米的正方体堆起来的立体图形,其中有一些正方体看不见,那么这个立体图形的表面积是多少?【分析与解答】仔细观察图形,虽然这个立体图形是不规则的,但是从前面看到的面与从后面看到的面个数是相等,同理从左、右看到的面个数是相等的,从上、下看到的面是一致的,所以这个立体图形的表面积等于(前面十上面+左面)×2,即(10+9+8)×2=54(平方厘米)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二讲数的整除
知识要点:
1.数的整除特征:
(1)能被4或25整除的数的特征:这个数的末两位上的数字所组成的数能被4或25整除。
(2)能被8或125整除的数的特征:这个数的末三位上的数字所组成的数能被8或125整除。
(3)能被3或9整除的数的特征:这个数的各个数位上的数字之和能被3或9整除。
(4)能被11整除的数的特征:这个数的奇数位上的数字之和与偶数位上的数字之和的差能被11整除。
(5)能被7、11、13整除的数的特征:这个数的末三位上的数字组成的数与末三位以前的数字所组成的数之差能被7、11、13整除。
2.数的整除性质:
(1)如果甲数能被乙数整除,乙数能被丙数整除,那么甲数一定能被丙数整除。
例如:72能被36整除,36能被9整除,那么72一定能被9整除。
(2)如果两个数都能被同一个自然数整除,那么这两个数的和与差一定能被这个自然数整除。
例如:84与63都能被7整除,那么84+63及84—63都能被7整除。
(3)如果一个数能分别被两个互质的自然数整除,那么这个数能被这两个互质的自然数的乘积整除。
例如:144能被4整除,又能被9整除,而且4与9互质,那么144能被4×9=36整除。
精选例题:
例1:在下面的数中,哪些能被4整除?哪些能被8整除?哪些能被25整除?哪些能被125整除?
100,234,728,7756,6648,2781,1750,8125。
思路点拨:
例2:学校为竖笛小组购买了75根竖笛,发票上的总价有两个数字模糊不清,只看到3□7.□元,你知道每根竖笛至少是多少元吗?
思路点拨:
例3:一个六位数165□□□能同时被4和9整除,这个六位数最大是多少?最小
是多少?
思路点拨:
例4:abcabc这个六位数能否被7整除?能否被11整除?能否被13整除?如果能,
请说明理由。
思路点拨:
例5: 173□是四位数,数学老师说:“我在这个□中先后填入3个数字,所得到的3个四位数,依次可被9、11、6整除”问:数学老师先后填入的3个数字的和是多少?
思路点拨:
例6: 将自然数1,2,3,…依次写下去组成一个数:12345678910111213….如果写到某个自然数时,所组成的数恰好第一次能被72整除,那么这个自然数是多少?
思路点拨:
例7: 自然数中1~100内共有多少个不能被3或11整除的数?
思路点拨:
例8:用1,2,3,4,5,6,7,8,9(每个数字用一次)组成三个能被9整除的、和尽可能大的三位数,这三个三位数分别是多少?
思路点拨:
例9:小明的两个衣服口袋中各有13张卡片,每张卡片上分别写着1,2,3,…,13。
如果从这两个口袋各拿出一张卡片来计算它们所写两数的乘积,可以得到许多不相等的乘积。
那么,其中能够被6整除的乘积共有多少个?
思路点拨:
应用与拓展
1.在下面的□里填上适当的数字。
能被4整除:93□,□可以填( ) 能被8整除:48□2,□可以填( )
能被9整除:20□308,□可以填( ) 能被25整除:71□□,□□可以填( )
能被125整除:8□50,□可以填( )
2.在下面的数中,哪些能被4整除,哪些能被25整除?哪些能被8整除?哪些能被除125整除?
①234②500③789④8865⑤3728⑥8064⑦5125⑧12000
能被4整除的数是:能被8整除的数是
能被25整除的数是能被125整除的数是:
3.用2,3,7,8四个数字组成没有重复数字的四位数,且它是11的倍数,并将这些数按从大到小排列出来。
4. 在42□0□的方框中填上合适的数字,使这个五位数能同时被2、3、5整除,请写出所有可能的情况。
5. 自然数N由两种数字0和8组成,且是15的倍数,当N尽可能小时,它是15的多少倍?
6.在97538□□的□里填上什么数字就能被45整除?填上什么数字就能被21整除?
7.实验小学五年级三班期末数学综合测试,平均分是90分,总分是A95B,求这个班有多少学生。
8.过新年,小明到大润发超市买了一箱饮料共24瓶,可收据上的钱数已模糊不清,只看到总价是□27.□元,这箱饮料至少多少钱?
9.一个七位数4352□□□,□中的各位数字互不相同,且这个七位数能同时被7和6整除,这个七位数最大是多少?
10. 一个六位数256□□□能同时被8和9整除,求这样的六位数中最小的数是多少?
11.有10个连续自然数,其中的奇数之和是85。
在这10个连续自然数中,是3的倍数的数之和最大是多少?
12.用1-9九个数字组成三个三位数,使其中最大的三位数被3除余2,且尽可能地小;次大的三位数被3除余1;最小的三位数能被3整除。
那么,最大的三位数是多少?(每个数字只用一次)。
