测试精度分析4
SDP4模型精度分析的开题报告

SGP4/SDP4模型精度分析的开题报告题目:SGP4/SDP4模型精度分析一、研究背景和意义卫星的轨道计算是卫星控制和运行的重要技术之一。
SGP4/SDP4模型是一种计算卫星轨道元素的模型,被广泛应用于卫星轨道计算的领域。
SGP4/SDP4模型的精度直接关系着卫星控制和运行的效果,因此精度分析对于提高卫星的运行效率、降低运行成本具有重要意义。
二、研究目标通过对SGP4/SDP4模型的精度进行分析,探讨影响SGP4/SDP4模型精度的因素,并提出提高SGP4/SDP4模型精度的方法和建议。
具体研究目标如下:1.总结和分析文献中有关SGP4/SDP4模型精度的研究成果和最新发展;2.分析SGP4/SDP4模型精度影响因素,包括天体测量误差、大气折射与运动学效应、地球引力势场、时间系统误差等因素的影响;3.采用数据分析和定量研究的方法,对SGP4/SDP4模型的精度进行评估,并与其他卫星轨道计算模型进行对比;4.提出提高SGP4/SDP4模型精度的方法和建议,包括模型改进、数据处理、算法优化等方面。
三、研究内容和方法1.文献综述通过检索相关的文献,总结和分析有关SGP4/SDP4模型精度的研究成果和最新发展,了解和掌握相关领域的研究现状。
2.影响因素分析分析SGP4/SDP4模型精度受到的影响因素,包括天体测量误差、大气折射与运动学效应、地球引力势场、时间系统误差等因素的影响。
通过理论分析和数值模拟来揭示这些因素的作用机制和影响程度。
3.精度评估采用数据分析和定量研究的方法,对SGP4/SDP4模型的精度进行评估,并与其他卫星轨道计算模型进行对比。
通过实验对比,分析不同因素对模型精度的影响。
4.提高精度的方法和建议提出提高SGP4/SDP4模型精度的方法和建议,包括模型改进、数据处理、算法优化等方面。
通过实验和数据分析,验证和比较不同方法的有效性和可行性。
四、预期成果完成本研究后,我们将得到以下预期成果:1.总结和分析有关SGP4/SDP4模型精度的研究成果和最新发展;2.深入剖析影响SGP4/SDP4模型精度的因素,提出有针对性的改进方法;3.通过实验对比,评估不同模型的精度,并提出提高精度的方法和建议;4.提出卫星轨道计算领域的未来研究方向和发展趋势。
同步轨道卫星四站时差统计定轨精度分析

P NGH a eg , H N h o , H NG T o E u - n Z E G C a 2Z A a 2 f
( . ao a K yLb r o f l dS n l Poes g C egu6 04 ,hn ; 1 N t nl e aoa r o i i a r s n , hnd 10 1 C i i ty B n g s c i a
2 Su w s Eet nc adT l o m nctnTcn l yR s r st e C e gu60 4 ,hn ) .o t et l r i n e cm ui i eho g ee c I tu , hnd 10 1 C ia h co s e ao o a h n it A s a tM au n m ie neo a i lT O bt c: esr gt ed f ec f rv ( D A)bsdo a lt Scm u i t ns a i oeo e r i i fr ra ae nst le o m nc i i l s n f h ei ao g n t
,
Pa sv b tM e s r m e t o o y c r n u a elt s i e Or i a u e n f Ge s n h o o s S t lie
Ba e n Fo r sa i n S Ti e Di e e e fAr i a s d o u .t to m f r n e o rv l
自校 准 方法 同步估计 系统误差 , 系统误差 估计精 度 约为4m, 置误 差约 为 10m, 报 1 的位 置 误 位 2 预 周
差 约 为 2 0 m。 0
关键 词 : 同步 卫 星 ; 四站 时差 ; 源测轨 ; 无 统计 定轨 ; 定轨精 度
斯坦福-比奈智力量表第四版的特色研究

斯坦福-比奈智力量表第四版的特色研究斯坦福-比奈智力量表第四版(SB4)是一种广泛应用于临床和教育领
域的智力测试。
下面是SB4的特色研究:
1.提高测试的精确度:SB4采用了新的子测试和任务,通过对测试的
评分和分析方法的改进,提高了测试的精确度,并提供了更可靠的智力得分。
2.将文化因素纳入考虑:SB4考虑到文化因素对智力测试的影响,采
用跨文化比较法,通过对不同文化背景的被试进行测试和分析,来更准确
地评估他们的智力水平。
3.强调认知过程:SB4注重评估认知过程,可以获得更全面的智力信息,包括注意力、工作记忆、推理和问题解决能力等方面。
4.推广应用领域:SB4广泛应用于学校、临床和研究领域,包括儿童、青少年、成人和老年人等人群。
5.融合计算机技术:SB4采用了计算机技术,可以更方便快捷地进行
测试和数据分析,并且可以提供更丰富的智力测试信息。
总的来说,SB4作为一种先进的智力测试工具,不断地引入新的研究
成果和技术,不断完善和改进测试方法,以更精准的评估结果满足不同领
域中的需求。
四点探针法

四探针测试方法分类
四探针测试技术方法分为直线四探针法和方形四探 针法。方形四探针法具有测量较小微区的优点,可以测 试样品的不均匀性,微区及微样品薄层电阻的测量多采 用此方法。
四探针法按发明人又分为Perloff法、Rymaszewski法、 范德堡法、改进的范德堡法等。值得提出的是每种方法 都对被测样品的厚度和大小有一定的要求,当不满足条 件时,必须考虑边缘效应和厚度效应的修正问题。
• 四探针法除了用来测量半导体材料的电阻率以外,在半 导体器件生产中广泛使用四探针法来测量扩散层薄层电 阻,以判断扩散层质量是否符合设计要求。
• 因此,薄层电阻是工艺中最常需要检测的工艺参数之一。
四点探针测试技术
1、概述
四探针法用于测量半导体材料(厚材和薄片)电阻率以 及硅片上的扩散层、离子注入层的方块电阻,也可以测量 玻璃或其他绝缘材料上所形成的导电膜方块电阻。四探针 测试技术已经成为半导体生产工艺中应用最为广泛的工艺 监控手段之一。
14
半导体材料的电阻率: 在半无穷大样品上的点电流源,若样品的电阻率ρ均匀,引 入点电流源的探针其电流强度为I,则所产生的电力线具有球 面的对称性,即等位面为一系列以点电流为中心的半球面, 如图所示。在以r为半径的半球面上,电流密度j的分布是均 匀的。
若E 为r处的电场强度,则:
E j I 2 r2
下面重点介绍直线四探针法。
13
2、直线四探针法测量原理
在直线四探针技术中,四根探针通常是等距排成一条直 线,给探针施加一定压力,使之垂直地压在一块相对于探针 间距可视为半无穷大的样品上。外侧的两个探针之间施加电 流,中间的两个探针之间放置高精度电压表,就可以测出被 测样品的电阻率。测量电路如下图所示:
扩散层的方块电阻测量
全站仪三角高程测量与四等水准测量的精度比较分析

全站仪三角高程测量与四等水准测量的精度比较分析作者:王继辉来源:《城市建设理论研究》2013年第16期摘要:根据全站仪三角高程测量的原理和方法,对一条附合水准路线分别进行全站仪三角高程测量和水准仪四等水准测量,应用误差传播定律对两者的测量精度进行了对比分析。
结果表明,全站仪的测量精度略高于水准仪的测量精度,且使用较方便,受地形限制小,作业效率高,全站仪三角高程测量可以代替四等水准测量。
关键词:全站仪三角高程测量;四等水准测量;误差分析中图分类号:P2 文献标识码:A 文章编号:引言随着测绘技术的发展,全站仪已广泛应用于控制测量、地形测量及工程测量中。
但是由于全站仪在测设竖直角时盘左和盘右的偏差较大且不稳定,全站仪三角高程测量能否代替水准测量,很多学者有不同的看法。
因此,本文根据全站仪三角高程测量的原理和方法,在平原微丘区的地形上,拟对一条附合水准路线分别进行全站仪三角高程测量和水准仪四等水准测量,应用误差传播定律对两者的测量精度进行比较分析,以确定两种测量方法的优劣。
1、工程概况本研究中主要对从大连市地铁D级GPS控制点DK027至控制点B2间的测点,分别进行全站仪三角高程测量与四等水准测量,并进行实测高程精度比较分析。
已知控制点DK027,B2的高程分别为66.788m和67.519m,测量长度约1.4km,附合水准路线走向图如图1所示。
全站仪采用PENTAXR-325N型,由江西南昌宾得全站仪生产供应商提供;水准仪采用科力达NL30A型,由南方测绘仪器有限公司生产。
在测量前均对仪器进行了校正,仪器精度均满足要求。
在天气晴好的情况下,先用全站仪进行测量,利用三角高程对向观测方法,仪器架设6站,完成了附合水准路线的测量;再用水准仪进行测量,按照四等水准双面尺法观测方法,仪器架设9站,完成测量。
图1附合水准路线走向图2、全站仪三角高程测量2.1三角高程测量原理如图2所示,设A,B为地面上高度不同的2点,已知A点的高程HA,只要知道A点对B 点的高差HAB,即可由HB=HA+HAB得到B点的高程HB。
电阻的高精度测试(四线开尔文测试)

电阻的高精度测试(四线开尔文测试)以下内容均为个人根据多年军品级电阻夹具设计、测试设备设计经验得出的一些知识以用于分享,对不正确有偏差的部分欢迎交流。
对于分立元件,阻容感是最常见最基本的元件,随着科学技术以及社会需求的发展,各类电子产品都呈现出模块化、集成化、小型化、低功耗的方向发展,模块化便于组装、维修更换,集成化便于多个功能集合于一体,小型化便于最终产品做出来空间更小,低功耗便于节能。
对于电阻类产品,主要参数为电阻值、功率、电阻温漂系数等,针对不同材料及工艺,电阻各个参数性能差异大,同时也在不同应用领域有着不同的作用,典型的比如普通陶瓷厚膜、薄膜电阻,在使用时设计人员都希望其阻值精度高,而温漂系数越低越好,这代表着电阻在不同温度下其阻值变化越小,例如在电源控制中,电源模块工作发热时或使用环境温度高时电阻阻值几乎不变,这样情况下电源稳定性兼容性更好,而对于测温领域的热敏电阻,则是希望温漂系数变化较大,与电阻值形成一定的比例关系,实时监控电阻的阻值,通过该比例关系换算出当时的温度,最常见的铂电阻PT100、PT1000。
所以根据不同使用环境,对电阻的不同参数要求不一样。
本次谈一下陶瓷电阻,现工艺主要为薄膜、厚膜这两种工艺,如果简单描述此类电阻的生产工艺就是:在陶瓷基板上印刷上一层有规则图形的金属浆料,一般在一块基板上印刷N多个电阻尺寸的图形或线条,再将该陶瓷基板根据单个电阻尺寸进行划片,划片后再经过激光调阻,把每一个电阻的阻值进行测试,通过激光将陶瓷基板上的浆料去除掉以得到想要的阻值,再将每个电阻分割下来,每个陶瓷片的两端进行金属化,然后将每个电阻片中间的金属浆料上增加玻璃釉,这样电阻就成形了(其它细节工艺暂不阐述)。
对于电阻的阻值,常规分为低阻、中阻、高阻,从电阻生产、分销行业内,从10Ω至2MΩ称为中阻,高于这个范围的为高阻,低于这个范围的称为低阻,对于中阻产品使用频率最高,其生产成本分摊下来也较低,一般售价几厘钱或几毛钱一颗,而对于mΩ、GΩ、TΩ级别的电阻,都要几块几十甚至几百一颗。
全站仪坐标放样的方法及精度分析

点号 01 02 03
测量坐标
X坐标 207901.320 207917.295 207899.602 Y坐标 300562.450 300554.979 300518.020
04
05 06 07 08 09 10
207883.640
207886.644 207911.585 207896.675 207923.555 207885.444 207912.850
误差和平均中误差均在误差允许范围内,都 符合精度要求。
但是第二种方法精度更高,所以我们在放样
精度要求较高时可选用此法。
目前全站仪已成为工程测量施工过程中 不可或缺的首选测量仪器,因此,对全站仪放 样进行精度分析 ,从而制定出简捷、适用的使 用方法和操作规程是十分必要的。本文通过 对以上各种问题的实验和研究,了解全站仪 坐标放样的操作方法与放样精度,为指导今 后的施工放样工作提供依据。
mp 8m m
m限 2mp 16mm
点号 01 02 03 04 05 06 07 08 09 10
设计坐标
X坐标 207901.311 207917.287 207899.610 207883.633 207886.652 207911.582 207896.668 207923.546 207885.436 207912.856 Y坐标 300562.440 300554.970 300518.027 300525.496 300571.091 300543.286 300545.394 300569.481 300565.218 300562.185
谢谢!
全站仪坐标放样的方法 及精度分析
目录
第1章
绪论 第2章 工程放样的原理与方法 第3章 全站仪的功能与使用 第4章 全站仪坐标放样的方法与步骤
精度设计第4章 几何公差
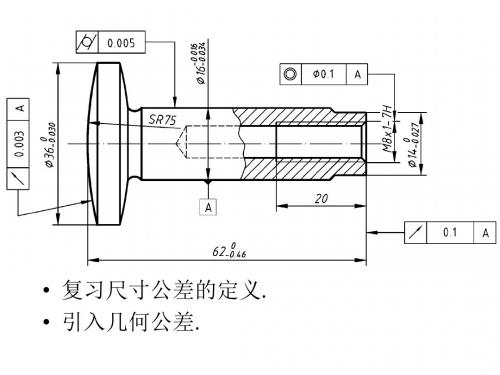
最小条件及最小包容区域
最小条件是提取被测要素对其拟合要素的最大变 动量为最小。
最小包容区域是包容被测提取要素并且有最小宽 度或直径的区域,即满足最小条件的包容区域。 方向位置公差要求的被测提取要素的最小包容区 域,构成要素与基准应保持方向要求。 位置公差要求的被测提取素的最小包容区域,构 成要素与基准既保持方向要求,还应保持理想位 置要求。
• 一、几何误差的评定 • 几何公差带与最小包容区域(包容被测实际要素 并且具有最小宽度或直径的区域)都具有大小、 形状和方位三要素,二者的形状和方位相同,大 小不同。 • 最小包容区域的尺度即为几何误差值; • 零件的几何误差合格条件: • f(几何误差值)<t(几何公差值),即被测要 素的最小包容区域必须被相应的几何公差带所包 容。
平行平 面形状
平行直线形状
四棱柱 形状
同心圆 形状 同轴圆柱面
t
圆柱 形状
形状公差
• 单一要素对其理想要素允许的变动量。其公 差带只有大小和形状,无方向和位置的限制。 • 直线度 _ • 平面度 _ • 圆度 _ • 圆柱度 _
直线度公差
•直 线 度 公 差 用 于 控 制 直线和轴线的形状误差, 根据零件的功能要求, 直线度可以分为在给定 平面内,在给定方向上 和在任意方向上三种情 •在给定平面内的直线度 况。 •在给定方向内的直线度
a)六孔组的图样标注 b)六孔组的几何框图 c)六孔组的位置度公差带
面轮廓度
• 面轮廓度公差带是包 络一系列直径为公差 值t的球的两包络面之 间的区域,诸球的球 心应位于理想轮廓面 上。如图所示。 • 面轮廓度也分无基准 要求的面轮廓度公差、 有基准要求的面轮廓 度公差。
公差带的特点
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、莱以特准则(3σ准则)
二、肖维特准则
三、格罗布斯准则 四、t 检验准则 五、狄克松准则
每次剔除一个 重新计算时数据个数 已经改变 计算自由度
重点掌握: 粗大误差剔除的基本原理 不同剔除方法的应用范围 等精度测量的误差分析流程
等 精 度 直 接 测 量 数 据 处 理 流 程
选择怀疑含有粗差的个体x(1)或x(n) 据不同测量次数,可由表(P53表4-5)计算 γ10(或γ11 或γ21或 γ22,公式不同)
同样,据不同的P(α)和n,可查表得临界值 γ0(n,α) 比较、检验:若计算得到的γij>γ0,则认为被 怀疑值存在粗差
粗大误差判断的基本原则: 残差是否超过极限误差
格罗布斯准则 分别考虑测量次数n和置信概率P 步骤:
一次剔除 一个
小→大排序
在x(1)、x(n
中确定最可怀疑值(残差绝对值最大者)
)
计算g(1)
x
x(1)
ˆ
或g(n)
x(1)
ˆ
x
据n、α查表(P51表4-3),求临界值g0
判断:若g(i)
g0
(n,
),则认为g(i
含有粗差
)
t检验准则 测量次数少时用
第四章 粗大误差
主要内容: 判断粗大误差的基本原则 各种剔除准则的应用范围及特点 五种剔除准则的使用
粗大误差判断的基本原则:
残差是否超过极限误差
一、莱以特准则(3σ准则)
二、肖维特准则
三、格罗布斯准则
四、t 检验准则
五、狄克松准则
填表
方法 准则内容 使用范围 特点
3σ准则
肖维勒 准则
格罗布 斯准则
步骤:
假设怀疑xd有粗差(残差最大者)
n
xi
i 1
计算:x id 、ˆ '
n 1
n
vi2
i 1 id
n2
K(n,α)与P(α)、 n有关,查
检验:若 xd x K(n,)ˆ '
P52表4-4
则认为xd 含有粗差,剔除
狄克松准则
极差比较法,不需计算标准偏差,尤其适于小样本 步骤:小→大排序
P考虑N 精度高
P、n 精度更高
P、n, 精度更高
不求σ 精 度最高
一次 剔除 一个
然后 再继 续按 照老 方法 判断, 直到 没有 粗差 存在
莱以特准则(3σ准则)
vi M 3
3ˆ 3
n
vi2
i1 3 n 1
n
vi2
i1 9
n
vi2 vi
t检验
狄克松 准则
注意
方法 莱以特
3σ
肖维勒准 则
格罗布斯 准则
t检验
狄克松准 则
内容
使用范围 特点 注意
v 3
M
N1
P N 2 得 M
P50
P52
P53
n>10 越大越好
不过大、小 40~50
n一般 20~100 n较少时用 一般n≤30 n较小最精
确 一般n≤25
P固定 简单
i 1
即n 10时, vi 3,判断不出粗差
n 10才有效
是ˆ,而非 x
一次剔除一个
肖维勒准则
根据测量次数确定置信概率,然后确定极限 误差,观察测量值是否在极限误差之外
N1 P 2 1
1
N
2N
N P t M
一般40~50个数据,比3σ准则好
一次剔除一个
