转动惯量和力矩
电机的转动惯量和转矩的关系

电机的转动惯量和转矩的关系
1 电机转动惯量和转矩的基本概念
电机的转动惯量指的是电机旋转时所表现出的惯性。
同样大小的
转动惯量会对不同大小的转矩产生不同的影响。
若转动惯量大,则给
定大小的转矩所产生的加速度就会小;而若转动惯量小,则同样大小
的转矩所产生的加速度就会大。
转矩指的是电机在旋转时对应用于轴上的力所产生的力矩。
一个
具有足够大的转矩的电机可以在一定程度上抵御阻力,而使旋转速度
不至于下降过快。
2 电机的转动惯量和转矩的关系
转动惯量和转矩之间的关系可以用牛顿第二定律来表示:F=ma。
其中,F为电机受到的作用力,m为电机的质量,a为加速度。
由于电
机受到的力是由转矩提供的,即F=T/r,其中T为转矩,r为轮子半径。
将电机的转动惯量记为J,则根据牛顿第二定律可得:
T = J * a / r
即,某一大小的转矩所产生的加速度与转动惯量成反比。
因此,
要在限制转矩的情况下增加电机的加速度,就需要减小电机的转动惯量。
另一方面,若要保持电机的加速度不变,可以通过增加转矩的大小来抵消转动惯量。
因此,一些需要较高加速度的机器人和机械装置通常使用低转动惯量的电机,同时加装较大转矩的减速器来调整其工作状态。
3 结语
转动惯量和转矩是电机中重要的机械参量,它们之间的关系对于电机的设计和性能优化具有重要的影响。
在实践应用中,需要根据具体的应用需求和工作环境来选择不同大小、不同类型的电机,以及相应的配套减速器、控制器等组件。
定轴转动刚体的转动定律度力矩角动量转动惯量

Iz Ix Iy
z
定理证明:
对于质量平面分布的刚体, 绕 x 轴的转动惯量为:
o
yy
Ix y2dm
x
dm
绕 y 轴的转动惯量为:
I y x2dm
x
绕 z 轴的转动惯量为:
19
z
Iz z2dm (x 2 y2 )dm
y2dm x 2dm I x I y 证毕
o
yy
x z dm
0
M
绕圆环质心轴的转动惯量为
dm
oR
I MR2
例2:在无质轻杆的 b 处 3b 处各系质量为 2m 和 m 的 质点,可绕 o 轴转动,求:质点系的转动惯量I。
解:由转动惯量的定义
I
2
mi ri 2
2mb 2
m
(3b)2
11mb 2
i 1
9
例3: 如图所示,一质量为m、长为l的均质空心圆柱
体(即圆筒圆筒)其内、外半径分别为R1和R2。试求
的质元受阻力矩大,
细杆的质量密度 m
l
质元质量 dm dx
o
xl dm m dx
x
质元受阻力矩:
dM 阻 dmgx
细杆受的阻力矩
m l
M阻
dM
阻
0l
gxdx
1 2
gl 2
1 2
mgl
4
二、定轴转动刚体的角动量
1 .质点对点的角动量
L
r
P
r
mv
作圆周运动的质点的角动量L=rmv;
l
x2dm
L
x2dx
1 L3
0
1 mL2
0
3
A
大学物理-第四章-力矩 转动定律 转动惯量
2 J ddt
1
1
1 dt
1 dt
2 1
Jd
1 2
J22
1 2
J12
2 Md (1 J2 )
1
2
力矩对刚体所做的功,等于刚体转动动能的增量。
26
Y
M
vC
C mi
yC yi
O
X
4、刚体的势能
EP mi gyi
i
mgyc
其中m为刚体的总质量, yc为刚体质心的高度
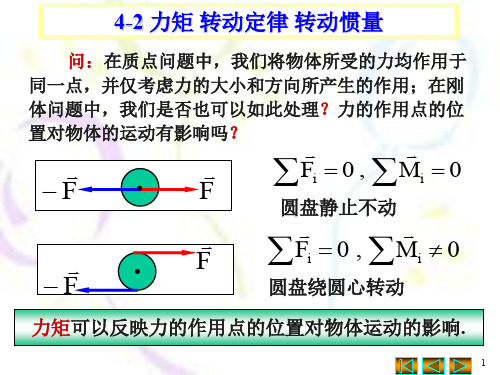
4-2 力矩 转动定律 转动惯量
问:在质点问题中,我们将物体所受的力均作用于
同一点,并仅考虑力的大小和方向所产生的作用;在刚
体问题中,我们是否也可以如此处理?力的作用点的位
置对物体的运动有影响吗?
F
F
Fi 0 , Mi 0
圆盘静止不动
F
Fi 0 , Mi 0
1、刚体的转动动能
i质点的动能
Eki
1 2
mi vi2
1 2
miri2 2
整个刚体的动能 — 对i求和
Ek
i
Eki
i
1 2
mivi2
i
1 2
mi
ri2
2
1 2
(
i
miri2 ) 2
1 2
J 2
可见,刚体的转动动能等于刚体的转动惯量与角速度
平方乘积的一半。
t
t0 Mdt L L0
动量守 恒定律
Fi 0,
mi vi
力矩转动定律转动惯量

❖ 质量连续分布
J mjrj2 r2dm dm:质量元 j
4-2 力矩 转动定律
上页 下页 首页 目录
物理学
第五版 刚体对某一转轴的转动惯量等于每个质元的质
量与这一质元到转轴的距离平方的乘积之总和。
质量为线分布 质量为面分布 质量为体分布
可见,转动惯量与l 无关。所以,实心圆柱对其
轴的转动惯量也是mR2/2。
4-2 力矩 转动定律
上页 下页 首页 目录
物第理五版学例2: 求长为L、质量为m的均匀细棒的转动惯量。 (1)转轴通过棒一端并与棒垂直。 (2)转轴通过棒 的中心并与棒垂直;
解:取如图坐标,dm=dx , =m/L
A L
B
J A r2dm
x
L x2dx mL2 / 3 0
AC L/2
B L/2 x
JC r2dm
L
Jc
2 L
x2dx
mL2
/12
2
4-2 力矩 转动定律
上页 下页 首页 目录
物理学
第五版
四、
平行轴定理
质量为 m 的刚体,如
果对其质心轴的转动惯量
为 JC ,则对任一与该轴平
行,相距为 d 的转轴的转
动惯量
JO JC md 2
dt
刚体定轴转动的角加速度与它所受的合外力
矩成正比,与刚体的转动惯量成反比.
讨论:
(1) M 一定,J
α 转动惯量是转动
惯性大小的量度;
(2) 是矢量式(但在定轴转动中力矩只有两个
方向)。
4-2 力矩 转动定律
上页 下页 首页 目录
物理学
转动惯量和飞轮力矩的关系

转动惯量和飞轮力矩的关系转动惯量和飞轮力矩的关系可不是一件简单的事,听起来就像是物理课上的一个老掉牙的话题,但其实这背后有很多有趣的故事哦。
想象一下,一个飞轮就像是个超级英雄,能在需要的时候给我们提供强大的动力。
它的转动惯量就像是它的身份牌,越重的身份牌,飞轮就越难以转动,但一旦它动起来,那可真是势不可挡。
你可能会想,飞轮和转动惯量之间到底有啥关系呢?哎,别急,慢慢来。
飞轮的力矩就像是小孩拉着风筝,风筝飞得越高,需要的力气就越大。
飞轮越重,转动惯量越大,要想让它转动起来,必须用更多的力矩。
这就好比你在运动的时候,想要举起一块大石头,光靠自己的力气可不够,得找个小伙伴帮忙。
这也解释了为什么在一些机械设备里,我们常常会看到飞轮的身影。
它们就是在帮助设备克服转动惯量,顺利运行。
大家都知道,惯性是物理中的“老大”,一旦飞轮转起来,简直就像是被施了魔法,转动的过程不再受到太多阻碍。
你会发现,飞轮在一些交通工具中尤其重要,像是汽车、火车、甚至是飞机。
想象一下,汽车在加速时,飞轮的力矩就像是给它打了一针强心剂,让它瞬间提速。
再比如,火车启动的时候,飞轮的转动惯量保证了它不会因为瞬间的加速而失控。
哇,这可真是个了不起的家伙,不是吗?而飞轮的设计就像是美食中的调味料,适当的添加才能让整体的性能达到最佳状态。
说到飞轮,咱们得提一下“平衡”这个概念。
飞轮在转动的时候,就像是一个调皮的小孩,随时可能摔倒,但如果设计得当,飞轮就能在转动中保持稳定。
想象一下,一个飞轮在快速旋转,它的重心就像是个魔术师,巧妙地保持平衡。
这个时候,转动惯量发挥了它的威力,让飞轮在各种环境中都能保持稳定,就算遇到风浪,也能轻松应对。
飞轮的力矩就像是一个坚实的后盾,让它在关键时刻展现出超强的能力。
再说说飞轮的应用吧,别小看它,这小东西在生活中可无处不在。
比如,洗衣机在甩干的时候,飞轮的力矩帮助衣物迅速脱水,几乎就像是给衣物上了个“干洗”的魔法。
健身器材中的飞轮,能够让你在锻炼时体验到更顺畅的感觉。
发电机的转动惯量和飞轮力矩的关联

发电机的转动惯量和飞轮力矩的关联【发电机的转动惯量和飞轮力矩的关联】引言:发电机作为一种电力设备在现代社会中扮演着重要的角色。
当我们探讨发电机的性能和工作原理时,转动惯量和飞轮力矩是两个必须考虑的关键概念。
本文将深入剖析发电机的转动惯量和飞轮力矩之间的关联,并分享对这个主题的观点和理解。
1. 转动惯量的概念和重要性转动惯量是物体绕轴旋转时,其惯性对旋转加速度的抵抗程度的物理量。
在发电机中,转动惯量决定了发电机在启动、停机和运行过程中的稳定性和响应能力。
较大的转动惯量意味着发电机能够存储更多的旋转能量,并能够在负载变化时提供更稳定的电能输出。
转动惯量是发电机设计和优化中需要考虑的重要因素。
2. 飞轮力矩的定义和作用飞轮力矩是指发电机转动时旋转部件所受到的力矩。
它产生的主要原因是转子的转动惯性和外部负载的影响。
飞轮力矩对发电机的运行和性能具有关键影响。
它可以平衡反作用力和负载变化,保持发电机的稳定运行。
较大的飞轮力矩使得发电机更能够应对外部负载的变化,减少启停时的能量波动,提高电能输出的质量。
3. 转动惯量与飞轮力矩的关联转动惯量与飞轮力矩之间存在着密切的关联。
较大的转动惯量会导致较大的飞轮力矩。
这是因为在转速恒定的情况下,较大的转动惯量需要较大的力矩才能改变其旋转速度。
而较大的飞轮力矩则可以提供更强的驱动力,以满足转动惯量的需求。
4. 转动惯量和飞轮力矩的影响因素转动惯量和飞轮力矩受到多种因素的影响。
其中包括发电机的物理结构和设计参数,如转子的质量和几何形状,转子轴承的摩擦和损耗等。
负载的变化和外部扰动也会对转动惯量和飞轮力矩产生影响。
通过合理的设计和优化,可以调整转动惯量和飞轮力矩以满足不同的运行需求。
5. 观点和理解转动惯量和飞轮力矩是发电机设计和性能优化中的重要考虑因素。
较大的转动惯量和飞轮力矩有助于提高发电机的稳定性和响应能力,从而提供更可靠的电能输出。
在实际应用中,我们需要根据具体的需求和运行条件,合理调整和控制转动惯量和飞轮力矩,以实现优化的发电机性能。
力矩与转动惯量

力矩与转动惯量力矩是物体受力后产生的旋转效应,它是描述物体转动能力的物理量。
转动惯量则是物体对转动运动的惯性度量,它和物体的质量分布和其转动轴的位置有关。
本文将介绍力矩和转动惯量的概念、计算公式以及影响因素。
一、力矩的概念与计算力矩是力对物体的转动效应的量度,通常用符号M表示。
在力的作用下,物体的转动效果取决于力的大小和作用点距离旋转轴的距离。
力矩的计算公式为:M = F × r × sinθ其中,F为力的大小,r为作用点距离转动轴的距离,θ为力和转动轴之间的夹角,sin表示正弦函数。
从公式中可以看出,力矩的大小与力的大小、作用点距离旋转轴的距离以及两者之间的夹角有关。
二、转动惯量的概念与计算转动惯量是物体对转动运动的惯性度量,它与物体的质量分布和转动轴的位置有关。
通常用符号I表示。
对于质点,其转动惯量可以直接通过质量m和离转动轴的距离r计算:I = m × r²对于复杂的物体,转动惯量的计算需要考虑物体的形状和质量分布情况。
例如,对于绕轴旋转的刚体,转动惯量的计算公式为:I = ∫r² dm其中,积分符号∫表示对整个物体进行质量分布的积分,r为质量元dm离转动轴的距离。
通过对物体进行积分求和,可以得到物体的总转动惯量。
三、影响力矩和转动惯量的因素1. 力的大小:力矩与力的大小成正比。
当施加在物体上的力增大时,力矩也会增大。
2. 作用点距离旋转轴的距离:力矩与作用点距离旋转轴的距离成正比。
当作用点距离旋转轴增大时,力矩也会增大。
3. 夹角θ:力矩与力和旋转轴之间的夹角正弦函数有关。
夹角θ越大,力矩越大。
4. 物体的形状和质量分布:转动惯量的大小与物体的形状和质量分布有关。
对于不同形状的物体,其转动惯量会有所不同。
综上所述,力矩和转动惯量分别描述了物体受力后的旋转效应和对转动运动的惯性度量。
力矩的大小与力的大小、作用点距离旋转轴的距离以及两者之间的夹角有关;转动惯量的计算需要考虑物体的形状和质量分布情况。
常用机构的转动惯量与扭矩的计算

常用机构的转动惯量与扭矩的计算引言:在机械工程中,常常需要计算机构的转动惯量和扭矩,这些参数是设计和分析机械系统的重要指标。
本文将介绍一些常用机构的转动惯量和扭矩的计算方法,以帮助读者更好地理解机械系统的运动行为。
一、刚性转动连杆机构刚性转动连杆机构是一种常见的机构,在此之前,我们需要对转动惯量和扭矩有所认识。
1.转动惯量的计算转动惯量是描述物体绕一些轴线转动的惯性大小。
对于刚性连杆机构而言,其转动惯量可以通过以下公式计算:I=m*r^2其中,I表示转动惯量,m表示物体的质量,r表示质点与轴线距离。
扭矩是描述物体受力作用下产生的转动效果的物理量。
对于刚性连杆机构而言,其扭矩可以通过以下公式计算:T=r*F其中,T表示扭矩,r表示力矩臂,F表示力的大小。
二、常见机构的转动惯量和扭矩计算1.单摆机构单摆机构由一个固定轴和一个摆动物体组成,其转动惯量和扭矩的计算公式如下:I=m*L^2T = m * g * L * sinθ其中,I表示摆动物体的转动惯量,m表示摆动物体的质量,L表示摆长,g表示重力加速度,θ表示摆动物体相对垂直方向的偏角。
2.齿轮传动机构齿轮传动机构由驱动轮和从动轮组成,其转动惯量和扭矩的计算公式如下:I=m*r^2T=F*r其中,I表示轮的转动惯量,m表示轮的质量,r表示轮的半径,F表示作用在轮上的力。
3.曲柄摇杆机构曲柄摇杆机构由曲柄和摇杆组成,其转动惯量和扭矩的计算公式如下:I=m*r^2T=F*r其中,I表示摇杆的转动惯量,m表示摇杆的质量,r表示摇杆的长度,F表示作用在摇杆上的力。
4.平行四边形机构平行四边形机构由两个平行的连杆和两个交叉连杆组成,其转动惯量和扭矩的计算公式如下:I = m * a^2 * (sinδ)^2 + 1/12 * m * b^2T = F * a * sinδ其中,I表示交叉连杆的转动惯量,m表示交叉连杆的质量,a表示平行连杆的长度,δ表示平行连杆与交叉连杆之间的夹角,b表示交叉连杆的长度,F表示作用在交叉连杆上的力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
r
p
L
m o r
转动惯量
J m r , J r dm
2 j j 2 j
物理意义:转动惯性的量度 .
转动惯性的计算方法
质量离散分布刚体的转惯量
2 j j 2 11 j
J m r m r m r
2 2 2
M z k r F M z rF sin
O
r
F
2)合力矩等于各分力矩的矢量和
M M1 M 2 M 3
3) 刚体内作用力和反作用力的力矩互相抵消
M ij
O
M ji
d
ri
F ji i F
ij
rj
j
Mij M ji
2 j j 2
质量连续分布刚体的转动惯量
J m r r dm
j
dm
:质量元
质量连续分布刚体的转动惯量
J m r r dm
2 j j 2 j
dm
:质量元
对质量线分布的刚体: dm
dl
:质量线密度
对质量面分布的刚体: dm
:质量面密度
:质量体密度
质点的角动量
在空间运动,某时刻相对原点 O 的位矢为 r,质点相对于原 点的角动量
质量为 m 的质点以速度 v
L
x
z
r
o
L r p r mv 大小 L rmv sin
m y
v
L
v
为 r 的圆运动,相对圆心的 角动量
L 的方向符合右手法则. 质点以角速度 作半径
P
R O m
力矩
刚体绕 O z 轴旋转 , 力 F
作用在刚体上点 P , 且在转动 平面内, r 为由点O 到力的 作用点 P 的径矢 . Z 的力矩 F 对转轴
M
M
O
z
M Fr sin Fd
M r F
r
F
*
d
P
Fi 0 , Mi 0
d F
: 力臂
F
Fi 0 , Mi 0
F
F
讨论
1)若力 F 不在转动平面内,把力分解为平行和垂 直于转轴方向的两个分量 z F Fz F F 其中 Fz 对转轴的力 k Fz
矩为零,故 F 对转轴的 力矩
dS
dV
对质量体分布的刚体:dm
注意
转动惯量的大小取决于刚体的质量、质 量分布、形状及转轴的位置 .
平行轴定理
质量为 m 的刚体,如果对 其质心轴的转动惯量为 J C ,则 对任一与该轴平行,相距为 d 的转轴的转动惯量 C
d
mO
J O J C md
2
1 圆盘对P 轴 J P mR 2 mR 2 的转动惯量 2
