Matlab中Bode图的绘制技巧复习进程
Matlab中Bode图的绘制技巧(精)
Matlab中Bode图的绘制技巧我们经常会遇到使用Matlab画伯德图的情况,可能我们我们都知道bode这个函数是用来画bode图的,这个函数是Matlab内部提供的一个函数,我们可以很方便的用它来画伯德图,但是对于初学者来说,可能用起来就没有那么方便了。
譬如我们要画出下面这个传递函数的伯德图:1.576e010 s^2H(s= ------------------------------------------------------------------------------------------s^4 + 1.775e005 s^3 + 1.579e010 s^2 + 2.804e012 s + 2.494e014(这是一个用butter函数产生的2阶的,频率范围为[20 20K]HZ的带通滤波器。
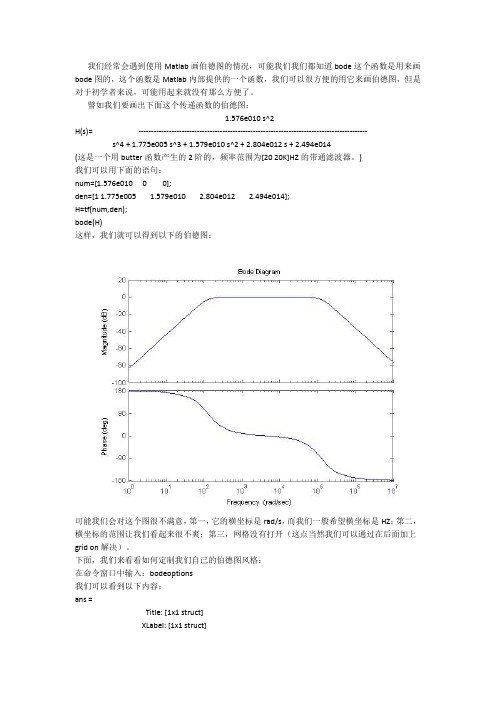
我们可以用下面的语句:num=[1.576e010 0 0];den=[1 1.775e005 1.579e010 2.804e012 2.494e014];H=tf(num,den;bode(H这样,我们就可以得到以下的伯德图:可能我们会对这个图很不满意,第一,它的横坐标是rad/s,而我们一般希望横坐标是HZ;第二,横坐标的范围让我们看起来很不爽;第三,网格没有打开(这点当然我们可以通过在后面加上grid on解决)。
下面,我们来看看如何定制我们自己的伯德图风格:在命令窗口中输入:bodeoptions我们可以看到以下内容:ans =Title: [1x1 struct] XLabel: [1x1 struct] YLabel: [1x1 struct] TickLabel: [1x1 struct] Grid: 'off'XLim: {[1 10]} XLimMode: {'auto'} YLim: {[1 10]} YLimMode: {'auto'} IOGrouping: 'none' InputLabels: [1x1 struct] OutputLabels: [1x1 struct] InputVisible: {'on'} OutputVisible: {'on'} FreqUnits: 'rad/sec' FreqScale: 'log' MagUnits: 'dB' MagScale: 'linear' MagVisible: 'on' MagLowerLimMode: 'auto' MagLowerLim: 0 PhaseUnits: 'deg' PhaseVisible: 'on' PhaseWrapping: 'off'PhaseMatching: 'off'PhaseMatchingFreq: 0PhaseMatchingValue: 0我们可以通过修改上面的每一项修改伯德图的风格,比如我们使用下面的语句画我们的伯德图:P=bodeoptions;P.Grid='on';P.XLim={[10 40000]};P.XLimMode={'manual'};P.FreqUnits='HZ';num=[1.576e010 0 0];den=[1 1.775e005 1.579e010 2.804e012 2.494e014];H=tf(num,den;bode(H,P这时,我们将会看到以下的伯德图:上面这张图相对就比较好了,它的横坐标单位是HZ,范围是[10 40K]HZ,而且打开了网格,便于我们观察-3DB处的频率值。
BODE图画图过程
电机定位系统校正(BODE图)MATLAB软件具有强大的计算能力和绘图功能,能够快速、准确地做出频域特性曲线。
利用MATLAB^制系统的Bode图,为控制系统设计和分析提供了极大的方便。
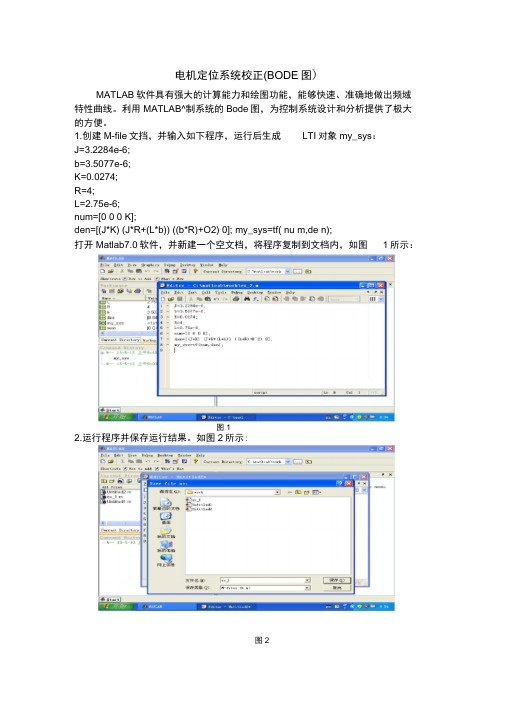
1.创建M-file文挡,并输入如下程序,运行后生成LTI对象my_sys:J=3.2284e-6;b=3.5077e-6;K=0.0274;R=4;L=2.75e-6;num=[0 0 0 K];den=[(J*K) (J*R+(L*b)) ((b*R)+O2) 0]; my_sys=tf( nu m,de n);打开Matlab7.0软件,并新建一个空文档,将程序复制到文档内,如图1所示:图12.运行程序并保存运行结果。
如图2所示:图2图43. 打开 Start-Toolboxes — ControlSystem — SISO Design Tool启动SISO Design,如图3所示4. 将my_sys 程序导入到SISO Design Tool 中, 如图4所示啪号TW Hi^vicn ToniP il ■ ErLE ・ Vi, mr r za-ipMi-i k t Dqri £x> al>1* E □'l'l. •冷日■丁 11*』]1卜l>] X o 4 T 11; »M s K 1 mi4||'=4Dp山 watLa ft — 15-S-IQ Jt 午肌"■存-i-s — 15-5-in 上午恥ny_2F2c !x|F L 1« Edu I 上LIM tmp viiK«l&rl 姿kl 尸L C. TadulllaJpIIH n y. L R ann曲闻出田画田田刚Dur r ■n.l 卫a r nryCtiaiTijinfl Hi ®f-15-5-JQ 上牛奔■■■jip.sygG ii — 15-5-10 上午和 iSB (TT = EJS >尺jgtrt.Hci nr ||T ^ nkm 1rn mfi B * njrtlini£>■ |si90 ・ui.fi 1 v f Ja S D .EM 1 色■'i -Fi'Mii ^mpp+if-slnrCi|r TBH.*: n i. B-Bf I arv^(Bft-olKl fir tiv? for “偷史 俺±&n )埔1口曲riw^uefCf rijSr.14 fftcrt图65.在View 菜单中,关闭根轨迹显示,只显示开环的 Bode 图。
BODE图 画图过程
电机定位系统校正(BODE图)MATLAB软件具有强大的计算能力和绘图功能,能够快速、准确地做出频域特性曲线。
利用MATLAB绘制系统的Bode图,为控制系统设计和分析提供了极大的方便。
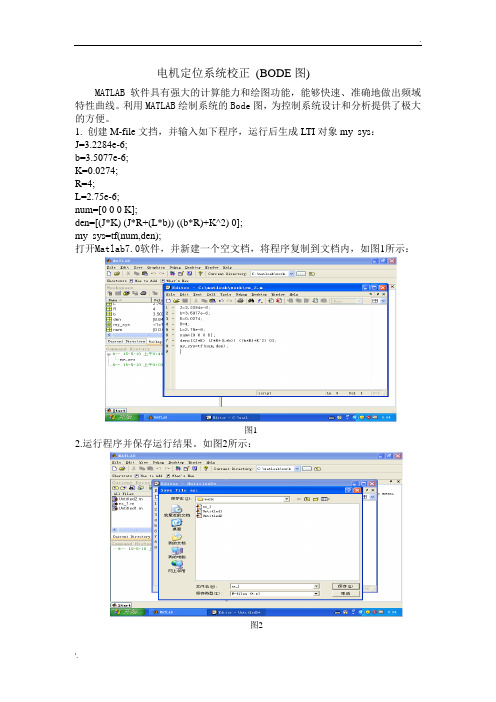
1. 创建M-file文挡,并输入如下程序,运行后生成LTI对象my_sys:J=3.2284e-6;b=3.5077e-6;K=0.0274;R=4;L=2.75e-6;num=[0 0 0 K];den=[(J*K) (J*R+(L*b)) ((b*R)+K^2) 0];my_sys=tf(num,den);打开Matlab7.0软件,并新建一个空文档,将程序复制到文档内,如图1所示:图12.运行程序并保存运行结果。
如图2所示:图23.打开Start-Toolboxes—Control System—SISO Design Tool。
启动SISO Design,如图3所示图34.将my_sys程序导入到SISO Design Tool中,如图4所示图45.在View菜单中,关闭根轨迹显示,只显示开环的Bode图。
如图5所示图56. 加积分环节;加零点(60角频率)将各个参数进行积分:空白处右键—Add Pole/Zero—Integrator。
如图6所示:图67.在magnitude曲线加零点,然后Analysis菜单下Response to Step Command 指令。
如图7所示:图78.在管理反馈界面中,只显示闭环的r与y的关系—LT1 Viewer For SISO Design Tool界面空白处右键—Systems—Closed Loop :r to u (green),如图8所示:图89.添加零点和极点,如图8所示,并移动极点、零点和线的位置,调整LT1 Viewer For SISO Design Tool窗口中函数图像的变化直到符合Bode图,如图9所示:图910.用鼠标上下移动观察阶越响应的超调量变化,满足校正要求。
自动控制原理基础-项目4-MATLAB绘制系统的Bode图和Nyquist图

MATLAB draws the Bode diagram and Nyquist diagram of the system
MATLAB R2020a基本操作
1. 鼠标双击MATLAB R2020a 图标,打开MATLAB软件。
2. 获得系统默认频率范围的Nyquist图
案例1
3. 在MATLAB软件命令框中输入如下命令
4. 获得系统自定义频率范围的Nyquist图
说明:除了在MATLAB软件命令框中直接输入命 令外,还可以利用脚本编辑器编写M文件,通过 运行M文件来绘图。
2. 等待MATLAB启动完毕。
MATLAB 绘制系统Bode图
案例1
1. 在MATLAB软件命令框中输入如下命令
2. 获得系统默认频率范围的Bode图
案例1
3. 在MATLAB软件命令框中输入如下命令
4. 获得系统自定义频率范围的Bode图
MATLAB 绘制系统Nyquist图
案例1ቤተ መጻሕፍቲ ባይዱ
1. 在MATLAB软件命令框中输入如下命令
matlab绘制Nyquist图与Bode图

MATLAB绘制开环传递函数的Nyquist图与Bode图电气101 1008140313 邱书恒(主导)一、问题重述1.1.已知开环传递函数,画Nyquist图G0(s)=10(0.5s+1)(1+s) ()1.2.已知开环传递函数,画波特图并计算相位裕度G0(s)=2083(s+3)s(s2+20s+625)二、求解过程2.1.画Nyquist图频率特性G(jω)是频率ω的复变函数,可以在复平面上用一个矢量来表示某一频率ω下的量G(jω)。
该矢量的幅值为G(ω)=|G(jω)|,它的相角为φ(ω)=∠[G(jω)]。
当ω从0→∞变化时,矢量轨迹就表示频率特性。
按上述办法,吧频率特性在复平面上用极坐标表示的几何图形,即为Nyquist图。
2.2.画Bode图频率特性的对数坐标图,就是Bode图。
三、Matlab命令解析3.1.nyquist命令nyquist命令可以求得连续系统的奈奎斯特曲线,命令语法如下:nyquist(sys)nyquist(sys,w)nyquist(sys1,sys2,…,sysN)nyquist(sys1,sys2,…sysN,w)[re,im,w,sdre,sdim]=nyquist(sys)Nyquist(sys)创建一个动态系统Nyquist图,该模型可以是连续的或离散,和单变量或多输入多输出。
当带有输出变量时,可得到相应的一组数据,不带输出变量时,则绘出奈奎斯特曲线。
也可用制定向量w指定所要绘制的曲线范围。
3.2. bode命令Bode命令可以求得连续系统的伯德图,命令语法如下:bode(sys)bode(sys1,…,sysN)bode(sys1,PlotStyle1,…,sysN,PlotStyleNbode(…,w)[mag,phase]=bode(sys,w)[mag,phase,wout]=bode(sys)[mag,phase,wout,sdmag,sdphase]=bode(sys)Bode(sys)创建一个动态系统的频率响应bode图。
bode图怎么绘制

bode图怎么绘制不过在系统辨识工具箱中有相应的函数能够完成该功能。
应该是invfrqs函数。
但这个是由频率响应得到的,所以你的对输入输出信号做傅里叶变换得到频率响应后在用这个函数拟合传递函数。
使用matlab工具箱更为方便和直观:1. 把u,y信号导入到工作空间里。
2. 用ident命令打开matlab系统辨识工具箱,然后点击import data,从新打开界面里导入工作空间的数据。
然后可以通过图形查看该输入输出信号,或者在proprocess进行信号预处理。
3. 根据你的模型在estimate里选择linear parameter models,个人觉得你应该选择ARX 结构,确定阶数,然后进行估计。
4. 在主界面里查看估计模型,并且可以和实际输出比较,看看拟合度。
详细使用方面参考帮助文档System Identification Toolbox User's Guide也只能是拟合吧,拟合的目标也只能是有限的一些典型传递函数。
做过这个,就是拟合吧在sisotool工具里放置合适的零极点,尽量使曲线吻合,得到传递函数我是大概知道实测的曲线的零极点分布的,然后去拟合的,这样好做点如果已经得到Bode plot,就幅度vs频率,相位vs频率曲线,根据+/-20db/dec,+/-40db/dec 渐近线先预测几个pole,zero,double pole double zero,然后再去近似了。
还有几个比较困难的地方是:1)实际系统引入的杂散参数和群延迟特性,才是拟合和预测的难点。
2)实际测量时仪器已经采用了离散化的数字处理手段,还有测量系统处理误差和测量时注入的扰动幅度所引起的误差,对低频还好,对高频都是很大的影响。
3)所以目前已有的模型,多是对1/2开关频率之前的预测,V2等新模型有所改进,但是还是有其局限性以我测试的为例吧,R=1e3; C=1e-7; L=0.1; Rl=1000;magdb_LCR=zeros(1,1e5);% -sL-R-|(1/sC)mag_LCR=zeros(1,1e5);phase_LCR=zeros(1,1e5);freq=(1:1e5);RCplot=zeros(1,1e5);LCRplot=zeros(1,1e5);for f=1:1:1e5LCR=1/((1i*2*pi*f)^2*L*C+1i*2*pi*f*C*Rl+1);LCRplot(f)=LCR;mag_LCR(f)=abs(LCR);magdb_LCR(f)=20*log10(abs(LCR));phase_LCR(f)=angle(LCR)*180/pi;end我用上方的函数写一个已知的传递函数,生成对应频率下的幅值和相位。
应用Matlab绘制Bode图及Nyquist图
解答:
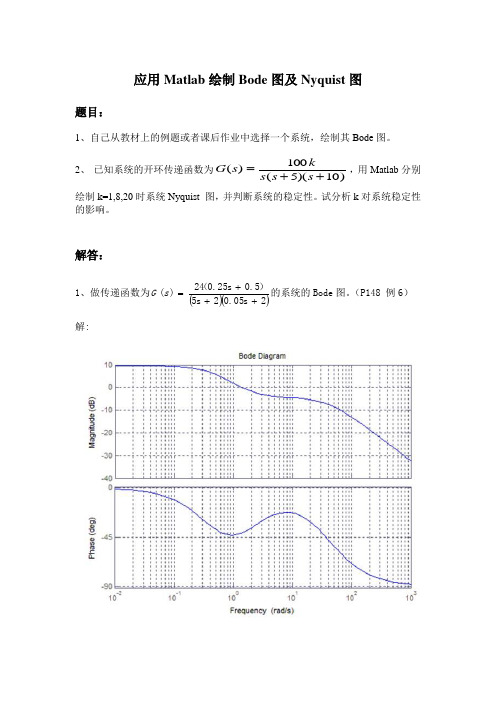
1、做传递函数为 G (s ) 解:
24 (0.25s 0.5) 的系统的 Bode 图。 (P148 例 6) 5s 20.05s 2
2、 已知系统的开环传递函数为 G ( s )
100k ,用 Matk=1,8,20 时系统 Nyquist 图,并判断系统的稳定性。试分析 k 对系统稳定 性的影响。 解: (1)当 K=1 时,由题意得 P=0,由 Bode 图得 N=0,则 Z=N+P=0,系统稳 定。
应用 Matlab 绘制 Bode 图及 Nyquist 图
题目:
1、自己从教材上的例题或者课后作业中选择一个系统,绘制其 Bode 图。 2、 已知系统的开环传递函数为 G ( s )
100k ,用 Matlab 分别 s ( s 5)(s 10)
绘制 k=1,8,20 时系统 Nyquist 图,并判断系统的稳定性。试分析 k 对系统稳定性 的影响。
(2) 当 K=8 时,由题意得 P=0,由 Bode 图得 N=2,则 Z=N+P=2,系统不稳 定。
(3)当 K=20 时,由题意得 P=0,由 Bode 图得 N=2,则 Z=N+P=2,系统 不稳定。
matlab绘制bode图技巧
我们经常会遇到使用Matlab画伯德图的情况,可能我们我们都知道bode这个函数是用来画bode图的,这个函数是Matlab内部提供的一个函数,我们可以很方便的用它来画伯德图,但是对于初学者来说,可能用起来就没有那么方便了。
譬如我们要画出下面这个传递函数的伯德图:1.576e010 s^2H(s)= ------------------------------------------------------------------------------------------s^4 + 1.775e005 s^3 + 1.579e010 s^2 + 2.804e012 s + 2.494e014(这是一个用butter函数产生的2阶的,频率范围为[20 20K]HZ的带通滤波器。
)我们可以用下面的语句:num=[1.576e010 0 0];den=[1 1.775e005 1.579e010 2.804e012 2.494e014];H=tf(num,den);bode(H)这样,我们就可以得到以下的伯德图:可能我们会对这个图很不满意,第一,它的横坐标是rad/s,而我们一般希望横坐标是HZ;第二,横坐标的范围让我们看起来很不爽;第三,网格没有打开(这点当然我们可以通过在后面加上grid on解决)。
下面,我们来看看如何定制我们自己的伯德图风格:在命令窗口中输入:bodeoptions我们可以看到以下内容:ans =Title: [1x1 struct]XLabel: [1x1 struct]YLabel: [1x1 struct]TickLabel: [1x1 struct]Grid: 'off'XLim: {[1 10]}XLimMode: {'auto'}YLim: {[1 10]}YLimMode: {'auto'}IOGrouping: 'none'InputLabels: [1x1 struct]OutputLabels: [1x1 struct]InputVisible: {'on'}OutputVisible: {'on'}FreqUnits: 'rad/sec'FreqScale: 'log'MagUnits: 'dB'MagScale: 'linear'MagVisible: 'on'MagLowerLimMode: 'auto'MagLowerLim: 0PhaseUnits: 'deg'PhaseVisible: 'on'PhaseWrapping: 'off'PhaseMatching: 'off'PhaseMatchingFreq: 0PhaseMatchingValue: 0我们可以通过修改上面的每一项修改伯德图的风格,比如我们使用下面的语句画我们的伯德图:P=bodeoptions;P.Grid='on';P.XLim={[10 40000]};P.XLimMode={'manual'};P.FreqUnits='HZ';num=[1.576e010 0 0];den=[1 1.775e005 1.579e010 2.804e012 2.494e014];H=tf(num,den);bode(H,P)这时,我们将会看到以下的伯德图:上面这张图相对就比较好了,它的横坐标单位是HZ,范围是[10 40K]HZ,而且打开了网格,便于我们观察-3DB处的频率值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
M a t l a b中B o d e图的
绘制技巧
Matlab中Bode图的绘制技巧
我们经常会遇到使用Matlab画伯德图的情况,可能我们我们都知道bode这个函数是用来画bode图的,这个函数是Matlab内部提供的一个函数,我们可以很方便的用它来画伯德图,但是对于初学者来说,可能用起来就没有那么方便了。
譬如我们要画出下面这个传递函数的伯德图:
1.576e010 s^2
H(s)= ------------------------------------------------------------------------------------------
s^4 + 1.775e005 s^3 + 1.579e010 s^2 + 2.804e012 s + 2.494e014
(这是一个用butter函数产生的2阶的,频率范围为[20 20K]HZ的带通滤波器。
)
我们可以用下面的语句:
num=[1.576e010 0 0];
den=[1 1.775e005 1.579e010 2.804e012 2.494e014];
H=tf(num,den);
bode(H)
这样,我们就可以得到以下的伯德图:
可能我们会对这个图很不满意,第一,它的横坐标是rad/s,而我们一般希望横坐标是HZ;第二,横坐标的范围让我们看起来很不爽;第三,网格没有打开(这点当然我们可以通过在后面加上grid on解决)。
下面,我们来看看如何定制我们自己的伯德图风格:
在命令窗口中输入:bodeoptions
我们可以看到以下内容:
ans =
Title: [1x1 struct]
XLabel: [1x1 struct]
YLabel: [1x1 struct]
TickLabel: [1x1 struct]
Grid: 'off'
XLim: {[1 10]}
XLimMode: {'auto'}
YLim: {[1 10]}
YLimMode: {'auto'}
IOGrouping: 'none'
InputLabels: [1x1 struct]
OutputLabels: [1x1 struct]
InputVisible: {'on'}
OutputVisible: {'on'}
FreqUnits: 'rad/sec'
FreqScale: 'log'
MagUnits: 'dB'
MagScale: 'linear'
MagVisible: 'on'
MagLowerLimMode: 'auto'
MagLowerLim: 0
PhaseUnits: 'deg'
PhaseVisible: 'on'
PhaseWrapping: 'off'
PhaseMatching: 'off'
PhaseMatchingFreq: 0
PhaseMatchingValue: 0
我们可以通过修改上面的每一项修改伯德图的风格,比如我们使用下面的语句画我们的伯德图:P=bodeoptions;
P.Grid='on';
P.XLim={[10 40000]};
P.XLimMode={'manual'};
P.FreqUnits='HZ';
num=[1.576e010 0 0];
den=[1 1.775e005 1.579e010 2.804e012 2.494e014];
H=tf(num,den);
bode(H,P)
这时,我们将会看到以下的伯德图:
上面这张图相对就比较好了,它的横坐标单位是HZ,范围是[10 40K]HZ,而且打开了网格,便于我们观察-3DB处的频率值。
当然,你也可以改变bodeoptions中的其它参数,做出符合你的风格的伯德图。
是这样的,运行命令ctrlpref,出现控制系统工具箱的设置页面,Units改为Hz就好了
R = abs(Z)
theta = angle(Z)。
