Matlab中Bode图的绘制技巧
matlab画幅频响应和相频响应

matlab画幅频响应和相频响应
要使用MATLAB绘制系统的幅频响应和相频响应,可以按照以下步骤进行:
1. 定义系统传递函数或频率响应函数。
假设你有一个系统的传递函数H(s),可以使用MATLAB的`tf`函数定义传递函数。
例如,假设传递函数为H(s) = (s+1)/(s^2+2s+3),可以使用以下代码定义传递函数:
matlab
num = [1 1];
den = [1 2 3];
H = tf(num, den);
2. 绘制幅频响应。
使用MATLAB的`bode`函数可以绘制系统的幅频响应曲线。
以下代码演示如何绘制幅频响应曲线:
matlab
bode(H);
这将绘制出系统的幅频响应曲线,并显示频率范围和幅度值。
3. 绘制相频响应。
使用MATLAB的`bode`函数的输出参数可以获取系统的相频响应数据。
以下代码演示如何获取相频响应数据并绘制相频响应曲线:
matlab
[mag, phase, wout] = bode(H);
semilogx(wout, squeeze(phase));
这将绘制出系统的相频响应曲线,并显示频率范围和相位值。
以上是基本的步骤,你可以根据实际需求和系统的特点进行相应的修改和调整。
控制系统Bode图的Matlab实验

红河学院工学院实验报告单
《机械工程控制基础》Matlab 仿真实验报告单
课程名称:
姓名:
日期:
成绩:
年级专业: 学号: 实验场地:
实验序号: 4
实验名称:控制系统Bode 图的Matlab 实验
一、实验内容。
已知控制系统开环传递函数,绘制开环传递函数Bode 图,。
1000()(1)(2)(5)
K G s s s s =
+++ 二、实验目的。
1、熟悉Matlab 操作
2、掌握Matlab 中,绘制传递函数的Bode 图。
三、相关Matlab 仿真程序。
已知控制系统开环传递函数,绘制开环传递函数Bode 图。
1000()(1)(2)(5)
K G s s s s =+++
相关程序:
clear
num=1000;
den=conv([1 1],conv([1 2],[1 5]));
GKs=tf(num,den)
w=logspace(-2,3,100);
bode(GKs,w);
grid on
margin(GKs)
四、相关Matlab仿真图形。
五、判断系统稳定性,并说明理由。
幅值裕度的值为-18dB
相位裕度的值为-44.4deg
剪切频率 4.12rad/sec
相位穿越频率9.51rad/sec
从图形中可以看出来,剪切频率大于相位穿越频率,又因为其开环传递是最小相位系统,所以其闭环系统不稳定。
另一方面,幅值裕度和相位裕度都为负值,也证明其闭环系统不稳定。
BODE图 画图过程
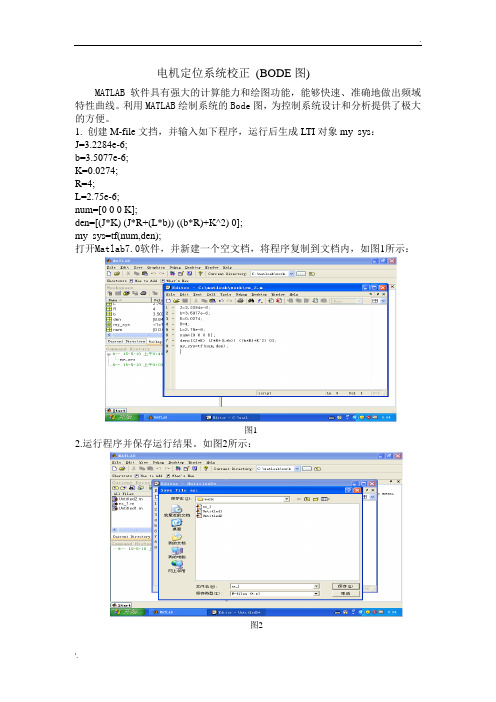
电机定位系统校正(BODE图)MATLAB软件具有强大的计算能力和绘图功能,能够快速、准确地做出频域特性曲线。
利用MATLAB绘制系统的Bode图,为控制系统设计和分析提供了极大的方便。
1. 创建M-file文挡,并输入如下程序,运行后生成LTI对象my_sys:J=3.2284e-6;b=3.5077e-6;K=0.0274;R=4;L=2.75e-6;num=[0 0 0 K];den=[(J*K) (J*R+(L*b)) ((b*R)+K^2) 0];my_sys=tf(num,den);打开Matlab7.0软件,并新建一个空文档,将程序复制到文档内,如图1所示:图12.运行程序并保存运行结果。
如图2所示:图23.打开Start-Toolboxes—Control System—SISO Design Tool。
启动SISO Design,如图3所示图34.将my_sys程序导入到SISO Design Tool中,如图4所示图45.在View菜单中,关闭根轨迹显示,只显示开环的Bode图。
如图5所示图56. 加积分环节;加零点(60角频率)将各个参数进行积分:空白处右键—Add Pole/Zero—Integrator。
如图6所示:图67.在magnitude曲线加零点,然后Analysis菜单下Response to Step Command 指令。
如图7所示:图78.在管理反馈界面中,只显示闭环的r与y的关系—LT1 Viewer For SISO Design Tool界面空白处右键—Systems—Closed Loop :r to u (green),如图8所示:图89.添加零点和极点,如图8所示,并移动极点、零点和线的位置,调整LT1 Viewer For SISO Design Tool窗口中函数图像的变化直到符合Bode图,如图9所示:图910.用鼠标上下移动观察阶越响应的超调量变化,满足校正要求。
自动控制原理基础-项目4-MATLAB绘制系统的Bode图和Nyquist图

MATLAB draws the Bode diagram and Nyquist diagram of the system
MATLAB R2020a基本操作
1. 鼠标双击MATLAB R2020a 图标,打开MATLAB软件。
2. 获得系统默认频率范围的Nyquist图
案例1
3. 在MATLAB软件命令框中输入如下命令
4. 获得系统自定义频率范围的Nyquist图
说明:除了在MATLAB软件命令框中直接输入命 令外,还可以利用脚本编辑器编写M文件,通过 运行M文件来绘图。
2. 等待MATLAB启动完毕。
MATLAB 绘制系统Bode图
案例1
1. 在MATLAB软件命令框中输入如下命令
2. 获得系统默认频率范围的Bode图
案例1
3. 在MATLAB软件命令框中输入如下命令
4. 获得系统自定义频率范围的Bode图
MATLAB 绘制系统Nyquist图
案例1ቤተ መጻሕፍቲ ባይዱ
1. 在MATLAB软件命令框中输入如下命令
浅议用Matlab绘制Bode图及频率特性分析

频率特性的描述: 极坐标形式:
这两种描述之间的关系:
系统的频率特性图主要有 Bode(波德)图、Nyquist(奈 奎斯特)曲线、Nichols(尼柯尔斯)图。
限于篇幅,本文以 Bode 图为例来说明。 2 用 Matlab 来绘制 Bode 图
Bode图是指由对数幅频特性和相频特性组成的对数频率 特性图。对数幅频特性和相频特性曲线的横轴都是频率,且 均是按对数分度的。对数幅频特性的纵轴为:
通过设计,构思出程序流程框图,以最典型的二阶系统 为例来说明。系统的传பைடு நூலகம்函数为
绘制出 w 取一系列不同值时的 Bode 图,如图一所示。
图一 Bode 图
251
科技广场 2007.11
浅议用 Matlab 绘制 Bode 图及频率特性分析
Drawing Bode Graphic with Matlab and Analysis of Frequency
黄 涛 郭玉婷 Huang Tao Guo Yuting (1.吉林师范大学信息技术学院, 吉林 四平 136000; 2.四平市第三高级中学, 吉林 四平 130001) (1.College of Information Technology, Jilin Normal University, Jilin Shping 136000; 2.The Third High School, Jilin Siping 136001)
分
版社.
析
[3]MATLAB电子仿真与应用[M].北京:国防工业出版社.
[4]电子系统仿真与MATLAB[M].北京:北京广播学院出版
社.
作者简介 黄涛,男,吉林师范大学信息技术学院教师,讲师,吉
用MatlabSimulink画波特图Bode图

用Matlab/Simulink画波特图Bode图在Matlab中,大多时候,我们都是用M语言,输入系统的传递函数后,用bode函数绘制bode图对系统进行频率分析,这样做,本人觉得效率远不如Simulink建模高。
如何在Matlab/Simulink中画bode图,以前也在网上查过些资料,没看到太多有用的参考。
今天做助教课的仿真,又要画电机控制中电流环的bode图,模型已经建好,step response也很容易看出来,可这bode图怎么也出不来,又不愿意用m语言写出传递函数再画。
baidu和google了好一阵,几乎没有一个帖子说的清清楚楚的,经过一番摸索,终于掌握了Simulink里画bode图的方法。
.其实,Simulink里画bode图,非常的easy,也很方便。
写此文的目的是希望对那些常用Simulink进行仿真希望画bode图又不愿用M语言的新手有所帮助。
以下均是以Matlab R2008a为例。
首先,在simulink里建好model。
如图1,这里需要注意的是,输入和输出要用input port和output port,这样以后画bode图的时候,系统就会知道是这两个变量之间的关系。
图1 建好model其次,选择线性分析。
Tools->Control Design ->Linear Analysis。
如图2。
图2 选择Linear Ansysis将出现如图3所示的Control and Estimation Tools Manager窗口。
图3 Control and Estimation Tools Manager窗口第三步,激动人心的时刻到了,哈哈。
如果你是按照前面的步骤来的,那么这时候,你就应该可以直接画出bode图,在窗口的下方,将“Plot linear analysis result in a ”前面的方框打上勾,已打的就不用管了,再在后面的下拉框里选择“bode response plot”,即画output port和input port之间的bode图,再点击“Linearize Model”按钮,就OK了。
应用Matlab绘制Bode图及Nyquist图
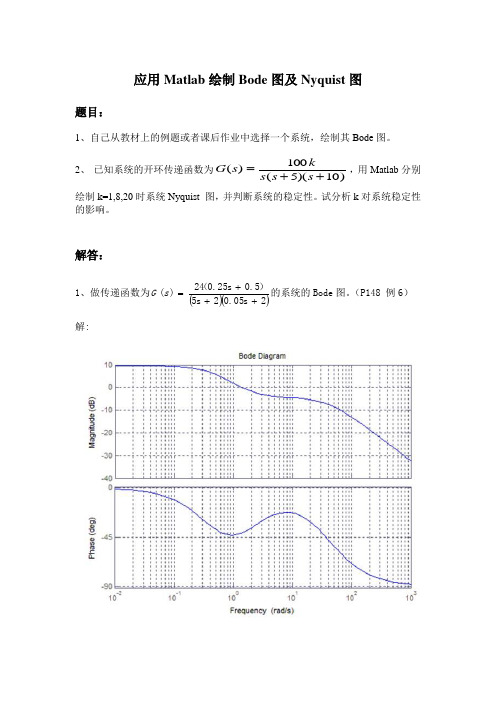
解答:
1、做传递函数为 G (s ) 解:
24 (0.25s 0.5) 的系统的 Bode 图。 (P148 例 6) 5s 20.05s 2
2、 已知系统的开环传递函数为 G ( s )
100k ,用 Matk=1,8,20 时系统 Nyquist 图,并判断系统的稳定性。试分析 k 对系统稳定 性的影响。 解: (1)当 K=1 时,由题意得 P=0,由 Bode 图得 N=0,则 Z=N+P=0,系统稳 定。
应用 Matlab 绘制 Bode 图及 Nyquist 图
题目:
1、自己从教材上的例题或者课后作业中选择一个系统,绘制其 Bode 图。 2、 已知系统的开环传递函数为 G ( s )
100k ,用 Matlab 分别 s ( s 5)(s 10)
绘制 k=1,8,20 时系统 Nyquist 图,并判断系统的稳定性。试分析 k 对系统稳定性 的影响。
(2) 当 K=8 时,由题意得 P=0,由 Bode 图得 N=2,则 Z=N+P=2,系统不稳 定。
(3)当 K=20 时,由题意得 P=0,由 Bode 图得 N=2,则 Z=N+P=2,系统 不稳定。
matlab bode指数

在MATLAB中,使用Bode图来分析系统的频率响应时,指数函数可能用于描述频率的幂次。
Bode图是一种图表示方法,用于显示系统的频率响应特性,包括幅频特性和相频特性。
在MATLAB中绘制Bode图时,可以使用bode函数来计算并绘制系统的频率响应。
该函数可以绘制幅频图和相频图,其中幅频图显示了系统在不同频率下的增益或幅度,而相频图显示了系统在不同频率下的相位延迟。
在描述频率响应时,可以使用指数函数来表示增益或相位的变化。
例如,可以使用形如A * exp(-alpha *
w)的指数函数来描述频率响应的幅度,其中A是常数,alpha是衰减系数,w是角频率。
类似地,可以使用形如phase_shift + alpha * w的指数函数来描述相位延迟。
在MATLAB中,可以使用exp函数来计算指数函数。
例如,要计算exp(-alpha * w),可以使用以下代码:matlab复制代码
w = 0:0.01:10; % 生成频率向量
alpha = 1; % 衰减系数
A = 1; % 常数
y = A * exp(-alpha * w); % 计算幅值
类似地,可以使用以下代码计算相位延迟:
matlab复制代码
phase_shift = 0; % 相位偏移量
y = phase_shift + alpha * w; % 计算相位延迟
然后,可以使用bode函数将计算得到的幅值或相位绘制成Bode图:
matlab复制代码bode(y); % 绘制Bode图
请注意,以上代码仅为示例,实际使用时需要根据具体的应用场景和需求进行修改和调整。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Matlab中Bode图的绘制技巧
我们经常会遇到使用Matlab画伯德图的情况,可能我们我们都知道bode这个函数是用来画bode图的,这个函数是Matlab内部提供的一个函数,我们可以很方便的用它来画伯德图,但是对于初学者来说,可能用起来就没有那么方便了。
譬如我们要画出下面这个传递函数的伯德图:
s^2
H(s)=
------------------------------------------------------------------------------------------
s^4 + s^3 + s^2 + s +
(这是一个用butter函数产生的2阶的,频率范围为[20 20K]HZ的带通滤波器。
)
我们可以用下面的语句:
num=[ 0 0];
den=[1 ];
H=tf(num,den);
bode(H)
这样,我们就可以得到以下的伯德图:
v1.0 可编辑可修改
可能我们会对这个图很不满意,第一,它的横坐标是rad/s,而我们一般希望横坐标是HZ;第二,横坐标的范围让我们看起来很不爽;第三,网格没有打开(这点当然我们可以通过在后面加上grid on解决)。
下面,我们来看看如何定制我们自己的伯德图风格:
在命令窗口中输入:bodeoptions
我们可以看到以下内容:
ans =
Title: [1x1 struct]
XLabel: [1x1 struct]
YLabel: [1x1 struct]
TickLabel: [1x1 struct]
Grid: 'off'
XLim: {[1 10]}
XLimMode: {'auto'}
YLim: {[1 10]}
YLimMode: {'auto'}
IOGrouping: 'none'
InputLabels: [1x1 struct]
OutputLabels: [1x1 struct]
InputVisible: {'on'}
OutputVisible: {'on'}
FreqUnits: 'rad/sec'
FreqScale: 'log'
MagUnits: 'dB'
MagScale: 'linear'
MagVisible: 'on'
MagLowerLimMode: 'auto'
MagLowerLim: 0
PhaseUnits: 'deg'
PhaseVisible: 'on'
PhaseWrapping: 'off'
PhaseMatching: 'off'
PhaseMatchingFreq: 0
PhaseMatchingValue: 0
我们可以通过修改上面的每一项修改伯德图的风格,比如我们使用下面的语句画我们的伯德图:P=bodeoptions;
='on';
={[10 40000]};
={'manual'};
='HZ';
num=[ 0 0];
den=[1 ];
H=tf(num,den);
bode(H,P)
这时,我们将会看到以下的伯德图:
上面这张图相对就比较好了,它的横坐标单位是HZ,范围是[10 40K]HZ,而且打开了网格,便于我们观察-3DB处的频率值。
当然,你也可以改变bodeoptions中的其它参数,做出符合你的风格的伯德图。
R = abs(Z)
theta = angle(Z)。
