最小生成树
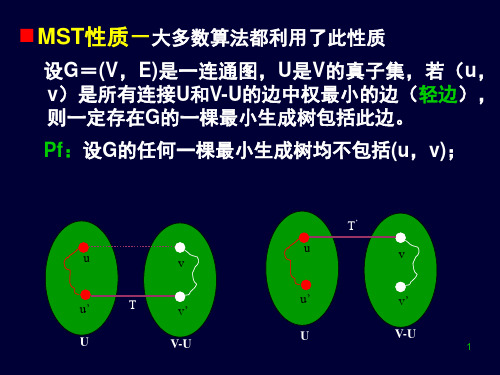
最小生成树MinimumSpanningTree
8
1、Prim算法
算法求精-初始化
将根r涂红加入红点集U,TE=φ。
对每个白点i (0≤i ≤n-1, i≠r ), i所关联的最短紫边(r,i)的 长度为G[r][i], 这n-1条最短紫边构成了初始的候选轻边集。
因为树边为空,故将T[0..n-2]全部用来存放候选轻边集。
❖设V(G)={0,1,…,n-1}
❖算法的每一步均是在连接红、白点集的紫 边中选一轻边扩充到T(贪心),T从任意 一点r开始(r为根),直至U=V为止。 MST性质保证了贪心选择策略的正确性。
3
1、Prim算法
如何找轻边?
❖可能的紫边集
设红点集|U|=k, 白点集|V-U|=n-k,则可能的紫边 数为:k(n-k)。
//将(u,v)涂红加入树中,白点v加入红点集
ModifyCandidateSet(…);
//根据新红点v调整候选轻边集
}
}
算法终止时U=V,T=(V,TE)
6
1、Prim算法
实例
6 1
5
35 4
05
1
3
27 2
4
5
6
60 5
1
1
3
∞2
∞
4
5
0
151
3
2
5
2 4
4
5
0
151
3
2
5
2 4
4
5
0
151 2
int i, minpos, min=Infinity; for (i=k; i<n-1; i++) //遍历候选集找轻边
最小生成树---普里姆算法(Prim算法)和克鲁斯卡尔算法(Kruskal算法)

最⼩⽣成树---普⾥姆算法(Prim算法)和克鲁斯卡尔算法(Kruskal算法)最⼩⽣成树的性质:MST性质(假设N=(V,{E})是⼀个连通⽹,U是顶点集V的⼀个⾮空⼦集,如果(u,v)是⼀条具有最⼩权值的边,其中u属于U,v属于V-U,则必定存在⼀颗包含边(u,v)的最⼩⽣成树)普⾥姆算法(Prim算法)思路:以点为⽬标构建最⼩⽣成树1.将初始点顶点u加⼊U中,初始化集合V-U中各顶点到初始顶点u的权值;2.根据最⼩⽣成树的定义:从n个顶点中,找出 n - 1条连线,使得各边权值最⼩。
循环n-1次如下操作:(1)从数组lowcost[k]中找到vk到集合U的最⼩权值边,并从数组arjvex[k] = j中找到该边在集合U中的顶点下标(2)打印此边,并将vk加⼊U中。
(3)通过查找邻接矩阵Vk⾏的各个权值,即vk点到V-U中各顶点的权值,与lowcost的对应值进⾏⽐较,若更⼩则更新lowcost,并将k存⼊arjvex数组中以下图为例#include<bits/stdc++.h>using namespace std;#define MAXVEX 100#define INF 65535typedef char VertexType;typedef int EdgeType;typedef struct {VertexType vexs[MAXVEX];EdgeType arc[MAXVEX][MAXVEX];int numVertexes, numEdges;}MGraph;void CreateMGraph(MGraph *G) {int m, n, w; //vm-vn的权重wscanf("%d %d", &G->numVertexes, &G->numEdges);for(int i = 0; i < G->numVertexes; i++) {getchar();scanf("%c", &G->vexs[i]);}for(int i = 0; i < G->numVertexes; i++) {for(int j = 0; j < G->numVertexes; j++) {if(i == j) G->arc[i][j] = 0;else G->arc[i][j] = INF;}}for(int k = 0; k < G->numEdges; k++) {scanf("%d %d %d", &m, &n, &w);G->arc[m][n] = w;G->arc[n][m] = G->arc[m][n];}}void MiniSpanTree_Prim(MGraph G) {int min, j, k;int arjvex[MAXVEX]; //最⼩边在 U集合中的那个顶点的下标int lowcost[MAXVEX]; // 最⼩边上的权值//初始化,从点 V0开始找最⼩⽣成树Tarjvex[0] = 0; //arjvex[i] = j表⽰ V-U中集合中的 Vi点的最⼩边在U集合中的点为 Vjlowcost[0] = 0; //lowcost[i] = 0表⽰将点Vi纳⼊集合 U ,lowcost[i] = w表⽰ V-U中 Vi点到 U的最⼩权值for(int i = 1; i < G.numVertexes; i++) {lowcost[i] = G.arc[0][i];arjvex[i] = 0;}//根据最⼩⽣成树的定义:从n个顶点中,找出 n - 1条连线,使得各边权值最⼩for(int i = 1; i < G.numVertexes; i++) {min = INF, j = 1, k = 0;//寻找 V-U到 U的最⼩权值minfor(j; j < G.numVertexes; j++) {// lowcost[j] != 0保证顶点在 V-U中,⽤k记录此时的最⼩权值边在 V-U中顶点的下标if(lowcost[j] != 0 && lowcost[j] < min) {min = lowcost[j];k = j;}}}printf("V[%d]-V[%d] weight = %d\n", arjvex[k], k, min);lowcost[k] = 0; //表⽰将Vk纳⼊ U//查找邻接矩阵Vk⾏的各个权值,与lowcost的对应值进⾏⽐较,若更⼩则更新lowcost,并将k存⼊arjvex数组中for(int i = 1; i < G.numVertexes; i++) {if(lowcost[i] != 0 && G.arc[k][i] < lowcost[i]) {lowcost[i] = G.arc[k][i];arjvex[i] = k;}}}int main() {MGraph *G = (MGraph *)malloc(sizeof(MGraph));CreateMGraph(G);MiniSpanTree_Prim(*G);}/*input:4 5abcd0 1 20 2 20 3 71 2 42 3 8output:V[0]-V[1] weight = 2V[0]-V[2] weight = 2V[0]-V[3] weight = 7最⼩总权值: 11*/时间复杂度O(n^2)克鲁斯卡尔算法(Kruskal算法)思路:以边为⽬标进⾏构建最⼩⽣成树在边集中依次寻找最⼩权值边,若构建是不形成环路(利⽤parent数组记录各点的连通分量),则将其添加到最⼩⽣成树中。
最小生成树唯一的充要条件

最小生成树唯一的充要条件最小生成树是一种在图论中常见的概念,它是一个连通无向图中的一棵生成树,其所有边的权值之和最小。
在实际应用中,最小生成树有着广泛的应用,比如在通信网络、电力网络和交通运输等领域。
要确定一个图的最小生成树是否唯一,需要满足以下充要条件:图中的每条边的权值互不相同。
这个条件是非常重要的,因为只有当图中的每条边的权值都不相同时,才能确保最小生成树的唯一性。
如果图中存在两条或多条边的权值相同,那么可能会有多个最小生成树。
为了更好地理解最小生成树唯一的充要条件,我们可以通过一个简单的例子来说明。
假设有一个无向图,其中包含4个顶点A、B、C、D,以及4条边AB、AC、BC、BD。
如果这些边的权值分别为1、2、3、4,那么根据最小生成树的算法,我们可以得到唯一的最小生成树,即连接顶点A、B、C的边AB、AC。
因为在这种情况下,每条边的权值都不相同,所以最小生成树是唯一的。
相反,如果图中存在两条或多条边的权值相同,那么就会出现多个最小生成树的情况。
比如,如果在上面的例子中,边AC的权值改为1,那么就会有两个最小生成树,一个是连接顶点A、B、C的边AB、AC,另一个是连接顶点A、C、D的边AC、CD。
这是因为存在两条权值相同的边AB和AC,所以会有多个最小生成树。
因此,最小生成树的唯一性与图中每条边的权值是否相同密切相关。
只有当图中的每条边的权值都不相同时,最小生成树才是唯一的。
这个充要条件在实际应用中非常重要,因为只有满足这个条件,我们才能准确地求解出最小生成树,从而优化网络结构,提高效率。
最小生成树唯一的充要条件是图中的每条边的权值互不相同。
只有当图中的每条边的权值都不相同时,最小生成树才是唯一的。
这个条件在实际应用中非常重要,因为只有满足这个条件,我们才能准确地求解出最小生成树,从而优化网络结构,提高效率。
希望通过本文的介绍,读者能够更好地理解最小生成树的唯一性条件,为实际应用提供参考。
最小生成树的概念

最小生成树的概念
在图论中,最小生成树是一个连通图的生成树,其边的权值之和最小。
通俗地说,最
小生成树是指在一个图中找到一棵权值最小的生成树,这个生成树包含了连通图的所有顶点,且边的数量最小。
怎么找到最小生成树呢?有两种常用算法:Prim算法和Kruskal算法。
Prim算法首先任选一个点作为起点,然后在剩余的点中选择与当前集合距离最短的点加入集合,直到所有点被加入。
在加入每一个点时,找到与当前集合连接的距离最短的边,加入到生成树中。
重复以上步骤,直到所有点都被加入到生成树中。
Kruskal算法则是将边按照权值从小到大排序,选择权值最小的边加入到生成树中,
如果加入当前边后不构成环,则加入,否则继续找下一条权值最小的边。
重复以上步骤,
直到所有点都被加入到生成树中。
最小生成树有很广泛的应用,如在通信、传输、路网规划等领域都有很重要的作用。
在有些应用中,最小生成树不仅要求边的权值之和最小,还要满足一些约束条件,比如边
的数量、每个点的度数等,这时我们需要采用更加复杂的算法来求解问题。
最小生成树的应用非常广泛,比如在计算机网络中,路由协议需要找到最短的数据传
输路径;在城市交通中,规划出最优的交通路径能够有效减少能源的消耗;在电力系统中,设计最短的输电线路可以节省能源成本。
最小生成树的运用如此广泛,它不仅在计算机科
学中有重要作用,也在其他各个领域有着不可替代的作用。
最小生成树

如此进行下去,每次往生成树里并入一 个顶点和一条边,直到n-1次后,把所有 n 个顶点都并入生成树T的顶点集U中, 此时U=V,TE中包含有(n-1)条边;
图
图6.10 图G 及其生成树
无向连通图 G 图
➢ 生成树
图6.10 图G 及其生成树
生成树
➢ 最小生成树
图
1.1 普里姆(prim)算法
假设G=(V,E)是一个具有n 个顶点的连通网络, T=(U,TE)是G的最小生成树,其中U是T的顶点 集,TE是T的边集,U和TE的初值均为空。
算法开始时,首先从V中任取一个顶点(假定 为V1),将此顶点并入U中,此时最小生成树 顶点集U={V1};
这样,T就是最后得到的最小生成树。
普里姆算法中每次选取的边两端,总是 一个已连通顶点(在U集合内)和一个未 连通顶点(在U集合外),故这个边选取 后一定能将未连通顶点连通而又保证不 会形成环路。
图
图6.11 普里姆算法例子
图
为了便于在顶点集合U和V-U之间选择权 最小的边,建立两个数组closest和 lowcost,closest[i]表示U中的一个顶点,该 顶点与V-U中的一个顶点构成的边具有最 小的权;lowcost表示该边对应的权值。
姆
{
算
min=lowcost[j];
法
k=j;
续
} printf(“(%d,%d)”,k,closest[j]);
/* 打印生成树的一条边*/
最小生成树(普里姆算法)

最⼩⽣成树(普⾥姆算法):所谓⽣成树,就是n个点之间连成n-1条边的图形。
⽽最⼩⽣成树,就是权值(两点间直线的值)之和的最⼩值。
⾸先,要⽤⼆维数组记录点和权值。
如上图所⽰⽆向图:int map[7][7];map[1][2]=map[2][1]=4;map[1][3]=map[3][1]=2;......然后再求最⼩⽣成树。
具体⽅法是:1.先选取⼀个点作起始点,然后选择它邻近的权值最⼩的点(如果有多个与其相连的相同最⼩权值的点,随便选取⼀个)。
如1作为起点。
visited[1]=1;pos=1;//⽤low[]数组不断刷新最⼩权值,low[i](0<i<=点数)的值为:i点到邻近点(未被标记)的最⼩距离。
low[1]=0; //起始点i到邻近点的最⼩距离为0low[2]=map[pos][2]=4;low[3]=map[pos][3]=2;low[4]==map[pos][4]=3;low[5]=map[pos][5]=MaxInt; //⽆法直达low[6]=map[pos][6]=MaxInt;2.再在伸延的点找与它邻近的两者权值最⼩的点。
//low[]以3作当前位置进⾏更新visited[3]=1;pos=3;low[1]=0; //已标记,不更新low[2]=map[1][2]=4; //⽐5⼩,不更新low[3]=2; //已标记,不更新low[4]=map[1][4]=3; //⽐1⼤,更新后为:low[4]=map[3][4]=1;low[5]=map[1][5]=MaxInt;//⽆法直达,不更新low[6]=map[1][6]=MaxInt;//⽐2⼤,更新后为:low[6]=map[3][6]=2;3.如此类推...当所有点都连同后,结果最⽣成树如上图所⽰。
所有权值相加就是最⼩⽣成树,其值为2+1+2+4+3=12。
⾄于具体代码如何实现,现在结合POJ1258例题解释。
最小生成树算法比较Prim和Kruskal算法的优劣

最小生成树算法比较Prim和Kruskal算法的优劣在图论中,最小生成树(Minimum Spanning Tree, MST)是指一个连通图的生成树,它的所有边的权值之和最小。
最小生成树算法是解决最小生成树问题的常用方法,而Prim算法和Kruskal算法是两种经典的最小生成树算法。
本文将比较Prim算法和Kruskal算法的优劣,为读者提供更全面的了解。
一、Prim算法Prim算法是一种贪心算法,通过逐步扩展生成树的方式来构建最小生成树。
Prim算法以一个初始节点开始,然后逐渐添加与当前生成树相连的最短边,直到生成树包含图中的所有节点为止。
以下是Prim算法的基本步骤:1. 选择任意一个节点作为初始节点,并将其加入生成树中。
2. 从生成树的节点中选择一个最短边,并将与该边相连的节点加入生成树。
3. 重复步骤2,直到生成树中包含所有节点。
相比于Kruskal算法,Prim算法在每一步只考虑一个节点,并且每次选择最短边,因此Prim算法的时间复杂度为O(V^2),其中V是图中的节点数。
二、Kruskal算法Kruskal算法也是一种贪心算法,通过按照边的权值递增的顺序来构建最小生成树。
Kruskal算法从图中所有边中选择最短边,并将其加入生成树中,同时保证生成树不形成环,直到生成树中包含所有节点为止。
以下是Kruskal算法的基本步骤:1. 对图中的所有边按照权值进行排序。
2. 依次遍历排序后的边,将权值最小的边加入生成树中,并检查是否形成环。
3. 重复步骤2,直到生成树中包含所有节点。
Kruskal算法中的关键步骤是判断是否形成环,可以使用并查集数据结构来实现。
Kruskal算法的时间复杂度为O(ElogE),其中E是图中的边数。
三、Prim算法与Kruskal算法的比较1. 时间复杂度:Prim算法的时间复杂度为O(V^2),而Kruskal算法的时间复杂度为O(ElogE)。
由于E通常小于V^2,所以Kruskal算法在大多数情况下更快。
最小生成树

对于图G=(V,E)的每一条e∈E, 赋予相应的权数 f(e),得到一个网络图,记为N=(V,E,F),
设T=(为T的权,N中权数最小的 生成树称为N的最小生成树。 许多实际问题,如在若干个城市之间建造铁路网、 输电网或通信网等,都可归纳为寻求连通赋权图 的最小生成树问题。 下面介绍两种求最小生成树的方法:
例1 求下图所示的最小生成树。
v2 e1 v1 e2 e6 v4 e 7 v3
v5
解:按各边的权的不减次序为:
e1 e 2 e3 e7 e6 e 4 e5 e8
所以,首先取 e1 , e2 ,尔后再取 e7 和 e6 , 则构成最小生成树 .
二、破圈法 破圈法就是在图中任取一个圈,从圈中去 掉权最大的边,将这个圈破掉。重复这个 过程,直到图中没有圈为止,保留下的边 组成的图即为最小生成树。 例2 同例1。 解:在圈v2v2v3中,去掉权最大的边e2或e3; 在圈v2v3v4中,去掉权最大的边e4; 在圈v3v4v5中,去掉权最大的边e5; 在圈中v2v3v5,去掉权最大的边e8;
在剩下的图中,已没有圈,于是得到最小生成树, 如下图:
v2 e1 v1 e2 e6 v4 v3 e7
v5
例3 求下图的最小生成树。
C1 1 B1 3 5 A 4 B2 6 5 8 7 6 C4 C3 3 3 4 D3 8 3 C2 8 D2 4 E A
4 3 B2 C4 4 D3 C3 3
B 2 A 3 5 J 2 2 H 5 G 1 F 2 1 S 3 1 4 C 3 4 1 4 E
5
D 2
A 2
B
1
C D 1 2 E
1 S 2 H
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
即最小k+1度限制生成树属于最小k度限制生成树的邻集。
假设我们已经得到了最小p度限制生成树, 如何通过它来求最小p+1度限制生成树呢?
如图,假设我们 已经得到了v0度为 2时的最小生成树, 现在要求v0度为3 时的最小生成树。 V0
枚举与V0关联且 不在树上的边, 添加到树上。
为了使V0的度增 加,下面两条边 红色的边是不能 删除的。
总复杂度:O(VlogV+E+kV);
例题3:还是通讯网络
某地区共有n座村庄,每座村庄的坐标用一 对整数(x, y)表示,现在要在村庄之间建立通 讯网络。 通讯工具有两种,分别是需要铺设的普通 线路和卫星设备。 只能给k个村庄配备卫星设备,拥有卫星设 备的村庄互相间直接通讯。 铺设了线路的村庄之间也可以通讯。
如何判断欲加入的一条边是否与生成树 中边构成回路。 将各顶点划分为所属集合的方法来解决, 每个集合的表示一个无回路的子集。开 始时边集为空,N个顶点分属N个集合, 每个集合只有一个顶点,表示顶点之间 互不连通。 当从边集中按顺序选取一条边时,若它 的两个端点分属于不同的集合,则表明 此边连通了两个不同的部分,因每个部 分连通无回路,故连通后仍不会产生回 路,此边保留,同时把相应两个集合合 并
动态规划
Best(v)的状态转移方程为 Best(v)=max(Best(Father(v)),w(Father(v),v)) 边界条件为 Best[v0]=-∞,{Best[v’]=-∞|(v0,v’)∈E(T)}。
动态规划
状态总共|V|个,而状态转移的时间复杂度 为O(1),因而总的时间复杂度是O(V),即通过 最小p度限制生成树求最小p+1度限制生成 树的时间复杂度是O(V)。
次小生成树有可能也是最小生成树
定理
定理:次小生成树属于最小生成树的邻集。 即次小生成树可以通过由最小生成树换一条 边来得到。
结论
另一个结论: T是某一棵最小生成树,T0是任一棵异于T 的树,则定可通过变换 T0 --> T1 --> T2 --> ... --> Tn (T) 变成最小生成树。 所谓的变换是,每次把Ti中的某条边换成T 中的一条边, 而且树T(i+1)的权小于等于Ti的 权。
还是应当掌握度限制生成树的正规算法
最小度限制生成树的定义
设G=(V,E,ω)是连通的无向图,v0 ∈V是特别 指定的一个顶点 , k为给定的一个正整数。 V0在T中的度为DT(v0)。
如果T是G的一个生成树且DT(v0) =k,则称T 为G的k度限制生成树。G中权值和最小的k 度限制生成树称为G的最小k度限制生成树。
例题2:POJ 1639 Picnic Planning
这是在一个特殊点V0所连边数有限制(不大于K)条件 下求最小生成树的问题。
最土解法: 枚举去掉V0的一些边,使得V0的度变为K 的方案数,对每种方案求一个最小生成树,然后在 所有的最小生成树里再取最小的。 复杂度极高,但是本题数据弱,可以过。
定理:设T是图G的最小k度限制树,E0是G中与v0有关联 的边的集合, E1=E0\E(T), E1即是和V0相连,但是不在T中的边的集合 E2=E(T)\E0, E2即是T中不和V0相连的边的集合 A={(+a,-b)| a∈E1,b∈E2}
设ω(a’)-ω(b’)=min{ω(a)-ω(b)| (+a,-b)∈A},则T + a’-b’是G 的一个最小k+1度限制生成树。
具体实现:从V0开始做一遍广搜即可。 问题:最先求几度的最小度限制生成树呢? 即p从多少开始求?
答案
因为求最小k度限制生成树,当 k < DG(v0) 时,问题并不总是有解的。如图。
V0
所以如果将v0去掉,图会被分成m个连通支, 那么就先求最小m度限制生成树。
如何求最小m度限制生成树
例题3:还是通讯网络
问:怎样合理的分配卫星和铺设线路,使 得在保证每两座村庄之间都可以直接或间 接地通讯的前提下,铺设线路的总长度最 短。? 数据规模:0 <= k <= n <= 500
分析
我们增加一个节点:卫星。卫星到所有节 点的权值都是 0 。 那么,我们要求的仍是一个最小生成树。 只不过卫星最多只能与 k 个节点相连。 也就是说,节点:卫星的度限制为 k 。 这是一个最小度限制生成树的问题!
答案
只需先求最小生成树,d 的最小值即为第 k 长边!
例题2:POJ 1639 Picnic Planning
矮人虽小却喜欢乘坐巨大的轿车,车大到可以装下 无论多少矮人。某天,N(N≤20)个矮人打算到野外 聚餐。为了集中到聚餐地点,矮人A 要么开车到 矮人B 家中,留下自己的轿车在矮人B 家,然后乘 坐B 的轿车同行;要么直接开车到聚餐地点,并 将车停放在聚餐地。虽然矮人的家很大,可以停 放无数量轿车,但是聚餐地点却最多只能停放K 辆轿车。给你一张加权无向图,描述了N 个矮人 的家和聚餐地点,求出所有矮人开车最短总路程。
算法:Kruskal 和 Prim
•
Kruskal:将所有边从小到大加入,在此过程中 判断是否构成回路
– – –
使用数据结构:并查集 时间复杂度:O(ElogE) 适用于稀疏图 使用数据结构:堆 时间复杂度:O(ElogV) 或 O(VlogV+E)(斐波那契堆) 适用于密集图 若不用堆则时间复杂度为O(V2)
删去边的权值越 大,所得到的生 成树的权值和就 越小,因此,需 要找到环上可删 除的权值最大的 边并将其删除。
简单的枚举,时 间复杂度非常高。
应该使用动态 规划!
动态规划
设最小p度限制生成树为T , T是无根树,为 了简便,我们把v0作为该树的根。 定义Father(v)为T中v的父结点,Father(v0) 无意义。 设Best(v)为路径v0->v上与v0无关联且权值 最大的边。
最小生成树(MST)问题
by yzc
图的生成树
在一个连通图G中,如果取它的全部顶点和 一部分边构成一个子图G’,即: V(G’)=V(G);E(G’) ∈E(G) 若边集E(G’)中的边既将图中的所有顶点连 通又不形成回路,则称子图G’是原图G的一 棵生成树。 一棵含有n个点的生成树,必含有n-1条边。
例题4:POJ1679 The Unique MST
题目:要求判断给定图的最小生成树是否唯一
解:显然,这是一个求次小生成树的问题, 如果求出来的次小生成树权值和与最小生 成树相同,则不唯一
次小生成树的定义
设G=(V , E , ω)是连通的无向图,T是图G的 一个最小生成树。如果有另一棵树T1,满 足不存在树T’ , T’ ≠ T , ω(T’)<ω(T1) , 则称T1是图G的次小生成树。
最小生成树
对于一个连通网(连通带权图,假定每条 边上的权均为大于零的实数)来说,每棵 树的权(即树中所有边的权值总和)也可 能不同 具有权最小的生成树称为最小生成树。
最小生成树
生成树
无向连通图的边的集合 无回路 连接所有的点 所有边的权值之和最小
最小
Prim算法
假设G=(V,E)是一个具有n个顶点的连通网, T=(U,TE)是G的最小生成树,U,TE初值均为空集。
1)我们可以先删去v0,对各个连通分量求 最小生成树。
具体实现:枚举每个顶点作为起点执行Prim算 法,执行的过程中对同一连通支的顶点用相同 数字标记。
2)再在每个连通分量中找最小边和v0相连。 3)得到最小m度限制生成树。
时间复杂度分析
求最小m度生成树:O(VlogV+E);
最多k次从p度到p+1度的递推:k*O(V);
图例
关键问题
每次如何从连接T中和T外顶点的所有边中,找 到一条最短的 1) 如果用邻接矩阵存放图,而且选取最短边的 时候遍历所有边进行选取,则时间复杂度为 O(V2), V 为顶点个数 2)用邻接表存放图,并使用堆来选取最短边,则 时间复杂度为O(ElogV) 不加堆的Prim 算法适用于密集图,加堆的适用 于稀疏图
首先从V中任取一个顶点(假定取v1),将它并入 U中,此时U={v1},然后只要U是V的真子集(U∈V), 就从那些一个端点已在T中,另一个端点仍在T外 的所有边中,找一条最短边,设为(vi,vj),其中 vi∈U,vj ∈V-U,并把该边(vi, vj)和顶点vj分别并入T 的边集TE和顶点集U,如此进行下去,每次往生成 树里并入一个顶点和一条边,直到n-1次后得到最 小生成树。
证:设最小生成树有n条边,任意两棵最小生成树分别称为A, B, 如果e是一条边,用w(e)表示该边 的权值。 A的边按权值递增排序后为a1, a2,……an w(a1)≤w(a2)≤……w(an) B的边按权值递增排序后为b1, b2,……bn w(b1)≤w(b2)≤……w(bn) 设i是两个边列表中,第一次出现不同边的位置,ai≠bi 不妨设w(ai)≥w(bi) 情形1 如果树A中包含边bi,则一定有j>i使得 bi=aj ,事实上,这时有 w(bi)=w(aj)≥w(ai) ≥w(bi) 故 w(bi)=w(aj)=w(ai),在树A的边列表中交换边ai和 aj的位置并不会影响树A的边权有序 列表,两棵树在第i个位置的边变成同一条边。 情形2 树A中并不包含边bi,则把bi加到树A上,形成一个圈,由于A是最小生成树,这个圈里任意 一条边的权值都不大于w(bi) ,另外,这个圈里存在边aj不在树B中。因此,有w(aj)≤w(bi),且 j>i (因为aj不在B中)。于是,有w(bi)≤w(ai)≤w(aj)≤w(bi),因此 w(ai)= w(aj) = w(bi)。那么在树A中把aj换成bi仍然保持它是一棵最小生成树,并不会影响树A的 边权有序列表,并且转换成情形1。
