2019-2020年高三上学期数学一轮复习教案:第1讲 集合
1高三数学第一轮复习——集合课案

( 3)表示一个集合可用列举法、描述法、图示法。
列举法:把集合中的元素一一列举出来,写在大括号内;例如:
A={ a1, a2,…… }. 。
描述法:把集合中的元素的公共属性描述出来,写在大括号
内。具体方法:在大括号内先写上表
示这个集合元素的一般符号及取值(或变化)范围,再画一条竖线,在竖线后写出这个集合中元素所具有
A . {2} B. {3} C. { - 3, 2}
D. { - 2, 3}
解析: 易得 B={ -3 , 2} ,故阴影为 A B ={2} 。 答案: A
2. 已知集合 A={y|y 2-(a2+a+1)y+a(a 2+1)>0},B={y|y 2-6y+8 ≤ 0,} 若 A∩ B≠ ,则实数 a 的取值范围为 (
的关系的韦恩( Venn)图如图 1 所示,则阴影部分所示的集合的元素共有
(
)
A. 3 个
B. 2 个
C. 1 个
解析: 由 M { x 2 x 1 2} 得 1 x 3 ,则 M
D. 无穷多个
N 1,3 ,有 2 个。 答案: B
题型 2:集合的性质
例 2. (2009 山东卷理 )集合 A 0,2, a , B 1,a2 ,若 A B 0,1,2,4,16 ,则 a 的值为 ( )
3.全集与补集:
( 1)全集:包含了我们所要研究的各个集合的全部元素的集合称为全集,记作
U;
( 2)补集:若 S 是一个集合, A S,则, CS = { x | x S且x A} 称为 S 中子集 A 的补集;
-1-
( 3)简单性质:
1) CS ( CS )=A;
高三数学一轮复习精品教案2:1.1集合教学设计

第一节集合1.集合的基本概念(1)集合中元素的三个特性:确定性、互异性、无序性.(2)元素与集合的关系:属于或不属于,表示符号分别为∈和∉.(3)集合的三种表示方法:列举法、描述法、V enn图法.2.集合间的基本关系(1)子集:若对∀x∈A,都有x∈B,则A⊆B或B⊇A.(2)真子集:若A⊆B,但∃x∈B,且x∉A,则A B或B A.(3)相等:若A⊆B,且B⊆A,则A=B.(4)空集的性质:∅是任何集合的子集,是任何非空集合的真子集.3.集合的基本运算续表1.(人教A版教材习题改编)若集合M={x∈N|x≤10},a=22,则下面结论中正确的是()A.{a}⊆M B.a⊆MC.{a}∈M D.a∉M『解析』∵M={x∈N|x≤10}={0,1,2,3},∴a∉M.『答案』 D2.(2013·慈溪模拟)设集合M={x|x<2 013},N={x|0<x≤2 013},则M∪N=() A.M B.NC.{x|x≤2 013} D.{x|0<x<2 012}『解析』M∪N={x|x≤2 013}.『答案』 C3.(2012·广东高考)设集合U={1,2,3,4,5,6},M={1,2,4},则∁U M=() A.U B.{1,3,5}C.{3,5,6} D.{2,4,6}『解析』∵U={1,2,3,4,5,6},M={1,2,4},∴∁U M={3,5,6}.『答案』 C4.若P={x|x<1},Q={x|x>-1},则()A.P⊆Q B.Q⊆PC.∁R P⊆Q D.Q⊆∁R P『解析』∵P={x|x<1},∴∁R P={x|x≥1},因此∁R P⊆Q.『答案』 C5.若集合A={x|x<1},B={x|x≥a},且A∩B≠∅,则实数a的取值范围为() A.{a|a≤1} B.{a|a<1}C.{a|a≥1} D.{a|a>1}『解析』∵A∩B≠∅,∴a<1,故选B.『答案』 B(1)(2013·洛阳模拟)设P 、Q 为两个非空实数集合,定义集合P +Q ={a +b |a ∈P ,b ∈Q },若P ={0,2,5},Q ={1,2,6},则P +Q 中元素的个数为( )A .9B .8C .7D .6(2)(2013·连云港模拟)已知集合A ={m +2,2m 2+m ,-3},若3∈A ,则m 的值为________.『思路点拨』 (1)先确定a 值,再确定b 值,注意元素的互异性. (2)根据元素与集合的关系知,m +2=3或2m 2+m =3,注意元素的互异性. 『尝试解答』 (1)当a =0,b =1,2,6时,P +Q ={1,2,6}; 当a =2,b =1,2,6时,P +Q ={3,4,8}; 当a =5,b =1,2,6时,P +Q ={6,7,11}.∴当P ={0,2,5},Q ={1,2,6}时,P +Q ={1,2,3,4,6,7,8,11}. 故集合P +Q 有8个元素.(2)∵3∈A ,∴m +2=3或2m 2+m =3,解得m =1或m =-32.当m =1时,m +2=2m 2+m =3,不满足集合元素的互异性,当m =-32时,A ={-3,12,3}满足题意.故m =-32. 『答案』 (1)B (2)-32,1.解答本题(1)时,若不按分类讨论计算,易漏掉元素,对于本题(2)易忽视元素的互异性而得到错误答案.2.用描述法表示集合,首先要弄清集合中代表元素的含义,再看元素的限制条件,明确集合类型,是数集、点集还是其它的集合.3.对于含有字母的集合,在求出字母的值后,要注意检验集合的元素是否满足互异性.(1)若定义:A *B ={z |z =xy ,x ∈A ,y ∈B }.设A ={1,2},B ={0,2},则集合A *B 的所有元素之和为( )A .0B .2C .3D .6(2)已知集合A ={x |ax 2-3x +2=0},若A =∅,则实数a 的取值范围为________. 『解析』 (1)∵A *B ={z |z =xy ,x ∈A ,y ∈B }, 又A ={1,2},B ={0,2},∴A *B ={0,2,4},其所有元素之和为6,故选D. (2)∵A =∅,∴方程ax 2-3x +2=0无实根, 当a =0时,x =23不合题意,当a ≠0时,Δ=9-8a <0,∴a >98.『答案』 (1)D (2)(98,+∞)(1)已知a ∈R ,b ∈R ,若{a ,ba ,1}={a 2,a +b ,0},则a 2 013+b 2 013=________.(2)已知集合A ={x |x 2-3x -10≤0},B ={x |m +1≤x ≤2m -1},若A ∪B =A ,则实数m 的取值范围是________.『思路点拨』 (1)0∈{a ,ba ,1},则b =0,1∈{a 2,a ,0},则a 2=1,a ≠1,从而a ,b 可求.(2)A ∪B =A ⇒B ⊆A ,分B =∅和B ≠∅两种情况求解. 『尝试解答』 (1)由已知得ba=0及a ≠0,所以b =0,于是a 2=1,即a =1或a =-1.又根据集合中元素的互异性可知a =1应舍去,因此a =-1,故a 2 013+b 2 013=(-1)2 013=-1.(2)A ={x |x 2-3x -10≤0}={x |-2≤x ≤5}, 又A ∪B =A ,所以B ⊆A .①若B =∅,则2m -1<m +1,此时m <2. ②若B ≠∅,则⎩⎪⎨⎪⎧2m -1≥m +1,m +1≥-2,2m -1≤5.解得2≤m ≤3.由①、②可得,符合题意的实数m 的取值范围为m ≤3. 『答案』 (1)-1 (2)(-∞,3』,1.解答本题(2)时应注意两点:一是A ∪B =A ⇒B ⊆A ;二是B ⊆A 时,应分B =∅和B ≠∅两种情况讨论.2.集合A 中元素的个数记为n ,则它的子集的个数为2n ,真子集的个数为2n -1,非空真子集的个数为2n -2.3.已知两集合间的关系求参数时,关键是将两集合间的关系转化为元素或区间端点间的关系,进而转化为参数满足的关系.解决这类问题常常合理利用数轴、V enn 图化抽象为直观.若集合M ={x |x 2+x -6=0},N ={x |ax +2=0,a ∈R },且M ∩N =N ,则实数a 的取值集合是________.『解析』 因为M ∩N =N ,所以N ⊆M . 又M ={-3,2}, 若N =∅,则a =0.若N ≠∅,则N ={-3}或N ={2}.所以-3a +2=0或2a +2=0,解得a =23或a =-1.所以a 的取值集合是{-1,0,23}.『答案』 {-1,0,23}(1)(2012·浙江高考)设集合A ={x |1<x <4},集合B ={x |x 2-2x -3≤0},则A ∩(∁R B )=( )A .(1,4)B .(3,4)C .(1,3)D .(1,2)∪(3,4)(2)(2012·天津高考)已知集合A ={x ∈R ||x +2|<3},集合B ={x ∈R |(x -m )(x -2)<0},且A ∩B =(-1,n ),则m =________,n =________.『思路点拨』 (1)先化简集合B ,求出∁R B ,再借助数轴求A ∩∁R B . (2)根据A ∩B 结构特征求解.『尝试解答』 (1)解x 2-2x -3≤0得-1≤x ≤3, ∴B =『-1,3』,则∁R B =(-∞,-1)∪(3,+∞), ∴A ∩(∁R B )=(3,4).(2)∵A ={x |-5<x <1},B ={x |(x -m )(x -2)<0}, 且A ∩B ={x |-1<x <n },∴m=-1,n=1.『答案』(1)B(2)-11,1.在进行集合的运算时要尽可能地借助Venn图和数轴使抽象问题直观化.一般地,集合元素离散时用Venn图表示;集合元素连续时用数轴表示,用数轴表示时要注意端点值的取舍.2.在解决有关A∩B=∅,A⊆B等集合问题时,往往忽略空集的情况,一定先考虑∅是否成立,以防漏解.3.要注意六个关系式A⊆B、A∩B=A、A∪B=B、∁U A⊇∁U B、A∩(∁U B)=∅、(∁U A)∪B =U的等价性.(2012·辽宁高考)已知全集U={0,1,2,3,4,5,6,7,8,9},集合A ={0,1,3,5,8},集合B={2,4,5,6,8},则(∁U A)∩(∁U B)=() A.{5,8}B.{7,9}C.{0,1,3} D.{2,4,6}『解析』因为∁U A={2,4,6,7,9},∁U B={0,1,3,7,9},所以(∁U A)∩(∁U B)={7,9}.『答案』 B一种方法正如数轴是研究实数的工具,Venn图是研究集合的工具,借助Venn图和数轴即数形结合能使抽象问题直观化,其中运用数轴图示法要特别注意端点是实心还是空心.两个防范1.空集在解题时具有特殊地位,它是任何集合的子集,是任何非空集合的真子集,应时刻关注对空集的讨论,防止漏解.2.在解决含参数的集合问题时,要检验集合中元素的互异性,否则很可能会因为不满足“互异性”而导致结论错误.(见学生用书第3页)从近两年课标区高考试题看,集合间的关系与集合的运算是高考命题的重点,常与函数、方程、不等式等知识结合命题,而以集合为背景的新定义题,则是高考命题的热点.创新探究之一以集合为背景的新定义题(2012·课标全国卷)已知集合A={1,2,3,4,5},B={(x,y)|x∈A,y∈A,x-y∈A},则B中所含元素的个数为()A.3B.6C.8D.10『解析』因为A={1,2,3,4,5},所以集合A中的元素都为正数,若x-y∈A,则必有x-y>0,即x>y.当y=1时,x可取2,3,4,5,共有4个数;当y=2时,x可取3,4,5,共有3个数;当y=3时,x可取4,5,共有2个数;当y=4时,x只能取5,共有1个数;当y=5时,x不能取任何值.综上,满足条件的实数对(x,y)的个数为4+3+2+1=10,即集合B中的元素共有10个,故选D.『答案』 D创新点拨:(1)本题以元素与集合的关系为载体,用附加条件“x∈A,y∈A,x-y∈A”定义以有序实数对(x,y)为元素的集合B,通过对新定义的理解与应用来考查阅读理解能力与知识迁移能力.(2)考查创新意识、化归转化能力,以及分类讨论思想.应对措施:(1)准确理解集合B是解决本题的关键,集合B中的元素是有序实数对(x,y),并且要求x∈A,y∈A,x-y∈A,所以要判断集合B中元素的个数,需要根据x-y是否是集合A中的元素进行判断.(2)为化复杂为简单,以y取何值为标准分类,分别求值.1.(2012·湖北高考)已知集合A={x|x2-3x+2=0,x∈R},B={x|0<x<5,x∈N},则满足条件A⊆C⊆B的集合C的个数为()A.1B.2C.3D.4『解析』由x2-3x+2=0得x=1或x=2,∴A={1,2}.由题意知B={1,2,3,4},∴满足条件的C可为{1,2},{1,2,3},{1,2,4},{1,2,3,4}.『答案』 D2.(2012·山东高考)已知全集U={0,1,2,3,4},集合A={1,2,3},B={2,4},则(∁U A)∪B为()A.{1,2,4} B.{2,3,4}C.{0,2,4} D.{0,2,3,4}『解析』∵∁U A={0,4},B={2,4},∴(∁U A)∪B={0,2,4}.『答案』 C。
2019-2020学年高考数学一轮复习 1.1集合教案.doc

2019-2020学年高考数学一轮复习 1.1集合教案教学目标:知识与技能:了解集合的含义,元素与集合的属于关系,理解集合之间的包含与相等关系,理解子集与补集的关系。
过程与方法:会求两个集合的交,并,补集,能使用韦恩图表达集合的关系及运算。
情感、态度与价值观:教学过程中,要让学生充分体验集合的具体应用,应用集合解决实际问题的方法。
教学重点:集合的交,并,补关系及运算教学难点:使用韦恩图表达集合的关系及运算教 具:多媒体、实物投影仪教学过程:一、复习引入:1.集合的含义与表示方法2.集合间的基本关系3.集合的基本运算二、例题讲解例1判断下面结论是否正确(请在括号中打“√”或“×”).(1)已知集合A={x|y=x2},B={y|y=x2},C={(x,y)|y=x2},则A=B=C.( )(2)含有n 个元素的集合的子集个数是2n ,真子集个数是2n-1,非空真子集的个数是2n-2.( )(3)A ∩B= 的充要条件是A=B= .( )(4)A ∩B=A ⇔A ⊆B.( )(5)A ∪B=A ⇔B ⊆A.( )(6) (A ∪B)=( A)∩( B).( )【解析】(1)错误.集合A 是函数y=x2的定义域,即A=(-∞,+∞);集合B 是函数y=x2的值域,即B=[0,+∞);集合C 是满足方程y=x2的实数x,y 的集合,也可以看作是函数y=x2图象上的点组成的集合,因此这三个集合互不相等.(2)正确.空集的子集个数为1个,即 ;含有1个元素的集合{a1}的子集个数为2个,即 ,{a1};含有2个元素的集合{a1,a2}的子集个数为4个,即 ,{a1},{a2},{a1,a2}……归纳可得含有n 个元素的集合的子集个数为2n 个,故其真子集个数是2n-1,非空真子集的个数是2n-2.(3)错误.A ∩B= 时,只要集合A,B 没有公共元素即可,不一定是A=B= .(4)正确.当A ⊆B 时,显然A ∩B=A ;当A ∩B=A 时,对任意x ∈A ,得x ∈A ∩B ,得x ∈B ,即x ∈A ⇒x ∈B ,故A ⊆B .(5)正确.当B ⊆A 时,显然A ∪B=A ;当A ∪B=A 时,对任意x ∈B ,则x ∈A ∪B , ∅∅得x∈A,即x∈B⇒x∈A,即B⊆A.(6)正确.设x∈ (A∪B),则x (A∪B),得x A且x B,即x∈ A且x∈ B,即x∈( A)∩( B),即 (A∪B)⊆( A)∩( B);反之,当x∈( A)∩( B)时,得x∈ A且x∈ B得x A且x B,得x (A∪B),得x∈ (A∪B),即 (A∪B) ( A)∩( B).根据集合相等的定义得 (A∪B)=( A)∩( B).答案:(1)× (2)√ (3)× (4)√ (5)√ (6)√考向 1 集合的基本概念【典例1】(1)(2012·新课标全国卷)已知集合A={1,2,3,4,5}, B={(x,y)|x∈A,y∈A,x-y ∈A},则B中所含元素的个数为( )(A)3 (B)6 (C)8 (D)10(2)已知A={a+2,(a+1)2,a2+3a+3},若1∈A,则实数a构成的集合B的元素个数是( )(A)0 (B)1 (C)2 (D)3【思路点拨】(1)集合B中的元素是满足x∈A,y∈A,x-y∈A的有序实数对,根据要求分类列举求解.(2)据1∈A逐个讨论求解a值,根据集合元素的互异性得集合B中元素的个数.【规范解答】(1)选D.方法:x=2时,y=1,x-y=1,此时(x,y)=(2,1),此时(x,y)有1个;x=3时,y=1,2,此时x-y=2,1,(x,y)有2个;x=4时,y=1,2,3,此时x-y=3,2,1,(x,y)有3个;x=5时,y=1,2,3,4,此时x-y=4,3,2,1,(x,y)有4个.所以集合B中的元素个数为1+2+3+4=10.(2)选B.若a+2=1,则a=-1,代入集合A,得A={1,0,1},与集合元素的互异性矛盾;若(a+1)2=1,得a=0或-2,代入集合A,得A={2,1,3}或A={0,1,1},后者与集合元素的互异性矛盾,故a=0符合要求;若a2+3a+3=1,则a=-1或-2,代入集合A,得A={1,0,1}或A={0,1,1},都与集合元素的互异性相矛盾.综上可知,只有a=0符合要求,故集合B中只有一个元素.【互动探究】在本例(1)的集合B中如果去掉x-y∈A的限制条件,其他条件均不变,则集合B中含有的元素个数是多少?【解析】当x=1时,y=1,2,3,4,5,同理当x=2,3,4,5时,y=1,2,3,4,5,所以集合B中含有5×5=25个元素【变式训练】定义集合运算:A*B={z|z=xy,x∈A,y∈B}.设A={1,2},B={0,2},则集合A*B的所有元素之和为( )(A)0 (B)2 (C)3 (D)6【解析】选D.根据指定的法则,集合A*B中的元素是A,B中的元素的乘积,根据集合元素的性质,得A*B={0,2,4},故集合A*B中所有元素之和为6.考向 2 集合间的基本关系【典例2】(1)(2014·三明模拟)已知集合A={x|x2-3x+2=0,x∈R},B={x|0<x<5,x∈N},则满足条件A⊆C⊆B的集合C的个数为 ( )(A)1 (B)2 (C)3 (D)4(2)若集合A={1,a,b},B={a,a2,ab},且A ∪B=A ∩B,则实数a 的取值集合是 .【思路点拨】(1)求出A,B 中的元素,由A ⊆C ⊆B,知集合C 的个数由B 中有A 中没有的元素个数决定.(2)A ∪B=A ∩B ⇔A=B ,得出关于a,b 的方程组,解出a,b ,再根据集合元素的性质加以检验得出结论.【规范解答】(1)选D.A={x|x2-3x+2=0,x ∈R}={1,2},B={x|0<x<5,x ∈N}={1,2,3,4},由A ⊆C ⊆B,方法一:则C 中含有除1,2之外的3,4两元素中的0个、1个、2个,即C 的个数可以看作是集合{3,4}的子集的个数,有22=4个.方法二:则C 可能为{1,2},{1,2,3},{1,2,4},{1,2,3,4}共4个(2)方法一:因为A ∪B=A ∩B,所以A=B ,所以{1,b}={a2,ab}, 所以 解得 反代回A,B 集合知,只有 适合, 所以 即实数a 的取值集合是{-1}.【变式训练】(1)已知M={x|x-a=0},N={x|ax-1=0},若M ∩N=N ,则实数a 的值为( )(A)1 (B)-1 (C)1或-1 (D)0或1或-1【解析】选D .M ∩N=N ⇔N ⊆M .当a=0时,N= ,符合要求, 当a ≠0时,只要 即a=±1即可.(2)设集合A={x,y,x+y},B={0,x2,xy},若A=B ,则实数对(x,y)的取值集合是_________.【解析】由A=B ,且0∈B ,故集合B 中的元素x2≠0,xy ≠0,故x ≠0,y ≠0,那么只能是集合A 中的x+y=0,此时就是在条件x+y=0下,{x,y}={x2,xy}, 答案:{(1,-1),(-1,1)}考向 3 集合的基本运算【典例3】(1)(2012·福建高考)已知集合M={1,2,3,4},N={-2,2},下列结论成立的是( )(A)N ⊆M (B)M ∪N=M (C)M ∩N=N (D)M ∩N={2} 221ab,1a b ab b a =⎧⎧=⎨⎨==⎩⎩,或,a 1a 1a 1,b 0b R b 1.=-==⎧⎧⎧⎨⎨⎨=∈=⎩⎩⎩,,或或a 1b 0=-⎧⎨=⎩,a 1b 0.=-⎧⎨=⎩,∅1a a =,22x y 0,x y 0,x x,x y,xy y xy x.+=+=⎧⎧⎪⎪==⎨⎨⎪⎪==⎩⎩即或,x 1,x 1,y 1y 1.==-⎧⎧⎨⎨=-=⎩⎩解得或,(2)(2012·辽宁高考)已知全集U={0,1,2,3,4,5,6,7,8,9},集合A={0,1,3,5,8},集合B={2,4,5,6,8},则( A)∩( B)为( )(A){5,8} (B){7,9} (C){0,1,3} (D){2,4,6}【思路点拨】(1)根据集合M,N中元素的特点逐一验证.(2)可以根据补集定义求出 A, B,再根据交集定义得出结论,还可以利用Venn图解决.【规范解答】(1)选D.显然M∩N={2}. (2)选B.方法:集合( A)∩( B)= (A∪B)={7,9}.如图所示:【拓展提升】小结:集合的运算律(1)交换律:A∪B=B∪A,A∩B=B∩A.(2)结合律:(A∪B)∪C=A∪(B∪C);(A∩B)∩C=A∩(B∩C).(3)分配律:A∩(B∪C)=(A∩B)∪(A∩C);A∪(B∩C)=(A∪B)∩(A∪C).【变式训练】(1)已知集合M={y|y=2x},集合N={x|y=lg(2x-x2)},则M∩N=( )(A)(0,2) (B)(2,+∞)(C)[0,+∞] (D)(-∞,0)∪(2,+∞)【解析】选A. 集合M为函数y=2x的值域,即M=(0,+∞),集合N是函数y=lg(2x-x2)的定义域,由不等式2x-x2>0,解得N=(0,2),所以M∩N=(0,2).三,布置作业思考辨析,考点自测,知能巩固。
(新人教)高三数学第一轮复习教案1.1.1集合(1)

一.课题:集合(1)二.教学目标:1.理解集合的概念和性质.2.了解元素与集合的表示方法.3.熟记有关数集.4.培养学生认识事物的能力三.教学重、难点:集合概念、性质.四.教学过程:(一)复习:回顾初中代数中涉及“集合”提法(二)新课讲解:1.定义:一般地,某些指定的对象集在一起就成为一个集合(集).进一步指出:集合中每个对象叫做这个集合的元素.由此上述例中集合的元素是什么?(例(1)的元素为1、3、5、7,例(2)的元素为到两定点距离等于两定点间距离的点,例(3)的元素为满足不等式323x x +>+的实数x ,例(4)的元素为所有直角三角形,例(5)为高一·三班全体男同学.)请同学们另外举出三个例子,并指出其元素.一般用大括号表示集合,则上几例可表示为……由以上四个问题可知,集合元素具有三个特征:(1)确定性;(2)互异性;(3)无序性.元素与集合的关系有“属于∈”及“不属于∉( ∉ 也可表示为 )两种.请同学们熟记上述符号及其意义.∈请同学回答:已知a b c m ++=,2{|}A x ax bx c m =++=,判断1与A 的关系. [1A ∈]五.课堂练习:课本P 5,练习1、2补充练习:若23{1,3,1}m m m -∈-+,求m 。
[1m =-或2]m =-六.小结:1.集合的概念2.集合元素的三个特征:其中“集合中的元素必须是确定的”应理解为:对于一个给定的集合,它的元素的意义是明确的.“集合中的元素必须是互异的”应理解为:对于给定的集合,它的任何两个元素都是不同的.3.常见数集的专用符号.七.课后作业:课本P 7,习题1.1 第1题.。
2019-2020年高考数学一轮总复习-1.1-集合及其运算教案-理-新人教A版
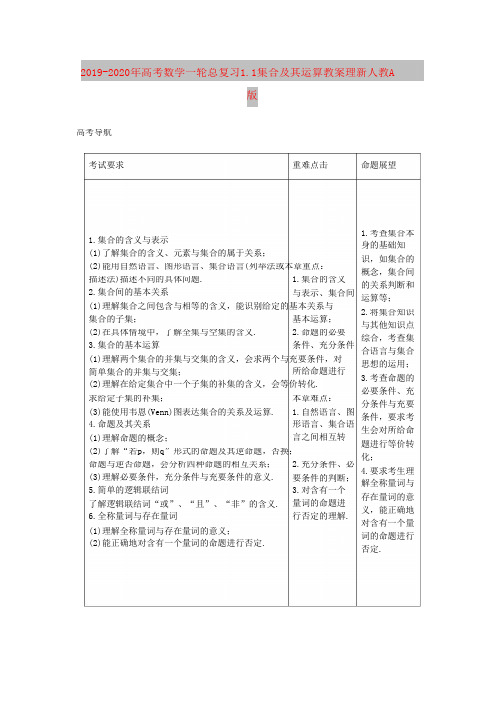
2019-2020年高考数学一轮总复习1.1集合及其运算教案理新人教A版高考导航考试要求 重难点击 命题展望1.考查集合本 身的基础知 识,如集合的 概念,集合间 的关系判断和 运算等; 1.集合的含义与表示 (1)了解集合的含义、元素与集合的属于关系; (2)能用自然语言、图形语言、集合语言(列举法或本章重点: 描述法)描述不同的具体问题.2.集合间的基本关系 1.集合的含义 与表示、集合间 (1)理解集合之间包含与相等的含义,能识别给定的基本关系与 2.将集合知识 与其他知识点 综合,考查集 合语言与集合 思想的运用;3.考查命题的 必要条件、充 分条件与充要 条件,要求考 生会对所给命 题进行等价转 化; 集合的子集; 基本运算; (2)在具体情境中,了解全集与空集的含义. 3.集合的基本运算 2.命题的必要 条件、充分条件 (1)理解两个集合的并集与交集的含义,会求两个与充要条件,对 所给命题进行 (2)理解在给定集合中一个子集的补集的含义,会等价转化. 简单集合的并集与交集; 求给定子集的补集; 本章难点: (3)能使用韦恩(Venn)图表达集合的关系及运算.4.命题及其关系 1.自然语言、图 形语言、集合语 言之间相互转 (1)理解命题的概念; (2)了解“若p ,则q”形式的命题及其逆命题,否换; 命题与逆否命题,会分析四种命题的相互关系; (3)理解必要条件,充分条件与充要条件的意义.5.简单的逻辑联结词 2.充分条件、必 4.要求考生理 解全称量词与 存在量词的意 义,能正确地 对含有一个量 词的命题进行 否定.要条件的判断; 3.对含有一个 量词的命题进 行否定的理解. 了解逻辑联结词“或”、“且”、“非”的含义. 6.全称量词与存在量词 (1)理解全称量词与存在量词的意义; (2)能正确地对含有一个量词的命题进行否定.知识网络1.1集合及其运算典例精析题型一集合中元素的性质【例1】设集合A={a+1,a-3,2a-1,a2+1},若-3∈A,求实数a的值.【解析】令a+1=-3⇒a=-4,检验合格;令a-3=-3⇒a=0,此时a+1=a2+1,舍去;令2a-1=-3⇒a=-1,检验合格;而a2+1≠-3;故所求a的值为-1或-4.【点拨】此题重在考查元素的确定性和互异性.首先确定-3是集合A的元素,但A中四个元素全是未知的,所以需要讨论;而当每一种情况求出a的值以后,又需要由元素的互异性检验a是否符合要求.b【变式训练1】若a、b∈R,集合{1,a+b,a}={0,,b},求a和b的值.ab【解析】由{1,a+b,a}={0,,b},aa b 0,a b 0,b b1, a,aa得① ba 或② b1 显然①无解;由②得a=-1,b=1.题型二集合的基本运算【例2】已知A={x|x2-8x+15=0},B={x|ax-1=0},若B⊆A,求实数a.1 【解析】由已知得A={3,5}.当a=0时,B=∅⊆A;当a≠0时,B={}.a1 1 11要使B⊆A,则=3或=5,即a=或.35a a11综上,a=0或或.35【点拨】对方程ax=1,两边除以x的系数a,能不能除,导致B是否为空集,是本题分类讨论的根源.【变式训练2】(xx江西模拟)若集合A={x||x|≤1,x∈R},B={y|y=x2,x∈R},则A∩B 等于( )A.{x|-1≤x≤1} C.{x|0≤x≤1}B.{x|x≥0} D.【解析】选C.A=[-1,1],B=[0,+∞),所以A∩B=[0,1].题型三集合语言的运用【例3】已知集合A=[2,log2t],集合B={x|x2-14x+24≤0},x,t∈R,且A⊆B.(1)对于区间[a,b],定义此区间的“长度”为b-a,若A的区间“长度”为3,试求t的值;(2)某个函数f(x)的值域是B,且f(x)∈A的概率不小于0.6,试确定t的取值范围.【解析】(1)因为A的区间“长度”为3,所以log2t-2=3,即log2t=5,所以t=32. (2)由x2-14x+24≤0,得2≤x≤12,所以B=[2,12],所以B的区间“长度”为10.设A的区间“长度”为y,因为f(x)∈A的概率不小于0.6,所以y≥0.6,所以y≥6,即log2t-2≥6,解得t≥28=256.10又A⊆B,所以log2t≤12,即t≤212=4096,所以t的取值范围为[256,4096](或[28,212]).2【变式训练3】设全集U是实数集R,M={x|x2>4},N={x| ≥1},则图中阴影部分所x-1表示的集合是(A.{x|-2≤x<1}B.{x|-2≤x≤2}C.{x|1<x≤2}D.{x|x<2})【解析】选C.化简得M={x<-2或x>2},N={x|1<x≤3},故图中阴影部分为∁RM∩N={x|1<x≤2}.总结提高1.元素与集合及集合与集合之间的关系对于符号∈,∉和⊆,⊈的使用,实质上就是准确把握两者之间是元素与集合,还是集合与集合的关系.2.“数形结合”思想在集合运算中的运用认清集合的本质特征,准确地转化为图形关系,是解决集合运算中的重要数学思想. (1)要牢固掌握两个重要工具:韦恩图和数轴,连续取值的数集运算,一般借助数轴处理,而列举法表示的有限集合则侧重于用韦恩图处理.(2)学会将集合语言转化为代数、几何语言,借助函数图象及方程的曲线将问题形象化、直观化,以便于问题的解决.3.处理集合之间的关系时,是一个不可忽视、但又容易遗漏的内容,如A⊆B,A∩B=A,A ∪B=B等条件中,集合A可以是空集,也可以是非空集合,通常必须分类讨论.2019-2020年高考数学一轮总复习1.3简易逻辑联结词、全称量词与存在量词教案理新人教A版典例精析题型一全称命题和特称命题的真假判断【例1】判断下列命题的真假.1(1)∀x∈R,都有x2-x+1>;2(2)∃α,β使cos(α-β)=cosα-cosβ;(3)∀x,y∈N,都有x-y∈N;(4)∃x0,y0∈Z,使得2x0+y0=3.1 331【解析】(1)真命题,因为x2-x+1=(x-)2+≥>.4422π(2)真命题,例如α=π,β=,符合题意.4 2(3)假命题,例如x=1,y=5,但x-y=-4∉N.(4)真命题,例如x0=0,y0=3,符合题意.【点拨】全称命题是真命题,必须确定对集合中的每一个元素都成立,若是假命题,举反例即可;特称命题是真命题,只要在限定集合中,至少找到一个元素使得命题成立.【变式训练1】已知命题p:∃x∈R,使tanx=1,命题q:∀x∈R,x2>0.则下面结论正确的是( )A.命题“p∧q”是真命题C.命题“p∨q”是真命题B.命题“p∧q”是假命题D.命题“p∧q”是假命题π【解析】选D.先判断命题p和q的真假,再逐个判断.容易知命题p是真命题,如x=,p4 是假命题;因为当x=0时,x2=0,所以命题q是假命题,q是真命题.所以“p∧q”是假命题,A错误;“p∧q”是真命题,B错误;“p∨q”是假命题,C错误;“p∧q”是假命题,D正确.题型二含有一个量词的命题的否定【例2】写出下列命题的否定,并判断其真假.1(1)p:∀x∈R,x2-x+≥0;4(2)q:所有的正方形都是矩形;(3)r:∃x∈R,x2+2x+2≤0;(4)s:至少有一个实数x,使x3+1=0.1【解析】(1)p:∃x∈R,x2-x+<0,是假命题.4(2)q:至少存在一个正方形不是矩形,是假命题.(3)r:∀x∈R,x2+2x+2>0,是真命题.(4)s:∀x∈R,x3+1≠0,是假命题.【点拨】含有一个量词的命题否定中,全称命题的否定是特称命题,而特称命题的否定是全 称命题,一般命题的否定则是直接否定结论即可.【变式训练2】已知命题p :∀x∈(1,+∞),log3x >0,则p 为【解析】∃x0∈(1,+∞),log3x0≤0.题型三命题的真假运用 .【例3】若r(x):sinx +cosx >m ,s(x):x2+mx +1>0,如果“对任意的x∈R,r(x)为 假命题”且“对任意的x∈R,s(x)为真命题”,求实数m 的取值范围.π 【解析】因为由m <sinx +cosx =2sin(x +)恒成立,得m <-2; 4而由x2+mx +1>0恒成立,得m2-4<0,即-2<m <2.依题意,r(x)为假命题且s(x)为真命题,所以有m≥-2且-2<m <2,故所求m 的取值范围为-2≤m<2.【点拨】先将满足命题p 、q 的m 的取值集合A 、B 分别求出,然后由r(x)为假命题(取A 的 补集),s(x)为真命题同时成立(取交集)即得.【变式训练3】(xx 广东模拟)设M 是由满足下列性质的函数f(x)构成的集合:在定义域内1 存在x0,使得f(x0+1)=f(x0)+f(1)成立.已知下列函数:①f(x)=;②f(x)=2x ;③f(x) x=lg(x2+2);④f(x)=cos πx ,其中属于集合M 的函数是 (写出所有满足要求的函 数的序号).1 =1+1,显然无实数解; 【解析】②④.对于①,方程 x +1x对于②,由方程2x +1=2x +2,解得x =1;对于③,方程lg[(x +1)2+2]=lg(x2+2)+lg3,显然也无实数解;对于④,方程cos[π(x +1)]=cos πx +cos π,1 即cos πx =,显然存在x 使等式成立.故填②④. 2总结提高1.同一个全称命题,特称命题,由于自然语言的不同,可能有不同的表述方法,在实际应用 中可以灵活选择.2.命题的否定,一定要注意与否命题的区别:全称命题的否定,先要将它变成特称命题,然 后将结论加以否定;反过来,对特称命题的否定,先将它变成全称命题,然后对结论加以否 定.而命题的否命题,则是将原命题中的条件否定当条件,结论否定当结论构成一个新的, 即否命题.。
高三数学一轮复习教学案集合

高三数学一轮复习教学案集合第1课时:集合的概念一、集合集合是一个原始概念,描述性定义为:某些指定的对象就成为一个集合,简称“集”。
集合中的每一个对象叫做这个集合的“元素”。
二、元素与集合的关系元素与集合是属于和从属关系,若a是集合A的元素,记作a∈A,若a不是集合B的元素,记作a∉B。
但是要注意元素与集合是相对而言的。
三、集合与集合的关系集合与集合的关系用符号表示:子集:若集合A中的所有元素都是集合B的元素,就说集合A包含于集合B(或集合B包含集合A),记作A⊆B。
相等:若集合A中的所有元素都是集合B的元素,同时集合B中的所有元素都是集合A的元素,就说集合A等于集合B,记作A=B。
真子集:若A是B的子集,但A不等于B,则说A是B 的真子集,记作A⊂B。
子集数量:若集合A含有n个元素,则A的子集有2^n 个,真子集有2^n-1个,非空真子集有2^n-1个。
四、集合的表示法集合的表示法常用的有列举法、描述法和韦恩图法三种。
有限集常用列举法,无限集常用描述法,图示法常用于表示集合之间的相互关系。
根据考试大纲的要求,结合2009年高考的命题情况,我们可以预测2010年集合部分在选择、填空和解答题中都有涉及。
高考命题热点有以下两个方面:一是集合的运算、集合的有关述语和符号、集合的简单应用等作基础性的考查,题型多以选择、填空题的形式出现;二是以函数、方程、三角、不等式等知识为载体,以集合的语言和符号为表现形式,结合简易逻辑知识考查学生的数学思想、数学方法和数学能力,题型常以解答题的形式出现。
空集 $\varnothing$ 是一个特殊而又重要的集合,它不含任何元素。
空集是任何集合的子集,也是任何非空集合的真子集。
在解题时,不能忽视空集的存在。
典型例题:例1.已知集合 $A=\{x\in \mathbb{N}|6-x$ 是 $8$ 的正约数$\}$,试求集合 $A$ 的所有子集。
解:由题意可知 $6-x$ 是 $8$ 的正约数,所以 $6-x$ 可以是$1,2,4,8$,相应的$x$ 为$2,4,5$,即$A=\{2,4,5\}$。
2020版高考数学一轮复习第一章集合与简易逻辑第1讲集合及其运算教案理(含解析)新人教A版

第1讲集合及其运算基础知识整合1.集合与元素02互异性、□03无序性.(1)集合中元素的三个特征:□01确定性、□07∉表示.(2)元素与集合的关系是□04属于或□05不属于两种,用符号□06∈或□09描述法、□10图示法.(3)集合的表示法:□08列举法、□(4)常见数集的记法2.集合间的基本关系3.集合的基本运算1.若有限集A中有n个元素,则集合A的子集个数为2n,真子集的个数为2n-1,非空真子集的个数为2n-2.2.A⊆B⇔A∩B=A⇔A∪B=B.3.A∩(∁U A)=∅;A∪(∁U A)=U;∁U(∁U A)=A.1.(2019·镇海中学模拟)设集合A={y|y=x2-1},B={x|y=x2-1},则下列结论正确的是( )A.A=B B.A⊆BC.B⊆A D.A∩B={x|x≥1}答案 D解析∵A={y|y=x2-1}={y|y≥0},B={x|y=x2-1}={x|x≥1或x≤-1},∴A∩B={x|x≥1},故选D.2.(2018·全国卷Ⅱ)已知集合A={(x,y)|x2+y2≤3,x∈Z,y∈Z},则A中元素的个数为( )A.9 B.8C.5 D.4答案 A解析∵x2+y2≤3,∴x2≤3.∵x∈Z,∴x=-1,0,1.当x=-1时,y=-1,0,1;当x=0时,y=-1,0,1;当x=1时,y=-1,0,1,综上,A中元素共有9个,故选A.3.(2018·天津高考)设全集为R,集合A={x|0<x<2},B={x|x≥1},则A∩(∁R B)=( )A.{x|0<x≤1}B.{x|0<x<1}C.{x|1≤x<2} D.{x|0<x<2}答案 B解析∵∁R B={x|x<1},∴A∩(∁R B)={x|0<x<1},故选B.4.(2019·兰州诊断)已知集合A ={x |x 2>9},B ={x |2x>1},则A ∪B =( ) A .{x |x <-3} B .{x |-3<x <3} C .{x |x >0} D .{x |x <-3或x >0}答案 D解析 由x 2>9,得x >3或x <-3,A ={x |x >3或x <-3}.又由2x>1,解得x >0,所以B ={x |x >0}.所以A ∪B ={x |x <-3或x >0}.故选D.5.(2018·武汉模拟)设全集U =R ,集合A ={x |2x -x 2>0},B ={y |y =e x+1},则A ∪B 等于( )A .{x |x <2}B .{x |1<x <2}C .{x |x >1}D .{x |x >0}答案 D解析 由2x -x 2>0得0<x <2,故A ={x |0<x <2},由y =e x+1得y >1,故B ={y |y >1},所以A ∪B ={x |x >0}.故选D.6.(2018·武昌模拟)设A ,B 是两个非空集合,定义集合A -B ={x |x ∈A ,且x ∉B }.若A ={x ∈N |0≤x ≤5},B ={x |x 2-7x +10<0},则A -B =( )A .{0,1}B .{1,2}C .{0,1,2}D .{0,1,2,5}答案 D解析 因为A ={x ∈N |0≤x ≤5}={0,1,2,3,4,5},B ={x |x 2-7x +10<0}={x |2<x <5},A -B ={x |x ∈A ,且x ∉B },所以A -B ={0,1,2,5}.故选D.核心考向突破考向一 集合的基本概念例1 (1)(2019·辽宁模拟)已知集合A ={y |y =x 2+2x +1},B ={x |y =x 2+2x +1},则集合A 与集合B 的关系为( )A .A =B B .A ∈BC .B ⊆AD .A B答案 D解析 集合A 表示二次函数y =x 2+2x +1=(x +1)2中y 的取值范围,显然y ≥0,即A ={y |y ≥0};集合B 表示函数y =x 2+2x +1中x 的取值范围,易知x ∈R ,即B =R ,所以A B .故选D.(2)设集合A ={x ,x 2,xy },B ={1,x ,y }且A =B ,则实数x =________,y =________. 答案 -1 0解析 ∵A =B ,∴⎩⎪⎨⎪⎧x 2=1,xy =y 或⎩⎪⎨⎪⎧x 2=y ,xy =1,解得⎩⎪⎨⎪⎧x =1,y ∈R或⎩⎪⎨⎪⎧x =-1,y =0或⎩⎪⎨⎪⎧x =1,y =1.当x =1,y ∈R 时,A =B ={1,1,y },不满足互异性,舍去;当x =-1,y =0时,A =B ={-1,1,0},符合题意;当x =y =1时,A =B ={1,1,1},不满足互异性,舍去.综上可知x =-1,y =0.触类旁通解决集合概念问题的一般思路(1)研究一个集合,首先要看集合中的代表元素,然后再看元素的限制条件.解本例(1)时要注意,集合A 是函数值域构成的数集,集合B 是函数定义域构成的数集.本例中参数的确定,往往要对集合中的元素进行分类讨论,构造方程组求解.同时注意对元素互异性的检验.即时训练 1.(2018·郑州模拟)已知集合A ={x |y =1-x 2,x ∈Z },B ={p -q |p ∈A ,q ∈A },则集合B 中元素的个数为( )A .1B .3C .5D .7答案 C解析 由题意知A ={-1,0,1},当p =-1,q =-1,0,1时,p -q =0,-1,-2;当p =0,q =-1,0,1时,p -q =1,0,-1;当p =1,q =-1,0,1时,p -q =2,1,0.根据集合中元素的互异性可知,集合B 中的元素为-2,-1,0,1,2,共计5个.故选C.2.设集合A =⎩⎨⎧⎭⎬⎫5,b a,a -b ,B ={b ,a +b ,-1},若A ∩B ={2,-1},则A ∪B =( )A .{2,3}B .{-1,2,5}C .{2,3,5}D .{-1,2,3,5}答案 D解析 由A ∩B ={2,-1},可得⎩⎪⎨⎪⎧b a=2,a -b =-1或⎩⎪⎨⎪⎧b a =-1,a -b =2.当⎩⎪⎨⎪⎧b a =2,a -b =-1时,⎩⎪⎨⎪⎧a =1,b =2,此时B ={2,3,-1},所以A ∪B ={-1,2,3,5};当⎩⎪⎨⎪⎧b a =-1,a -b =2时,⎩⎪⎨⎪⎧a =1,b =-1,此时不符合题意,舍去.故选D.考向二 集合间的基本关系例 2 (1)(2019·山东模拟)已知集合A =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x -2x ≤0,x ∈N ,B ={x |x ≤2,x ∈Z },则满足条件A ⊆C ⊆B 的集合C 的个数为( )A .1B .2C .4D .8答案 D 解析 由x -2x≤0得0<x ≤2,故A ={1,2};由x ≤2得0≤x ≤4,故B ={0,1,2,3,4}.满足条件A ⊆C ⊆B 的集合C 的个数为23=8.(2)已知集合A ={x |x 2-3x -10≤0},B ={x |m +1≤x ≤2m -1},若B ⊆A ,则实数m 的取值范围为________.答案 (-∞,3]解析 若B ⊆A ,则①当B =∅时,有m +1>2m -1,即m <2,此时满足B ⊆A ;②当B ≠∅时,有⎩⎪⎨⎪⎧m +1≤2m -1,m +1≥-2,2m -1≤5,解得2≤m ≤3.由①②得,m 的取值范围是(-∞,3].触类旁通解本例时,要能够将集合间的关系进行等价转化,转化为集合C 中哪些元素必有,哪些元素可能有,不要忽略任何非空集合是它自身的子集.已知两个集合间的关系求参数时,关键是将条件转化为元素或区间端点间的关系,进而转化为参数所满足的关系,常用数轴、Venn 图等来直观解决这类问题.解题时要关注空集的特殊性,本例中,易忽视B =∅而误解.即时训练 3.设集合A ={1,2,3,4,5,6},B ={4,5,6,7,8},则满足S ⊆A 且S ∩B ≠∅的集合S 的个数是( )A .57B .56C .49D .8答案 B解析 集合S 的个数为26-23=64-8=56.4.设A ={x |x 2-8x +15=0},B ={x |ax -1=0},若B ⊆A ,则实数a 的取值组成的集合C =________.答案⎩⎨⎧⎭⎬⎫0,13,15 解析 a =0时,B =∅,B ⊆A ;a ≠0时,1a =3或1a =5,解得a =13或a =15,所以C =⎩⎨⎧⎭⎬⎫0,13,15.考向三 集合的基本运算角度1 集合间的交、并、补运算例3 (1)(2019·海南模拟)已知全集U =R ,集合A ={x |x 2-x -6≤0},B =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x +1x -4>0,那么集合A ∩(∁U B )=( ) A .{x |-2≤x <4} B .{x |x ≤3或x ≥4} C .{x |-2≤x <-1} D .{x |-1≤x ≤3}答案 D解析 依题意A ={x |-2≤x ≤3},B ={x |x <-1或x >4},故∁U B ={x |-1≤x ≤4},故A ∩(∁UB )={x |-1≤x ≤3},故选D.(2)设全集U =R ,集合M ={x |y =3-2x },N ={y |y =3-2x},则图中阴影部分表示的集合是( )A.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ 32<x ≤3 B.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ 32<x <3 C.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ 32≤x <2 D.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪32<x <2 答案 B解析 由3 -2x ≥0,得x ≤32,即M =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ x ≤32;由2x >0,得3-2x <3,即N ={y |y <3}.因此图中阴影部分表示的集合是(∁U M )∩N =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪32<x <3. 触类旁通集合的基本运算问题一般应注意的几点(1)看元素组成.集合是由元素组成的,从研究集合中元素的构成入手是解决运算问题的前提.对集合化简.有些集合是可以化简的,如果先化简再研究其关系并进行运算,可使问题变得简单明了,易于解决.注意数形结合思想的应用.集合运算常用的数形结合形式有数轴和Venn 图. 即时训练 5.设集合U =R ,A ={x |x =3k +1,k ∈N *},B ={x |x ≤5,x ∈Q }(Q 为有理数集),则图中阴影部分表示的集合是( )A .{1,3,4,5}B .{2,4,5}C .{2,5}D .{1,2,3,4,5}答案 B解析 ∵集合A ={x |x =3k +1,k ∈N *},∴A ={2,7,10,13,4,19,22,5,…}.∵B ={x |x ≤5,x ∈Q },题中Venn 图中的阴影部分表示A ,B 两集合的交集,又A ∩B ={2,4,5},∴图中阴影部分表示的集合为{2,4,5}.故选B.6.(2019·汕头模拟)已知集合P ={x ∈R |2(x -1)(x -3)≤1},Q =⎩⎨⎧⎭⎬⎫x ∈R ⎪⎪⎪y =x 2-43,则P ∪(∁R Q )=( )A .[2,3]B .(-2,3]C .[1,2)D .(-∞,-2]∪[1,+∞)答案 B解析 因为P ={x ∈R |2(x -1)(x -3)≤1},所以P ={x ∈R |(x -1)(x -3)≤0},所以P ={x∈R |1≤x ≤3}.因为Q =⎩⎨⎧⎭⎬⎫x ∈R ⎪⎪⎪y =x 2-43,所以Q ={x ∈R |x 2≥4},所以Q ={x ∈R |x ≤-2或x ≥2},所以P ∪(∁R Q )=[1,3]∪(-2,2)=(-2,3].故选B.角度2 利用集合运算求参数例4 (1)(2019·广西模拟)设集合A ={x |x (4-x )≥3},B ={x |x >a },若A ∩B =A ,则a 的取值范围是( )A .a ≤1B .a <1C .a ≤3D .a <3答案 B解析 由x (4-x )≥3解得1≤x ≤3,即集合A ={x |1≤x ≤3}.因A ∩B =A ,则A ⊆B ,而B ={x |x >a },所以a <1,故选B.(2)已知集合A ={x ∈R ||x +2|<3},集合B ={x ∈R |(x -m )(x -2)<0},且A ∩B =(-1,n ),则m =________,n =________.答案 -1 1解析 由|x +2|<3,得-3<x +2<3,即-5<x <1,所以集合A ={x |-5<x <1}.因为A ∩B =(-1,n ),所以-1是方程(x -m )(x -2)=0的根,解得m =-1.此时不等式(x +1)(x -2)<0的解集为-1<x <2,所以B =(-1,2).所以A ∩B =(-1,1),即n =1.触类旁通将两个集合之间的关系准确转化为参数所满足的条件时,应注意子集与真子集的区别,此类问题多与不等式组的解集相关.确定参数所满足的条件时,一定要把端点值代入进行验证,否则易产生增解或漏解.本例易忽视a ≠1,而误选A.即时训练 7.(2019·江西南昌模拟)已知集合A ={x |y =4-x 2},B ={x |a ≤x ≤a +1},若A ∪B =A ,则实数a 的取值范围为( )A .(-∞,-3]∪[2,+∞)B .[-1,2]C .[-2,1]D .[2,+∞) 答案 C解析 集合A ={x |y =4-x 2}={x |-2≤x ≤2},因为A ∪B =A ,则B ⊆A ,所以有⎩⎪⎨⎪⎧a ≥-2,a +1≤2,所以-2≤a ≤1,故选C.8.已知集合P ={y |y 2-y -2>0},Q ={x |x 2+ax +b ≤0},若P ∪Q =R ,P ∩Q =(2,3],则a +b =________.答案 -5解析 P ={y |y 2-y -2>0}={y |y >2或y <-1}, ∵P ∪Q =R ,P ∩Q =(2,3],∴Q ={x |-1≤x ≤3},∴-1,3是方程x 2+ax +b =0的两根,由根与系数的关系得,-a =-1+3=2,b =-3,∴a +b =-5.1.(2019·宁夏模拟)已知集合A ={x ∈N |x 2-2x -3≤0},B ={1,3},定义集合A ,B 之间的运算“*”:A *B ={x |x =x 1+x 2,x 1∈A ,x 2∈B },则A *B 中的所有元素之和为( )A .15B .16C .20D .21答案 D解析 由x 2-2x -3≤0,得(x +1)(x -3)≤0,故集合A ={0,1,2,3}.∵A *B ={x |x =x 1+x 2,x 1∈A ,x 2∈B },∴A *B 中的元素有0+1=1,0+3=3,1+1=2,1+3=4,2+1=3(舍去),2+3=5,3+1=4(舍去),3+3=6.∵A *B ={1,2,3,4,5,6},∴A *B 中的所有元素之和为21.2.已知非空集合A ,B 满足以下两个条件: (1)A ∪B ={1,2,3,4},A ∩B =∅;(2)A 的元素个数不是A 中的元素,B 的元素个数不是B 中的元素.则有序集合对(A ,B )的个数为( )A .1B .2C .4D .6答案 B解析 若集合A 中只有1个元素,则集合B 中有3个元素,则1∉A,3∉B ,即3∈A,1∈B ,此时有1对;同理,若集合B 只有1个元素,则集合A 中有3个元素,有1对;若集合A 中有2个元素,则集合B 中有2个元素,2∉A ,2∉B ,不满足条件.所以满足条件的有序集合对(A ,B )的个数为1+1=2,故选B.答题启示解决以集合为背景的新定义问题,要抓住两点:(1)紧扣新定义.首先分析新定义的特点,把新定义所叙述的问题的本质弄清楚,并能够应用到具体的解题过程之中,这是破解新定义型集合问题难点的关键所在;(2)用好集合的性质.解题时要善于从试题中发现可以使用集合性质的一些因素,在关键之处用好集合的运算与性质.对点训练1.设集合S ={A 0,A 1,A 2,A 3},在S 上定义运算⊕:A i ⊕A j =A k ,k 为i +j 除以4的余数(i,j=0,1,2,3),则满足关系式(x⊕x)⊕A2=A0的x(x∈S)的个数为( ) A.4 B.3C.2 D.1答案 C解析因为x∈S={A0,A1,A2,A3},故x的取值有四种情况.若x=A0,根据定义A i ⊕A j=A k,其中k为i+j除以4的余数(i,j=0,1,2,3),则(x⊕x)⊕A2=A0⊕A2=A2,不符合题意,同理可以验证x=A1,x=A2,x=A3三种情况,其中x=A1,x=A3符合题意,故选C.2.对于非空集合P,Q,定义集合间的一种运算“★”:P★Q={x|x∈P∪Q且x∉P∩Q}.如果P={x|-1≤x-1≤1},Q={x|y=x-1},则P★Q=( )A.{x|1≤x≤2} B.{x|0≤x≤1或x≥2}C.{x|0≤x≤1或x>2} D.{x|0≤x<1或x>2}答案 D解析因为P={x|-1≤x-1≤1}={x|0≤x≤2},Q={x|x-1≥0}={x|x≥1},所以P ∪Q={x|x≥0},P∩Q={x|1≤x≤2},所以P★Q={x|x∈P∪Q且x∉P∩Q}={x|0≤x<1或x>2}.故选D.。
2019-2020年高三数学第一轮复习教案人教版

2019-2020年高三数学第一轮复习教案人教版【教学目标】1.让学生掌握函数关于点(或直线)的对称函数解析式的求法;2.让学生了解函数图象的自对称和两函数图象之间的相互对称问题.【教学重点】函数(或曲线)关于点(或直线)的对称问题的解法 【教学难点】自对称和相互对称的区别【例题设置】例1、例2、例3(函数(或曲线)关于点(或直线)的对称问题的解法),例4(函数的对称问题)【教学过程】一、函数关于点(或直线)的对称函数解析式的求法 〖例1★ 点评:将点改为函数图象或曲线解法类似,其步骤大致如下:将所求曲线上的任意一点,求其关于点(或直线)的对称点,再将点的坐标代入原方程,即可得到所求的轨迹方程.因此所有的对称问题最终都将归结为点的对称问题,只要记住对称点的写法,问题便迎刃而解.〖例2〗 已知函数,则其关于原点对称的函数解析式为 ;关于直线对称的函数解析式为 . 答案:;当对称轴斜率为1时,点坐标符合口诀:用代,用代.〖例3〗 已知定义在上的奇函数的图象与函数的图象关于点对称,且当时,,求的解析式.解:① 设()为的图象上的任意一点,则其关于点的对称点()必在的图象上,故 ∴当时, ② 当时,,且为奇函数∴33()()()f x f x x x =--=--= 综上所述, .〖例4〗 设函数的定义域为,则下列命题中: ① 若为偶函数,则的图象关于轴对称; ② 若是偶函数,则的图象关于直线对称; ③ 若,则的图象关于直线对称; ④ 若,则的图象关于直线对称; ⑤ 与图象关于直线对称. ⑥ 与图象关于直线对称.其中正确命题的序号为: . 答案:④⑥★点评:其中注意④⑤的区别,指的是的图象自身的一种对称关系;而与是函数通过复合变换后得到的两个新的函数图象,要求的应是这两个函数图象的对称关系.二、函数图象本身的对称性(自身对称)命题1:设函数的定义域为,若对于一切的,都有,则函数的图象关于直线对称. 推 论:设函数的定义域为,若对于一切的,都有,则函数的图象关于直线()()22a xb x a bx ++-+==对称.命题2:设函数的定义域为,若对于一切的,都有,则函数的图象关于点对称. 推 论:设函数的定义域为,若对于一切的,都有,则函数的图象关于点对称.三、两个函数的图象对称性(相互对称)(利用解析几何中的对称曲线轨迹方程理解) 命题3:函数与的图象关于直线对称. 命题4:函数与的图象关于点成中心对称.下面只给出命题1的证明,其它命题及推论的证明类似. 证法一:由知函数为偶函数,其图象关于轴对称思考: 情形一中的范围是如何给出的,为何要限定其范围?另一方面,将的图象向右()或向左()平移个单位得到的图象,故函数的图象关于直线对称.证法二:由知点与点都是函数上的点,而的中点为,即点关于直线对称,由点的任意性可知,函数的图象关于直线对称.证法三:设点为函数的图象上的任意一点,其关于直线对称的点为. ∵对于一切的,都有∴0000(2)[()]()f a x f a a x f x y -=--==即点也在函数的图象上 由点的任意性可知,函数的图象关于直线对称.四、函数的周期性命题5:设函数的定义域为,若对于一切的,都有,则函数是以为周期的周期函数. 命题6:设函数的定义域为,若对于一切的,都有,则函数是以为周期的周期函数.【课堂小结】1.所有的对称问题最终都将归结为点的对称问题,要牢记例1的结论;2.给出的如果是函数自身的一个关系,则:若前系数互为相反数,则是有关对称性;若前系数相同,则有关周期性.3.自对称和相互对称的区别:第一类,是反映函数自身内部的对称关系;第二类中,是研究由函数复合变换后得两个新的函数图象间的关系.【教后反思】2019-2020年高三数学第一轮复习教案数列的求和方法及应用[素质教育目标] 一、 知识目标要求学生熟练掌握和运用等差、等比数列的前n 项和的公式及一个数列求前n 项和的基本方法和技巧。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解析:阴影部分表示的集合为A∩C∩(∁UB)={2,8}.
答案:{2,8}
(4)常用数集及其记法:
非负整数集(或自然数集),记作N;
正整数集,记作N*或N+;
整数集,记作Z;
有理数集,记作Q;
实数集,记作R。
2.集合的包含关系:
(1)集合A的任何一个元素都是集合B的元素,则称A是B的子集(或B包含A),记作A B(或 );
集合相等:构成两个集合的元素完全一样。若A B且B A,则称A等于B,记作A=B;若A B且A≠B,则称A是B的真子集,记作AB;
解析:选B选项A错,应当是B⊆A.选项B对,正方形一定是矩形,但矩形不一定是正方形.选项C错,正方形一定是菱形,但菱形不一定是正方形.选项D错,应当是D⊆A.
2.(2012·浙江高考)设集合A={x|1<x<4},集合B={x|x2-2x-3≤0},则A∩(∁RB)=()
A.(1,4)B.(3,4)
5.(教材习题改编)已知全集U={-2,-1,0,1,2},集合A=,则∁UA=________.
解析:因为A=,当n=0时,x=-2;n=1时不合题意;
n=2时,x=2;n=3时,x=1;n≥4时,x∉Z;n=-1时,x=-1;
n≤-2时,x∉Z.故A={-2,2,1,-1},又U={-2,-1,0,1,2},所以∁UA={0}.
C.(1,3)D.(1,2)∪(3,4)
解析:选B因为∁RB={x|x>3,或x<-1},所以A∩(∁RB)={x|3<x<4}.
3.(教材习题改编)A={1,2,3},B={x∈R|x2-ax+1=0,a∈A},则A∩B=B时a的值是()
A.2B.2或3
C.1或3D.1或2
解析:选D验证a=1时B=∅满足条件;验证a=2时B={1}也满足条件.
5.集合的简单性质:
(1)
(2)
(3)
(4) ;
(5) (A∩B)=( A)∪( B), (A∪B)=( A)∩( B)。
典例解析:
1.(2012·大纲全国卷)已知集合A={x|x是平行四边形},B={x|x是矩形},C={x|x是正方形},D={x|x是菱形},则()
A.A⊆BB.C⊆B
C.D⊆CD.A⊆D
预测2017年高考将继续体现本章知识的工具作用,多以小题形式出现,也会渗透在解答题的表达之中,相对独立。具体题型估计为:
(1)题型是1个选择题或1个填空题;
(2)热点是集合的基本概念、运算和工具作用。
教学准备
多媒体
教学过程
要点精讲:
1.集合:某些指定的对象集在一起成为集合。
(1)集合中的对象称元素,若a是集合A的元素,记作 ;若b不是集合A的元素,记作 ;
答案:{0}
1.正确理解集合的概念
研究一个集合,首先要看集合中的代表元素,然后再看元素的限制条件,当集合用描述法表示时,注意弄清其元素表示的意义是什么.注意区分{x|y=f(x)}、{y|y=f(x)}、{(x,y)|y=f(x)}三者的不同.
命题走向
有关集合的高考试题,考查重点是集合与集合之间的关系,近年试题加强了对集合的计算化简的考查,并向无限集发展,考查抽象思维能力,在解决这些问题时,要注意利用几何的直观性,注意运用Venn图解题方法的训练,注意利用特殊值法解题,加强集合表示方法的转换和化简的训练。考试形式多以一道选择题为主,分值5分。
(3)表示一个集合可用列举法、描述法或图示法;
列举法:把集合中的元素一一列举出来,写在大括号内;
描述法:把集合中的元素的公共属性描述出来,写在大括号{}内。
具体方法:在大括号内先写上表示这个集合元素的一般符号及取值(或变化)范围,再画一条竖线,在竖线后写出这个集合中元素所具有的共同特征。
注意:列举法与描述法各有优点,应该根据具体问题确定采用哪种表示法,要注意,一般集合中元素较多或有无限个元素时,不宜采用列举法。
(1)理解集合之间包含与相等的含义,能识别给定集合的子集;
(2)在具体情境中,了解全集与空集的含义;
3.集合的基本运算
(1)理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集;
(2)理解在给定集合中一个子集的补集的含义,会求给定子集的补集;
(3)能使用Venn图表达集合的关系及运算,体会直观图示对理解抽象概念的作用且属于集合B的元素所组成的集合,叫做集合A与B的交集。交集 。
(2)一般地,由所有属于集合A或属于集合B的元素所组成的集合,称为集合A与B的并集。 。
注意:求集合的并、交、补是集合间的基本运算,运算结果仍然还是集合,区分交集与并集的关键是“且”与“或”,在处理有关交集与并集的问题时,常常从这两个字眼出发去揭示、挖掘题设条件,结合Venn图或数轴进而用集合语言表达,增强数形结合的思想方法。
(2)简单性质:1)A A;2) A;3)若A B,B C,则A C;4)若集合A是n个元素的集合,则集合A有2n个子集(其中2n-1个真子集);
3.全集与补集:
(1)包含了我们所要研究的各个集合的全部元素的集合称为全集,记作U;
(2)若S是一个集合,A S,则, = 称S中子集A的补集;
(3)简单性质:1) ( )=A;2) S= , =S。
2019-2020年高三上学期数学一轮复习教案:第1讲集合
课题
集合(共2课时)
修改与创新
课标要求
1.集合的含义与表示
(1)通过实例,了解集合的含义,体会元素与集合的“属于”关系;
(2)能选择自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题,感受集合语言的意义和作用;
2.集合间的基本关系
(2)集合中的元素必须满足:确定性、互异性与无序性;
确定性:设A是一个给定的集合,x是某一个具体对象,则或者是A的元素,或者不是A的元素,两种情况必有一种且只有一种成立;
互异性:一个给定集合中的元素,指属于这个集合的互不相同的个体(对象),因此,同一集合中不应重复出现同一元素;
无序性:集合中不同的元素之间没有地位差异,集合不同于元素的排列顺序无关;
