16二端口网络
二端口网络相关知识简介
对称二端口只有两个参数是独立的。
对称二端口是指两个端口电气特性上对称。电路结 构左右对称的,端口电气特性对称;电路结构不对称的 二端口,其电气特性也可能是对称的。这样的二端口也 是对称二端口。使用时可以不分彼此。
•
I1 2
+
•
U1
5
10 10
•
•
I2
I1 2
++
U U •
•
21
2
•
I2
+ 4 •
U2 2
U 2
Y21 Δ
I1
Y11 Δ
I2
Z 21 I1
Z22 I2
其中 =Y11Y22 –Y12Y21
其矩阵形式为
U U
1 2
Z11
Z
21
Z12 Z 22
I1 I2
Z
Z11
Z
21
Z12
Z
22
称为Z参数矩阵
Z参数的实验测定
U 1 Z11I1 Z12 I2 U 2 Z21I1 Z22 I2
互易 对称
Y Y12=Y21 Y11=Y22
Z Z12=Z21 Z11=Z22
T
H
detA=1 H12= -H21 T11=T22 detH=1
5 .含有受控源的电路四个独立参数。
§3 二端口的等效电路
(1) 两个二端口网络等效: 是指对外电路而言,端口的电压、电流关系相同。
(2) 求等效电路即根据给定的参数方程画出电路。
i2
–
1 i1 3
4 i2
1-1’ 2-2’是二端口
3-3’ 4-4’不是二端口,是四端网络
i1' i1 i i1 i2' i2 i i2
电气工程电路笔记教案 (16)二端口网络

CH16 二端口网络本章介绍二端口(网络)及其方程,二端口的Y 、Z 、A 、H 等参数矩阵以及它们之间的相互关系,还介绍转移函数,T 型和Π型等效电路及二端口的连接,最后介绍回转器和负阻抗变换器。
§16-1 二端口网络的基本概念教学目的:学习二端口网络的概念,了解常见的二端口。
教学重点:二端口网络的基本概念。
教学难点:二端口和一端口的区别。
教学方法:课堂讲授。
教学内容:一、二端网络(一端口网络):通过引出一对端钮与外电路连接的网络常称为二端网络,通常分为两类即无源二端网络和有源二端网络。
二端网络中电流从一个端钮流入,从另一个端钮流出,这样一对端钮形成了网络的一个端口,故二端网络也称为一端口网络。
如图'i i =。
在正弦稳态电路中,....U Z II Y U ==可见,端口的两个物理量仅需一个参数去联系。
二、四端网络(二端口网络):定义:如图所示,该四端网络如果满足,'11I I =,'22I I =,则称该网络为二端口网络。
其中,11′ 端口称为输入端口,22′ 端口称为输出端口。
在输入端口处加上激励,在输出端口处产生响应。
对于线性无源的二端口网络,端口共有四个物理量, 要研究端口的电压和电流之间的关系,任选其+ _.2U +_.1U1+ _u中两个为自变量,则另外两个就为因变量。
11111222211222()()()()()()f t W x t W x t f t W x t W x t =+=+可见,两个端口上的四个物理量需四个参数去联系。
根据不同的组合方式,就有六种不同的二端口参数方程,这里只介绍常用的四种参数。
可逆二端口网络:满足互易定理的二端口网络。
对称二端口网络:如果将二端口网络的输入端口(端口11′)与输出端口(端口22′)对调后,其各端口电流、电压关系均不改变,这种二端口网络称为对称二端口网络,这种网络从联接结构看也是对称的。
§16-2 二端口网络的方程及参数 教学目的:二端口网络的方程及其参数。
二端口网络课件

2. Y 参数表达旳等效电路(宜选用形等效电路)
I1
I2
Y11 Y21
Y12 Y22
U1 U 2
••
II11
++
••
UU11
--YY1122 YY111++YY1122
I2
••
II22
YY222++YY1122
++
••
UU22
(Y21 Y12 )U1
假如网络是互易旳,上图变为型等效电路。
串联后复合二端口Z 参数矩阵等于原二端口Z 参数矩 阵相加。可推广到 n 端口串联。
16-6 回转器和负阻抗转换器
1. 回转器
回转器是一种线性非互易旳多端元件,能够用晶体管电路
或运算放大器来实现。理想回转器是不储能、不耗能旳无源
线性两端口元件。
i1 理想回转器旳基本特征 +
uu12
ri2 ri1
第16章 二端口网络
工程实际中,研究信号及能量旳传播和信号变换时,经 常遇到如下两端口电路。
n:1 R
C
C
变压器
传播线
滤波器
(1)线性一端口网络旳外部性能用戴维南或诺顿等效电路替 代去分析;
(2)线性二端口网络旳端口处旳i, u 间旳关系可经过某些只 取决于构成二端口本身旳元件及连接方式旳参数表达。
us
u2
uc
N
4(t) V
uc
运算电路模型: I1(s)
12 V
s
N
uc (t ) 4 3e0.231t V (t 0)
I2(s)
1s U2(s) 1s V
12 s 3U2 (s) 13I2 (s)
第十六章 二端口网络

第十六章 二端口网络16-1 求图示二端口的Y ,Z 和T 参数矩阵。
解:(1)对图(a)所示电路,标出端口电压21,U U 和电流21,I I及其参考方向,由KVL ,KCL 和元件VCR ,得:2121111)(1U L j U L j U U L j I ωωω+-=-= 212212)1(1)(1U L C j U L j U C j U U L j I ωωωωω-+=+-= 所以,Y 参数矩阵为:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=)1(111L C j Lj L j Lj Y ωωωωω同理可得2121111)1()(1I C j I C L j I I C j I L j U ωωωωω+-=++= 2121211)(1I C j I C j I I C j U ωωω+=+=得出Z 参数矩阵为:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=C j C j C j C L j Z ωωωωω111)1(根据KCL ,KVL 和元件VCR ,可得出端口11'-处电压1U 和电流1I为:211U I j U +=ω(1)221I U C j I -=ω(2)将式(2)代入(1)中,得:2222221)1()(I L j U LC U I U C j L j U ωωωω--=+-=(3)将方程式(3)与式(2)联立可得T 参数矩阵为:⎥⎦⎤⎢⎣⎡-=112Cj L j LCT ωωω(2)对图(b )所示电路,指定端口电压1U ,2U 和电流1I ,2I及参考方向,由KCL ,KVL 和元件VCR ,得:2121111)1()(1U L j U L C j U U L j U C j I ωωωωω+-=-+= 2121211)(1U L j U L j U U j I ωωω-=--=所以,Y 参数矩阵为:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=L j L j L j L C j Y ωωωωω111)1(同理,可得Z 参数方程2121111)(1I C j I C j I I C j U ωωω+=+=212122)1(1)(1I C L j I C j I I C j I L j U ωωωωω-+=++= 故,Z 参数矩阵为:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=)1(111C L j Cj Cj C j Z ωωωωω 又因为端口1-1`处的电压1U 和电流1I为:221I L j U U ω-= (1) 211I U C j I -=ω (2)将式(1)代入到式(2)中,得2222221)1()(I LC U C j I I L j U C j Iωωωω--=--= (3)将方程式(1)与式(3)联立,可得出T 参数矩阵为⎥⎦⎤⎢⎣⎡-=LC C j L j T 211ωωω注:本题也可采用教材中各参数的定义求解。
第16章-b-二端口网络

L di1 dt
L r 2C
BACK NEXT
从端口1看,u1, i1关系为一等效电感关系,L= r2C. 若 r =50k, C =1F 则 等效电感 L=2500H !
3. 回转器不消耗功率(能量),也不储能。是线性无源元件。
u1i1 u2i2 ri2i1 ri1i2 0
4. 回转器是非互易元件。
T11 T21
T12 T11
T22
T21
T12 T22
UI22
得 T T T
结论: 级联后所得复合二端口T 参数矩阵等于级联旳二 端口T 参数矩阵相乘。上述结论可推广到n个二端 口级联旳关系。
...
T1
T2
... Tn
T=[T1][T2] …. [Tn]
BACK NEXT
例
4
Z11 Z 21
Z12
Z
22
结论:
串联后复合二端口Z 参数矩阵等于原二端口Z 参数 矩阵相加。可推广到n端口串联。
BACK NEXT
注意: (1)串联后端口条件可能被破坏。
2A
2 Z” 2
1A
1.5A
3A 1¸
3 1¸ 1.5A
2A
1A
1¸
1¸
1.5A
1.5A 2
2A
2 2 端口条件破坏
1A
[Z] [Z'][Z"]
i2
+ u1
UNIC
+ u2
电压反向型
ui11
ku2 i2
u1
i1
k
0
0 u2
1
i
2
T 参数矩阵
BACK NEXT
第16章习题课 二端口网络

Z 21 = r + Z 3
Z 22 = Z 2 + Z 3
可见,网络内含有受控源时,Z12 ≠ Z 21。 同样的有 Y12 ≠ Y21。
传输参数 【例4】求图示二端口网络的传输参数。 】求图示二端口网络的传输参数。 解 直接建立传输参数方程
& & & U1 = (10 + 20) I1 = 30 I1 & & & & U = −3I + 20 I = 17 I
2 − 1 1 3 3 3 Yb = S ,Yc = 1 −1 2 − 3 3 6 − 1 6 S 1 3 1 − 1 2 Y = Yb + Yc = S −1 1 2
【例10】求图示二端口网络的 参数。 】求图示二端口网络的T 参数。
由以上结果求得
A = 30 = 1.765 17 C = 1 = 0.0588 S 17
参数。 【例5】求图示二端口网络的 参数。 】求图示二端口网络的H参数 解 直接建立H参数方程
& & & & & & U1 = 2 I1 + 6( I1 + I 2 ) = 8 I1 + 6 I 2 & & & & & & U = 2 I + 6( I + I ) = 6 I + 8I
参数。 【例2】求图示网络的 参数。 】求图示网络的Z参数 解 方法一 用开路法求Z参数
1
+ I & 1 & U
1
Z1 Z3
Z2
& I2 + & U2
第十六章二端口网络优秀课件

1. 确定二端口处电压、电流之间的关系,写出参数矩阵, 在分析中一般使用相量法或运算法。
2. 利用端口参数比较不同的二端口的性能和作用。
3. 对于给定的一种二端口参数矩阵,会求其它的参数矩阵。
4. 对于复杂的二端口,可以看作由若干简单的二端口组 成。由各简单的二端口参数推导出复杂的二端口参数。
16-2 二端口的方程和参数
+ i1 u1 -
i2 + u2 -
端口物理量4个 i1 i2 u1 u2
下:
•
•
I1
•
U1
•
I2 U 2
•
•
U
•
1
U
•
2
I1 I2
•
•
U
•
1
I1
•
I2 U 2
假 一、设Y 端 参数口 和U 方1电 和 程U压 2已知• , + I• 1
端口电 I1和 流 I2未知 •
U1
•
-
线性 无源
•
I2
+
•
-U 2
U
•
1
I1
•
U 2 I2
端U1口和电U流2共同I1和 作用I可2 产视生为。
1
外
NS
电
1 Req +
路
uoc
1’
1’
-
(a)
1 +
外电路 开路电压
十六章 二端口网络
U 2
11
二端口网络的Y、Z参数特性:
1、对于线性R、L(M)、C元件构成的 任何无源二端口,Z12=Z21,Y12=Y21
2、对于对称的二端口,Z11=Z22,Y11=Y22 3、Z=Y-1参数
I 1 I 2
方法一:分别求Z四个 参数
+ -
+
-
U 1
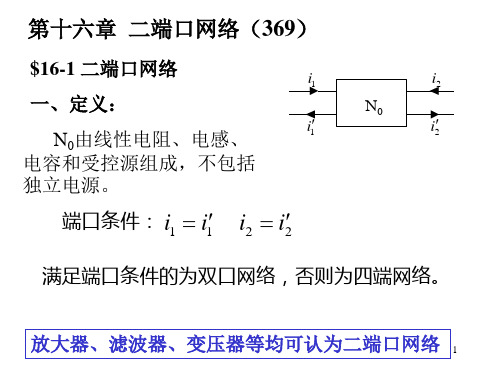
第十六章 二端口网络(369)
$16-1 二端口网络 一、定义: N0由线性电阻、电感、 电容和受控源组成,不包括 独立电源。 端口条件: i1
i1
i1
i2
N0
i2
i1
i2 i2
满足端口条件的为双口网络,否则为四端网络。 放大器、滤波器、变压器等均可认为二端口网络
1
二端口网络分析特性: 1、对于二端口网络,主要分析端口的电流和电压, 不涉及内部电路的工作状况。因此,本章主要讨论 端口u、i为变量的电路方程(二端口VAR约束方程) 2、二端口网络端口有四个物理量(u1、i1、u2、i2), 若其中两个为自变量,另两个为应变量,可有六组 表征网络特性的独立方程:
4
方法二:分别求出四个Y参数,从而得出Y矩阵
根据方程
1 Y1 1U 1 Y1 2U 2 I 2 Y2 1U 1 Y2 2U 2 I
0 ,U 1V,则如图 1、令 U 1 2
I Y1 2 1 U2
I 1 U 1
0 U 1
I 1
二、电流控制型二端口VAR方程
+
I 1
U 1 -
No
+
i2 ) u1 f(i1 , i2 ) u 2 f(i1 , 结构电 路 如 图
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
式中:△z = z11 z22 - z12z21、 △y = y11 y22 - y12y21
并非所有的二端口均有Z,Y 参数。
+
I1
Z
I2
+
U1 U 2 Z ( I1 I 2 )
Z Z Z Z Z
1
U1
U2
YZ
不存在
例16-2 求图中T形电路的Z参数。 解: 方法1:列电路方程法。
I2 y22 |U1 0 U2
入口短路时 的输出导纳
Y参数具有导纳的量纲, 而且是在端口短路的
情况下, 通过计算或测量得到的, 因此称为短路导
I1 y11 将Y方程写成矩阵形式为: I 2 y 21
纳参数。
y12 U 1 y 22 U 2
第十六章
二端口网络
本章内容
概述 两端口的参数和方程 两端口的等效电路 两端口的连接
§16-1
二端口概述
在工程实际中,研究信号及能量的传输和信号变换时, 经常碰到如下形式的电路……四端网络。
R C C
滤波器
一. 端口 (port)
+ u1 i1 ′ i1 + u1 i1 i1′ i2 + u2
出端导纳
互易性和对称性
互易二端口:
对称二端口:
H12 H 21
H11 H 22 H12 H 21 1
I1
I2
+ R1
例题:求三极 管等效电路的 H参数
+
U1
β I1
R2 U 2
U1 R1I1
I 1 U I2 1 2 R2
U2 z 21 |I2 0 Z 2 I1
2.令输入口开路,即: I1 0
I1 I0 Z1 1
Z3 I 2
U 2 (Z 2 Z3 ) I 2
U1 Z 2 I 2
U1
-
+
Z2
U2
-
+
U1 z12 | Z2 I1 0 I2 U2 z 22 |I1 0 Z 2 Z 3 I
四、混合参数(H 参数)
H 参数也称为混合参数,
常用于晶体管等效电路。
U1
-
+
I1
二端口 电路
I2
U2
-
+
混合参数方程:
U 1 H 11 I 1 H 12U 2 I 2 H 21 I 1 H 22U 2
I1 H 12 I 1 H H 22 U 2 U 2
即: Y y11 y 21
z11 Z z 21
1
或:Z Y 1
y12 1 z 22 z12 z y22 z11 21 z
z12 1 y22 y12 y z 22 y11 21 Y
U1
-
+
I1
二端口 电路
I2
U2
-
+
I1
+
U1
-
二端口 电路
+
I2
U2
-
根据替代定理,画出二端口的等效电路:
U 根据叠加定理可得: 1
z11I1 z12 I 2 U 2 z21I1 z22 I 2
(16-2)
称为二端口的Z方程。式中z11、 z12、z21、z22称为Z参数。
例 16 –1:求电路的Y参数。 解:
(1) 根据节点电流方程求Y矩 阵
I 1 YaU 1Yb (U 1 U 2 )
(Ya Yb )U 1 YbU 2
+
I1
Yb
I2
+
U1
-
Ya Yc
U2
-
得Y参数矩阵:
I 2 Yb (U 2 U 1) YcU 2
2
三、 传输参数(T/A参数)
当研究信号传输的各种问题时, 以 U 、 I 为自变量,
2
U1
-
+
I1
二端口 电路
I2
U2
-
+
2
U 1 、I 1 为应变量。其方程称为传输方程: U 1 A B U 2 U2 A I1 C D I 2 I 2
U1 z11 | I2 0 入口开路时的 I1
2
2
Z参数又称为开路阻抗参数。
入口开路时的输出 阻抗(或策动点阻抗
U1 z11 将式(16-2)写成矩阵形式为: U 2 z 21
定义:
z12 I1 I1 Z z 22 I 2 I 2
混合参数矩 阵(H矩阵)
矩阵形式:
U 1 H 11 I 2 H 21
H参数的物理意义计算与测定
I1
+
U1
-
I2 + 二端口 U U 22 0 电路
-
U 1 H 11 I 1 H 12U 2 I 2 H 21 I 1 H 22U 2
U1
-
U2
-
二端口电路端口方程:
在二端口变量中任选两 个作自变量, 而另外两个作应 变量, 列写出的描述二端口电 路端口伏安特性的方程。
+
I1
二端口 电路
I2
+
U1
-
U2
-
共有六种形式的电路方程和参数。
I1 U1 I2 U2
U1 U2 I1 I2
Z 2 Z3 Z2
方法2:由Z参数的定义求。
1.令输出口开路,即:I 2 0
I 1 Z1
I2 0 Z3 I2
U2
+
U1 ( Z1 Z 2 ) I1
U 2 Z 2 I1
U1
-
+
Z2
U1 z11 |I2 0 Z1 Z 2 I1
U1 -
I 2 -YbU 1 I1 于是得: y |U 0 Ya Yb 11 U 2
1
I1 (Ya Yb )U 1
I2 y21 |U 0 Yb U1 2
令输入口短路,即 U 1 =0,
I1
+
Yb
I2
I 2 (Yb Yc )U 2 I1 YbU 2
i2
i1 i3
N
i4.
四端网络
满足:i1 i2 i3 i4 0
§16-2 二端口的方程和参数
本章主要讨论二端口电路,且二端口电路内不含独立电源。 只讨论端口的伏安关系,不涉及电路内部。 采用在频域中讨论。
输入端口
输出端口
二端口电路的相量模型:
+
I1
二端口 电路
I2
+
电路变量:
U 1 I1 U 2 I 2
U1 U 1=0 Ya Y c -
U2
-
+
I2 于是得: y22 |U10 Yb Yc U2 I1 y12 |U 0 Yb U2 1
二、开路参数(Z参数)
选端口电流 I 1 、I 2为自变量
U 端口电压 U 1、 2 为应变量。
I1 0 I2 + + 二端口 U1 U2 电路
-
U1 H 11 I1
I2 H 21 I
1
U 2 0
输入阻抗 短路参数
U 2 0
电流转移比
U1 H 12 U2 I2 H 22 I1 0
……出口开路时的转移导纳
I1
I2
二端口 电路
U1
-
+
U22 0
-
+
短 路 参 数
U1 B I2 U 2 0 ......出口短路时的转移阻抗 I1 D I2 U 2 0
......出口短路时的电流比
( 1)对于互易电路, A参数满足: AD- BC = 1 这时 A参数中有3个是独立参数。 (2)如果电路是互易的, 并且是对称的, 则还有: A =D 这时 A参数中有3个是独立参数。
A B A …….传输参数矩阵(A/T 矩阵) C D
def
注意方程式中负号的含义。
传输参数的其物理含义:
I1
+
I2I 0 2
二端口 电路
U1
-
U2
-
+
开 路 参 数
U1 A U 2 I2 0
I1 C U 2 I2 0
……出口开路时的电压比
出口短路时的 正向转移导纳
其物理含义:
1. 出口短路时: U 2 0 I1 出口短路时 y11 的输入导纳 U1 U 2 0 2. 入口短路时: U1 0
I2 y21 U1
U 2 0
入口短路时的 反向转移导纳
I1 y12 |U1 0 U2
Ya Yb Y Yb
Yb Yb YC
YbU 1 (Yb Yc )U 2
由于y12 = y21`, 该电路是互易电路。
