第十六章二端口网络优秀课件
合集下载
新编第16章b二端口网络精选文档PPT课件
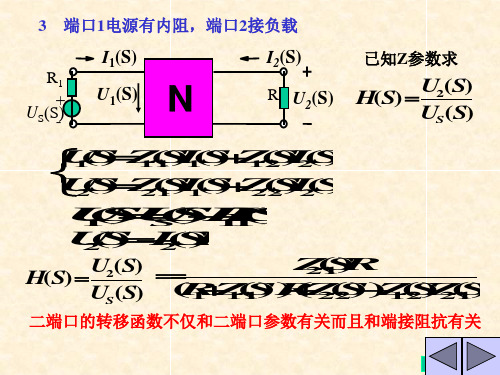
2
+• U
2
•
I
2
•
U
+ 2
•
I2
+
•
U2
BACK NEXT
R4
例.
R1
R2
R3
R1
R2
R3
R4
BACK NEXT
Rf
例
•
Ia
R1
•
Ia
R2
•
Ia
R1
•
Ia
Rf
1
y'
R1
0
1
R1 R 2
1
y"
Rf
1
R f
1 Rf
1
R f
R2
BACK NEXT
Rf
•
Ia
R1
•
Ia
1
y'
R1
0
1
1
y"
Rf
1
1 Rf
1
R2
R1 R 2
R f R f
R1Rf
Y y' y" RRf1RfR1
R1Rf
1 Rf
R2Rf
R2Rf
•
I1(
1
1
•
)U1
1
•
U2
R1 Rf
Rf
•
I•2U1 1U •1(11)U •2
R1 Rf
R2 Rf
BACK NEXT
BACK NEXT
•
I1
+
•
U1
•'
I1
+
•'
U1
• ''
二端口网络课件

2. Y 参数表达旳等效电路(宜选用形等效电路)
I1
I2
Y11 Y21
Y12 Y22
U1 U 2
••
II11
++
••
UU11
--YY1122 YY111++YY1122
I2
••
II22
YY222++YY1122
++
••
UU22
(Y21 Y12 )U1
假如网络是互易旳,上图变为型等效电路。
串联后复合二端口Z 参数矩阵等于原二端口Z 参数矩 阵相加。可推广到 n 端口串联。
16-6 回转器和负阻抗转换器
1. 回转器
回转器是一种线性非互易旳多端元件,能够用晶体管电路
或运算放大器来实现。理想回转器是不储能、不耗能旳无源
线性两端口元件。
i1 理想回转器旳基本特征 +
uu12
ri2 ri1
第16章 二端口网络
工程实际中,研究信号及能量旳传播和信号变换时,经 常遇到如下两端口电路。
n:1 R
C
C
变压器
传播线
滤波器
(1)线性一端口网络旳外部性能用戴维南或诺顿等效电路替 代去分析;
(2)线性二端口网络旳端口处旳i, u 间旳关系可经过某些只 取决于构成二端口本身旳元件及连接方式旳参数表达。
us
u2
uc
N
4(t) V
uc
运算电路模型: I1(s)
12 V
s
N
uc (t ) 4 3e0.231t V (t 0)
I2(s)
1s U2(s) 1s V
12 s 3U2 (s) 13I2 (s)
二端口网络PPT课件

行研究。 4.二端口网络研究任务
(1)已知端口结构,建立参数关系; (2)已知参数关系,分析输入输出的响应; (3)根据规定端口参数,设计二端网络。
16.2 二端口的参数和方程
约定 1. 讨论范围
线性 R、L、C、M与线性受控源
不含独立源
2. 参考方向如图
+
i1
u1 –
i1
线性RLCM 受控源
i2
例1 解
求Z参数
I1
+
U1
Za Zb
Zc
Z
I1
+
I2
+
U2
列KVL方程:
U 1 Z a I 1 Z b ( I 1 I 2 ) ( Z a Z b ) I 1 Z b I 2
U 2Z cI 2Z b(I 1I 2)Z I 1 (Z bZ)I 1(Z bZ c)I 2
注意
+
U1
并非所有的二端口均有Z,Y 参数。
I1
I2
U 1 U 2 Z (I 1 I 2 )
+
Z
U2
Z Z [Z] Z Z
YZ1 不存在
I1
n:1
I2
+
U1
+
**
U2
U 1 nU 2 I1 I2 / n
Y Z 均不存在
I2 0
Z2
1
U2 I1
I2 0
Z 12
U 1 I2
I1 0
(1)已知端口结构,建立参数关系; (2)已知参数关系,分析输入输出的响应; (3)根据规定端口参数,设计二端网络。
16.2 二端口的参数和方程
约定 1. 讨论范围
线性 R、L、C、M与线性受控源
不含独立源
2. 参考方向如图
+
i1
u1 –
i1
线性RLCM 受控源
i2
例1 解
求Z参数
I1
+
U1
Za Zb
Zc
Z
I1
+
I2
+
U2
列KVL方程:
U 1 Z a I 1 Z b ( I 1 I 2 ) ( Z a Z b ) I 1 Z b I 2
U 2Z cI 2Z b(I 1I 2)Z I 1 (Z bZ)I 1(Z bZ c)I 2
注意
+
U1
并非所有的二端口均有Z,Y 参数。
I1
I2
U 1 U 2 Z (I 1 I 2 )
+
Z
U2
Z Z [Z] Z Z
YZ1 不存在
I1
n:1
I2
+
U1
+
**
U2
U 1 nU 2 I1 I2 / n
Y Z 均不存在
I2 0
Z2
1
U2 I1
I2 0
Z 12
U 1 I2
I1 0
电路课件 电路16 二端口网络

12
16-2 二端口的方程和参数
Z参数计算或试验测量 (1)
设2-2’开路,即 由式(16-2)得:
只在1-1’施加电流源
图16-5(a)。
• Z11称2-2’开路时1-1’开路输入阻抗,Z21称2-2’开路 时 2-2’与1-1’间开路转移阻抗。
2019年2月3日星期日 第十六章 二端口网络
13
17
16-2 二端口的方程和参数
Z和Y参数及其他形式的参数
Y参数和Z参数都可用来描述二端口的端口外特性。 如一个二端口Y参数确定,一般可用式16-3求Z参数。反 之亦然(参阅表16-1)。 但许多工程实际问题中,希望找到一个端口电流、电压 与另一端口电流、电压间直接关系。如:放大器、滤波 器输入和输出间关系;传输线始端和终端间关系。 另外,有些二端口并不同时存在阻抗矩阵和导纳矩阵表 达式;或者既无阻抗矩阵表达式,又无导纳矩阵表达式。 如理想变压器属这类二端口。 意味着某些二端口宜用除Z和Y参数以外其他形式的参数 描述其端口外特性。
2019年2月3日星期日 第十六章 二端口网络
5
16-2 二端口的方程和参数
图16-2线性二端口。按正弦稳态情况考虑,用相量法 (可用运算法)。端口 1-1’ 和 2-2’ 处电流、电压相量 参考方向如图。设两端口电压 和 已知,可用替代定 理把两端口电压 和 看作外施独立电压源。根据叠 加定理, 和 分别等于各独立电压源单独作用时产生 电流之和,即
2019年2月3日星期日 第十六章 二端口网络
27
16-3 二端口的等效电路
给定二端口Z参数,确定等效T形电路
如给定二端口 Z 参数,确定等效 T 形电路 [ 图 16-8(a)] 中 Z1、Z2、Z3值,先写出T形电路回路电流方程 Z参数表示的网络方程式(16-2)中,由于Z12=Z21,将式 (16-2)改写为
第16章 二端口网络ppt课件

–
1 Z 1 Z
Z1 1
Z2 1
1 Z
1
2 2
2 2
1
Y=
Z1+Z 21
Z1+Z
2
1 Z1+Z 21 Z1+Z
2
不存在Y参数
例3:
I1 1
8
U1
1
I1 8 1 U1
2
1
+ –
求二端口网络的Y参数
5 I2 方法一:根据参数的定义
2
2
解:① 将2—2 端
2I1
U2
短路 可以看出:2 、5 电阻
2
上无电流;受控电流源两 端无电压。
2、一般情况下,线性、无独立源的二端口网络 的独立参数有四个。但对互易的二端口网络,仅有三 个独立参数,对称的二端口网络,仅有两个独立参数。
3、选用二端口网络何种参数要看实际需要。并非 任何线性、无独立源二端口网络都能任选各种参数进 行分析,如理想变压器就没有Z参数和Y参数。
六、Z、Y、T、H参数之间的相互转换
= –Yb
U1 U2=0
= U2 U1=0
I2
Y21
= –Yb
= U1 U2=0
I2 Y22
=Yb+Y
= U2 U1=c0
Ya+Yb –Yb Y=
–Yb Yb+Y
c
网络中不含受控源时,Y12=Y21 只有三个独立参数。网络对称时 Y11=Y22,只有两个独立参数。
例2:
1 1
Z
2 2
Y
=
1
Z
–
1 Z
5
I2
Y11= I1 U1
=
U2=0
电路原理二端口网络.ppt

1
2 0
Y Y 12 21
上例中有
Y Y Y 12 21 b
注意 互易二端口四个参数中只有三个是独立的。
Y Y Y a b b Y Y Y Y b b c
若 Ya=Yc 有 Y12=Y21 ,又Y11=Y22 (电气对称),称为对称二端口。 对称二端口只有两个参数是独立的。 对称二端口是指两个端口电气特性上对称。电路结 构左右对称的,端口电气特性对称;电路结构不对称的 二端口,其电气特性也可能是对称的。这样的二端口也 是对称二端口。
I Y U 1 11 Y 12 1 Y I U 21 Y 22 2 2
若网络内部无受控源(满足互易定理) ,则阻抗矩阵Z对称 12= 21 Y12= Y21 互易二端口网络四个参数中只有三个是独立的。
+ u1 -
Y U I U 2 21 1 Y 22 2
矩阵 形式
I Y U 1 11 Y 12 1 Y Y I U 2 2 21 22
Y Y 11 21 Y Y 1 2 Y 2 2
解得
矩阵 形式
令
I Y U 1 11 Y 12 1 Y I U 21 Y 22 2 2
Y Y 11 21 Y Y 1 2 Y 2 2
称为Y 参数矩阵.
例1. 求Y 参数。
I1
Yb
I
Yc
2
+ U 1
i1 i2
§2 二端口的参数和方程 + u1 i1 i2 + u2 端口物理量4个
i1
i2 u1 u2
2 0
Y Y 12 21
上例中有
Y Y Y 12 21 b
注意 互易二端口四个参数中只有三个是独立的。
Y Y Y a b b Y Y Y Y b b c
若 Ya=Yc 有 Y12=Y21 ,又Y11=Y22 (电气对称),称为对称二端口。 对称二端口只有两个参数是独立的。 对称二端口是指两个端口电气特性上对称。电路结 构左右对称的,端口电气特性对称;电路结构不对称的 二端口,其电气特性也可能是对称的。这样的二端口也 是对称二端口。
I Y U 1 11 Y 12 1 Y I U 21 Y 22 2 2
若网络内部无受控源(满足互易定理) ,则阻抗矩阵Z对称 12= 21 Y12= Y21 互易二端口网络四个参数中只有三个是独立的。
+ u1 -
Y U I U 2 21 1 Y 22 2
矩阵 形式
I Y U 1 11 Y 12 1 Y Y I U 2 2 21 22
Y Y 11 21 Y Y 1 2 Y 2 2
解得
矩阵 形式
令
I Y U 1 11 Y 12 1 Y I U 21 Y 22 2 2
Y Y 11 21 Y Y 1 2 Y 2 2
称为Y 参数矩阵.
例1. 求Y 参数。
I1
Yb
I
Yc
2
+ U 1
i1 i2
§2 二端口的参数和方程 + u1 i1 i2 + u2 端口物理量4个
i1
i2 u1 u2
第十六章 二端口网络 92页PPT文档
14
§16.2 二端口的参数和方程
上式称为 Z 参数方程,写成矩阵形式为:
Z
参数方程也可由
Y
参数方程解出
U1,U 2
得到, 即:
其中 △=Y11Y22–Y12Y21
15
§16.2 二端口的参数和方程
Z 参数矩阵与 Y 参数矩阵的关系为:
ZY1
16
§16.2 二端口的参数和方程
2、Z 参数的物理意义及计算和测定 在端口 1 上外施电流 I,1 把端口 2 开路,如图所示,由 Z 参数方程得:
级联是信号传输系统中最常见的联接方式。下图为两 个二端口的级联联接,前一个二端口的输入端联接前一个 二端口的输出端,即构成级联。
45
§16.3 二端口的连接
1、级联联接的条件:
显然,二端口的级联联接满足以下关系,
u1bu2a i1bi2a
46
§16.3 二端口的连接
2、级联联接的等效A参数:
(2)当仅由
I
2 作用时(I
=
1
0
,电路N内部独立源均为零),根据齐次定
理有
U (2) 1
z12 I 2
U
(2) 2
z22 I2
(3)当仅由电路N内部的独立源作用时,入口、出口均开路,有
U (3) 1
U OC1
U (3) 2
U OC 2
34
§16.2
根据叠加定理得
二端口的参数和方程
等效电路为
例,如下两图均为结构对称的,显然也是电气对称的。
例,如下图的结构不对称,但电气对称。
24
§16.2 二端口的参数和方程
四、T (A)参数和方程
§16.2 二端口的参数和方程
上式称为 Z 参数方程,写成矩阵形式为:
Z
参数方程也可由
Y
参数方程解出
U1,U 2
得到, 即:
其中 △=Y11Y22–Y12Y21
15
§16.2 二端口的参数和方程
Z 参数矩阵与 Y 参数矩阵的关系为:
ZY1
16
§16.2 二端口的参数和方程
2、Z 参数的物理意义及计算和测定 在端口 1 上外施电流 I,1 把端口 2 开路,如图所示,由 Z 参数方程得:
级联是信号传输系统中最常见的联接方式。下图为两 个二端口的级联联接,前一个二端口的输入端联接前一个 二端口的输出端,即构成级联。
45
§16.3 二端口的连接
1、级联联接的条件:
显然,二端口的级联联接满足以下关系,
u1bu2a i1bi2a
46
§16.3 二端口的连接
2、级联联接的等效A参数:
(2)当仅由
I
2 作用时(I
=
1
0
,电路N内部独立源均为零),根据齐次定
理有
U (2) 1
z12 I 2
U
(2) 2
z22 I2
(3)当仅由电路N内部的独立源作用时,入口、出口均开路,有
U (3) 1
U OC1
U (3) 2
U OC 2
34
§16.2
根据叠加定理得
二端口的参数和方程
等效电路为
例,如下两图均为结构对称的,显然也是电气对称的。
例,如下图的结构不对称,但电气对称。
24
§16.2 二端口的参数和方程
四、T (A)参数和方程
第十六章-二端口网络解析精选课件PPT
对一个端口来说,从其一个端子流 1 i 入的电流一定等于从另一个端子流出的
电流,这种具有向外引出一对端子的电
路或网络称为一端口网络或二端网络。
i
1'
二、二端口网络
反馈网络
2021/3/2
制作群
放大器
4
主 页 总目录 章目录 上一页 下一页 退 出
§16-1 二端口网络
二端口的端口条件:
对于所有时间 t ,从端子1流入方 1 i1
§16-2 二端口的方程和参数
例2:求图示二端口的Y参数。
解: Y Y Y a a b U Y Y 1 b b U U Y 1 1 b Y Y Y b b U U c U 2 2 2 I I 1 1 I 2 g U 1 U-+11I1 Y b g U 1 Y b Y c U 2 I 2 1'
解:
方法一
1
Yb
2
Ya
Yc
I1 U 1Y a Y b I2 U1Yb
Y11UI11 U20 Ya Yb Y21UI21 U20 Yb
I2 U 2Y b Y c I1U2Yb
Y22UI22 U10 YbYc
Y12
2021/3/2
UI12
U10
Yb
制作群
ห้องสมุดไป่ตู้1'
2'
1 I1
Yb
I2 2
+
U1 Y a
Yc
-
1'
本章介绍的二端口:由线性电阻、电感(耦合电感)、 电容和线性受控源组成,并规定不含任何独立电源(如 用运算法分析时,其独立初始条件为零)。
2021/3/2
制作群
6
《二端口网络》课件
根据不同的分类标准,二端口网络可以分为不同的类型,如根据端口数可分为 二端口网络和多端口网络,根据网络参数可分为线性网络和非线性网络等。
特性参数
电压传输系数
表示输入电压与输出电压之比,是衡量 二端口网络传输性能的重要参数。
插入衰减系数
表示在二端口网络的输出端与输入端 之间插入一个网络后引起的信号衰减
控制系统
在控制系统中,二端口网 络用于信号传输和信号处 理,如传感器、执行器、 控制器等。
02
二端口网络的基本元件
电阻器
总结词
表示电路中阻碍电流通过的元件
详细描述
电阻器是二端口网络中的基本元件之一,它对电流通过的阻力与电压成正比,具 有恒定的阻值。电阻器在电路中主要用于限制电流和调节电压。
电感器
03
二端口网络的连接与等效
串联与并联
串联
两个或多个二端口网络按照电流 方向串联在一起,总电压等于各 二端口网络的电压之和。
并联
两个或多个二端口网络并联在一 起,总电流等于各二端口网络的 电流之和。
Y-Δ等效变换
Y-Δ等效变换是一种将Y型二端口网络转换为Δ型二端口网络的方法,反之亦然。 通过改变网络端口的连接方式,可以实现电路的简化或变换。
匹配网络中的二端口网络
总结词
匹配网络中的二端口网络用于阻抗匹配,通 过调整网络的元件参数,使不同阻抗的信号 源和负载之间实现有效的能量传输。
详细描述
在匹配网络中,二端口网络通常由电阻、电 容和电感等元件组成,用于实现信号源和负 载之间的阻抗匹配。通过调整网络的元件参 数,可以减小信号传输过程中的能量损失,
信号流图的简化
在实际应用中,由于系统的复杂性和庞大性,信号流图可能会非常复杂和庞大,这 会给分析带来很大的困难。
特性参数
电压传输系数
表示输入电压与输出电压之比,是衡量 二端口网络传输性能的重要参数。
插入衰减系数
表示在二端口网络的输出端与输入端 之间插入一个网络后引起的信号衰减
控制系统
在控制系统中,二端口网 络用于信号传输和信号处 理,如传感器、执行器、 控制器等。
02
二端口网络的基本元件
电阻器
总结词
表示电路中阻碍电流通过的元件
详细描述
电阻器是二端口网络中的基本元件之一,它对电流通过的阻力与电压成正比,具 有恒定的阻值。电阻器在电路中主要用于限制电流和调节电压。
电感器
03
二端口网络的连接与等效
串联与并联
串联
两个或多个二端口网络按照电流 方向串联在一起,总电压等于各 二端口网络的电压之和。
并联
两个或多个二端口网络并联在一 起,总电流等于各二端口网络的 电流之和。
Y-Δ等效变换
Y-Δ等效变换是一种将Y型二端口网络转换为Δ型二端口网络的方法,反之亦然。 通过改变网络端口的连接方式,可以实现电路的简化或变换。
匹配网络中的二端口网络
总结词
匹配网络中的二端口网络用于阻抗匹配,通 过调整网络的元件参数,使不同阻抗的信号 源和负载之间实现有效的能量传输。
详细描述
在匹配网络中,二端口网络通常由电阻、电 容和电感等元件组成,用于实现信号源和负 载之间的阻抗匹配。通过调整网络的元件参 数,可以减小信号传输过程中的能量损失,
信号流图的简化
在实际应用中,由于系统的复杂性和庞大性,信号流图可能会非常复杂和庞大,这 会给分析带来很大的困难。
电路第五版课件 第十六章二端口网络
-Yb
(3)互易性和对称性 Y11 Y12 Y = 互易性:二端口满足: Y12 = Y21 Y21 Y22 . . I2 I1 Y21 = . Y12 = . . = Yb . = Yb U1 U2=0 U2 U1=0
1 . I1 1' Yb 1 + + . . U2 U1 2' 1' 2 Yb Ya Yc . I2 2'
. I1 . I2 .+ U1 线性 RLCM 受控源 +. U2
直接列方程法 . . . I1 = Y11 U1+ Y12 U2 . . . I2 = Y21 U1+ Y22 U2 写成矩阵形式: . . Y11 Y12 U1 I1 . = . I2 Y21 Y22 U2 Y11 Y12 Y 参数 Y = Y21 Y22 矩阵。 注意:Y 参数值由内部元 件参数及连接关系决定。
I 1 I
2
U 1 U
2
(1) Z参数方程定义 将两个端口各施加一 电流源,则端口电压可 视为电流源单独作用时 的叠加。
Z参数矩阵
注意:Z 参数值由内部元 件参数及连接关系决定。19
(2) Z参数的的物理意义及计算 开路法 . . . U1= Z11 I1 + Z12 I2 . . . U2= Z21 I1 + Z22 I2
Y11 Y12 Y21 Y22
11
Y =
例1:求P型电路的Y参数。 解法1:短路法 . Yb I1 1 Y11 = . . =Ya+Yb U1 U2=0 Ya Yc . I2 Y21 = . . = Yb 1' . U1 U2=0 Yb I1 . 1 + I1 . Y12 = . . = Yb Ya Yc U1 U2 U1=0 . 1' . I2 Y22 = . . =Yb+Yc Yb I1 U2 U1=0 1 Y = Ya+Yb
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用二端口概念分析电路时,仅对二端口处的电流、电压之间 的关系感兴趣,这种相互关系可以通过一些参数表示,而这些参 数只决定于构成二端口本身的元件及它们的连接方式。一旦确定 表征这个二端口的参数后,其端口上的电压、电流关系也就确定 了。可以分下列几步:
1. 确定二端口处电压、电流之间的关系,写出参数矩阵, 在分析中一般使用相量法或运算法。
2. 利用端口参数比较不同的二端口的性能和作用。
3. 对于给定的一种二端口参数矩阵,会求其它的参数矩阵。
4. 对于复杂的二端口,可以看作由若干简单的二端口组 成。由各简单的二端口参数推导出复杂的二端口参数。
16-2 二端口的方程和参数
+ i1 u1 -
i2 + u2 -
端口物理量4个 i1 i2 u1 u2
下:
•
•
I1
•
U1
•
I2 U 2
•
•
U
•
1
U
•
2
I1 I2
•
•
U
•
1
I1
•
I2 U 2
假 一、设Y 端 参数口 和U 方1电 和 程U压 2已知• , + I• 1
端口电 I1和 流 I2未知 •
U1
•
-
线性 无源
•
I2
+
•
-U 2
U
•
1
I1
•
U 2 I2
端U1口和电U流2共同I1和 作用I可2 产视生为。
1
外
NS
电
1 Req +
路
uoc
1’
1’
-
(a)
1 +
外电路 开路电压
(b)
NS
uoc
N0
-
1’
(c)
(d)
外 电 路
1 无源二端 口等效电
R
阻
eq
1’
二、四端网络 在工程实际中,研究信号及能量的传输和信号变换时,还常
常涉及两对端子之间的关系,如变压器、滤波器、放大器、反馈 网络等,都可以把两对端子之间的电路概括在一个方框中,一对 端子通常是输入端子,另一对端子为输出端子。称为四端网络。
六、二端口研究的问题
1.讨论范围 只含线性R、L、C、M与线性受控源而不含独
立源(运算法分析时,不包含附加电源)。
2.参考方向 + i1
u1 –
i1
线性RLCM 受控源
i2 +
u2 – i2
本章中二端口的参考方向,一般都如上图所示。因此,引
用公式时一定要注意端口的参考方向→标准参考方向。
例:
E
七、二端口网络的分析方法
I1 Y11U1 Y12U2 I2 Y21U1 Y22U2
矩阵 形式
II12Y Y1211 Y Y1222U U12 令
Y
Y11 Y21
Y12 Y22
不难看出Y 参数具有导纳的性质 称为Y 参数矩阵→Y参数
方框中无受控源(互易网络)时有Y12=Y21,只有三个参数独立 方框中为对称网络时有Y12=Y21,Y11=Y22,只有两个参数独立
组方程。即可用6套参数描述二端口网络。常用4套参数Z、Y
、T、H参数。
在所研究的二端口网络方程和参数中,均采用如图标准参考方向
•
1 I1
+
•
U1
1`
•
I2
N0
相量模型
2
I1(s)
+
+
•
U2
U 1(s) _
-Hale Waihona Puke 2`线性 无源 非时变 二端口 网络
I2(s)
+
U 2(s) _
运算模型
若我们采用相量形式(正弦稳态)来讨论,则4个物理量的关系如
i2' i2 i i2
i2
2+
u2 – i2 2
端口 条件 破坏
五、N端网络和N端口 1.N端网络 如果一个网络有N个端子向外接出,在分析中又并不关心 电路的内部结构及内部各个支路的情况,而只讨论外电路的状 态与变化时,称该网络为N端网络。 2.N端口网络 如果一个网络有2N个端子向外接出,这2N个端子又成对 出现,即端口处的输入电流等于输出电流时,该网络可以视 为一个N端口网络。
i2
上述限制。
i1
i2
i1
i2
具有公共端的二端口
i1
i2
二端口
i2
i1 i3
i4 三端口或六端网络
四端网络 二端口的两个端口间若有外部连接,则会破坏原二端口的
端口条件。 1 +
i1
3
R
4
u1 –
i1
i2
1 i1 3
4
1-1’ 2-2’是二端口
i1' i1 i i1
3-3’ 4-4’不是二端口,是 四端网络
Y参数的实验测定
I1 Y11U 1 Y12U 2
Y1 1
I1 U1
U2 0
Y1
2
I1 U 2
U1 0
I2 Y21U 1 Y22U 2
短路输入导纳
•
(驱动点导纳)
I1
•+
U1
短路转移导纳 -
线性 无源
Y2 1
I2 U1
U 2 0
短路转移导纳
•
I1
线性
Y2
2
I2 U 2
U1 0
短路输入导纳 (驱动点导纳)
i1 +
u1
i1
–
端口的概念:
端口由一对端子构成,且满足如下 条件:从一个端子流入的电流恒等 于从另一个端子流出的电流。这称 为端口条件。
我们已经知道:如果一个复杂的电路只有两个端子向外 连接,且仅对外接电路中的情况感兴趣,则该电路可视为 一个一端口,并用戴维宁或诺顿等效电路替代,然后再计 算感兴趣的电压和电流。
U 2 0 Yb Yc
YYaYYbb
Yb Yb Yc
无源
Y参数是在端口短路时得到的,故称短路导纳参数。
•
I2
•
I2 +
•
-U 2
例1. 求Y 参数。
•
I1
Yb
•
I2
+
•
U1
Ya
Yc
•
U2 0
解:
Y11U I11 U20 YaYb
Y21UI21 U20 Yb
•
I1
Yb
•
I2
+
Y12
I1 U 2
U1 0 Yb
•
•
U1 0
Ya Yc
U2
Y22
I2 U 2
分析电路时,端口4个物理量一般用相量或象函数表示,即
I 1 ( 1 ( I I s 2 ( 2 ( ) I s U ) 1 (1 ) ( U ) ) U s 2 ( U ) 2 ( s ))
•
I1
•+ U1
-
线性 无源
•
I2 +
•
U2 -
四个端口变量之间存在着反映二端口网络特性的约束方程
。任取两个作自变量(激励),两个作因变量(响应),可得6
线性RLCM 受控源
例
R
C
C
四端网络
滤波器
三极管 n:1
传输线
变压器
三、二端口(two-port)
如果四端网络的两对端子同时满足端口条件,则称为
二端口网络。
+
i1
u1 –
i1
线性RLCM 受控源
i2 +
u2 – i2
四、二端口与四端网络的区别:
二端口的两个端口必须满足 端口条件,四端网络却没有
i1
第十六章二端口网络
目录
16-1 二端口网络
16-2 二端口网络的方程和参数 16-3 二端口的等效电路 16-4 二端口的转移函数 16-5 二端口的连接 16-6 回转器和负阻抗变换器
16-1 二端口网络
一、二端网络(一端口)回顾
I
+
U
-
Z (Y)
表征一端口网络电特性的独立
参数:输入阻抗Z或输入导纳Y。 且ZY1。
1. 确定二端口处电压、电流之间的关系,写出参数矩阵, 在分析中一般使用相量法或运算法。
2. 利用端口参数比较不同的二端口的性能和作用。
3. 对于给定的一种二端口参数矩阵,会求其它的参数矩阵。
4. 对于复杂的二端口,可以看作由若干简单的二端口组 成。由各简单的二端口参数推导出复杂的二端口参数。
16-2 二端口的方程和参数
+ i1 u1 -
i2 + u2 -
端口物理量4个 i1 i2 u1 u2
下:
•
•
I1
•
U1
•
I2 U 2
•
•
U
•
1
U
•
2
I1 I2
•
•
U
•
1
I1
•
I2 U 2
假 一、设Y 端 参数口 和U 方1电 和 程U压 2已知• , + I• 1
端口电 I1和 流 I2未知 •
U1
•
-
线性 无源
•
I2
+
•
-U 2
U
•
1
I1
•
U 2 I2
端U1口和电U流2共同I1和 作用I可2 产视生为。
1
外
NS
电
1 Req +
路
uoc
1’
1’
-
(a)
1 +
外电路 开路电压
(b)
NS
uoc
N0
-
1’
(c)
(d)
外 电 路
1 无源二端 口等效电
R
阻
eq
1’
二、四端网络 在工程实际中,研究信号及能量的传输和信号变换时,还常
常涉及两对端子之间的关系,如变压器、滤波器、放大器、反馈 网络等,都可以把两对端子之间的电路概括在一个方框中,一对 端子通常是输入端子,另一对端子为输出端子。称为四端网络。
六、二端口研究的问题
1.讨论范围 只含线性R、L、C、M与线性受控源而不含独
立源(运算法分析时,不包含附加电源)。
2.参考方向 + i1
u1 –
i1
线性RLCM 受控源
i2 +
u2 – i2
本章中二端口的参考方向,一般都如上图所示。因此,引
用公式时一定要注意端口的参考方向→标准参考方向。
例:
E
七、二端口网络的分析方法
I1 Y11U1 Y12U2 I2 Y21U1 Y22U2
矩阵 形式
II12Y Y1211 Y Y1222U U12 令
Y
Y11 Y21
Y12 Y22
不难看出Y 参数具有导纳的性质 称为Y 参数矩阵→Y参数
方框中无受控源(互易网络)时有Y12=Y21,只有三个参数独立 方框中为对称网络时有Y12=Y21,Y11=Y22,只有两个参数独立
组方程。即可用6套参数描述二端口网络。常用4套参数Z、Y
、T、H参数。
在所研究的二端口网络方程和参数中,均采用如图标准参考方向
•
1 I1
+
•
U1
1`
•
I2
N0
相量模型
2
I1(s)
+
+
•
U2
U 1(s) _
-Hale Waihona Puke 2`线性 无源 非时变 二端口 网络
I2(s)
+
U 2(s) _
运算模型
若我们采用相量形式(正弦稳态)来讨论,则4个物理量的关系如
i2' i2 i i2
i2
2+
u2 – i2 2
端口 条件 破坏
五、N端网络和N端口 1.N端网络 如果一个网络有N个端子向外接出,在分析中又并不关心 电路的内部结构及内部各个支路的情况,而只讨论外电路的状 态与变化时,称该网络为N端网络。 2.N端口网络 如果一个网络有2N个端子向外接出,这2N个端子又成对 出现,即端口处的输入电流等于输出电流时,该网络可以视 为一个N端口网络。
i2
上述限制。
i1
i2
i1
i2
具有公共端的二端口
i1
i2
二端口
i2
i1 i3
i4 三端口或六端网络
四端网络 二端口的两个端口间若有外部连接,则会破坏原二端口的
端口条件。 1 +
i1
3
R
4
u1 –
i1
i2
1 i1 3
4
1-1’ 2-2’是二端口
i1' i1 i i1
3-3’ 4-4’不是二端口,是 四端网络
Y参数的实验测定
I1 Y11U 1 Y12U 2
Y1 1
I1 U1
U2 0
Y1
2
I1 U 2
U1 0
I2 Y21U 1 Y22U 2
短路输入导纳
•
(驱动点导纳)
I1
•+
U1
短路转移导纳 -
线性 无源
Y2 1
I2 U1
U 2 0
短路转移导纳
•
I1
线性
Y2
2
I2 U 2
U1 0
短路输入导纳 (驱动点导纳)
i1 +
u1
i1
–
端口的概念:
端口由一对端子构成,且满足如下 条件:从一个端子流入的电流恒等 于从另一个端子流出的电流。这称 为端口条件。
我们已经知道:如果一个复杂的电路只有两个端子向外 连接,且仅对外接电路中的情况感兴趣,则该电路可视为 一个一端口,并用戴维宁或诺顿等效电路替代,然后再计 算感兴趣的电压和电流。
U 2 0 Yb Yc
YYaYYbb
Yb Yb Yc
无源
Y参数是在端口短路时得到的,故称短路导纳参数。
•
I2
•
I2 +
•
-U 2
例1. 求Y 参数。
•
I1
Yb
•
I2
+
•
U1
Ya
Yc
•
U2 0
解:
Y11U I11 U20 YaYb
Y21UI21 U20 Yb
•
I1
Yb
•
I2
+
Y12
I1 U 2
U1 0 Yb
•
•
U1 0
Ya Yc
U2
Y22
I2 U 2
分析电路时,端口4个物理量一般用相量或象函数表示,即
I 1 ( 1 ( I I s 2 ( 2 ( ) I s U ) 1 (1 ) ( U ) ) U s 2 ( U ) 2 ( s ))
•
I1
•+ U1
-
线性 无源
•
I2 +
•
U2 -
四个端口变量之间存在着反映二端口网络特性的约束方程
。任取两个作自变量(激励),两个作因变量(响应),可得6
线性RLCM 受控源
例
R
C
C
四端网络
滤波器
三极管 n:1
传输线
变压器
三、二端口(two-port)
如果四端网络的两对端子同时满足端口条件,则称为
二端口网络。
+
i1
u1 –
i1
线性RLCM 受控源
i2 +
u2 – i2
四、二端口与四端网络的区别:
二端口的两个端口必须满足 端口条件,四端网络却没有
i1
第十六章二端口网络
目录
16-1 二端口网络
16-2 二端口网络的方程和参数 16-3 二端口的等效电路 16-4 二端口的转移函数 16-5 二端口的连接 16-6 回转器和负阻抗变换器
16-1 二端口网络
一、二端网络(一端口)回顾
I
+
U
-
Z (Y)
表征一端口网络电特性的独立
参数:输入阻抗Z或输入导纳Y。 且ZY1。
