机械动力学.
机械动力学

…………………② …………………③ 阻力(矩)不变。
M r0 r M d d
0 Md Md
=
不计摩擦驱动力(矩)
计摩擦驱动力(矩) 计摩擦阻力(矩)
Mr = 0 Mr
不计摩擦阻力(矩)
驱动力(矩)不变。
第四节 刚性转子的平衡设计
1.静平衡设计(D/b5)
o表征几何形状对摩擦力的影响。
θ
Q
θ
N 21 2
②
N 21 2
①
3)o 总汇 (1) 简单平面移动副
o =
N21
v12 P
f21 1 2 Q
3)o 总汇
(2) V形槽移动副
Q
o=/sin
θ
θ
N 21 2
②
N 21 2
①
3)o 总汇
比较槽面摩擦:o=/sin
(3) 三角螺旋副 Q
34
FR R32
1 4
2
R41
R43
R12
21 23
Md R41
2
R43
FR
1
4
3 V34
R32
【教师例7-2】图示平底摆动从动件盘状凸轮机构的 凸轮为圆盘,摩擦圆、摩擦角、驱动力矩Md、阻力FR 如图所示。试画出图示机构的静力分析图。
【解】 R12 2 R32 FR
1、Md
二、单自由度系统等效力学模型的建立 1.建立系统运动方程 建立依据: dE dW Ndt
1 1 1 1 2 2 2 2 J J m m E S1 1 S2 2 2 S2 3 S3 2 2 2 2 N M d 1 m2 g S 2 cos Fr S 3
机械动力学课程教学大纲

机械动力学课程教学大纲一、课程简介机械动力学是机械工程中的重要基础课程之一,主要研究物体的运动规律和动力学原理。
本课程旨在培养学生对物体运动的分析和动力学理论的理解能力,为学生提供运动学和动力学的基础知识,为他们今后的学习和研究奠定牢固基础。
二、教学目标1. 培养学生对物体运动的观察和分析能力;2. 熟悉运动学和动力学的基本概念和原理;3. 掌握常见的力学定律和公式;4. 培养学生的问题解决能力和实践能力;5. 培养学生的团队合作能力和沟通能力。
三、教学内容1. 运动学基础1.1 位置、位移和速度1.2 加速度和曲线运动 1.3 圆周运动和角速度1.4 相对运动2. 动力学基础2.1 牛顿运动定律2.2 动量和动量守恒2.3 力和加速度2.4 动能和功2.5 能量守恒和机械能3. 静力学3.1 弹簧力和弹性势能 3.2 引力和万有引力定律3.3 惯性力和离心力4. 动力学4.1 圆周运动的力学分析4.2 非惯性系和转动惯量4.3 力矩和角动量4.4 角动量守恒和刚体转动4.5 飞行器的运动学和动力学四、教学方法1. 讲授理论知识:通过课堂讲解、示范等方式,向学生介绍理论知识和基本概念。
2. 实验教学:设计相关实验,让学生进行实验操作和数据分析,提高他们的实践能力。
3. 小组讨论:设置小组活动,让学生在团队中合作解决问题,培养团队合作和沟通能力。
4. 课堂练习:布置课后作业和练习题,加强对知识的巩固和运用能力。
五、考核方式1. 平时表现(20%):包括课堂参与、作业完成情况等。
2. 实验报告(30%):根据实验要求撰写实验报告并提交。
3. 期中考试(20%):考察对课程内容的理解和掌握程度。
4. 期末考试(30%):综合考察整个课程的学习成果。
六、参考教材1. 赵凤岐,机械动力学,高等教育出版社,2015年。
2. 谢振波,机械力学基础,清华大学出版社,2013年。
七、参考网址无。
八、备注本课程的教学大纲可根据实际教学需求进行调整和补充,以确保教学内容的连贯性和可操作性。
机械动力学分析

机械动力学分析机械动力学是研究物体受到外力作用时的运动规律和力学性质的学科。
它对于机械设计和工程分析非常重要。
本文将对机械动力学的基本概念、分析方法和实际应用进行详细探讨。
第一部分:机械动力学基础1.运动和力学运动是物体的位置随时间变化的过程。
力学是研究物体运动和力之间关系的学科。
在机械动力学中,重要的概念包括位移、速度、加速度和质量等。
2.牛顿定律牛顿定律是机械动力学的基石。
根据牛顿定律,物体受到的合力等于物体质量乘以加速度。
这个定律适用于解决物体在恒力作用下的运动问题。
3.动力学原理动力学原理描述了物体在受到外力作用时的运动规律。
其中,动量守恒原理和能量守恒原理是常用的分析工具。
动量守恒原理指出,在没有外力作用的情况下,物体的动量保持不变。
能量守恒原理指出,在封闭系统中,能量的总量保持不变。
第二部分:机械动力学分析方法1.静力学分析静力学是机械动力学的基础。
它研究物体在平衡状态下的受力和受力转矩。
静力学分析常使用受力图和受力平衡方程来求解。
2.运动学分析运动学研究物体的运动状态,包括位置、速度和加速度等。
运动学分析常使用位移、速度和加速度的关系式进行计算。
3.动力学分析动力学分析研究物体在受力作用下的运动规律。
它涉及物体的质量、力、加速度和位移等参数的计算。
常见的动力学分析方法包括牛顿第二定律、动量守恒和能量守恒的应用。
第三部分:机械动力学的实际应用1.机械设计机械动力学分析在机械设计中起着重要的作用。
通过对机械系统的动力学分析,可以评估机械的工作性能和可靠性,优化设计方案,减少能量消耗和材料使用等。
2.工程分析机械动力学分析在工程领域中广泛应用。
例如,在桥梁设计中,需要对桥梁受力和振动进行动力学分析,以保证结构的安全性和可靠性。
在汽车工程中,需要对汽车的运动性能和悬挂系统进行动力学分析,以提高驾驶舒适性和行驶稳定性。
3.故障诊断与维修机械动力学分析可以用于故障诊断和设备维修。
通过对受损机械的动力学分析,可以确定故障原因,并采取相应的维修措施。
第7章机械动力学
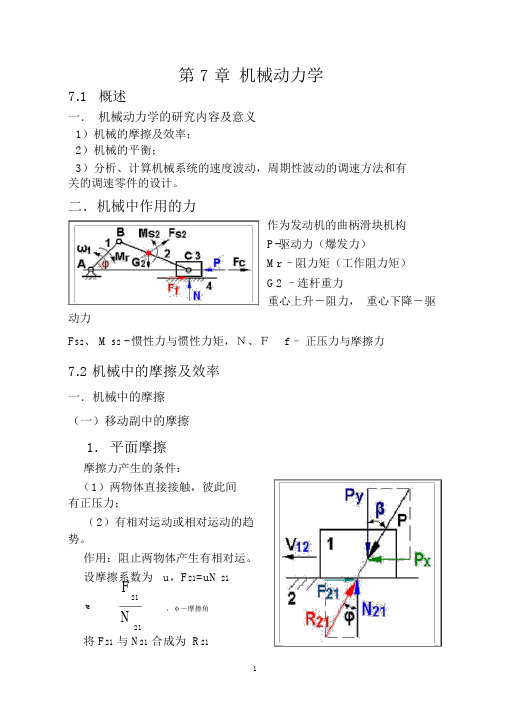
第 7 章机械动力学7.1概述一.机械动力学的研究内容及意义1)机械的摩擦及效率;2)机械的平衡;3)分析、计算机械系统的速度波动,周期性波动的调速方法和有关的调速零件的设计。
二.机械中作用的力作为发动机的曲柄滑块机构P-驱动力(爆发力)Mr –阻力矩(工作阻力矩)G2 –连杆重力重心上升-阻力,重心下降-驱动力F S2、 M S2 - 惯性力与惯性力矩,N、F f –正压力与摩擦力7.2 机械中的摩擦及效率一.机械中的摩擦(一)移动副中的摩擦1.平面摩擦摩擦力产生的条件:(1)两物体直接接触,彼此间有正压力;(2)有相对运动或相对运动的趋势。
作用:阻止两物体产生有相对运。
设摩擦系数为u,F21=uN 21F21tg,φ-摩擦角N21将 F21与 N21合成为 R21R21-总反力(全反力)P X P分解为 P和 P ,tgX Y P Y( P X P sin、 P Y P cos )F21P X,有F21tgY 方向平衡: Py=N 21,即:tg tg P Xtg讨论:①总反力 R21恒与相对速度V 12成 90° +φ②当β >φ, P X > F21,滑块作加速运动;当β =φ, P X = F21,动则恒动,静则恒静;当β <φ, P X < F21,原来运动,作减速运动,原来静止,永远静止,称自锁。
③ 自锁条件:β≤φβ=φ,条件自锁(静止);β<φ,无条件自锁。
2.斜面摩擦斜面机构如图,滑块置于升角α的斜面上,摩擦角为φ,作用于滑块上的铅垂力为Q,求滑块等速上升和下降时所需水平平衡力P 和 P’。
(1)求等速上升水平平衡力 PP-驱动力, Q-阻力PQ R 21 0 ,tg ()P,P Qtg () (1)Q( 2)求等速下降水平平衡力 P ’Q -驱动力, P ’-阻力P'Q R 21 0 ,tg () P ',P 'Qtg () (2)Q讨论:① 欲求下滑 (反行程) P ’,只需将式 ( 1)中 P →P ’,φ→ (-φ )② 下滑时,当α >φ, P ’为平衡力α <φ, P ’为负,成为驱动力的一部分,该条件下,若无 P ’,则无论 Q 多大,滑块不下滑,称自锁,自锁条件:α≤φ。
机械动力学动力分析原理

机械动力学动力分析原理机械动力学是力学的一个重要分支,研究机械系统在外力作用下的运动规律。
在机械系统的设计、制造和优化过程中,动力分析起着重要的作用。
动力分析主要是指通过计算和分析力学参数,来研究机械系统的运动学特性、力学特性和动力学特性。
本文将介绍机械动力学动力分析的基本原理。
一、动力学基本概念在进行机械动力学动力分析之前,我们首先要了解一些基本概念。
1. 动力学:研究物体的运动是如何受到力的作用而改变状态的学科。
2. 动力学分析:通过对机械系统的力学参数进行计算和分析,以研究机械系统的运动规律和力学特性。
3. 动力:物体改变其状态所受到的力。
4. 动力学平衡:在机械系统中,当物体的运动状态不发生变化时,称为动力学平衡。
5. 力矩:力在力臂上的作用产生的力矩。
6. 动力矩:力矩与角速度的乘积,反映了物体绕固定轴旋转的难易程度。
二、动力分析的原理机械动力学动力分析的原理主要基于牛顿第二定律和动量定理。
1. 牛顿第二定律牛顿第二定律是机械动力学的基础,表明物体的加速度与作用力成正比,与物体的质量成反比。
在直线运动中,牛顿第二定律可以表达为F=ma,其中F是物体所受的合外力,m是物体的质量,a是物体的加速度。
在旋转运动中,牛顿第二定律可以表达为τ=Iα,其中τ是物体所受的合外力矩,I是物体的转动惯量,α是物体的角加速度。
2. 动量定理动量定理表明,当物体所受的合外力矩为零时,物体的角动量守恒。
动量定理可以表达为Στ=0,其中Στ是物体所受的合外力矩。
三、动力分析的应用机械动力学动力分析的应用非常广泛,涉及到各种机械系统的设计和优化。
1. 运动学分析通过对机械系统的运动学参数进行计算和分析,可以了解机械系统的运动规律和运动状态。
例如,可以计算机械系统的速度、加速度和位移等参数。
2. 力学分析通过对机械系统的力学参数进行计算和分析,可以了解机械系统所受的各种力和力矩的大小和方向,从而为机械系统的设计提供依据。
机械动力学

机械动力学
机械动力学是一种力学分支,用来研究物体的运动规律。
机械力学的基本原理是,物体受力时要考虑它的动量、势能和力学运动状态。
机械力学研究物体受力后,如何协调运动以实现力学系统的最终目标。
机械动力学的基本方程是力学平衡方程,它描述了物体在力学运动中,受力的情况下,动能、势能和运动状态变化的情况。
力学平衡方程主要由三个部分组成:力学定制、力学规律和力学流形。
力学定制是机械动力学的基本原理,它涉及物体的力学变化,包括物体的运动状态、势能和动能。
力学定制可以用来计算物体受力时,各变量的变化速率。
力学规律是机械动力学的第二个基本原理,它涉及物体在力学运动中受力所产生的力学变化。
力学规律具体表示为:物体受力时,质量、动量、势能和动能会发生变化。
力学流形是机械动力学的第三个基本原理,它涉及物体在力学运动中受力的情况下,力学参数的变化。
力学流形是由力学规律的积累,它可以提供物体在各种力学变化状态下的精确的运动状态。
机械动力学是一种比较复杂的力学,研究不仅仅限于物体受力时的运动状态,还可以涉及力学设计与分析、力学模拟、力学断裂以及力学仿真等方面。
它可以帮助科学家们深入了解物体运动规律,为人们在有限工作环境中分析残缺机械参数提供技术支持,实现更加省力、精确且有效的力学分析。
在当今社会,机械动力学已成为一门重要的科学,广泛应用于工
程设计、航天技术、发动机技术、精密仪器等领域。
未来,机械动力学将继续发挥重要作用,在复杂的工程设计及技术开发过程中,与其他科学形成有机结合,以实现精确、有效的力学应用。
机械动力学

机械动力学机械动力学是机械工程的一个重要分支,它是一门研究物体的大小、形状、机构及运动的科学。
内容涵盖物理、力学、化学、材料科学、计算机科学和生物学等学科领域,并研究机械系统、工程机械以及各种物质运动问题,为机械工程领域提供理论支持。
机械动力学主要攻克三大难题:第一是关于物质在力械系统中传递、转换及被能量影响的机制。
第二个难题是关于机械系统的动力学性能,包括阻尼、刚度、转动惯量等,它们在物理学中被称作系统参数,它们能反映出物质运动的宏观特性。
第三个难题是关于物体的结构、机构、形状等,这反映出物质运动的宏观特性,例如物体的柔性或者刚性。
机械动力学的研究方法和应用广泛,有数学分析法,特别是拉格朗日多元微分方程,以描述物质在运动中变换的过程;还有实验测量法,如力计、振动计和粒子传感器,它们可以快速准确测量物质运动中的参数变化;有数值模拟法,如有限元法、离散元法、库伦法等,它们可以模拟物质在各种复杂条件下的运动;还有控制理论和正反控制等,这些也是机械动力学领域的重要研究内容。
机械动力学的应用领域非常广泛,如机械工程中的机械设计、机械制造、机械运动分析、机械传动系统、阻尼控制、模型分析、机械修理等;航空航天工程中的空气动力学、宇宙物理学、力学、气动学等;军事工程中的弹道学、飞行动力学、航空发动机等;还有汽车工程、核工程等,机械动力学的理论及技术应用极为广泛。
未来,机械动力学将会给对机械工程设计、制造及保养带来积极变化,有助于各种设备的优化设计和更高效的运行,改善机械系统的可靠性和可用性,缩短交付时间,降低成本。
未来,机械动力学将会发展为一门非常重要的工程学科,以实现更高质量、更低成本的技术进步。
从机械动力学的发展及应用来看,它为机械工程领域提供了重要理论支持。
它极大地促进了现代机械设计、制造和修理,使机械系统具有更高的可靠性和可用性,对现代工程技术的发展有着重要的意义。
机械动力学

机械动力学机械动力学是研究机械构件运动的科学,它强调机械构件的物理性质、物理规律和运动规律的分析以及所产生的结果。
它是工程学和物理学的一门重要学科。
机械动力学的研究对象也包括机械系统和机械结构,它涵盖了机械中所有的构件和元件,其中包括弹簧、螺栓、联接杆以及多节折杆、活动构件等等。
机械动力学的研究包括动力分析、结构动力分析、运动学模型以及弹性动力学研究等多方面的研究。
动力分析是研究机械构件的运动规律、受力规律以及受力的来源。
结构动力分析是分析机械构件的结构特性,包括构件的静态特性、动态特性和动态反应特性。
运动学模型是利用运动学分析来求解机械系统或机械构件的运动规律,找出其位置、速度和加速度的关系。
弹性动力学研究是分析机械构件或机械系统在受力时位移和变形的变化规律,研究机械构件弹性变形特性和稳定性等方面的内容。
机械动力学在工程设计和研究中占据重要地位。
在工程中,机械动力学的研究主要集中在机械设备的动力设计和动力分析方面。
例如,在设计某种机械设备时,需要对机械构件的运动规律进行动力分析,以便确定机械设备的动态特性,使机械设备能够满足其安全、可靠和持续可用的要求。
在工程研究中,机械动力学要求研究者清楚地了解机械构件的运动规律,以及构件可能出现的不确定性和冲击力对机械构件的影响,使其能有效的研究机械系统的运动特性。
在实际工程应用中,机械动力学的研究是应用最广泛的,它不仅能够发掘机械系统的运动规律,而且能够发现机械构件或机械系统在运行过程中可能出现的缺陷和质量问题,从而帮助设计和实现更高效、更安全的机械设备。
机械动力学是实际工程应用中重要的科学,它不仅能够提供基础理论,而且能够有效地帮助设计和实现高效、安全的机械设备,使机械设备的效率有所提高。
本文就机械动力学的基本概念、研究内容以及在工程设计和研究中的应用进行了阐述,以期提供一定的理论参考,促进对机械动力学的研究。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、判断题4、优化平衡就是采用优化的方法获得一个绝对最佳解。
()5、在动力分析中主要涉及的力是驱动力和生产阻力。
()6、通路定理是用来判断能否实现摆动力完全平衡的理论。
()7、惯性力的计算是建立在主动构件作理想运动的假定的基础上的。
()8、当取直线运动的构件作为等效构件时,作用于系统上的全部外力折算到该构件上得到等效力。
()9、无论如何,等效力与机械驱动构件的真实速度无关。
()10、等效质量和等效转动惯量与机械驱动构件的真实速度无关。
()11、摆动力的平衡一定会导致机械结构的复杂化。
()12、综合平衡不仅考虑机构在机座上的平衡,同时也考虑运动副动压力的平衡和输入转矩的平衡。
()26、拉格朗日方程是研究约束系统静力动力学问题的一个普遍的方法。
()27、当以电动机为原动机时,驱动力矩是速度的函数。
()28、等效质量和等效转动惯量与质量有关。
()29、在不含有变速比传动而仅含定速比传动的系统中,传动比为常数。
()30、为了使得等效构件的运动与机构中该构件的运动一致,要将全部外力等效地折算到该机构上,这一折算是依据功能原理进行的。
()二、单选题36、机构摆动力矩完全平衡的条件为机构的()为常数。
A、质量矩B、动量矩C、转动惯量D、惯性矩37、摆动力的完全平衡常常会导致机械结构的()。
A、简单化B、轻量化C、复杂化D、大型化38、当取定轴转动的构件作为等效构件时,作用于系统上的全部外力折算到该构件上得到()。
A、等效质量B、等效转动惯量C、等效力D、等效力矩39、等效质量和等效转动惯量与()有关。
A、传动比B、质量C、转动惯量D、等效力40、输入功大于输出功,其差值是()。
A、盈功B、亏功C、正功D、负功41、在以下所有方法中,概念最清晰、易于理解的是()。
A、广义质量代换法B、线性独立矢量法C、质量矩替代法D、有限位置法42、优化平衡就是采用优化的方法获得一个()。
A、绝对最佳解B、相对最佳解C、实际解D、理论解43、在含有连杆机构或凸轮机构等变速比传动的系统中,传动比仅与机构的()有关。
A、速度B、角速度C、加速度D、位置44、当以电动机为原动机时,驱动力矩是()的函数。
A、加速度B、角加速度C、速度D、角速度45、机器本身是振源,将其与地基隔离开来,以减少其对周围的影响,称为()。
A、隔振B、减振C、被动隔振D、主动隔振46、在研究摆动力的平衡时,不涉及惯性力矩,可以采用()。
A、静代换B、动代换C、静力代换D、摆动力代换51、机构的总质心为零的是()。
A、总质心作匀速直线运动B、总质心作变速直线运动C、总质心作圆周运动D、总质心作减速运动52、机构摆动力完全平衡的条件为:机构运动时机构的动量矩为()。
A、0B、关于速度的函数C、关于质量的函数D、常数53、无法实现摆动力完全平衡的方法有()。
A、加配重B、合理布置机构C、设置附加机构D、减小体积54、可以引起机构在机座上的振动的是()。
A、速度的变化B、摆动力C、速度的周期变化D、加速度的变化55、摆动力完全平衡的缺点有()。
A、减少振动B、减小摩擦C、使机械结构复杂化D、使机械体积增加56、以下选项中,不能归为阻尼的是()。
A、物体的内力B、物体表面间的摩擦力C、周围介质的阻力D、材料的内摩擦57、飞轮有()的作用。
A、平衡器B、储能器C、加大系统加速度D、减小系统惯性58、描述等效构件运动的方程式形式有()。
A、能量形式B、动量形式C、加速度形式D、平衡力形式59、为了使得等效构件的运动与机构中该构件的运动一致,不能将()等效地折算到该机构上。
A、全部外力B、所有质量C、所有转动惯量D、全部内力60、当取直线运动的构件作为等效构件时,作用于系统上的全部()折算到该构件上得到等效质量。
A、全部外力B、质量和转动惯量C、转动惯量D、全部内力三、多选题62、假定构件为刚体,且忽略构件的弹性变形的分析方法有()。
A、静力分析B、动态静力分析C、弹性动力分析D、动力分析63、根据惯性载荷造成的危害,机构的平衡可分为以下几种()。
A、机构在机座上的平衡B、机构输入转矩的平衡C、机构滑动副中动压力的平衡D、运动副中动压力的平衡64、机构的总质心为零,有()这些可能。
A、总质心作匀速直线运动B、总质心作变速直线运动C、总质心作圆周运动D、总质心静止不动67、作用在机械上的力有()。
A、驱动力B、重力C、摩擦力D、生产阻力68、当取直线运动的构件作为等效构件时,作用于系统上的全部()折算到该构件上得到等效质量。
A、全部外力B、质量C、转动惯量D、全部内力69、描述等效构件运动的方程式有()。
A、能量形式B、动量形式C、力矩形式D、平衡力形式70、工业机器人通常由()组成。
A、执行机构B、驱动装置C、控制系统D、传感系统71、机械系统运转的全过程可分为()这几个阶段。
A、急停阶段B、启动阶段C、稳定运转阶段D、停车阶段72、在动力分析中,主要涉及的力是()。
A、驱动力B、重力C、摩擦力D、生产阻力73、以下选项中,与等效力有关的是()。
A、外力B、传动比C、ωj/vD、v k/v74、以下选项中,与等效力矩有关的是()。
A、外力据B、传动比C、ωj/ωD、v k/ω75、以下选项中,可归为阻尼的有()。
A、物体的内力B、物体表面间的摩擦力C、周围介质的阻力D、材料的内摩擦四、填空题76、从惯性载荷被平衡的程度看,平衡可分为、和。
77、机械动力学的分析方法按功能分类可分为和。
78、动力学的分析方法按水平分类,可分为、、和。
79、用质量再分配实现摆动力的完全平衡,其分析方法主要有、、和。
80、机械系统运转的全过程可分为、和这几个阶段。
81、机器人动力学是机器人、和的基础。
82、工业机器人通常由、、和组成。
83、二自由度系统的等效转动惯量是系统的、、和的函数。
84、实现摆动力完全平衡的方法有、和。
期末复习题《机械动力学》参考答案一、判断题1-5√×√×√ 6-10×√√√√ 11-15 ×√××× 16-20 ×√√×√21-25 √××√× 26-30 √××√√二、单选题31-35 BCBCD 36-40 AABCC 41-45 BBDDD 46-50 ABCDA 51-55 ADDBC56-60 ABADB三、多选题61.AB 62.ABD 63.ABD 64.AD 65.BC 66.ABCD 67.ABCD 68.BC 69.AC 70.ABCD71.BCD 72.AD 73.ABCD 74.ABCD 75.BCD四、填空题76、部分平衡、完全平衡、优化综合平衡77、动力学反问题、动力学正问题78、静力分析、动态静力分析、动态分析、弹性动态分析79、广义质量代换法、线性独立矢量法、质量矩替代法、有限位置法80、启动阶段、稳定运转阶段、停车阶段81、操作机设计、控制器设计、动态性能分析82、执行机构、驱动装置、控制系统、传感系统83、时间、惯性参数、几何参数、广义坐标84、加配重、合理布置机构、设置附加机构五、计算题85、解:1)各个构件的受力图如下所示:(曲柄连杆滑块各5分,共15分)2)根据受力图可以得到曲柄平衡方程如下:(各个构件的平衡方程分别为5分,共15分)RB RA 1RBd F F 0P F M 0⎧-=⎪⎨⨯+=⎪⎩化为标量式为:RBX RAX RBy RAy B F F 0F F 0x 0RByB RBx d F y F M ⎧-=⎪-=⎨⎪-+=⎩其中:11x cos ,sin B B r y r θθ==根据受力图可以得到连杆平衡方程如下:RC RB 222222F F m RC RB S P F q F J θ⎧-=⎪⎨⨯-⨯=⎪⎩化为标量式为:222222RCx RBx 2RCy RBy 222F F F F ()()()()s s c s RCy c s RCx B s RBy B s RBx m xm y x x F y y F x x F y y F J θ⎧-=⎪⎪-=⎨⎪-----+-=⎪⎩ 其中:221212x cos cos ,sin sin s s r L y r L θθθθ=+=-12c x cos cos y 0c r l θθ=+=,根据受力图可以得到滑块平衡方程如下:RC 33F m S -=化为标量式为:33RCx 33F 0s RDy RCy s m x F F m y -=⎧⎪⎨-==⎪⎩其中:3312x cos cos ,0s c s c x r l y y θθ==+==86、解:(2分)图2以构件1为等效构件时,等效动力学模型如上图2。
等效构件的角速度与构件1的角速度同为ω1。
根据等效构件所具有的动能等于原机械系统的总动能;等效转动惯量J e 为:2133212221221⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+=ωωωωv m v m J J J c c e (12分)根据等效构件的瞬时功率等于原机械系统的总瞬时功率,等效力矩M e 为:⎪⎪⎭⎫⎝⎛+=13331cos ωαv F M M e (6分)其中,3α为F 3与V 3的夹角,下同。
等效驱动力矩M d :1M M d =(4分)等效阻力矩M r :⎪⎪⎭⎫⎝⎛-=1333cos ωαv F M r (6分)87、解:重物可视为一个集中的质量块,而梁则可视为一个没有质量的弹簧。
重物落到梁上以后可将此系统视为一个单自由度振动系统。
重物振动位移计算的坐标原点取其静力平衡位置。
那么,这一自由振动的初始位移的绝对值应等于梁在重物作用下的静挠度,而重物下落所获得的速度即为自由振动的初始速度。
根据材料力学可知,简支梁在重物作用下的中点静挠度为31st 48G l EIδ=由此可计算出梁的静变形为δst=0.735cm 。
(2分)梁的刚度为1k stG δ=(4分)固有频率为n 36rad s ω (4分)88、解:由0=++kx x c x m代入数据后得 08501501017300203=++=⨯++x x x x x x(8分)其中,152=a ,8502=n ω,计算阻尼比和固有圆频率17.2826.012.291126.02.295.722=-⨯=-=<===ζωωωζn d na(4分)将初始条件代入00020020arctan)(ax xx ax xx A d d +=++= ωϕω (4分)得:od d ax xx mm ax xx A 3.555.25.730017.2825arctanarctan)(4.30)17.2825.7300(25)(0002220020⨯+⨯=+==⨯++=++= ωϕω(2分)则系统的振动响应为)96.017.28sin(4.305.7+=-t e x t (2分)。
