九年级数学上册(人教版)课件:24章24.4第二课时
合集下载
秋九年级数学人教版上册课件:第24章整理与复习 (共10张PPT)

第24章 整理与复习
• 复习目标:
1.复习本章的重点内容,整理本章知识,形成知识 体系.
2.体会利用圆的知识综合解决问题的思路和方法.
知识梳理,体系构建
1.圆是如何定义的? 2.同圆或等圆中的弧、弦、圆心角有什么关系? 垂直于弦的直径有什么性质?一条弧所对的圆周角和它 所对的圆心角有什么关系? 3.点和圆有怎样的位置关系?直线和圆呢?圆和 圆呢?怎样判断这些位置关系?
13、He who seize the right moment, is the right man.谁把握机遇,谁就心想事成。2021/9/142021/9/142021/9/142021/9/149/14/2021 •14、谁要是自己还没有发展培养和教育好,他就不能发展培养和教育别人。2021年9月14日星期二2021/9/142021/9/142021/9/14 •15、一年之计,莫如树谷;十年之计,莫如树木;终身之计,莫如树人。2021年9月2021/9/142021/9/142021/9/149/14/2021 •16、教学的目的是培养学生自己学习,自己研究,用自己的头脑来想,用自己的眼睛看,用自己的手来做这种精神。2021/9/142021/9/14September 14, 2021 •17、儿童是中心,教育的措施便围绕他们而组织起来。2021/9/142021/9/142021/9/142021/9/14
• You have to believe in yourself. That's the secret of success. 人必须相信自己,这是成功的秘诀。
•
例2 如图, ⊙O 的弦 AB=8 cm,直径CE⊥AB 于 D, DC=2 cm,求半径 OC 的长.
E
• 复习目标:
1.复习本章的重点内容,整理本章知识,形成知识 体系.
2.体会利用圆的知识综合解决问题的思路和方法.
知识梳理,体系构建
1.圆是如何定义的? 2.同圆或等圆中的弧、弦、圆心角有什么关系? 垂直于弦的直径有什么性质?一条弧所对的圆周角和它 所对的圆心角有什么关系? 3.点和圆有怎样的位置关系?直线和圆呢?圆和 圆呢?怎样判断这些位置关系?
13、He who seize the right moment, is the right man.谁把握机遇,谁就心想事成。2021/9/142021/9/142021/9/142021/9/149/14/2021 •14、谁要是自己还没有发展培养和教育好,他就不能发展培养和教育别人。2021年9月14日星期二2021/9/142021/9/142021/9/14 •15、一年之计,莫如树谷;十年之计,莫如树木;终身之计,莫如树人。2021年9月2021/9/142021/9/142021/9/149/14/2021 •16、教学的目的是培养学生自己学习,自己研究,用自己的头脑来想,用自己的眼睛看,用自己的手来做这种精神。2021/9/142021/9/14September 14, 2021 •17、儿童是中心,教育的措施便围绕他们而组织起来。2021/9/142021/9/142021/9/142021/9/14
• You have to believe in yourself. That's the secret of success. 人必须相信自己,这是成功的秘诀。
•
例2 如图, ⊙O 的弦 AB=8 cm,直径CE⊥AB 于 D, DC=2 cm,求半径 OC 的长.
E
人教版九年级数学上册课时课件24

∠D=180°-67.5°=112.5°.
当堂练习
✓ 当堂反馈 ✓ 即学即用
当堂练习
1.判断 (1)同一个圆中等弧所对的圆周角相等 ( √ ) (2)相等的弦所对的圆周角也相等 ( × ) (3)同弦所对的圆周角相等 ( × )
当堂练习
2.已知△ABC的三个顶点在⊙O上,∠BAC=60°, ∠ABC=45°, 则∠AOB= 150°.
O C A
O
B
讲授新课
圆周角定理
要点归纳
圆周角定理: 一条弧所对的圆周角等于该弧它所对的圆心角的一半;
讲授新课
互动探究
问题1 如图,OB,OC都是⊙O的半径,点A ,D 是上
任意两点,连接AB,AC,BD,CD.∠BAC与∠BDC 相等吗?请说明理由.
答:相等.
D
证明:在⊙O中, BAC 1 BOC, 2
OA=OC ∠A= ∠C ∠BOC= ∠ A+ ∠C
BAC 1 BOC 2
讲授新课
圆心O在∠BAC的内部
A
A
A
O
OO
O
B
B
C
D
D
BAD 1 BOD 2
BAC
BAD DAC
1
1
(BOD DOC ) BOC
2
2
C
D
DAC 1 DOC 2
讲授新课
圆心O在∠BAC的外部
A
OO
D
D
C
B
D
DAC 1 DOC A2
✓ 教学目标 ✓ 教学重点
新课导入
回顾旧知 什么是圆心角?它具有哪些性质?
讲授新课
✓ 典例精讲 ✓ 归纳总结
讲授新课
当堂练习
✓ 当堂反馈 ✓ 即学即用
当堂练习
1.判断 (1)同一个圆中等弧所对的圆周角相等 ( √ ) (2)相等的弦所对的圆周角也相等 ( × ) (3)同弦所对的圆周角相等 ( × )
当堂练习
2.已知△ABC的三个顶点在⊙O上,∠BAC=60°, ∠ABC=45°, 则∠AOB= 150°.
O C A
O
B
讲授新课
圆周角定理
要点归纳
圆周角定理: 一条弧所对的圆周角等于该弧它所对的圆心角的一半;
讲授新课
互动探究
问题1 如图,OB,OC都是⊙O的半径,点A ,D 是上
任意两点,连接AB,AC,BD,CD.∠BAC与∠BDC 相等吗?请说明理由.
答:相等.
D
证明:在⊙O中, BAC 1 BOC, 2
OA=OC ∠A= ∠C ∠BOC= ∠ A+ ∠C
BAC 1 BOC 2
讲授新课
圆心O在∠BAC的内部
A
A
A
O
OO
O
B
B
C
D
D
BAD 1 BOD 2
BAC
BAD DAC
1
1
(BOD DOC ) BOC
2
2
C
D
DAC 1 DOC 2
讲授新课
圆心O在∠BAC的外部
A
OO
D
D
C
B
D
DAC 1 DOC A2
✓ 教学目标 ✓ 教学重点
新课导入
回顾旧知 什么是圆心角?它具有哪些性质?
讲授新课
✓ 典例精讲 ✓ 归纳总结
讲授新课
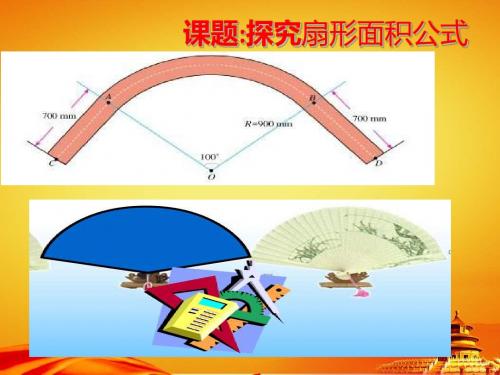
人教版九年级数学上册第24章 圆 弧长和扇形面积

24.4 弧长和扇形面积
第1课时 弧长和扇形面积
1.通过自主探究得出弧长的计算公式,体验从特殊到一般的学习
方法,发展学生的推理能力.
2.通过小组讨论推导出扇形面积公式,会推导弧长和扇形面积之
间的关系,学会利用类比的思想方法解决问题.
3.通过练习恰当熟练地运用公式计算弧长、扇形的面积,增强学
生的数学运用能力.
3
4.试着总结圆心角为 ᵒ的扇形面积公式.
扇形 =
=
教师讲评
知识点1.弧长(重点)
n°的圆心角所对的弧长为l= .
知识点2.扇形面积(重点)
1.扇形:由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.如
图,黄色部分是一个扇形,记作扇形OAB.
2.扇形面积:
旧知回顾
还记得小学学过的圆的周长和面积公式吗?
(C=πd=2πr,S=πr²)
“欲穷千里目,更上一层楼”是唐朝诗人王之涣在《登鹳雀楼》一诗中的诗句
,那么同学们想过没有,如果真的要看千里之遥,要“站”多高呢?
如图,地球上B、C两点间的距离指的是球面上两点间的距离,也就是什么的
长?(弧BC的长)
假设弧BC的长为500km,如果地球的半径是6400km,你能算出视线AC的
(2)由(1)易得 =
,
=
, ∠
= °.
∴阴影部分的面积=扇形OAB的面积 −△ 的面积
=
×
− × ×
×
= −
.
第1课时 弧长和扇形面积
1.通过自主探究得出弧长的计算公式,体验从特殊到一般的学习
方法,发展学生的推理能力.
2.通过小组讨论推导出扇形面积公式,会推导弧长和扇形面积之
间的关系,学会利用类比的思想方法解决问题.
3.通过练习恰当熟练地运用公式计算弧长、扇形的面积,增强学
生的数学运用能力.
3
4.试着总结圆心角为 ᵒ的扇形面积公式.
扇形 =
=
教师讲评
知识点1.弧长(重点)
n°的圆心角所对的弧长为l= .
知识点2.扇形面积(重点)
1.扇形:由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.如
图,黄色部分是一个扇形,记作扇形OAB.
2.扇形面积:
旧知回顾
还记得小学学过的圆的周长和面积公式吗?
(C=πd=2πr,S=πr²)
“欲穷千里目,更上一层楼”是唐朝诗人王之涣在《登鹳雀楼》一诗中的诗句
,那么同学们想过没有,如果真的要看千里之遥,要“站”多高呢?
如图,地球上B、C两点间的距离指的是球面上两点间的距离,也就是什么的
长?(弧BC的长)
假设弧BC的长为500km,如果地球的半径是6400km,你能算出视线AC的
(2)由(1)易得 =
,
=
, ∠
= °.
∴阴影部分的面积=扇形OAB的面积 −△ 的面积
=
×
− × ×
×
= −
.
2014年秋人教版九年级数学上册:24.4《弧长及扇形的面积》ppt课件
则450
S 的圆心角所对的扇形面积表示为 扇 形
S 扇形
45 R 360
1 R 2 360
2
则 10的圆心角所对的扇形面积表示为
则n0圆心角是所对的扇形面积表示为
S 扇形
nR 2 360
O n° A
B
即:n0圆心角的扇形面积公式表示为
O n°
A
B
注意: 1.扇形面积的大小由圆的大小(半径)、圆心角的度 数决定. 2. 公式中 n 的意义. n 表示 1 °圆心角的倍数,它是不 带单位的;
四 课堂程序
6 π (1)半径为3的圆,周长是_________
1.学生回答
固旧知,为后面 (2)半径为R的圆,周长是_________ C=2πR 巩 学习作铺垫 4π (3)半径为2的圆,面积是_________ (4)半径为R的圆,面积是_________ S=πR2 设计意图 2.学生自主学习, 通过学生 自主学习从 学生自主阅读数学九年上册课本第二 提问方式进 行小结,让 十四章 圆 第112页 扇形面积部分 学生养成学 —总结— 在小学我们已经学习过有关圆的面积公 习 培养自主学 式,扇形与圆有怎样的关系,那么扇形面 习的良好学 习习惯,确 积应怎样计算?它与圆的面积之间有怎样 定本节课的 学习目标。 的关系呢?本节课我们将进行探索.
本节知识在中招考试中所占的分值:
2012年 2013年 4分 4分
一、教材分析
2.学情分析
在学习这节课知识之前,学生已经学习了与圆相关的概念,垂径定理,圆心 角,圆周角定理及扇形的弧长公式等内容,是有一定的学科基础,同时学生 也想继续探究新的知识.
3.学习目标:
(一) 知识目标 1). 了解扇形的概念 2) 理解n°的圆心角所对的扇形面积的计算公式 3) 会运用公式求扇形面积. (二) 能力目标 1).经历探索扇形面积计算公式的过程,培养学生的探索能 力. 2).了解扇形面积公式后,能用公式解决问题,训练学生的 数学运用能力. (三)情感与价值观目标 1).经历探索扇形面积计算公式,让学生体验教学活动充满 着探索与创造,感受数学的严谨性以及数学结论的确定 性. 2).通过用扇形面积公式解决实际问题,让学生体验数学与 人类生活的密切联系,激发学生学习数学的兴趣,提高他 们的学习积极性,同时提高大家的运用能力.
S 的圆心角所对的扇形面积表示为 扇 形
S 扇形
45 R 360
1 R 2 360
2
则 10的圆心角所对的扇形面积表示为
则n0圆心角是所对的扇形面积表示为
S 扇形
nR 2 360
O n° A
B
即:n0圆心角的扇形面积公式表示为
O n°
A
B
注意: 1.扇形面积的大小由圆的大小(半径)、圆心角的度 数决定. 2. 公式中 n 的意义. n 表示 1 °圆心角的倍数,它是不 带单位的;
四 课堂程序
6 π (1)半径为3的圆,周长是_________
1.学生回答
固旧知,为后面 (2)半径为R的圆,周长是_________ C=2πR 巩 学习作铺垫 4π (3)半径为2的圆,面积是_________ (4)半径为R的圆,面积是_________ S=πR2 设计意图 2.学生自主学习, 通过学生 自主学习从 学生自主阅读数学九年上册课本第二 提问方式进 行小结,让 十四章 圆 第112页 扇形面积部分 学生养成学 —总结— 在小学我们已经学习过有关圆的面积公 习 培养自主学 式,扇形与圆有怎样的关系,那么扇形面 习的良好学 习习惯,确 积应怎样计算?它与圆的面积之间有怎样 定本节课的 学习目标。 的关系呢?本节课我们将进行探索.
本节知识在中招考试中所占的分值:
2012年 2013年 4分 4分
一、教材分析
2.学情分析
在学习这节课知识之前,学生已经学习了与圆相关的概念,垂径定理,圆心 角,圆周角定理及扇形的弧长公式等内容,是有一定的学科基础,同时学生 也想继续探究新的知识.
3.学习目标:
(一) 知识目标 1). 了解扇形的概念 2) 理解n°的圆心角所对的扇形面积的计算公式 3) 会运用公式求扇形面积. (二) 能力目标 1).经历探索扇形面积计算公式的过程,培养学生的探索能 力. 2).了解扇形面积公式后,能用公式解决问题,训练学生的 数学运用能力. (三)情感与价值观目标 1).经历探索扇形面积计算公式,让学生体验教学活动充满 着探索与创造,感受数学的严谨性以及数学结论的确定 性. 2).通过用扇形面积公式解决实际问题,让学生体验数学与 人类生活的密切联系,激发学生学习数学的兴趣,提高他 们的学习积极性,同时提高大家的运用能力.
人教版九年级数学上册作业课件 第二十四章 圆 弧长和扇形面积 第2课时 圆锥的侧面积与全面积

7.已知圆锥的侧面展开图是一个半径为12 cm,弧长为12π cm的扇形, 求这个圆锥的侧面积及高.
解:侧面积为12 ×12×12π=72π(cm2).设底面半径为 r cm,则有 2πr =12π,∴r=6.由于高、母线、底面圆的半径恰好构成直角三角形, 根据勾股定理可得,高 h= 122-62 =6 3 (cm)
知识点 2:圆锥的全面积 8.圆锥的底面半径为 4 cm,高为 5 cm,则它的表面积为( D ) A.12π cm2 B.26π cm2 C. 41 π cm2 D.(4 41 +16)π cm2
9.已知直角三角形 ABC 的一条直角边 AB=12 cm,另一条直角边 BC =5 cm,则以 AB 为轴旋转一周,所得到的圆锥的表面积是( A ) A.209π cm2 B.155π cm2 C.90π cm2 D.65π cm2
解:l=2π×3=nπ18×0 6 ,∴n=180,∴圆锥侧面展开图是一个半圆,如 图所示,∠BAP=90°,AB=6 m,AP=3 m,∴BP=3 5 m,∴小猫 所经过的最短路程是 3 5 m
人教版
第二十四章 圆
24.4 弧长和扇形面积 第2课时 圆锥的侧面积与全面积
1.圆锥是由一个底面和一个__侧__面围成的几何体,连接圆锥_顶__点__和底面 圆周上任意一点的线段叫做圆锥的母线.
练习1:一圆锥的母线长为5,高为4,则该圆锥底面圆的周长为_6_π__.
2.圆锥的侧面展开图是一个__扇__形,扇形的半径为圆锥的_母__线__长,扇形 的弧长即为圆锥底面圆的_周__长__.圆锥的全面积等于底面积+_侧__面__积__.
则圆锥的侧面积为12 π·AC2=18π(cm2)
17.(2020·广东中考改编)如图,从一块半径为1 m的圆形铁皮上剪出一个 圆周角为120°的扇形ABC,如果将剪下来的扇形围成一个圆锥,求该圆锥 的底面圆的半径r.
解:侧面积为12 ×12×12π=72π(cm2).设底面半径为 r cm,则有 2πr =12π,∴r=6.由于高、母线、底面圆的半径恰好构成直角三角形, 根据勾股定理可得,高 h= 122-62 =6 3 (cm)
知识点 2:圆锥的全面积 8.圆锥的底面半径为 4 cm,高为 5 cm,则它的表面积为( D ) A.12π cm2 B.26π cm2 C. 41 π cm2 D.(4 41 +16)π cm2
9.已知直角三角形 ABC 的一条直角边 AB=12 cm,另一条直角边 BC =5 cm,则以 AB 为轴旋转一周,所得到的圆锥的表面积是( A ) A.209π cm2 B.155π cm2 C.90π cm2 D.65π cm2
解:l=2π×3=nπ18×0 6 ,∴n=180,∴圆锥侧面展开图是一个半圆,如 图所示,∠BAP=90°,AB=6 m,AP=3 m,∴BP=3 5 m,∴小猫 所经过的最短路程是 3 5 m
人教版
第二十四章 圆
24.4 弧长和扇形面积 第2课时 圆锥的侧面积与全面积
1.圆锥是由一个底面和一个__侧__面围成的几何体,连接圆锥_顶__点__和底面 圆周上任意一点的线段叫做圆锥的母线.
练习1:一圆锥的母线长为5,高为4,则该圆锥底面圆的周长为_6_π__.
2.圆锥的侧面展开图是一个__扇__形,扇形的半径为圆锥的_母__线__长,扇形 的弧长即为圆锥底面圆的_周__长__.圆锥的全面积等于底面积+_侧__面__积__.
则圆锥的侧面积为12 π·AC2=18π(cm2)
17.(2020·广东中考改编)如图,从一块半径为1 m的圆形铁皮上剪出一个 圆周角为120°的扇形ABC,如果将剪下来的扇形围成一个圆锥,求该圆锥 的底面圆的半径r.
九年级数学上册(人教版)教学课件:24.4.2

◆要点导航 ◆典例全解
▲题型一 ▲题型二
◆反馈演练
§基础夯实 §能力跃升 §思维拓展
◆要点导航 ◆典例全解
▲题型一 ▲题型二
◆反馈演练
§基础夯实 §能力跃升 §思维拓展
◆要点导航 ◆典例全解
▲题型一 ▲题型二
◆反馈演练
§基础夯实 §能力跃升 §思维拓展
◆要点导航 ◆典例全解
▲题型一 ▲题型二
◆反馈演练
§基础夯实 §能力跃升 §思维拓展
◆要点导航 ◆典例全解
▲题型一 ▲题型二
◆反馈演练
§基础夯实 §能力跃升 §思维拓展
◆要点导航 ◆典例全解
▲题型一 ▲题型二
◆反馈演练
§基础夯实 §能力跃升 §思维拓展
◆要点导航 ◆典例全解
▲题型一 ▲题型二
◆反馈演练
§基础夯实 §能力跃升 §思维拓展
◆要点导航 ◆典例全解
▲题型一 ▲题型二
◆反馈演练
§基础夯实 §能力跃升 §思维拓展
◆要点导航 ◆典例全解
▲题型一 ▲题型二
◆反馈演练
§基础夯实 §能力跃升 §思维拓展
◆要点导航 ◆典例全解
▲题型一 ▲题型二
◆反馈演练
§基础夯实 §能力跃升 §思维拓展
◆要点导航 ◆典例全解
▲题型一 ▲题型二
◆反馈演练
§基础夯实 §能力跃升 §思维拓展
◆要点导航 ◆典例全解实 §能力跃升 §思维拓展
◆要点导航 ◆典例全解
▲题型一 ▲题型二
◆反馈演练
§基础夯实 §能力跃升 §思维拓展
◆要点导航 ◆典例全解
▲题型一 ▲题型二
◆反馈演练
§基础夯实 §能力跃升 §思维拓展
◆要点导航 ◆典例全解
▲题型一 ▲题型二
◆反馈演练
§基础夯实 §能力跃升 §思维拓展
◆要点导航 ◆典例全解
▲题型一 ▲题型二
◆反馈演练
§基础夯实 §能力跃升 §思维拓展
◆要点导航 ◆典例全解
▲题型一 ▲题型二
◆反馈演练
§基础夯实 §能力跃升 §思维拓展
◆要点导航 ◆典例全解
▲题型一 ▲题型二
◆反馈演练
§基础夯实 §能力跃升 §思维拓展
◆要点导航 ◆典例全解
▲题型一 ▲题型二
◆反馈演练
§基础夯实 §能力跃升 §思维拓展
◆要点导航 ◆典例全解
▲题型一 ▲题型二
◆反馈演练
§基础夯实 §能力跃升 §思维拓展
◆要点导航 ◆典例全解
▲题型一 ▲题型二
◆反馈演练
§基础夯实 §能力跃升 §思维拓展
◆要点导航 ◆典例全解
▲题型一 ▲题型二
◆反馈演练
§基础夯实 §能力跃升 §思维拓展
◆要点导航 ◆典例全解
▲题型一 ▲题型二
◆反馈演练
§基础夯实 §能力跃升 §思维拓展
◆要点导航 ◆典例全解
▲题型一 ▲题型二
◆反馈演练
§基础夯实 §能力跃升 §思维拓展
◆要点导航 ◆典例全解
▲题型一 ▲题型二
◆反馈演练
§基础夯实 §能力跃升 §思维拓展
◆要点导航 ◆典例全解实 §能力跃升 §思维拓展
◆要点导航 ◆典例全解
▲题型一 ▲题型二
◆反馈演练
§基础夯实 §能力跃升 §思维拓展
◆要点导航 ◆典例全解
▲题型一 ▲题型二
◆反馈演练
§基础夯实 §能力跃升 §思维拓展
◆要点导航 ◆典例全解
人教版九年级数学上册课件:24.4弧长和扇形面积(共19张PPT)

-
1353π6×0 152=375π(cm2).
9
能力提升
11.如图,图1是由若干个相同的图形(图2)组成的美丽图案的一部分.图2中, 图形的相关数据:半径OA=2 cm,∠AOB=120°,则图2的周长为 83π ________cm.(结果保留π)
10
12.如图,在△ABC中,AC=4,将△ABC绕点C逆时针旋 转30°得到△FGC,则图43中π 阴影部分的面积为________.
第二十四章 圆
弧长和扇形面积
第一课时
知识展示
知识点 1 弧长公式 n°的圆心角所对的弧长 l 的计算公式为 l=n1π8R0 ,其中 R 为半径. 核心提示:在弧长公式中,已知 l、n、R 中的任意两个量,都可以求出第三个 量. 知识点 2 扇形的定义 由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.
分析:先用扇形OAB的面积-三角形OAB的面积求出上面空白部分面积,再用扇形OCD的面积-三角形OCD的面积-上面空白部分的面
积7.,如即图可,求5分出.别阴以影【五部边分黑形的A龙面BC积D江.E的顶哈点尔为圆滨心,中以1考为半】径作一五个个圆,扇则图形中的阴影弧部分长的面是积之1和1为π__c___m___.,半径是18
2
知识点 3 扇形面积公式 (1)n°圆心角的扇形面积公式:S 扇形=n3π6R02 ,其中 R 为半径. (2)弧长为 l 的扇形面积公式:S 扇形=12lR,其中 R 为半径. 【典例】如图,半径为 12 的圆中,两圆心角∠AOB=60°、∠COD=120°,连接 AB、CD,求图中阴影部分的面积.
cm,则此扇形的圆心角是__________度. 71.2.如如图图,,分在别△以AB五C中边,形AACB=CD4E,的将顶△点AB为C圆绕心点,C逆以时11为针1半旋0 径转作30五°得个到圆△,FG则C,图则中图阴中影阴部影分部的分面的积面之积和为为________________.. 一列火车以6每.小时【28 江km的苏速度泰经州过10中秒通考过弯】道.如那么图弯,道所分对的别圆心以角为正___三_____角__度形.(π的取3.3个顶点为圆心, 98..一已段知铁扇边路形弯所长道在成圆为圆半弧 径半形为,4径,圆弧弧画长的为弧半6径π,,是则2三扇km形.段面积弧为_围_____成____.的图形称为莱洛三角形.若正三角 分 积析,:即先 可用 求形扇 出形 阴边影OA部长B的分面为的积面6-积三.c角m形,OAB则的面该积求莱出上洛面三空白角部分形6面π积的,再周用扇长形为OCD_的_面__积_-__三_角c形mOC. D的面积-上面空白部分的面
人教版九年级数学上册第二十四章《圆》课件

算一算:设在例3中,⊙O的半径为10,则正方形
ABCD的边长为 4 5 .
A
D
?2x 10 Ⅱ
M
x B O
C
图4
连OA,OD即可, 同圆的半径相等.
N 在Rt△ABO中,AB2 BO2 AO2
即(2x)2 x2 102
变式:如图,在扇形MON中, MON =45 ,半径 MO=NO=10,,正方形ABCD的顶点B、C、D在半径上, 顶点A在圆弧上,求正方形ABCD的边长.
视频:生活中的圆
骑车运动
看了此画,你有何想法?
思考:车轮为什么做成圆形?做成三角形、正方形 可以吗?
车轮为圆形的原理分析:(下图为FLASH动画,点击)
讲授新课
一 探究圆的概念
合作探究
情景:一些学生正在做投圈游戏,他们呈“一”字排 开.这样的队形对每一人都公平吗?你认为他们应当 排成什么样的队形?
固定的端点O叫做圆心,线段OA叫 做半径,一般用r表示.
视频:画圆实际操作演示
确定一个圆的要素
一是圆心,圆心确定其位置;二是半径,半径确定其大小.
同心圆
圆心相同,半径不同
等圆
半径相同,圆心不同
圆也可以看成是由多个点组成的
到定点的距离等于定长 的点都在同一个圆上吗?
有间隙吗?
圆可以看成到定满点足距什离么等条于件定的长?的所有点组成的.
解:连结OA. ∵ABCD为正方形
N
A
D
xx
∴DC=CO
x
x
MB
C
O
图5
设OC=x,则AB=BC=DC=OC=x 又∵OA=OM=10
∴在Rt△ABO中, AB2 BO2 AO2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二十四章 圆 24.4 弧长和扇形面积
第二课时 圆锥的侧面积和全面积
新知 1 圆锥的侧面展开图及面积
(1)圆锥及母线:圆锥是由一个底面和一个侧面围 成的,如图24-4-14所示.
连接圆锥顶点和底面圆周上 任意一点的线段叫做圆锥的母线.
(2)圆锥的侧面展开图是一个扇形,如图24-4- 14所示.
A. 240π cm2 B. 480π cm2 C. 1200π cm2 D. 2400π cm2
3. 将弧长为2π cm,圆心角为120°的扇形围成一个圆
锥的侧面,则这个圆锥的高
,侧面积
.
新知 2 圆锥的全面积 圆锥的侧面积与底面积之和称为圆锥的全面积.
例题精讲 【例2】要在如图24-4-17所示的一个机器零件表面 涂上防锈漆,请你帮助计算一下这个零件的表面积. 解析 这个机器零件的表面由三部分组成:底面圆、 圆柱侧面和圆锥侧面,分别计算各部分面积即可.
的底面圆周长=扇形的弧长,列方程求解.
解 设圆锥的底面圆半径为r,依题意,得
2πr=
解得r=4.
故圆锥的底面半径为4.
举一反三
1. 一个圆柱的侧面展开图是两邻边长分别为6和8的矩 形,则该圆柱的底面圆半径是( C )
2. 如图24-4-16,用一张半径为24 cm的扇形纸板 制作一顶圆锥形帽子(接缝忽略不计),如果圆锥形帽子 的底面半径为10 cm,那么这张扇形纸板的面积是 ( A)
∴圆锥的侧面积为
1
lR=12
×12π×18=108π,
故该圆锥的侧面积为108πcm2.
(3)设圆锥的母线长为l,底面圆的半径为r,那么 这个扇形的半径为l,扇形的弧长为2πr,因此圆锥的 侧面积为 S侧=12 ·l·2πr=πrl.
例题精讲
【例1】在长方形ABCD中AB=16,如图24-4-15
所示裁出一扇形ABE,将扇形围成一个圆锥(AB和AE
重合),求此圆锥的底面半径.
解析 圆锥的底面圆半径为r,根据圆锥
解:过点C作CD⊥AB于点D. Rt△ABC中,∠ACB=90°,AC=BC. ∴AB= AC=4. ∴CD=2. 以CD为半径的圆的周长是4π. 故直线旋转一周则所得的几何体得表面 积是:
4. (4分)如图KT24-4-2,分别以等腰直角三角板的 直角边、斜边为旋转轴旋转,所形成的旋转体的全面 积依次记为S1,S2,则S1与S2的大小关系为A( )
解 如图24-4-18所示,点O′为AD的中点,
连接PO′,则PO′⊥AD.
在Rt△APO′中,AO′= AD=40(mm),
∴ AP=
=50(mm),
∴ S圆锥侧=πrl=π×40×50=2 000π(mm2), S圆柱侧=π×80×100=8 000π(mm2), S底=402×π=1 600π(mm2), ∴ S全=1 600π+8 000π+2 000π=11 600π(mm2). 答:这个零件的表面积是11 600π mm2.,
A. S1>S2
B. S1<S2 C. S1=S2
D. 无法判断
6. (10分)如图KT24-4-3所示的扇形是一个圆锥的
侧面展开图, 若∠AOB=120° , 弧AB 的长为12π
cm, 求该圆锥的侧面积.
解:设AO=BO=R,
∵∠AOB=120°,
弧AB 的长为12π cm ,
∴
解得R=18.
举一反三
1. 已知圆锥的母线长为4,底面半径为2,则圆锥的
全面积为( B )
A. 8π
B. 12π
C. π
D. 4π
2. 一个圆锥的侧面积为8π,母线长为4,则这个圆锥
的全面积为 12π .
3. 如图24-4-19,Rt△ABC中,∠ACB=90°, AC=BC=2 ,若把Rt△ABC绕边AB所在直线旋 转一周,求所得几何体的表面积(结果保留π).
第二课时 圆锥的侧面积和全面积
新知 1 圆锥的侧面展开图及面积
(1)圆锥及母线:圆锥是由一个底面和一个侧面围 成的,如图24-4-14所示.
连接圆锥顶点和底面圆周上 任意一点的线段叫做圆锥的母线.
(2)圆锥的侧面展开图是一个扇形,如图24-4- 14所示.
A. 240π cm2 B. 480π cm2 C. 1200π cm2 D. 2400π cm2
3. 将弧长为2π cm,圆心角为120°的扇形围成一个圆
锥的侧面,则这个圆锥的高
,侧面积
.
新知 2 圆锥的全面积 圆锥的侧面积与底面积之和称为圆锥的全面积.
例题精讲 【例2】要在如图24-4-17所示的一个机器零件表面 涂上防锈漆,请你帮助计算一下这个零件的表面积. 解析 这个机器零件的表面由三部分组成:底面圆、 圆柱侧面和圆锥侧面,分别计算各部分面积即可.
的底面圆周长=扇形的弧长,列方程求解.
解 设圆锥的底面圆半径为r,依题意,得
2πr=
解得r=4.
故圆锥的底面半径为4.
举一反三
1. 一个圆柱的侧面展开图是两邻边长分别为6和8的矩 形,则该圆柱的底面圆半径是( C )
2. 如图24-4-16,用一张半径为24 cm的扇形纸板 制作一顶圆锥形帽子(接缝忽略不计),如果圆锥形帽子 的底面半径为10 cm,那么这张扇形纸板的面积是 ( A)
∴圆锥的侧面积为
1
lR=12
×12π×18=108π,
故该圆锥的侧面积为108πcm2.
(3)设圆锥的母线长为l,底面圆的半径为r,那么 这个扇形的半径为l,扇形的弧长为2πr,因此圆锥的 侧面积为 S侧=12 ·l·2πr=πrl.
例题精讲
【例1】在长方形ABCD中AB=16,如图24-4-15
所示裁出一扇形ABE,将扇形围成一个圆锥(AB和AE
重合),求此圆锥的底面半径.
解析 圆锥的底面圆半径为r,根据圆锥
解:过点C作CD⊥AB于点D. Rt△ABC中,∠ACB=90°,AC=BC. ∴AB= AC=4. ∴CD=2. 以CD为半径的圆的周长是4π. 故直线旋转一周则所得的几何体得表面 积是:
4. (4分)如图KT24-4-2,分别以等腰直角三角板的 直角边、斜边为旋转轴旋转,所形成的旋转体的全面 积依次记为S1,S2,则S1与S2的大小关系为A( )
解 如图24-4-18所示,点O′为AD的中点,
连接PO′,则PO′⊥AD.
在Rt△APO′中,AO′= AD=40(mm),
∴ AP=
=50(mm),
∴ S圆锥侧=πrl=π×40×50=2 000π(mm2), S圆柱侧=π×80×100=8 000π(mm2), S底=402×π=1 600π(mm2), ∴ S全=1 600π+8 000π+2 000π=11 600π(mm2). 答:这个零件的表面积是11 600π mm2.,
A. S1>S2
B. S1<S2 C. S1=S2
D. 无法判断
6. (10分)如图KT24-4-3所示的扇形是一个圆锥的
侧面展开图, 若∠AOB=120° , 弧AB 的长为12π
cm, 求该圆锥的侧面积.
解:设AO=BO=R,
∵∠AOB=120°,
弧AB 的长为12π cm ,
∴
解得R=18.
举一反三
1. 已知圆锥的母线长为4,底面半径为2,则圆锥的
全面积为( B )
A. 8π
B. 12π
C. π
D. 4π
2. 一个圆锥的侧面积为8π,母线长为4,则这个圆锥
的全面积为 12π .
3. 如图24-4-19,Rt△ABC中,∠ACB=90°, AC=BC=2 ,若把Rt△ABC绕边AB所在直线旋 转一周,求所得几何体的表面积(结果保留π).
