八年级数学上册 7.4 平行线的判定导学案(新版)北师大版
八年级数学上册7.3平行线的判定导学案(无答案)(新版)北师大版
①分析教材P173随堂联系
②分析P173的知识技能第一题纠错题,总结解决这一类型题的注意点。
方案预设三:
如果两条直线都和第三条直线垂直,那
么这两条直线平行。
方案预设四:
分析P174数学理解第二题。
方案预设五:
分析P174数学理解第三题。
方案预设六:
分析P174问题解决。
【重点识记】
1、同位角相等,两直线平行———公理
平行线的判定
【学习目标】1.熟练掌握平行线的判定公理及定理。
2、能对平行线的判定进行灵活运用,并把它们应用于几何证明中
【定向导学·互动展示·当堂反馈】
自研自探 环节
展示提升 环节
质疑评价 环节
总结归纳 环节
自 学 指 导
( 内容·学法·时间 )
展 示 方 案
(内容·学法·时间)
随 堂 笔 记
(成果记录·知识生成·)
(见课本P172的证明二)
同学们可要记得几何题型的作图便于做题哦!!
同学们认真看一下作几何的文字题的过程,一定要写出已知、求证、证明及其作图的相关过程。
内错角相等,两直线平行
同旁内角互补,两直线平行
两条直线都和第三条直线平行,则这两条直线互相平行
在同一平面内,不相交的两条直线叫做平行线.
【例题导析】
1、证明:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
(见课本P172的证明一)
2、两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
【学法指导】
自研教材P172的内容特别是定理的推理过程,学着课本书写定理的数学转化、比如已知、求证、证明等。
思考一下,我们来感受一下:
北师大版八年级上册数学7.3《平行线的判定》教学设计

北师大版八年级上册数学7.3《平行线的判定》教学设计一. 教材分析《平行线的判定》是北师大版八年级上册数学的一节重要内容,主要介绍了同位角相等、内错角相等、同旁内角互补三种平行线的判定方法。
这部分内容是学生学习几何的基础,对于培养学生的逻辑思维能力和空间想象能力具有重要意义。
在教材中,通过生活实例引入平行线的概念,然后引导学生通过观察、思考、交流、总结出平行线的判定方法,最后通过练习来巩固所学知识。
二. 学情分析八年级的学生已经具备了一定的数学基础,对于图形的认知和观察能力也有一定的提高。
但是,学生在空间想象能力和逻辑思维能力方面还有待提高。
此外,学生的学习习惯和动手操作能力也存在一定的差异。
因此,在教学过程中,教师需要关注学生的个体差异,引导他们积极参与课堂活动,提高他们的空间想象能力和逻辑思维能力。
三. 教学目标1.知识与技能:使学生掌握同位角相等、内错角相等、同旁内角互补三种平行线的判定方法,能够运用这些方法判断两条直线是否平行。
2.过程与方法:通过观察、思考、交流等活动,培养学生的空间想象能力和逻辑思维能力。
3.情感态度与价值观:激发学生对数学的兴趣,培养他们勇于探究、合作学习的良好习惯。
四. 教学重难点1.教学重点:同位角相等、内错角相等、同旁内角互补三种平行线的判定方法。
2.教学难点:如何引导学生观察、思考、总结出平行线的判定方法。
五. 教学方法1.情境教学法:通过生活实例引入平行线的概念,激发学生的学习兴趣。
2.引导发现法:引导学生观察、思考、交流,总结出平行线的判定方法。
3.实践操作法:让学生通过动手操作,巩固所学知识。
4.激励评价法:关注学生的个体差异,及时给予鼓励和评价,提高他们的学习积极性。
六. 教学准备1.教具:多媒体课件、黑板、粉笔、直线模型、角度模型。
2.学具:学生用书、练习册、直线模型、角度模型。
七. 教学过程1.导入(5分钟)利用多媒体课件展示生活实例,引导学生观察并提出问题:为什么说这两条直线平行?激发学生的学习兴趣。
秋八年级数学上册 7.3 平行线的判定学案 北师大版(2021年整理)

2017年秋八年级数学上册 7.3 平行线的判定学案(新版)北师大版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2017年秋八年级数学上册 7.3 平行线的判定学案(新版)北师大版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2017年秋八年级数学上册 7.3 平行线的判定学案(新版)北师大版的全部内容。
7。
3 平行线的判定【学习目标】1.会用“同位角相等,两直线平行"证明“内错角相等,两直线平行”及“同旁内角互补,两直线平行”的正确性.2.会用平行线的三个判定定理解决问题.【学习重点】平行线的三个判定定理.【学习难点】灵活应用平行线的三个判定定理解决问题.学习行为提示:让学生通过阅读教材后,独立完成“自学互研”的所有内容,并要求做完了的小组长督促组员迅速完成.学习行为提示:教会学生看书,独学时对于书中的问题一定要认真探究,书写答案.教会学生落实重点.情景导入生成问题前面我们探索过两直线平行的哪些判别条件?利用“同位角相等,两直线平行”这个基本事实,你能证明它们吗?试试看.【说明】通过复习旧知识,为本节课进一步学习直线平行的条件做准备.两条直线被第三条直线所截,形成的角中,有同位角、内错角和同旁内角.同位角相等,两直线平行,那么利用内错角、同旁内角的关系,能否判定两直线平行?【说明】这个问题的提出,直截了当地切入本节课的中心内容,通过学生的猜想、讨论,引起学生的探究欲望.自学互研生成能力错误!先阅读教材第172页定理1的内容及其证明过程,然后完成下面的问题.问题1如右图,∠1与∠2是什么位置关系?问题2当∠1=∠2时,直线a、b有什么关系?为什么?【说明】通过观察、思考、讨论培养学生分析图形的能力,感受转化的思想.由未知转化为已知,把已知条件转化为以前学过的旧知识,从而达到解决问题的目的.为了给学生一个清晰的证明过程,教师展示如下:证明:∵∠1=∠2(已知),∠1=∠3(对顶角相等).∴∠3=∠2(等量代换).∴a∥b (同位角相等,两直线平行).错误!先阅读教材第172页定理2的内容及证明过程,然后完成下面的问题.问题3如下图,∠2与∠3是什么位置关系?学习行为提示:教会学生怎么交流.先对学,再群学.充分在小组内展示自己,分析答案,提出疑惑,共同解决(可按结对子学—帮扶学-组内群学来开展).在群学后期教师可有意安排每组展示问题,并给学生板书题目和组内演练的时间.问题4当∠2+∠3=180°时,直线a、b有什么关系?为什么?【说明】让学生自己口述,培养学生的口语表达能力和推理论证的能力.在思考探究的过程中,体会判断两条直线平行的条件.这个证明的过程,老师可以引导学生自己书写.【归纳结论】已给的基本事实、定义和已经证明的定理以后都可以作为依据,用来证明新的结论.仿例:如图所示,一个合格的弯形管道经两次拐弯后,如果∠C=68°,∠B=112°,则AB 与CD的位置关系是__平行__,理由是__同旁内角互补,两直线平行__.交流展示生成新知1.将阅读教材时“生成的问题”和通过“自主探究、合作探究”得出的“结论"展示在各小组的小黑板上,并将疑难问题也板演到黑板上,再一次通过小组间就上述疑难问题相互释疑.2.各小组由组长统一分配展示任务,由代表将“问题和结论”展示在黑板上,通过交流“生成新知”.知识模块一内错角相等,两直线平行知识模块二同旁内角互补,两直线平行检测反馈达成目标【当堂检测】见所赠光盘和学生用书;【课后检测】见学生用书.课后反思查漏补缺1.收获:_______________________________________________________________2.存在困惑:________________________________________________________________________。
八年级数学上册7.3平行线的判定教学设计 (新版北师大版)

八年级数学上册7.3平行线的判定教学设计(新版北师大版)一. 教材分析《八年级数学上册7.3平行线的判定》这一节内容主要让学生掌握平行线的判定方法,理解平行线的性质,并能运用这些方法解决实际问题。
教材通过丰富的图片和实例,引导学生探索平行线的判定规律,培养学生的逻辑思维能力和空间想象能力。
二. 学情分析学生在学习这一节内容时,已具备了一定的数学基础,如掌握了直线、射线、线段的性质,具备了一定的观察和分析能力。
但部分学生对于平行线的概念和判定方法可能还较为模糊,因此,在教学过程中,教师需要关注这部分学生的学习需求,通过具体实例和操作,帮助他们理解和掌握平行线的判定方法。
三. 教学目标1.让学生掌握平行线的判定方法,理解平行线的性质。
2.培养学生观察、分析、解决问题的能力。
3.培养学生的逻辑思维能力和空间想象能力。
四. 教学重难点1.平行线的判定方法。
2.平行线性质的应用。
五. 教学方法1.采用问题驱动法,引导学生主动探索平行线的判定方法。
2.利用多媒体辅助教学,展示实例和操作过程,增强学生的直观感受。
3.采用小组合作学习,让学生在讨论中巩固知识,提高解决问题的能力。
4.注重个体差异,针对不同学生提供个性化的指导。
六. 教学准备1.准备相关的多媒体教学课件。
2.准备实例和练习题。
3.准备教学用具,如直尺、三角板等。
七. 教学过程1.导入(5分钟)利用多媒体展示一些生活中的平行线现象,如楼梯、轨道等,引导学生关注平行线,激发学生的学习兴趣。
2.呈现(10分钟)讲解平行线的定义和性质,通过实例和动画演示,让学生直观地理解平行线的概念。
3.操练(10分钟)让学生分组讨论,尝试找出判定两条直线平行的方法。
教师巡回指导,给予个别学生必要的帮助。
4.巩固(10分钟)出示一些判断题和练习题,让学生运用所学知识解决问题,巩固对平行线判定方法的理解。
5.拓展(10分钟)引导学生思考:在实际生活中,平行线有哪些应用?如何运用平行线的性质解决实际问题?6.小结(5分钟)对本节课的内容进行总结,强调平行线的判定方法和性质,提醒学生注意在实际问题中的应用。
2019版八年级数学上册 第七章 平行线的证明 7.3 平行线的判定学案(新版)北师大版

2019版八年级数学上册第七章平行线的证明 7.3 平行线的判定学案(新版)北师大版3. 平行线的判定:⑴________相等,两直线平行;⑵________相等,两直线平行;⑶________互补,两直线平行;⑷平行于同一条直线的两条直线互相______.四、课堂探究——质疑解疑、合作探究简述为:__________________________.已知:∠1和∠2是直线被直线c截出的内错角,且∠1=∠2,求证:∥证明:2019版八年级数学上册第七章平行线的证明7.3 平行线的判定学案(新版)北师大版3. 平行线的判定:⑴ ________相等,两直线平行;⑵________相等,两直线平行;⑶________互补,两直线平行;⑷ 平行于同一条直线的两条直线互相______. 四、课堂探究——质疑解疑、合作探究 探究点1:平行线判定定理的证明你能利用“同位角相等,两直线平行”这个基本事实,证明“内错角相等,两直线平行”吗?定理:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行. 简述为:__________________________.已知:∠1和∠2是直线,a b 被直线c 截出的内错角,且∠1=∠2,求证:a ∥b证明:你能利用“同位角相等,两直线平行”这个基本事实,证明“同旁内角互补,两直线平行”吗?定理:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行. 简述为:__________________________.已知:∠1和∠2是直线,a b 被直线c 截出的同旁内角,且∠1与∠2互补. 求证:a ∥b证明:例题:如图1,能判定AB ∥CD 的是( )A .∠1=∠2B .∠3=∠4C .∠1=∠4D .∠2=∠3A 41BEDA1练习:1. 如图2,能判定直线AB∥CD的条件是()A.∠1=∠2 B.∠3=∠4 C.∠1+∠4=180°D.∠3+∠4=90°2.如图3,∠1=∠2,则下列结论正确的是()A.AB∥CD B.AD∥BC C.AB∥CE D.AD ∥CE探究点2:平行线判定定理的综合应用例题:如图,∠AOB=120°,∠OBD=30°,OA⊥AC,求证:AC∥DB•练习:1. 如图,已知∠OEB=130°,∠FOD=25°,OF平分∠EOD,求证:AB∥CD.2.如图,AB⊥BC,BC⊥CD,BF和CE是射线,并且∠1=∠2,求证:BF∥CE.探究点:平行线判定定理的实际应用例题:木工师傅用角尺画出工件边缘的两条垂线,就可以再找出两条平行线,a∥b,你能说明是什么道理吗?练习:物理实验发现:光线从空气射入玻璃中,会发生折射现象,•光线从玻璃射入空气中,同样也会发生折射现象.如图所示的是光线从空气射入玻璃中,再从玻璃射入空气中的示意图,已知∠1=∠2,∠3=∠4,那么光线AB与CD是否平行?并说明理由.五、巩固提升——(有效训练、反馈矫正)1.如图4,点E在AD•的延长线上,•下列条件中不能判断AB∥CD的是()A.∠3=∠4B.∠A+∠ADC=180°C.∠1=∠2D.∠A=∠52.如图5,在下列条件中不能判断L1∥L2的是()A.∠1=∠3B.∠2=∠3C.∠4+∠5=180°D.∠2+∠4=180°3.如图6,能说明AD∥BC的条件是()A.∠2=∠3B.∠1=∠4C.∠1+∠2=∠3+∠4D.∠A+∠C=180°4.如图7,能说明AB∥DE的有()①∠1=∠D;②∠CFB+∠D=180°;③∠B=∠D;④∠BFD=∠D.A.1个B.2个C.3个D.4个5.如图8,下列条件中,不能判定直线AB∥CD 的是()A.∠BAD=∠ADCB.∠A EC=∠ADCC.∠A EF=∠GCED.∠A EC+∠GCE=180°6.如图9,不能说明AE∥BD的有()A.∠1=∠2B.∠A=∠CBDC.∠BDE+∠DEA=180°D.∠3=∠47. 如图10,下列条件中,能判断AB∥CD的是( )A.∠BAD=∠BCDB.∠1=∠2C.∠3=∠4D.∠BAC=∠ACD8.如图,已知DE、BF分别平分∠ADC和∠ABC,∠1=∠2,∠ADC=∠ABC,那么AB与CD 平行吗?说明你的理由.图9图8图5 图4图6 图734DCBA21图10。
八年级数学上册 第七章 平行线的证明导学案2(新版)北师大版

八年级数学上册第七章平行线的证明导学案2(新版)北师大版2、了解定义、命题、公理和定理的含义、3、平行线的性质定理和判定定理、4、三角形的内角和定理及推论、5、使学生在证明过程中积极投入,全力以赴,享受合作的快乐。
重点:1、平行线的性质定理和判定定理的应用、2、三角形内角和定理及其推论的应用、3、证明的步骤及书写格式、难点:证明过程的书写、一、梳理本章的知识结构图、(举例说明)本章重点:证明一个命题是真命题的基本步骤是:(1)根据题意,(2)根据条件、结论,结合图形,(3)经过分析,找出由已知推出求证的途径,专题研究:1、下列语句中,是命题的为()、A、延长线段AB到CB、垂线段最短C、过点O作直线a∥bD、锐角都相等吗判断的依据是、2、下列命题中是真命题的为()、A、两锐角之和为钝角B、两锐角之和为锐角C、钝角大于它的补角D、锐角大于它的余角3、下列四个命题中,真命题有()、(1)两条直线被第三条直线所截,内错角相等、(2)如果∠1和∠2是对顶角,那么∠1=∠2、(3)一个角的余角一定小于这个角的补角、(4)如果∠1和∠3互余,∠2与∠3的余角互补,那么∠1和∠2互补、A、1个B、2个C、3个D、4个解题方法:4、“两条直线相交,有且只有一个交点”的题设是()、A、两条直线B、交点C、两条直线相交D、只有一个交点5、“同角的余角相等”的题设是__________,结论是__________。
解题方法:。
6、若三角形的一个外角等于与它不相邻的一个内角的4倍,等于与它相邻的内角的2倍,则三角形各角的度数为( )、A、45,45,90B、30,60,90C、25,25,130D、36,72,72应用的知识点有:。
7、如图所示,∠B=∠C,则∠ADC与∠AEB的大小关系是()、A、∠ADC>∠AEBB、∠ADC=∠AEBC、∠ADC<∠AEBD、大小关系不能确定应用的知识点是:8、补充理由:如图所示,若∠1+∠2=180,∠1=∠3,EF与GH 平行吗?解:EF∥GH,理由如下∠1+∠2=180()∴AB∥_______()又∠1=∠3()∴∠2+∠________=180()∴EF∥GH ()9、如图所示,已知直线BF∥DE,∠1=∠2,求证:GF∥BC、解题技巧:要求两直线平行,需找。
八年级数学上册 第七章 7.3 平行线的判定导学案(无答

平行线的判定学习目标: 1、掌握直线平行的条件,并会进行简单的应用。
2、领悟归纳和转化的数学思想方法。
学习重点: 运用平行线的判定方法判断两直线平行学习难点: 运用平行线的判定方法进行简单的推理。
一、复习回顾:1、证明几何命题的步骤是什么呢?2、两条直线被第三条直线所截,如果同位角相等,那么这两条直线______。
(简记为:同位角相等,两直线________。
)二、探索新知:(1)平行线判定定理一证明:平行线的判定定理一:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
(简记为:内错角相等,两直线平行。
1、指出定理的条件和结论,并画出图形,结合图形写出已知和求证。
已知:求证:证明:(2)平行线判定定理二证明:平行线判定定理二:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
(简记为:同旁内角互补,两直线平行。
)1、指出定理的条件和结论,并画出图形,结合图形写出已知和求证。
已知:求证:证明:三、应用新知:1、如图,填空:(1)∠A 与_________互补,则AB ∥_______( )(2)∠A 与_________互补,则AD ∥_______( )2、如图:∠5=∠CDA=∠ABC, ∠1=∠4, ∠2=∠3, ∠BAD+∠CDA=180°,填空:∵∠BAD+∠CDA=180°(已知)∴_____∥_____( , )∵∠5=∠CDA (已知), ∠5+∠BCD=180°( ), 621ADE∠CDA+∠______=180°( )∴∠BCD=∠6 ( )∴_____∥_____( , )3、已知,如图∠1+∠2=180°,填空。
∵∠1+∠2=180°()∠2=∠3()∴∠1+∠3=180°()∴_____∥_____( , )四、课堂练习:1、请你说说用直尺和平移三角尺画出两条直线平行的理由。
7.4 平行线的性质 八年级上册北师大版
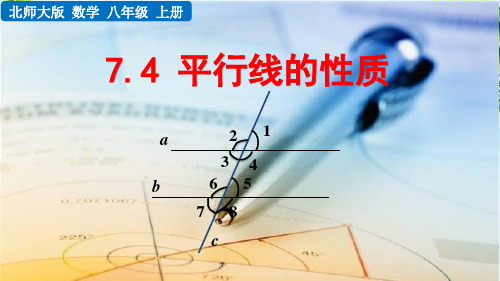
38°,则∠2的度数为 ( B )
A. 38° B. 52°
C. 76°
D. 142°
课堂检测
基础巩固题
4.如图所示,AB∥CD,∠E=40°,∠A=110°,则∠C的
度数为( D )
A. 60°
B. 80°
C. 75°
D. 70°
课堂检测
基础巩固题
5. 如图所示,直线a∥b,Rt△ABC的直角顶点C在直线b上,
简单说成:两直线平行,同位角相等.
几何语言:
∵a∥b(已知),
a
1
b
2
∴∠1=∠2 (两直线平行,同位角相等). c
探究新知
素养考点 利用“两直线平行,同位角相等”求角的度数
例 如图,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,
∠AED=40°.
(1)DE和BC平行吗?为什么?(2)∠C是多少度?为什么?
自主安排 配套练习册练习
2 CN
AB∥CD,∠1和∠2
D 是直线AB,CD被 直线EF截出的同
符号 语言
F
位角.
求证:∠1=∠2.
探究新知
思考3 你能说说证明的思路吗?
G
E 1
A
M 2
HB
CN
D
F
如果∠1 ≠ ∠2,AB与 CD的位置关 系会怎样呢?
证明:假设∠1 ≠ ∠2,那么我们可 以过点M作直线GH,使∠EMH= ∠2,如图所示.
∠1=20°,则∠2= 70 °.
课堂检测
能力提升题
有这样一道题:如图,若AB∥DE , AC∥DF,试说明
∠A+∠D=180o.请补全下面的解答过程,括号内填写依据. F
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级数学上册 7.4 平行线的判定导学案(新
版)北师大版
【学习目标】
1、掌握平行线的性质定理,了解平行于同一条直线的两条直线平行。
2、了解性质定理与判定定理的联系,初步感受互逆的思维过程。
3、进一步理解证明的步骤、格式和方法,发展演绎推理能力。
学习重点:掌握平行线的性质。
学习难点:平行线的性质的应用。
ABCDE
【复习引入】
1、平行线的判定有哪些?
2、如图所示,△ABC中,∠A=46,∠B=74,∠ADE=60,求证:BC∥ED。
【自主学习】
如图所示,l1∥l2,图中有哪些相等的角?你能说明理由吗?
【探究学习】
1、如果两条直线被第三条直线所截,那么
_________________________________________________________
________________________________简述为:两直线平行,
_______________________;两直线平行,
_______________________;两直线平行,
____________________。
几何语言:∵l1∥l2 ∴∠1=∠5 ()___________() ___________()
2、例题分析:已知:如图7-11,b∥a,c∥a,∠1,∠2,∠3是直线a,b,c被直线d截出的同位角。
求证:b∥c由上面例题,你发现了什么?写下你的结论。
_________________________________________________________ _对于上面结论,你还有其他的证明方法吗?小结:(1)平行线的性质。
(2)平行于同一条直线的两直线平行。
【巩固练习】
11、下列图形中,由,能得到的是()
BABA1BA1ABCD21DCDC22CD2
D、
C、
B、
A、2、已知:如图,AD∥BC,∠ABD=∠D,求证:BD平分
∠ABC。
ABCD
3、如图,AB∥CD,AD∥BC。
求证:∠A=∠C,∠B=∠D。
【布置作业】。
