C2数学模型1
车辆控制数学模型

车辆控制数学模型全文共四篇示例,供读者参考第一篇示例:车辆控制数学模型是指在控制工程中用数学方法描述车辆运动控制的模型,通过对车辆动力学、控制系统和环境参数的建模,可以准确地预测车辆在不同情况下的运动行为,并在实际控制中提供指导。
车辆控制数学模型广泛应用于汽车、飞行器、船舶等各种交通工具的控制系统中,是现代交通运输领域的重要技术之一。
一辆车辆在道路上行驶时,需要受到外部环境、车辆自身动力学和控制系统等多种因素的影响,而车辆控制数学模型正是为了分析和描述这些影响而建立的。
通常来说,车辆控制数学模型可以分为横向运动控制模型和纵向运动控制模型两部分。
横向运动控制模型描述的是车辆在横向方向(左右方向)的运动控制。
在这个模型中,主要考虑的是车辆的转向动作,包括转向角、横向速度、侧滑角等因素。
通过分析车辆的横向运动状态和控制输入(例如方向盘转角、制动力矩等),可以建立横向运动控制模型,并进一步设计控制策略来实现车辆的横向运动控制。
在实际应用中,车辆控制数学模型可以根据具体的车辆类型和运动需求进行调整和优化,以满足不同的控制要求。
对于自动驾驶系统来说,车辆控制数学模型需要考虑更多的感知与决策因素,以实现智能化的自动行驶控制。
又如,在交通拥堵时,车辆控制数学模型需要考虑更多的交通流动力学因素,以实现更有效的交通管理和控制。
车辆控制数学模型是对车辆运动行为进行量化和建模的重要方法,它为车辆控制系统的设计与实现提供了理论基础和技术支持。
随着科学技术的发展和控制理论的进步,车辆控制数学模型将不断进行优化与完善,以更好地适应不断变化的交通运输需求,为交通运输领域的发展和改善提供更加可靠和高效的技术支撑。
第二篇示例:车辆控制数学模型是指通过数学方法描述和分析车辆运动过程中的控制行为和规律的模型。
在现代汽车工程领域,控制系统设计和优化是提高车辆性能、安全性和舒适性的关键因素之一。
根据不同的控制目标和需求,能够建立合适的数学模型对车辆进行控制,可以提高车辆驾驶性能,并且广泛应用于自动驾驶系统、电动汽车控制系统以及智能交通系统等领域。
自动控制原理第三章二阶系统的数学模型及单位阶跃响应.ppt

定义: 由二阶微分方程描述的系统称为二阶 系统。
➢二阶系统数学模型
二阶系统的微分方程一般式为:
dd 2c t(2t)2 ndc d (tt)n 2c(t)n 2r(t)
(n 0)
阻尼比 n 无阻尼振荡频率
二阶系统的反馈结构图
R(s)
22 nn
ss((ss 22nn))
形式,而闭环零点的微分作用,将在保证响应特性 平稳的情况下,显著地提高系统的快速性。
2.输出量的速度反馈控制
将输出量的速度信号c(t)采用负反馈形式,反馈到输 入端并与误差信号e(t)比较,构成一个内回路,称为 速度反馈控制。如下图示。
闭环传函为:
(s)C R ( (s s) )s2(2 n n K 2tn 2)s n 2
等效阻尼比:
t
1 2
Ktn
等效阻尼比增大了,振荡倾向和超调量减小,改 善了系统的平稳性。
3.比例-微分控制和速度反馈控制比较
➢从实现角度看,比例-微分控制的线路结构比较简 单,成本低;而速度反馈控制部件则较昂贵。
➢从抗干扰来看,前者抗干扰能力较后者差。
➢从控制性能看,两者均能改善系统的平稳性,在相 同的阻尼比和自然频率下,采用速度反馈不足之处是 其会使系统的开环增益下降,但又能使内回路中被包 围部件的非线性特性、参数漂移等不利影响大大削弱。
3.发展 (1)原因: ①甲午战争以后列强激烈争夺在华铁路的 修。筑权 ②修路成为中国人 救的亡强图烈存愿望。 (2)成果:1909年 京建张成铁通路车;民国以后,各条商路修筑 权收归国有。 4.制约因素 政潮迭起,军阀混战,社会经济凋敝,铁路建设始终未入 正轨。
由此知道:
c(t)c1(t)c2(t)
姜启源 数学模型第五版-第1章

1.3
问题
建模示例之一 包饺子中的数学
通常,1kg馅, 1kg面, 包100个饺子. 今天,馅比 1kg多, 1kg面不变, 要把馅包完.
应多包几个(每个小些), 还是少包几个(每个大些)?
分析
直观认识——“大饺子包的馅多”! 但是:“用的面皮也多”!
需要比较:饺子从小变大时馅和面增加的数量关系.
C
C´ B´ B A´
O
A
x
D´
D
A,C 两脚与地面距离之和 ~ f() B,D 两脚与地面距离之和 ~ g()
正方形ABCD 绕O点旋转
模型建立
地面为连续曲面 椅子在任意位置 至少三只脚着地 椅子旋转900, 对 角线AC和BD互换 f() , g()是连续函数 对任意, f(), g() 至少一个为0 g(0)=0,f(0) > 0, f(/2)=0, g(/2)>0.
不平的地面上的椅子, 通常三只脚着地—— 放不稳! 挪动几下,使四只脚着地——椅子放稳!
讨论椅子能放稳的条件.
椅子能在不平的地面上放稳吗
模型假设
四腿一样长,椅脚与地面点接触,四脚连线呈正方形. 地面高度连续变化,可视为数学上的连续曲面. 地面相对平坦,椅子在任意位置至少三只脚着地.
模型建立
椅子位置 利用正方形(椅脚连线)的对称性. 用表示椅子位置. 四只脚着地 椅脚与地面距离为零 距离是的函数. 四个距离 (四只脚) 对称性 两个距离
模 型 构 成
尽量采用简单的数学工具
数学建模的一般步骤 模型 求解 模型 分析 模型 检验 各种数学方法、软件和计算机技术. 如结果的误差分析、统计分析、 模型对数据的稳定性分析. 与实际现象、数据比较, 检验模型的合理性、适用性.
第02章 评价规模有效和技术有效的C2R模型

I
第2章 评价规模有效和技术有效的C2R模型
2.1 第一个DEA模型C2R 0 0 ( , ) R
I2 ) 是等价的。 R,所以 ( PI2 ) 与( P 又由于R CR CR 由模型(C2R)I可知,hj0是在满足 uT y j 1, j 1, , j0 , , n T v xj 的前提下,追求 DMU-j0 对应的效率 hj0 的最大值 hj0 ,因 此hj0是相对于n个决策单元的相对效率值(简称效率指数)。 I 不难看出, (P )的最优值满足 C2R
t (v xj u yj ) 0,
T T
j 1,2,, n
即 并且,由
T xj T yj 0,
j 1,2,, n 1 t T v x0
得到一个新的约束
T x0 tvT x0 1 I ) 此时模型(C2R)I化为等价的模型 ( P CR
2
2016年11月22日星期二
u y0 hj0 0T 1 v x0 则称DMU-j0为弱DEA有效。
2016年11月22日星期二
0T
19第2章 评价规模有效和技术有效的 Nhomakorabea2R模型
2.1 第一个DEA模型C2R
定义2.2 若(C2R)I的最优解v0、u0 ,满足(效率指数) u0T y0 hj0 0T 1 v x0 并且 v0 >0, u0 >0 则称DMU-j0为DEA有效。 I ) 等价,利用线性规 由于(C2R)I模型与线性规划( P C2R 划 ( PI2 ) ,有下面的等价定义。
2016年11月22日星期二
12
第2章 评价规模有效和技术有效的C2R模型
2.1 第一个DEA模型C2R
微分方程的经典模型

模型分析
问题中并未出现“变化率”、“导数”这样的关键词,但要寻找的是体重 (记为W)关于时间t的函数。如果我们把体重W看作是时间t的连续可微函数, 我们就能找到一个含有的
dW 微分方程。 dt
模型假设
W0 ; 1.W ( t ) 表示 t 时刻某人的体重,并设一天开始时人的体重为 2. W ( t ) 关于 t 连续而且充分光滑;
模型建立
游击作战模型的形式:
,
(t) f (x, y) x (t) g(x, y) y x(0) x , y(0) y 0 0
, 由假设2、3,甲乙双方的战斗减员率分别为
f(x ,y ) c x y
g (x ,y )dxy
结合以上两表达式,并代入 c、d 的值,可得游击作战的数学模型
或被歼灭)的一方为败。因此,如果 K K0 ,则乙的兵力减少到
甲方兵力降为“零”,从而乙方获胜。同理可知, K0
K0 胜。而当
a
时
时,甲方获
时,双方战平。
2 2 bx ay 0 甲方获胜的充要条件为 0 0
代入a 、b 的表达式,进一步可得甲方获胜的充要条件为
2 2 r p x r p y x x 0 y y 0
模型建立 根据假设得到一般的战争模型
x ( t) f( x ,y ) x u ( t) y ( t) g ( x ,y ) y v ( t) x ( 0 )x , y ( 0 )y 0 0
正规作战模型
模型假设
1.不考虑增援,并忽略非战斗减员;
得:
其解为:
i(t) i0e
k0t
模型分析与解释
这个结果与传染病初期比较吻合,但它表明病人人数将按指数规律 无限增加,显然与实际不符
数学模型第01章第五版ppt课件

3)据连续函数的基本性质, 必存在0 ( 0< 0 < /2) , 使h(0)=0, 即 f(0) = g(0) . 4)因为 f(0) • g(0)=0, 所以 f(0) = g(0) = 0.
结论:在模型假设条件下,将椅子绕中心旋转, 一定能找到四只脚着地的稳定点.
表现特性 建模目的
确定和随机
静态和动态
离散和连续
线性和非线性
描述、优化、预报、决策、…
了解程度 白箱
灰箱
黑箱
1.8 怎样学习数学建模—— 学习课程和参加竞赛
数学建模与其说是一门技术,不如说是一门艺术.
技术大致有章可循. 艺术无法归纳成普遍适用的准则.
• 着重培养数学建模的意识和能力 数学建模的意识 对于日常生活和工作中那些需要 或者可以用数学知识分析、解决的实际问题,能够 敏锐地发现并从建模的角度去积极地思考、研究.
用 x 表示船速,y 表示水速,列出方程:
(x y) 30 750
x=20
( x y) 50 750 求解 y =5
答:船速为20km/h.
航行问题建立数学模型的基本步骤
• 作出简化假设(船速、水速为常数) • 用符号表示有关量(x, y分别表示船速和水速) • 用物理定律(匀速运动的距离等于速度乘以 时间)列出数学式子(二元一次方程) • 求解得到数学解答(x=20, y=5)
1.4 建模示例之二 路障间距的设计
背景 校园、居民小区道路需要限制车速——设置路障 问题 限制车速≤40km/h, 相距多远设置一个路障?
分析 汽车过路障时速度接近零, 过路障后加速.
车速达到40km/h时让司机看到下一路障而 减速, 至路障处车速又接近零. 如此循环以达到限速的目的.
一级动力学反应模型
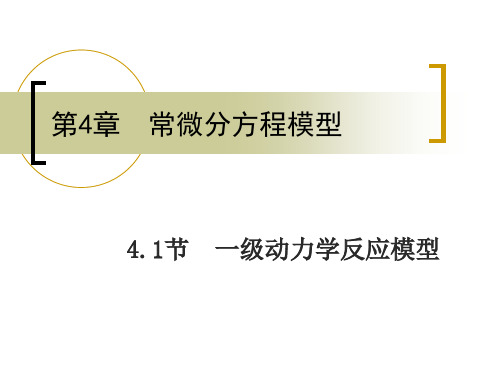
一级动力学反应的指数衰减过程和半衰期 x=x 0
x=x 0/2
x
t=0
t=
t
图4.1
4.1.2 碳-14测年法
当人们看见一件很古老的东西,最常见的疑问是 “这是多少年前的东西”?考古学家一直在努力发展 新技术来考证古物的年代. 在诸多考证年代的的方法之中,以“碳-14 定年 法”最为普遍. 它的原理是根据生物体死亡之后,体 内碳-14 衰减的速率来估计年代. 美国化学家威拉得· 法兰克· 利比(Willard Frank Libby)因在 20 世纪 40 年代发明碳-14 定年法而于 1960 年获得诺贝尔化学奖.
4.1.4 海拔与大气压
根据物理学知识,可以假设大气压对海拔的变化 率与大气压成正比,因此在海拔 y 米处,大气压 p 满 足微分方程初值问题 (4.1.10) dp dy kp , p(0) p0 其中比例系数
Mg (4.1.11) k RT 其中, T 为海拔 y 米处的气温(单位: K ) ,常数 R 8.315J/mol K . M 28.8 103 kg/mol , g =9.8m/s2 ,
4.1.1 一级动力学 反应模型及其性质
在初始时刻 t 0 , 设反应物的含量为 x0 . (4.1.1)式满 足初始条件 x(t0 ) x0 的特解为 (4.1.2) x(t ) x0e 0 (4.1.2)式表明:系统中反应物的含量按指数规律随时 间衰减.
k t t
4.1.1 一级动力学 反应模型及其性质
4.1.2 碳-14测年法
碳是一种很常见的非金属元素,以多种形式广泛 存在于大气和地壳之中,常见的碳单质有石墨和金刚 石,碳的一系列化合物——有机物是生命的根本. 自然界中存在三种碳的同位素:碳-12(98.9%) 、 碳-13 及碳-14(极少). 碳-12 和碳-13 属稳定型,碳 -14 具有放射性. 碳-14 是由宇宙射线撞击空气中的氮 原子而产生,衰变方式为 β 衰变,碳-14 原子转变为 氮原子. 碳-14 的半衰期长达 5730 年,考古学家就是 根据碳-14 的半衰期计算年代.
车辆控制数学模型

车辆控制数学模型
车辆控制的数学模型是用于描述车辆在运动过程中受到的各种力和力矩以及其响应的数学方程。
这些模型通常涉及多个方面,包括车辆的动力学(运动学和动力学)、悬挂系统、轮胎特性等。
以下是一些常见的车辆控制数学模型的要素:
运动学模型:
位置和姿态:描述车辆在空间中的位置和朝向。
速度和角速度:描述车辆在不同方向上的线速度和角速度。
动力学模型:
质量和惯性:车辆的质心质量和绕各轴的惯性矩。
动力:引擎或电动机提供的动力。
阻力:空气阻力、滚动阻力等对车辆运动的阻碍。
摩擦:轮胎与路面之间的摩擦力。
悬挂系统模型:
弹簧和阻尼:描述车辆悬挂系统的弹簧刚度和阻尼特性。
悬挂几何:车轮与车身之间的几何关系,对车辆姿态的影响。
轮胎模型:
轮胎力:描述轮胎受力与滑移关系,通常使用Pacejka Magic Formula 或其他轮胎模型。
侧向和纵向力:描述轮胎在横向和纵向上产生的力。
车辆控制输入:
转向输入:车辆转向角度或转向速度。
加速度输入:车辆纵向的加速度控制。
这些要素可以通过运动学和动力学方程来描述车辆的运动行为。
数学模型的建立和求解可以使用传统的动力学方法、控制理论、优化方法等。
在实际应用中,这些模型可以用于开发车辆动态控制系统,包括制动系统、转向系统、巡航控制系统等,以提高车辆的性能、稳定性和安全性。
不同类型的车辆(小轿车、卡车、无人车辆等)可能会采用不同的数学模型来更好地适应其特定的运动特性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
进行仿真研究,分析系统性能
根据仿真分析结果,进行系统设计方案的确定
根据仿真分析结果,整定调节器参数
建立数学模型的方法有 1
采用物理机理方法建模
2 采用确定性信号实验方法建模
3 数学模型的辩识
2.1 采用物理机理方法建模
3
过程控制系统其他环节的数学模型
检测仪表数学模型 Km (s) = 1 / ( 0.1s + 1 ) 执行器和调节阀数学模型 Ka (s) = 1 / ( 0.1s + 1 ) T0 PID 调节器的数学模型 Wc (s) = P +I /s +D· s
P:比例增益,I:积分系数,D:微分系数
K0 / ( T0 s K+ 1 )
0
一阶惯性环节
y(t) = P· e(t) + I· ∫e(t) · dt + D· de(t)/dt
Y (s) k0 s k1 s kn1 s kn W ( s) n n 1 X (s) j0 s j1 s jn1 s jn
n
n 1Biblioteka 用一阶线性常系数微分方程描述的对象的模型称为一阶惯 性环节。
用二阶线性常系数微分方程描述的对象的模型称为二阶惯 性环节。 建立被控过程数学模型的目的
2. 被控对象数学模型
物理对象的输入与输出的关系一般要用微分方程表示 这种微分方程,就叫做对象的数学模型。
k0 • d(n)y(t)/dt(n) + k1 • d(n-1)y(t)/dt(n-1) +…+ kn-1 • x(t)/dt +kn • y(t) = j0 • d(n)x(t)/dt(n) + j1 • d(n-1)x(t)/dt(n-1) +…+jn-1 • x(t)/dt +jn • x(t) k0,k1,… kn,j0,j1,… jn都是常数 设初始状态为0,对方程两边取拉氏变换, 得对象数学模型的传递函数形式的表达方式W(s)
