2018-2019北京期八年级下期末试卷分类汇编八下期末数学试卷分类-几何综合【含答案】
北京市八年级上册期末数学试卷精选汇编:几何综合专题(含答案)

F ED FAED几何综合专题海淀区24.如图所示,将两个含30°角的三角尺摆放在一起,可以证得△ABD 是等边三角形,于是我们得到:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半. 交换命题的条件和结论,得到下面的命题: 在直角△ABC 中,∠ACB =90°,如果12CB AB=,那么∠BAC =30°. 请判断此命题的真假,若为真命题,请给出证明;若为假命题,请说明理由.26. (1)………………………1分(2)连接AE由题意可知,,EAD CAD α∠=∠= AC =AE , ∴902,BAE α∠=︒- ∵AB=AC ,∴AB=AE , ∴,ABE AEB ∠=∠∴180452BAEABF α︒-∠∠==︒+.………………………3分(3)12EF BC =, 证明:由(2)可知45,AEB ABE α∠=∠=︒+∴.CBF α∠= ………………………4分CAF EG A'F E C ∵点C 关于直线AD 的对称点为点E , ∴135,ACF AEF α∠=∠=︒- ∴90,BCF α∠=︒-∵90,CBF BCF ∠+∠=︒ ………………………5分 ∴△BCF 是直角三角形.∵△ACE 是等边三角形, ∴30.α=︒∴30CBF ∠=︒ ∴1.2EF CF BC ==………………………6分东城区23.在三角形纸片ABC 中,∠B =90°,∠A =30°,AC =4,点E 在AC 上,AE =3.将三角形纸片按图1方式折叠,使点A 的对应点A '落在AB 的延长线上,折痕为ED ,A E '交BC 于点F. (1)求∠CFE 的度数;(2)如图2,,继续将纸片沿BF 折叠,点A '的对应点为A '',A F ''交DE 于点G .求线段DG 的长.图1图224. 如图,△ABC .(1)尺规作图:过点C 作AB 的垂线交AB 于点O .不写作法,保留作图痕迹; (2)分别以直线AB ,OC 为x 轴,y 轴建立平面直角坐标系,使点B ,C 均在正半轴上.若AB=7.5,OC =4.5,∠A =45°,写出点B 关于y 轴的对称点D 的坐标; (3)在(2)的条件下,求△ACD 的面积.23.解:(1)∵∠A =30°,∴∠A '=30°. ……………………1分∵∠A BF '=90°,∴∠A FB '=60°. ……………………2分∵∠CFE =∠A FB ',A'F E∴∠CFE =60°. ……………………3分(2)∵点A 与点A '关于直线DE 对称, ∴DE ⊥AA '. ∵∠A =30°,AE =3, ∴1322DE AE == . ……………………4分 由(1)知,∠CFE =60°,∠C =60°,∴△CFE 是等边三角形.∴EF =CE =AC -AE =1. ……………………5分 同理,△EFG 也是等边三角形,∴12DG DE EG =-=DG =DE -EG =.……………………6分24.解:(1)……………………………………………………………………………………2分(2)D (-3,0); ……………………4分 (3)13927==2228ACD S ⨯⨯△.……………………6分 密云区25.已知如图,点A 、点B 在直线l 异侧,以点A 为圆心,AB 长为半径作弧交直线l 于C 、D 两点.分别以C 、D 为圆心,AB 长为半径作弧,两弧在l 下方交于点E,连结AE. (1)根据题意,利用直尺和圆规补全图形; (2)证明:l 垂直平分AE.lAB25.(1)GFEC图2O ED CBAl………………2分(2)证明:AC=AD=AB,CE=ED=AB,∴AC=CE,AD=DE又CD=CD∴△ACD ≌△ECD………………4分∴∠ACD=∠ECD∵AC=CE ∴l 垂直平分AE.………………6分门头沟区24.如图,在△ABC 中,AC 的垂直平分线交AC 于点D , 交BC 延长线交于点E ,连接AE ,如果∠B =50°,∠BAC =21°,求∠CAE 的度数.24.解答题(本小题满分5分) ∵AC 的垂直平分线交AC 于点D ∴EA =EC ……………………………………… 1分 ∴∠E AC =∠ECA ………………………… 2分∵∠B =50°,∠BAC =21°∴∠ECA=∠B+∠BAC=71°………………… 4分∴∠E AC =71° ………………… 5分27. 如图,在△ABC 中,AB=AC ,点M 在△ABC 内,AM 平分∠BAC .点D 与点M 在AC 所在直线的两侧,AD ⊥AB ,AD= BC ,点E 在AC 边上,CE=AM ,连接MD 、BE . (1) 补全图形;(2) 请判断MD 与BE 的数量关系,并进行证明;(3) 点M 在何处时,BM+BE 会有最小值,画出图形确定点M 的位置;如果AB =5,BC = 6,求出BM+BE的最小值.DBCD BC BCM27.解答题(本小题满分7分) 解:(1)补全图形正确 ………………………………………………………1分 (2)MD =BE ………………………………………………………2分证明:延长AM 交BC 于点F (如图2). ∵ AM 平分∠BAC , ∴ ∠BAM =∠CAM .∵ AD ⊥AB , ∴ ∠MAD +∠BAM =90°. ∴ ∠MAD +∠CAM =90°∵ AB=AC ,AM 平分∠BAC ,∴ AF ⊥BC .∴ ∠C +∠CAM =90°.∴ ∠MAD =∠C . ………………………………3分 又∵ AM= CE ,AD= BC ,∴ △AMD ≌△CEB . …………………………………………… 4分 ∴ MD =BE . …………………………………………… 5分(3) 点M 的位置如图 …………………………………………… 6分∵ AB=5,BC = 6, ∴ AD = BC=6,.∴22225661BD AB AD =++=∴ BM+BE 61……………… 7分朝阳区26.如图,△ABC 是等边三角形,△ADC 与△ABC 关于直线AC 对称,AE 与CD 垂直交BC 的延长线于点E ,∠EAF=45º,且AF 与AB 在AE 的两侧,EF ⊥AF . (1)依题意补全图形.(2)①在AE 上找一点P ,使点P 到点B ,点C 的距离和最短;②求证:点D 到AF ,EF 的距离相等.26.(1)补全图形,如图………………………..2分(2与AE 的交点.F E B C MFE BCMF DAP F DA…………..4分②证明:连接DE ,DF .∵△ABC ,△ADC 是等边三角形,∴AC =AD ,∠ACB =∠CAD =60°. ∵AE ⊥CD , ∴∠CAE =21∠CAD =30°. ∴∠CEA =∠ACB -∠CAE =30°. ∴∠CAE =∠CEA. ∴CA =CE . ∴CD 垂直平分AE . ∴DA =DE .∵EF ⊥AF ,∠EAF =45°, ∴∠FEA =45°. ∴∠FEA =∠EAF . ∴F A =FE .∴△F AD ≌△FED .∴∠AFD =∠EFD .点D 到AF ,EF 的距离相等. ……………..7分顺义区27.在平面内,给定∠AOB =60°,及OB 边上一点C ,如图所示.到射线OA ,OB 距离相等的所有点组成图形G ,线段OC 的垂直平分线交图形G 于点D ,连接CD .(1)依题意补全图形;直接写出∠DCO 的度数;(2)过点D 作OD 的垂线,交OA 于点E ,OB 于点F .求证:CF =DE .OA27.(5分)FD AF EDCBA(1)画图………………………………… 2分30°………………………………… 3分(2) 证明:∵OD 是∠AOB 的平分线,∠AOB =60°, ∴∠1 =∠2=30°,又∵点D 在OC 的垂直平分线上, ∴CD =OD ,∴∠3 =∠2=30°, ∵EF ⊥OD ,∴∠EDO =∠FDO =90°, ∴∠DFO =60°,∴∠4 =30°,∠4 =∠3, ∴CF =DF ,又∵△OED ≌△OFD ,……………………………………4分 ∴DE =DF ,∴CF =DE .…………………………………………………5分昌平区27.如图,将△ABC 分别沿 AB ,AC 翻折得到△ABD 和△AEC ,线段 BD 与AE交于点 F ,连接BE .(1)如果∠ABC =16º,∠ACB =30°,求∠DAE 的度数; (2)如果BD ⊥CE ,求∠CAB 的度数.27. 解:(1)∵△ABC 沿AC 、AB 翻折得到△AEC 和△ABD , ∴△AEC ≌△ABC ,△ABD ≌△ABC.∴∠2=∠1=30°, ∠4=∠3=16°. …………1分 ∠EAC =∠BAD =∠BAC =180°-30°--16°=134°. ……2分∵∠DAC =360°-∠BAD -∠BAC ,4321OC B ADEF54321F EDCBA∴∠DAC=360°-134°-134°=92°. ………………3分∴∠DAE=∠EAC -∠DAC=134°-92°=42°. …………4分(2)∵BD ⊥CE ,∴∠5=90°. . …………………………………………………………………… 5分∴∠DBC+∠ECB=90°.∵∠1=∠2,∠3=∠4,∴∠DBC+∠ECB=2∠3+2∠1=90°.∴∠3+∠1=45°. . …………………………………………… 6分 在△ABC 中,∠CAB =180°-(∠3+∠1)=180°-45°=135°. …… 7分平谷区27. 已知:在△ABC 中,∠ABC =45°,BD ⊥AC 于点D ,过点C 作CE ⊥AB 于点E ,交BD 于点F .(1)依题意补全图形; (2)求证:∠ABD =∠ACE (3)求证:EF =AE27. (1) 依题意补全图形………………………………………………… 1 (2)证明:∵CE ⊥AB ,BD ⊥AC∴∠BEC=∠BDC=90°………………………2 ∴∠ABD+∠EFB=90°∠ACE+∠CFD=90° ∵∠EFB=∠CFD∴∠ABD=∠ACE (3)(3)∵∠BEC=90°,∠ABC=45° ∴ BE=EC (4)在△BEF 和△AEC 中 ⎪⎩⎪⎨⎧∠∠=∠=∠ACE =ABD ECBE AEC BEC∴BEF ∆≌AEC ∆)(ASA (5)DAFDEA∴EF =AE燕山地区27.阅读下面材料:学习了三角形全等的判定方法(即“SAS ”“ASA ”“AAS ”“SSS ”)和直角三角形全等的判定方法(即“HL ”)后,明明继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行探究明明将命题用符号语言表示为:在△ABC 和△DEF 中,AC=DF ,BC=EF ,∠B =∠E . 明明的探究方法是把∠B 分为“直角、钝角、锐角”三种情况进行探究.(1) 当∠B 是直角时,如图甲,△ABC 和△DEF 中,AC=DF ,BC=EF ,∠B =∠E =90°, 根据“HL ”定理,可以知道Rt △ABC ≌ Rt △DEF.(2)当∠B 是锐角时,如图乙,BC=EF ,∠B =∠E ﹤90°,在射线EM 上有点D,使DF=AC,画出符合条件的点D ,则△ABC 和△DEF 的关系是 ;A. 全等B. 不全等C.不一定全等(3)当∠B 是钝角时,如图丙,在△ABC 和△DEF 中,AC=DF ,BC=EF ,∠B =∠E ﹥90°.过点C 作AB 边的垂线交AB 延长线于点M;同理过点F 作DE 边的垂线交DE 延长线于N ,根据“ASA ”,可以知道△CBM ≌△FEN,请补全图丙,进而证出△ABC ≌△DEF.A27.(2)画出点D 正确,选C ………………… 2分 (3)补全图 ………………… 3分证明:由△CBM ≌△FEN得,CM=FN,BD=EN 又在Rt △CMA 和Rt △FND 中⎩⎨⎧==FN CM DF AC ∴△CMA ≌△FND ∴AM=DN∴AB=DE ……………… 4分 又在△ABC 和△DEF 中 ⎪⎩⎪⎨⎧===DE AB EF BC DFAC ∴△ABC ≌△DEF ……………… 5分图甲 图乙图丙BF房山区26.(1)证明:∵AB AD =,=60A ∠︒,∴△ABD 是等边三角形.∴60ADB ∠=︒. …….………..……….1分∵CE ∥AB ,∴60CED A ∠=∠=︒. …….………..……….2分 ∴CED ADB ∠=∠. (2)解:连接AC 交BD 于点O ,∵AB AD =,BC DC =, ∴AC 垂直平分BD . ∴30BAO DAO ∠=∠=︒. ∵△ABD 是等边三角形,8AB = ∴8AD BD AB ===,∴4BO OD ==. ………….………..……….3分 ∵CE ∥AB , ∴ACE BAO ∠=∠.∴6AE CE ==, 2DE AD AE =-=.O F EDBA∵60CED ADB ∠=∠=︒.∴60EFD ∠=︒.∴△EDF 是等边三角形.∴2EF DF DE ===,∴4CF CE EF =-=,2OF OD DF =-=.在Rt △COF 中, ∴2223OC CF OF =-=. …….………..……….4分 在Rt △BOC 中, ∴22224(23)27BC BO OC =+=+= …….………..……….5分大兴区26. 解:∵AD 是△ABC 的高∴90ADB ADC ∠=∠= ………………………… 1分∵45ABC ∠=∴45DBA ABC ∠=∠=∴BD =AD ………………………… 2分∵BE 是△ABC 的高∴90BEC ∠=∴90EBC C ∠+∠=∵90ADC ∠=∴90DAC C ∠+∠=∴EBC DAC ∠=∠ ………………………… 3分在△BDF 和△ADC 中,EBC DAC BD ADBDF ADC ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BDF ≌△ADC . ………………………… 4分∴DF =CD . ………………………… 5分∵CD =4∴DF =4 ………………………… 6分27.解:(1)EB CA ………………………… 2分(2)∵将线段CD 绕点C 逆时针旋转90°得到线段CE ,∴90DCE ∠=,CD =CE∵ ∠ACB =90°∴ACD BCE ∠=∠ ………………………… 3分在△ACD 和△BCE 中,AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩∴△ACD ≌△BCE ………………………… 5分∴CBE A ∠=∠ ………………………………………… 6分 ∵90,ACB AC BC ∠==∴45A ∠=∴45CBE ∠=∵90DCE ∠=,CD =CE∴45CED ∠=……………………………………………………… 7分 在△BCE 中,BCE ACD α∠=∠=.∴90DEB ∠=-α…………………………………………………… 8分 石景山区通州区。
初二数学期末试卷西城

北京市各区数学期末复习资料-初二下学期(几何综合+新定义问题)

每日一题—几何部分1.如图,在Rt △ABC 中,∠A =90°,AB =AC ,将线段BC 绕点B 逆时针旋转α°(0<α<180),得到线段BD ,且AD ∥BC . (1)依题意补全图形;(2)求满足条件的α的值; (3)若AB =2,求AD 的长.2.在Rt △ABC 中,∠ACB =90°,CA =CB .点D 为线段BC 上一个动点(点D 不与点B ,C重合),连接AD ,点E 在射线AB 上,连接DE ,使得DE =DA .作点E 关于直线BC 的对称点F ,连接BF , DF . (1)依题意补全图形; (2)求证:∠CAD =∠BDF ; (3)用等式表示线段AB ,BD ,BF 之间的数量关系,并证明.3.如图,在正方形ABCD 中,E 是边BC 上一动点(不与点B ,C 重合),连接DE ,点C 关于直线DE 的对称点为C ʹ,连接ACʹ并延长交直线DE 于点P ,F 是AC ′中点,连接DF . (1)求∠FDP 的度数;(2)连接BP ,请用等式表示AP ,BP ,DP 三条线段之间的数量关系,并证明. (3)连接AC ,若正方形的边长为2,请直接写出△ACC ′的面积最大值.FP C'BCA DE4.已知:Rt △ABC 中,∠ACB =90°,AC =BC .(1) 如图1,点D 是BC 边上一点(不与点B ,C 重合),连接AD ,过点B 作BE ⊥AD ,交AD 的延长线于点E ,连接CE . 若∠BAD =α,求∠DBE 的大小 (用含α的式子表示) ; (2) 如图2,点D 在线段BC 的延长线上时,连接AD ,过点B 作BE ⊥AD ,垂足E 在线段AD 上,连接CE . ①依题意补全图2;②用等式表示线段EA ,EB 和EC 之间的数量关系,并证明.图1 图25.在△ABC 中,∠ACB =90°,AC =BC , D 为AB 的中点,点E 为AC 延长线上一点,连接DE ,过点D 作DF ⊥DE 交CB 的延长线于点F .(1)求证:BF= CE ; (2)若CE =AC ,用等式表示线段DF 与AB 的数量关系,并证明.ABA6.如图,在等腰直角△ABC中,90CA CD),连接BD,ABC°,D是线段AC上一点(2过点C作BD的垂线,交BD的延长线于点E,交BA的延长线于点F.(1)依题意补全图形;(2)若ACE α,求ABD的大小(用含α的式子表示);(3)若点G在线段CF 上,CG BD,连接DG.①判断DG与BC的位置关系并证明;②用等式表示DG,CG,AB之间的数量关系为.7.如图,等边△ABC中,P是AB上一点,过点P作PD⊥AC于点D,作PE⊥BC于点E,M是AB的中点,连接ME,MD.(1)依题意补全图形;(2)用等式表示线段BE ,AD 与AB的数量关系,并加以证明;(3)求证:MD=ME.C8.如图,∠AOB = 90°,OC 为∠AOB 的平分线,点P 为OC 上一个动点,过点P 作射线PE交OA 于点E .以点P 为旋转中心,将射线PE 沿逆时针方向旋转90°,交OB 于点F . (1)根据题意补全图1,并证明PE = PF ;(2)如图1,如果点E 在OA 边上,用等式表示线段OE ,OP 和OF 之间的数量关系,并证明;(3)如图2,如果点E 在OA 边的反向延长线上,直接写出线段OE ,OP 和OF 之间的数量关系.图1 图29.已知ABC ∆为等边三角形,点D 是线段AB 上一点(不与A 、B 重合).将线段CD 绕点C 逆时针旋转60︒得到线段CE.连结DE 、BE. (1)依题意补全图1并判断AD 与BE 的数量关系. (2)过点A 作AF EB ⊥交EB 延长线于点F.用等式表示线段EB 、DB 与AF 之间的数量关系并证明.PPEECCBBOOAA图2D CBA图1A B CD10.在△ABC 中,∠ABC =120°,线段AC 绕点A 逆时针旋转60°得到线段AD ,连接CD ,BD 交AC 于P .(1)若∠BAC =α,直接写出∠BCD 的度数 (用含α的代数式表示); (2)求AB ,BC ,BD 之间的数量关系;(3)当α=30°时,直接写出AC ,BD 的关系.11,如图,在等边△ABC 中,D 为边AC 的延长线上一点()CD AC ,平移线段BC ,使点C 移动到点D ,得到线段ED ,M 为ED 的中点,过点M 作ED 的垂线,交BC 于点F ,交AC 于点G . (1)依题意补全图形; (2)求证:AG = CD ;(3)连接DF 并延长交AB 于点H ,用等式表示线段AH 与CG 的数量关系,并证明.12.已知:如图,在△ABC 中,AB >AC ,∠B =45°, 点D 是BC 边上一点,且AD=AC ,过点C 作CF ⊥AD 于点E ,与AB 交于点F .(1)若∠CAD =α,求∠BCF 的大小(用含α的式子表示); (2)求证:AC =FC ;(3)用等式直接表示线段BF 与DC 的数量关系.D BAB CDFE13.如图,在等边ABC △中,点D 是线段BC 上一点.作射线AD ,点B 关于射线AD 的对称点为E .连接CE 并延长,交射线AD 于点F .(1)设BAF α∠=,用α表示BCF ∠的度数;(2)用等式表示线段AF 、CF 、EF 之间的数量关系,并证明.14.如图,在△ABC 中,∠ABC =90°,BA =BC .将线段AB 绕点A 逆时针旋转90°得到线段AD ,E 是边BC 上的一动点,连接DE 交AC 于点F ,连接BF . (1)求证:FB =FD ;(2)点H 在边BC 上,且BH =CE ,连接AH 交BF 于点N .①判断AH 与BF 的位置关系,并证明你的结论;②连接CN .若AB =2,请直接写出线段CN 长度的最小值.H O DCBA15.已知:四边形ABCD 中,120ABC ∠=︒,60ADC ∠=︒,AD =CD ,对角线AC ,BD相交于点O ,且BD 平分∠ABC ,过点A 作AH BD ⊥,垂足为H . (1)求证:ADB ACB ∠=∠;(2)判断线段BH ,DH ,BC 之间的数量关系;并证明.16.如图,在△ABC 中,AB =BC ,∠B =90°,点D 为线段BC 上一个动点(不与点B ,C 重合),连接AD ,将线段AD 绕点D 顺时针旋转90°得到线段DE ,连接EC .(1) ① 依题意补全图1;② 求证:∠EDC =∠BAD ;(2) ① 小方通过观察、实验,提出猜想:在点D 运动的过程中,线段CE 与BD 的数量关系始终不变,用等式表示,并证明.图1 D C B A备用图AB CD每日一题—新定义部分1.在平面直角坐标系xOy 中,如果等边三角形的一边与x 轴平行或在x 轴上,则称这个等边三角形为水平正三角形.(1)已知A (1,0),B (-1,0),若△ABC 是水平正三角形,则点C 坐标的是 (只填序号); ①,②,③,④(2)已知点O ,E ,F ,以这三个点中的两个点及平面内的另一个点P为顶点,构成一个水平正三角形,则这两个点是 ,并求出此时点P 的坐标.2.在平面直角坐标系xOy 中,对于P ,Q 两点给出如下定义:若点P 到x 、y 轴的距离中的最大值等于点Q 到x 、y 轴的距离中的最大值,则称P ,Q 两点为“等距点”.下图中的P ,Q 两点即为“等距点”.(1)已知点A 的坐标为(-3,1),①在点E (0,3),F (3,-3),G (2,-5)中,为点A 的“等距点”的是________;②若点B 在直线y =x +6上,且A ,B 两点为“等距点”,则点B 的坐标为________; (2)直线l :y =kx -3(k >0)与x 轴交于点C ,与y 轴交于点D ,若T 1(-1,t 1),T 2(4,t 2),是直线l 上的两点,且T 1与T 2为“等距点”,求k 的值.()12,(0()01,-(0()00,(1()02,-3.对于平面直角坐标系xOy 中的点P 和图形G ,给出如下定义:若在图形G 上存在两个点A ,B ,使得以P ,A ,B 为顶点的三角形为等边三角形,则称P 为图形G 的“等边依附点”.已知M (-3,N (3,. ①在点C (-2,2),D (0,1),E (1,3)中,是线段MN 的“等边依附点”的是 ;②点P (m ,0)在x 轴上运动,若P 为线段MN 的“等边依附点”,求点P 的横坐标m 的取值范围。
2018-2019学年北京市海淀区八年级(下)期末数学试卷(解析版)

2018-2019学年北京市海淀区八年级(下)期末数学试卷一、选择题(本题共30分,每小题3分)在下列各题的四个选项中,只有一个是符合题意的1.(3分)下列实数中,是方程x2﹣4=0的根的是()A.1B.2C.3D.42.(3分)如图,在Rt△ABC中,∠C=90°,BC=6,AC=8,则AB的长度为()A.7B.8C.9D.103.(3分)在下列条件中,能判定四边形为平行四边形的是()A.两组对边分别平行B.一组对边平行且另一组对边相等C.两组邻边相等D.对角线互相垂直4.(3分)下列各曲线中,不表示y是x的函数的是()A.B.C.D.5.(3分)数据2,6,4,5,4,3的平均数和众数分别是()A.5和4B.4和4C.4.5和4D.4和56.(3分)一元二次方程x2﹣8x﹣1=0配方后可变形为()A.(x+4)2=17B.(x+4)2=15C.(x﹣4)2=15D.(x﹣4)2=17 7.(3分)若点A(﹣3,y1),B(1,y2)都在直线y=x+2上,则y1与y2的大小关系是()A.y1<y2B.y1=y2C.y1>y2D.无法比较大小8.(3分)如图,正方形ABCD的边长为,对角线AC,BD交于点O,E是AC延长线上一点,且CE=CO,则BE的长度为()A.B.C.D.29.(3分)对于一次函数y=kx+b(k,b为常数),下表中给出5组自变量及其对应的函数值,其中恰好有1个函数值计算有误,则这个错误的函数值是()X﹣10123Y2581214 A.5B.8C.12D.1410.(3分)博物馆作为征集、典藏、陈列和研究代表自然和人类文化遗产实物的场所,其存在的目的是为众提供知识、教育及欣赏服务.近年来,人们到博物馆学习参观的热情越来越高,2012﹣2018年我国博物馆参观人数统计如下:小明研究了这个统计图,得出四个结论:①2012年到2018年,我国博物馆参观人数持续增②2019年末我国博物馆参观人数估计将达到1082亿人次③2012年到2018年,我国博物馆参观人数年增幅最大的是2017年;④2016年到2018年,我国博物馆参观人数平均年增长率超过10%其中正确的是()A.①③B.①②③C.①②④D.①②二、填空题(本题共18分,每小题3分)11.(3分)在▱ABCD中,若∠B=110°,则∠D=°.12.(3分)八年级(1)班甲、乙两个小组的10名学生进行飞镖训练,某次训练成绩如下甲组成绩(环)87889乙组成绩(环)98797由上表可知,甲、乙两组成绩更稳定的是.13.(3分)若关于x的一元二次方程x2+6x+m=0有实数根,且所有实数根均为整数,请写出一个符合条件的常数m的值:m=.14.(3分)如图,某港口P位于南北延伸的海岸线上,东面是大海远洋号,长峰号两艘轮船同时离开港P,各自沿固定方向航行,“远洋”号每小时航行12nmile,“长峰”号每小时航行16nmile,它们离开港口1小时后,分别到达A,B两个位置,且AB=20nmile,已知“远洋”号沿着北偏东60°方向航行,那么“长峰”号航行的方向是.15.(3分)若一个矩形的长边的平方等于短边与其周长一半的积,则称这样的矩形为“优美矩形”.某公园在绿化时工作人员想利用如图所示的直角墙角(两边足够长)和长为38m的篱笆围成一个“优美矩形”形状的花园ABCD,其中边AB,AD为篱笆且AB大于AD.设AD为xm,依题意可列方程为.16.(3分)在平面直角坐标系xOy中,直线y=kx+3与x,y轴分别交于点A,B,若将该直线向右平移5单位,线段AB扫过区域的边界恰好为菱形,则k的值为.三、解答题(本题共26分,第17题8分,第18,20题各5分,第19,21题各4分)17.(8分)解下列方程:(1)x2+2x﹣3=0(用配方法)(2)2x2+5x﹣1=0(用公式法)18.(5分)在平面直角坐标系xOy中,函数y=kx+b的图象与直线y=2x平行,且经过点A(1,6)(1)求一次函数y=kx+b的解析式;(2)求一次函数y=kx+b的图象与坐标轴围成的三角形的面积.19.(5分)下面是小丁设计的“利用直角三角形和它的斜边中点作矩形的尺规作图过程:已知:如图,在Rt△ABC中,∠ABC=90°,O为AC的中点,求作:四边形ABCD,使得四边形ABCD为矩形.作法:①作射线BO,在线段BO的延长线上取点D,使得DO=BO②连接AD,CD,则四边形ABCD为矩形根据小丁设计的尺规作图过程(1)使用直尺和圆规,在图中补全图形(保留作图痕迹)(2)完成下面的证明证明:∵点O为AC的中点,∴AO=CO又∵DO=BO,∴四边形ABCD为平行四边形()∵∠ABC=90°,∴▱ABCD为矩形()20.(4分)方程x 2+2x +k ﹣4=0有实数根 (1)求k 的取值范围;(2)若k 是该方程的一个根,求2k 2+6k ﹣5的值.21.(4分)小东和小明要测量校园里的一块四边形场地ABCD (如图所示)的周长,其中边CD 上有水池及建筑遮挡,没有办法直接测量其长度小东经测量得知AB =AD =5m ,∠A =60°,BC =12m ,∠ABC =150°小明说根据小东所得的数据可以求出CD 的长度.你同意小明的说法吗?若同意,请求出CD 的长度;若不同意,请说明理由.四、解答题(本题共13分,第22题7分,第23题6分)22.(7分)三月底,某学校迎来了以“学海通识品墨韵,开卷有益览书山”为主题的学习节活动为了让同学们更好的了解二十四节气的知识,本次学习节在沿袭以往经典项目的基础上,增设了十四节气之旅项目,并开展了相关知识竞赛该学校七、八年级各有400名学生参加了这次竞赛,现从七、八年级各随机抽取20名学生的成绩进行抽样调查 七年级:74 97 96 72 98 99 72 73 76 74 74 69 76 89 78 74 99 97 98 99 八年级:76 88 93 89 78 94 89 94 95 50 89 68 65 88 77 87 89 88 92 91 整理数据如下成绩 人数 年级 50≤x ≤5960≤x ≤6970≤x ≤7980≤x ≤8990≤x ≤100七年级 0 1 10 1 a 八年级 12386分析数据如下年级平均数中位数众数方差七年级84.27774138.56八年级84b89129.7根据以上信息,回答下列问题(1)a=b=;(2)你认为哪个年级知识竞赛的总体成绩较好,说明理由(至少从两个不同的角度说明推断的合理性).(3)学校对知识竞赛成绩不低于80分的学生颁发优胜奖,请你估计学校七、八年级所有学生中获得优胜奖的大约有人.23.(6分)如图,在▱ABCD中,对角线AC,BD交于点O,过点B作BE⊥CD于点E,延长CD到点F,使DF=CE,连接AF.(1)求证:四边形ABEF是矩形;(2)连接OF,若AB=6,DE=2,∠ADF=45°,求OF的长度.五、解答题(本题共13分,第24题6分,第25题7分)24.(6分)如图,在平面直角坐标系xOy中,直线y=kx+7与直线y=x﹣2交于点A(3,m)(1)求k,m的值;(2)已知点P(n,n),过点P作垂直于y轴的直线与直线y=x﹣2交于点M,过点P 作垂直于x轴的直线与直线y=kx+7交于点N(P与N不重合).若PN≤2PM,结合图象,求n的取值范围.25.(7分)在Rt△ABC中,∠BAC=90°,点O是△ABC所在平面内一点,连接OA,延长OA到点E,使得AE=OA,连按OC,过点B作BD与OC平行,并使∠DBC=∠OCB,且BD=OC,连按DE.(1)如图一,当点O在Rt△ABC内部时,①按题意补全图形;②猜想DE与BC的数量关系,并证明.(2)若AB=AC(如图二),且∠OCB=30°,∠OBC=15°,求∠AED的大小.2018-2019学年北京市海淀区八年级(下)期末数学试卷参考答案与试题解析一、选择题(本题共30分,每小题3分)在下列各题的四个选项中,只有一个是符合题意的1.(3分)下列实数中,是方程x2﹣4=0的根的是()A.1B.2C.3D.4【分析】先把方程化为x2=4,方程两边开平方得到x=±=±2,即可得到方程的两根.【解答】解:移项得x2=4,开方得x=±2,∴x1=2,x2=﹣2.故选:B.【点评】本题考查了解一元二次方程﹣直接开平方法,用直接开方法求一元二次方程的解的类型有:x2=a(a≥0),ax2=b(a,b同号且a≠0),(x+a)2=b(b≥0),a (x+b)2=c(a,c同号且a≠0).法则:要把方程化为“左平方,右常数,先把系数化为1,再开平方取正负,分开求得方程解”;2.(3分)如图,在Rt△ABC中,∠C=90°,BC=6,AC=8,则AB的长度为()A.7B.8C.9D.10【分析】根据勾股定理即可得到结论.【解答】解:在Rt△ABC中,∠C=90°,BC=6,AC=8,∴AB===10,故选:D.【点评】本题考查了勾股定理,熟练掌握勾股定理是解题的关键.3.(3分)在下列条件中,能判定四边形为平行四边形的是()A.两组对边分别平行B.一组对边平行且另一组对边相等C.两组邻边相等D.对角线互相垂直【分析】根据平行四边形的判定定理逐个判断即可.【解答】解:A、两组对边分别平行的四边形是平行四边形,故本选项符合题意;B、一组对边平行且另一组对边相等的四边形是等腰梯形,不是平行四边形,故本选项不符合题意;C、两组邻边相等的四边形不一定是平行四边形,故本选项不符合题意;D、对角线互相平分的四边形才是平行四边形,故本选项不符合题意;故选:A.【点评】本题考查了平行四边形的判定定理,能熟记平行四边形的判定定理的内容是解此题的关键,注意:平行四边形的判定定理有:①两组对边分别平行的四边形是平行四边形,②两组对边分别相等的四边形是平行四边形,③两组对角分别平行的四边形是平行四边形,④一组对边平行且相等的四边形是平行四边形,⑤对角线互相平分的四边形是平行四边形.4.(3分)下列各曲线中,不表示y是x的函数的是()A.B.C.D.【分析】设在一个变化过程中有两个变量x与y,对于x的每一个确定的值,y都有唯一的值与其对应,那么就说y是x的函数,x是自变量.根据函数的意义即可求出答案.【解答】解:显然A、B、D选项中,对于自变量x的任何值,y都有唯一的值与之相对应,y是x的函数;C选项对于x取值时,y都有2个值与之相对应,则y不是x的函数;故选:C.【点评】本题主要考查了函数的定义,在定义中特别要注意,对于x的每一个值,y都有唯一的值与其对应.5.(3分)数据2,6,4,5,4,3的平均数和众数分别是()A.5和4B.4和4C.4.5和4D.4和5【分析】根据平均数和众数的概念求解.【解答】解:这组数据的平均数是:(2+6+4+5+4+3)=4;∵4出现了2次,出现的次数最多,∴这组数据的众数是4;故选:B.【点评】本题考查了众数和平均数的知识,一组数据中出现次数最多的数据叫做众数;平均数是指在一组数据中所有数据之和再除以数据的个数.6.(3分)一元二次方程x2﹣8x﹣1=0配方后可变形为()A.(x+4)2=17B.(x+4)2=15C.(x﹣4)2=15D.(x﹣4)2=17【分析】先把常数项移到方程右边,再把方程两边加上16,然后把方程左边写成完全平方形式即可.【解答】解:x2﹣8x=1,x2﹣8x+16=17,(x﹣4)2=17.故选:D.【点评】本题考查了解一元二次方程﹣配方法:将一元二次方程配成(x+m)2=n的形式,再利用直接开平方法求解,这种解一元二次方程的方法叫配方法.7.(3分)若点A(﹣3,y1),B(1,y2)都在直线y=x+2上,则y1与y2的大小关系是()A.y1<y2B.y1=y2C.y1>y2D.无法比较大小【分析】先根据直线y=x+2判断出函数图象的增减性,再根据各点横坐标的大小进行判断即可.【解答】解:∵直线y=x+2,k=>0,∴y随x的增大而增大,又∵﹣3<1,∴y1<y2.故选:A.【点评】本题考查的是一次函数的增减性,即一次函数y=kx+b(k≠0)中,当k>0,y 随x的增大而增大;当k<0,y随x的增大而减小.8.(3分)如图,正方形ABCD的边长为,对角线AC,BD交于点O,E是AC延长线上一点,且CE=CO,则BE的长度为()A.B.C.D.2【分析】利用正方形的性质得到OB=OC=BC=1,OB⊥OC,则OE=2,然后根据勾股定理计算BE的长.【解答】解:∵正方形ABCD的边长为,∴OB=OC=BC=×=1,OB⊥OC,∵CE=OC,∴OE=2,在Rt△OBE中,BE==.故选:C.【点评】本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;正方形具有四边形、平行四边形、矩形、菱形的一切性质.9.(3分)对于一次函数y=kx+b(k,b为常数),下表中给出5组自变量及其对应的函数值,其中恰好有1个函数值计算有误,则这个错误的函数值是()X﹣10123Y2581214 A.5B.8C.12D.14【分析】经过观察5组自变量和相应的函数值得(﹣1,2),(0,5),(1,8),(3,14)符合解析式y=3x+5,(2,12)不符合,即可判定.【解答】解:∵(﹣1,2),(0,5),(1,8),(3,14)符合解析式y=3x+5,当x=2时,y=11≠12∴这个计算有误的函数值是12,故选:C.【点评】本题考查了一次函数图象上点的坐标特征,图象上点的坐标符合解析式是解决本题的关键.10.(3分)博物馆作为征集、典藏、陈列和研究代表自然和人类文化遗产实物的场所,其存在的目的是为众提供知识、教育及欣赏服务.近年来,人们到博物馆学习参观的热情越来越高,2012﹣2018年我国博物馆参观人数统计如下:小明研究了这个统计图,得出四个结论:①2012年到2018年,我国博物馆参观人数持续增②2019年末我国博物馆参观人数估计将达到1082亿人次③2012年到2018年,我国博物馆参观人数年增幅最大的是2017年;④2016年到2018年,我国博物馆参观人数平均年增长率超过10%其中正确的是()A.①③B.①②③C.①②④D.①②【分析】根据条形统计图中的信息对4个结论矩形判断即可.【解答】解:①2012年到2018年,我国博物馆参观人数持续增,正确;②10.08×(1+)=10.45,故2019年末我国博物馆参观人数估计将达到10.45亿人次;故错误;③2012年到2018年,我国博物馆参观人数年增幅最大的是2017年;正确;④设平均年增长率为x,则8.50(1+x)2=10.08,解得:x=0.0889,故2016年到2018年,我国博物馆参观人数平均年增长率是8.89%,故错误;故选:A.【点评】此题考查了条形统计图,弄清题中图形中的数据是解本题的关键.二、填空题(本题共18分,每小题3分)11.(3分)在▱ABCD中,若∠B=110°,则∠D=110°.【分析】直接利用平行四边形的对角相等即可得出答案.【解答】解:∵四边形ABCD是平行四边形,∴∠B=∠D=110°.故答案为:110.【点评】此题主要考查了平行四边形的性质,正确得出对角相等是解题关键.12.(3分)八年级(1)班甲、乙两个小组的10名学生进行飞镖训练,某次训练成绩如下甲组成绩(环)87889乙组成绩(环)98797由上表可知,甲、乙两组成绩更稳定的是甲.【分析】根据方差计算公式,进行计算,然后比较方差,小的稳定,在计算方差之前还需先计算平均数.【解答】解:甲==8,乙==8,=[(8﹣8)2+(7﹣8)2+(8﹣8)2+(8﹣8)2+(9﹣8)2]=0.4,=[(9﹣8)2+(8﹣8)2+(7﹣8)2+(9﹣8)2+(7﹣8)2]=0.8∵<∴甲组成绩更稳定.故答案为:甲.【点评】考查平均数、方差的计算方法,理解方差是反映一组数据的波动大小的统计量,方差越小,数据越稳定.13.(3分)若关于x的一元二次方程x2+6x+m=0有实数根,且所有实数根均为整数,请写出一个符合条件的常数m的值:m=9.【分析】利用判别式的意义得到△=62﹣4m≥0,解不等式得到m的范围,在此范围内取m=0即可.【解答】解:△=62﹣4m≥0,解得m≤9;当m=0时,方程变形为x2+6x=0,解得x1=0,x2=﹣6,所以m=9满足条件.故答案为9.【点评】本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2﹣4ac 有如下关系:当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程无实数根.14.(3分)如图,某港口P位于南北延伸的海岸线上,东面是大海远洋号,长峰号两艘轮船同时离开港P,各自沿固定方向航行,“远洋”号每小时航行12nmile,“长峰”号每小时航行16nmile,它们离开港口1小时后,分别到达A,B两个位置,且AB=20nmile,已知“远洋”号沿着北偏东60°方向航行,那么“长峰”号航行的方向是南偏东30°.【分析】由题意得:P与O重合,得出OA2+OB2=AB2,由勾股定理的逆定理得出△PAB 是直角三角形,∠AOB=90°,求出∠COP=30°,即可得出答案.【解答】解:由题意得:P与O重合,如图所示:OA=12nmile,OB=16nmile,AB=20nmile,∵122+162=202,∴OA2+OB2=AB2,∴△PAB是直角三角形,∴∠AOB=90°,∵∠DOA=60°,∴∠COP=180°﹣90°﹣60°=30°,∴“长峰”号航行的方向是南偏东30°,故答案为:南偏东30°.【点评】此题主要考查了直角三角形的判定、勾股定理的逆定理及方向角的理解及运用.利用勾股定理的逆定理得出△PAB为直角三角形是解题的关键.15.(3分)若一个矩形的长边的平方等于短边与其周长一半的积,则称这样的矩形为“优美矩形”.某公园在绿化时工作人员想利用如图所示的直角墙角(两边足够长)和长为38m的篱笆围成一个“优美矩形”形状的花园ABCD,其中边AB,AD为篱笆且AB大于AD.设AD为xm,依题意可列方程为(38﹣x)2=38x.【分析】设AD为xm,根据“矩形的长边的平方等于短边与其周长一半的积”列出列出方程即可.【解答】解:设AD的长为x米,则AB的长为(38﹣x)m,根据题意得:(38﹣x)2=38x,故答案为:(38﹣x)2=38x.【点评】考查了由实际问题抽象出一元二次方程的知识,解题的关键是表示出另一边的长,难度不大.16.(3分)在平面直角坐标系xOy中,直线y=kx+3与x,y轴分别交于点A,B,若将该直线向右平移5单位,线段AB扫过区域的边界恰好为菱形,则k的值为±.【分析】根据菱形的性质知AB=5,由一次函数图象的性质和两点间的距离公式解答.【解答】解:令y=0,则x=﹣,即A(﹣,0).令x=0,则y=3,即B(0,3).∵将该直线向右平移5单位,线段AB扫过区域的边界恰好为菱形,∴AB=5,则AB2=25.∴(﹣)2+32=25.解得k=±.故答案是:±.【点评】考查了菱形的性质和一次函数图象与几何变换,解题的关键是根据菱形的性质得到AB=5.三、解答题(本题共26分,第17题8分,第18,20题各5分,第19,21题各4分)17.(8分)解下列方程:(1)x2+2x﹣3=0(用配方法)(2)2x2+5x﹣1=0(用公式法)【分析】(1)根据配方法的步骤,可得答案;(2)根据公式法,可得答案.【解答】解:(1)移项,得x2+2x=3配方,得x2+2x+1=3+1即(x+1)2=3开方得x+1=±2,x1=1,x2=﹣3;(2)a=2,b=5,c=﹣1,△=b2﹣4ac=25﹣4×2×(﹣1)=33>0,x==,x1=,x2=.【点评】本题考查了解一元二次方程,配方得出完全平方公式是解题关键.18.(5分)在平面直角坐标系xOy中,函数y=kx+b的图象与直线y=2x平行,且经过点A(1,6)(1)求一次函数y=kx+b的解析式;(2)求一次函数y=kx+b的图象与坐标轴围成的三角形的面积.【分析】(1)根据函数y=kx+b的图象与直线y=2x平行,且经过点A(1,6),即可得出k和b的值,即得出了函数解析式.(2)先求出与x轴及y轴的交点坐标,然后根据三角形面积公式求解即可.【解答】解:(1)∵函数y=kx+b的图象与直线y=2x平行,∴k=2,又∵函数y=2x+b的图象经过点A(1,6),∴6=2+b,解得b=4,∴一次函数的解析式为y=2x+4;(2)在y=2x+4中,令x=0,则y=4;令y=0,则x=﹣2;∴一次函数y=kx+b的图象与坐标轴交于(0,4)和(﹣2,0),∴一次函数y=kx+b的图象与坐标轴围成的三角形的面积为×2×4=4.【点评】本题考查待定系数法求函数解析式及三角形的面积的知识,关键是正确得出函数解析式及坐标与线段长度的转化.19.(5分)下面是小丁设计的“利用直角三角形和它的斜边中点作矩形的尺规作图过程:已知:如图,在Rt△ABC中,∠ABC=90°,O为AC的中点,求作:四边形ABCD,使得四边形ABCD为矩形.作法:①作射线BO,在线段BO的延长线上取点D,使得DO=BO②连接AD,CD,则四边形ABCD为矩形根据小丁设计的尺规作图过程(1)使用直尺和圆规,在图中补全图形(保留作图痕迹)(2)完成下面的证明证明:∵点O为AC的中点,∴AO=CO又∵DO=BO,∴四边形ABCD为平行四边形(对角线互相平分的四边形是平行四边形)∵∠ABC=90°,∴▱ABCD为矩形(有一个角是直角的平行四边形是矩形)【分析】(1)根据要求画出图形即可.(2)根据有一个角是直角的平行四边形是矩形即可证明.【解答】解:(1)如图,矩形ABCD即为所求.(2)理由:∵点O为AC的中点,∴AO=CO又∵DO=BO,∴四边形ABCD为平行四边形(对角线互相平分的四边形是平行四边形)∵∠ABC=90°,∴▱ABCD为矩形(有一个角是直角的平行四边形是矩形).故答案为:对角线互相平分的四边形是平行四边形,有一个角是直角的平行四边形是矩形【点评】本题考查作图﹣复杂作图,矩形的判定等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.20.(4分)方程x2+2x+k﹣4=0有实数根(1)求k的取值范围;(2)若k是该方程的一个根,求2k2+6k﹣5的值.【分析】(1)根据判别式的意义得到△=22﹣4(k﹣4)≥0,然后解不等式即可;(2)利用方程解的定义得到k2+3k=4,再变形得到2k2+6k﹣5=2(k2+3k)﹣5,然后利用整体代入的方法计算.【解答】解:(1)△=22﹣4(k﹣4)≥0,解得k≤5;(2)把x=k代入方程得k2+2k+k﹣4=0,即k2+3k=4,所以2k2+6k﹣5=2(k2+3k)﹣5=2×4﹣5=3.【点评】本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2﹣4ac 有如下关系:当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程无实数根.21.(4分)小东和小明要测量校园里的一块四边形场地ABCD(如图所示)的周长,其中边CD上有水池及建筑遮挡,没有办法直接测量其长度小东经测量得知AB=AD=5m,∠A=60°,BC=12m,∠ABC=150°小明说根据小东所得的数据可以求出CD的长度.你同意小明的说法吗?若同意,请求出CD的长度;若不同意,请说明理由.【分析】直接利用等边三角形的判定方法得出△ABD是等边三角形,再利用勾股定理得出答案.【解答】解:同意小明的说法.理由:连接BD,∵AB=AD=5m,∠A=60°,∴△ABD是等边三角形,∴BD=5m,∠ABD=60°,∵∠ABC=150°,∴∠DBC=90°,∵BC=12m,BD=5m,∴DC ==13(m ),答:CD 的长度为13m .【点评】此题主要考查了勾股定理的应用以及等边三角形的判定,正确得出△ABD 是等边三角形是解题关键.四、解答题(本题共13分,第22题7分,第23题6分)22.(7分)三月底,某学校迎来了以“学海通识品墨韵,开卷有益览书山”为主题的学习节活动为了让同学们更好的了解二十四节气的知识,本次学习节在沿袭以往经典项目的基础上,增设了十四节气之旅项目,并开展了相关知识竞赛该学校七、八年级各有400名学生参加了这次竞赛,现从七、八年级各随机抽取20名学生的成绩进行抽样调查 七年级:74 97 96 72 98 99 72 73 76 74 74 69 76 89 78 74 99 97 98 99 八年级:76 88 93 89 78 94 89 94 95 50 89 68 65 88 77 87 89 88 92 91 整理数据如下成绩 人数 年级 50≤x ≤5960≤x ≤6970≤x ≤7980≤x ≤8990≤x ≤100七年级 0 1 10 1 a 八年级 12386分析数据如下年级 平均数 中位数 众数 方差 七年级 84.2 77 74 138.56 八年级84b89129.7根据以上信息,回答下列问题 (1)a =8 b = 88.5 ;(2)你认为哪个年级知识竞赛的总体成绩较好,说明理由(至少从两个不同的角度说明推断的合理性).(3)学校对知识竞赛成绩不低于80分的学生颁发优胜奖,请你估计学校七、八年级所有学生中获得优胜奖的大约有180,280人.【分析】(1)从调查的七年级的人数20减去前几组的人数即可,将八年级的20名学生的成绩排序后找到第10、11个数的平均数即是八年级的中位数,(2)从中位数、众数、方差进行分析,调查结论,(3)用各个年级的总人数乘以样本中优秀人数所占的比即可.【解答】解:(1)a=20﹣1﹣10﹣1=8,b=(88+89)÷2=88.5故答案为:8,88.5.(2)八年级成绩较好,八年级成绩的众数、中位数比七年级成绩相应的众数、中位数都要大,说明八年级成绩的集中趋势要高,方差八年级较小,说明八年级的成绩比较稳定.(3)七年级优秀人数为:400×=180人,八年级优秀人数为:400×=280人,故答案为:180,280.【点评】考查频数分布表、众数、中位数、平均数、方差的意义及计算方法,明确各自的意义和计算方法是解决问题的前提.23.(6分)如图,在▱ABCD中,对角线AC,BD交于点O,过点B作BE⊥CD于点E,延长CD到点F,使DF=CE,连接AF.(1)求证:四边形ABEF是矩形;(2)连接OF,若AB=6,DE=2,∠ADF=45°,求OF的长度.【分析】(1)根据平行四边形的性质得到AD∥BC且AD=BC,等量代换得到BC=EF,推出四边形AEFD是平行四边形,根据矩形的判定定理即可得到结论;(2)根据直角三角形斜边中线可得:OF=AC,利用勾股定理计算AC的长,可得结论.【解答】(1)证明:∵在▱ABCD中,∴AD∥BC且AD=BC,∴∠ADF=∠BCE,在△ADF和△BCE中,∵∴△ADF≌△BCE(SAS),∴AF=BE,∠AFD=∠BEC=90°,∴AF∥BE,∴四边形ABEF是矩形;(2)解:由(1)知:四边形ABEF是矩形,∴EF=AB=6,∵DE=2,∴DF=CE=4,∴CF=4+4+2=10,Rt△ADF中,∠ADF=45°,∴AF=DF=4,由勾股定理得:AC===2,∵四边形ABCD是平行四边形,∴OA=OC,∴OF=AC=.【点评】本题考查了矩形的判定和性质,平行四边形的性质,勾股定理,正确的识别图形是解题的关键.五、解答题(本题共13分,第24题6分,第25题7分)24.(6分)如图,在平面直角坐标系xOy中,直线y=kx+7与直线y=x﹣2交于点A(3,m)(1)求k,m的值;(2)已知点P(n,n),过点P作垂直于y轴的直线与直线y=x﹣2交于点M,过点P 作垂直于x轴的直线与直线y=kx+7交于点N(P与N不重合).若PN≤2PM,结合图象,求n的取值范围.【分析】(1)把A点坐标代入y=x﹣2中,求得m的值,再把求得的A点坐标代入y =kx+7中,求得k的值;(2)根据题意,用n的代数式表示出M、N点的坐标,再求得PM、PN的值,根据PN ≤2PM,列出n的不等式,再求得结果.【解答】解:(1)把A(3,m)代入y=x﹣2中,得m=3﹣2=1,∴A(3,1),把A(3,1)代入y=kx+7中,得1=3k+7,解得,k=﹣2;(2)由(1)知,直线y=kx+7为y=﹣2x+7,根据题意,作出草图如下:∵点P(n,n),∴M(n+2,n),N(n,﹣2n+7),∴PM=2,PN=|3n﹣7|,∵PN≤2PM,∴|3n﹣7|≤2×2,∴1≤n≤,∵P与N不重合,∴n≠﹣2n+7,∴n≠,综上,1≤n≤,且n≠【点评】本题是一次函数图象的相交与平行的问题,主要考查了待定系数法求一次函数的解析式,第(2)小题关键是用n的代数式表示PM与PN的长度.25.(7分)在Rt△ABC中,∠BAC=90°,点O是△ABC所在平面内一点,连接OA,延长OA到点E,使得AE=OA,连按OC,过点B作BD与OC平行,并使∠DBC=∠OCB,且BD=OC,连按DE.(1)如图一,当点O在Rt△ABC内部时,①按题意补全图形;②猜想DE与BC的数量关系,并证明.(2)若AB=AC(如图二),且∠OCB=30°,∠OBC=15°,求∠AED的大小.【分析】(1)①根据要求画出图形即可解决问题.②结论:DE=BC.连接OD交BC于F,连接AF.证明AF为Rt△ABC斜边中线,为△ODE的中位线,即可解决问题.(2)分两种情形:如图二中,当点O在△ABC内部时,连接OD交BC于F,连接AF,延长CO交AF于M.连接BM.证明△BMA≌△BMO(AAS),推出AM=OM,∠BMO=∠BMA=120°,推出∠AMO=120°,即可解决问题.如图三中,当点O在△ABC外部时,当点O在△ABC内部时,连接OD交BC于F,连接AF,延长CO交AF于M.连接BM.分别求解即可.【解答】解:(1)①补全图形如图所示:②结论:DE=BC.理由:如图一中,连接OD交BC于F,连接AF.∵OC∥BD,∴∠FCO=∠FBD,∵∠CFO=∠BFD,OC=BD,∴△FCO≌△FBD(AAS),∴BF=CF,∵OA=AE,∵DE=2AF,∵∠BAC=90°,BF=CF,∴BC=2AF,∴DE=BC.(2)如图二中,当点O在△ABC内部时,连接OD交BC于F,连接AF,延长CO交AF于M.连接BM.由(1)可知:AF为Rt△ABC斜边中线,为△ODE的中位线,∵AB=AC,∴AF垂直平分线段BC,∴MB=MC,∵∠OCB=30°,∠OBC=15°,∴∠MBC=∠MCB=30°,∵∠BAC=90°,AB=AC,∴∠ABC=∠ACB=45°,∠MBO=∠MBA=15°,∵∠BAM=∠BOM=45°,BM=BM,∴△BMA≌△BMO(AAS),∴AM=OM,∠BMO=∠BMA=120°,∴∠AMO=120°,∴∠MAO=∠MOA=30°,∴∠AED=∠MAO=30°.如图三中,当点O在△ABC外部时,当点O在△ABC内部时,连接OD交BC于F,连接AF,延长CO交AF于M.连接BM.由∠BOM=∠BAM=45°,可知A,B,M,O四点共圆,∴∠MAO=∠MBO=30°﹣15°=15°,∵DE∥AM,∴∠AED=∠MAO=15°,综上所述,满足条件的∠AED的值为15°或30°.【点评】本题属于三角形综合题,考查了全等三角形的判定和性质,直角三角形斜边中线的性质,三角形中位线定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.。
2023北京西城区初二(下)期末数学试题及答案

2023北京西城初二(下)期末数 学2023.7注意事项:1.本试卷共8页,共两部分,四道大題,26道小题.其中第一大题至第三大题为必做题,第四大道为选做道,计入总分,考试时间100分钟.2.在试卷和答题卡上准确填写学校、班级、姓名和学号.3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效.4.在答题卡上,选择题、作图题用2B 铅笔作答,其他试题用黑色字迹签字笔作答.5.考试结束,请将考试材料一并交回.第一部分 选择题一、选择题(第1-8题均有四个选项,符合题意的选项只有一个)1. 下列各式中,是最简二次根式的是( )2. 以下列各组数为边长,能构成直角三角形的是( )A. 2,3,3B. 2,3,4C. 2,3,5D. 233. 下列计算,正确的是( )3=-=23=⨯2÷=4. 下列命题正确的是( )A. 对角线相等的四边形是平行四边形B. 对角线相等且互相平分的四边形是菱形C. 对角线垂直且互相平分的四边形是矩形D. 对角线垂直、相等且互相平分的四边形是正方形5. 在Rt ABC △中,90ACB ∠=︒,D 为斜边AB 的中点.若8AC =,6BC =,则CD 的长为( )A. 10B. 6C. 5D. 46. 小雨在参观故宫博物馆时,被太和殿窗棂的三交六椀菱花图案所吸引,他从中提取出一个含60︒角的菱形ABCD (如图1所示).若AB 的长度为a ,则菱形ABCD 的面积为( )C. 2a 27. 台风影响着人们的生产和生活.人们为研究台风,将研究条件进行一定的合理简化,把近地面风速画在一个以台风中心为原点,以台风半径为横轴,风速为纵轴的坐标系中,并在图中标注了该台风的12级、10级和7级风圈半径,如12级风圈半径是指近地面风速衰减至32.7m /s 时,离台风中心的距离约为150km .那么以下关于这场台风的说法中,正确的是( )A. 越靠近台风中心位置,风速越大B. 距台风中心150km 处,风速达到最大值C. 10级风圈半径约为280kmD. 在某个台风半径达到最大风速之后,随台风半径的增大,风速又逐渐衰减8. 在平面直角坐标系xOy 中,矩形OABC ,()0,3A ,()2,3B ,()2,0C ,点M 在边OA 上,1OM =.点P 在边AB 上运动,连接PM ,点A 关于直线PM 的对称点为A '.若PA x =,MA A B y +'=',下列图像能大致反映y 与x 的函数关系的是( ).A. B.C. D.第二部分 非选择题二、填空题9. 在实数范围内有意义,则实数x 的取值范围是______.10. 0=,则=a ______,b =______.11. 若ABC 的周长为6,则以ABC 三边的中点为顶点的三角形的周长等于______.12. 某商场招聘员工,现有甲、乙两人参加竞聘,通过计算机、语言和商品知识三项测试,他们各自成绩(百分制)和各项占比如下表所示,那么从甲、乙两人各自的平均成绩看,应该录取:______测试项目计算机语言商品知识在平均成绩中的占比50%30%20%甲的成绩708090乙的成绩90807013. 如图,直线y mx n =+与直线y kx b =+的交点为A ,则关于x ,y 的方程组,y mx n y kx b =+⎧⎨=+⎩的解是______.14. 小杰利用教材中的剪纸活动设计了一个魔术.他将一个长方形纸片对折两次,剪下一个45︒角(图1),展平后得到一个带正方形孔洞的魔术道具(图2),这个正方形孔洞ABCD 的边长为2cm (图4).他试图将一个直径为3cm 的圆形铁环(铁环厚度忽略不计)穿过这个孔洞,没有成功,于是他对这个道具进行折叠、旋转(图5、图6),并调整纸片产生一个新的“孔洞”(图3).请你计算调整前后的孔洞最“宽”处的“宽度”来说明魔术的效果.图4中的“宽度”BD =______cm ;图6中的“宽度”BD ''=______cm .15. 如图,在ABCD Y 中,BE 平分ABC ∠交AD 于点E ,CF 平分BCD ∠交AD 于点F ,BE 与CF 的交点在ABCD Y 内.若5BC =,3AB =,则EF =______.16. 在ABC 中,3BC =,BD 平分ABC ∠交AC 于点D ,DE BC ∥交AB 于点E ,EF AC ∥交BC 于点F .有以下结论:①四边形EFCD 一定是平行四边形;②连接DF 所得四边形EBFD 一定是平行四边形;③保持ABC ∠的大小不变,改变BA 的长度可使BF FC =成立;④保持BA 的长度不变,改变ABC ∠的大小可使BF FC =成立.共中所有的正确结论是:______.(填序号即可)三、解答题17. 计算:(1(2)+--.18. 在平面直角坐标系xOy 中,直线:26m y x =+与x 轴的交点为A ,与y 轴的交点为B ,将直线m 向右平移3个单位长度得到直线l .(1)求点A ,点B 的坐标,画出直线m 及直线l ;(2)求直线l 的解析式;(3)直线l 还可以看作由直线m 经过其他方式的平移得到的,请写出一种平移方式.19. 尺规作图:过直线外一点作这条直线的平行线.已知:如图,直线l 及直线l 外一点P .求作:直线m ,使得m l ∥,且直线m 经过点P .;作法:①在直线l 上取一点A ,连接AP ,以点A 为圆心,AP 的长为半径画弧,交直线l 于点B ;②分别以点P ,点B 为圆心,AP 的长为半径画弧,两弧交于点C (不与点A 重合);③经过P ,C 两点作直线m .直线m 就是所求作的直线.(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);(2)完成下面的证明.证明:连接BC .∵AP = = = ,∴四边形PABC 是(填“矩形”“菱形”或“正方形”)( )(填推理的依据).∴m l ∥( )(填推理的依据).20. 如图,在ABCD Y 中,AE BC ⊥于点E ,CF AD ⊥于点F .(1)求证:四边形AECF 是矩形;(2)连接BD ,若30CBD ∠=︒,5BC =,BD =DF 的长.21. 已知甲、乙两地相距60km ,小徐和小马两人沿同一条公路从甲地到乙地,小徐骑自行车3h 到达.小马骑摩托车比小徐晩1h 出发,骑行30km 时追上小徐,停留h n 后继续以原速骑行.在整个行程中,两人与甲地的距离y 与小徐骑行时间x 的对应关系分别如图中线段OA 和折线段BCDE 所示,DE 与OA 的交点为F .(1)线段OA 所对应的函数表达式为 ,相应自变量x 的取值范围是 ,线段BC 所对应的函数表达式为 ,相应自变量x 的取值范围是 ;(2)小马在BC 段的速度为 km/h ,n = ;(3)求小马第二次追上小徐时与乙地的距离.22. 某校为了解课外阅读情况,在初二年级的两个班中,各随机抽取部分学生调查了他们一周的课外阅读时长(单位:小时),并对数据进行了整理、描述和分析.下面给出了部分信息.a .甲班学生课外阅读时长(单位:小时):7,7,8,9,9,11,12b .乙班学生课外阅读时长的折线图:c .甲、乙两班学生阅读时长的平均数、众数、中位数:平均数中位数众数甲班m9t乙班9n9根据以上信息,回答下列问题:(1)写出表中m ,t ,n 的值;(2)设甲、乙两班数据的方差分别为21s ,22s ,则21s 22s (填“>”“=”或“<”).23. 在平面直角坐标系xOy 中,对于非零的实数a ,将点(),P x y 变换为,y P ax a ⎛⎫⎪⎝⎭'称为一次“a -变换”.例如,对点()2,3P 作一次“3-变换”,得到点()6,1P '.已知直线24y x =-+与x 轴交于点A ,与y 轴交于点B .若对直线l 上的各点分别作同样的“a -变换”,点A ,B 变换后的对应点分别为A ',B '.(1)当2a =-时,点A '的坐标为 ;(2)若点B '的坐标为()0,6,则a 的值为 ;(3)以下三个结论:①线段AB 与线段A B ''始终相等;②BAO ∠与B A O ∠''始终相等;③AOB 与A OB ''△的面积始终相等.其中正确的是 (填写序号即可),并对正确的结论加以证明.24. 在菱形ABCD 中,60ABC ∠=︒,M ,N 两点分别在AB ,BC 边上,BM BN =.连接DM ,取DM 的中点K ,连接AK ,NK .(1)依题意补全图1,并写出AKN ∠的度数;(2)用等式表示线段NK 与AK 的数量关系,并证明;(3)若6AB =,AC ,BD 的交点为O ,连接OM ,OK ,四边形AMOK 能否成为平行四边形?若能,求出此时AM 的长;若不能,请说明理由.四、选做题25. 在单位长度为1的正方形网格中,如果一个凸四边形的顶点都是网格线交点,我们称其为格点凸四边形.如图,在平面直角坐标系xOy 中,矩形ORST 的四个顶点分别为()0,0O ,()0,5R,()8,0T ,()8,5S .已知点()2,4E ,()0,3F ,()4,2G .若点P 在矩形ORST 的内部,以P ,E ,F ,G 四点为顶点的格点凸四边形的面积为6,所有符合题意的点P 的坐标为 .26. 在平面直角坐标系xOy 中,对于正方形ABCD 和它的边上的动点P ,作等边OPP '△,且O ,P ,P '三点按顺时针方向排列,称点P '是点P 关于正方形ABCD 的“友好点”.已知(),A a a -,(),B a a ,(),C a a -,(),D a a --(其中0a >).(1)如图1,若3a =,AB 的中点为M ,当点P 在正方形的边AB 上运动时,①若点P 和点P 关于正方形ABCD 的“友好点”点P '佮好都在正方形的边AB 上,则点P '的坐标为 ;点M 关于正方形ABCD 的“友好点”点M '的坐标为 ;②若记点P 关于正方形ABCD 的“友好点”为(),P m n ',直接写出n 与m 的关系式(不要求写m 的取值范围);(2)如图2,()1,1E --,()2,2F .当点P 在正方形ABCD 的四条边上运动时,若线段EF 上有且只有一个点P 关于正方形ABCD 的“友好点”,求a 的取值范围;(3)当24a ≤≤时,直接写出所有正方形ABCD 的所有“友好点”组成图形的面积.参考答案第一部分 选择题一、选择题(第1-8题均有四个选项,符合题意的选项只有一个)题号12345678答案BDCDCBDA第二部分 非选择题二、填空题9. 2x ≥.10. 1,5-.11. 3.12.乙.13. 13x y =⎧⎨=⎩14. 4.15. 1.16.①③.三、解答题17. (1)2=+=+=.(2)+--225=--1=-.18. (1)解:对于直线:26m y x =+,当0x =时,6y =当0y =时,260x +=,解得3x =-,∴()30A -,,()06B ,,经过()30A -,,()06B ,两点的直线即为直线m ,然后将直线m 向右平移3个单位长度得到直线l ,所以m l ∥,且直线l 经过()00O ,;作出直线m 及直线l 的图象如图所示:(2)解:因为直线:26m y x =+向右平移3个单位长度得到直线l ,所以直线():236l y x =-+,即直线l 的解析式为2y x =;(3)解:∵直线:26m y x =+,直线:2l y x =,∴直线m 向下平移6个单位长度得到直线l (答案不唯一).19. (1)如图,直线m 即为所求作;(2)证明:连接BC ,∵AP AB PC BC ===,∴四边形PABC 是菱形.(四条边相等的四边形是菱形).∴m l ∥(菱形的对边平行).故答案为:AB ;PC ;BC ;菱形;四条边相等的四边形是菱形;菱形的对边平行.20. (1)证明:如图3.∵四边形ABCD 是平行四边形,∴AD BC ∥.∴180AEC EAF ∠+∠=︒,∵AE BC ⊥于点E ,CF AD ⊥于点F ,∴90AEC ∠=︒,90AFC ∠=︒.∴18090EAF AEC ∠=︒-∠=︒.∴90AEC EAF AFC ∠=∠=∠=︒.∴四边形AECF 是矩形.(2)如图4,作DG BC ⊥,交BC 的延长线于点G .∵在Rt DBG △中,90DGB ∠=︒,30DBG ∠=︒,BD =,∴2BDDG ==6BG ==.∵5BC =,∴1CG BG BC =-=.同理可得四边形FCGD 是矩形.∴1DF CG ==.21. (1)解:由题意得,线段OA 是小徐的函数图象,折线段BCDE 是小马的函数图象,∴小徐的骑行速度为60320km /h ÷=,∴线段OA 所对应的函数表达式为20y x =,其中相应自变量x 的取值范围是03x ≤≤;在20y x =中,当2030y x ==, 1.5x =,∴在小徐出发1.5h 时,小马追上小徐,∴小马的骑行速度为3060km/h 1.51=-,∴线段BC 所对应的函数表达式为()6016060y x x =-=-,其中相应自变量x 的取值范围是1 1.5x ≤≤;故答案为:20y x =,03x ≤≤,6060y x =-,1 1.5x ≤≤;(2)解:由(1)得小马在BC 段的速度为60km/h ,2 1.50.5n =-=,故答案为:60,0.5;(3)解:设小马在小徐出发t 小时后第二次追上小徐,由题意得,()2030602t t =+-,解得 2.25t =,∴小马在小徐出发2.25小时后第二次追上小徐,∴小马第二次追上小徐时与乙地的距离为60 2.252015km -⨯=.22. (1)平均数1(778991112)97=++++++=,故9m =,出现次数最多的有7和9,故7,9t =;由图知,乙班中位数为9,故9n =.(2)222222221122(79)(79)(89)(99)(99)(119)(129)77s ⎡⎤=-+-+-+-+-+-+-=⎣⎦222222222146(59)(79)(99)(99)(99)(109)(149)77s ⎡⎤=-+-+-+-+-+-+-=⎣⎦∴2212S S <.23. (1)直线24y x =-+与x 轴交于点A ,令0y =,即240x -+=,解得2x =,(2,0)A ∴,当2a =-时,点A '的坐标为0(22,)2-⨯-,即(4,0)-;故答案为(4,0)-(2)直线24y x =-+与y 轴交于点B ,令0x =时,4y =,(0,4)B ∴,若点B '的坐标为()0,6,即4(0,)a a ⨯,46a ∴=,解得23a =,经检验23a =是分式方程的解,则a 的值为23;故答案为23(3)③正确,理由如下:证明:∵直线24y x =-+与x 轴交于点A ,与y 轴交于点B ,∴()2,0A ,()0,4B .∵点A ,B 变抰后的对应点分别为A ',B ',∴()2,0A a ',40,B a ⎛⎫⎪⎝⎭'.∵12442AOB S =⨯⨯=△,14242A OB S a a ''=⨯⨯=△,∴A OB AOB S S ''= ,即③正确.故答案为③24. (1)解:补全图形如图所示:.延长AK 与CD 交于点E ,连接NM ,NA ,NE .∵在菱形ABCD 中,60ABC ∠=︒,∴AB BC CD AD ===,AB DC ,120BCD ∠=︒.∴MAK DEK ∠=∠.K 为DM 的中点,∴MK DK =.∵AKM EKD ∠=∠,∴AMK EDK ≅△△.∴AK EK =,AM ED =.∴AB AM DC ED -=-,即BM CE =.∵BM BN =,60ABC ∠=︒,∴BMN 为等边三角形.∴MN BM BN ==,60BMN ∠=︒.∴MN CE =,AM NC =,180120AMN BMN ∠=︒-∠=︒.∴AMN NCE ∠=∠.∴AMN NCE ≅△△.∴AN NE =,∵AK EK =,∴NK AE ⊥,即90AKN ∠=︒.(2)解:NK ,证明如下:延长AK 与CD 交于点E ,连接NM ,NA ,NE .∵在菱形ABCD 中,60ABC ∠=︒,∴AB BC CD AD ===,AB DC ,120BCD ∠=︒.∴MAK DEK ∠=∠.∵K 为DM 的中点,∴MK DK =.∵AKM EKD ∠=∠,∴AMK EDK ≅△△.∴AK EK =,AM ED =.∴AB AM DC ED -=-,即BM CE =.∵BM BN =,60ABC ∠=︒,∴BMN 为等边三角形.∴MN BM BN ==,60BMN ∠=︒.∴MN CE =,AM NC =,180120AMN BMN ∠=︒-∠=︒.∴AMN NCE ∠=∠.∴AMN NCE ≅△△.∴AN NE =,MAN CNE ∠=∠.∵ANC ABC BAN ∠=∠+∠,ANC ANE CNE ∠=∠+∠,∴60ANE ABC ︒∠=∠=∴ANE 为等边三角形,60NAK ∠=︒,在Rt ANK △中,90AKN ∠=︒,60NAK ∠=︒,可得30ANK ∠=︒,∴2AN AK=∴NK ==.(3)解:如图:四边形AMOK 能成为平行四边形,理由如下:∵菱形ABCD 的对角线AC ,BD 的交点为O ,∴BO OD =.∵DM 的中点为K ,∴OK 为DMB 的中位线.∴2BM OK =.∵四边形AMOK 为平行四边形,∴AM OK =.∴23AB AM BM AM OK AM =+=+=.∵6AB =,∴123AM AB ==.四、选做题25. 解:如图,111421214223222EFG S =⨯-⨯⨯-⨯⨯-⨯⨯=V ,113232P EG S =⨯⨯= ,∴11336EFG P EG P EFG S S S =+=+=四边形 ,此时,格点1P 的坐标为()5,4,过格点1P 作EG 的平行线,过格点23,P P ,则有:2313P EG P EG P EG S S S === ,∴26P EFG S =四边形,36P EFG S =四边形,∴()26,3,P ()37,2,P 又()411112422213,222P FG S =⨯+⨯-⨯⨯-⨯⨯= ∴41336EFG P FG P EFG S S S =+=+=四边形 ∴()42,1,P 所以,以P ,E ,F ,G 四点为顶点的格点凸四边形的面积为6的点P 有四处,坐标为()()()()6,3,5,4,7,2,2,1,故答案为:()()()()6,3,5,4,7,2,2,1.26. (1)①);32⎫⎪⎪⎭;如图,OP OP PP ''==∴PM P M '=,3OM =,30MOP MOP ¢Ð=Ð=°∴2OP MP ¢¢=∴Rt OMP ¢ 中,222OM MP OP ¢¢+=,2223(2)MP MP ¢¢+=,解得MP '=∴P ;如图,过点M '作M F x '⊥轴,垂足为F ,则90OFM ¢Ð=°,3OM ¢=,∴9030M OF MOM ¢¢Ð=°-Ð=°∴1322M F OM ¢¢==∴OF ===∴32M ⎫'⎪⎪⎭②6n +.如图,直线P M ''交x 轴于点G ,∵60POP MOM ¢¢Ð=Ð=°∴POP MOP MOM MOP ¢¢¢¢Ð-Ð=Ð-Ð即POM P OM ¢¢Ð= 又,OP OP OM OM ¢¢==∴POM P OM ¢¢@ ∴90OM P OMP ¢¢Ð=Ð=°∵906030M OG ¢Ð=°-°=°,∴90903060OGM M OG ¢¢Ð=°-Ð=°-°=°,点(,)P m n '在直线M G '上,设直线解析式为(0)y kx b k =+≠,则332b b +=+=解得6k b ⎧=⎪⎨=⎪⎩∴6n +;(2)如上图,由(1)知若 (),A a a -,则OM OM a ¢==,Rt OM G ¢ 中,12M G OG ¢=,2221()2a OG OG +=,解得OG =,即点,0)G ,由(1)知点P 在线段AB 上时,直线P M ''与x 轴相交锐角为60︒,可设直线M G '为y q =-+,代入,0)G a ,解得2q a =,故点P '在直线2y a =-+上,即A B ''解析式为2y a =-+;如下图所示,同理可得,直线C D ''解析式为2y a =-,经过()1,1E --,则1(1)2a -=--,解得a =;如下图所示时,直线A B ''的解析式为2y a =+,经过()2,2F,则222a =+解得1a =+.1a <+.(3)如图,当2a =时,点P '轨迹所在四边形A B C D ''''的面积为2(22)16´=,当4a =时,点P '轨迹所在四边形的面积为2(24)64´=,故24a ≤≤时,正方形ABCD 的所有“友好点”组成图形的面积为641648-=.。
2018-2019学年上期北京市各区期末考试八年级数学分类汇编 几何综合题
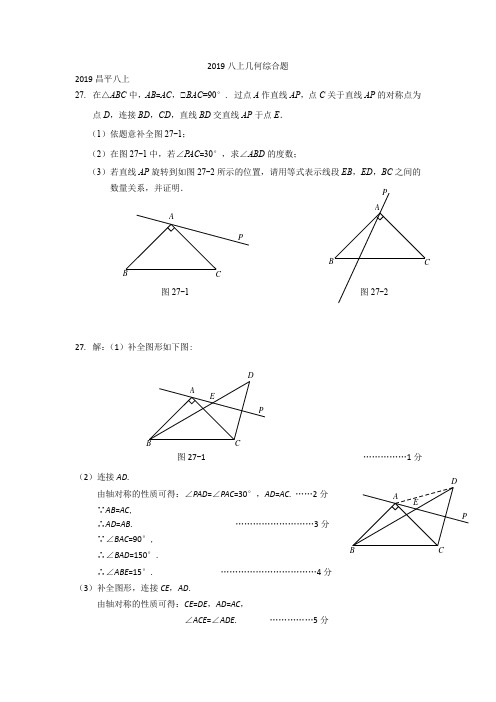
2019八上几何综合题2019昌平八上27. 在△ABC 中,AB =AC ,∠BAC =90°. 过点A 作直线AP ,点C 关于直线AP 的对称点为点D ,连接BD ,CD ,直线BD 交直线AP 于点E . (1)依题意补全图27-1;(2)在图27-1中,若∠P AC =30°,求∠ABD 的度数;(3)若直线AP 旋转到如图27-2所示的位置,请用等式表示线段EB ,ED ,BC 之间的27. 解:(1)补全图形如下图:(2)连接AD .由轴对称的性质可得:∠PAD =∠PAC =30°,AD =AC . ……2分 ∵AB =AC ,∴AD =AB . ………………………3分 ∵∠BAC =90°,∴∠BAD =150°.∴∠ABE =15°. ……………………………4分 (3)补全图形,连接CE ,AD .由轴对称的性质可得:CE =DE ,AD =AC ,∠ACE =∠ADE . ……………5分ABCPED图27-1 ……………1分ABCPED∵AB =AC , ∴AD =AB . ∴∠ADB =∠ABD . ∴∠ACE =∠ABD . ∵∠ABD +∠ABE =180°, ∴∠ACE +∠ABE =180°. 在四边形ABEC 中,∵∠BAC +∠ABE +∠BEC +∠ACE =360°, 又∵∠BAC =90°,∴∠BEC=90°. ……………………………………………………………6分 ∴BE 2+CE 2=BC 2. ∴EB 2+ED 2=BC 2. …………………………………………………………7分2019朝阳八上27.已知C 是线段AB 垂直平分线m 上一动点,连接AC ,以AC 为边作等边三角形ACD ,点D 在直线AB 的上方,连接DB 与直线m 交于点E ,连接BC ,AE . (1)如图1,点C 在线段AB 上.①根据题意补全图1; ②求证:∠EAC =∠EDC ;(2)如图2,点C 在直线AB 的上方, 0°<∠CAB <30°,用等式表示线段BE ,CE ,DE 之间的数量关系,并证明.27.解:(1)①补全图形如图所示.DPA BCE图1图2②证明:∵直线m是AB的垂直平分线,∴EA=EB,CA=CB.∴∠EAC=∠B.∵△ACD是等边三角形,∴CA=CD.∴CD=CB.∴∠EDC=∠B.∴∠EAC=∠EDC.(2)BE=CE+DE.证明:如图,在EB上截取EF,使EF=CE,连接CF.∵直线m是AB的垂直平分线,∴EA=EB,CA=CB.∴∠EAB=∠EBA,∠CAB=∠CBA.∴∠EAC=∠EBC.∵△ACD是等边三角形,∴CA=CD,∠ACD=60°.∴CD=CB.∴∠EDC=∠EBC.∴∠EDC=∠EAC.∵∠1=∠2,∴∠DEA=∠ACD=60°.∴∠AEB=120°.∵EA=EB,m⊥AB,∴∠AEC=∠BEC=60°.∴△CEF是等边三角形.∴∠CEF=∠CFE=60°.∴△CDF≌△CBE.∴DF=BE.∴BE=CE+DE.2019大兴八上28. 已知:如图, 过等腰直角三角形AB C的直角顶点A作直线AP,点B关于直线AP的对称点为E,连接BE,C E,其中CE交直线AP于点F.(1)依题意补全图形;(2)若∠PAB=16°,求∠ACF的度数;(3)如图,若45°<∠PAB<90°,用等式表示线段AB,FE,FC之间的数量关系,并证明.28.(1)补全图形,如图所示.………………………………1分(2)解:连接AE,∵点E与点B关于直线AP对称,∴对称轴AP是EB的垂直平分线.∴AE=AB,∠EAP=∠BAP=16°…………………………………2分∵等腰直角三角形AB C,∴AB=AC,∠BAC=90°∴AE=AC.∴∠AEC=∠ACF. …………………………………………………3分∴2∠ACF+32°+90°=180°.∴∠ACF=29°……………………………………………………4分(3)AB,FE,FC满足的数量关系:FE2+FC2=2AB2…………………5分证明:连接AE,BF,设BF交AC于点G,∵点E与点B关于直线AP对称,∴对称轴AP是EB的垂直平分线.∴AE=AB,FE=FB.∵AF=AF,∴△AEF≌△ABF∴∠FEA=∠FBA.∵AB=AC,∴AE=AC.∴∠ACE=∠AEC.∴∠ACE=∠ABF. …………………………………………6分又∵∠CGF=∠AGB,∴∠CFB=∠BAC=90°. ………………………………………7分∴FB2+FC2=BC2.∵BC2=2AB2,∴FE2+FC2=2AB2 ………………………………………………8分2019东城八上27.(本小题6分)QPF EDCBA(1)老师在课上给出了这样一道题目:如图(1),等边△ABC 边长为2,过AB 边上一点P 作PE ⊥AC 于E ,Q 为BC 延长线上一点,且AP=CQ ,连接PQ 交AC 于D ,求DE 的长.小明同学经过认真思考后认为,可以通过过点P 作平行线构造等边三角形的方法来解决这个问题.请根据小明同学的思路直接写出DE 的长. (2)【类比探究】老师引导同学继续研究:1.等边△ABC 边长为2,当P 为BA 的延长线上一点时,作PE ⊥CA 的延长线于点E ,Q 为边BC 上一点,且AP=CQ ,连接PQ 交AC 于D .请你在图(2)中补全图形并求DE 的长.2. 已知等边△ABC ,当P 为AB 的延长线上一点时,作PE ⊥射线AC 于点E , Q 为(○1BC 边上;○2BC 的延长线上;○3CB 的延长线上)一点,且AP =CQ ,连接PQ 交直线AC 于点D ,能使得DE 的长度保持不变.(将答案的编号填在横线上)图(1) 图(2) (备用图)27. 解:(1)DE=1. ………………………1分(2) 1. 正确补全图形. ……………2分 过点P 作PF ∥BC 交CA 的延长线与点F . ∴ ∠PF A =∠C .∵ △ABC 是等边三角形, ∴ 可证 △APF 为等边三角形. ∴ AP =PF .C B A C B A又∵ PE ⊥CA 的延长线于点E , ∴ AE =FE =12AF . ……………3分 ∵ AP=CQ , ∴ PF =QC .∵ ∠FDP =∠CDQ ,∴ △FDP ≌△CDQ .∴ FD =CD =12CF . ……………4分 ∵ DE =DF -EF =1111222CF AF AC -==. ……………5分2. ○2. ……………6分2019东城八上28. (本小题6分)在平面直角坐标系xOy 中,△ABO 为等边三角形,O 为坐标原点,点A 关于y 轴的对称点为D ,连接AD ,BD ,OD ,其中AD ,BD 分别交y 轴于点E ,P . (1)如图1,若点B 在x 轴的负半轴上时,直接写出BDO ∠的度数;(2)如图2,将△ABO 绕点O 旋转,且点A 始终在第二象限,此时AO 与y 轴正半轴夹角为α,60︒<α<90︒,依题意补全图形,并求出BDO ∠的度数;(用含α的式子表示)(3)在第(2)问的条件下,用等式表示线段BP ,PE ,PO 之间的数量关系.(直接写出结果)图1 图228. 解:(1)120°; ……………1分 (2)正确画出图形. ……………2分 ∵ ,60AOE DOE AOB α∠=∠=∠=︒,∴ 3602603002BOD αα∠=︒--︒=︒-. …………3分 ∵ BO =BD , ∴ ∠OBD =∠ODB . ∴ 180602BODBDO α︒-∠∠==-︒. ……………4分(3)2PE BP PO =+. ……………6分 说明:本试卷中的试题都只给出了一种解法,对于其他解法请参照评分标准相应给分.2019房山八上30. 如图9,BN 是等腰ABC Rt ∆的外角CBM ∠内部的一条射线,090=∠ABC ,CB AB =,点C 关于BN 的对称点为D ,连接AD ,BD ,CD ,其中CD ,AD 分别交射线BN 于点E ,P . (1)依题意补全图形;(2)若CBN α∠=,求BDA ∠的大小(用含α的式子表示); (3)用等式表示线段PB ,PA 与PE 之间的数量关系,并证明.30、解:(1) ---------------------------2分FPDEBAO(2)∵∠ABC=90°∴∠MBC=∠ABC=90°∵点C 关于BN 的对称点为D∴BC =BD ,∠CBN=∠DBN=α ---------------------------3分 ∵AB =BC∴AB =BD ---------------------------4分 ∴∠BAD=∠ADB=()α29018021-︒-︒=45°-α ---------------------------5分 (3) 猜想:()PE PB PA +=2 ---------------------------4分 证明:过点B 作BQ ⊥BE 交AD 于Q ---------------------------6分 ∵∠BPA=∠DBN+∠ADB ,∠ADB=45°-α,∠DBN=α ∴∠BPA=∠DPE=45°∵点C 关于BN 的对称点为D ∴BE ⊥CD∴PD =2PE ,PQ =2PB , ---------------------------7分 ∵BQ ⊥BE ,∠BPA=45° ∴∠BPA=∠BQP=45° ∴∠AQB=∠DPB=135° 又∵AB =BD ,∠BAD=∠ADB ∴△AQB ≌△BPD (AAS ) ∴AQ =PD ∵PA =AQ +PQ∴()PE PB PA +=2 ---------------------------8分2019怀柔八上27.如图1,在△ABC 中,AB =AC , D 为直线BC 上一动点(不与B ,C 重合),在AD 的右侧作△ADE ,使得AE =AD ,∠DAE =∠BAC ,连接CE . (1)当D 在线段BC 上时,求证:△BAD ≌△CAE ; (2)当点D 运动到何处时,AC ⊥DE ,并说明理由;(3)当CE ∥AB 时,若△ABD 中最小角为20°,直接写出∠ADB 的度数.27.解:(1)∵∠DAE =∠BAC , ∴∠BAD =∠CAE . ∵AB=AC ,AD=AE ,∴△BAD ≌△CAE (SAS ).……………………………………………………2分 (2)当D 运动到BC 中点时,AC ⊥DE . …………………………………………3分∵D 是BC 中点,AB=AC ,∴∠1=∠2. ∵△BAD ≌△CAE ,∴∠1=∠3.∴∠2=∠3. ∵AD=AE ,∴AC ⊥DE .B EDCBA 图1ABC备用图∴当D 运动到BC 中点时,AC ⊥DE .……………………………5分 (3)∠ADB =20°或40°或100° .…………………………7分 28.解:(1)如图:…………………………………………………1分 (2)在△ACE 和△BCD 中,∴△ACE ≌△BCD (SAS ). ∴∠1=∠2.∵∠AEC =∠BEF , ∴∠BFE =∠ACE .∵∠ACE =90°,∴∠AFB=90°.∴AF ⊥BD .………………………………………3分 (3)数量关系是:CQ =CF .………………………………………4分过C 作CG ⊥CF 交AF 于G . ∴∠GCF =90°.∵∠ACB =90°,∴∠3=∠4. ∵∠1=∠2,AC=BC , ∴△ACG ≌△BCF (ASA ).∴CG =CF .∴△CGF 是等腰直角三角形. ∴∠CFG =45°.∴∠CFD =45°.∵点C 与 Q 关于BD 对称,∴CF =FQ . ∠CFD =∠QFD =45°.∴△CFQ 是等腰直角三角形. ∴CQ =CF .………………………………………………………7分2019门头沟八上28.已知:△ABC 是等边三角形,D 是直线BC 上一动点,连接AD ,在线段AD 的右侧作射线DP 且使∠ADP =30°,作点A 关于射线DP 的对称点E ,连接DE 、CE . (1)当点D 在线段BC 上运动时,① 依题意将图1补全;② 请用等式表示线段AB 、CE 、CD 之间的数量关系,并证明;(2)当点D 在直线BC 上运动时,请直接写出AB 、CE 、CD 之间的数量关系,不需证明.21FEBD4321GFEBD∴ △ADE 是等边三角形.…………………………………………………………………3分∴ AD =AE ,∠DAE =∠ADE =60°. 又∵△ABC 是等边三角形, ∴ AB =AC=BC ,∠BAC =60°.∴ ∠BAC -∠DAC =∠DAE -∠DAC , 即:∠BAD =∠CAE . 在△BAD 和△CAE 中AB AC BAD CAE AD AE =⎧⎪=⎨⎪=⎩∠∠ ∴△BAD≌△CAE …………………………………………………………………………4分∴ BD =CE∴ AB =BC =BD+CD= CE+CD .(2)AB = CE+CD ,AB = CE -CD ,AB = CD -CE .…………………………………………………7分说明:若考生的解法与给出的解法不同,正确者可参照评分参考相应给分.2019密云八上27. 已知:在△ABC 中,∠ABC =45°,CD AB ⊥于点D ,点E 为CD 上一点,且DE=AD ,连接BE 并延长交AC 于点F ,连接DF . (1)求证:BE=AC(2)用等式表示线段FB 、FD 、FC 之间的数量关系,并加以证明.27 . (1) ∵ ∴∵∴ ∴ …………………………1分∴∴ …………………………3分 (2) …………………………4分证明:∵ ∴ ∴ ∴ F EDCBABD CD =BDE CDA BD CD BDC ADC DE AD ∆∆=⎧⎪∠=∠⎨⎪=⎩在和中BDE CDA ∆≅∆BE AC =2FB FD FC =+°90CD AB BDC ADC ⊥∠=∠=°45ABC BDC ∠=∆是等腰直角三角形°DH DF BF H HDF=BDC=90HDF-HDE=BDC-HDE BDH=CDF⊥∠∠∠∠∠∠∠∠作交于FEDC B A∵, ∴∴∴ ∴ ∴∵∴ ………………………………7分2019平谷八上26.阅读下面材料:学习了三角形全等的判定方法(即“SAS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,小聪继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.小聪将命题用符号语言表示为:在△ABC 和△DEF 中,AC =DF ,BC =EF ,∠B =∠E . 小聪想:要想解决问题,应该对∠B 进行分类研究. ∠B 可分为“直角、钝角、锐角”三种情况进行探究. (1)当∠B 是直角时,如图1,在△ABC 和△DEF 中,AC =DF ,BC =EF ,∠B =∠E =90°,则Rt △ABC ≌Rt △DEF (依据:________)(2)当∠B 是锐角时,如图2,BC =EF ,∠B =∠E<90°,在射线EM 上有点D ,使DF =AC ,画出符合条件的点D ,则△ABC 和△DEF 的关系是________;A .全等B .不全等C .不一定全等(3)第三种情况:当∠B 是钝角时,如图3,在△ABC 和△DEF 中,AC =DF ,BC =EF ,BDE CDA ∆≅∆ABEDCF ∠=∠BDH CDF ABE DCF BD DCBDH CDF ∆∆∠=∠⎧⎪=⎨⎪∠=∠⎩在和中BDH CDF ∆≅∆,DH DF BH FC ==HDF ∆是等腰直角三角形HF =图1图2FB FH BH FB FC=+=+∠B =∠E >90°,求证:△ABC ≌△DEF .26.解:(1)△ABC ≌△DEF (依据:HL )…………………………………………1分…………………………………………………3分(2)选择C ……………………………………………………4分 (3)证明:如图,过点C 作CG ⊥AB 交AB 的延长线于点G , 过点F 作DH ⊥DE 交DE 的延长线于点H , ∵∠CBA =∠FED ,∴180°﹣∠CBA =180°﹣∠FED ,即∠CBG =∠FEH , ……………………………………………………………… 5分 在△CBG 和△FEH 中,90CBG FEHG H BC EF ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩, ∴△CBG ≌△FEH (AAS ), ∴CG =FH ,在Rt △ACG 和Rt △DFH 中,AC DFCG FH =⎧⎨=⎩,Rt △ACG ≌Rt △DFH (HL ),∴∠A =∠D , ………………………………………………………………………6分在△ABC 和△DEF 中,CBA FE A D A D C DF ∠=∠⎧⎪⎨⎪=∠∠⎩=,∴△ABC ≌△DEF (AAS ).…………………………………………………………7分图32019石景山八上28.ABC △是等边三角形,2AC =,点C 关于AB 对称的点为C ',点P 是直线C B '上 的一个动点,连接AP ,作60APD ∠=°交射线..BC 于点D . (1)若点P 在线段C B '上(不与点C ',点B 重合).①如图1,若点P 是线段C B '的中点,则AP 的长为 ; ②如图2,点P 是线段C B '上任意一点,求证:PD PA =; (2)若点P 在线段C B '的延长线上. ①依题意补全图3;②直接写出线段BD ,AB ,BP 之间的数量关系为: .28.(1. ………………………… 2分 ②证法一:作60BPE ∠=°交AB 于点E ,如图1.…… 3分 ∵ABC △是等边三角形,∴60ABC ∠=°(等边三角形的三个角都是60°). ∵点C '与点C 关于AB 对称, ∴60C BA CBA BPE '∠=∠=∠°=, ∴460∠=°.∴PBE △ ∴PB PE =(等边三角形的三边都相等), 5120PBD ∠=∠°=.∵1260∠+∠=°,3260∠+∠=°,∴13∠=∠(等量减等量,差相等). ………………………… 4分 在PBD △和PEA △中,13,,5,PB PE PBD ∠=∠=∠=∠⎧⎪⎨⎪⎩∴PBD △≌PEA △(ASA ).∴PD PA =( 全等三角形的对应边相等). ……………………… 5分 证法二:延长AB 到点E ,使BE BD =,连接PE ,如图2. ……………… 3分 ∵ABC △是等边三角形(已知),∴60ABC ∠=°(等边三角形的三个角都是60°). ∵点C '与点C 关于AB 对称(已知), ∴60C BA CBA '∠=∠=°. ∴1120PBD ∠=∠°=. 在PBE △和PBD △中,,1,,PB PB PBD BE BD =∠=∠=⎧⎪⎨⎪⎩∴PBE △≌PBD △(SAS ).∴PE PD =(全等三角形的对应边相等), ……………………… 4分 3E ∠=∠(全等三角形的对应角相等). ∵60APF FBD ∠=∠=°, AFP BFD ∠=∠(对顶角相等), ∴23∠=∠(三角形内角和定理). ∴2E ∠=∠(等量代换). ∴PE PA =(等角对等边). 又∵PE PD =(已证),∴PD PA =(等量代换). ……………………… 5分 证法三:延长CB 到点E ,使BE BA =, 连接PE ,如图3.可证PEB △≌PAB △(SAS ). 再证PED △是等腰三角形. 证法四:连接C A ',在C A '上截取C E C P ''=, 连接PE ,如图4. 可证PBD △≌AEP △(ASA ).证法五:过点P 作PM CB ⊥交CB 的延长线于点M ,PN AB ⊥于点N ,如图5. 可证PMD △≌PNA △(AAS ).(2)①补全图形,如图6所示;……… 6分②BD AB BP =+. ……… 7分2019通州八上28. 在等边ABC ∆中,(1)如图1,P ,Q 是BC 边上两点,AP=AQ ,20BAP ∠=︒,求AQB ∠的度数; (2)点,P Q 是BC 边上的两个动点(不与,B C 重合),点P 在点Q 的左侧,且AP AQ =,点Q 关于直线AC 的对称点为M ,连接,.AM PM ①依题意将图2补全; ②求证:.PA PM = 图1 图228. (1)解:∵ △ABC 为等边三角形∴∠B =60°∴∠APC =∠BAP +∠B=80° ∵AP=AQ∴∠AQB=∠APC =80°……………………………..(2分)(2)① 补全图形如图所示. …………………………………..(4分)②证法不唯一CB CB 图4 图5B证明:过点A作AH⊥BC于点H,如图.由△ABC为等边三角形,AP=AQ,可得∠PAB=∠QAC. …………………………………..(5分)∵点Q,M关于直线AC对称,∴∠QAC=∠MAC,AQ=AM∴∠PAB=∠MAC,AQ=AM∴∠PAM=∠BAC=60°…………………………………..(6分)∴△APM为等边三角形∴PA=PM. …………………………………..(7分)2019西城八上26.在△ABC中,AB=AC,在△ABC的外部作等边三角形△ACD,E为AC的中点,连接DE 并延长交BC于点F,连接BD.(1)如图1,若∠BAC=100°,求∠BDF的度数;(2)如图2,∠ACB的平分线交AB于点M,交EF于点N,连接BN.①补全图2;②若BN=DN,求证:MB=MN.图1 图2(1)解:在等边三角形△ACD中,∠CAD =∠ADC =60°,AD=AC.∵E为AC的中点,∴∠ADE=12∠ADC=30°.···················································································2分BDACEF BDACEFMB∵AB=AC,∴AD=AB.∵∠BAD=∠BAC+∠CAD=160°.∴∠ADB=∠ABD=10°.∴∠BDF=∠ADF -∠ADB=20°.·····································································4分(2)①补全图形;②证明:连接AN.∵CM平分∠ACB,∴设∠ACM=∠BCM=α.∵AB=AC,∴∠ABC=∠ACB=2α.在等边三角形△ACD中,∵E为AC的中点,∴DN⊥AC.∴NA=NC.∴∠NAC=∠NCA=α.∴∠DAN=60°+ α.在△ABN和△ADN中,∵,,, AB AD BN DN AN AN=⎧⎪=⎨⎪=⎩∴△ABN≌△ADN.∴∠ABN=∠ADN=30°,∠BAN=∠DAN=60°+ α.∴∠BAC=60°+ 2α.在△ABC中,∠BAC+∠ACB +∠ABC=180°,∴60°+ 2α+ 2α+2α=180°.∴α=20°.NBD ACEFM∴∠NBC=∠ABC-∠ABN= 10°.∴∠MNB=∠NBC+ ∠NCB=30°.∴∠MNB=∠MBN.∴MB=MN. ···················································································································8分2019延庆八上27.如图,∠MON =45°,点A 是OM 上一点,点B ,C 是ON 上两点,且AB =AC ,作出点B 关于OM 对称的点D ,连接AD ,CD . (1)按要求补全图形; (2)判断∠DAC = °;(3)判断AD 与DC 的数量关系 ,并证明.27.解:(1)如图 ………… ……2分(2)∠DAC =90° ………… ……3分 (3)AD DC 2=………… ……4分证明:∵点B 与点D 关于AO 对称 ∵BD 被AO 垂直平分 ∵AD =AB 又∵AB =AC∵AD =AC ………… … 5分∵∵ABC =∵ACB =∵O +∵OAB ∵∵BAC =OAB ∠-︒290∵∵DAC =90° ………… … 6分 ∴△ADC 是等腰直角三角形 ∴AD DC 2= …………………7分2019延庆八上28.如图,在△ABC 中,∠ABC =15°,AB =2,BC =2,以AB 为直角边向外作等腰直角△BAD ,且∠BAD=90°;以BC 为斜边向外作等腰直角△BEC ,连接DE . (1)按要求补全图形; (2)求DE 长;(3)直接写出△ABC 的面积.28.解:(1)如图所示………… ……2分(2) 连接DC解:∵△ABD 是等腰直角三角形, AB =2,∠BAD =90°.∴ AB =AD =2 ,∠ABD =45°. 由勾股定理得DB =2.EDCBAFEDCBA∴ ∠DBC =∠ABC +∠ABD =60°. ∵BC =2. ∴ BC =BD .∴△BCD 是等边三角形. ∴BD =CD =2.∴D 点在线段BC 的垂直平分线上. 又∵△BEC 是等腰直角三角形. ∴BE =CE ,∠CEB =45°∴E 点在线段BC 的垂直平分线上. ∴DE 垂直平分BC . ∴BF =21BC =1, ∠BFE =90° ∵∠FBE =∠BEF =45° ∴BF =EF =1Rt △BFD 中,BF =1,BD =2由勾股定理得DF =3∴ DE =DF +EF =13+ ………… ……6分(3)213-………… ……7分2019燕山八上27.已知BC =5,AB =1,AB ⊥BC ,射线CM ⊥BC ,动点P 在线段BC 上(不与点B ,C 重合),过点P 作DP ⊥AP 交射线CM 于点D ,连接AD .(1) 如图1,若BP =4,判断△ADP 的形状,并加以证明.(2) 如图2,若BP =1,作点C 关于直线DP 的对称点C ′,连接AC ′. ① 依题意补全图2;AB CDM P图2图1PMDCBA②请直接写出线段AC′的长度.27.(1) △ADP是等腰直角三角形.………………………………1分证明:∵BC=5,BP=4,∴PC=1,∵AB=1,∴PC=AB.………………………………2分∵AB⊥BC,CM⊥BC,DP⊥AP,∴∠B=∠C=90°,∠APB+∠DPC=90°,∠PDC+∠DPC=90°,∴∠APB=∠PDC,………………………………3分在△ABP和△PCD中,B CAPB PDC AB PC∠=∠⎧⎪∠=∠⎨⎪=⎩,,,∴△ABP≌△PCD,………………………………4分∴AP=PD,∵∠APD=90°,∴△ADP………………………………5分(2) ①依题意补全图2;………………………………6分②AC.………………………………7分2019顺义八上30.数学课上,老师给出了如下问题:已知:如图1,在Rt△ABC中,∠C=90°,AC=BC,延长CB到点D,∠DBE=45°,点F 是边BC上一点,连结AF,作FE⊥AF,交BE于点E.(1)求证:∠CAF=∠DFE;(2)求证:AF=EF.经过独立思考后,老师让同学们小组交流.小辉同学说出了对于第二问的想法:“我想通过构造含有边AF 和EF 的全等三角形,因此我过点E 作EG ⊥CD 于G (如图2所示),如果能证明Rt △ACF 和Rt △FGE 全等,问题就解决了.但是这两个三角形证不出来相等的边,好像这样做辅助线行不通.”小亮同学说:“既然这样做辅助线证不出来,再考虑有没有其他添加辅助线的方法.”请你顺着小亮同学的思路在图3中继续尝试,并完成(1)、(2)问的证明. 30.证明:(1)∵∠C=90°,∵ ∠CAF + ∠1 = 90︒ . ....................... 1 分 ∵FE ∵AF ,∵ ∠DFE + ∠1 = 90︒ . ....................... 2 分 ∵ ∠CAF = ∠DFE . .......................... 3 分(2)在 A C 上截取 A G=BF ,连结 F G ,如图 4. ............................................ 4 分∵AC= BC ,∵ AC - AG = BC -BF . 即 CG= CF .∵∵C=90°,∵ ∠CGF = ∠CFG = 45︒ . ∵ ∠AGF = 180︒ - ∠CGF = 135︒ . ∵∵DBE=45°,∵ ∠FBE = 180︒ - ∠DBE = 135︒ .∵ ∠AGF = ∠FBE . ................................................................................. 5 分 由: ∠CAF = ∠DFE . ∵A G F ∵∵FB E (A. ................................................................................................................ 6 分∵AF=EF . ...................................................................................................7 分G 图3图2图1ACB DEF ACB DEF F EDB CA2019丰台八上28.如图,Rt△ABC中,∠ACB = 90°,AC = BC,点D为AB边上的一个动点(不与点A,B及AB中点重合),连接CD,点A关于直线CD的对称点为点E,直线BE,CD交于点F.(1)如图1,当∠ACD = 15°时,根据题意将图形补充完整,并直接写出∠BFC的度数;(2)如图2,当45°<∠ACD<90°时,用等式表示线段AC,EF,BF之间的数量关系,并加以证明.图1 图2ACDA BC。
2022-2023学年北京市顺义区八年级(下)期末数学试卷【答案版】

2022-2023学年北京市顺义区八年级(下)期末数学试卷一、选择题(本题共16分,每题2分)第1-8题均有四个选项,符合题意的选项只有一个1.在平面直角坐标系中,点(2,3)关于x轴对称的点的坐标是()A.(2,﹣3)B.(3,2)C.(﹣2,3)D.(﹣2,﹣3)2.下列几何体中,圆柱体是()A.B.C.D.3.若一个多边形的内角和与外角和相等,则这个多边形是()A.三角形B.六边形C.五边形D.四边形4.方程(x+2)(x+1)=x+2的解为()A.x1=0,x2=2B.x1=0,x2=﹣2C.x1=﹣1,x2=﹣2D.x1=x2=﹣15.平行四边形ABCD中,对角线AC、BD交于点O(如图),则图中全等三角形的对数为()A.2B.3C.4D.56.如图,顺次连接矩形各边中点,得到由矩形和菱形组成的图形,则关于这个图形的描述正确的是()A.是轴对称图形但不是中心对称图形B.不是轴对称图形也不是中心对称图形C.不是轴对称图形但是中心对称图形D.既是轴对称图形又是中心对称图形7.用配方法解一元二次方程x2﹣8x+2=0,此方程可化为的正确形式是()A.(x﹣4)2=14B.(x﹣4)2=18C.(x+4)2=14D.(x+4)2=188.下面的三个问题中都有两个变量:①正方形的面积y与边长x;②将水箱中的水匀速放出,直至放完,水箱中剩余水量y与放水时间x;③汽车从A地匀速行驶到B地,汽车距离B地的路程y与行驶时间x;其中,变量y与变量x之间的函数关系可以利用如图所示的图象表示的是()A.①②B.①③C.②③D.①②③二、填空题(本题共16分,每题2分)9.﹣2的相反数是.10.方程(x﹣1)2=3的解为.11.如图,在△ABC中,∠ACB=90°,∠A=50°,D为边AB的中点,则∠BCD=°.12.如图,在平行四边形ABCD中,CE平分∠BCD,BC=6,AE=2,则CD=.13.某校举办“五月的鲜花”演唱比赛,十位评委对每位同学的演唱进行现场打分.已知甲、乙两位同学得分的平均数都是8.6,如图是甲、乙两位同学得分的折线图及表示得分平均数的水平直线:如果某同学得分的10个数据的方差越小,则认为评委对该同学演唱的评价越一致,据此推断:甲、乙两位同学中,评委对的评价更一致(填“甲”或“乙”).14.已知关于x 的方程x 2+4x +m =0有两个不相等的实数根,写出一个符合条件的m 的值为 .15.小红和小明从甲地出发,骑自行车沿同一条路到距甲地24千米的乙地参加活动.如图,折线OA ﹣AB 和线段CD 分别表示小红和小明离甲地的距离y (单位:km )与时间t (单位:h )之间函数关系的图象.根据图中提供的信息,当小明到达乙地时,小红还有 小时到达乙地,此时小红距乙地 千米.16.如图,在矩形ABCD 中,AB =4,AD =6,P ,Q 分别是边AD ,BC 上的动点,点P 从A 出发到D 停止运动,点Q 从C 出发到B 停止运动,若P ,Q 两点以相同的速度同时出发,匀速运动.下面四个结论中,①存在四边形APCQ 是矩形;②存在四边形APCQ 是菱形;③存在四边形APQB 是矩形;④存在四边形APQB 是正方形;所有正确结论的序号是 .三、解答题(本题共68分,第17-19题,每题5分,第20-22题,每题6分,第23题5分,第24,25题,每题6分,第26题5分,第27题7分,第28题6分)17.解不等式组:{x >2x −1x −1<x 2. 18.解方程:x 2+4x ﹣5=0.19.如表是一次函数y =kx +b (k ≠0)中x 与y 的两组对应值.(1)求该一次函数的表达式;(2)求该一次函数的图象与x轴的交点坐标.20.(6分)下面是小红设计的“已知直角作矩形”的尺规作图过程.已知:如图,∠A=90°.求作:矩形ABCD.作法:如图,①在∠A的两边上分别任取点B,D(不与点A重合);②以点B为圆心,AD长为半径画弧,以点D为圆心,AB长为半径画弧,两弧在∠A的内部交于点C;③连接BC,CD.所以四边形ABCD即为所求作的矩形.根据小红设计的尺规作图过程,(1)使用直尺和圆规,补全图形(保留作图痕迹);(2)完成下列证明.证明:∵AB=CD,AD=,∴四边形ABCD是平行四边形()(填推理的依据),又∵∠A=90°,∴四边形ABCD是矩形()(填推理的依据).21.(6分)已知关于x的一元二次方程x2+bx﹣3=0.(1)求证:方程总有两个不相等的实数根;(2)若方程的一个根是1,求b的值及方程的另一个根.22.(6分)如图,在△ABC中,AB=BC,D,E分别是AB,AC的中点,AF∥DE,EF∥AD.(1)求证:四边形ADEF是菱形;(2)连接DF,若AB=10,AC=12,求DF的长.23.某校打算用14m的篱笆,在墙边(墙足够长)围成一个矩形区域,作为“养殖基地”(篱笆只围AB,BC,CD三边),当矩形区域的面积是24m2时,求它的长和宽.24.(6分)在平面直角坐标系xOy中,直线l1:y=﹣x+1与x轴交于点A,直线l2:y=kx﹣3(k≠0)与y轴交于点B,与l1交于点C.(1)求△OAB的面积;(2)若△OBC的面积是△OAB面积的2倍,求k的值.25.(6分)2023年5月30日,神舟十六号载人飞船发射取得圆满成功.为普及航天知识,某中学举办了一次“航天知识竞赛”,共有1000名学生参加.为更好的了解本次比赛得分的分布情况,随机抽取了部分学生的比赛得分,进行收集、整理、描述和分析.下面给出了部分信息(数据分成5组:50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100):a.学生比赛得分频数分布表:b.学生比赛得分频数分布直方图:c .学生比赛得分在80≤x <90这一组的是:80,81,83,82,86,87,85,81,89,88,85,86,80,83;根据以上信息,回答下列问题:(1)e = ,f = ;(2)请补全频数分布直方图;(3)若得分在85分及以上均为“优秀”,请估计参加这次比赛的1000名学生中得分优秀的人数.26.在平面直角坐标系xOy 中,一次函数y =kx +2(k ≠0)的图象经过点(﹣1,0).(1)求k 的值;(2)当x >0时,对于x 的每一个值,一次函数y =﹣x +b 的值小于一次函数y =kx +2(k ≠0)的值,直接写出b 的取值范围.27.(7分)如图,在正方形ABCD 中,E 是边BC 上的一动点(不与点B ,C 重合),AF ⊥AE 于点A ,AF =AE ,连接BF ,DE .(1)求证:∠ABF =∠ADE ;(2)延长FB ,DE ,交于点G ,连接AG .①依题意补全图形;②用等式表示线段EG ,FG ,AG 之间的数量关系,并证明.28.(6分)在平面直角坐标系xOy 中,给出如下定义:若在图形M 上存在一点P ,且点P 的纵坐标是横坐标的n (n 为正整数)倍,则称点P 为图形M 的“n 倍点”.例如,点(1,4)是直线y =﹣x +5的“4倍点”.(1)在点P 1(1,2),P 2(2,0),P 3(2,4),P 4(85,45)中, 是直线y =﹣2x +4的“2倍点”;(2)已知点A的坐标为(m,0),点B的坐标为(m+2,0),以线段AB为矩形的一边向上作矩形ABCD.①若m=1,AD=4,判断是否存在矩形ABCD的“3倍点”,若存在,求出矩形ABCD的“3倍点”的坐标,若不存在,请说明理由;②若AD=nAB,且存在矩形ABCD的“n倍点”,直接写出m的取值范围.2022-2023学年北京市顺义区八年级(下)期末数学试卷参考答案与试题解析一、选择题(本题共16分,每题2分)第1-8题均有四个选项,符合题意的选项只有一个1.在平面直角坐标系中,点(2,3)关于x轴对称的点的坐标是()A.(2,﹣3)B.(3,2)C.(﹣2,3)D.(﹣2,﹣3)解:点(2,3)关于x轴对称的点的坐标是(2,﹣3),故选:A.2.下列几何体中,圆柱体是()A.B.C.D.解:A、是正方体,故该选项不符合题意;B、是圆锥,故该选项不符合题意;C、是三棱锥,故该选项不符合题意;D、是圆柱体,故该选项符合题意;故选:D.3.若一个多边形的内角和与外角和相等,则这个多边形是()A.三角形B.六边形C.五边形D.四边形解:设多边形的边数为n,根据题意得(n﹣2)•180°=360°,解得n=4.所以这个多边形是四边形.故选:D.4.方程(x+2)(x+1)=x+2的解为()A.x1=0,x2=2B.x1=0,x2=﹣2C.x1=﹣1,x2=﹣2D.x1=x2=﹣1解:(x+2)(x+1)=x+2,整理,得x2+2x=0,x(x+2)=0,x=0或x+2=0,∴x1=0,x2=﹣2.故选:B.5.平行四边形ABCD中,对角线AC、BD交于点O(如图),则图中全等三角形的对数为()A.2B.3C.4D.5解:∵四边形ABCD是平行四边形,∴AB=CD,AD=BC;OD=OB,OA=OC;∵OD=OB,OA=OC,∠AOD=∠BOC;∴△AOD≌△COB(SAS);①同理可得出△AOB≌△COD(SAS);②∵BC=AD,CD=AB,BD=BD;∴△ABD≌△CDB(SSS);③同理可得:△ACD≌△CAB(SSS).④因此本题共有4对全等三角形,故选:C.6.如图,顺次连接矩形各边中点,得到由矩形和菱形组成的图形,则关于这个图形的描述正确的是()A.是轴对称图形但不是中心对称图形B.不是轴对称图形也不是中心对称图形C.不是轴对称图形但是中心对称图形D.既是轴对称图形又是中心对称图形解:根据长方形和菱形的对称的特点:它们既是轴对称图形,又是中心对称图形.则它们的这种组合图形,既是轴对称图形又是中心对称图形.故选:D.7.用配方法解一元二次方程x2﹣8x+2=0,此方程可化为的正确形式是()A.(x﹣4)2=14B.(x﹣4)2=18C.(x+4)2=14D.(x+4)2=18解:x2﹣8x+2=0,x2﹣8x=﹣2,x2﹣8x+16=﹣2+16,(x﹣4)2=14,故选:A.8.下面的三个问题中都有两个变量:①正方形的面积y与边长x;②将水箱中的水匀速放出,直至放完,水箱中剩余水量y与放水时间x;③汽车从A地匀速行驶到B地,汽车距离B地的路程y与行驶时间x;其中,变量y与变量x之间的函数关系可以利用如图所示的图象表示的是()A.①②B.①③C.②③D.①②③解:正方形的面积y是边长x的二次函数,故①不符合题意;将水箱中的水匀速放出,直至放完,根据水箱中的剩余水量y随放水时间x的增大而减小,故②符合题意;汽车从A地匀速行驶到B地,根据汽车的剩余路程y随行驶时间x的增加而减小,故③符合题意;所以可以利用如图所示的图象表示的是②③.故选:C.二、填空题(本题共16分,每题2分)9.﹣2的相反数是2.解:﹣2的相反数是:﹣(﹣2)=2,故答案为:2.10.方程(x﹣1)2=3的解为x=1±√3.解:(x﹣1)2=3开平方得,x﹣1=±√3所以x=1±√3.故答案为:1±√3.11.如图,在△ABC中,∠ACB=90°,∠A=50°,D为边AB的中点,则∠BCD=40°.解:在△ABC 中,∠ACB =90°,∠A =50°,∴∠B =40°,∵D 为线段AB 的中点,∴CD =BD ,∴∠BCD =∠B =40°.故答案为:40.12.如图,在平行四边形ABCD 中,CE 平分∠BCD ,BC =6,AE =2,则CD = 4 .解:∵在▱ABCD 中,CE 平分∠BCD 交AD 于点E ,∴∠DEC =∠ECB ,∠DCE =∠BCE ,BC =AD ,∴∠DEC =∠DCE ,∴DE =DC ,∵AD =BC =6,AE =2,∴DE =DC =6﹣2=4.故答案为:4.13.某校举办“五月的鲜花”演唱比赛,十位评委对每位同学的演唱进行现场打分.已知甲、乙两位同学得分的平均数都是8.6,如图是甲、乙两位同学得分的折线图及表示得分平均数的水平直线:如果某同学得分的10个数据的方差越小,则认为评委对该同学演唱的评价越一致,据此推断:甲、乙两位同学中,评委对 甲 的评价更一致(填“甲”或“乙”).解:甲同学的方差S 2甲=110×[2×(7﹣8.6)2+2×(8﹣8.6)2+4×(9﹣8.6)2+2×(10﹣8.6)2]=1.04, 乙同学的方差S 2乙=110×[4×(7﹣8.6)2+2×(9﹣8.6)2+4×(10﹣8.6)2]=1.84,∵S 2甲<S 2乙,∴评委对甲同学演唱的评价更一致.故答案为:甲.14.已知关于x 的方程x 2+4x +m =0有两个不相等的实数根,写出一个符合条件的m 的值为 3(答案不唯一) .解:∵关于x 的方程x 2+4x +m =0有两个不相等的实数根,∴Δ=42﹣4m >0,解得:m <4,则m =3,故答案为:3(答案不唯一).15.小红和小明从甲地出发,骑自行车沿同一条路到距甲地24千米的乙地参加活动.如图,折线OA ﹣AB 和线段CD 分别表示小红和小明离甲地的距离y (单位:km )与时间t (单位:h )之间函数关系的图象.根据图中提供的信息,当小明到达乙地时,小红还有 0.5 小时到达乙地,此时小红距乙地 4 千米.解:由图象可得,当小明到达乙地时,小红还有2.5﹣2=0.5(小时)到达乙地,设AB 段对应的函数解析式为y =kx +b ,∵点(0.5,8),(2.5,24)在该函数图象上,∴{0.5k +b =82.5k +b =24, 解得{k =8b =4, ∴AB 段对应的函数解析式为y =8x +4,当x =2时,y =8×2+4=20,∵24﹣20=4(千米),∴当小明到达乙地时,此时小红距乙地4千米,故答案为:0.5,4.16.如图,在矩形ABCD中,AB=4,AD=6,P,Q分别是边AD,BC上的动点,点P从A出发到D停止运动,点Q从C出发到B停止运动,若P,Q两点以相同的速度同时出发,匀速运动.下面四个结论中,①存在四边形APCQ是矩形;②存在四边形APCQ是菱形;③存在四边形APQB是矩形;④存在四边形APQB是正方形;所有正确结论的序号是①②③.解:在矩形ABCD中,AB=4,AD=6,∴AB=CD=4,AD=BC=6,∠A=∠B=∠C=∠D=90°,①当点P与D重合,点C与B重合时,存在四边形APCQ是矩形;故①正确;②∵AP=CQ,AP∥CQ,∴四边形APCQ是平行四边形,当AP=CP时,四边形APCQ是菱形,设AP=x,则CP=x,PD=6﹣x,∵∠D=90°,∴PC2=PD2+CD2,∴x2=(6﹣x)2+42,解得x=13 2,故当AP=132时,四边形APCQ是菱形;故②正确;③当AP=BQ时,四边形APQB是矩形,∵AP=CQ,∴BQ=CQ=12BC=3,当AP=3时,四边形APQB是矩形,故③正确;④不存在四边形APQB是正方形,理由:当AP =AB =BQ =4,则CQ =2,∵AP =CQ ,∴BQ =CQ =4,∵BC =BQ +CQ =6,∴不存在四边形APQB 是正方形,故答案为:①②③.三、解答题(本题共68分,第17-19题,每题5分,第20-22题,每题6分,第23题5分,第24,25题,每题6分,第26题5分,第27题7分,第28题6分)17.解不等式组:{x >2x −1x −1<x 2. 解:{x >2x −1①x −1<x 2②, 解不等式①,得x <1;解不等式②,得x <2;∴不等式组的解集是x <1.18.解方程:x 2+4x ﹣5=0.解:原方程变形为(x ﹣1)(x +5)=0∴x 1=﹣5,x 2=1.19.如表是一次函数y =kx +b (k ≠0)中x 与y 的两组对应值.(1)求该一次函数的表达式;(2)求该一次函数的图象与x 轴的交点坐标.解:(1)设函数解析式为y =kx +b (k ≠0),把(0,﹣4)和(3,2)分别代入解析式,得{b=−4,3k+b=2,∴{k=2b=−4∴一次函数的表达式:y=2x﹣4;(2)令y=0,∴2x﹣4=0,∴x=2,∴该一次函数的图象与x轴的交点坐标(2,0).20.(6分)下面是小红设计的“已知直角作矩形”的尺规作图过程.已知:如图,∠A=90°.求作:矩形ABCD.作法:如图,①在∠A的两边上分别任取点B,D(不与点A重合);②以点B为圆心,AD长为半径画弧,以点D为圆心,AB长为半径画弧,两弧在∠A的内部交于点C;③连接BC,CD.所以四边形ABCD即为所求作的矩形.根据小红设计的尺规作图过程,(1)使用直尺和圆规,补全图形(保留作图痕迹);(2)完成下列证明.证明:∵AB=CD,AD=BC,∴四边形ABCD是平行四边形(对边相等的四边形是平行四边形)(填推理的依据),又∵∠A=90°,∴四边形ABCD是矩形(有一个角是90°的平行四边形是矩形)(填推理的依据).(1)解:图形如图所示:(2)证明:∵AB=CD,AD=BC,∴四边形ABCD是平行四边形(对边相等的四边形是平行四边形),又∵∠A=90°,∴四边形ABCD是矩形(有一个角是90°的平行四边形是矩形),故答案为:BC,对边相等的四边形是平行四边形,有一个角是90°的平行四边形是矩形.21.(6分)已知关于x的一元二次方程x2+bx﹣3=0.(1)求证:方程总有两个不相等的实数根;(2)若方程的一个根是1,求b的值及方程的另一个根.解:(1)∵b2﹣4ac=b2﹣4×1×(﹣3)=b2+12>0,∴方程总有两个不相等的实数根;(2)设方程的另一个根为m,由根与系数关系得1×m=﹣3,解得m=﹣3,∴方程的另一个根为﹣3.∵x1+x2=−b a,∴﹣b=1+(﹣3),∴b=2.22.(6分)如图,在△ABC中,AB=BC,D,E分别是AB,AC的中点,AF∥DE,EF∥AD.(1)求证:四边形ADEF是菱形;(2)连接DF,若AB=10,AC=12,求DF的长.(1)证明:∵AF∥DE,EF∥AD,∴四边形ADEF是平行四边形,∵D,E分别是AB,AC的中点,∴AD=12AB,DE是△ABC的中位线,∴DE=12 BC,∵AB=BC,∴AD=DE,∴四边形ADEF是菱形;(2)解:连接DF交AE于O,∵四边形ADEF是菱形,∴AE⊥DF,AO=12AE,OD=12DF,∵D,E分别是AB,AC的中点,AB=10,AC=12,∴AD=5,AC=6,∴AO=3,∴DO=√AD2−AO2=√52−32=4,∴DF=8.23.某校打算用14m的篱笆,在墙边(墙足够长)围成一个矩形区域,作为“养殖基地”(篱笆只围AB,BC,CD三边),当矩形区域的面积是24m2时,求它的长和宽.解:矩形区域的宽为x m,则它的长为(14﹣2x)m,根据题意得,x(14﹣2x)=24,解得,x1=3,x2=4,∴14﹣2x =8或6,答:矩形区域的宽为3m 或4m ,则它的长为8m 或6m .24.(6分)在平面直角坐标系xOy 中,直线l 1:y =﹣x +1与x 轴交于点A ,直线l 2:y =kx ﹣3(k ≠0)与y 轴交于点B ,与l 1交于点C .(1)求△OAB 的面积;(2)若△OBC 的面积是△OAB 面积的2倍,求k 的值.解:(1)∵直线l 1:y =﹣x +1与x 轴交于点A ,∴A (1,0),∵直线l 2:y =kx ﹣3(k ≠0)与y 轴交于点B ,∴B (0,﹣3),∴OA =1,OB =3,∴△OAB 的面积:12OA ⋅OB =12×1×3=32; (2)∵△OBC 的面积是△OAB 面积的2倍,∴12OB ⋅|x C |=32×2,即12×3×|x C |=3, ∴点C 的横坐标为x =2或x =﹣2,把x =2代入y =﹣x +1得,y =﹣1;把x =﹣2代入y =﹣x +1得,y =3;∴点C 的坐标为(2,﹣1)或(﹣2,3),把(2,﹣1)代入y =kx ﹣3得,﹣1=2k ﹣3,解得k =1,把(﹣2,3)代入y =kx ﹣3得,3=﹣2k ﹣3,解得k =﹣3,∴k 的值为1或﹣3.25.(6分)2023年5月30日,神舟十六号载人飞船发射取得圆满成功.为普及航天知识,某中学举办了一次“航天知识竞赛”,共有1000名学生参加.为更好的了解本次比赛得分的分布情况,随机抽取了部分学生的比赛得分,进行收集、整理、描述和分析.下面给出了部分信息(数据分成5组:50≤x <60,60≤x <70,70≤x <80,80≤x <90,90≤x ≤100):a .学生比赛得分频数分布表:b .学生比赛得分频数分布直方图:c .学生比赛得分在80≤x <90这一组的是:80,81,83,82,86,87,85,81,89,88,85,86,80,83;根据以上信息,回答下列问题:(1)e = 0.28 ,f = 50 ;(2)请补全频数分布直方图;(3)若得分在85分及以上均为“优秀”,请估计参加这次比赛的1000名学生中得分优秀的人数. 解:(1)由题意得,f =5÷0.10=50,e =1.00﹣0.10﹣0.12﹣0.30﹣0.20=0.28,故答案为:0.28,50;(2)m =50×0.12=6,n =50×0.28=14,补全频数分布直方图如下:(3)1000×7+1050=340(名),答:估计参加这次比赛的1000名学生中得分优秀的人数大约为340名.26.在平面直角坐标系xOy 中,一次函数y =kx +2(k ≠0)的图象经过点(﹣1,0).(1)求k 的值;(2)当x >0时,对于x 的每一个值,一次函数y =﹣x +b 的值小于一次函数y =kx +2(k ≠0)的值,直接写出b 的取值范围.解:(1)∵一次函数y =kx +2(k ≠0)的图象经过点(﹣1,0).∴﹣k +2=0,解得k =2,∴一次函数解析式:y =2x +2;(2)解不等式﹣x +b <2x +2得x >b−23, 由题意得b−23≤0,即b ≤2.27.(7分)如图,在正方形ABCD 中,E 是边BC 上的一动点(不与点B ,C 重合),AF ⊥AE 于点A ,AF =AE ,连接BF ,DE .(1)求证:∠ABF =∠ADE ;(2)延长FB ,DE ,交于点G ,连接AG .①依题意补全图形;②用等式表示线段EG ,FG ,AG 之间的数量关系,并证明.(1)证明:∵四边形ABCD 为正方形,∴AB =AD ,∠BAC =90°,∴∠DAE +∠BAE =90°,又∵AF ⊥AE ,AF =AE ,∴∠EAF =90°,∴∠BAF +∠BAE =90°,∴∠BAF =∠DAE ,在△ABF 和△ADE 中,{AB =AD∠BAF =∠DAE AF =AE,∴△ABF ≌△ADE (SAS ),∴∠ABF =∠ADE ,(2)①解:依题意补全图形如下:②线段EG ,FG ,AG 之间的数量关系是:EG +FG =√2AG .证明如下:过点A 作AH ⊥AG 与GD 的延长线交于H ,∵∠BAC =90°,∴∠BAG +∠GAD =90°,∵AH ⊥AG ,则∠GAH =90°,∴∠GAD +∠DAH =90°,∴∠BAG =∠DAH ,∵∠ABG =180°﹣∠ABF ,∠ADH =180°﹣∠ADE ,由(1)知:∠ABF =∠ADE ,∴∠ABG =∠ADH ,在△ABG 和△ADH 中,{∠BAG =∠DAHAB =AD ∠ABG =∠ADH,∴△ABG ≌△ADH (ASA )∴AG =AH ,又∠GAH =90°,∴△AGH 为等腰直角三角形,由勾股定理得:GH =√AG 2+AH 2=√2AG ,即:EG +EH =√2AG ,∵∠EAF =∠GAH =90°,即:∠F AG +∠GAE =∠GAE +∠EAH =90°,∴∠F AG =∠EAH ,在△AFG 和△AEH 中,{AF =AE∠FAG =∠EAH AG =AH,∴△AFG ≌△AEH (SAS ),∴FG =EH ,∴EG +FG =√2AG .28.(6分)在平面直角坐标系xOy 中,给出如下定义:若在图形M 上存在一点P ,且点P 的纵坐标是横坐标的n (n 为正整数)倍,则称点P 为图形M 的“n 倍点”.例如,点(1,4)是直线y =﹣x +5的“4倍点”.(1)在点P 1(1,2),P 2(2,0),P 3(2,4),P 4(85,45)中, P 1(1,2) 是直线y =﹣2x +4的“2倍点”;(2)已知点A 的坐标为(m ,0),点B 的坐标为(m +2,0),以线段AB 为矩形的一边向上作矩形ABCD . ①若m =1,AD =4,判断是否存在矩形ABCD 的“3倍点”,若存在,求出矩形ABCD 的“3倍点”的坐标,若不存在,请说明理由;②若AD =nAB ,且存在矩形ABCD 的“n 倍点”,直接写出m 的取值范围.解:(1)∵P 2(2,0),P 4(85,45)不满足纵坐标是横坐标的2倍, ∴P 2(2,0),P 4(85,45)不是直线y =﹣2x +4的“2倍点”; 而P 3(2,4)不在直线y =﹣2x +4上,∴P 3(2,4)不是直线y =﹣2x +4的“2倍点”;根据“2倍点“定义,P 1(1,2)在直线y =﹣2x +4上,纵坐标是横坐标的2倍,∴P 1(1,2)是直线y =﹣2x +4的“2倍点”;故答案为:P 1(1,2);(2)①当m =1,AD =4时,存在矩形ABCD 的“3倍点”,理由如下:如图:此时A (1,0),B (3,0),C (3,4),D (1,4),若矩形ABCD 的“3倍点”在AD 上,则矩形ABCD 的“3倍点”为(1,3)满足条件; 若矩形ABCD 的“3倍点”在CD 上,则矩形ABCD 的“3倍点”为(43,4)满足条件; 根据定义,AB ,BC 上不存在矩形ABCD 的“3倍点”,∴矩形ABCD 的“3倍点”的坐标为(1,3)或(43,4); ②如图:∵A (m ,0),B (m +2,0),∴AB =2,∵AD =nAB ,∴AD =2n =BC ,∴A (m ,0),B (m +2,0),C (m +2,2n ),D (m ,2n ),若矩形ABCD 的“n 倍点”在AD 上,则矩形ABCD 的“n 倍点”坐标为(m ,mn ), ∴0≤mn ≤2n ,∵n 为正整数,∴0≤m ≤2;若矩形ABCD 的“n 倍点”在CD 上,则矩形ABCD 的“n 倍点”坐标为(2,2n ),∴m≤2≤m+2,解得:0≤m≤2;若矩形ABCD的“n倍点”在BC上,则矩形ABCD的“n倍点”坐标为(m+2,mn+2n),∴0≤mn+2n≤2n,即﹣2n≤mn≤0,∵n为正整数,∴﹣2≤m≤0;根据定义,AB上不可能存在矩形ABCD的“n倍点”,综上所述,存在矩形ABCD的“n倍点”,m的范围是0≤m≤2或﹣2≤m≤0.。
2024届北京市海淀中学八年级数学第二学期期末教学质量检测试题含解析

2024届北京市海淀中学八年级数学第二学期期末教学质量检测试题注意事项1.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置. 3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.4.作答选择题,必须用2B 铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效. 5.如需作图,须用2B 铅笔绘、写清楚,线条、符号等须加黑、加粗.一、选择题(每小题3分,共30分)1.若一次函数(2)y m x m =-+的图像经过第一,二,三象限,则m 的取值范围是( ) A .02m <<B .02m <≤C .2m >D .02m ≤<2.如图,在ABC ∆中,90C ∠=︒,8AC =,6BC =,点P 为斜边AB 上一动点,过点P 作PE AC ⊥于E ,PF BC ⊥于点F ,连结EF ,则线段EF 的最小值为( )A .24B .3.6C .4.8D .53.如图,在菱形ABCD 中,E ,F 分别是AB ,AC 的中点,若2EF =,6AC =,则菱形ABCD 的面积为( )A .67B .12C .15D .1054.如图,平行四边形ABCD 中,2,AD AB CE AB =⊥于点E ,CE 的垂真平分线MV 分别交AD 、BC 于M 、N ,交CE 于O ,连接CM 、EM ,下列结论:(1)AFM DCM ∠=∠(2)AM DM =(3)2BCD DCM ∠=∠(4)CDMBEON S S=四边形·其中正确的个数有( )A .1个B .2个C .3个D .4个5.下列式子是分式的是( )A .2019x B .2019xC .2019xπD .2019x y+ 6.已知一个多边形的内角和是它的外角和的两倍,那么它的边数为( ) A .8B .6C .5D .47.小明到单位附近的加油站加油,如图是小明所用的加油机上的数据显示牌,则数据中的变量有( )A .金额B .数量C .单价D .金额和数量8.如图,不等式组1010x x +⎧⎨-≤⎩的解集在数轴上表示正确的是( )A .B .C .D .9.计算的2(4)-的结果是( ) A .4- B .4±C .4D .1610.如果()22x -=2﹣x ,那么( ) A .x <2B .x≤2C .x >2D .x≥2二、填空题(每小题3分,共24分)11.若一直角三角形的两边长为4、5,则第三边的长为________ .12.如图,已知直线AB 、CD 相交于点O ,OE 平分BOC ∠,如果50BOE ∠=︒,那么AOC ∠=__________度.13.如图,正方形CDEF 内接于Rt ABC ,1AE =,2BE =,则正方形的面积是________.14.如图是由16个边长为1的正方形拼成的图案,任意连结这些小格点的三个顶点可得到一些三角形.与A ,B 点构成直角三角形ABC 的顶点C 的位置有___________个.15.已知点1,0A ,()4,0B ,()0,2C ,在平面内找一点M ,使得以M 、A 、B 、C 为顶点的四边形为平行四边形,则点M 的坐标为__________.16.如图,平行四边形ABCD 中,点E 为BC 边上一点, AE 和BD 交于点F ,已知ABF ∆的面积等于6, BEF ∆的面积等于4,则四边形CDFE 的面积等于__________.17.甲、乙两学生在军训打靶训练中,打靶的总次数相同,且所中环数的平均数也相同,但甲的成绩比乙的成绩稳定,那么两者的方差的大小关系是2S 甲___________ 2S 乙. (填“>”,“<”或“=”) 18.如图,AO=OC ,BD=16cm ,则当OB=___cm 时,四边形ABCD 是平行四边形.三、解答题(共66分)19.(10分)如图,在△ABC 中,D 是BC 边的中点,分别过B 、C 做射线AD 的垂线,垂足分别为E 、F ,连接BF 、CE .(1)求证:四边形BECF 是平行四边形;(2)我们知道S △ABD =S △ACD ,若AF =FD ,在不添加辅助线的条件下,直接写出与△ABD 、△ACD 面积相等的所有三角形.20.(6分)已知:关于的方程.(1)不解方程,判断方程的根的情况;(2)若为等腰三角形,腰,另外两条边是方程的 两个根,求此三角形的周长.21.(6分)如图,在菱形ABCD 中,AB=2,∠DAB=60°,点E 是AD 边的中点,点M 是AB 边上一动点(不与点A 重合),延长ME 交射线CD 于点N ,连接MD ,AN.(1)求证:四边形AMDN 是平行四边形;(2)填空:①当AM 的值为 时,四边形AMDN 是矩形;②当AM 的值为 时,四边形AMDN 是菱形.22.(8分)如图,在平面直角坐标系中,直线y =12x +2与x 轴、y 轴分别交于A 、B 两点,以A B 为边在第二象限内作正方形ABCD .(1)求点A 、B 的坐标,并求边AB 的长; (2)求点D 的坐标;(3)在x 轴上找一点M ,使△MDB 的周长最小,请求出M 点的坐标.23.(8分)如图,在ABC 中,点E ,F 分别为边AB ,AC 的中点,延长EF 到点G 使FG EF . 求证:四边形EGCB 是平行四边形.24.(8分)(1)探究新知:如图1,已知ABC △与ABD △的面积相等,试判断AB 与CD 的位置关系,并说明理由.(2)结论应用:①如图2,点M ,N 在反比例函数(0)k y k x=>的图像上,过点M 作ME y ⊥轴,过点N 作NF x ⊥轴,垂足分别为E ,F ,连接EF .试证明:MN EF ∥.②若①中的其他条件不变,只改变点M ,N 的位置如图3所示,请画出图形,判断MN 与EF 的位置关系并说明理由.25.(10分)作图题:在图(1)(2)所示抛物线中,抛物线与x 轴交于A 、B ,与y 轴交于C ,点D 是抛物线的顶点,过D 平行于y 轴的直线是它的对称轴,点P 在对称轴上运动.仅用无刻度的直尺画线的方法,按要求完成下列作图:图① 图②+最小;(1)在图①中作出点P,使线段PA PC-最大.(2)在图②中作出点P,使线段PB PC26.(10分)一分钟投篮测试规定,得6分以上为合格,得9分以上为优秀,甲、乙两组同学的一次测试成绩如下:成绩(分) 4 5 6 7 8 9甲组(人) 1 2 5 2 1 4乙组(人) 1 1 4 5 2 2(1)请你根据上述统计数据,把下面的图和表补充完整;一分钟投篮成绩统计分析表:统计量平均分方差中位数合格率优秀率甲组 2.56 6 80.0% 26.7%乙组 6.8 1.76 86.7% 13.3%(2)下面是小明和小聪的一段对话,请你根据(1)中的表,写出两条支持小聪的观点的理由.参考答案一、选择题(每小题3分,共30分) 1、B 【解题分析】已知一次函数(2)y m x m =-+的图像经过第一,二,三象限,根据一次函数的性质可得不等式组20m m ->⎧⎨>⎩,解不等式组即可求得m 的取值范围. 【题目详解】∵一次函数(2)y m x m =-+的图像经过第一,二,三象限,∴200m m ->⎧⎨>⎩,解得02m << . 故选B. 【题目点拨】本题考查了一次函数的性质,利用一次函数的性质得到不等式组200m m ->⎧⎨>⎩是解决问题的关键.2、C 【解题分析】连接PC ,先证明四边形ECFP 是矩形,从而得EF=PC ,当CP ⊥AB 时,PC 最小,利用三角形面积解答即可. 【题目详解】 连接PC ,∵PE ⊥AC ,PF ⊥BC , ∴∠PEC=∠PFC=∠C=90°,∴四边形ECFP是矩形,∴EF=PC,∴当PC最小时,EF也最小,即当CP⊥AB时,PC最小,∵AC=1,BC=6,∴AB=10,∴PC的最小值为:AC BCAB⋅=4.1.∴线段EF长的最小值为4.1.故选C.【题目点拨】本题主要考查的是矩形的判定与性质,关键是根据矩形的性质和三角形的面积公式解答.3、A【解题分析】根据EF是△ABC的中位线,由三角形中位线定理求出BC的长.连接BD,然后根据菱形的对角线互相垂直的性质用勾股定理求出BD的长,最后用菱形的面积公式求解.【题目详解】解:连接BD∵E、F分别是AB,AC边上的中点,∴EF是△ABC的中位线,∴BC=2EF=4,ABCD是菱形AC与BD互相垂直平分,BD经过F点,2222437BF BC CF=-=-=7BD=则S菱形ABCD=1162767 22AC BD=⋅=⨯⨯=故选:A.【题目点拨】本题考查了三角形的中位线定理和菱形的性质,理解中位线定理BC、用勾股定理求出BF是关键.4、C【解题分析】①由平行四边形性质可得AB∥CD,由线段垂直平分线性质可得ME=MC,再根据等角的余角相等可得①正确;②构造△AME≌△DMG(ASA),即可证明②正确;③利用平行四边形性质、线段垂直平分线性质和AD=2AB可得四边形CDMN是菱形,依据菱形性质即可证明③正确;④S△CDM=12S菱形CDMN,S四边形BEON<34S菱形CDMN,④不一定成立;【题目详解】解:延长EM交CD的延长线于G,如图,∵ABCD是平行四边形,∴AB∥CD∴∠AEM=∠G∵CE⊥AB∴CE⊥CD∵MN垂直平分CE,∴ME=MC∴∠MEC=∠MCE∵∠MEC+∠G=90°,∠MCE+∠DCM=90°∴∠DCM=∠G∴∠AEM=∠DCM故①正确;∵∠DCM=∠G∴MC=MG∴ME=MG∵∠AME=∠DMG∴△AME≌△DMG(ASA)∴AM=DM故②正确;∵ABCD是平行四边形,∴AB∥CD,AB=CD,AD∥BC,AD=BC∵CE⊥AB,MN⊥CE∴AB∥MN∥CD∴四边形ABNM、四边形CDMN均为平行四边形∴MN=AB∵AM=MD=12AD,AD=2AB∴MD=CD=MN=NC∴四边形CDMN是菱形∴∠BCD=2∠DCM,故③正确;设菱形ABNM的高为h,则S△CDM=12S菱形CDMN,S四边形BEON=12(BE+ON)×h=32ON×h∵OM=12(AE+CD)∴12CD<OM<AB∴ON<12CD∴S四边形BEON<34CD×h=34S菱形CDMN,故④不一定成立;故选C.【题目点拨】本题主要考查平行四边形的性质,熟练掌握平行四边形的性质是解答本题的关键.5、B【解题分析】根据分母中含有字母的式子是分式,可得答案.【题目详解】解:2019x是分式,故选:B.【题目点拨】本题考查了分式的定义,分母中含有字母的式子是分式,否则是整式.6、B【解题分析】根据多边形的外角和是360°,以及多边形的内角和定理即可求解.【题目详解】解:设多边形的边数是n,则(n−2)•180=2×360,解得:n=6,故选:B.【题目点拨】本题考查了多边形的内角和定理以及外角和定理,正确理解定理是关键.7、D【解题分析】根据常量与变量的定义即可判断.【题目详解】常量是固定不变的量,变量是变化的量,单价是不变的量,而金额是随着数量的变化而变化,故选:D.【题目点拨】本题考查常量与变量,解题的关键是正确理解常量与变量,本题属于基础题型.8、B【解题分析】首先分别解出两个不等式,再确定不等式组的解集,然后在数轴上表示即可.【题目详解】解:解第一个不等式得:x>-1;解第二个不等式得:x≤1,在数轴上表示,故选B.【题目点拨】此题主要考查了解一元一次不等式组,以及在数轴上表示解集,把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时 “≥” ,“≤” 要用实心圆点表示; “ <“ >” 要用空心圆点表示.9、C【解题分析】根据算术平方根和平方根进行计算即可【题目详解】=4故选:C【题目点拨】此题考查算术平方根和平方根,掌握运算法则是解题关键10、B【解题分析】a =,可知x-2≤0,即x≤2.故选B考点:二次根式的性质二、填空题(每小题3分,共24分)11 或1【解题分析】解:当4和5=;当53= ;1.12、1【解题分析】先根据角平分线的定义,求出∠BOC 的度数,再根据邻补角的和等于11°求解即可.【题目详解】解:∵OE 平分BOC ∠,50BOE ∠=︒,∴2250100∠=∠=⨯︒=︒BOC BOE ,∴180********∠=︒-∠=︒-︒=︒AOC BOC ,故答案为:1.【题目点拨】本题考查了角平分线的定义以及邻补角的性质,属于基础题.13、0.8【解题分析】根据题意分析可得△ADE ∽△EFB ,进而可得2DE=BF ,2AD=EF=DE ,由勾股定理得,DE 2+AD 2=AE 2,可解得DE ,正方形的面积等于DE 的平方问题得解.【题目详解】∵根据题意,易得△ADE ∽△EFB ,∴BE:AE=BF:DE=EF:AD=2:1,∴2DE=BF ,2AD=EF=DE ,由勾股定理得,DE 2+AD 2=AE 2,解得:DE=EF=5,故正方形的面积是25⎛ ⎝⎭=45, 故答案为:0.8【题目点拨】本题考查相似三角形,熟练掌握相似三角形的判定及基本性质是解题关键.14、1【解题分析】根据题意画出图形,根据勾股定理的逆定理进行判断即可.【题目详解】如图所示:当∠C 为直角顶点时,有C 1,C 2两点;当∠A 为直角顶点时,有C 3一点;当∠B 为直角顶点时,有C 4,C 1两点,综上所述,共有1个点,故答案为1.【题目点拨】本题考查的是勾股定理的逆定理,根据题意画出图形,利用数形结合求解是解答此题的关键.15、()5,2-,()3,2,()3,2-【解题分析】根据题意画出图形,由平行四边形的性质两组对边分别平行且相等来确定点M 的坐标.【题目详解】解:①当如图1时,∵C (0,2),A (1,0),B (4,0),∴AB=3,∵四边形ABMC 是平行四边形,∴M (3,2);②当如图2所示时,同①可知,M (-3,2);③当如图3所示时,过点M 作MD ⊥x 轴,∵四边形ACBM是平行四边形,∴BD=OA=1,MD=OC=2,∴OD=4+1=5,∴M(5,-2);综上所述,点M坐标为(3,2)、(-3,2)、(5,-2).【题目点拨】本题考查了平行四边形的性质和判定,利用分类讨论思想是本题的关键.16、11【解题分析】由△ABF的面积等于6,△BEF的面积等于4,可得EF:AF=2:3,进而证明△ADF∽△EBF,根据相似三角形的性质可得249EBFADFS EFS AF⎛⎫==⎪⎝⎭,继而求出S△ABD=15,再证明△BCD≌△DAB,从而得S△BCD=S△DAB=15,进而利用S四边形CDFE=S△BCD-S△BEF即可求得答案.【题目详解】∵△ABF的面积等于6,△BEF的面积等于4,∴EF:AF=4:6=2:3,∵四边形ABCD是平行四边形,∴AD//BC,∴△ADF∽△EBF,∴249 EBFADFS EFS AF⎛⎫==⎪⎝⎭,∵S△BEF=4,∴S△ADF=9,∴S△ABD=S△ABF+S△AFD=6+9=15,∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,∵BD是公共边,∴△BCD≌△DAB,∴S△BCD=S△DAB=15,∴S四边形CDFE=S△BCD-S△BEF=15-4=11,故答案为11.【题目点拨】本题考查了平行四边形的性质,相似三角形的判定与性质等,熟练掌握并灵活运用相关知识是解题的关键.17、<【解题分析】根据方差的意义可作出判断,方差是用来衡量一组数据波动大小的量,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.【题目详解】解:∵甲的成绩比乙的成绩稳定,∴S2甲<S2乙,故答案为:<.【题目点拨】本题考查方差的意义,方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.18、1【解题分析】根据对角线互相平分的四边形是平行四边形可得OB=1cm时,四边形ABCD是平行四边形.【题目详解】当OB=1cm时,四边形ABCD是平行四边形,∵BD=16cm,OB=1cm,∴BO=DO,又∵AO=OC,∴四边形ABCD是平行四边形,故答案为1.【题目点拨】本题考查了平行四边形的判定,熟练掌握平行四边形的判定方法是解题的关键.三、解答题(共66分)19、(1)详见解析;(2)与△ABD和△ACD面积相等的三角形有△CEF、△BEF、△BEC、△BFC.【解题分析】(1)根据全等三角形的判定和性质得出ED=FD,进而利用平行四边形的判定证明即可;(2)利用三角形的面积解答即可.【题目详解】(1)证明:在△ABF与△DEC中∵D是BC中点,∴BD=CD∵BE⊥AE,CF⊥AE∴∠BED=∠CFD=90︒,在△ABF与△DEC中BED CFDBDE CDF BD CD∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BED≌△CFD(AAS),∴ED=FD,∵BD=CD,∴四边形BFEC是平行四边形;(2)与△ABD和△ACD面积相等的三角形有△CEF、△BEF、△BEC、△BFC.理由:∵四边形BECF是平行四边形,∴S△BDF=S△BDE=S△CDE=S△CDF,∵AF=DF,∴S△ABF=S△BDF,S△ACF=S△CDF∴S△BDF=S△BDE=S△CDE=S△CDF=S△ABF=S△ACF,∴S△ABD=S△ACD=S△CEF=S△BEF=S△BEC=S△BFC.【题目点拨】本题考查了全等三角形的判定与性质以及平行四边形形的判定,关键是根据全等三角形的判定和性质得出ED=FD.20、(1)无论为何值,该方程总有两个不相等的实数根;(2)此三角形的周长为或.【解题分析】(1)根据判别式即可求出答案.(2)由题意可知:该方程的其中一根为5,从而可求出m的值,最后根据m的值即可求出三角形的周长;【题目详解】解:(1),无论为何值,该方程总有两个不相等的实数根(2),为等腰三角形,另外两条边是方程的根,是方程的根.将代入原方程,得:,解得:.当时,原方程为,解得:,能够组成三角形,该三角形的周长为;当时,原方程为,解得:,,能够组成三角形,该三角形的周长为.综上所述:此三角形的周长为或.【题目点拨】本题考查一元二次方程,等腰三角形的定义,三角形三边的关系,解题的关键是熟练运用根与系数的关系,本题属于中等题型.21、(1)见解析(2)①1;②2【解题分析】试题分析:(1)利用菱形的性质和已知条件可证明四边形AMDN的对边平行且相等即可;(2)①有(1)可知四边形AMDN是平行四边形,利用有一个角为直角的平行四边形为矩形即∠DMA=90°,所以AM=12AD=1时即可;②当平行四边形AMND的邻边AM=DM时,四边形为菱形,利用已知条件再证明三角形AMD是等边三角形即可.试题解析:(1)证明:∵四边形ABCD是菱形,∴ND∥AM,∴∠NDE=∠MAE,∠DNE=∠AME,又∵点E是AD边的中点,∴DE=AE,∴△NDE≌△MAE,∴ND=MA,∴四边形AMDN是平行四边形;(2)解:①当AM的值为1时,四边形AMDN是矩形.理由如下:∵AM=1=12AD , ∴∠ADM=30°∵∠DAM=60°,∴∠AMD=90°,∴平行四边形AMDN 是矩形;②当AM 的值为2时,四边形AMDN 是菱形.理由如下:∵AM=2,∴AM=AD=2,∴△AMD 是等边三角形,∴AM=DM ,∴平行四边形AMDN 是菱形,考点:1.菱形的判定与性质;2.平行四边形的判定;3.矩形的判定.22、(1)(2)D (-6,4);(3)M (-2,0)【解题分析】(1)由题意将y=0和x=0分别代入即可求出点A 、B 的坐标,进而求出边AB 的长;(2)根据题意作DH ⊥x 轴于H ,并利用全等三角形的判定与性质求得△DAH ≌△ABO ,进而得出DH 和OH 的值即可;(3)根据题意作D 点关于x 轴的对称点为E ,并连接BE 交x 轴于点M ,△MDB 的周长为DB DM MB ++,有DB 为定值,只需满足DM MB +的值最小即可,将=DM EM 进行转化,根据两点间线段最短即可知道此时的M 即为所求,解出直线BE 的解析式即可得到M 点的坐标.【题目详解】解:(1)由题意直线y=12x+2与x 轴、y 轴分别交于A 、B 两点,将y=0和x=0分别代入即可求出点A 、B 的坐标为:A (-4,0),B (0,2),所以AB (2)作DH ⊥x 轴于H ,由于∠DHA =∠BAD =90°,∠DAH +∠BAO=90°,∠BAO+∠ABO =90°,∴∠DAH =∠ABO ,又DA =AB ,∴△DAH ≌△ABO (AAS ),则DH =OA =4,AH =OB =2,OH=4+2=6,∵点D 的坐标在第二象限,∴D (-6,4).(3)作D 点关于x 轴的对称点为E ,并连接BE 交x 轴于点M ,根据轴对称的性质可知=DM EM ,E (-6,-4),△MDB 的周长为:DB DM MB ++,有DB 为定值,只需满足DM MB +的值最小即可, 将=DM EM 进行转化,根据两点间线段最短即可知道此时的M 即为所求, 利用待定系数法求得直线BE 的解析式为2y x =+,直线2y x =+与x 轴的交点坐标为(-2,0),故M (-2,0).【题目点拨】本题考查一次函数与正方形,涉及的知识有待定系数法求一次函数解析式,坐标与图形性质,勾股定理,全等三角形的判定与性质,正方形的性质,对称性质,以及一次函数与坐标轴的交点,熟练掌握相关性质及定理是解答本题的关键.23、证明见解析.【解题分析】 根据中位线的性质得到12EF BC =∥,再得到EG BC =∥,故可证明. 【题目详解】解:∵E ,F 分别为AB ,AC 的中点,∴EF 是△ABC 的中位线,∴12EF BC =∥. ∵EF FG =,∴EG BC =.∴EG BC =∥∴四边形EGCB 是平行四边形.【题目点拨】此题主要考查平行四边形的判定,解题的关键是熟知三角形的中位线定理及平行四边形的判定方法.24、(1)AB CD ∥,理由见解析;(2)①见解析;②MN EF ∥,理由见解析.【解题分析】(1)分别过点C ,D ,作CG ⊥AB ,DH ⊥AB ,垂足为G ,H ,则∠CGA=∠DHB=90°,根据△ABC 与△ABD 的面积相等,证明AB 与CD 的位置关系;(2)连结MF ,NE ,设点M 的坐标为(x 1,y 1),点N 的坐标为(x 2,y 2),进一步证明S △EFM =S △EFN ,结合(1)的结论即可得到MN ∥EF ;(3)连接FM 、EN 、MN ,结合(2)的结论证明出MN ∥EF ,GH ∥MN ,于是证明出EF ∥GH .【题目详解】(1)如图1,分别过点C 、D 作CG AB ⊥、DH AB ⊥,垂足分别为G 、H ,则90CGA DHE ∠=∠=︒,∴CG DH ,∵ABC ABD S S =△△且12ABC S AB CG =⋅△, 12ABD S AB DH =⋅△, ∴CG DH =,∴四边形CGHD 为平行四边形,∴AB CD ∥;(2)①如图2,连接MF ,NE ,设点M 的坐标为()11,x y ,点N 的坐标为()22,x y ,∵点M ,N 在反比例函数的图像上,∴11x y k =,22x y k =.∵ME y ⊥轴,NF x ⊥轴,且点M ,N 在第一象限, ∴1OE y =,1ME x =,2NF y =,2OF x =.∴ 11111||222EFM S x y k k ===△,()()22221111||2222EFN S x y x y k k =--===△, ∴EFM EFN S S =△△,从而,由(1)中的结论可知:MN EF ∥;②如图MN EF ∥,理由:连接MF ,NE ,设点M 的坐标为()11,x y ,点N 的坐标为()22,x y ,由(2)①同理可得:11111||222EFM S x y k k ===△,()()22221111||2222EFN S x y x y k k =--===△, ∴EFM EFN S S =△△,从而,由(1)中的结论可知:MN EF ∥.【题目点拨】本题主要考查反比例函数的综合题,解答本题的关键是根据同底等高的两个三角形面积相等进行解答问题,此题难度不是很大,但是三问之间都有一定的联系.25、(1)见解析;(2)见解析【解题分析】(1)作A 关于对称轴的对称点B,连接BC ,与对称轴的交点即为P 点;(2)由于点A 和点B 关于对称轴对称,则PA=PB,那么只要P 、A 、C 三点共线即可,即连接AC 并延长与对称轴的交点,就是所求的P 点.【题目详解】解:如图:(1)作A 关于对称轴的对称点B,连接BC ,与对称轴的交点即为P 点;点P即为所求作(2)如图:延长AC与对称轴的交点即为P点.点P即为所求作【题目点拨】本题在函数图像中考查了两点之间直线最短和轴对称方面的知识,考查方式新颖,灵活运用所学知识成为解答本题的关键.26、 (1)见解析;(2)乙组成绩好于甲组,理由见解析【解题分析】(1)根据测试成绩表求出乙组成绩为1分和9分的人数,补全统计图,再根据平均数的计算方法和中位数的定义求出平均数和中位数,即可补全分析表;(2)根据平均分、方差、中位数、合格率的意义即可写出支持小聪的观点的理由.【题目详解】(1)根据测试成绩表即可补全统计图(如图):补全分析表:甲组平均分(4×1+5×2+6×5+1×2+8×1+9×4)÷15=6.8,乙组中位数是第8个数,是1.统计量平均分方差中位数合格率优秀率甲组 6.8 2.56 6 80.0% 26.1%乙组 6.8 1.16 1 86.1% 13.3%(2)甲乙两组平均数一样,乙组的方差低于甲组,说明乙组成绩比甲组稳定,又乙组合格率比甲组高,所以乙组成绩好于甲组.【题目点拨】此题考查频数(率)分布直方图,方差,中位数,加权平均数,解题关键在于掌握中位数和方差的运算公式.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018-2019年初二期末分类—几何证明1、【海淀】在Rt△ABC 中,∠BAC = 90︒,点O 是△ABC 所在平面内一点,连接OA,延长OA 到点E,使得AE=OA,连接OC,过点B 作BD 与OC 平行,并使∠DBC=∠OCB,且BD=OC,连接DE.(1)如图一,当点O 在Rt△ABC 内部时.① 按题意补全图形;②猜想DE 与BC 的数量关系,并证明.图一(2)若A B = AC(如图二),且∠OCB = 30︒, ∠OBC = 15︒,求∠AED的大小.图二备用图备用图26.四边形ABCD是正方形,AC是对角线,E是平面内一点,且CE<BC.过点C作FC⊥CE,且CF=CE.连接AE,AF.M是AF的中点,作射线DM交AE于点N.(1)如图1,若点E,F分别在BC,CD边上.求证:①∠BAE=∠DAF;②DN⊥AE;(2)如图2,若点E在四边形ABCD内,点F在直线BC的上方.求∠EAC与∠ADN的和的度数.图1 图227.在正方形ABCD中,点E是射线AC上一点,点F是正方形ABCD外角平分线CM上一点,且CF=AE,连接BE,EF.(1)如图1,当E是线段AC的中点时,直接写出BE与EF的数量关系;(2)当点E不是线段AC的中点,其它条件不变时,请你在图2中补全图形,判断(1)中的结论是否成立,并证明你的结论;的度数. (直接写出结果即可)(3)当点B,E,F在一条直线上时,求CBE27.已知,点E在正方形ABCD的AB边上(不与点A,B重合),BD是对角线,延长AB 到点F,使BF=AE,过点E作BD的垂线,垂足为M,连接AM,CF.(1)根据题意补全图形,并证明MB=ME;(2)①用等式表示线段AM与CF的数量关系,并证明;②用等式表示线段AM,BM,DM之间的数量关系(直接写出即可).C27.正方形ABCD 中,点P 是直线AC 上的一个动点,连接BP ,将线段BP 绕点B 顺时针旋转90°得到线段BE ,连接CE .(1)如图1,若点P 在线段AC 上, ①直接写出ACE ∠的度数为 °; ②求证:2222PA PC PB +=;(2)如图2,若点P 在CA 的延长线上,1PA =,PB = ①依题意补全图2;②直接写出线段AC 的长度为 .图1 图2CE正方形ABCD 中,点M 是直线BC 上的一个动点(不与点B 、C 重合),作射线DM ,过点B 作BN ⊥DM 于点N ,连接CN 。
(1)如图1,当点M 在BC 上时,如果∠CDM =25°,那么∠MBN 的度数是_________; (2)如图2,当点M 在BC 的延长线上时,①依题意补全图2;②用等式表示线段NB ,NC 和ND图1 图2NMABCD27.如图,在正方形ABCD中,点E是BC边所在直线上一动点(不与点B、C重合),过点B 作BF⊥DE,交射线DE于点F,连接CF.(1)如图1,当点E在线段BC上时,∠BDF=α.①按要求补全图形;②∠EBF=______________(用含α的式子表示);③判断线段BF,CF,DF之间的数量关系,并证明.(2)当点E在直线BC上时,直接写出线段BF,CF,DF之间的数量关系,不需证明.图1备用图27. 我们规定:一组邻边相等且对角互补的四边形叫作“完美四边形”.(1)在①平行四边形,②菱形,③矩形,④正方形中,一定为“完美”四边形的是(请填序号);(2)“完美”四边形ABCD中,AB=AD,∠B+∠D=180°,连接AC.①如图1,求证:AC平分∠BCD;小明通过观察、实验,提出以下两种想法,证明AC平分∠BCD:想法一:通过∠B+∠D=180°,可延长CB到E,使BE=CD,通过证明△AEB≌△ACD,从而可证AC平分∠BCD;想法二:通过AB=AD,可将△ACD绕点A顺时针旋转,使AD与AB重合,得到△AEB,可证C,B,E三点在条直线上,从而可证AC平分∠BCD.请你参考上面的想法,帮助小明证明AC平分∠BCD;②如图2,当∠BAD=90°,用等式表示线段AC,BC,CD之间的数量关系,并证明.27. 在矩形ABCD 中,AB =3,AD =2,点E 是射线DA 上一点,连接EB ,以点E 为圆心EB 长为半径画弧,交射线CB 于点F ,作射线FE 与CD 延长线交于点G . (1)如图1,若DE =5,则∠DEG = °;(2)若∠BEF =60°,请在图2中补全图形,并求EG 的长;(3)若以E ,F ,B ,D 为顶点的四边形是平行四边形,此时EG 的长为 .C B A D图1图2备用图AB DEFGD A B C27.如图,E为正方形ABCD内一点,点F在CD边上,且∠BEF=90°,EF=2BE.点G为EF的中点,点H为DG的中点,连接EH并延长到点P,使得PH=EH,连接DP.(1)依题意补全图形;(2)求证:DP=BE;(3)连接EC,CP,猜想线段EC和CP的数量关系并证明.27.已知:在正方形ABCD中,点H在对角线BD上运动(不与B,D重合)连接AH,过H点作HP⊥AH于H交直线CD于点P,作HQ⊥BD于H交直线CD于点Q.(1)当点H在对角线BD上运动到图1位置时,则CQ与PD的数量关系是__________.(2)当H点运动到图2所示位置时①依据题意补全图形.②上述结论还成立吗?若成立,请证明.若不成立,请说明理由.(3)若正方形边长为3,∠PHD=30°,直接写出PC长.图1图227.如图,四边形ABCD 是平行四边形,A , B 是直线l 上的两点,点B 关于AD 的对称点为M ,连接CM 交AD 于F 点. (1)若90ABC ∠=︒,如图,①依题意补全图形;②判断MF 与FC 的数量关系是 ;(2)如图,当135ABC ∠=︒时,AM ,CD 的延长线相交于点E ,取M E 的中点H ,连结HF ,用等式表示线段CE 与AF 的数量关系,并证明.27.正方形ABCD中,M为边CB延长线上一点,过点A作直线AM,设∠BAM=α,点B关于直线AM的对称点为点E,连接AE、DE,DE交AM于点N.(1)依题意补全图形;当α=30°时,直接写出∠AND的度数;(2)当α发生变化时,∠AND的度数是否发生变化?说明理由;(3)探究线段AN,EN,DN的数量关系,并证明.备用图27.如图,正方形ABCD中,点P在BC边上,连接AP,将线段PA绕点P顺时针旋转90°得到线段PE,过点E作EF⊥BC,分别交直线BC,AC于点F,G.(1) 依题意补全图形;(2) 求证:BP=EF;(3) 连接PG,CE,用等式表示线段PG,CE,CD之间的数量关系,并证明.P15、【清华附中】24.如图,四边形ABCD 是正方形,ABE ∆是等边三角形,M 为对角线BD (不含B 点)上任意一点,将BM 绕点B 逆时针旋转60°得到BN ,连接EN 、AM 、CM . (1)证明:EBN ABM ∆≅∆(2)当M 点在何处时,CM BM AM ++的值最小,并说明理由;(3)当CM BM AM ++的最小值为13+时,则正方形的边长为 .16、【房山】27. 如图,在正方形ABCD中,P为边AD上的一动点(不与点A、D重合),连接BP,点A 关于直线BP的对称点为E,连接AE,CE.(1)依题意补全图形,(2)求∠AEC的大小;(3)过点B作BF⊥CE于F,用等式表示线段AE、CF和BF的数量关系,并证明.B【答案】1、【海淀】2、【西城】26.(1)证明:①在正方形ABCD中,∴∠ABE=∠ADF=90°,AB = BC= CD = AD.∵CE = CF,∴BE =DF.∴△ABE ≌△ADF.∴∠BAE=∠DAF.·························2分②∵M是AF的中点,∴∠DAF=∠ADN.由①可知∠BAE=∠DAF.∴∠BAE=∠ADN.∵∠BAE +∠EAD =90°,∴∠AND +∠EAD =90°.∴AN⊥DN.································································· 4分(2)解:延长AD至H,使得DH=AD,连接FH,CH.又∵ CE =CF , ∴ △ACE ≌△HCF . ∴ ∠EAC =∠FHC .∵ M 是AF 的中点,D 是AH 的中点, ∴ DM ∥FH . ∴ ∠ADN =∠AHF .∴ ∠ADN +∠EAC =∠AHF +∠FHC =∠AHC =45°. ······················ 8分3、【东城】 27.解:(1)EF =. …………………………………………1分(2)补全图形如图所示.(1)中的结论仍然成立,即EF =.证明:连接ED ,DF由正方形的对称性可知,BE =DE ,∠CBE =∠CDE . ∵ 正方形ABCD , ∴ AB =CD ,∠BAC =45°.∵ 点F 是正方形ABCD 外角平分线CM 上一点, ∴ ∠DCF =45°. ∴ ∠BAC =∠DCF . 由∵ CF =AE , ∴ △ABE ≌△CDF . ∴ BE =DF ,∠ABE =∠CDF . ∴ DE =DF .又∵ ∠ABE +∠CBE =90°, ∴ ∠CDF +∠CDE =90°. 即 ∠EDF =90°.∴ △EDF 是等腰直角三角形. ∴ EF=.∴ EF =. …………………………………………5分(3) 当点B ,E ,F 在一条直线上时,CBE ∠=22.5°. …………………………………7分4、【朝阳】27.(1)补全的图形,如图所示.…..……………………………….……….1分证明:∵四边形ABCD 是正方形, ∴1452ABD ABC ∠=∠=︒. ∵EM ⊥BD ,∴45ABD MEB ∠=∠=︒.∴MB =ME .….……………………………….……..………………………..……….…2分 (2FC =.…………………………….……..………………………..……….…3分 证明:如图,连接MC ,MF , ∵四边形ABCD 是正方形,∴AB =BC ,45ABD DBC ∠=∠=︒. ∵45ABD MEB ∠=∠=︒,, ∴AEM FBM ∠=∠.∵AE =BF , ∴△AEM ≌△FBM .∴AM =MF . ……………………….……..………………………..……….…4分 ∵AE =BF , ∴EF =BC =AB . ∴△MEF ≌△MBC .∴∠EMF =∠BMC ,FM =MC . ∴∠FMC =90°.AFA∴△FCM 是等腰直角三角形. …….……..…………..………..……….…5分FC =.②2222AM BM DM =+.……………….……..……………………………….…7分 5、【石景山】27.(1)①90. ………… 1分 ②证明:连接PE ,如图1. ∵四边形ABCD 是正方形,∴CB AB =,1245∠=∠=°,3490∠+∠=°. ∵将线段BP 绕点B 顺时针旋转90°得到线段BE , ∴BE BP =,5490∠+∠=°.∴PE =,53∠=∠.∴CBE △≌ABP △(SAS ). ………………………… 3分 ∴EC PA =,6145∠=∠=°. ∴2690PCE ∠=∠+∠=°.在Rt PCE △中,由勾股定理,得222EC PC PE +=. ……… 4分 ∵EC PA =,PE =,∴2222PA PC PB +=. ………………………… 5分(2)①补全的图形如图2所示. ………………………… 6分 ②4. ………………………… 7分654321EPDCB A 图1 图26、【丰台】27. 解:(1)25°;…………………………………1分(2)①正确补全图形;……………………2分②猜想: NC +ND =NB . ……………3分 证明:在DM 延长线上取一点E ,使DE =BN . ∵BN ⊥DM , ∴∠BND =90°.∵四边形ABCD 是正方形, ∴CD =CB ,∠BND =∠BCD . ∵∠1=∠2, ∴∠3 =∠4.∴△CDE ≌ △CBN . …………………………………………………………5分 ∴CE =CN ,∠DCE =∠BCN . ∴∠NCE =∠BCD =90°. ∵在Rt △NCP 中,CN =CE , ∴NE =2NC . ∵NE +ND =DE ,∴2NC +ND =NB . ………………………………………………………6分 证法不唯一,其他证法请参照示例相应步骤给分.7、【门头沟】27.(1)①略;…………………………………………………………1分②45°-α;…………………………………………………………………………2分③线段BF ,CF ,DF 之间的数量关系是DF BF =+. ……………3分证明如下:在DF 上截取DM =BF ,连接CM .∵ 正方形ABCD ,∴ BC =CD ,∠BDC =∠DBC =45°,∠BCD =90° ∴∠CDM =∠CBF =45°-α,∴△CDM ≌△CBF (SAS ). ……………………………………4分 ∴ DM =BF , CM =CF ,∠DCM =∠BCF .∴ ∠MCF =∠BCF +∠MCE =∠DCM +∠MCE=∠BCD =90°∴ MF .…………………5分∴.DF DM MF BF =+=(2)DF BF =,BF DF =,BF DF +=.………………7分8、【平谷】27.(1)○4 (1)(2)解:○1想法一:延长CB 使BE=CD ,连接AE ∵∠ADC +∠ABC =180°,∠ABE +∠ABC =180°,∴∠ADC =∠ABE . ········································································2 ∵AD=AB , ∴△ADC ≌△ABE . ∴∠ACD =∠AEB ;AC=AE . ·····················································································3 ∴∠ACB =∠AEB . ∴∠ACD =∠ACB .即AC 平分∠BCD (4)想法二:将△ACD 绕点A 顺时针旋转,使AD 边与AB 边重合,得到△ABE ,∴△ADC ≌△ABE . ∴∠ADC =∠ABE ; ∠ACD =∠AEB;AC=AE . ··················································································2 ∵∠ADC +∠ABC =180°,∴∠ABE +∠ABC =180°.∴点C ,B ,E 在一条直线上. ······························································3 ∵AC=AE , ∴∠ACB =∠AEB . ∴∠ACD =∠ACB .即AC 平分∠BCD . (4)○2 延长CB 使BE=CD ,连接AE , 由 ○1得△ACE 为等腰三角形. ∵∠BAD =90°,∴∠EAC =90°. ..........................................................................5 ∴222CE AC =. . (6)∴CE =.∴BC +CDAC . (7)9、【昌平】27. 解:(1)45°. ……………………1分(2)如图所示. ………………………………2分∵ 四边形ABCD 是矩形,∴∠1=∠2=∠3=∠ABF =∠C =90°.∵∠4=60°, EF =EB ,∴∠F =∠5=60°.∴∠6=∠G = 30°. ………………3分 ∴AE =12BE .∵AB =3,∴根据勾股定理可得:AE. …………………4分 ∵AD =2,∴DE =2. ……………………5分 ∴EG =4+ ……………………6分 (3)EG= ………………………7分654321GED CA27.解:(1)依题意补全图形如下:……………………………………………1分(2)∵点H为线段DG的中点,∴DH=GH.在ΔPDH和ΔEGH中,∵EH=PH,∠EHG=∠PHD,∴ΔPDH≌ΔEGH(SAS).∴DP=EG.∵G为EF的中点,∴EF=2EG.∵EF=2EB,∴BE=EG=DP.……………………………………………………4分(3)猜想:EC=CP.…………………………………………………………5分由(2)可知ΔPDH≌ΔEGH.∴∠HEG=∠HPD.∴DP∥EF.∴∠PDC=∠DFE.又∵∠BEF=∠BCD=90°,∴∠EBC+∠EFC=180°.又∵∠DFE+∠EFC=180°,∴∠EBC=∠DFE=∠PDC.∵BC=DC,DP=BE,∴ΔEBC≌ΔPDC(SAS).∴EC=PC.……………………………………………………………7分27.(1)相等(CQ=PD)………… ……1分(2)①……………2分②结论成立,证明如下:证明:连接HC,………………3分∵正方形ABCD,BD为对角线∴∠5=45°,可证△ADH≌△CDH,得∠1=∠2又∵QH⊥BD,∠5=45°∴∠4=45°,∴∠4=∠5∴QH=HD,∠HQC=∠HDP=135°………………4分∵AH⊥HP,AD⊥DP,∴∠AHP=∠ADP=90°又∵∠AOH=∠DOP∴∠1=∠3∴∠2=∠3可证△CQH≌△PDH(AAS)∴CQ=PD 成立………………5分(3)第一种情况如图解释PC= 1-3…6分第二种情况如图解释:3 ……7分PC=112、【大兴】27.(1)①1分②FM=FC.………………………………………………………2分(2)CE与AF的数量关系是CE AF………………………………3分证明:过点M作MG∥CD交AD于点G.∵B,M关于AD对称,∴∠1=∠2,AB=AM.∵四边形ABCD 为平行四边形 ∴AB ∥CD . ∵MG ∥CD , ∴MG ∥AB . ∴∠2=∠3. ∴∠1=∠3.∴AM =MG .………………………………………………………………4分 ∵AB =AM ,AB =CD , ∴MG =CD . ∵MG ∥CD , ∴ ∠4=∠FDC . ∵∠MFG =∠CFD , ∴ △MFG ≌ △CFD .∴ FM =FC .……………………………………………………………………5分 ∴F 为CM 的中点, ∵H 为ME 的中点, ∴ FH ∥CE ,12FH CE∴= …………………………………………………………………6分 ∵∠ABC =135°, ABCD 中,AD ∥BC , ∴∠2=180°-∠ABC =45°. ∴由对称性,∠1=∠2=45°. ∵FH ∥CD ,AB ∥CD ,∴FH ∥AB . ∴∠HFA =∠2=45°. ∴∠FHA =90°,HA =HF . ∴222FH AH AF +=∴222FH AF =……………………………………………………………………7分 又12FH CE=∴22)212(AFCE = 2221AF CE =∴ AF CE 2=∴.………………………………………………………………8分13、【怀柔】27. (1)∵∠BAM =∠EAM =α=30°, ∴∠EAD =90°+30°+30°=150° ∵AE = AB =AD ,∴∠E =∠ADE =15 °,∴∠AND =45 ° …………………2分 (2)∠AND 的度数不发生变化∵∠BAM =∠EAM =α,∴∠EAD =90°+2α.∵AE =AB =AD ,∴∠E =∠ADE =2α)290(180+-o o =45o -α.∴∠AND =∠EAN +∠E =45o -α+α=45o ………4分(3) 过点 A 作AG ⊥AM ,交DE 于点G ,连接BN∵点B 与 点E 关于直线AM 对称,∴△ABN ≌△AEN .∴∠E =∠ABN 又∵∠E =∠ADE ,∴∠ ABN =∠ADE .∵∠DAB =∠GAN =90∴∠DAG =∠BAN . 又∵AN =AG ,∴△ABN ≌△ADG (ASA ∴AN =AG . △ANG 为等腰直角三角形.∴AN 2+AN 2=NG 2.∴NG =AN 2.又∵EN =BN =DG ∴DN =EN AN +2. ……………7分 14、【燕山】27.(1) 补全的图形如图所示; ………………………………1分(2) 证明:如图,∵四边形ABCD 是正方形,∴∠B =90°, ………………………………2分 ∴∠1+∠2=90°.∵线段PA 绕点P 顺时针旋转90°得到线段PE , ∴PA =PE ,∠APE =90°, ∴∠2+∠3=90°,∴∠1=∠3. ………………………………3分 ∵EF ⊥BC 于F , ∴∠EFP =90°=∠B , 在△ABP 和△PFE 中,∠B =∠EFP ,∠1=∠3,PA =PE , ∴△ABP ≌△PFE ,∴BP =EF . ………………………………4分 (3) 22212PG CD CE =. ………………………………5分证明:如图,∵四边形ABCD 是正方形, ∴AB =BC =CD . ∵△ABP ≌△PFE , ∴AB =PF , ∴BC =PF =CD ,∴BC -PC =PF -PC ,即BP =CF . 又∵BP =EF ,PF GCDBA E31∴EF =CF ,∴△CEF 是等腰直角三角形,EFCE . ∵∠FCG =∠ACB =12∠DCB =45°, ∴CF =FG =EF , ∴PF 为线段EG 的垂直平分线,∴PE =PG .在Rt △PFE 中,有222PE PF EF +=, ∴22212PG CD CE +=. ………………………………7分 15、【清华附中】解:(1)∵A B E ∆是等边三角形,∴B E B A =,︒=∠60AB E .∵︒=∠60MB N ,∴AB N AB E AB N MB N ∠-∠=∠-∠,即NB E B MA ∠=∠. 又∵NB MB =,∴()SAS ENB AMB ∆≅∆. …………3 分(2)如图,连接CE ,当M 点位于BD 与CE 的交点处时,CM B M AM ++的值最小. …………4 分 理由如下:连接MN ,由(1)知,ENB AMB ∆≅∆,∴EN AM =.∵︒=∠60MB N ,NB MB =,∴BMN ∆是等边三角形,∴MN B M =.∴CM MN EN CM B M AM ++=++根据“两点之间线段最短”,得 EC CM MN EN =++最短∴当M 点位于BD 与CE 的交点处时,CM B M AM ++的值最小,即等于EC 的长 …………………6 分(3)正方形的边长为2 …………7 分32 过E 点作CB EF ⊥交CB 的延长线于F ,∴︒=︒-︒=∠306090EB F . 设正方形的边长为x ,则=B F x 23,=EF 2x.在EFC Rt ∆中,∵222EC FC EF =+,∴ ()22213232+=⎪⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛x x x 解得,2=x (舍去负值).∴正方形的边长为216、【房山】。
