2018-2020三年高考数学分类汇编
新课标高考数学分类精编(精华文档)(2020-2021) (13)
2018年-2020年新课标高考数学(理科)试题分类精编
第12部分-三视图
一.选择题
1.(2020年陕西理7).若某空间几何体的三视图如图所示,则该几何体的体积是
)2
(第7小题图)
【答案】C
【解析】由所给三视图知,对应的几何体为一倒放的直三棱柱
'''C B A ABC -(如下图所示)
,其高为2,底面ABC 满足:
1,2,==⊥AC AB AC AB . 故该几何体的体积为12122
1'=⨯⎪⎭⎫ ⎝⎛⨯⨯=⋅=∆AA S V ABC .故选C . 2.( 2020年广东理6)如图1,△ ABC 为三角形,AA '//BB ' //CC ' , CC ' ⊥平面ABC 且3AA '=32
BB '=CC ' =AB,则多面体△ABC -A B C '''的正视图(也称主视图)是
【答案】D .
3.( 2020年安徽理8)一个几何体的三视图如图,
该几何体的表面积为
A 、280
B 、292
C 、360
D 、372
【解析】该几何体由两个长方体组合而成,其表面
积等于下面长方体的全面积加上面长方体的4个侧面积之和。
2(10810282)2(6882)360S =⨯+⨯+⨯+⨯+⨯=.
【方法技巧】把三视图转化为直观图是解决问题的关键.又三视图很容易知道是两个长方体的组合体,画出直观图,得出各个棱的长度.把几何体的表面积转化为下面长方体的全面积加上面长方体的4个侧面积之和。
4.(2020年北京理3)一个长方体去掉一个小长方体,所得几何体的
B。
2018-2020年近三年高考数学真题解答题汇编:专题4.3 统计与概率(学生版+解析版)
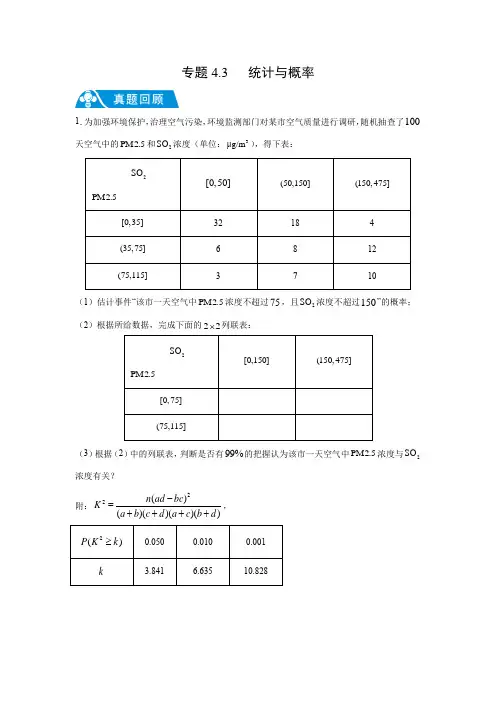
专题4.3 统计与概率1.为加强环境保护,治理空气污染,环境监测部门对某市空气质量进行调研,随机抽查了100天空气中的PM2.5和2SO 浓度(单位:3μg/m ),得下表:(1)估计事件“该市一天空气中PM2.5浓度不超过75,且2SO 浓度不超过150”的概率; (2)根据所给数据,完成下面的22⨯列联表:(3)根据(2)中的列联表,判断是否有99%的把握认为该市一天空气中PM2.5浓度与2SO 浓度有关?附:22()()()()()n ad bc K a b c d a c b d -=++++,2.某校为举办甲、乙两项不同活动,分别设计了相应的活动方案:方案一、方案二.为了解该校学生对活动方案是否支持,对学生进行简单随机抽样,获得数据如下表:假设所有学生对活动方案是否支持相互独立.(1)分别估计该校男生支持方案一的概率、该校女生支持方案一的概率;(2)从该校全体男生中随机抽取2人,全体女生中随机抽取1人,估计这3人中恰有2人支持方案一的概率;(3)将该校学生支持方案的概率估计值记为0p ,假设该校一年级有500名男生和300名女生,除一年级外其他年级学生支持方案二的概率估计值记为1p ,试比较0p 与1p 的大小.(结论不要求证明)3.为加强环境保护,治理空气污染,环境监测部门对某市空气质量进行调研,随机抽查了100天空气中的PM2.5和2SO 浓度(单位:3μg/m ),得下表:(1)估计事件“该市一天空气中PM2.5浓度不超过75,且2SO 浓度不超过150”的概率;(2)根据所给数据,完成下面的22⨯列联表:(3)根据(2)中的列联表,判断是否有99%的把握认为该市一天空气中PM2.5浓度与2SO 浓度有关?附:22()()()()()n ad bcKa b c d a c b d-=++++,4.某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当天到某公园锻炼的人次,整理数据得到下表(单位:天):(1)分别估计该市一天的空气质量等级为1,2,3,4的概率;(2)求一天中到该公园锻炼的平均人次的估计值(同一组中的数据用该组区间的中点值为代表);(3)若某天的空气质量等级为1或2,则称这天“空气质量好”;若某天的空气质量等级为3或4,则称这天“空气质量不好”.根据所给数据,完成下面的2×2列联表,并根据列联表,判断是否有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关?附:22()()()()()n ad bcKa b c d a c b d-=++++,5.甲、乙、丙三位同学进行羽毛球比赛,约定赛制如下:累计负两场者被淘汰;比赛前抽签决定首先比赛的两人,另一人轮空;每场比赛的胜者与轮空者进行下一场比赛,负者下一场轮空,直至有一人被淘汰;当一人被淘汰后,剩余的两人继续比赛,直至其中一人被淘汰,另一人最终获胜,比赛结束.经抽签,甲、乙首先比赛,丙轮空.设每场比赛双方获胜的概率都为12,(1)求甲连胜四场的概率;(2)求需要进行第五场比赛的概率;(3)求丙最终获胜的概率.6.某沙漠地区经过治理,生态系统得到很大改善,野生动物数量有所增加.为调查该地区某种野生动物的数量,将其分成面积相近的200个地块,从这些地块中用简单随机抽样的方法抽取20个作为样区,调查得到样本数据(x i ,y i )(i =1,2,…,20),其中x i 和y i 分别表示第i 个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,并计算得20160i ix==∑,2011200i iy==∑,2021)80i i x x =-=∑(,2021)9000i i y y =-=∑(,201))800i i i x y x y =--=∑((. (1)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数);(2)求样本(x i ,y i )(i =1,2,…,20)的相关系数(精确到0.01);(3)根据现有统计资料,各地块间植物覆盖面积差异很大.为提高样本的代表性以获得该地区这种野生动物数量更准确的估计,请给出一种你认为更合理的抽样方法,并说明理由.附:相关系数r =12211))))ni iiiin ni i x y x x y y y x ===----∑∑∑((((,≈1.414.7.改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A ,B 两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中A ,B 两种支付方式都不使用的有5人,样本中仅使用A 和仅使用B 的学生的支付金额分布情况如下:交付金额(元) 支付方式(1)从全校学生中随机抽取1人,估计该学生上个月A,B两种支付方式都使用的概率;(2)从样本仅使用A和仅使用B的学生中各随机抽取1人,以X表示这2人中上个月支付金额大于1000元的人数,求X的分布列和数学期望;(3)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用A的学生中,随机抽查3人,发现他们本月的支付金额都大于2000元.根据抽查结果,能否认为样本仅使用A的学生中本月支付金额大于2000元的人数有变化?说明理由.8.为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成,A B 两组,每组100只,其中A组小鼠给服甲离子溶液,B组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:P C的估计值为记C为事件:“乙离子残留在体内的百分比不低于5.5”,根据直方图得到()0.70.(1)求乙离子残留百分比直方图中,a b的值;(2)分别估计甲、乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表).9.设甲、乙两位同学上学期间,每天7:30之前到校的概率均为23.假定甲、乙两位同学到校情况互不影响,且任一同学每天到校情况相互独立.(1)用X表示甲同学上学期间的三天中7:30之前到校的天数,求随机变量X的分布列和数学期望;(2)设M为事件“上学期间的三天中,甲同学在7:30之前到校的天数比乙同学在7:30之前到校的天数恰好多2”,求事件M发生的概率.10.某商场为提高服务质量,随机调查了50名男顾客和50名女顾客,每位顾客对该商场的服务给出满意或不满意的评价,得到下面列联表:(1)分别估计男、女顾客对该商场服务满意的概率;(2)能否有95%的把握认为男、女顾客对该商场服务的评价有差异?附:22()()()()()n ad bcKa b c d a c b d-=++++.11.11分制乒乓球比赛,每赢一球得1分,当某局打成10:10平后,每球交换发球权,先多得2分的一方获胜,该局比赛结束.甲、乙两位同学进行单打比赛,假设甲发球时甲得分的概率为0.5,乙发球时甲得分的概率为0.4,各球的结果相互独立.在某局双方10:10平后,甲先发球,两人又打了X 个球该局比赛结束. (1)求P (X =2);(2)求事件“X =4且甲获胜”的概率.12.为了治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验.试验方案如下:每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠,随机选一只施以甲药,另一只施以乙药.一轮的治疗结果得出后,再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止试验,并认为治愈只数多的药更有效.为了方便描述问题,约定:对于每轮试验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分,乙药得1-分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分,甲药得1-分;若都治愈或都未治愈则两种药均得0分.甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X . (1)求X 的分布列;(2)若甲药、乙药在试验开始时都赋予4分,(0,1,,8)i p i =表示“甲药的累计得分为i 时,最终认为甲药比乙药更有效”的概率,则00p =,81p =,11i i i i p ap bp cp -+=++(1,2,,7)i =,其中(1)a P X ==-,(0)b P X ==,(1)c P X ==.假设0.5α=,0.8β=. ①证明:1{}i i p p +-(0,1,2,,7)i =为等比数列;②求4p ,并根据4p 的值解释这种试验方案的合理性.13.电影公司随机收集了电影的有关数据,经分类整理得到下表:好评率是指:一类电影中获得好评的部数与该类电影的部数的比值. 假设所有电影是否获得好评相互独立.(1)从电影公司收集的电影中随机选取1部,求这部电影是获得好评的第四类电影的概率; (2)从第四类电影和第五类电影中各随机选取1部,估计恰有1部获得好评的概率; (3)假设每类电影得到人们喜欢的概率与表格中该类电影的好评率相等,用“1k ξ=”表示第k 类电影得到人们喜欢,“0k ξ=”表示第k 类电影没有得到人们喜欢(k =1,2,3,4,5,6).写出方差1D ξ,2D ξ,3D ξ,4D ξ,5D ξ,6D ξ的大小关系.14.某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min )绘制了如下茎叶图:(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;(2)求40名工人完成生产任务所需时间的中位数m ,并将完成生产任务所需时间超过m 和不超过m 的工人数填入下面的列联表:(3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?附:()()()()()22n ad bc K a b c d a c b d -=++++,15.下图是某地区2000年至2016年环境基础设施投资额y (单位:亿元)的折线图.为了预测该地区2018年的环境基础设施投资额,建立了y 与时间变量t 的两个线性回归模型.根据2000年至2016年的数据(时间变量t 的值依次为1,2,,17)建立模型①:ˆ30.413.5yt =-+;根据2010年至2016年的数据(时间变量t 的值依次为1,2,,7)建立模型②:ˆ9917.5yt =+. (1)分别利用这两个模型,求该地区2018年的环境基础设施投资额的预测值; (2)你认为用哪个模型得到的预测值更可靠?并说明理由.16.已知某单位甲、乙、丙三个部门的员工人数分别为24,16,16.现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查.(1)应从甲、乙、丙三个部门的员工中分别抽取多少人?(2)若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.①用X 表示抽取的3人中睡眠不足..的员工人数,求随机变量X 的分布列与数学期望; ②设A 为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,求事件A 发生的概率.17.某工厂的某种产品成箱包装,每箱200件,每一箱产品在交付用户之前要对产品作检验,如检验出不合格品,则更换为合格品.检验时,先从这箱产品中任取20件作检验,再根据检验结果决定是否对余下的所有产品作检验,设每件产品为不合格品的概率都为(01)p p <<,且各件产品是否为不合格品相互独立.(1)记20件产品中恰有2件不合格品的概率为()f p ,求()f p 的最大值点0p ; (2)现对一箱产品检验了20件,结果恰有2件不合格品,以(1)中确定的0p 作为p 的值.已知每件产品的检验费用为2元,若有不合格品进入用户手中,则工厂要对每件不合格品支付25元的赔偿费用.①若不对该箱余下的产品作检验,这一箱产品的检验费用与赔偿费用的和记为X ,求EX ; ②以检验费用与赔偿费用和的期望值为决策依据,是否该对这箱余下的所有产品作检验?专题4.3 统计与概率1.为加强环境保护,治理空气污染,环境监测部门对某市空气质量进行调研,随机抽查了100天空气中的PM2.5和2SO 浓度(单位:3μg/m ),得下表:(1)估计事件“该市一天空气中PM2.5浓度不超过75,且2SO 浓度不超过150”的概率; (2)根据所给数据,完成下面的22⨯列联表:(3)根据(2)中的列联表,判断是否有99%的把握认为该市一天空气中PM2.5浓度与2SO 浓度有关?附:22()()()()()n ad bc K a b c d a c b d -=++++,【试题来源】2020年海南省高考数学试卷(新高考全国Ⅱ卷) 【答案】(1)0.64;(2)答案见解析;(3)有.【分析】(1)根据表格中数据以及古典概型的概率公式可求得结果;(2)根据表格中数据可得22⨯列联表; (3)计算出2K ,结合临界值表可得结论.【解析】(1)由表格可知,该市100天中,空气中的 2.5PM 浓度不超过75,且2SO 浓度不超过150的天数有32618864+++=天,所以该市一天中,空气中的 2.5PM 浓度不超过75,且2SO 浓度不超过150的概率为640.64100=; (2)由所给数据,可得22⨯列联表为(3)根据22⨯列联表中的数据可得222()100(64101610)()()()()80207426n ad bc K a b c d a c b d -⨯⨯-⨯==++++⨯⨯⨯36007.4844 6.635481=≈>,因为根据临界值表可知,有99%的把握认为该市一天空气中 2.5PM 浓度与2SO 浓度有关. 2.某校为举办甲、乙两项不同活动,分别设计了相应的活动方案:方案一、方案二.为了解该校学生对活动方案是否支持,对学生进行简单随机抽样,获得数据如下表:假设所有学生对活动方案是否支持相互独立.(1)分别估计该校男生支持方案一的概率、该校女生支持方案一的概率;(2)从该校全体男生中随机抽取2人,全体女生中随机抽取1人,估计这3人中恰有2人支持方案一的概率;(3)将该校学生支持方案的概率估计值记为0p ,假设该校一年级有500名男生和300名女生,除一年级外其他年级学生支持方案二的概率估计值记为1p ,试比较0p 与1p 的大小.(结论不要求证明)【试题来源】2020年北京市高考数学试卷 【答案】(1)该校男生支持方案一的概率为13,该校女生支持方案一的概率为34; (2)1336,(3)01p p < 【解析】(1)该校男生支持方案一的概率为2001200+4003=,该校女生支持方案一的概率为3003300+1004=;(2)3人中恰有2人支持方案一分两种情况,(1)仅有两个男生支持方案一,(2)仅有一个男生支持方案一,一个女生支持方案一,所以3人中恰有2人支持方案一概率为2121311313()(1)()(1)3433436C -+-=; (3)01p p <3.为加强环境保护,治理空气污染,环境监测部门对某市空气质量进行调研,随机抽查了100天空气中的PM2.5和2SO 浓度(单位:3μg/m ),得下表:(1)估计事件“该市一天空气中PM2.5浓度不超过75,且2SO 浓度不超过150”的概率; (2)根据所给数据,完成下面的22⨯列联表:(3)根据(2)中的列联表,判断是否有99%的把握认为该市一天空气中PM2.5浓度与2SO 浓度有关?附:22()()()()()n ad bc K a b c d a c b d -=++++,【试题来源】2020年新高考全国卷Ⅱ(海南卷) 【答案】(1)0.64;(2)答案见解析;(3)有.【分析】(1)根据表格中数据以及古典概型的概率公式可求得结果;(2)根据表格中数据可得22⨯列联表;(3)计算出2K ,结合临界值表可得结论.【解析】(1)由表格可知,该市100天中,空气中的 2.5PM 浓度不超过75,且2SO 浓度不超过150的天数有32618864+++=天,所以该市一天中,空气中的 2.5PM 浓度不超过75,且2SO 浓度不超过150的概率为640.64100=; (2)由所给数据,可得22⨯列联表为(3)根据22⨯列联表中的数据可得222()100(64101610)()()()()80207426n ad bc K a b c d a c b d -⨯⨯-⨯==++++⨯⨯⨯36007.4844 6.635481=≈>,因为根据临界值表可知,有99%的把握认为该市一天空气中 2.5PM 浓度与2SO 浓度有关. 【名师点睛】本题考查了古典概型的概率公式,考查了完善22⨯列联表,考查了独立性检验,属于中档题.4.某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当天到某公园锻炼的人次,整理数据得到下表(单位:天):(1)分别估计该市一天的空气质量等级为1,2,3,4的概率;(2)求一天中到该公园锻炼的平均人次的估计值(同一组中的数据用该组区间的中点值为代表);(3)若某天的空气质量等级为1或2,则称这天“空气质量好”;若某天的空气质量等级为3或4,则称这天“空气质量不好”.根据所给数据,完成下面的2×2列联表,并根据列联表,判断是否有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关?附:22()()()()()n ad bc K a b c d a c b d -=++++,【试题来源】2020年全国统一高考数学试卷(文)(新课标Ⅱ)【答案】(1)该市一天的空气质量等级分别为1、2、3、4的概率分别为0.43、0.27、0.21、0.09;(2)350;(3)有,理由见解析. 【分析】(1)根据频数分布表可计算出该市一天的空气质量等级分别为1、2、3、4的概率;(2)利用每组的中点值乘以频数,相加后除以100可得结果;(3)根据表格中的数据完善22⨯列联表,计算出2K 的观测值,再结合临界值表可得结论. 【解析】(1)由频数分布表可知,该市一天的空气质量等级为1的概率为216250.43100++=,等级为2的概率为510120.27100++=,等级为3的概率为6780.21100++=,等级为4的概率为7200.09100++=;(2)由频数分布表可知,一天中到该公园锻炼的人次的平均数为100203003550045350100⨯+⨯+⨯=(3)22⨯列联表如下:()221003383722 5.820 3.84155457030K ⨯⨯-⨯=≈>⨯⨯⨯,因此,有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关. 【名师点睛】本题考查利用频数分布表计算频率和平均数,同时也考查了独立性检验的应用,考查数据处理能力,属于基础题.5.甲、乙、丙三位同学进行羽毛球比赛,约定赛制如下:累计负两场者被淘汰;比赛前抽签决定首先比赛的两人,另一人轮空;每场比赛的胜者与轮空者进行下一场比赛,负者下一场轮空,直至有一人被淘汰;当一人被淘汰后,剩余的两人继续比赛,直至其中一人被淘汰,另一人最终获胜,比赛结束.经抽签,甲、乙首先比赛,丙轮空.设每场比赛双方获胜的概率都为12, (1)求甲连胜四场的概率; (2)求需要进行第五场比赛的概率; (3)求丙最终获胜的概率.【试题来源】2020年全国统一高考数学试卷(理)(新课标Ⅱ) 【答案】(1)116;(2)34;(3)716. 【分析】(1)根据独立事件的概率乘法公式可求得事件“甲连胜四场”的概率;(2)计算出四局以内结束比赛的概率,然后利用对立事件的概率公式可求得所求事件的概率;(3)列举出甲赢的基本事件,结合独立事件的概率乘法公式计算出甲赢的概率,由对称性可知乙赢的概率和甲赢的概率相等,再利用对立事件的概率可求得丙赢的概率.【解析】(1)记事件:M 甲连胜四场,则()411216P M ⎛⎫== ⎪⎝⎭;(2)记事件A 为甲输,事件B 为乙输,事件C 为丙输, 则四局内结束比赛的概率为()()()()411424P P ABAB P ACAC P BCBC P BABA ⎛⎫'=+++=⨯= ⎪⎝⎭,所以,需要进行第五场比赛的概率为314P P '=-=; (3)记事件A 为甲输,事件B 为乙输,事件C 为丙输, 记事件:M 甲赢,记事件:N 丙赢,则甲赢的基本事件包括:BCBC 、ABCBC 、ACBCB 、BABCC 、BACBC 、BCACB 、BCABC 、BCBAC , 所以,甲赢的概率为()4511972232P M ⎛⎫⎛⎫=+⨯= ⎪ ⎪⎝⎭⎝⎭.由对称性可知,乙赢的概率和甲赢的概率相等, 所以丙赢的概率为()97123216P N =-⨯=. 【名师点睛】本题考查独立事件概率的计算,解答的关键就是列举出符合条件的基本事件,考查计算能力,属于中等题.6.某沙漠地区经过治理,生态系统得到很大改善,野生动物数量有所增加.为调查该地区某种野生动物的数量,将其分成面积相近的200个地块,从这些地块中用简单随机抽样的方法抽取20个作为样区,调查得到样本数据(x i ,y i )(i =1,2,…,20),其中x i 和y i 分别表示第i 个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,并计算得20160i ix==∑,2011200i iy==∑,2021)80i i x x =-=∑(,2021)9000i i y y =-=∑(,201))800i i i x y x y =--=∑((. (1)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数);(2)求样本(x i ,y i )(i =1,2,…,20)的相关系数(精确到0.01);(3)根据现有统计资料,各地块间植物覆盖面积差异很大.为提高样本的代表性以获得该地区这种野生动物数量更准确的估计,请给出一种你认为更合理的抽样方法,并说明理由.附:相关系数r=12211))))ni iiiin ni i x y x x y y y x ===----∑∑∑((((,≈1.414.【试题来源】2020年全国统一高考数学试卷(理)(新课标Ⅱ) 【答案】(1)12000;(2)0.94;(3)详见解析【分析】(1)利用野生动物数量的估计值等于样区野生动物平均数乘以地块数,代入数据即可;(2)利用公式20()()iix x y y r --=∑计算即可;(3)各地块间植物覆盖面积差异较大,为提高样本数据的代表性,应采用分层抽样.【解析】(1)样区野生动物平均数为201111200602020ii y ==⨯=∑,地块数为200,该地区这种野生动物的估计值为2006012000⨯=(2)样本(,)i ix y(i=1,2,…,20)的相关系数为20()()0.943i ix x y yr--===≈∑(3)由(2)知各样区的这种野生动物的数量与植物覆盖面积有很强的正相关性,由于各地块间植物覆盖面积差异很大,从俄各地块间这种野生动物的数量差异很大,采用分层抽样的方法较好地保持了样本结构与总体结构得以执行,提高了样本的代表性,从而可以获得该地区这种野生动物数量更准确的估计.【点晴】本题主要考查平均数的估计值、相关系数的计算以及抽样方法的选取,考查学生数学运算能力,是一道容易题.7.改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:交付金额(元)支付方式(1)从全校学生中随机抽取1人,估计该学生上个月A,B两种支付方式都使用的概率;(2)从样本仅使用A和仅使用B的学生中各随机抽取1人,以X表示这2人中上个月支付金额大于1000元的人数,求X的分布列和数学期望;(3)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用A的学生中,随机抽查3人,发现他们本月的支付金额都大于2000元.根据抽查结果,能否认为样本仅使用A的学生中本月支付金额大于2000元的人数有变化?说明理由.【试题来源】2019年北京市高考数学试卷(理)【答案】(1) 25;(2)见解析;(Ⅱ)见解析. 【分析】(1)由题意利用古典概型计算公式可得满足题意的概率值;(2)首先确定X 可能的取值,然后求得相应的概率值可得分布列,最后求解数学期望即可. (Ⅱ)由题意结合概率的定义给出结论即可.【解析】(1)由题意可知,两种支付方式都是用的人数为1003025540---=人,则: 该学生上个月A ,B 两种支付方式都使用的概率4021005p ==. (2)由题意可知,仅使用A 支付方法的学生中,金额不大于1000的人数占35,金额大于1000的人数占25, 仅使用B 支付方法的学生中,金额不大于1000的人数占25,金额大于1000的人数占35, 且X 可能的取值为0,1,2.()32605525p X ==⨯=,()22321315525p X ⎛⎫⎛⎫==+= ⎪ ⎪⎝⎭⎝⎭,()32625525p X ==⨯=, X 的分布列为其数学期望:()0121252525E X =⨯+⨯+⨯=. (Ⅱ)我们不认为样本仅使用A 的学生中本月支付金额大于2000元的人数有变化.理由如下: 随机事件在一次随机实验中是否发生是随机的,是不能预知的,随着试验次数的增多,频率越来越稳定于概率.学校是一个相对消费稳定的地方,每个学生根据自己的实际情况每个月的消费应该相对固定,出现题中这种现象可能是发生了“小概率事件”.【名师点睛】本题以支付方式相关调查来设置问题,考查概率统计在生活中的应用,考查概率的定义和分布列的应用,使学生体会到数学与现实生活息息相关.8.为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成,A B 两组,每组100只,其中A 组小鼠给服甲离子溶液,B 组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:记C 为事件:“乙离子残留在体内的百分比不低于5.5”,根据直方图得到()P C 的估计值为0.70.(1)求乙离子残留百分比直方图中,a b 的值;(2)分别估计甲、乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表).【试题来源】2019年全国统一高考数学试卷(理)(新课标Ⅱ)【答案】(1) 0.35a =,0.10b =;(2) 4.05,6.【分析】(1)由()0.70P C =及频率和为1可解得a 和b 的值;(2)根据公式求平均数.【解析】(1)由题得0.200.150.70a ++=,解得0.35a =,由0.050.151()10.70b P C ++=-=-,解得0.10b =.(2)由甲离子的直方图可得,甲离子残留百分比的平均值为0.1520.2030.3040.2050.1060.057 4.05⨯+⨯+⨯+⨯+⨯+⨯=,乙离子残留百分比的平均值为0.0530.1040.1550.3560.2070.1586⨯+⨯+⨯+⨯+⨯+⨯=【名师点睛】本题考查频率分布直方图和平均数,属于基础题.9.设甲、乙两位同学上学期间,每天7:30之前到校的概率均为23.假定甲、乙两位同学到校情况互不影响,且任一同学每天到校情况相互独立.(1)用X 表示甲同学上学期间的三天中7:30之前到校的天数,求随机变量X 的分布列和数学期望;(2)设M 为事件“上学期间的三天中,甲同学在7:30之前到校的天数比乙同学在7:30之前到校的天数恰好多2”,求事件M 发生的概率.。
2018-2020年近三年高考数学真题解答题汇编:专题4.5 圆锥曲线(学生版+解析版)

专题4.5 圆锥曲线1.已知椭圆C :22221(0)x y a b a b+=>>过点M (2,3),点A 为其左顶点,且AM 的斜率为12, (1)求C 的方程;(2)点N 为椭圆上任意一点,求△AMN 的面积的最大值.2.已知椭圆22221(0)x y a b a b+=>>的一个顶点为(0,3)A -,右焦点为F ,且||||OA OF =,其中O 为原点. (1)求椭圆的方程;(2)已知点C 满足3OC OF =,点B 在椭圆上(B 异于椭圆的顶点),直线AB 与以C 为圆心的圆相切于点P ,且P 为线段AB 的中点.求直线AB 的方程.3.已知椭圆2222:1x y C a b+=过点(2,1)A --,且2a b =.(1)求椭圆C 的方程:(2)过点(4,0)B -的直线l 交椭圆C 于点,M N ,直线,MA NA 分别交直线4x =-于点,P Q .求||||PB BQ 的值.4.如图,已知椭圆221:12x C y +=,抛物线22:2(0)C y px p =>,点A 是椭圆1C 与抛物线2C 的交点,过点A 的直线l 交椭圆1C 于点B ,交抛物线2C 于M (B ,M 不同于A ).(1)若116=p ,求抛物线2C 的焦点坐标; (2)若存在不过原点的直线l 使M 为线段AB 的中点,求p 的最大值.5.已知椭圆C :22221(0)x y a b a b +=>>的离心率为2,且过点()2,1A .(1)求C 的方程:(2)点M ,N 在C 上,且AM AN ⊥,AD MN ⊥,D 为垂足.证明:存在定点Q ,使得DQ 为定值.6.在平面直角坐标系xOy 中,已知椭圆22:143x y E +=的左、右焦点分别为F 1,F 2,点A在椭圆E 上且在第一象限内,AF 2⊥F 1F 2,直线AF 1与椭圆E 相交于另一点B . (1)求△AF 1F 2的周长;(2)在x 轴上任取一点P ,直线AP 与椭圆E 的右准线相交于点Q ,求OP QP ⋅的最小值; (3)设点M 在椭圆E 上,记△OAB 与△MAB 的面积分别为S 1,S 2,若S 2=3S 1,求点M 的坐标.7.已知椭圆222:1(05)25x y C m m +=<<,A ,B 分别为C 的左、右顶点. (1)求C 的方程;(2)若点P 在C 上,点Q 在直线6x =上,且||||BP BQ =,BP BQ ⊥,求APQ 的面积.8.已知A 、B 分别为椭圆E :2221x y a+=(a >1)的左、右顶点,G 为E 的上顶点,8AG GB ⋅=,P 为直线x =6上的动点,P A 与E 的另一交点为C ,PB 与E 的另一交点为D . (1)求E 的方程;(2)证明:直线CD 过定点.9.已知椭圆C 1:22221x y a b+=(a >b >0)的右焦点F 与抛物线C 2的焦点重合,C 1的中心与C 2的顶点重合.过F 且与x 轴垂直的直线交C 1于A ,B 两点,交C 2于C ,D 两点,且|CD |=43|AB |.(1)求C 1的离心率;(2)若C 1的四个顶点到C 2的准线距离之和为12,求C 1与C 2的标准方程.10.已知椭圆C 1:22221x y a b+=(a >b >0)的右焦点F 与抛物线C 2的焦点重合,C 1的中心与C 2的顶点重合.过F 且与x 轴垂直的直线交C 1于A ,B 两点,交C 2于C ,D 两点,且|CD |=43|AB |. (1)求C 1的离心率;(2)设M 是C 1与C 2的公共点,若|MF |=5,求C 1与C 2的标准方程.11.已知椭圆2222:1x y C a b+=的右焦点为(1,0),且经过点(0,1)A .(1)求椭圆C 的方程;(2)设O 为原点,直线:(1)l y kx t t =+≠±与椭圆C 交于两个不同点P ,Q ,直线AP 与x 轴交于点M ,直线AQ 与x 轴交于点N ,若|OM |·|ON |=2,求证:直线l 经过定点.12.已知抛物线C :x 2=−2py 经过点(2,−1). (1)求抛物线C 的方程及其准线方程;(2)设O 为原点,过抛物线C 的焦点作斜率不为0的直线l 交抛物线C 于两点M ,N ,直线y =−1分别交直线OM ,ON 于点A 和点B .求证:以AB 为直径的圆经过y 轴上的两个定点.13.已知曲线C :y =22x ,D 为直线y =12-上的动点,过D 作C 的两条切线,切点分别为A ,B .(1)证明:直线AB 过定点: (2)若以E (0,52)为圆心的圆与直线AB 相切,且切点为线段AB 的中点,求四边形ADBE 的面积.14.设椭圆22221(0)x ya ba b+=>>的左焦点为F,左顶点为A,上顶点为B.已知|2||OA OB=(O为原点).(1)求椭圆的离心率;(2)设经过点F且斜率为34的直线l与椭圆在x轴上方的交点为P,圆C同时与x轴和直线l相切,圆心C在直线4x=上,且OC AP∥,求椭圆的方程.15.如图,已知点(10)F,为抛物线22(0)y px p=>的焦点,过点F的直线交抛物线于,A B 两点,点C在抛物线上,使得ABC的重心G在x轴上,直线AC交x轴于点Q,且Q在点F右侧.记,AFG CQG△△的面积为12,S S.(1)求p的值及抛物线的准线方程;(2)求12SS的最小值及此时点G的坐标.16.设椭圆22221(0)x ya ba b+=>>的左焦点为F,上顶点为B.已知椭圆的短轴长为4,.(1)求椭圆的方程;(2)设点P在椭圆上,且异于椭圆的上、下顶点,点M为直线PB与x轴的交点,点N在y轴的负半轴上.若||||ON OF=(O为原点),且OP MN⊥,求直线PB的斜率.17.已知12,F F 是椭圆2222:1(0)x y C a b a b+=>>的两个焦点,P 为C 上一点,O为坐标原点.(1)若2POF 为等边三角形,求C 的离心率;(2)如果存在点P ,使得12PF PF ⊥,且12F PF △的面积等于16,求b 的值和a 的取值范围.18.已知点A ,B 关于坐标原点O 对称,│AB │ =4,⊙M 过点A ,B 且与直线x +2=0相切. (1)若A 在直线x +y =0上,求⊙M 的半径.(2)是否存在定点P ,使得当A 运动时,│MA │-│MP │为定值?并说明理由.19.已知点A (−2,0),B (2,0),动点M (x ,y )满足直线AM 与BM 的斜率之积为−12.记M 的轨迹为曲线C .(1)求C 的方程,并说明C 是什么曲线;(2)过坐标原点的直线交C 于P ,Q 两点,点P 在第一象限,PE ⊥x 轴,垂足为E ,连结QE 并延长交C 于点G . ①证明:PQG 是直角三角形; ②求PQG 面积的最大值.20.已知抛物线C :y 2=3x 的焦点为F ,斜率为32的直线l 与C 的交点为A ,B ,与x 轴的交点为P .(1)若|AF |+|BF |=4,求l 的方程; (2)若3AP PB =,求|AB |.21.设椭圆22221(0)x y a b a b +=>>的右顶点为A ,上顶点为B .AB =(1)求椭圆的方程;(2)设直线:(0)l y kx k =<与椭圆交于P ,Q 两点,l 与直线AB 交于点M ,且点P ,M 均在第四象限.若BPM △的面积是BPQ 面积的2倍,求k 的值.22.已知椭圆2222:1(0)x y M a b a b +=>>,焦距为斜率为k 的直线l与椭圆M 有两个不同的交点A 、B . (1)求椭圆M 的方程; (2)若1k =,求||AB 的最大值;(3)设()2,0P -,直线PA 与椭圆M 的另一个交点为C ,直线PB 与椭圆M 的另一个交点为D .若C 、D 和点71,44Q ⎛⎫- ⎪⎝⎭共线,求k .23.如图,在平面直角坐标系xOy 中,椭圆C 过点1)2,焦点12(F F ,圆O 的直径为12F F .(1)求椭圆C 及圆O 的方程;(2)设直线l 与圆O 相切于第一象限内的点P .①若直线l 与椭圆C 有且只有一个公共点,求点P 的坐标;②直线l 与椭圆C 交于,A B 两点.若OAB 的面积为7,求直线l 的方程.24.已知抛物线C :2y =2px 经过点P (1,2).过点Q (0,1)的直线l 与抛物线C 有两个不同的交点A ,B ,且直线P A 交y 轴于M ,直线PB 交y 轴于N . (1)求直线l 的斜率的取值范围;(2)设O 为原点,QM QO λ=,QN QO μ=,求证:11λμ+为定值.25.已知斜率为k 的直线l 与椭圆22143x y C +=:交于A ,B 两点,线段AB 的中点为()()10M m m >,.(1)证明:12k <-; (2)设F 为C 的右焦点,P 为C 上一点,且0FP FA FB ++=.证明:FA ,FP ,FB 成等差数列,并求该数列的公差.26.已知斜率为k 的直线l 与椭圆22143x y C +=:交于A ,B 两点.线段AB 的中点为(1,)(0)M m m >.(1)证明:12k <-; (2)设F 为C 的右焦点,P 为C 上一点,且0FP FA FB ++=.证明:2FP FA FB =+.27.如图,已知点P 是y 轴左侧(不含y 轴)一点,抛物线C :y 2=4x 上存在不同的两点A ,B 满足PA ,PB 的中点均在C 上.(1)设AB 中点为M ,证明:PM 垂直于y 轴;(2)若P 是半椭圆x 2+24y=1(x<0)上的动点,求△PAB 面积的取值范围.28.设抛物线22C y x =:,点()20A ,,()20B -,,过点A 的直线l 与C 交于M ,N 两点.(1)当l 与x 轴垂直时,求直线BM 的方程; (2)证明:ABM ABN ∠=∠.29.设抛物线24C y x =:的焦点为F ,过F 且斜率为(0)k k >的直线l 与C 交于A ,B 两点,||8AB =. (1)求l 的方程;(2)求过点A ,B 且与C 的准线相切的圆的方程.30.设椭圆22221x y a b +=(a >b >0)的左焦点为F ,上顶点为B .A 的坐标为(),0b ,且FB AB ⋅= (1)求椭圆的方程;(2)设直线l :(0)y kx k =>与椭圆在第一象限的交点为P ,且l 与直线AB 交于点Q . 若sin 4AQ AOQ PQ=∠(O 为原点) ,求k 的值.31.设椭圆22:12x C y +=的右焦点为F ,过F 的直线l 与C 交于,A B 两点,点M 的坐标为(2,0).(1)当l 与x 轴垂直时,求直线AM 的方程; (2)设O 为坐标原点,证明:OMA OMB ∠=∠.专题4.5 圆锥曲线1.已知椭圆C :22221(0)x y a b a b+=>>过点M (2,3),点A 为其左顶点,且AM 的斜率为12, (1)求C 的方程;(2)点N 为椭圆上任意一点,求△AMN 的面积的最大值. 【试题来源】2020年新高考全国卷Ⅱ(海南卷)【答案】(1)2211612x y +=;(2)18. 【解析】(1)由题意可知直线AM 的方程为13(2)2y x -=-,即24-=-x y . 当y =0时,解得4x =-,所以a =4,椭圆()2222:10x y C a b a b+=>>过点M (2,3),可得249116b +=, 解得b 2=12.所以C 的方程:2211612x y +=.(2)设与直线AM 平行的直线方程为2x y m -=,如图所示,当直线与椭圆相切时,与AM 距离比较远的直线与椭圆的切点为N ,此时△AMN 的面积取得最大值.联立直线方程2x y m -=与椭圆方程2211612x y +=,可得()2232448m y y ++=,化简可得2216123480y my m ++-=,所以()221444163480m m ∆=-⨯-=,即m 2=64,解得m =±8,与AM 距离比较远的直线方程:28x y -=,直线AM 方程为24-=-x y , 点N 到直线AM 的距离即两平行线之间的距离,利用平行线之间的距离公式可得d ==,由两点之间距离公式可得||AM ==.所以△AMN 的面积的最大值:1182⨯=. 【名师点睛】解决直线与椭圆的综合问题时,要注意:(1)注意观察应用题设中的每一个条件,明确确定直线、椭圆的条件;(2)强化有关直线与椭圆联立得出一元二次方程后的运算能力,重视根与系数之间的关系、弦长、斜率、三角形的面积等问题.2.已知椭圆22221(0)x y a b a b+=>>的一个顶点为(0,3)A -,右焦点为F ,且||||OA OF =,其中O 为原点. (1)求椭圆的方程;(2)已知点C 满足3OC OF =,点B 在椭圆上(B 异于椭圆的顶点),直线AB 与以C 为圆心的圆相切于点P ,且P 为线段AB 的中点.求直线AB 的方程. 【试题来源】2020年天津市高考数学试卷【答案】(1)221189x y +=;(2)132y x =-,或3y x =-. 【分析】(1)根据题意,并借助222a b c =+,即可求出椭圆的方程;(2)利用直线与圆相切,得到CP AB ⊥,设出直线AB 的方程,并与椭圆方程联立,求出B 点坐标,进而求出P 点坐标,再根据CP AB ⊥,求出直线AB 的斜率,从而得解.【解析】(1)椭圆()222210x y a b a b+=>>的一个顶点为()0,3A -,∴3b =,由OA OF =,得3c b ==,又由222a b c =+,得2228313a =+=,所以,椭圆的方程为221189x y +=;(2)直线AB 与以C 为圆心的圆相切于点P ,所以CP AB ⊥,根据题意可知,直线AB 和直线CP 的斜率均存在, 设直线AB 的斜率为k ,则直线AB 的方程为3y kx ,即3y kx =-,2231189y kx x y =-⎧⎪⎨+=⎪⎩,消去y ,可得()2221120k x kx +-=,解得0x =或21221k x k =+. 将21221k x k =+代入3y kx =-,得222126321213k y k k k k =⋅--=++, 所以,点B 的坐标为2221263,2121k k k k ⎛⎫- ⎪++⎝⎭, 因为P 为线段AB 的中点,点A 的坐标为()0,3-,所以点P 的坐标为2263,2121kk k -⎛⎫⎪++⎝⎭,由3OC OF =,得点C 的坐标为()1,0, 所以,直线CP 的斜率为222303216261121CPk kk k k k --+=-+-+=,因为CP AB ⊥,所以231261k k k ⋅=--+,整理得22310k k -+=,解得12k =或1k =. 所以,直线AB 的方程为132y x =-或3y x =-. 【名师点睛】本题考查了椭圆标准方程的求解、直线与椭圆的位置关系、直线与圆的位置关系、中点坐标公式以及直线垂直关系的应用,考查学生的运算求解能力,属于中档题.当看到题目中出现直线与圆锥曲线位置关系的问题时,要想到联立直线与圆锥曲线的方程.3.已知椭圆2222:1x y C a b+=过点(2,1)A --,且2a b =.(1)求椭圆C 的方程:(2)过点(4,0)B -的直线l 交椭圆C 于点,M N ,直线,MA NA 分别交直线4x =-于点,P Q .求||||PB BQ 的值. 【试题来源】2020年北京市高考数学试卷【答案】(1)22182x y +=;(2)1. 【分析】(1)由题意得到关于a ,b 的方程组,求解方程组即可确定椭圆方程;(2)首先联立直线与椭圆的方程,然后由直线MA ,NA 的方程确定点P ,Q 的纵坐标,将线段长度的比值转化为纵坐标比值的问题,进一步结合根与系数关系可证得0P Q y y +=,从而可得两线段长度的比值.【解析】(1)设椭圆方程为()222210x y a b a b+=>>,由题意可得224112a ba b ⎧+=⎪⎨⎪=⎩,解得2282a b ⎧=⎨=⎩,故椭圆方程为22182x y +=. (2)设()11,M x y ,()22,N x y ,直线MN 的方程为()4y k x =+,与椭圆方程22182x y +=联立可得()222448x k x ++=,即()()222241326480k x k x k +++-=,则2212122232648,4141k k x x x x k k --+==++. 直线MA 的方程为()111122y y x x ++=++, 令4x =-可得()()()1111111141214122122222P k x k x y x y x x x x ++-++++=-⨯-=-⨯-=++++, 同理可得()()222142Q k x y x -++=+.很明显0P Q y y <,且:P Q PB yPQ y =,注意到: ()()()()()()()()122112121242424421212222P Q x x x x x x y y k k x x x x +++++⎛⎫+++=-++=-+⨯ ⎪++++⎝⎭,而:()()()()()122112124242238x x x x x x x x +++++=+++⎡⎤⎣⎦2222648322384141k k k k ⎡⎤⎛⎫--=+⨯+⎢⎥ ⎪++⎝⎭⎣⎦()()()22226483328412041k k k k -+⨯-++=⨯=+, 故0,P Q P Q y y y y +==-.从而1PQPB y BQy ==. 【名师点睛】解决直线与椭圆的综合问题时,要注意:(1)注意观察应用题设中的每一个条件,明确确定直线、椭圆的条件;(2)强化有关直线与椭圆联立得出一元二次方程后的运算能力,重视根与系数之间的关系、弦长、斜率、三角形的面积等问题.4.如图,已知椭圆221:12x C y +=,抛物线22:2(0)C y px p =>,点A 是椭圆1C 与抛物线2C 的交点,过点A 的直线l 交椭圆1C 于点B ,交抛物线2C 于M (B ,M 不同于A ).(1)若116=p ,求抛物线2C 的焦点坐标; (2)若存在不过原点的直线l 使M 为线段AB 的中点,求p 的最大值. 【试题来源】2020年浙江省高考数学试卷 【答案】(1)1(,0)32;(2【解析】(1)当116=p 时,2C 的方程为218y x =,故抛物线2C 的焦点坐标为1(,0)32;(2)设()()()112200,,,,,,:A x y B x y M x y I x y m λ=+,由()22222222220x y y my m x y mλλλ⎧+=⇒+++-=⎨=+⎩,1200022222,,222m m my y y x y m λλλλλλ--∴+===+=+++, 由M 在抛物线上,所以()222222244222m pm mp λλλλλ=⇒=+++, 又22222()220y pxy p y m y p y pm x y mλλλ⎧=⇒=+⇒--=⎨=+⎩, 012y y p λ∴+=,2101022x x y m y m p m λλλ∴+=+++=+,2122222m x p m λλ∴=+-+.由2222142,?22x y x px y px⎧+=⎪⇒+=⎨⎪=⎩即2420x px +-=12x p ⇒==-+222221822228162p p p m p p p λλλλλ+⇒-=+⋅=++≥+,18p ≥,21160p ≤,p ≤ 所以,p的最大值为40,此时(55A . 法2:设直线:(0,0)l x my t m t =+≠≠,()00,A x y .将直线l 的方程代入椭圆221:12x C y +=得()2222220m y mty t +++-=,所以点M 的纵坐标为22M mty m =-+.将直线l 的方程代入抛物线22:2C y px =得2220y pmy pt --=,所以02M y y pt =-,解得()2022p m y m+=,因此()220222p m xm+=,由220012x y +=解得22212242160m m p m m ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭,所以当m t ==p取到最大值为40.5.已知椭圆C :22221(0)x y a b a b +=>>,且过点()2,1A .(1)求C 的方程:(2)点M ,N 在C 上,且AM AN ⊥,AD MN ⊥,D 为垂足.证明:存在定点Q ,使得DQ 为定值.【试题来源】2020年山东省高考数学试卷(新高考全国Ⅱ卷)【答案】(1)22163x y +=;(2)详见解析. 【分析】(1)由题意得到关于,,a b c 的方程组,求解方程组即可确定椭圆方程;(2)设出点M ,N 的坐标,在斜率存在时设方程为y kx m =+, 联立直线方程与椭圆方程,根据已知条件,已得到,m k 的关系,进而得直线MN 恒过定点,在直线斜率不存在时要单独验证,然后结合直角三角形的性质即可确定满足题意的点Q 的位置.【解析】(1)由题意可得222222411c aa b a b c ⎧=⎪⎪⎪+=⎨⎪=+⎪⎪⎩,解得226,3a b ==,故椭圆方程为22163x y +=.(2)设点()()1122,,,M x y N x y ,若直线MN 斜率存在时,设直线MN 的方程为y kx m =+, 代入椭圆方程消去y 并整理得()22212k4260xkmx m +++-=,可得122414km x x k +=-+,21222614m x x k-=+, 因为AM AN ⊥,所以·0AM AN =,即()()()()121222110x x y y --+--=, 根据1122,kx m y kx m y =+=+,代入整理可得()()()()22121212140x x km k x x k m ++--++-+=,所以()()()22222264121401414m km k km k m k k -⎛⎫++---+-+= ⎪++⎝⎭, 整理化简得()()231210k m k m +++-=,因为2,1A ()不在直线MN 上,所以210k m +-≠,故2310k m ++=,1k ≠,于是MN 的方程为2133y k x ⎛⎫=-- ⎪⎝⎭,1k ≠ 所以直线过定点直线过定点21,33P ⎛⎫-⎪⎝⎭, 当直线MN 的斜率不存在时,可得()11,N x y -,由·0AM AN =得()()()()111122110x x y y --+---=, 得()1221210x y -+-=,结合2211163x y +=可得2113840x x -+=,解得123x =,或22x =,当22x =时与A 横坐标重合舍去, 此时直线MN 过点21,33P ⎛⎫-⎪⎝⎭,令Q 为AP 的中点,即41,33Q ⎛⎫ ⎪⎝⎭, 若D 与P 不重合,则由题设知AP 是Rt ADP 的斜边,故123DQ AP ==,若D 与P 重合,则12DQ AP =, 故存在点41,33Q ⎛⎫⎪⎝⎭,使得DQ 为定值. 【名师点睛】本题的关键点是利用AM AN ⊥得 ·0AM AN =,转化为坐标运算,需要设直线MN 的方程,点()()1122,,,M x y N x y ,因此需要讨论斜率存在与不存在两种情况,当直线MN 斜率存在时,设直线MN 的方程为y kx m =+,与椭圆方程联立消去y 可12x x +,12x x 代入·0AM AN =即可,当直线MN 的斜率不存在时,可得()11,N x y -,利用坐标运算以及三角形的性质即可证明,本题易忽略斜率不存在的情况,属于难题.6.在平面直角坐标系xOy 中,已知椭圆22:143x y E +=的左、右焦点分别为F 1,F 2,点A在椭圆E 上且在第一象限内,AF 2⊥F 1F 2,直线AF 1与椭圆E 相交于另一点B . (1)求△AF 1F 2的周长;(2)在x 轴上任取一点P ,直线AP 与椭圆E 的右准线相交于点Q ,求OP QP ⋅的最小值; (3)设点M 在椭圆E 上,记△OAB 与△MAB 的面积分别为S 1,S 2,若S 2=3S 1,求点M 的坐标.【试题来源】2020年江苏省高考数学试卷 【答案】(1)6;(2)-4;(3)()2,0M 或212,77⎛⎫-- ⎪⎝⎭.【解析】(1)因为椭圆E 的方程为22143x y +=,所以()11,0F -,()21,0F由椭圆定义可得124AF AF +=.所以12AF F △的周长为426+=; (2)设()0,0P x ,根据题意可得01x ≠.因为点A 在椭圆E 上,且在第一象限,212AF F F ⊥,所以31,2A ⎛⎫⎪⎝⎭因为准线方程为4x =,所以()4,Q Q y ,所以()()()()200000,04,4244Q OP QP x x y x x x ⋅=⋅--=-=--≥-,当且仅当02x =时取等号.所以OP QP ⋅的最小值为4-.(3)设()11,M x y ,点M 到直线AB 的距离为d . 因为31,2A ⎛⎫⎪⎝⎭,()11,0F -,所以直线1AF 的方程为()314y x =+, 因为点O 到直线AB 的距离为35,213S S =, 所以2113133252S S AB AB d ==⨯⨯⨯=⋅,所以95d =, 所以113439x y -+=①,因为2211143x y +=②,所以联立①②解得1120x y =⎧⎨=⎩,1127127x y ⎧=-⎪⎪⎨⎪=-⎪⎩.所以()2,0M 或212,77⎛⎫-- ⎪⎝⎭. 【名师点睛】本题考查了椭圆的定义,直线与椭圆相交问题、点到直线距离公式的运用,熟悉运用公式以及根据213S S =推出95d =是解答本题的关键. 7.已知椭圆222:1(05)25x y C m m +=<<的离心率为4,A ,B 分别为C 的左、右顶点. (1)求C 的方程;(2)若点P 在C 上,点Q 在直线6x =上,且||||BP BQ =,BP BQ ⊥,求APQ 的面积. 【试题来源】2020年全国统一高考数学试卷(新课标Ⅱ)【答案】(1)221612525x y +=;(2)52. 【分析】(1)因为222:1(05)25x y C m m +=<<,可得5a =,b m =,根据离心率公式,结合已知,即可求得答案;(2)点P 在C 上,点Q 在直线6x =上,且||||BP BQ =,BP BQ ⊥,过点P 作x 轴垂线,交点为M ,设6x =与x 轴交点为N ,可得PMB BNQ ≅△△,可求得P 点坐标,求出直线AQ 的直线方程,根据点到直线距离公式和两点距离公式,即可求得APQ 的面积. 【解析】(1)222:1(05)25x y C m m +=<<,∴5a =,b m =,根据离心率4c e a ====,解得54m =或54m =-(舍), ∴C 的方程为22214255x y ⎛⎫ ⎪⎝⎭+=,即221612525x y +=;(2)不妨设P ,Q 在x 轴上方点P 在C 上,点Q 在直线6x =上,且||||BP BQ =,BP BQ ⊥,过点P 作x 轴垂线,交点为M ,设6x =与x 轴交点为N ,根据题意画出图形,如图:||||BP BQ =,BP BQ ⊥,90PMB QNB ∠=∠=︒,又90PBM QBN ∠+∠=︒,90BQN QBN ∠+∠=︒,∴PBM BQN ∠=∠,根据三角形全等条件“AAS ”,可得PMB BNQ ≅△△,221612525x y +=,∴(5,0)B ,∴651PM BN ==-=,设P 点为(,)P P x y , 可得P 点纵坐标为1P y =,将其代入221612525x y +=,可得21612525P x +=,解得3P x =或3P x =-,∴P 点为(3,1)或(3,1)-, ①当P 点为(3,1)时,故532MB =-=,PMB BNQ ≅△△,∴||||2MB NQ ==,可得Q 点为(6,2),画出图象,如图(5,0)A -,(6,2)Q ,可求得直线AQ 的直线方程为211100x y -+=,根据点到直线距离公式可得P 到直线AQ 的距离为5d ===,根据两点间距离公式可得AQ ==,∴APQ 面积为15252⨯=;②当P 点为(3,1)-时,故5+38MB ==,PMB BNQ ≅△△,∴||||8MB NQ ==,可得Q 点为(6,8),画出图象,如图(5,0)A -,(6,8)Q ,可求得直线AQ 的直线方程为811400x y -+=,根据点到直线距离公式可得P 到直线AQ 的距离为d ===,根据两点间距离公式可得AQ ==∴APQ面积为1522=,综上所述,APQ 面积为52. 【名师点睛】本题主要考查了求椭圆标准方程和求三角形面积问题,解题关键是掌握椭圆的离心率定义和数形结合求三角形面积,考查了分析能力和计算能力,属于中档题.8.已知A 、B 分别为椭圆E :2221x y a+=(a >1)的左、右顶点,G 为E 的上顶点,8AG GB ⋅=,P 为直线x =6上的动点,P A 与E 的另一交点为C ,PB 与E 的另一交点为D . (1)求E 的方程;(2)证明:直线CD 过定点.【试题来源】2020年全国统一高考数学试卷(新课标Ⅱ)【答案】(1)2219x y +=;(2)证明详见解析. 【分析】(1)由已知可得(),0A a -, (),0B a ,()0,1G ,即可求得21AG GB a ⋅=-,结合已知即可求得29a =,问题得解.(2)设()06,P y ,可得直线AP 的方程为()039y y x =+,联立直线AP 的方程与椭圆方程即可求得点C 的坐标为20022003276,99y y y y ⎛⎫-+ ⎪++⎝⎭,同理可得点D 的坐标为2002200332,11y y y y ⎛⎫-- ⎪++⎝⎭,当203y ≠时,可表示出直线CD 的方程,整理直线CD 的方程可得()02043233y y x y ⎛⎫=- ⎪-⎝⎭即可知直线过定点3,02⎛⎫ ⎪⎝⎭,当203y =时,直线CD :32x =,直线过点3,02⎛⎫⎪⎝⎭,命题得证. 【解析】(1)依据题意作出如下图象:由椭圆方程222:1(1)x E y a a+=>可得(),0A a -, (),0B a ,()0,1G ,∴(),1AG a =,(),1GB a =-,∴218AG GB a ⋅=-=,∴29a =,∴椭圆方程为2219x y +=; (2)设()06,P y ,则直线AP 的方程为()()00363y y x -=+--,即()039y y x =+联立直线AP 的方程与椭圆方程可得()2201939x y y y x ⎧+=⎪⎪⎨⎪=+⎪⎩,整理得()2222000969810y x y x y +++-=,解得3x =-或20203279y x y -+=+将20203279y x y -+=+代入直线()039y y x =+可得02069y y y =+ 所以点C 的坐标为20022003276,99y y y y ⎛⎫-+ ⎪++⎝⎭.同理可得点D 的坐标为2002200332,11y y y y ⎛⎫-- ⎪++⎝⎭, 当203y ≠时,∴直线CD 的方程为0022********2000022006291233327331191y y y y y y y x y y y y y y ⎛⎫-- ⎪++⎛⎫⎛⎫--⎝⎭-=-⎪ ⎪-+-++⎝⎭⎝⎭-++, 整理可得()()()2220000002224200000832338331116963y y y y y y y x x y y y y y +⎛⎫⎛⎫--+=-=- ⎪ ⎪+++--⎝⎭⎝⎭, 整理得()()0002220004243323333y y y y x x y y y ⎛⎫=+=- ⎪---⎝⎭,所以直线CD 过定点3,02⎛⎫ ⎪⎝⎭.当203y =时,直线CD :32x =,直线过点3,02⎛⎫ ⎪⎝⎭. 故直线CD 过定点3,02⎛⎫⎪⎝⎭. 9.已知椭圆C 1:22221x y a b+=(a >b >0)的右焦点F 与抛物线C 2的焦点重合,C 1的中心与C 2的顶点重合.过F 且与x 轴垂直的直线交C 1于A ,B 两点,交C 2于C ,D 两点,且|CD |=43|AB |.(1)求C 1的离心率;(2)若C 1的四个顶点到C 2的准线距离之和为12,求C 1与C 2的标准方程. 【试题来源】2020年全国统一高考数学试卷(新课标Ⅱ)【答案】(1)12;(2)1C :2211612x y +=,2C : 28y x =.【分析】(1)根据题意求出2C 的方程,结合椭圆和抛物线的对称性不妨设,A C 在第一象限,运用代入法求出,,,A B C D 点的纵坐标,根据4||||3CD AB =,结合椭圆离心率的公式进行求解即可;(2)由(1)可以得到椭圆的标准方程,确定椭圆的四个顶点坐标,再确定抛物线的准线方程,最后结合已知进行求解即可;【解析】(1)因为椭圆1C 的右焦点坐标为(c,0)F ,所以抛物线2C 的方程为24y cx =,其中c =不妨设,A C 在第一象限,因为椭圆1C 的方程为22221x y a b+=,所以当x c =时,有222221c y b y a b a +=⇒=±,因此,A B 的纵坐标分别为2b a ,2ba -;因为抛物线2C 的方程为24y cx =,所以当x c =时,有242y c c y c =⋅⇒=±,所以,C D 的纵坐标分别为2c ,2c -,故22||b AB a=,||4CD c =.由4||||3CD AB =得2843b c a=,即2322()c c a a ⋅=-,解得2c a =-(舍去),12c a =.所以1C 的离心率为12.(2)由(1)知2a c =,b =,故22122:143x y C c c +=,所以1C 的四个顶点坐标分别为(2,0)c ,(2,0)c -,),(0,),2C 的准线为x c =-.由已知得312c c c c +++=,即2c =.所以1C 的标准方程为2211612x y +=,2C 的标准方程为28y x =.10.已知椭圆C 1:22221x y a b+=(a >b >0)的右焦点F 与抛物线C 2的焦点重合,C 1的中心与C 2的顶点重合.过F 且与x 轴垂直的直线交C 1于A ,B 两点,交C 2于C ,D 两点,且|CD |=43|AB |. (1)求C 1的离心率;(2)设M 是C 1与C 2的公共点,若|MF |=5,求C 1与C 2的标准方程.【试题来源】2020年全国统一高考数学试卷(新课标Ⅱ)【答案】(1)12;(2)221:13627x y C +=,22:12C y x =.【分析】(1)求出AB 、CD ,利用43CD AB =可得出关于a 、c 的齐次等式,可解得椭圆1C 的离心率的值;(2)由(1)可得出1C 的方程为2222143x y c c+=,联立曲线1C 与2C 的方程,求出点M 的坐标,利用抛物线的定义结合5MF =可求得c 的值,进而可得出1C 与2C 的标准方程.【解析】(1)(),0F c ,AB x ⊥轴且与椭圆1C 相交于A 、B 两点,则直线AB 的方程为x c =,联立22222221x cx y a b a b c=⎧⎪⎪+=⎨⎪=+⎪⎩,解得2x c b y a =⎧⎪⎨=±⎪⎩,则22bAB a =,抛物线2C 的方程为24y cx =,联立24x c y cx =⎧⎨=⎩,解得2x cy c =⎧⎨=±⎩,4CD c ∴=,43CD AB =,即2843b c a=,223b ac =,即222320c ac a +-=,即22320e e +-=,01e <<,解得12e =,因此,椭圆1C 的离心率为12;(2)由(1)知2ac =,b =,椭圆1C 的方程为2222143x y c c+=,联立222224143y cx x y c c ⎧=⎪⎨+=⎪⎩,消去y 并整理得22316120x cx c +-=, 解得23x c =或6x c =-(舍去),由抛物线的定义可得25533c MF c c =+==,解得3c =. 因此,曲线1C 的标准方程为2213627x y +=,曲线2C 的标准方程为212y x =.11.已知椭圆2222:1x y C a b+=的右焦点为(1,0),且经过点(0,1)A .(1)求椭圆C 的方程;(2)设O 为原点,直线:(1)l y kx t t =+≠±与椭圆C 交于两个不同点P ,Q ,直线AP 与x 轴交于点M ,直线AQ 与x 轴交于点N ,若|OM |·|ON |=2,求证:直线l 经过定点. 【试题来源】2019年北京市高考数学试卷【答案】(1)2212x y +=;(2)见解析.【分析】(1)由题意确定a ,b 的值即可确定椭圆方程;(2)设出直线方程,联立直线方程与椭圆方程确定OM ,ON 的表达式,结合根与系数关系确定t 的值即可证明直线恒过定点. 【解析】(1)因为椭圆的右焦点为(1,0),所以1225; 因为椭圆经过点(0,1)A ,所以1b =,所以2222a b c =+=,故椭圆的方程为2212x y +=.(2)设1122(,),(,)P x y Q x y ,联立2212(1)x y y kx t t ⎧+=⎪⎨⎪=+≠⎩得222(12)4220k x ktx t +++-=,21212224220,,1212kt t x x x x k k -∆>+=-=++,121222()212ty y k x x t k +=++=+,222212121222()12t k y y k x x kt x x t k-=+++=+. 直线111:1y AP y x x --=,令0y =得111x x y -=-,即111x OM y -=-; 同理可得221x ON y -=-.因为2OM ON =,所以1212121212211()1x x x x y y y y y y --==---++;221121t t t -=-+,解之得0t =,所以直线方程为y kx =,所以直线l 恒过定点(0,0). 【名师点睛】解决直线与椭圆的综合问题时,要注意:(1)注意观察应用题设中的每一个条件,明确确定直线、椭圆的条件;(2)强化有关直线与椭圆联立得出一元二次方程后的运算能力,重视根与系数之间的关系、弦长、斜率、三角形的面积等问题.12.已知抛物线C :x 2=−2py 经过点(2,−1). (1)求抛物线C 的方程及其准线方程;(2)设O 为原点,过抛物线C 的焦点作斜率不为0的直线l 交抛物线C 于两点M ,N ,直线y =−1分别交直线OM ,ON 于点A 和点B .求证:以AB 为直径的圆经过y 轴上的两个定点.【试题来源】2019年北京市高考数学试卷 【答案】(1) 24x y =-,1y =;(2)见解析.【分析】(1)由题意结合点的坐标可得抛物线方程,进一步可得准线方程;(2)联立准线方程和抛物线方程,结合根与系数关系可得圆心坐标和圆的半径,从而确定圆的方程,最后令x =0即可证得题中的结论.【解析】(1)将点()2,1-代入抛物线方程:()2221p =⨯-可得2p =,故抛物线方程为24x y =-,其准线方程为1y =. (2)很明显直线l 的斜率存在,焦点坐标为()0,1-,设直线方程为1y kx =-,与抛物线方程24x y =-联立可得2440x kx +-=.故:12124,4x x k x x +=-=-.设221212,,,44x x M x N x ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭,则12,44OM ON x x k k =-=-, 直线OM 的方程为14x y x =-,与1y =-联立可得14,1A x ⎛⎫- ⎪⎝⎭,同理可得24,1B x ⎛⎫- ⎪⎝⎭, 易知以AB 为直径的圆的圆心坐标为1222,1x x ⎛⎫+-⎪⎝⎭,圆的半径为1222x x -,且:()1212122222x x k x x x x ++==,12222x x -==则圆的方程为()()()2222141x k y k -++=+,令0x =整理可得2230y y +-=,解得123,1y y =-=,即以AB 为直径的圆经过y 轴上的两个定点()()0,3,0,1-.【名师点睛】本题主要考查抛物线方程的求解与准线方程的确定,直线与抛物线的位置关系,圆的方程的求解及其应用等知识,意在考查学生的转化能力和计算求解能力.13.已知曲线C :y =22x ,D 为直线y =12-上的动点,过D 作C 的两条切线,切点分别为A ,B .(1)证明:直线AB 过定点: (2)若以E (0,52)为圆心的圆与直线AB 相切,且切点为线段AB 的中点,求四边形ADBE 的面积.【试题来源】2019年全国统一高考数学试卷(新课标Ⅱ) 【答案】(1)见详解;(2) 3或【分析】(1)可设11(,)A x y ,22(,)B x y ,1(,)2D t -然后求出A ,B 两点处的切线方程,比如AD :1111()2y x x t +=-,因为BD 也有类似的形式,从而求出带参数直线AB 方程,最后求出它所过的定点.(2)由(1)得带参数的直线AB 方程和抛物线方程联立,再通过M 为线段AB 的中点,EM AB ⊥得出t 的值,从而求出M 坐标和EM 的值,12,d d 分别为点,D E 到直线AB 的距离,则12d d ==,结合弦长公式和根与系数关系代入求解即可.【解析】(1)设1(,)2D t -,11(,)A x y ,则21112y x =. 因为212y x =,所以y'x =.则切线DA 的斜率为1x ,故1111()2y x x t +=-,整理得112210tx y -+=.设22(,)B x y ,同理得222210tx y -+=. 11(,)A x y ,22(,)B x y 都满足直线方程2210tx y -+=.于是直线2210tx y -+=过点,A B ,而两个不同的点确定一条直线,所以直线AB 方程为2210tx y -+=.即2(21)0tx y +-+=,当20,210x y =-+=时等式恒成立.所以直线AB 恒过定点1(0,)2.(2)由(1)得直线AB 的方程为12y tx =+.由2122y tx xy ⎧=+⎪⎪⎨⎪=⎪⎩,可得2210x tx --=, 于是2121212122,1,()121x x t x x y y t x x t +==-+=++=+212|||2(1)AB x x t =-==+.设12,d d 分别为点,D E 到直线AB的距离,则12d d ==.因此,四边形ADBE 的面积()(2121||32S AB d d t =+=+ 设M 为线段AB 的中点,则21,2M t t ⎛⎫+⎪⎝⎭, 由于EM AB ⊥,而()2,2EM t t =-,AB 与向量(1,)t 平行, 所以()220t t t +-=,解得0t =或1t =±. 当0t =时,3S =;当1t =±时S =因此,四边形ADBE 的面积为3或.【名师点睛】此题第一问是圆锥曲线中的定点问题和第二问是求面积类型,属于常规题型,按部就班的求解就可以.思路较为清晰,但计算量不小.14. 设椭圆22221(0)x y a b a b+=>>的左焦点为F ,左顶点为A ,上顶点为B.已知|2||OA OB =(O 为原点). (1)求椭圆的离心率;(2)设经过点F 且斜率为34的直线l 与椭圆在x 轴上方的交点为P ,圆C 同时与x 轴和直线l 相切,圆心C 在直线4x =上,且OC AP ∥,求椭圆的方程. 【试题来源】2019年天津市高考数学试卷【答案】(1)12;(2)2211612x y +=.【分析】(1)2b =,结合椭圆中,,a b c 的关系,得到222()2a c =+,化简得出12c a =,从而求得其离心率;(2)结合(1)的结论,设出椭圆的方程2222143x y c c+=,写出直线的方程,两个方程联立,求得交点的坐标,利用直线与圆相切的条件,列出等量关系式,求得2c =,从而得到椭圆的方程.【解析】(1)设椭圆的半焦距为c2b =, 又由222a b c =+,消去b得222)a c =+,解得12c a =,所以,椭圆的离心率为12. (2)由(1)知,2,a c b ==,故椭圆方程为2222143x y c c+=,由题意,(,0)F c -,则直线l 的方程为3()4y x c =+, 点P 的坐标满足22221433()4x y c c y x c ⎧+=⎪⎪⎨⎪=+⎪⎩,消去y 并化简,得到2276130x cx c +-=,解得1213,7c x c x ==-,代入到l 的方程,解得1239,214y c y c ==-, 因为点P 在x 轴的上方,所以3(,)2P c c ,由圆心在直线4x =上,可设(4,)C t ,因为OC AP ∥,且由(1)知(2,0)A c -,故3242ct c c=+,解得2t =,因为圆C 与x 轴相切,所以圆的半径为2,又由圆C 与l2=,解得2c =, 所以椭圆的方程为2211612x y +=.15.如图,已知点(10)F ,为抛物线22(0)y px p =>的焦点,过点F 的直线交抛物线于,A B两点,点C 在抛物线上,使得ABC 的重心G 在x 轴上,直线AC 交x 轴于点Q ,且Q 在点F 右侧.记,AFG CQG △△的面积为12,S S .(1)求p 的值及抛物线的准线方程;(2)求12S S 的最小值及此时点G 的坐标.【试题来源】2019年浙江省高考数学试卷 【答案】(1)2,1x =-;(2)12+,()2,0G . 【分析】(1)由焦点坐标确定p 的值和准线方程即可;(2)设出直线方程,联立直线方程和抛物线方程,结合根与系数关系求得面积的表达式,最后结合均值不等式的结论即可求得12S S 的最小值和点G 的坐标. 【解析】(1)由题意可得12p=,则2,24p p ==, 抛物线方程为24y x =,准线方程为1x =-. (2)设()()1122,,,A x y B x y ,设直线AB 的方程为()1,0y k x k =->,与抛物线方程24y x =联立可得()2222240k x k x k -++=,故:2222242,1kx x x x +=+=, ()12121242,4y y k x x y y k+=+-==-⨯=-,设点C 的坐标为()33,C x y ,由重心坐标公式可得1233G x x x x ++=321423x k ⎛⎫++ ⎝=⎪⎭,1233G y y y y ++=3143y k =⎛⎫+ ⎪⎝⎭, 令0G y =可得34y k =-,则233244y x k==.即222144123382G k x k k ⎛⎫⎛⎫+++ ⎪ ⎪⎝⎭⎝=⎭=,由斜率公式可得131322311313444AC y y y y k y y x x y y --===-+-,直线AC 的方程为()33134y y x x y y -=-+,令0y =可得()()231331331334444Q y y y y y y y y yx x -+-+=+=+=-,故()11112218121323118223G F y S x x y y k k ⎡⎤⎛⎫⎛⎫+-⨯=⨯- ⎪=⨯-⨯ ⎪⎢⎥⎝⎭⎝=⨯⎭⎣⎦, 且()()32213311822423Q G y y y S x x y k ⎛⎫+ ⎪⎝⎭⎡⎤=⨯-⨯-=---⎢⎥⎣⎦, 由于34y k=-,代入上式可得12222833y S k k k ⎛⎫=-- ⎪⎝⎭,由12124,4y y y y k +==-可得1144y y k -=,则12144y k y =-,则()()()2211122121112281233222284433y y S y S y y k k k y k -==⎛⎫-+--⎛⎫⨯- ⎭⎪⎝⎭⎪⎝()212142488168y y =--++-()212132124828168yy ≥-=+-⨯+-.当且仅当21214888y y -=-,即21843y =+162y = 此时121424y k y ==-,281223G x k ⎛⎫+= ⎪⎝⎭=,则点G 的坐标为()2,0G . 【名师点睛】直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似,一般要用到根与系数的关系,本题主要考查了抛物线准线方程的求解,直线与抛物线的位置关系,三角形重心公式的应用,基本不等式求最值的方法等知识,意在考查学生的转化能力和计算求解能力.16.设椭圆22221(0)x y a b a b+=>>的左焦点为F ,上顶点为B .已知椭圆的短轴长为4,5. (1)求椭圆的方程;(2)设点P 在椭圆上,且异于椭圆的上、下顶点,点M 为直线PB 与x 轴的交点,点N 在y 轴的负半轴上.若||||ON OF =(O 为原点),且OP MN ⊥,求直线PB 的斜率.【试题来源】2019年天津市高考数学试卷【答案】(1)22154x y +=(2230230. 【分析】(1)由题意得到关于a ,b ,c 的方程,解方程可得椭圆方程;(2)联立直线方程与椭圆方程确定点P 的坐标,从而可得OP 的斜率,然后利用斜率公式可得MN 的斜率表达式,最后利用直线垂直的充分必要条件得到关于斜率的方程,解方程可得直线的斜率. 【解析】(1) 设椭圆的半焦距为c ,依题意,524,5c b a ==,又222a b c =+,可得5a =b =2,c =1.所以,椭圆方程为22154x y +=.(2)由题意,设()()(),0,,0P P P M P x y x M x ≠.设直线PB 的斜率为()0k k ≠,。
2018--2020年高考数学试题分类汇编数列附答案详解

2018--2020年⾼考数学试题分类汇编数列附答案详解2018---2020年⾼考数学试题分类汇编数列⼀、选择题.1、(2018年⾼考全国卷1理科4)记S n 为等差数列{a n }的前n 项和.若3S 3=S 2+S 4,a 1=2,则a 5=()A .﹣12B .﹣10C .10D .12答案:B解析:∵S n 为等差数列{a n }的前n 项和,3S 3=S 2+S 4,a 1=2,∴=a 1+a 1+d +4a 1+d ,把a 1=2,代⼊得d=﹣3 ∴a 5=2+4×(﹣3)=﹣10.故选:B .2、(2019年⾼考全国I 卷理科9)记n S 为等差数列{}n a 的前n 项和.已知4505S a ==,,则 A .25n a n =- B . 310n a n =-C .228n S n n =-D .2122n S n n =- 答案:A解析:有等差数列的性质可知54,0641514=+==+=d a a d a S ,解得2,31=-=d a所以52,42-=-=n a n n S n n ,故选A 。
3、(2019年⾼考全国III 卷理科5⽂科6)已知各项均为正数的等⽐数列{a n }的前4项和为15,且a 5=3a 3+4a 1,则a 3=A . 16B . 8C .4D . 2答案:C解析:由题意有154=S ,即151)1(414=--=qq a S 由题意有a 5=3a 3+4a 1,即1214143a q a q a +=,故 (q 2-4)(q 2+1)=0因为各项均为正数,所以q>0,所以q=2将q=2代⼊151)1(414=--=qq a S .得a 1=1、所以43=a 故选C 4、(2019年⾼考全国III 卷⽂理科9)执⾏下边的程序框图,如果输⼊的ε为0.01,则输出s 的值等于 A.4122-B.5122-C.6122-D.7122-答案:C解析:等⽐数列前n 项和,0,1==s x 不满⾜01.0s x 不满⾜01.011,41+==s x 不满⾜01.01....41211,1281++++==s x 满⾜01.05、(2019年⾼考北京卷理科2⽂科4)执⾏如图所⽰的程序框图,输出的s 值为(A )1(B )2(C )3(D )4 答案:B解析:k=1,s=1, s=2212312?=?-,k<3,故执⾏循环体k=1+1=2,2222322s ?==?-;此时k=2<3,故继续执⾏循环体k=3,2222322s ?==?-,此时k=3,结束循环,输出s=2.故答案为:B.6、(2019年⾼考浙江卷10)设,a b R ∈,数列{}n a 中1a a =,21n n a a b +=+,21n n a a b +=+,则()A.当12b =时,1010a > B.当14b =时,1010a >C.当2b =-时,1010a >D.当2b =-时,1010a > 答案:A解答:选项B :不动点满⾜2211()042x x x -+=-=,如图,若11(0,)2a a =∈,12n a <,排除;如图若a 为不动点12,则12n a =;选项C :不动点满⾜22192()024x x x --=--=,不动点为2x =,令2a =,则210n a =<,排除;选项D :不动点满⾜221174()024x x x --=--=,不动点为1712x =,令1712a =,则171102n a =<,排除;选项A :证明:当12b =时,2211122a a =+≥,2321324a a =+≥,2431171216a a =+≥≥,处理⼀:可依次迭代到n a ;处理⼆:当4n ≥时,221112n n n a a a +=+≥≥,则117117171161616log 2log log 2n n n n a a a -++>?>,则1217()(4)16n n a n +≥≥,则641022617164(64631 1114710161616210()6a ?≥=+=++?+>++>,故选A.7、(2020?北京卷)在等差数列{}n a 中,19a =-,31a =-.记12(1,2,)n n T a a a n ==……,则数列{}n T (). A. 有最⼤项,有最⼩项 B. 有最⼤项,⽆最⼩项 C. ⽆最⼤项,有最⼩项 D. ⽆最⼤项,⽆最⼩项答案:B解:由题意可知,等差数列的公差511925151a a d --+===--,则其通项公式为:()()11912211n a a n d n n =+-=-+-?=-,注意到123456701a a a a a a a <<<<<<=<<,且由50T <可知()06,i T i i N <≥∈,由()117,ii i T a i i N T -=>≥∈可知数列{}n T 不存在最⼩项,由于1234569,7,5,3,1,1a a a a a a =-=-=-=-=-=,故数列{}n T 中的正项只有有限项:263T =,46315945T =?=.故数列{}n T 中存在最⼤项,且最⼤项为4T .故选:B.8、(2020?全国2卷)北京天坛的圜丘坛为古代祭天的场所,分上、中、下三层,上层中⼼有⼀块圆形⽯板(称为天⼼⽯),环绕天⼼⽯砌9块扇⾯形⽯板构成第⼀环,向外每环依次增加9块,下⼀层的第⼀环⽐上⼀层的最后⼀环多9块,向外每环依次也增加9块,已知每层环数相同,且下层⽐中层多729块,则三层共有扇⾯形⽯板(不含天⼼⽯)()A. 3699块B. 3474块C. 3402块D. 3339块答案:C解:设第n 环天⽯⼼块数为n a ,第⼀层共有n 环,则{}n a 是以9为⾸项,9为公差的等差数列,9(1)99n a n n =+-?=,设n S 为{}n a 的前n 项和,则第⼀层、第⼆层、第三层的块数分别为232,,n n n n n S S S S S --,因为下层⽐中层多729块,所以322729n n n n S S S S -=-+,即3(927)2(918)2(918)(99)7292222n n n n n n n n ++++-=-+即29729n =,解得9n =,所以32727(9927)34022n S S +?===. 故选:C9、(2020?全国2卷)数列{}n a 中,12a =,m n m n a a a +=,若155121022k k k a a a ++++++=-,则k =()A. 2B. 3C. 4D. 5答案:C解:在等式m n m n a a a +=中,令1m =,可得112n n n a a a a +==,12n na a +∴=,所以,数列{}n a 是以2为⾸项,以2为公⽐的等⽐数列,则1222n nn a -=?=,()()()()1011011105101210122122212211212k k k k k k a a a a ++++++?-?-∴+++===-=---,1522k +∴=,则15k +=,解得4k =.故选:C.10、(2020?全国2卷)0-1周期序列在通信技术中有着重要应⽤.若序列12na a a 满⾜{0,1}(1,2,)i a i ∈=,且存在正整数m ,使得(1,2,)i m i a a i +==成⽴,则称其为0-1周期序列,并称满⾜(1,2,)i m i a a i +==的最⼩正整数m 为这个序列的周期.对于周期为m 的0-1序列12na a a ,11()(1,2,,1)mi i k i C k a a k m m +===-∑是描述其性质的重要指标,下列周期为5的0-1序列中,满⾜1()(1,2,3,4)5C k k ≤=的序列是()A. 11010B. 11011C. 10001D. 11001答案:C解:由i m i a a +=知,序列i a 的周期为m ,由已知,5m =,511(),1,2,3,45i i k i C k a a k +===∑,对于选项A ,511223344556111111(1)()(10000)55555i i i C a a a a a a a a a a a a +===++++=++++=≤∑52132435465711112(2)()(01010)5555i i i C a a a a a a a a a a a a +===++++=++++=∑,不满⾜;对于选项B ,51122334455611113(1)()(10011)5555i i i C a a a a a a a a a a a a +===++++=++++=∑,不满⾜;对于选项D ,51122334455611112(1)()(10001)5555i i i C a a a a a a a a a a a a +===++++=++++=∑,不满⾜;故选:C⼆、填空题.1、(2018年⾼考全国卷1理科14)记S n 为数列{a n }的前n 项和.若S n =2a n +1,则S 6= ﹣63 .答案:63-解析:S n 为数列{a n }的前n 项和,S n =2a n +1,①当n=1时,a 1=2a 1+1,解得a 1=﹣1,当n ≥2时,S n ﹣1=2a n ﹣1+1,②,由①﹣②可得a n =2a n ﹣2a n ﹣1,∴a n =2a n ﹣1,∴{a n }是以﹣1为⾸项,以2为公⽐的等⽐数列,∴S 6==﹣63,故答案为:﹣632、(2018年⾼考北京卷理科9)设{a n }是等差数列,且a 1=3,a 2+a 5=36,则{a n }的通项公式为 a n =6n ﹣3 .解:∵{a n }是等差数列,且a 1=3,a 2+a 5=36,∴,解得a 1=3,d=6,∴a n =a 1+(n ﹣1)d=3+(n ﹣1)×6=6n ﹣3.∴{a n }的通项公式为a n =6n ﹣3.故答案为:a n =6n ﹣3.3、(2018年⾼考浙江卷10)已知a 1,a 2,a 3,a 4成等⽐数列,且a 1+a 2+a 3+a 4=ln (a 1+a 2+a 3),若a 1>1,则()A .a 1<a 3,a 2<a 4B .a 1>a 3,a 2<a 4C .a 1<a 3,a 2>a 4D .a 1>a 3,a 2>a 4【解答】解:a 1,a 2,a 3,a 4成等⽐数列,由等⽐数列的性质可知,奇数项符号相同,偶数项符号相同, a 1>1,设公⽐为q ,当q >0时,a 1+a 2+a 3+a 4>a 1+a 2+a 3,a 1+a 2+a 3+a 4=ln (a 1+a 2+a 3),不成⽴,即:a 1>a 3,a 2>a 4,a 1<a 3,a 2<a 4,不成⽴,排除A 、D .当q=﹣1时,a 1+a 2+a 3+a 4=0,ln (a 1+a 2+a 3)>0,等式不成⽴,所以q ≠﹣1;当q <﹣1时,a 1+a 2+a 3+a 4<0,ln (a 1+a 2+a 3)>0,a 1+a 2+a 3+a 4=ln (a 1+a 2+a 3)不成⽴,当q ∈(﹣1,0)时,a 1>a 3>0,a 2<a 4<0,并且a 1+a 2+a 3+a 4=ln (a 1+a 2+a 3),能够成⽴,故选:B .4、(2019年⾼考全国I 卷⽂科14)记S n 为等⽐数列{a n }的前n 项和.若13314a S ==,,则S 4=___________.答案:85 解析:设数列的公⽐为q ,则有43123213=++=++=q q a a a S 解得21-=q ,所以854=S 5、(2019年⾼考全国I 卷理科14)记S n 为等⽐数列{a n }的前n 项和.若214613a a a ==,,则S 5=____________.答案:3121解析:由624a a =得51621q a q a =,解得3=q ,所以31211)1(515=--=q q a S6、(2019年⾼考全国III 卷理科14)记S n 为等差数列{a n }的前n 项和,12103a a a =≠,,则105S S =___________. 答案:4解析:因为,312a a =所以1a +,13a d =即d a =12,则()()4215211051101510=?+?+=a a a a S S 7、(2019年⾼考全国III 卷⽂科14)记S n 为等差数列{a n }的前n 项和,若375,13a a ==,则10S =___________.答案:100解析:由题意得136,521713=+==+=d a a d a a ,解得2,11==d a 所以100291010110=?+=d a S8、(2019年⾼考北京卷理科10)设等差数列{a n }的前n 项和为S n ,若a 2=-3,S 5=-10,则a 3= ________ . S n 的最⼩值为_______。
2018--2020年高考数学试题分类汇编三角函数附答案详解

2018-2019年高考数学试题分类汇编三角函数一、选择题.1、(2018年高考全国卷1文科8)已知函数f(x)=2cos2x﹣sin2x+2,则()A.f(x)的最小正周期为π,最大值为3B.f(x)的最小正周期为π,最大值为4C.f(x)的最小正周期为2π,最大值为3D.f(x)的最小正周期为2π,最大值为4解:函数f(x)=2cos2x﹣sin2x+2,=2cos2x﹣sin2x+2sin2x+2cos2x,=4cos2x+sin2x,=3cos2x+1,=,=,故函数的最小正周期为π,函数的最大值为,故选:B.2、(2018年高考全国卷1文科11)已知角α的顶点为坐标原点,始边与x轴的非负半轴重合,终边上有两点A(1,a),B(2,b),且cos2α=,则|a﹣b|=()A.B.C.D.1解:∵角α的顶点为坐标原点,始边与x轴的非负半轴重合,终边上有两点A(1,a),B(2,b),且cos2α=,∴cos2α=2cos2α﹣1=,解得cos2α=,∴|cosα|=,∴|sinα|==,|tanα|=||=|a﹣b|===.故选:B.3、(2018年高考全国卷3理科4)若sinα=,则cos2α=()A.B.C.﹣ D.﹣解:∵sinα=,∴cos2α=1﹣2sin2α=1﹣2×=.故选:B.4、(2018年高考全国卷3理科9文科11)△ABC的内角A,B,C的对边分别为a,b,c.若△ABC的面积为,则C=()A.B.C.D.解:∵△ABC的内角A,B,C的对边分别为a,b,c.△ABC的面积为,∴S△ABC==,∴sinC==cosC,∵0<C<π,∴C=.故选:C.5、(2018年高考全国卷2理科6文科7)在△ABC中,cos=,BC=1,AC=5,则AB=()A.4 B. C. D.2解:在△ABC中,cos=,cosC=2×=﹣,BC=1,AC=5,则AB====4.故选:A.6、(2018年高考全国卷2理科10)若f(x)=cosx﹣sinx在[﹣a,a]是减函数,则a的最大值是()A.B.C. D.π解:f(x)=cosx﹣sinx=﹣(sinx﹣cosx)=,由,k∈Z,得,k∈Z,取k=0,得f(x)的一个减区间为[,],由f(x)在[﹣a,a]是减函数,得,∴.则a的最大值是.故选:A.7、(2018年高考全国卷2文科)10.(5分)若f(x)=cosx﹣sinx在[0,a]是减函数,则a的最大值是()A.B.C. D.π解:f(x)=cosx﹣sinx=﹣(sinx﹣cosx)=﹣sin(x﹣),由﹣+2kπ≤x﹣≤+2kπ,k∈Z,得﹣+2kπ≤x≤+2kπ,k∈Z,取k=0,得f(x)的一个减区间为[﹣,],由f(x)在[0,a]是减函数,得a≤.则a的最大值是.故选:C8、(2018年高考全国卷3文科4)若sinα=,则cos2α=()A.B.C.﹣ D.﹣解:∵sinα=,∴cos2α=1﹣2sin2α=1﹣2×=.故选:B.9、(2018年高考全国卷3文科6)函数f(x)=的最小正周期为()A.B.C.πD.2π解:函数f(x)===sin2x的最小正周期为=π,故选:C.10、(2018年高考北京卷理科7)在平面直角坐标系中,记d为点P(cosθ,sinθ)到直线x﹣my﹣2=0的距离.当θ、m变化时,d的最大值为()A.1 B.2 C.3 D.4解:由题意d==,tanα=﹣,∴当sin(θ+α)=﹣1时,d max=1+≤3.∴d的最大值为3.故选:C.11、(2018年高考北京卷文科7)在平面直角坐标系中,,,,是圆x2+y2=1上的四段弧(如图),点P其中一段上,角α以Ox为始边,OP为终边.若tanα<cosα<sinα,则P所在的圆弧是()A.B.C.D.解:A.在AB段,正弦线小于余弦线,即cosα<sinα不成立,故A不满足条件.B.在CD段正切线最大,则cosα<sinα<tanα,故B不满足条件.C.在EF段,正切线,余弦线为负值,正弦线为正,满足tanα<cosα<sinα,D.在GH段,正切线为正值,正弦线和余弦线为负值,满足cosα<sinα<tanα不满足tanα<cosα<sinα.故选:C.12、(2018年高考天津卷文理科6)将函数y=sin(2x+)的图象向右平移个单位长度,所得图象对应的函数()A.在区间[,]上单调递增B.在区间[,π]上单调递减C.在区间[,]上单调递增D.在区间[,2π]上单调递减解:将函数y=sin(2x+)的图象向右平移个单位长度,得到的函数为:y=sin2x,增区间满足:﹣+2kπ≤2x ≤,k ∈Z , 减区间满足:≤2x ≤,k ∈Z ,∴增区间为[﹣+kπ,+kπ],k ∈Z , 减区间为[+kπ,+kπ],k ∈Z ,∴将函数y=sin (2x+)的图象向右平移个单位长度,所得图象对应的函数在区间[,]上单调递增.故选:A .13、(2019年高考全国I 卷文理科5)函数f (x )=2sin cos ++x xx x 在[,]-ππ的图像大致为A .B .C .D .答案:D解析:因为)()(x f x f -=-,所以)(x f 为奇函数又01)(2>-=πππf ,124412)2(22>+=+=πππππf ,故选D 14、(2019年高考全国I 卷理科11)关于函数()sin |||sin |f x x x =+有下述四个结论:①f (x )是偶函数②f (x )在区间(2π,π)单调递增③f (x )在[,]-ππ有4个零点 ④f (x )的最大值为2其中所有正确结论的编号是 A .①②④ B .②④C .①④D .①③答案:C解析:由)(|sin |||sin |)sin(|||sin )(x f x x x x x f =+=-+-=-,故①正确;),2(ππ∈x 时,x x x x f sin 2sin sin )(=+=,函数递减,故②错误;],0[π∈x 时,x x x x f sin 2sin sin )(=+=,函数有2个零点,0)()0(==πf f ,而],0[π∈x 时0)()0(=-=πf f ,所以函数有且只有3个零点,故③错误;函数为偶函数,只需讨论0>x ,N k k k x ∈+∈),2,2(πππ时,x x x x f sin 2sin sin )(=+=,最大值为2,N k k k x ∈++∈),22,2(ππππ时,0sin sin )(=-=x x x f ,故函数最大值为2,故④正确。
2018高考数学试题分类汇编

设变量x ,y 满足约束条件5,24,1,0,x y x y x y y +≤⎧⎪-≤⎪⎨-+≤⎪⎪≥⎩ 则目标函数35z x y =+的最大值为(A) 6 (B) 19 (C) 21 (D) 45 已知,a b ∈R ,且360a b -+=,则128ab +的最小值为 . 我国古代数学著作《张邱建算经》中记载百鸡问题:“今有鸡翁一,值钱五;鸡母一,值钱三;鸡雏三,值钱一。
凡百钱,买鸡百只,问鸡翁、母、雏各几何?”设鸡翁,鸡母,鸡雏个数分别为x ,y ,z ,则100,153100,3x y z x y z ++=⎧⎪⎨++=⎪⎩当81z =时,x =___________,y =___________. 若,x y 满足约束条件0,26,2,x y x y x y -≥⎧⎪+≤⎨⎪+≥⎩则3z x y =+的最小值是___________,最大值是___________.在51()2x x-的展开式中,2x 的系数为 .已知圆2220x y x +-=的圆心为C ,直线21,2232⎧=-+⎪⎪⎨⎪=-⎪⎩x t y t (t 为参数)与该圆相交于A ,B 两点,则ABC△的面积为 .二项式831()2x x+的展开式的常数项是___________. 从1,3,5,7,9中任取2个数字,从0,2,4,6中任取2个数字,一共可以组成___________个没有重复数字的四位数.(用数字作答)有编号互不相同的五个砝码,期中5克,3克,1克砝码各两个,从中随机挑选三个,则这三个砝码的总质量为9克的概率为___________(结果用最简分数表示)一卷理科一卷文科二卷理科三卷文科北京文科江苏解析:()()'1,'22f x g x x ==+,若存在,则有()()200002211222x x x x ⎧+-=⋅⋅⋅⎪⎨=+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⎪⎩; 由()2可得:012x =-代入()1不符合,因此不存在;()()1'2,'f x ax g x x ==;根据题意有:()()200001ln 1122ax x ax x⎧-=⋅⋅⋅⎪⎨=⋅⋅⋅⋅⋅⋅⋅⋅⋅⎪⎩且00x >; 根据()2得到012x a =代入()1得到2ea =;()()()21'2,'x be x f x x g x x -=-=;根据题意有:()()()020000201122x x be x a x be x x x ⎧-+=⋅⋅⋅⋅⋅⋅⋅⎪⎪⎨-⎪-=⋅⋅⎪⎩根据()2有:0200020011x x be x x -=>⇒<<-;问题转化为:22000201x x a x -++=-;()3220000120x x a x x -++-+=()()32310m x x x a x =-++-=,转化为()m x 存在零点0x ,且001x <<;因为:()()00,120m a m =-<=>; 所以:恒存在零点001x <<;所以:对任意0a >,均存在0b >,使得存在"S 点"已知2log e =a ,ln 2b =,11log 3c =,则a ,b ,c 的大小关系为(A) a b c >> (B) b a c >> (C) c b a >> (D) c a b >>将函数sin(2)5y x π=+的图象向右平移10π个单位长度,所得图象对应的函数 (A)在区间35[,]44ππ上单调递增(B)在区间3[,]4ππ上单调递减 (C)在区间53[,]42ππ上单调递增(D)在区间3[,2]2ππ上单调递减 已知0a >,函数222,0,()22,0.x ax a x f x x ax a x ⎧++≤=⎨-+->⎩若关于x 的方程()f x ax =恰有2个互异的实数解,则a的取值范围是 .已知13313711log ,(),log 245a b c ===,则,,a b c 的大小关系为(A )a b c >> (B )b a c >> (C )c b a >>(D )c a b >>将函数sin(2)5y x π=+的图象向右平移10π个单位长度,所得图象对应的函数(A )在区间[,]44ππ- 上单调递增 (B )在区间[,0]4π上单调递减(C )在区间[,]42ππ 上单调递增 (D )在区间[,]2ππ 上单调递减已知函数f (x )=e x ln x ,f ′(x )为f (x )的导函数,则f ′(1)的值为__________.已知a ∈R ,函数()22220220x x a x f x x x a x ⎧++-≤⎪=⎨-+->⎪⎩,,,.若对任意x ∈[–3,+∞),f (x )≤x 恒成立,则a 的取值范围是__________.函数y =||2x sin2x 的图象可能是A .B .C .D .在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .若a =7,b =2,A =60°,则sin B =___________,c =___________.已知λ∈R ,函数f (x )=24,43,x x x x x λλ-≥⎧⎪⎨-+<⎪⎩,当λ=2时,不等式f (x )<0的解集是___________.若函数f (x )恰有2个零点,则λ的取值范围是___________.设常数a R ∈,函数()()2log f x x a =+,若()f x 的反函数的图像经过点()3,1,则()a =;已知112,1,,,1,2,322α⎧⎫∈---⎨⎬⎩⎭.若函数()f x x α=为奇函数,且在()0,+∞上递减,则()α=;已知常数0a >,函数()22x x f x ax =+的图像经过点61,,,55P p Q q ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭,若236p qpq +=,则()a =;设D 是含l 的的有限实数集, ()f x 是定义在D 上的函数。
专题06 立体几何(解答题)——三年(2018-2020)高考真题理科数学分项汇编
专题06立体几何(解答题)1.【2020年高考全国Ⅰ卷理数】如图,D 为圆锥的顶点,O 是圆锥底面的圆心,AE 为底面直径,AE AD =.ABC △是底面的内接正三角形,P 为DO 上一点,PO =.(1)证明:PA ⊥平面PBC ;(2)求二面角B PC E --的余弦值.【解析】(1)设DO a =,由题设可得,,63PO a AO a AB a ===,2PA PB PC a ===.因此222PA PB AB +=,从而PA PB ⊥.又222PA PC AC +=,故PA PC ⊥.所以PA ⊥平面PBC .(2)以O 为坐标原点,OE的方向为y 轴正方向,||OE 为单位长,建立如图所示的空间直角坐标系O xyz -.由题设可得1(0,1,0),(0,1,0),(,,0),(0,0,222E A C P --.所以1(,,0),(0,1,222EC EP =--=- .设(,,)x y z =m 是平面PCE 的法向量,则00EP EC ⎧⋅=⎪⎨⋅=⎪⎩m m,即021022y z x y ⎧-+=⎪⎪⎨⎪--=⎪⎩,可取3(3=-m .由(1)知2(0,1,)2AP =是平面PCB 的一个法向量,记AP = n ,则cos ,|||5⋅==n m n m n m |.所以二面角B PC E --的余弦值为5.【点晴】本题主要考查线面垂直的证明以及利用向量求二面角的大小,考查学生空间想象能力,数学运算能力,是一道容易题.2.【2020年高考全国Ⅱ卷理数】如图,已知三棱柱ABC -A 1B 1C 1的底面是正三角形,侧面BB 1C 1C 是矩形,M ,N 分别为BC ,B 1C 1的中点,P 为AM 上一点,过B 1C 1和P 的平面交AB 于E ,交AC 于F.(1)证明:AA 1∥MN ,且平面A 1AMN ⊥平面EB 1C 1F ;(2)设O 为△A 1B 1C 1的中心,若AO ∥平面EB 1C 1F ,且AO =AB ,求直线B 1E 与平面A 1AMN 所成角的正弦值.【解析】(1)因为M ,N 分别为BC ,B 1C 1的中点,所以1MN CC ∥.又由已知得AA 1∥CC 1,故AA 1∥MN .因为△A 1B 1C 1是正三角形,所以B 1C 1⊥A 1N .又B 1C 1⊥MN ,故B 1C 1⊥平面A 1AMN .所以平面A 1AMN ⊥平面11EB C F .(2)由已知得AM ⊥BC .以M 为坐标原点,MA的方向为x 轴正方向, MB 为单位长,建立如图所示的空间直角坐标系M -xyz ,则AB =2,AM连接NP ,则四边形AONP 为平行四边形,故1(,0)333PM E =.由(1)知平面A 1AMN ⊥平面ABC ,作NQ ⊥AM ,垂足为Q ,则NQ ⊥平面ABC .设(,0,0)Q a,则1(NQ B a =,故112(,,|333B E a B E =--=.又(0,1,0)=-n 是平面A 1AMN的法向量,故1111πsin(,)cos ,2||B E B E B E B E ⋅-===⋅n n n |n |所以直线B 1E 与平面A 1AMN.3.【2020年高考全国Ⅱ卷理数】如图,在长方体1111ABCD A B C D -中,点,E F 分别在棱11,DD BB 上,且12DE ED =,12BF FB =.(1)证明:点1C 在平面AEF 内;(2)若2AB =,1AD =,13AA =,求二面角1A EF A --的正弦值.【解析】设AB a =,AD b =,1AA c =,如图,以1C 为坐标原点,11C D的方向为x 轴正方向,建立空间直角坐标系1C xyz -.(1)连结1C F ,则1(0,0,0)C ,(,,)A a b c ,2(,0,)3E a c ,1(0,,)3F b c ,1(0,,)3EA b c = ,11(0,,)3C F b c = ,得1EA C F = .因此1EA C F ∥,即1,,,A E F C 四点共面,所以点1C 在平面AEF 内.(2)由已知得(2,1,3)A ,(2,0,2)E ,(0,1,1)F ,1(2,1,0)A ,(0,1,1)AE =-- ,(2,0,2)AF =-- ,1(0,1,2)A E =-,1(2,0,1)A F =-.设1(,,)x y z =n 为平面AEF 的法向量,则110,0,AE AF ⎧⋅=⎪⎨⋅=⎪⎩n n 即0,220,y z x z --=⎧⎨--=⎩可取1(1,1,1)=--n .设2n 为平面1A EF 的法向量,则22110,0,A E A F ⎧⋅=⎪⎨⋅=⎪⎩n n 同理可取21(,2,1)2=n .因为1212127cos ,||||⋅〈〉==⋅n n n n n n ,所以二面角1A EF A --的正弦值为427.4.【2020年高考江苏】在三棱柱ABC -A 1B 1C 1中,AB ⊥AC ,B 1C ⊥平面ABC ,E ,F 分别是AC ,B 1C 的中点.(1)求证:EF ∥平面AB 1C 1;(2)求证:平面AB 1C ⊥平面ABB 1.【解析】因为,E F 分别是1,AC B C 的中点,所以1EF AB ∥.又/EF ⊂平面11AB C ,1AB ⊂平面11AB C ,所以EF ∥平面11AB C .(2)因为1B C ⊥平面ABC ,AB ⊂平面ABC ,所以1B C AB ⊥.又AB AC ⊥,1B C ⊂平面11AB C ,AC ⊂平面1AB C ,1,B C AC C = 所以AB ⊥平面1AB C .又因为AB ⊂平面1ABB ,所以平面1AB C ⊥平面1ABB .【点睛】本小题主要考查线面平行的证明,考查面面垂直的证明,属于中档题.5.【2020年高考浙江】如图,在三棱台ABC —DEF 中,平面ACFD ⊥平面ABC ,∠ACB =∠ACD =45°,DC =2BC .(Ⅰ)证明:EF ⊥DB ;(Ⅱ)求直线DF 与平面DBC 所成角的正弦值.【解析】(Ⅰ)如图,过点D 作DO AC ⊥,交直线AC 于点O ,连结OB .由45ACD ∠=︒,DO AC ⊥得CD =,由平面ACFD ⊥平面ABC 得DO ⊥平面ABC ,所以DO BC ⊥.由45ACB ∠=︒,122BC CD ==得BO BC ⊥.所以BC ⊥平面BDO ,故BC ⊥DB .由三棱台ABC DEF -得BC EF ∥,所以EF DB ⊥.(Ⅱ)方法一:过点O 作OH BD ⊥,交直线BD 于点H ,连结CH .由三棱台ABC DEF -得DF CO ∥,所以直线DF 与平面DBC 所成角等于直线CO 与平面DBC 所成角.由BC ⊥平面BDO 得OH BC ⊥,故OH ⊥平面BCD ,所以OCH ∠为直线CO 与平面DBC 所成角.设CD =.由2,DO OC BO BC ====,得BD OH ==所以sin OH OCH OC ∠==因此,直线DF 与平面DBC 所成角的正弦值为3.方法二:由三棱台ABC DEF -得DF CO ∥,所以直线DF 与平面DBC 所成角等于直线CO 与平面DBC 所成角,记为θ.如图,以O 为原点,分别以射线OC ,OD 为y ,z 轴的正半轴,建立空间直角坐标系O xyz -.设CD =.由题意知各点坐标如下:(0,0,0),(1,1,0),(0,2,0),(0,0,2)O B C D .因此(0,2,0),(1,1,0),(0,2,2)OC BC CD ==-=-.设平面BCD 的法向量(,,z)x y =n .由0,0,BC CD ⎧⋅=⎪⎨⋅=⎪⎩ n n 即0220x y y z -+=⎧⎨-+=⎩,可取(1,1,1)=n .所以|sin |cos ,|3|||OC OC OC θ⋅===⋅n |n n |.因此,直线DF 与平面DBC所成角的正弦值为3.【点睛】本题主要考查空间点、线、面位置关系,线面垂直的判定定理的应用,直线与平面所成的角的求法,意在考查学生的直观想象能力和数学运算能力,属于基础题.6.【2020年高考天津】如图,在三棱柱111ABC A B C -中,1CC ⊥平面,,2ABC AC BC AC BC ⊥==,13CC =,点,D E 分别在棱1AA 和棱1CC 上,且2,1,AD CE M ==为棱11A B 的中点.(Ⅰ)求证:11C M B D ⊥;(Ⅱ)求二面角1B B E D --的正弦值;(Ⅲ)求直线AB 与平面1DB E 所成角的正弦值.【解析】依题意,以C 为原点,分别以1,,CA CB CC的方向为x 轴,y 轴,z 轴的正方向建立空间直角坐标系(如图),可得1(0,0,0),(2,0,0),(0,2,0),(0,0,3)C A B C ,11(2,0,3),(0,2,3),(2,0,1),(0,0,2)A B D E ,(1,1,3)M .(Ⅰ)证明:依题意,1(1,1,0)C M = ,1(2,2,2)B D =-- ,从而112200C M B D ⋅=-+=,所以11C M B D ⊥.(Ⅱ)解:依题意,(2,0,0)CA = 是平面1BB E 的一个法向量,1(0,2,1)EB =,(2,0,1)ED =- .设(,,)x y z =n 为平面1DB E 的法向量,则10,0,EB ED ⎧⋅=⎪⎨⋅=⎪⎩n n 即20,20.y z x z +=⎧⎨-=⎩不妨设1x =,可得(1,1,2)=-n .因此有|||6cos ,6|A CA C CA ⋅〈〉==n n n ,于是30sin ,6CA 〈〉= n .所以,二面角1B B E D --的正弦值为306.(Ⅲ)解:依题意,(2,2,0)AB =-.由(Ⅱ)知(1,1,2)=-n 为平面1DB E 的一个法向量,于是3cos ,3||||AB AB AB ⋅==-n n n .所以,直线AB 与平面1DB E所成角的正弦值为3.7.【2019年高考全国Ⅰ卷理数】如图,直四棱柱ABCD–A 1B 1C 1D 1的底面是菱形,AA 1=4,AB =2,∠BAD =60°,E ,M ,N 分别是BC ,BB 1,A 1D 的中点.(1)证明:MN ∥平面C 1DE ;(2)求二面角A−MA 1−N 的正弦值.【答案】(1)见解析;(2)105.【解析】(1)连结B 1C ,ME .因为M ,E 分别为BB 1,BC 的中点,所以ME ∥B 1C ,且ME =12B 1C .又因为N 为A 1D 的中点,所以ND =12A 1D .由题设知A 1B 1= DC ,可得B 1C = A 1D ,故ME =ND ,因此四边形MNDE 为平行四边形,MN ∥ED .又MN ⊄平面EDC 1,所以MN ∥平面C 1DE .(2)由已知可得DE ⊥DA .以D 为坐标原点,DA的方向为x 轴正方向,建立如图所示的空间直角坐标系D −xyz ,则(2,0,0)A ,A 1(2,0,4),2)M ,(1,0,2)N ,1(0,0,4)A A =-,1(2)A M =--,1(1,0,2)A N =--,(0,MN =.设(,,)x y z =m 为平面A 1MA 的法向量,则1100A M A A ⎧⋅=⎪⎨⋅=⎪⎩m m ,所以2040x z z ⎧-+-=⎪⎨-=⎪⎩,.可取=m .设(,,)p q r =n 为平面A 1MN 的法向量,则100MN A N ⎧⋅=⎪⎨⋅=⎪⎩,.n n所以020p r ⎧=⎪⎨--=⎪⎩,.可取(2,0,1)=-n .于是15cos ,||5⋅〈〉==‖m n m n m n ,所以二面角1A MA N --的正弦值为5.【名师点睛】本题考查线面平行关系的证明、空间向量法求解二面角的问题.求解二面角的关键是能够利用垂直关系建立空间直角坐标系,从而通过求解法向量夹角的余弦值来得到二面角的正弦值,属于常规题型.8.【2019年高考全国Ⅱ卷理数】如图,长方体ABCD –A 1B 1C 1D 1的底面ABCD 是正方形,点E 在棱AA 1上,BE ⊥EC 1.(1)证明:BE ⊥平面EB 1C 1;(2)若AE =A 1E ,求二面角B –EC –C 1的正弦值.【答案】(1)证明见解析;(2)2.【解析】(1)由已知得,11B C ⊥平面11ABB A ,BE ⊂平面11ABB A ,故11B C ⊥BE .又1BE EC ⊥,所以BE ⊥平面11EB C .(2)由(1)知190BEB ∠=︒.由题设知Rt ABE △≌11Rt A B E △,所以45AEB ∠=︒,故AE AB =,12AA AB =.以D 为坐标原点,DA 的方向为x 轴正方向,||DA为单位长,建立如图所示的空间直角坐标系D –xyz ,则C (0,1,0),B (1,1,0),1C (0,1,2),E (1,0,1),(1,0,0)CB = ,(1,1,1)CE =- ,1(0,0,2)CC = .设平面EBC 的法向量为n =(x ,y ,x ),则0,0,CB CE ⎧⋅=⎪⎨⋅=⎪⎩ n n 即0,0,x x y z =⎧⎨-+=⎩所以可取n =(0,1,1)--.设平面1ECC 的法向量为m =(x ,y ,z ),则10,0,CC CE ⎧⋅=⎪⎨⋅=⎪⎩ m m 即20,0.z x y z =⎧⎨-+=⎩所以可取m =(1,1,0).于是1cos ,||||2⋅<>==-n m n m n m .所以,二面角1B EC C --的正弦值为32.【名师点睛】本题考查了利用线面垂直的性质定理证明线线垂直以及线面垂直的判定,考查了利用空间向量求二角角的余弦值,以及同角的三角函数关系,考查了数学运算能力.9.【2019年高考全国Ⅲ卷理数】图1是由矩形ADEB ,Rt △ABC 和菱形BFGC 组成的一个平面图形,其中AB =1,BE =BF =2,∠FBC =60°,将其沿AB ,BC 折起使得BE 与BF 重合,连结DG ,如图2.(1)证明:图2中的A ,C ,G ,D 四点共面,且平面ABC ⊥平面BCGE ;(2)求图2中的二面角B−CG−A 的大小.【答案】(1)见解析;(2)30 .【解析】(1)由已知得AD BE ,CG BE ,所以AD CG ,故AD ,CG 确定一个平面,从而A ,C ,G ,D 四点共面.由已知得AB ⊥BE ,AB ⊥BC ,故AB ⊥平面BCGE .又因为AB ⊂平面ABC ,所以平面ABC ⊥平面BCGE .(2)作EH ⊥BC ,垂足为H .因为EH ⊂平面BCGE ,平面BCGE ⊥平面ABC ,所以EH ⊥平面ABC .由已知,菱形BCGE 的边长为2,∠EBC =60°,可求得BH =1,EH 3.以H 为坐标原点,HC的方向为x 轴的正方向,建立如图所示的空间直角坐标系H –xyz,则A (–1,1,0),C (1,0,0),G (2,03),CG =(1,0,3),AC =(2,–1,0).设平面ACGD 的法向量为n =(x ,y ,z ),则0,0,CG AC ⎧⋅=⎪⎨⋅=⎪⎩ n n 即30,20.x x y ⎧=⎪⎨-=⎪⎩所以可取n =(3,6,3又平面BCGE 的法向量可取为m =(0,1,0),所以3cos ,||||2⋅〈〉==n m n m n m .因此二面角B –CG –A 的大小为30°.【名师点睛】本题是很新颖的立体几何考题,首先是多面体折叠问题,考查考生在折叠过程中哪些量是不变的,再者折叠后的多面体不是直棱柱,最后通过建系的向量解法将求二面角转化为求二面角的平面角问题,突出考查考生的空间想象能力.10.【2019年高考北京卷理数】如图,在四棱锥P –ABCD 中,PA ⊥平面ABCD ,AD ⊥CD ,AD ∥BC ,PA =AD =CD =2,BC =3.E 为PD 的中点,点F 在PC 上,且13PF PC =.(1)求证:CD ⊥平面PAD ;(2)求二面角F–AE–P 的余弦值;(3)设点G 在PB 上,且23PG PB =.判断直线AG 是否在平面AEF内,说明理由.【答案】(1)见解析;(2)33;(3)见解析.【解析】(1)因为PA ⊥平面ABCD ,所以PA ⊥CD .又因为AD ⊥CD ,所以CD ⊥平面PAD .(2)过A 作AD 的垂线交BC 于点M .因为PA ⊥平面ABCD ,所以PA ⊥AM ,PA ⊥AD .如图建立空间直角坐标系A −xyz ,则A (0,0,0),B (2,-1,0),C (2,2,0),D (0,2,0),P (0,0,2).因为E 为PD 的中点,所以E (0,1,1).所以(0,1,1),(2,2,2),(0,0,2)AE PC AP ==-= .所以1222224,,,,,3333333PF PC AF AP PF ⎛⎫⎛⎫==-=+= ⎪ ⎪⎝⎭⎝⎭.设平面AEF 的法向量为n =(x ,y ,z ),则0,0,AE AF ⎧⋅=⎪⎨⋅=⎪⎩ n n 即0,2240.333y z x y z +=⎧⎪⎨++=⎪⎩令z =1,则1,1y x =-=-.于是=(1,1,1)--n .又因为平面PAD 的法向量为p =(1,0,0),所以cos ,||3⋅〈〉==-‖n p n p n p .由题知,二面角F −AE −P 为锐角,所以其余弦值为33.(3)直线AG 在平面AEF 内.因为点G 在PB 上,且2,(2,1,2)3PG PB PB ==-- ,所以2424422,,,,,3333333PG PB AG AP PG ⎛⎫⎛⎫==--=+=- ⎪ ⎪⎝⎭⎝⎭.由(2)知,平面AEF 的法向量=(1,1,1)--n .所以4220333AG ⋅=-++= n .所以直线AG 在平面AEF 内.【名师点睛】(1)由题意利用线面垂直的判定定理即可证得题中的结论;(2)建立空间直角坐标系,结合两个半平面的法向量即可求得二面角F −AE −P 的余弦值;(3)首先求得点G 的坐标,然后结合平面AEF 的法向量和直线AG 的方向向量即可判断直线是否在平面内.11.【2019年高考天津卷理数】如图,AE ⊥平面ABCD ,,CF AE AD BC ∥∥,,AD AB ⊥1,2AB AD AE BC ====.(1)求证:BF ∥平面ADE ;(2)求直线CE 与平面BDE 所成角的正弦值;(3)若二面角E BD F --的余弦值为13,求线段CF的长.【答案】(1)见解析;(2)49;(3)87.【解析】依题意,可以建立以A 为原点,分别以AB AD AE ,,的方向为x 轴,y 轴,z 轴正方向的空间直角坐标系(如图),可得(0,0,0),(1,0,0),(1,2,0),(0,1,0)A B C D ,(0,0,2)E .设(0)CF h h =>>,则()1,2,F h .(1)依题意,(1,0,0)AB = 是平面ADE 的法向量,又(0,2,)BF h = ,可得0BF AB ⋅=,又因为直线BF ⊄平面ADE ,所以BF ∥平面ADE .(2)依题意,(1,1,0),(1,0,2),(1,2,2)BD BE CE =-=-=-- .设(,,)x y z =n 为平面BDE 的法向量,则0,0,BD BE ⎧⋅=⎪⎨⋅=⎪⎩ n n 即0,20,x y x z -+=⎧⎨-+=⎩不妨令1z =,可得(2,2,1)=n .因此有4cos ,9||||CE CE CE ⋅==- n n n .所以,直线CE 与平面BDE 所成角的正弦值为49.(3)设(,,)x y z =m 为平面BDF 的法向量,则0,0,BD BF ⎧⋅=⎪⎨⋅=⎪⎩ m m 即0,20,x y y hz -+=⎧⎨+=⎩不妨令1y =,可得21,1,h ⎛⎫=- ⎪⎝⎭m .由题意,有||1cos ,||||3⋅〈〉===m n m n m n ,解得87h =.经检验,符合题意.所以,线段CF 的长为87.【名师点睛】本小题主要考查直线与平面平行、二面角、直线与平面所成的角等基础知识.考查用空间向量解决立体几何问题的方法.考查空间想象能力、运算求解能力和推理论证能力.12.【2019年高考江苏卷】如图,在直三棱柱ABC -A 1B 1C 1中,D ,E 分别为BC ,AC 的中点,AB =BC .求证:(1)A 1B 1∥平面DEC 1;(2)BE ⊥C 1E.【答案】(1)见解析;(2)见解析.【解析】(1)因为D ,E 分别为BC ,AC 的中点,所以ED ∥AB .在直三棱柱ABC−A 1B 1C 1中,AB ∥A 1B 1,所以A 1B 1∥ED .又因为ED ⊂平面DEC 1,A 1B 1⊄平面DEC 1,所以A 1B 1∥平面DEC 1.(2)因为AB =BC ,E 为AC 的中点,所以BE ⊥AC .因为三棱柱ABC−A 1B 1C 1是直棱柱,所以CC 1⊥平面ABC .又因为BE ⊂平面ABC ,所以CC 1⊥BE .因为C 1C ⊂平面A 1ACC 1,AC ⊂平面A 1ACC 1,C 1C ∩AC =C ,所以BE ⊥平面A 1ACC 1.因为C 1E ⊂平面A 1ACC 1,所以BE ⊥C 1E .【名师点睛】本小题主要考查直线与直线、直线与平面、平面与平面的位置关系等基础知识,考查空间想象能力和推理论证能力.13.【2019年高考浙江卷】如图,已知三棱柱111ABC A B C -,平面11A ACC ⊥平面ABC ,90ABC ∠=︒,1130,,,BAC A A A C AC E F ∠=︒==分别是AC ,A 1B 1的中点.(1)证明:EF BC ⊥;(2)求直线EF 与平面A 1BC 所成角的余弦值.【答案】(1)见解析;(2)35.【解析】方法一:(1)连接A 1E ,因为A 1A =A 1C ,E 是AC 的中点,所以A 1E ⊥AC .又平面A 1ACC 1⊥平面ABC ,A 1E ⊂平面A 1ACC 1,平面A 1ACC 1∩平面ABC =AC ,所以,A 1E ⊥平面ABC ,则A 1E ⊥BC .又因为A 1F ∥AB ,∠ABC =90°,故BC ⊥A 1F .所以BC ⊥平面A 1EF .因此EF ⊥BC .(2)取BC 中点G ,连接EG ,GF ,则EGFA 1是平行四边形.由于A 1E ⊥平面ABC ,故A 1E ⊥EG ,所以平行四边形EGFA 1为矩形.由(1)得BC ⊥平面EGFA 1,则平面A 1BC ⊥平面EGFA 1,所以EF 在平面A 1BC 上的射影在直线A 1G 上.连接A 1G 交EF 于O ,则∠EOG 是直线EF 与平面A 1BC 所成的角(或其补角).不妨设AC =4,则在Rt △A 1EG 中,A 1E ,EG .由于O 为A 1G 的中点,故122A G EO OG ===,所以2223cos 25EO OG EG EOG EO OG +-∠==⋅.因此,直线EF 与平面A 1BC 所成角的余弦值是35.方法二:(1)连接A 1E ,因为A 1A =A 1C ,E 是AC 的中点,所以A 1E ⊥AC .又平面A 1ACC 1⊥平面ABC ,A 1E ⊂平面A 1ACC 1,平面A 1ACC 1∩平面ABC =AC ,所以,A 1E ⊥平面ABC .如图,以点E 为原点,分别以射线EC ,EA 1为y ,z 轴的正半轴,建立空间直角坐标系E –xyz .不妨设AC =4,则A 1(0,0,3),B 3,1,0),1(3,3,23)B ,33,,3)22F ,C (0,2,0).因此,33,,23)22EF = ,(3,1,0)BC = .由0EF BC ⋅=得EF BC ⊥.(2)设直线EF 与平面A 1BC 所成角为θ.由(1)可得1=(310)=(0223)BC A C -- ,,,.设平面A 1BC 的法向量为n ()x y z =,,,由100BC A C ⎧⋅=⎪⎨⋅=⎪⎩ n n ,得3030x y y z ⎧+=⎪⎨-=⎪⎩,取n (131)=,,故||4sin |cos |=5|||EF EF EF θ⋅==⋅ ,n n n |,因此,直线EF 与平面A 1BC 所成的角的余弦值为35.【名师点睛】本题主要考查空间点、线、面位置关系,直线与平面所成的角等基础知识,同时考查空间想象能力和运算求解能力.14.【2018年高考全国Ⅰ卷理数】如图,四边形ABCD 为正方形,,E F 分别为,AD BC 的中点,以DF 为折痕把DFC △折起,使点C 到达点P 的位置,且PF BF ⊥.(1)证明:平面PEF ⊥平面ABFD ;(2)求DP 与平面ABFD 所成角的正弦值.【答案】(1)见解析;(2)3 4 .【解析】方法一:(1)由已知可得,BF⊥PF,BF⊥EF,所以BF⊥平面PEF.又BF⊂平面ABFD,所以平面PEF⊥平面ABFD.(2)在平面DEF中,过P作PH⊥EF于点H,连接DH,如图,由于EF为平面ABCD和平面PEF的交线,PH⊥EF,则PH⊥平面ABFD,故PH⊥DH.则DP与平面ABFD所成的角为PDH∠.在三棱锥P-DEF中,可以利用等体积法求PH.因为DE∥BF且PF⊥BF,所以PF⊥DE,又△PDF≌△CDF,所以∠FPD=∠FCD=90°,所以PF⊥PD,由于DE∩PD=D,则PF⊥平面PDE,故13F PDE PDE V PF S-=⋅△,因为BF∥DA且BF⊥平面PEF,所以DA⊥平面PEF,所以DE⊥EP.设正方形的边长为2a,则PD=2a,DE=a,在△PDE 中,PE =,所以22PDE S a =△,故36F PDE V a -=,又2122DEF S a a a =⋅=△,所以232F PDE V PH a a -==,所以在△PHD 中,sin 4PH PDH PD ∠==,故DP 与平面ABFD 所成角的正弦值为34.方法二:(1)由已知可得,BF ⊥PF ,BF ⊥EF ,所以BF ⊥平面PEF .又BF ⊂平面ABFD ,所以平面PEF ⊥平面ABFD .(2)作PH ⊥EF ,垂足为H .由(1)得,PH ⊥平面ABFD .以H 为坐标原点,HF 的方向为y 轴正方向,||BF 为单位长,建立如图所示的空间直角坐标系H −xyz .由(1)可得,DE ⊥PE .又DP =2,DE =1,所以PE .又PF =1,EF =2,故PE ⊥PF .可得33,22PH EH ==.则33(0,0,0),(0,0,(1,,0),(1,,2222H P D DP --= (0,0,2HP = 为平面ABFD 的法向量.设DP 与平面ABFD 所成角为θ,则34sin ||4||||HP DP HP DP θ⋅=== .所以DP 与平面ABFD 所成角的正弦值为34.15.【2018年高考全国II 卷理数】如图,在三棱锥P ABC -中,AB BC ==,4PA PB PC AC ====,O 为AC 的中点.(1)证明:PO ⊥平面ABC ;(2)若点M 在棱BC 上,且二面角M PA C --为30︒,求PC 与平面PAM 所成角的正弦值.C【答案】(1)见解析;(2)4.【解析】(1)因为4AP CP AC ===,O 为AC 的中点,所以OP AC ⊥,且OP =连结OB .因为2AB BC AC ==,所以ABC △为等腰直角三角形,且OB AC ⊥,122OB AC ==.由222OP OB PB +=知PO OB ⊥.由,OP OB OP AC ⊥⊥知PO ⊥平面ABC .(2)如图,以O 为坐标原点,OB uu u r 的方向为x 轴正方向,建立空间直角坐标系O xyz -.由已知得(0,0,0),(2,0,0),(0,2,0),(0,2,0),(0,0,23),(0,2,23),O B A C P AP -=uu u r 取平面PAC 的法向量(2,0,0)OB =uu u r.设(,2,0)(02)M a a a -<≤,则(,4,0)AM a a =-uuu r .设平面PAM 的法向量为(,,)x y z =n .由0,0AP AM ⋅=⋅=uu u r uuu r n n 得230(4)0y z ax a y ⎧+=⎪⎨+-=⎪⎩,可取3(3,)a a a =--n ,所以2223(cos ,23(4)3OB a a a =-++uu u r n .由已知可得3|cos ,|2OB =uu u r n .222233223(4)3a a a -++.解得4a =-(舍去),43a =.所以83434(,,333=--n .又(0,2,23)PC =-uu u r ,所以3cos ,4PC =uu u r n .所以PC 与平面PAM 所成角的正弦值为34.16.【2018年高考全国Ⅲ卷理数】如图,边长为2的正方形ABCD 所在的平面与半圆弧 CD所在平面垂直,M 是 CD上异于C ,D 的点.(1)证明:平面AMD ⊥平面BMC ;(2)当三棱锥M ABC -体积最大时,求面MAB 与面MCD 所成二面角的正弦值.【答案】(1)见解析;(2)255.【解析】(1)由题设知,平面CMD ⊥平面ABCD ,交线为CD .因为BC ⊥CD ,BC ⊂平面ABCD ,所以BC ⊥平面CMD ,故BC ⊥DM .因为M 为 CD上异于C ,D 的点,且DC 为直径,所以DM ⊥CM .又BC CM =C ,所以DM ⊥平面BMC .而DM ⊂平面AMD ,故平面AMD ⊥平面BMC .(2)以D 为坐标原点,DA的方向为x 轴正方向,建立如图所示的空间直角坐标系D −xyz .当三棱锥M −ABC 体积最大时,M 为 CD的中点.由题设得(0,0,0),(2,0,0),(2,2,0),(0,2,0),(0,1,1)D A B C M ,(2,1,1),(0,2,0),(2,0,0)AM AB DA =-== 设(,,)x y z =n 是平面MAB 的法向量,则0,0.AM AB ⎧⋅=⎪⎨⋅=⎪⎩ n n 即20,20.x y z y -++=⎧⎨=⎩可取(1,0,2)=n .DA 是平面MCD 的法向量,因此cos ,5||||DA DA DA ⋅== n n n,sin ,5DA = n ,所以面MAB 与面MCD所成二面角的正弦值是5.17.【2018年高考江苏卷】如图,在正三棱柱ABC −A 1B 1C 1中,AB =AA 1=2,点P ,Q 分别为A 1B 1,BC 的中点.(1)求异面直线BP 与AC 1所成角的余弦值;(2)求直线CC 1与平面AQC 1所成角的正弦值.【答案】(1)20;(2)5.【解析】如图,在正三棱柱ABC −A 1B 1C 1中,设AC ,A 1C 1的中点分别为O ,O 1,则OB ⊥OC ,OO 1⊥OC ,OO 1⊥OB ,以1,{},OB OC OO 为基底,建立空间直角坐标系O −xyz .因为AB =AA 1=2,所以1110,1,0,,0,1,0,0,1,())()()2,,0,1,2)()A B C A B C --.(1)因为P 为A 1B 1的中点,所以31(,2)22P -,从而131(,2)(0,2,222),BP AC ==- ,故111||310|cos ,|20||||522BP AC BP AC BP AC ⋅==⋅⨯ .因此,异面直线BP 与AC 1所成角的余弦值为31020.(2)因为Q 为BC 的中点,所以31(,0)2Q ,因此33(,0)2AQ = ,11(0,2,2),(0,0,2)AC CC == .设n =(x ,y ,z )为平面AQC 1的一个法向量,则10,0,AQ AC ⎧⎪⎨⎪⎩⋅=⋅= n n 即330,22220.x y y z +=⎨⎪+=⎩不妨取(3,1,1)=-n ,设直线CC 1与平面AQC 1所成角为θ,则111||5sin |cos |,|||552CC CC CC |θ==⋅⨯⋅== n n n ,所以直线CC 1与平面AQC 1所成角的正弦值为55.18.【2018年高考江苏卷】在平行六面体1111ABCD A B C D -中,1111,AA AB AB B C =⊥.求证:(1)AB ∥平面11A B C ;(2)平面11ABB A ⊥平面1A BC .【答案】(1)见解析;(2)见解析.【解析】(1)在平行六面体ABCD -A 1B 1C 1D 1中,AB ∥A 1B 1.因为AB ⊄平面A 1B 1C ,A 1B 1⊂平面A 1B 1C ,所以AB ∥平面A 1B 1C .(2)在平行六面体ABCD -A 1B 1C 1D 1中,四边形ABB 1A 1为平行四边形.又因为AA 1=AB ,所以四边形ABB 1A 1为菱形,因此AB 1⊥A 1B .又因为AB 1⊥B 1C 1,BC ∥B 1C 1,所以AB 1⊥BC .又因为A 1B ∩BC =B ,A 1B ⊂平面A 1BC ,BC ⊂平面A 1BC ,所以AB 1⊥平面A 1BC .因为AB 1⊂平面ABB 1A 1,所以平面ABB 1A 1⊥平面A 1BC .19.【2018年高考浙江卷】如图,已知多面体ABCA 1B 1C 1,A 1A ,B 1B ,C 1C 均垂直于平面ABC ,∠ABC =120°,A 1A =4,C 1C =1,AB =BC =B 1B =2.(1)证明:AB 1⊥平面A 1B 1C 1;(2)求直线AC 1与平面ABB 1所成的角的正弦值.【答案】(1)见解析;(2)3913.【解析】方法一:(1)由11112,4,2,,AB AA BB AA AB BB AB ===⊥⊥得11122AB A B ==,所以2221111A B AB AA +=.故111AB A B ⊥.由2BC =,112,1,BB CC ==11,BB BC CC BC ⊥⊥得115B C =,由2,120AB BC ABC ==∠=︒得23AC =由1CC AC ⊥,得113AC =2221111AB B C AC +=,故111AB B C ⊥.因此1AB ⊥平面111A B C .(2)如图,过点1C 作111C D A B ⊥,交直线11A B 于点D ,连结AD .由1AB ⊥平面111A B C 得平面111A B C ⊥平面1ABB ,由111C D A B ⊥得1C D ⊥平面1ABB ,所以1C AD ∠是1AC 与平面1ABB 所成的角.由1111115,22,21B C A B AC ===得1111116cos 77C A B C A B ∠=∠=,所以13C D =,故11139sin 13C D C AD AC ∠==.因此,直线1AC 与平面1ABB 所成的角的正弦值是3913.方法二:(1)如图,以AC 的中点O 为原点,分别以射线OB ,OC 为x ,y 轴的正半轴,建立空间直角坐标系O -xyz.由题意知各点坐标如下:111(0,3,0),(1,0,0),(0,3,4),(1,0,2),3,1),A B A B C --因此111112),(1,2),(0,3),AB A B A C ==-=-uuu r uuu u r uuu u r 由1110AB A B ⋅=uuu r uuu u r 得111AB A B ⊥.由1110AB A C ⋅=uuu r uuu u r 得111AB A C ⊥.所以1AB ⊥平面111A B C .(2)设直线1AC 与平面1ABB 所成的角为θ.由(1)可知11(0,(1,(0,0,2),AC AB BB ===uuu r uu u r uuu r 设平面1ABB 的法向量(,,)x y z =n .由10,0,AB BB ⎧⋅=⎪⎨⋅=⎪⎩uu u r uuu r n n即0,20,x z ⎧+=⎪⎨=⎪⎩可取(=n .所以111|sin |cos ,|13|||AC AC AC θ⋅===⋅uuu r uuu r uuu r n |n n |.因此,直线1AC 与平面1ABB所成的角的正弦值是13.【名师点睛】本题主要考查空间点、线、面位置关系,直线与平面所成的角等基础知识,同时考查空间想象能力和运算求解能力.20.【2018年高考北京卷理数】如图,在三棱柱ABC −111A B C 中,1CC ⊥平面ABC ,D ,E ,F ,G 分别为1AA ,AC ,11A C ,1BB 的中点,AB=BC,AC =1AA =2.(1)求证:AC ⊥平面BEF ;(2)求二面角B−CD −C 1的余弦值;(3)证明:直线FG 与平面BCD 相交.【答案】(1)见解析;(2)(3)见解析.【解析】(1)在三棱柱ABC -A 1B 1C 1中,∵CC 1⊥平面ABC ,∴四边形A 1ACC 1为矩形.又E ,F 分别为AC ,A 1C 1的中点,∴AC ⊥EF .∵AB =BC .∴AC ⊥BE ,∴AC ⊥平面BEF .(2)由(1)知AC ⊥EF ,AC ⊥BE ,EF ∥CC 1.又CC 1⊥平面ABC ,∴EF ⊥平面ABC .∵BE ⊂平面ABC ,∴EF ⊥BE .如图建立空间直角坐标系E -xyz.由题意得B (0,2,0),C (-1,0,0),D (1,0,1),F (0,0,2),G (0,2,1).∴=(201)=(120)CD CB uu u r uu r ,,,,,,设平面BCD 的法向量为()a b c =,,n ,∴00CD CB ⎧⋅=⎪⎨⋅=⎪⎩uu u r uu r n n ,∴2020a c a b +=⎧⎨+=⎩,令a =2,则b =-1,c =-4,∴平面BCD 的法向量(214)=--,,n ,又∵平面CDC 1的法向量为=(020)EB uu r ,,,∴cos =||||EB EB EB ⋅<⋅>=uu r uu r uu r n n n .由图可得二面角B -CD -C 1为钝角,所以二面角B -CD -C 1的余弦值为21.(3)由(2)知平面BCD 的法向量为(214)=--,,n ,∵G (0,2,1),F (0,0,2),∴=(021)GF -uuu r ,,,∴2GF ⋅=-uuu r n ,∴n 与GF uuu r 不垂直,∴GF 与平面BCD 不平行且不在平面BCD 内,∴GF 与平面BCD 相交.21.【2018年高考天津卷理数】如图,AD BC ∥且AD =2BC ,AD CD ⊥,EG AD ∥且EG =AD ,CD FG ∥且CD =2FG ,DG ABCD ⊥平面,DA =DC =DG =2.(1)若M 为CF 的中点,N 为EG 的中点,求证:MN CDE ∥平面;(2)求二面角E BC F --的正弦值;(3)若点P 在线段DG 上,且直线BP 与平面ADGE 所成的角为60°,求线段DP 的长.【答案】(1)见解析;(2)10;(3)3.【解析】本小题主要考查直线与平面平行、二面角、直线与平面所成的角等基础知识.考查用空间向量解决立体几何问题的方法.考查空间想象能力、运算求解能力和推理论证能力.满分13分.依题意,可以建立以D 为原点,分别以DA ,DC ,DG 的方向为x 轴,y 轴,z 轴的正方向的空间直角坐标系(如图),可得D (0,0,0),A (2,0,0),B (1,2,0),C (0,2,0),E (2,0,2),F (0,1,2),G (0,0,2),M (0,32,1),N (1,0,2).(1)依题意DC =(0,2,0),DE =(2,0,2).设n 0=(x ,y ,z )为平面CDE 的法向量,则0000DC DE ⎧⋅=⎪⎨⋅=⎪⎩ ,,n n 即20220y x z =⎧⎨+=⎩,,不妨令z=–1,可得n 0=(1,0,–1).又MN =(1,32-,1),可得00MN ⋅= n ,又因为直线MN ⊄平面CDE ,所以MN ∥平面CDE .(2)依题意,可得BC =(–1,0,0),(122)BE =- ,,,CF =(0,–1,2).设n =(x ,y ,z )为平面BCE 的法向量,则00BC BE ⎧⋅=⎪⎨⋅=⎪⎩,,n n 即0220x x y z -=⎧⎨-+=⎩,,不妨令z =1,可得n =(0,1,1).设m =(x ,y ,z )为平面BCF 的法向量,则00BC CF ⎧⋅=⎪⎨⋅=⎪⎩ ,,m m 即020x y z -=⎧⎨-+=⎩,,不妨令z =1,可得m =(0,2,1).因此有cos<m ,n>=||||⋅=m n m n ,于是sin<m ,n>=10.所以,二面角E –BC –F.(3)设线段DP 的长为h (h ∈[0,2]),则点P 的坐标为(0,0,h ),可得(12)BP h =-- ,,.易知,DC =(0,2,0)为平面ADGE的一个法向量,故cos BP DC BP DC BP DC ⋅<⋅>== ,2,解得h=3∈[0,2]..所以线段DP的长为3专题06立体几何(解答题)1.【2020年高考全国Ⅰ卷理数】如图,D 为圆锥的顶点,O 是圆锥底面的圆心,AE 为底面直径,AE AD =.ABC △是底面的内接正三角形,P 为DO 上一点,6PO DO =.(1)证明:PA ⊥平面PBC ;(2)求二面角B PC E --的余弦值.2.【2020年高考全国Ⅱ卷理数】如图,已知三棱柱ABC -A 1B 1C 1的底面是正三角形,侧面BB 1C 1C 是矩形,M ,N 分别为BC ,B 1C 1的中点,P 为AM 上一点,过B 1C 1和P 的平面交AB 于E ,交AC 于F .(1)证明:AA 1∥MN ,且平面A 1AMN ⊥平面EB 1C 1F ;(2)设O 为△A 1B 1C 1的中心,若AO ∥平面EB 1C 1F ,且AO =AB ,求直线B 1E 与平面A 1AMN 所成角的正弦值.3.【2020年高考全国Ⅱ卷理数】如图,在长方体1111ABCD A B C D -中,点,E F 分别在棱11,DD BB 上,且12DE ED =,12BF FB =.(1)证明:点1C 在平面AEF 内;(2)若2AB =,1AD =,13AA =,求二面角1A EF A --的正弦值.4.【2020年高考江苏】在三棱柱ABC -A 1B 1C 1中,AB ⊥AC ,B 1C ⊥平面ABC ,E ,F 分别是AC ,B 1C 的中点.(1)求证:EF ∥平面AB 1C 1;(2)求证:平面AB 1C ⊥平面ABB 1.5.【2020年高考浙江】如图,在三棱台ABC —DEF 中,平面ACFD ⊥平面ABC ,∠ACB =∠ACD =45°,DC =2BC .(Ⅰ)证明:EF ⊥DB ;(Ⅱ)求直线DF 与平面DBC 所成角的正弦值.6.【2020年高考天津】如图,在三棱柱111ABC A B C -中,1CC ⊥平面,,2ABC AC BC AC BC ⊥==,13CC =,点,D E 分别在棱1AA 和棱1CC 上,且2,1,AD CE M ==为棱11A B 的中点.(Ⅰ)求证:11C M B D ⊥;(Ⅱ)求二面角1B B E D --的正弦值;(Ⅲ)求直线AB 与平面1DB E 所成角的正弦值.7.【2019年高考全国Ⅰ卷理数】如图,直四棱柱ABCD–A 1B 1C 1D 1的底面是菱形,AA 1=4,AB =2,∠BAD =60°,E ,M ,N 分别是BC ,BB 1,A 1D 的中点.(1)证明:MN ∥平面C 1DE ;(2)求二面角A−MA 1−N 的正弦值.8.【2019年高考全国Ⅱ卷理数】如图,长方体ABCD –A 1B 1C 1D 1的底面ABCD 是正方形,点E 在棱AA 1上,BE ⊥EC 1.(1)证明:BE⊥平面EB1C1;(2)若AE=A1E,求二面角B–EC–C1的正弦值.9.【2019年高考全国Ⅲ卷理数】图1是由矩形ADEB,Rt△ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°,将其沿AB,BC折起使得BE与BF重合,连结DG,如图2.(1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;(2)求图2中的二面角B−CG−A的大小.10.【2019年高考北京卷理数】如图,在四棱锥P–ABCD中,PA⊥平面ABCD,AD⊥CD,AD∥BC,PA=AD=CD=2,BC=3.E为PD的中点,点F在PC上,且13 PFPC .(1)求证:CD⊥平面PAD;(2)求二面角F–AE–P 的余弦值;(3)设点G 在PB 上,且23PG PB =.判断直线AG 是否在平面AEF 内,说明理由.11.【2019年高考天津卷理数】如图,AE ⊥平面ABCD ,,CF AE AD BC ∥∥,,AD AB ⊥1,2AB AD AE BC ====.(1)求证:BF ∥平面ADE ;(2)求直线CE 与平面BDE 所成角的正弦值;(3)若二面角E BD F --的余弦值为13,求线段CF 的长.12.【2019年高考江苏卷】如图,在直三棱柱ABC -A 1B 1C 1中,D ,E 分别为BC ,AC 的中点,AB =BC .求证:(1)A 1B 1∥平面DEC 1;(2)BE ⊥C 1E .13.【2019年高考浙江卷】如图,已知三棱柱111ABC A B C -,平面11A ACC ⊥平面ABC ,90ABC ∠=︒,1130,,,BAC A A A C AC E F ∠=︒==分别是AC ,A 1B 1的中点.(1)证明:EF BC ⊥;(2)求直线EF 与平面A 1BC 所成角的余弦值.14.【2018年高考全国Ⅰ卷理数】如图,四边形ABCD 为正方形,,E F 分别为,AD BC 的中点,以DF 为折痕把DFC △折起,使点C 到达点P 的位置,且PF BF ⊥.(1)证明:平面PEF ⊥平面ABFD ;(2)求DP 与平面ABFD 所成角的正弦值.15.【2018年高考全国II 卷理数】如图,在三棱锥P ABC -中,22AB BC ==,4PA PB PC AC ====,O为AC的中点.(1)证明:PO⊥平面ABC;--为30︒,求PC与平面PAM所成角的正弦值.(2)若点M在棱BC上,且二面角M PA CC16.【2018年高考全国Ⅲ卷理数】如图,边长为2的正方形ABCD所在的平面与半圆弧 CD所在平面垂直,M是 CD上异于C,D的点.(1)证明:平面AMD⊥平面BMC;-体积最大时,求面MAB与面MCD所成二面角的正弦值.(2)当三棱锥M ABC17.【2018年高考江苏卷】如图,在正三棱柱ABC−A1B1C1中,AB=AA1=2,点P,Q分别为A1B1,BC的中点.(1)求异面直线BP与AC1所成角的余弦值;(2)求直线CC1与平面AQC1所成角的正弦值.18.【2018年高考江苏卷】在平行六面体1111ABCD A B C D -中,1111,AA AB AB B C =⊥.求证:(1)AB ∥平面11A B C ;(2)平面11ABB A ⊥平面1A BC .19.【2018年高考浙江卷】如图,已知多面体ABCA 1B 1C 1,A 1A ,B 1B ,C 1C 均垂直于平面ABC ,∠ABC =120°,A 1A =4,C 1C =1,AB =BC =B 1B =2.(1)证明:AB 1⊥平面A 1B 1C 1;(2)求直线AC 1与平面ABB 1所成的角的正弦值.20.【2018年高考北京卷理数】如图,在三棱柱ABC −111A B C 中,1CC ⊥平面ABC ,D ,E ,F ,G 分别为1AA ,AC ,11A C ,1BB 的中点,AB=BC ,AC =1AA =2.(1)求证:AC ⊥平面BEF ;(2)求二面角B−CD −C 1的余弦值;(3)证明:直线FG 与平面BCD 相交.21.【2018年高考天津卷理数】如图,AD BC ∥且AD =2BC ,AD CD ⊥,EG AD ∥且EG =AD ,CD FG ∥且CD =2FG ,DG ABCD ⊥平面,DA =DC =DG =2.(1)若M 为CF 的中点,N 为EG 的中点,求证:MN CDE ∥平面;(2)求二面角E BC F --的正弦值;(3)若点P 在线段DG 上,且直线BP 与平面ADGE 所成的角为60°,求线段DP 的长.。
新课标高考数学分类精编(精华文档)(2020-2021) (11)
2018年-2020年新课标高考数学(理科)试题分类精编第10部分-不等式一. 选择题1.(2020年天津理6)设0,0.a b >>1133a b a b+与的等比中项,则的最小值为即2的6< 为312<-<a 3.(2019年海南理6)已知1230a a a >>>,则使得2(1)1(123)i a x i -<=,,都成立的x 取值范围是( )A .110a ⎛⎫⎪⎝⎭, B .120a ⎛⎫ ⎪⎝⎭, C .310a ⎛⎫ ⎪⎝⎭, D .320a ⎛⎫ ⎪⎝⎭,解:22222(1)120()0i i i i i a x a x a x a x x a -<⇒-<⇒-<,所以解集为2(0,)ia ,又123222a a a <<,因此选B 。
二. 填空题1.(2020年山东理14)若对任意0x >,xa ≤恒成立,则a 的取。
4.(2020年山东理13)不等式0212<---x x 的解集为 . 【解析】:解集为{|11}x x -<<.5.(2019年山东理16)若不等式34x b -<的解集中的整数有且仅有123,,,则b 的取值范围为 .解:34x b-<4433b bx-+⇒<<,4013574343bbb-⎧<<⎪⎪⇒⇒<<⎨+⎪<<⎪⎩即范围为(5,7)6.(2019年江苏11)设,,x y z为正实数,满足230x y z-+=,则2yxz的最得集。
2018--2020年高考数学试题分类汇编不等式选讲附答案详解
2018-2020年高考数学试题分类汇编不等式选讲1、(2018年高考全国卷1文理科第23题)(10分)已知f(x)=|x+1|﹣|ax﹣1|.(1)当a=1时,求不等式f(x)>1的解集;(2)若x∈(0,1)时不等式f(x)>x成立,求a的取值范围.【解答】解:(1)当a=1时,f(x)=|x+1|﹣|x﹣1|=,由f(x)>1,∴或,解得x>,故不等式f(x)>1的解集为(,+∞),(2)当x∈(0,1)时不等式f(x)>x成立,∴|x+1|﹣|ax﹣1|﹣x>0,即x+1﹣|ax﹣1|﹣x>0,即|ax﹣1|<1,∴﹣1<ax﹣1<1,∴0<ax<2,∵x∈(0,1),∴a>0,∴0<x<,∴a<∵>2,∴0<a≤2,故a的取值范围为(0,2].2、(2018年高考全国卷II文理科第23题)[选修4-5:不等式选讲](10分)设函数f(x)=5﹣|x+a|﹣|x﹣2|.(1)当a=1时,求不等式f(x)≥0的解集;(2)若f(x)≤1,求a的取值范围.【解答】解:(1)当a=1时,f(x)=5﹣|x+1|﹣|x﹣2|=.当x≤﹣1时,f(x)=2x+4≥0,解得﹣2≤x≤1,当﹣1<x<2时,f(x)=2≥0恒成立,即﹣1<x<2,当x≥2时,f(x)=﹣2x+6≥0,解得2≤x≤3,综上所述不等式f(x)≥0的解集为[﹣2,3],(2)∵f(x)≤1,∴5﹣|x+a|﹣|x﹣2|≤1,∴|x+a|+|x﹣2|≤4,∴|x+a|+|x﹣2|=|x+a|+|2﹣x|≥|x+a+2﹣x|=|a+2|,∴|a+2|≤4,即﹣4≤a+2≤4,解得﹣6≤a≤2,故a的取值范围[﹣6,2].3、(2018年高考全国卷III文理科第23题)[选修4-5:不等式选讲](10分)设函数f(x)=|2x+1|+|x﹣1|.(1)画出y=f(x)的图象;(2)当x∈[0,+∞)时,f(x)≤ax+b,求a+b的最小值.【解答】解:(1)当x≤﹣时,f(x)=﹣(2x+1)﹣(x﹣1)=﹣3x,当﹣<x<1,f(x)=(2x+1)﹣(x﹣1)=x+2,当x≥1时,f(x)=(2x+1)+(x﹣1)=3x,则f(x)=对应的图象为:画出y=f(x)的图象;(2)当x∈[0,+∞)时,f(x)≤ax+b,当x=0时,f(0)=2≤0•a+b,∴b≥2,当x>0时,要使f(x)≤ax+b恒成立,则函数f(x)的图象都在直线y=ax+b的下方或在直线上,∵f(x)的图象与y轴的交点的纵坐标为2,且各部分直线的斜率的最大值为3,故当且仅当a≥3且b≥2时,不等式f(x)≤ax+b在[0,+∞)上成立,即a+b的最小值为5.4、(2018年高考江苏卷第24题)[选修4-5:不等式选讲](本小题满分10分)若x ,y ,z 为实数,且x +2y +2z=6,求x 2+y 2+z 2的最小值.【解答】解:由柯西不等式得(x 2+y 2+z 2)(12+22+22)≥(x +2y +2z )2, ∵x +2y +2z=6,∴x 2+y 2+z 2≥4 是当且仅当时,不等式取等号,此时x=,y=,z=,∴x 2+y 2+z 2的最小值为45、(2019全国III 卷文理科)[选修4-5:不等式选讲](10分) 设,,x y z ∈R ,且1x y z ++=.(1)求222(1)(1)(1)x y z -++++的最小值;(2)若2221(2)(1)()3x y z a -+-+-≥成立,证明:3a ≤-或1a ≥-. 解:(1)由于2[(1)(1)(1)]x y z -++++222(1)(1)(1)2[(1)(1)(1)(1)(1)(1)]x y z x y y z z x =-+++++-++++++-2223(1)(1)(1)x y z ⎡⎤≤-++++⎣⎦,故由已知得2224(1)(1)(1)3x y z -++++≥, 当且仅当x =53,y =–13,13z =-时等号成立.所以222(1)(1)(1)x y z -++++的最小值为43. (2)由于2[(2)(1)()]x y z a -+-+-222(2)(1)()2[(2)(1)(1)()()(2)]x y z a x y y z a z a x =-+-+-+--+--+--2223(2)(1)()x y z a ⎡⎤≤-+-+-⎣⎦,故由已知2222(2)(2)(1)()3a x y z a +-+-+-≥,当且仅当43a x -=,13a y -=,223a z -=时等号成立. 因此222(2)(1)()x y z a -+-+-的最小值为2(2)3a +.由题设知2(2)133a +≥,解得3a ≤-或1a ≥-.6、(2019全国II 卷文理科)[选修4-5:不等式选讲](10分)已知()|||2|().f x x a x x x a =-+-- (1)当1a =时,求不等式()0f x <的解集; (2)若(,1]x ∈-∞时,()0f x <,求a 的取值范围. 解:(1)当a =1时,()=|1| +|2|(1)f x x x x x ---.当1x <时,2()2(1)0f x x =--<;当1x ≥时,()0f x ≥. 所以,不等式()0f x <的解集为(,1)-∞. (2)因为()=0f a ,所以1a ≥.当1a ≥,(,1)x ∈-∞时,()=() +(2)()=2()(1)<0f x a x x x x a a x x ----- 所以,a 的取值范围是[1,)+∞.7、(2019全国I 卷文理科)[选修4—5:不等式选讲](10分)已知a ,b ,c 为正数,且满足abc =1.证明:(1)222111a b c a b c++≤++; (2)333()()()24a b b c c a +++≥++.解:(1)因为2222222,2,2a b ab b c bc c a ac +≥+≥+≥,又1abc =,故有222111ab bc ca a b c ab bc ca abc a b c++++≥++==++.所以222111a b c a b c++≤++. (2)因为, , a b c 为正数且1abc =,故有333()()()a b b c c a +++++≥=3(+)(+)(+)a b b c a c3≥⨯⨯⨯=24.所以333()()()24a b b c c a +++++≥. 8、(2019江苏卷21C )C.[选修4-5:不等式选讲](本小题满分10分) 设x ∈R ,解不等式||+|2 1|>2x x -.解:当x <0时,原不等式可化为122x x -+->,解得x <-13; 当0≤x ≤12时,原不等式可化为x +1–2x >2,即x <–1,无解; 当x >12时,原不等式可化为x +2x –1>2,解得x >1. 综上,原不等式的解集为1{|1}3x x x <->或. 9、(2020•全国1卷)已知函数()|31|2|1|f x x x =+--. (1)画出()y f x =的图像;(2)求不等式()(1)f x f x >+的解集. 答案:(1)详解解析;(2)7,6⎛⎫-∞-⎪⎝⎭. 解析:(1)根据分段讨论法,即可写出函数()f x 的解析式,作出图象; (2)作出函数()1f x +的图象,根据图象即可解出.解:(1)因为()3,1151,1313,3x x f x x x x x ⎧⎪+≥⎪⎪=--<<⎨⎪⎪--≤-⎪⎩,作出图象,如图所示:(2)将函数()f x 的图象向左平移1个单位,可得函数()1f x +的图象,如图所示: 由()3511x x --=+-,解得76x =-. 所以不等式()(1)f x f x >+的解集为7,6⎛⎫-∞-⎪⎝⎭. 10、(2020•全国2卷)已知函数2()|21|f x x a x a =-+-+. (1)当2a =时,求不等式()4f x 的解集; (2)若()4f x ,求a 的取值范围. 答案:(1)32x x ⎧≤⎨⎩或112x ⎫≥⎬⎭;(2)(][),13,-∞-+∞.解析:(1)分别在3x ≤、34x <<和4x ≥三种情况下解不等式求得结果; (2)利用绝对值三角不等式可得到()()21f x a ≥-,由此构造不等式求得结果. 解:(1)当2a =时,()43f x x x =-+-.当3x ≤时,()43724f x x x x =-+-=-≥,解得:32x ≤; 当34x <<时,()4314f x x x =-+-=≥,无解; 当4x ≥时,()43274f x x x x =-+-=-≥,解得:112x ≥; 综上所述:()4f x ≥的解集为32x x ⎧≤⎨⎩或112x ⎫≥⎬⎭. (2)()()()()22222121211f x x a x a x ax a aa a =-+-+≥---+=-+-=-(当且仅当221a x a -≤≤时取等号),()214a ∴-≥,解得:1a ≤-或3a ≥, a ∴的取值范围为(][),13,-∞-+∞.11、(2020•全国3卷)设a ,b ,c ∈R ,a +b +c =0,abc =1. (1)证明:ab +bc +ca <0;(2)用max{a ,b ,c }表示a ,b ,c 中的最大值,证明:max{a ,b ,c . 答案:(1)证明见解析(2)证明见解析.解析:(1)由2222()2220a b c a b c ab ac bc ++=+++++=结合不等式的性质,即可得出证明;(2)不妨设max{,,}a b c a =,由题意得出0,,0a b c ><,由()222322b c b c bc a a a bcbc+++=⋅==,结合基本不等式,即可得出证明. 解:(1)2222()2220a b c a b c ab ac bc ++=+++++=,()22212ab bc ca a b c ∴++=-++. 1,,,abc a b c =∴均不为0,则2220a b c ++>,()222120ab bc ca a b c ∴++=-++<; (2)不妨设max{,,}a b c a =,由0,1a b c abc ++==可知,0,0,0a b c ><<,1,a b c a bc =--=,()222322224b c b c bc bc bc a a a bc bc bc++++∴=⋅==≥=.当且仅当b c =时,取等号,a ∴≥,即3max{,,}4a b c .12、(2020•江苏卷)设x ∈R ,解不等式2|1|||4x x ++≤. 答案:22,3⎡⎤-⎢⎥⎣⎦解析:根据绝对值定义化为三个方程组,解得结果解:因为1224x x x <-⎧⎨---≤⎩或10224x x x -≤≤⎧⎨+-≤⎩或0224x x x >⎧⎨++≤⎩21x ∴-≤<-或10x -≤≤或203x <≤所以解集为22,3⎡⎤-⎢⎥⎣⎦。
2018年全国各地高考数学试题及解答分类汇编大全(04 导数及其应用)
则曲线 y 2ln x 在点 1,0 处的切线的斜率为 k f 1 2 , 则所求切线方程为 y 0 2 x 1 ,即 y 2x 2 .
4.(2018 全国新课标Ⅱ理)曲线 y 2 ln(x 1) 在点 (0, 0) 处的切线方程为__________.
4.【答案】 y 2x
x
,1
1
1,1a
f x
0
f x
Z
极大值
]
f x 在 x 1处取得极大值,不合题意. ③当 x1 x2 ,即 a 1时, f x , f x 随 x 的变化情况如下表:
x
,1 a
1 a
1 a
,1
f x
0
1 a 0 极小值
1 0
1 a
,
Z
1,
f x
Z
极大值
]
极小值
Z
f x 在 x 1处取得极小值,即 a 1满足题意.
1 x
1)2 k 1
4
16
0 ,得 h(x) 有两个极值点 x1, x2 (x1 x2 ) ,
∴
1 x1
1 4
,∴ 0
x1
16 .
可知 h(x) 在 (0, x1) 递增, (x1, x2 ) 递减, (x2 , ) 递增,
∴ h(x1) kx1
x1
ln x1
a
( 2
1 x1
1) x1
(1)证明:函数 f (x) x 与 g(x) x2 2x 2 不存在“S 点”;
(2)若函数 f (x) ax2 1与 g(x) ln x 存在“S 点”,求实数 a 的值; (3)已知函数 f (x) x2 a ,g(x) bex .对任意 a 0 ,判断是否存在 b 0 ,使函数 f (x) 与 g(x)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A. B.
C. D.
19.(2018全国卷Ⅲ)已知集合 , ,则
A. B. C. D.
20.(2018天津)设全集为R,集合 , ,则
A. B. C. D.
21.(2018浙江)已知全集 , ,则
A. B.{1,3}C.{2,4,5}D.{1,2,3,4,5}
2.(2020•全国2卷)设有下列四个命题:
p1:两两相交且不过同一点的三条直线必在同一平面内.
p2:过空间中任意三点有且仅有一个平面.
p3:若空间两条直线不相交,则这两条直线平行.
p4:若直线l 平面α,直线m⊥平面α,则m⊥l.
则下述命题中所有真命题的序号是__________.
① ② ③ ④
3.(2020•天津卷)设 ,则“ ”是“ ”的()
D.若S有3个元素,则S∪T有个元素
10.(2020•上海卷)已知集合 , ,求 _______
11.(2019全国Ⅰ理)已知集合 ,则 =
A. B. C. D.
12.(2019全国Ⅱ理)设集合A={x|x2-5x+6>0},B={x|x-1<0},则A∩B=
A.(-∞,1)B.(-2,1)
C.(-3,-1)D.(3,+∞)
A. B.
C. D.
9.(2020•浙江卷)设集合S,T,S N*,T N*,S,T中至少有两个元素,且S,T满足:
①对于任意x,y S,若x≠y,都有xy T
②对于任意x,y T,若x<y,则 S;
下列命题正确的是()
A.若S有4个元素,则S∪T有7个元素
B.若S有4个元素,则S∪T有6个元素
C.若S有3个元素,则S∪T有4个元素
13.(2019全国Ⅲ理)已知集合 ,则
A. B. C. D.
14.(2019江苏)已知集合 , ,则 .
15.(2019浙江)已知全集 ,集合 , ,则 =
A. B. C. D.
16.(2019天津理1)设集合 ,则
A. B. C. D.
17.(2018北京)已知集合 , ,则
A.{0,1}B.{–1,0,1} C.{–2,0,1,2} D.{–1,0,1,2}
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
4.(2020•浙江卷)已知空间中不过同一点的三条直线m,n,l,则“m,n,l在同一平面”是“m,n,l两两相交”的()
A.充分不必要条件B.必要不充分条件
C.充分必要条件D.既不充分也不必要条件
5.(2019全国Ⅱ理16)设有下列四个命题:
C.充要条件 D.既不充分也不必要条件
11.(2018上海)已知 ,则“ ”是“ ”的( )
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既非充分又非必要条件
12.(2018浙江)已知平面 ,直线 , 满足 , ,则“ ∥ ”是“ ∥ ”的
A.充分不必要条件B.必要不充分条件
C.充分必要条件D.既不充分也不必要条件
A.α内有无数条直线与β平行B.α内有两条相交直线与β平行
C.α,β平行于同一条直线D.α,β垂直于同一平面
7.(2019北京理7)设点 不共线,则“ 与 的夹角是锐角”是“ ”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
8.(2019天津理3)设 ,则“ ”是“ ”的
专题一 集合与常用逻辑用语
第一讲 集合
2018------2020年
1.(2020•北京卷)已知集合 , ,则 ().
A. B. C. D.
2.(2020•全国1卷)设集合A={x|x2–4≤0},B={x|2x+a≤0},且A∩B={x|–2≤x≤1},则a=()
A. –4B. –2C. 2D. 4
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
9.(2018北京)设 , 均为单位向量,则“ ”是“ ⊥ ”的
A.充分而不必要条件B.必要而不充分条件
C.充分必要条件D.既不充分也不必要条件
10.(2018天津)设 ,则“ ”是“ ”的
A.充分而不必要条件 B.必要而不充分条件
p1:两两相交且不过同一点的三条直线必在同一平面内.
p2:过空间中任意三点有且仅有一个平面.
p3:若空间两条直线不相交,则这两条直线平行.
p4:若直线l 平面α,直线m⊥平面α,则m⊥l.
则下述命题中所有真命题的序号是__________.
① ② ③ ④
6.(2019全国Ⅱ理7)设α,β为两个平面,则α∥β的充要条件是
C.是偶函数,且在 单调递增D.是奇函数,且在 单调递减
4.(2020•全国2卷)若 ,则()
A. B. C. D.
5.(2020•江苏卷)已知y=f(x)是奇函数,当x≥0时, ,则f(-8)的值是____.
专题二 函数概念与基本初等函数Ⅰ
第三讲 函数的概念和性质
2018------2020年
1.(2020•北京卷)函数 的定义域是____________.
2.(2020•全国1卷)若 ,则()
A. B. C. D.
3.(2020•全国2卷)设函数 ,则f(x)()
A.是偶函数,且在 单调递增B.是奇函数,且在 单调递减
22.(2018全国卷Ⅱ)已知集合 ,则 中元素的个数为
A.9B.8C.5D.4
专题一 集合与常用逻辑用语
第2讲常用逻辑用语
2018------2020年
1.(2020•北京卷)已知 ,则“存在 使得 ”是“ ”的().
A.充分而不必要条件B.必要而不充分条件
C.充分必要条件D.既不充分也不必要条件
6.(2020•新全国1山东)设集合A={x|1≤x≤3},B={x|2<x<4},则A∪B=()
A.{x|2<x≤3}B.{x|2≤x≤3}
C.{x|1≤x<4}D.{x|1<x<4}
7.(2020•天津卷)设全集 ,集合 ,则 ()
A. B. C. D.
8.(2020•浙江卷)已知集合P= , ,则P Q=()
3.(2020•全国2卷)已知集合U={−2,−1,0,1,2,3},A={−1,0,1},B={1,2},则 ()
A.{−2,3}B.{−2,2,3}C.{−2,−1,0,3}D.{−2,−1,0,2,3}
4.(2020•全国3卷)已知集合 , ,则 中元素的个数为()
A.2B.3C.4D.6
5.(2020•江苏卷)已知集合 ,则 _____.
