2011—2017年新课标全国卷1理科数学分类汇编——9.解析几何
2011-2017年高考全国卷1理科数学客观题汇编
2011—2017年新课标高考全国Ⅰ卷理科数学客观题分类汇编1．集合与常用逻辑用语一、选择题【2017，1】已知集合，，则（）A．B．C．D．【2016，1】设集合，，则（）A．B．C．D．【2015，3】设命题：，，则为（）A．，B．，C．，D．，【2014，1】已知集合A={|}，B=，则=( ) ．[-2,-1] ．[-1,2）．[-1,1] ．[1,2）【2013，1】已知集合A＝{x|x2－2x＞0}，B＝{x|－＜x＜}，则( ) A．A∩B＝B．A∪B＝R C．B A D．A B【2012，1】已知集合A={1，2，3，4，5}，B={（，）|，，}，则B中包含元素的个数为（）A．3 B．6 C．8 D．102．函数及其性质一、选择题【2017，5】函数在单调递减，且为奇函数．若，则满足的的取值范围是（）A．B．C．D．【2017，11】设为正数，且，则（）A．2x<3y<5z B．5z<2x<3y C．3y<5z<2x D．3y<2x<5z【2016，7】函数在的图像大致为（）A．B．C．D．【2016，8】若，，则（）A ．B ．C ．D ．【2014，3】设函数，的定义域都为R ，且是奇函数，是偶函数，则下列结论正确的是（）．是偶函数．||是奇函数．||是奇函数．||是奇函数【2013，11】已知函数f(x)＝若|f(x)|≥ax，则a的取值范围是( ) A．(－∞，0] B．(－∞，1] C．[－2,1] D．[－2,0]【2012，10】已知函数，则的图像大致为（）【2011，12】函数的图像与函数的图像所有交点的横坐标之和等于（）A．2 B．4 C．6 D．8【2011，2】下列函数中，既是偶函数又在单调递增的函数是（）A．B．C．D．xyO 11A．1yxO 1xyO 111xy1OB．C．D．二、填空题【2015，13】若函数f(x)=x ln（x+）为偶函数，则a=3．导数及其应用一、选择题【2014，11】已知函数=，若存在唯一的零点，且＞0，则的取值范围为．（2，+∞）．（-∞，-2）．（1，+∞）．（-∞，-1）【2012，12】设点P在曲线上，点Q在曲线上，则的最小值为（）A．B．C．D．【2011，9】由曲线，直线及轴所围成的图形的面积为（）A．B．4 C．D．6二、填空题【2017，16】如图，圆形纸片的圆心为O，半径为5cm，该纸片上的等边三角形ABC的中心为O．D、E、F为圆O上的点，△DBC，△ECA，△F AB分别是以BC，CA，AB为底边的等腰三角形．沿虚线剪开后，分别以BC，CA，AB为折痕折起△DBC，△ECA，△F AB，使得D，E，F重合，得到三棱锥．当△ABC．的边长变化时，所得三棱锥体积（单位：cm3）的最大值为_______．【2013，16】若函数f(x)＝(1－x2)(x2＋ax＋b)的图像关于直线x＝－2对称，则f(x)的最大值为__________．4．三角函数、解三角形一、选择题【2017，9】已知曲线C1：y=cos x，C2：y=sin (2x+)，则下面结正确的是（）A．把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得到曲线C2B．把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移个单位长度，得到曲线C2C．把C1上各点的横坐标缩短到原来的倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得到曲线C2D．把C1上各点的横坐标缩短到原来的倍，纵坐标不变，再把得到的曲线向左平移个单位长度，得到曲线C2【2016，12】已知函数，为的零点，为图像的对称轴，且在单调，则的最大值为（）A．11 B．9 C．7 D．5【2015，8】函数=的部分图象如图所示，则的单调递减区间为（）A．B．C．D．【2015，2】（）A．B．C．D．【2014，6】如图，圆O的半径为1，A是圆上的定点，P是圆上的动点，角的始边为射线，终边为射线，过点作直线的垂线，垂足为，将点到直线的距离表示为的函数，则=在[0,]上的图像大致为（）【2014，8】设，，且，则（）．．．．【2012，9】已知，函数在（，）上单调递减，则的取值范围是（）A．[，] B．[，] C．（0，] D．（0，2] 【2011，5】已知角的顶点与原点重合，始边与轴的正半轴重合，终边在直线上，则=A．B．C．D．【2011，11】设函数的最小正周期为，且，则（）A．在单调递减B．在单调递减C．在单调递增D．在单调递增二、填空题【2015，16】在平面四边形中，，，则的取值范围是．【2014，16】已知分别为的三个内角的对边，=2，且，则面积的最大值为．【2013，15】设当x＝θ时，函数f(x)＝sin x－2cos x取得最大值，则cos θ＝__________．【2011，16】在中，，则的最大值为．5．平面向量一、选择题【2015，7】设为所在平面内一点，则（）A．B．C．D．【2011，10】已知a与b均为单位向量，其夹角为，有下列四个命题其中的真命题是（）A．B．C．D．二、填空题【2017，13】已知向量a，b的夹角为60°，|a|=2， | b |=1，则| a +2 b |= ．【2016，13】设向量a，b，且a b a b，则．【2014，15】已知A，B，C是圆O上的三点，若，则与的夹角为．【2013，13】已知两个单位向量a，b的夹角为60°，c＝t a＋(1－t)b．若b·c＝0，则t＝_____ _____．【2012，13】已知向量，夹角为45°，且，，则_________．6．数列一、选择题【2017，4】记为等差数列的前项和．若，，则的公差为（）A．1 B．2 C．4 D．8【2017，12】几位大学生响应国家的创业号召，开发了一款应用软件．为激发大家学习数学的兴趣，他们推出了“解数学题获取软件激活码”的活动．这款软件的激活码为下面数学问题的答案：已知数列1，1，2，1，2，4，1，2，4，8，1，2，4，8，16 ，…，其中第一项是20，接下来的两项是20，21，再接下来的三项是20，21，22，依此类推．求满足如下条件的最小整数N：N>100且该数列的前N项和为2的整数幂．那么该款软件的激活码是（）A．440 B．330 C．220 D．110 【2016，3】已知等差数列前项的和为，，则（）A．B．C．D．【2013，7】设等差数列{a n}的前n项和为S n，若S m－1＝－2，S m＝0，S m＋1＝3，则m＝( )．A．3 B．4 C．5 D．6【2013，12】设△A n B n C n的三边长分别为a n，b n，c n，△A n B n C n的面积为S n，n＝1,2,3，….若b1＞c1，b1＋c1＝2a1，a n＋1＝a n，b n＋1＝，c n＋1＝，则( )．A．{S n}为递减数列B．{S n}为递增数列C．{S2n－1}为递增数列，{S2n}为递减数列D．{S2n－1}为递减数列，{S2n}为递增数列【2013，14】若数列{a n}的前n项和，则{a n}的通项公式是a n＝__________．【2012，5】已知{}为等比数列，，，则（）A．7 B．5 C．－5 D．－7二、填空题【2016，15】设等比数列满足，，则的最大值为．【2012，16】数列{}满足，则{}的前60项和为__________．7．不等式、推理与证明一、选择题【2014，9）】不等式组的解集记为．有下面四个命题：：；：；：；：．其中真命题是（）．，．，．，．，二、填空题【2017，14】设x，y满足约束条件，则的最小值为．【2016，16】某高科技企业生产产品A和产品B需要甲、乙两种新型材料．生产一件产品A 需要甲材料1．5kg，乙材料1kg，用5个工时；生产一件产品B需要甲材料0．5kg，乙材料0．3kg，用3个工时．生产一件产品A的利润为2100元，生产一件产品B的利润为900元．该企业现有甲材料150kg，乙材料90kg，则在不超过600个工时的条件下，生产产品A、产品B 的利润之和的最大值为元．【2015，15】若x,y满足约束条件，则的最大值为．【2014，14】甲、乙、丙三位同学被问到是否去过A，B，C三个城市时，甲说：我去过的城市比乙多，但没去过B城市；乙说：我没去过C城市；丙说：我们三人去过同一个城市．由此可判断乙去过的城市为．【2012，14】设，满足约束条件，则的取值范围为__________ _．【2011，13】若变量满足约束条件则的最小值为．8．立体几何一、选择题【2017，7】某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形，该多面体的各个面中有若干个是梯形，这些梯形的面积之和为（）A．10 B．12 C．14 D．16【2016，11】平面过正方体的顶点，平面，平面，平面，则所成角的正弦值为A．B．C．D．【2016，6】如图，某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径．若该几何体的体积是，则它的表面积是（）A． B． C．D．【2015，6】《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺．问：积及为米几何？”其意思为：“在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一），米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1．62立方尺，圆周率约为3，估算出堆放的米约有（ ）A ．14斛B ．22斛C ．36斛D ．66斛【2015，11】圆柱被一个平面截去一部分后与半球(半径为)组成一个几何体，该几何体三视图中的正视图和俯视图如图所示． 若该几何体的表面积为，则（ ）A ．1B ．2C ．4D ．8【2015年，11题】 【2014年，12题】 【2013年，6题】【2014，12】如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的个条棱中，最长的棱的长度为（ ）．．．6．4【2013，6】如图，有一个水平放置的透明无盖的正方体容器，容器高8 cm ，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6 cm ，如果不计容器的厚度，则球的体积为( )3cm D ．3cm C ．3 cm B ．3cm A ．【2013，8】某几何体的三视图如图所示，则该几何体的体积为( )．A ．16＋8πB ．8＋8πC ．16＋16πD ．8＋16π【2013年，8】【2012年，7】【2011年，6】【2012，7】如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为（）A．6 B．9 C．12 D．15【2012，11】已知三棱锥S－ABC的所有顶点都在球O的球面上，△ABC是边长为1的正三角形，SC为球O的直径，且SC=2，则此棱锥的体积为（）A．B．C．D．【2011，6】在一个几何体的三视图中，正视图和俯视图如右图所示，则相应的侧视图可以为（）二、填空题【2011，15】已知矩形的顶点都在半径为4的球的球面上，且,则棱锥的体积为．9．解析几何一、选择题【2017，10】已知F为抛物线C：y2=4x的焦点，过F作两条互相垂直的直线l1，l2，直线l1与C交于A、B两点，直线l2与C交于D、E两点，则|AB|+|DE|的最小值为（）A．16 B．14 C．12 D．10【2016，10】以抛物线的顶点为圆心的圆交于两点，交的准线于两点，已知,，则的焦点到准线的距离为（）A．2 B．4 C．6 D．8【2016，5】已知方程表示双曲线，且该双曲线两焦点间的距离为，则的取值范围是（）A．B．C．D．【2015，5】已知是双曲线：上的一点，是的两个焦点，若，则的取值范围是（）A．B．C．D．【2014，4】已知是双曲线：的一个焦点，则点到的一条渐近线的距离为．．3 ．．【2014，10】已知抛物线：的焦点为，准线为，是上一点，是直线与的一个交点，若，则=（）．．．3 ．2【2013，4】已知双曲线C：(a＞0，b＞0)的离心率为，则C的渐近线方程为( )．A．y＝B．y＝C．y＝D．y＝±x【2013，10】已知椭圆E：(a＞b＞0)的右焦点为F(3,0)，过点F的直线交E于A，B两点．若AB 的中点坐标为(1，－1)，则E的方程为( )A．B．C．D．【2012，4】设、是椭圆E：（）的左、右焦点，P为直线上一点，是底角为30°的等腰三角形，则E的离心率为（）A．B．C．D．【2012，8】等轴双曲线C的中心在原点，焦点在轴上，C与抛物线的准线交于A，B两点，，则C的实轴长为（）A．B．C．4 D．8【2011，7】设直线L过双曲线C的一个焦点，且与C的一条对称轴垂直，L与C交于A ,B两点，为C的实轴长的2倍，则C的离心率为（）A．B．C．2 D．3二、填空题【2017，15】已知双曲线C：（a>0，b>0）的右顶点为A，以A为圆心，b为半径作圆A，圆A与双曲线C的一条渐近线交于M、N两点．若∠MAN=60°，则C的离心率为________．【2015，14】一个圆经过椭圆的三个顶点，且圆心在轴的正半轴上，则该圆的标准方程为．【2011，14】在平面直角坐标系中，椭圆的中心为原点，焦点在轴上，离心率为．过的直线L交C于两点，且的周长为16，那么的方程为．10．统计、概率分布列、计数原理一、选择题【2017，2】如图，正方形ABCD内的图形来自中国古代的太极图，正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称．在正方形内随机取一点，则此点取自黑色部分的概率是（）A．B．C．D．【2017，6】展开式中的系数为（）A．15 B．20 C．30 D．35【2016，4】某公司的班车在，，发车，小明在至之间到达发车站乘坐班车，且到达发车丫的时候是随机的，则他等车时间不超过10分钟的概率是（）A．B．C．D．【2015，10】的展开式中，的系数为（）A．10 B．20 C．30 D．60【2015，4】投篮测试中，每人投3次，至少投中2次才能通过测试．已知某同学每次投篮投中的概率为0．6，且各次投篮是否投中相互独立，则该同学通过测试的概率为（）A．0．648 B．0．432 C．0．36 D．0．312【2014，5】4位同学各自在周六、周日两天中任选一天参加公益活动，则周六、周日都有同学参加公益活动的概率（）．．．．【2013，3】为了解某地区的中小学生的视力情况，拟从该地区的中小学生中抽取部分学生进行调查，事先已了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异，而男女生视力情况差异不大．在下面的抽样方法中，最合理的抽样方法是( )A．简单随机抽样B．按性别分层抽样C．按学段分层抽样D．系统抽样【2013，9】设m为正整数，展开式的二项式系数的最大值为，展开式的二项式系数的最大值为．若13a＝7b，则m＝( )A．5 B．6 C．7 D．8【2012，2】将2名教师，4名学生分成2个小组，分别安排到甲、乙两地参加社会实践活动，每个小组由1名教师和2名学生组成，不同的安排方案共有（）A．12种B．10种C．9种D．8种【2011，8】的展开式中各项系数的和为2，则该展开式中常数项为（）A．B．C．20 D．40【2011，4】有3个兴趣小组，甲、乙两位同学各自参加其中一个小组，每位同学参加各个小组的可能性相同，则这两位同学参加同一个兴趣小组的概率为（）A．B．C．D．二、填空题【2016，14】的展开式中，的系数是．（用数字填写答案）【2014，13】的展开式中的系数为．(用数字填写答案) 【2012，15】某一部件由三个电子元件按下图方式连接而成，元件1或元件2正常工作，且元件3正常工作，则部件正常工作．设三个电子元件的使用寿命（单位：小时）均服从正态分布N（1000，502），且各个元件能否正常工作相互独立，那么该部件的使用寿命超过1000小时的概率为_________．11．复数及其运算一、选择题【2017，3】设有下面四个命题若复数满足，则；若复数满足，则；若复数满足，则；若复数，则．其中的真命题为（）A．B．C．D．【2016，2】设，其中是实数，则（）A．B．C．D．【2015，1】设复数满足，则=（）A．1 B．C．D．2 【2014，2）】=（）．．．．【2013，2】若复数z满足(3－4i)z＝|4＋3i|，则z的虚部为( )．A．－4 B．C．4 D．【2012，3】下面是关于复数的四个命题：：；：；：的共轭复数为；：的虚部为．其中的真命题为（）A．，B．，C．，D．，【2011，1】复数的共轭复数是（）A．B．C．D．11．程序框图一、选择题【2017，8】右面程序框图是为了求出满足的最小偶数n，那么在和和两个空白框中，可以分别填入A．A>1000和n=n+1 B．A>1000和n=n+2C．A1000和n=n+1 D．A1000和n=n+2【2017，8】【2016，9】【2015，9】【2016，9】执行右面的程序框图，如果输入的，，，则输出的值满足（）A．B．C．D．【2015，9】执行右面的程序框图，如果输入的，则输出的（）A．B．C．D．【2014，7】执行下图的程序框图，若输入的分别为1,2,3，则输出的=（）．．．．【2013，5】执行下面的程序框图，如果输入的t∈[－1,3]，则输出的s属于( )．A．[－3,4] B．[－5,2] C．[－4,3] D．[－2,5]【2012，6】如果执行右边和程序框图，输入正整数（）和实数，，…，，输出A，B，则（）A．为，，…，的和B．为，，…，的算术平均数C．和分别是，，…，中最大的数和最小的数D．和分别是，，…，中最小的数和最大的数【2013，5】 【2012，6】 【2011，3】 【2011,3】执行右面的程序框图，如果输入的N 是6，那么输出的p 是（ ） A ．120 B ．720 C ．1440 D ．5040。
2011年—2017年新课标全国1卷理科数学题型分类汇编(含答案)
2011 年—2017 年新课标高考全国Ⅰ卷理科数学分类汇编（含答案）说明：2017 年高考中，安徽、湖北、福建、湖南、山西、河北、江西、广东、河南等9 个省份选择使用新课标全国Ⅰ卷．2017 年，除了保留北京、天津、上海、江苏、浙江实行自主命题外（山东省语文、数学卷最后一年使用），大陆其他省区全部使用全国卷．研究发现，新课标全国卷的试卷结构和题型具有一定的稳定性和连续性．每个题型考查的知识点、考查方法、考查角度、思维方法等相对固定．掌握了全国卷的各种题型，就把握住了全国卷命题的灵魂．正所谓知己知彼，才能百战不殆，为了方便老师和同学们备考2018 年高考，本人认真研究近7 年新课标高考全国Ⅰ卷理科数学和高考数学考试说明，将2011 年—2017 年新课标全国Ⅰ卷进行了分类整理．2011 年—2017 年新课标高考全国Ⅰ卷理科数学分类汇编1．集合与常用逻辑用语 (2)2．函数与导数 (3)3．三角函数、解三角形 (7)4．平面向量 (10)5．数列 (11)6．不等式、推理与证明 (13)7．立体几何 (14)8．解析几何 (18)9．统计、概率分布列、计数原理 (23)10．复数及其运算 (30)11．程序框图 (31)12．坐标系与参数方程 (33)13．不等式选讲 (36)1．集合与常用逻辑用语一、选择题【2017，1】已知集合A ={x x <1}，B ={x 3x <1}，则（）A．A B = {x | x <0}B．A B =R C．A B = {x | x >1}D．A B=∅【2016，1】设集合A = {x x2 - 4x + 3 <0}，B = {x 2x - 3 > 0} ，则A B =（）A．(-3,-3)2B．(-3,3)2C．(1,3)2D．(3,3)2【2015，3】设命题p ：∃n∈N，n2 > 2n ，则⌝p 为（）A．∀n ∈N ，n2 >2n B．∃n∈N，n2 ≤2n C．∀n ∈N ，n2 ≤2n D．∃n∈N ，n2 =2n【2014，1】已知集合A={ x | x2 - 2x - 3 ≥ 0 }，B= {x -2 ≤x < 2}，则A ⋂B =( )A ．[-2,-1]B ．[-1,2）C ．[-1,1]D ．[1,2）【2013，1】已知集合A＝{x|x2－2x＞0}，B＝{x|－x＜，则( )A．A∩B＝B．A∪B＝R C．B ⊆A D．A ⊆B【2012，1】已知集合A={1，2，3，4，5}，B={（x ，y ）| x∈A，y ∈A ，x -y ∈A }，则B 中包含元素的个数为（）A．3 B．6 C．8 D．102．函数与导数一、选择题【2017，5】函数f (x) 在(-∞, +∞) 单调递减，且为奇函数．若f (1) =-1 ，则满足-1 ≤f (x - 2) ≤1的x 的取值范围是（）A．[-2, 2]B．[-1,1]C．[0, 4] D．[1, 3]【2017，11】设x, y, z 为正数，且2x = 3y = 5z ，则（）A．2x<3y<5z B．5z<2x<3y C．3y<5z<2x D．3y<2x<5z【2016，7】函数y =2x2 -e x 在[-2,2] 的图像大致为（）A．B．C．D．【2016，8】若a >b >1，0 <c <1，则（）A．a c <b c B．ab c <ba c C．a logb c <b logac D．logac <logbc【2015，12】设函数f (x) = e x (2x -1) -ax +a ,其中a <1，若存在唯一的整数x ，使得f (x ) < 0 ，00则a 的取值范围是（）A．⎡-3,1⎫B．⎡-3,3 ⎫C．⎡3,3 ⎫D．⎡3,1⎫ ⎣⎢2e⎪ ⎢2e 4 ⎪ ⎢2e 4 ⎪ ⎢2e ⎪⎭⎣ ⎭ ⎣⎭⎣ ⎭【2014，3】设函数f (x) ，g(x) 的定义域都为R，且f (x) 是奇函数，g(x) 是偶函数，则下列结论正确的是（）A ．f (x) g(x) 是偶函数B ．| f (x) | g(x) 是奇函数C ．f (x) | g(x) |是奇函数D ．| f (x) g(x) |是奇函数【2014，11】已知函数f (x) = ax3 - 3x2 +1 ，若f (x) 存在唯一的零点x ，且x ＞0，则a 的取值范围为0 0A ．（2，+∞）B ．（-∞，-2）C ．（1，+∞）D ．（-∞，-1）⎧-x2 + 2x，x ≤ 0，【2013，11】已知函数f(x)＝⎨⎩ln( x+1)，x > 0.若|f(x)|≥ax，则a 的取值范围是( ) A．(－∞，0] B．(－∞，1] C．[－2,1] D．[－2,0]【2012，10】已知函数f ( x) =1，则y =f (x) 的图像大致为（）A．B．D．【2012，12】设点P 在曲线y =1e x 上，点Q 在曲线y = ln(2x) 上，则| PQ |的最小值为（）2A．1- ln 2B- ln 2)C．1+ ln 2D+ ln 2)【2011，12】函数y =1x -1的图像与函数y =2s in πx(-2 ≤x ≤ 4) 的图像所有交点的横坐标之和等于（）A．2 B．4 C．6 D．8【2011，2】下列函数中，既是偶函数又在（0，+∞）单调递增的函数是（）A．y =x3B．y = x +1C．y =-x2 +1D．y = 2-x【2011，9】由曲线y =，直线y =x - 2 及y 轴所围成的图形的面积为（）A．103二、填空题B．4 C．163D．6【2017，16】如图，圆形纸片的圆心为O，半径为5 cm，该纸片上的等边三角形ABC 的中心为O．D、E、F 为圆O 上的点，△DBC，△ECA，△F AB 分别是以BC，CA，AB 为底边的等腰三角形．沿虚线剪开后，分别以BC，CA，AB 为折痕折起△DBC，△ECA，△F AB，使得D，E，F 重合，得到三棱锥．当△ABC．的边长变化时，所得三棱锥体积（单位：cm3）的最大值为．【2015，13】若函数f(x)=x ln（x a=【2013，16】若函数f(x)＝(1－x2)(x2＋ax＋b)的图像关于直线x＝－2 对称，则f(x)的最大值为．三、解答题【2017，12】已知函数f (x)=ae2 x +(a -2)e x -x ．（1）讨论f ( x) 的单调性；（2）若f ( x) 有两个零点，求a 的取值范围．【2016，12】已知函数f (x) = (x -2)e x +a(x -1)2 有两个零点．（Ⅰ）求a 的取值范围；（Ⅱ）设x1 , x2 是f (x) 的两个零点，证明：x1 +x2 < 2 ．【2015，12】已知函数f ( x) =x3 +ax +1，g(x) =-l n x ．4（Ⅰ）当a 为何值时，x 轴为曲线y =f (x) 的切线；（Ⅱ）用min{m, n} 表示m, n 中的最小值，设函数h(x) = min{ f (x), g(x)} （x > 0 ），讨论h(x) 零点的个数．【2014，21】设函数f ( x0 =ae x ln x +be x-1，曲线y =f (x) 在点（1，f (1) 处的切线为y =e(x -1) + 2 ．(Ⅰ) x求a,b；（Ⅱ）证明：f (x) >1．【2013，21】设函数f(x)＝x2＋ax＋b，g(x)＝e x(cx＋d)．若曲线y＝f(x)和曲线y＝g(x)都过点P(0,2)，且在点P 处有相同的切线y＝4x＋2．(1)求a，b，c，d 的值；(2)若x≥－2 时，f(x)≤kg(x)，求k 的取值范围．【2012，21】已知函数f (x) 满足f (x) =f '(1)e x-1 -f (0)x+1x2 ．2（1）求f (x) 的解析式及单调区间；（2）若f (x) ≥1x2 +ax +b ，求(a +1)b 的最大值．2【2011，21】已知函数f (x) =a ln x+b，曲线y =f (x) 在点(1, f (1)) 处的切线方程为x +2y- 3 = 0 ．x +1x（Ⅰ）求a 、b 的值；（Ⅱ）如果当x > 0 ，且x ≠1时，f (x) > ln x+k，求k 的取值范围．x -1 x3．三角函数、解三角形一、选择题2π 【2017，9】已知曲线 C 1：y =cos x ，C 2：y =sin (2x +3)，则下面结正确的是（ ）πA ．把 C 1 上各点的横坐标伸长到原来的 2 倍，纵坐标不变，再把得到的曲线向右平移 6得到曲线C 2 个单位长度，πB ．把C 1 上各点的横坐标伸长到原来的 2 倍，纵坐标不变，再把得到的曲线向左平移 12得到曲线C 2个单位长度，1 C ．把 C 1 上各点的横坐标缩短到原来的 2得到曲线C 2π 倍，纵坐标不变，再把得到的曲线向右平移 6个单位长度，1D ．把 C 1 上各点的横坐标缩短到原来的 2π倍，纵坐标不变，再把得到的曲线向左平移 12个单位长度，得到曲线 C 2【2016，12】已知函数 f ( x ) = sin(ωx + ϕ )(ω > 0, ϕ≤ π ， x = - π为 f ( x ) 的零点， x = π 为244y = f (x ) 图像的对称轴，且 f ( x ) 在 ( π 18 , 5π单调，则ω 的最大值为（）36A ．11B ．9C ．7D ．5【2015，8】函数 f ( x ) = cos(ω x + ϕ) 的部分图象如图所示，则 f ( x ) 的单调递减区间为（）A ． (k π - 1 , k π + 3), k ∈ ZB ． (2k π - 1 , 2k π + 3), k ∈ Z4 4 4 4 C ． (k - 1 , k + 3k ∈ ZD ． (2k - 1 , 2k + 3), k ∈ Z4 4【2015，2】 sin 20 cos10- cos160 sin10 4 4= （ ）A ．BC ． - 12D ． 12【2014，6】如图，圆 O 的半径为 1，A 是圆上的定点，P 是圆上的动点，角 x 的始边为射线OA ，终边为射线 OP ，过点 P 作直线OA 的垂线，垂足为 M ，将点 M 到直线OP 的距离表示为 x 的函数 f ( x ) ，则y= f ( x ) 在[0, π ]上的图像大致为（）【2014，8】设α ∈ (0, π ) ， β ∈ (0, π) ，且 tan α =1 + sin β，则（）2A ． 3α - β = π2 2B ． 2α - β = π2cos βC ． 3α + β = π 2D ． 2α + β = π2【2012，9】已知ω > 0 ，函数 f ( x ) = sin(ω x + π ) 在（ π，π ）上单调递减，则ω 的取值范围是（）4 2A ．[ 1 ， 5 ]B ．[ 1 ， 3 ]C ．（0， 1 ]D ．（0，2]2 4 2 4 2【2011，5】已知角θ 的顶点与原点重合，始边与 x 轴的正半轴重合，终边在直线 y = 2x 上，则 cos 2θ =A ． - 45B ． - 35C ． 35D ． 45【2011，11】设函数 f ( x ) = sin(ω x + ϕ ) + cos(ω x + ϕ)(ω > 0, ϕ且 f (-x ) = f (x ) ，则（ ）< π 的最小正周期为π ， 2A ． f ( x ) 在 ⎛ 0, π ⎫单调递减 B ． f ( x ) 在 ⎛ π ,3π ⎫单调递减2 ⎪ 4 4 ⎪⎝ ⎭⎝ ⎭C ． f ( x ) 在 ⎛ 0, π ⎫单调递增 D ． f ( x ) 在 ⎛ π ,3π ⎫单调递增2 ⎪ 4 4 ⎝ ⎭⎝ ⎭二、填空题【2015，16】在平面四边形 ABCD 中，∠A = ∠B = ∠C = 75 ，BC = 2 ，则 AB 的取值范围是．【2014，16】已知 a , b , c 分别为 ∆ABC 的三个内角 A , B , C 的对边， a =2，且 (2 + b )(sin A - sin B ) = (c - b ) sin C ，则 ∆ABC 面积的最大值为．【2013，15】设当 x ＝θ 时，函数 f (x )＝sin x －2cos x 取得最大值，则 cos θ＝．【2011，16】在 ABC 中， B = 60 , AC =AB + 2BC 的最大值为 ．三、解答题【2017，17】△ABC 的内角A ，B ，C 的对边分别为 a ，b ，c ，已知△ABC 的面积为 a 23sin A（1）求 sin B sin C ；（2）若 6cos B cos C =1,a =3,求△ABC 的周长【2016，17】∆ABC 的内角A, B,C的对边分别为a,b, c ，已知2c os C(a cos B +b cos A) =c ．（Ⅰ）求C ；（Ⅱ）若c = 7 ，∆ABC 的面积为3 3，求∆ABC 的周长．2【2013，17】如图，在△ABC 中，∠ABC＝90°，AB＝BC＝1，P 为△ABC 内一点，∠BPC＝90°．(1)若PB＝1，求P A；(2)若∠APB＝150°，求tan∠PBA．2【2012，17】已知a ，b ，c 分别为△ABC 三个内角A，B，C 的对边，a cos C +s in C -b -c = 0 ．（1）求A；（2）若a = 2 ，△ABC 的面积为 b ，c ．⎭⎝ ⎦4．平面向量一、选择题【2015，7】设 D 为 ∆ABC 所在平面内一点 BC = 3CD ，则（）A ． AD = - 1 AB + 4AC3 3 C ． AD =4 AB + 1AC3 3B ． AD = 1 AB - 4AC3 3 D ． AD =4 AB - 1AC3 3【2011，10】已知 a 与 b 均为单位向量，其夹角为θ ，有下列四个命题P : a + b > 1 ⇔ θ ∈ ⎡0, 2π ⎫P : a + b > 1 ⇔ θ ∈ ⎛ 2π ,π ⎤1 ⎢⎣ 3 ⎪⎭ 2 3⎥ ⎝ ⎦⎡ π ⎫⎛ π ⎤P 3 : a - b > 1 ⇔ θ ∈ ⎢⎣0, 3 ⎪P 4 : a - b > 1 ⇔ θ ∈ 3 ,π ⎥其中的真命题是（）A ． P 1 , P 4B ． P 1 , P 3C ． P 2 , P 3D ． P 2 , P 4二、填空题【2017，13】已知向量 a ，b 的夹角为 60°，|a |=2， | b |=1，则| a +2 b |=．【2016，13】设向量 a = (m ,1) ，b = (1,2) ，且| a + b |2= | a |2+ | b |2，则 m =．【2014，15】已知 A ，B ，C 是圆 O 上的三点，若 AO = 1( A B + AC ) ，则 AB 与 AC 的夹角为 ． 2【2013，13】已知两个单位向量 a ，b 的夹角为 60°，c ＝t a ＋(1－t )b ．若 b ·c ＝0，则 t ＝．【2012，13】已知向量 a ， b 夹角为 45°，且| a |= 1，| 2a - b |= 10 ，则| b |=．n 2 15．数列一、选择题【2017，4】记S n 为等差数列{a n } 的前 n 项和．若 a 4 + a 5 = 24 ， S 6 = 48 ，则{a n } 的公差为（ ）A ．1B ．2C ．4D ．8【2017，12】几位大学生响应国家的创业号召，开发了一款应用软件．为激发大家学习数学的兴趣，他们 推出了“解数学题获取软件激活码”的活动．这款软件的激活码为下面数学问题的答案：已知数列1，1，2， 1，2，4，1，2，4，8，1，2，4，8，16 ，…，其中第一项是 20，接下来的两项是 20，21，再接下来的三项是 20，21，22，依此类推．求满足如下条件的最小整数 N ：N >100 且该数列的前 N 项和为 2 的整数幂．那么该款软件的激活码是（ ）A ．440B ．330C ．220D ．110【2016，3】已知等差数列{a n } 前 9 项的和为 27 ， a 10 = 8 ，则 a 100 = （ ）A ．100B ． 99C ．98D ．97 【2013，7】设等差数列{a n }的前 n 项和为 S n ，若 S m －1＝－2，S m ＝0，S m ＋1＝3，则 m ＝( )．A ．3B ．4C ．5D ．6 【2013，12】设△A n B n C n 的三边长分别为 a n ，b n ，c n ，△A n B n C n 的面积为 S n ，n ＝1,2,3，….c + a b + a 若 b 1＞c 1，b 1＋c 1＝2a 1，a n ＋1＝a n ，b n ＋1＝ nn，c n ＋1＝2nn，则( )．2A ．{S n }为递减数列B ．{S n }为递增数列C ．{S 2n －1}为递增数列，{S 2n }为递减数列D ．{S 2n －1}为递减数列，{S 2n }为递增数列2 1【2013，14】若数列{a n }的前 n 项和 S n =a n 3+ ，则{a n }的通项公式是 a n ＝ ．3 【2012，5】已知{ a n }为等比数列， a4 + a 7 = 2 ， a 5a 6 = -8 ，则 a 1 + a 10 = （）A ．7B ．5C ．－5D ．－7二、填空题【2016，15】设等比数列{a n } 满足 a 1 + a 3 = 10 ， a 2 + a 4 = 5 ，则 a 1a 2a n 的最大值为．【2012，16】数列{ a n }满足 a n +1 + (-1) a n = 2n -1 ，则{ a n }的前 60 项和为 ．三、解答题【2015，17】 S n 为数列{a n } 的前 n 项和．已知 a n ＞0， a+ 2a n = 4S n + 3 ． n（Ⅰ）求{a n } 的通项公式；（Ⅱ）设 b n =，求数列{b n } 的前n 项和． a n a n +12【2014，17】已知数列{ a n }的前 n 项和为 S n ， a 1 =1， a n ≠ 0 ， a n a n +1 = λS n -1，其中 λ 为常数．(Ⅰ)证明： a n +2 - a n = λ ；（Ⅱ）是否存在 λ ，使得{ a n }为等差数列？并说明理由．【2011，17】等比数列{a n } 的各项均为正数，且 2a 1 + 3a 2 = 1, a 3 = 9a 2 a 6 .（Ⅰ)求数列{a n } 的通项公式；（Ⅱ）设 ⎧ 1 ⎫ b n = log 3 a 1 + log 3 a 2 + ...... + log 3 a n , 求数列 ⎨ ⎬ 的前n 项和． ⎩ b n ⎭⎩⎨⎩⎪ ⎨ x ≥ 06．不等式、推理与证明一、选择题⎧ x + y ≥ 1 【2014，9）】不等式组 ⎨⎩ x - 2 y ≤ 4的解集记为D ．有下面四个命题： p 1 ： ∀(x , y ) ∈ D , x + 2 y ≥ -2 ；p 2 ： ∃(x , y ) ∈ D , x + 2 y ≥ 2 ； P 3 ： ∀(x , y ) ∈ D , x + 2 y ≤ 3 ； p 4 ： ∃(x , y ) ∈ D , x + 2 y ≤ -1 ．其中真命题是（）A ． p 2 ， P 3B ． p 1 ， p 4C ． p 1 ， p 2D ． p 1 ， P 3二、填空题⎧ x + 2 y ≤ 1⎪【2017，14】设 x ，y 满足约束条件 ⎨2x + y ≥ -1，则z = 3x - 2 y 的最小值为 ．⎪ x - y ≤ 0 【2016，16】某高科技企业生产产品 A 和产品 B 需要甲、乙两种新型材料．生产一件产品 A 需要甲材料 1．5kg ， 乙材料 1kg ，用 5 个工时；生产一件产品 B 需要甲材料 0．5kg ，乙材料 0．3kg ，用 3 个工时．生产一件 产品 A 的利润为 2100 元，生产一件产品 B 的利润为 900 元．该企业现有甲材料 150kg ，乙材料 90kg ，则 在不超过 600 个工时的条件下，生产产品 A 、产品 B 的利润之和的最大值为 元．⎧ x -1 ≥ 0【2015，15】若 x ,y 满足约束条件 ⎪x - y ≤ 0 ⎪ x + y - 4 ≤ 0，则 y 的最大值为 ．x【2014，14】甲、乙、丙三位同学被问到是否去过 A ，B ，C 三个城市时，甲说：我去过的城市比乙多，但没去过 B 城市； 乙说：我没去过 C 城市； 丙说：我们三人去过同一个城市．由此可判断乙去过的城市为．⎧ x - y ≥ -1⎪x + y ≤ 3【2012，14】设 x ， y 满足约束条件 ⎪ ⎪⎩ y ≥ 0，则 z = x - 2 y 的取值范围为 ．⎧3 ≤ 2x + y ≤ 9,【2011，13】若变量 x , y 满足约束条件 ⎨⎩6 ≤ x - y ≤ 9,则 z = x + 2 y 的最小值为 ．7．立体几何一、选择题【2017，7】某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为 2，俯视图为等腰直角三角形，该多面体的各个面中有若 干个是梯形，这些梯形的面积之和为（ ） A ．10B ．12C ．14D ．16【2016，11】平面α 过正方体 ABCD - A 1 B 1C 1 D 1 的顶点 A ，α // 平面CB 1 D 1 ，α 平面 ABCD= m ，α 平面 ABB 1 A 1 = n ，则 m , n 所成角的正弦值为3A ．B ．2 3 1 C ．D ．2233【2016，6】如图，某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直 的半径．若该几何体的体积是28π，则它的表面积是（ ）3A ．17πB ．18πC ． 20πD ． 28π【2015，6】《九章算术》是我国古代内容极为丰富的数学名著，书中有如下 问题：“今有委米依垣内角，下周八尺，高五尺．问：积及为米几何？”其意思 为：“在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一），米堆底部的 弧长为 8 尺，米堆的高为 5 尺，问米堆的体积和堆放的米各为多少？”已知 1 斛米的体积约为 1．62 立方尺，圆周率约为 3，估算出堆放的米约有（ ）A ．14 斛B ．22 斛C ．36 斛D ．66 斛【2015，11】圆柱被一个平面截去一部分后与半球(半径为 r )组成一个几何体，该几何体三视图中的正视 图和俯视图如图所示． 若该几何体的表面积为16 + 20π ，则 r =（）A ．1B ．2C ．4D ．8【2015 年，11 题】【2014 年，12 题】 【2013 年，6 题】【2014，12】如图，网格纸上小正方形的边长为 1，粗实线画出的是某多面体的三视图，则该多面体的个 条棱中，最长的棱的长度为（）A ． 6 2B ． 4 2C ．6D ．4【2013，6】如图，有一个水平放置的透明无盖的正方体容器，容器高 8 cm ，将一个球放在容器口，再向 容器内注水，当球面恰好接触水面时测得水深为 6 cm ，如果不计容器的厚度，则球的体积为( )A ．500π cm 3B ．866π cm 3C ．1372π cm 3D ．2048π cm 33333【2013，8】某几何体的三视图如图所示，则该几何体的体积为( )．A ．16＋8πB ．8＋8πC ．16＋16πD ．8＋16π【2013 年，8】【2012 年，7】【2011 年，6】【2012，7】如图，网格纸上小正方形的边长为 1，粗线画出的是某几何体的三视图，则此几何体的体积为 （ ）A ．6B ．9C ．12D ．15 【2012，11】已知三棱锥 S －ABC 的所有顶点都在球 O 的球面上，△ABC 是边长为 1 的正三角形，SC 为球O 的直径，且 SC =2，则此棱锥的体积为（ ）A6B C ．3D ．2【2011，6】在一个几何体的三视图中，正视图和俯视图如右图所示，则相应的侧视图可以为（）二、填空题【2011，15】已知矩形 ABCD 的顶点都在半径为 4 的球 O 的球面上，且 AB = 6, BC =则棱锥O - ABCD 的体积为．三、解答题【2017，18】如图，在四棱锥 P-ABCD 中，AB//CD ，且 ∠BAP = ∠CDP = 90（1）证明：平面P AB ⊥平面 P AD ；（2）若P A =PD =AB =DC , ∠APD = 90 ,求二面角 A -PB -C 的余弦值．o 【2016，18】如图，在以 A , B , C , D , E , F 为顶点的五面体中，面 ABEF 为正方形，AF = 2FD , ∠AFD = 90︒ ，C且二面角 D - AF - E 与二面角 C - BE - F 都是 60︒ ．DEB（Ⅰ）证明：平面 ABEF ⊥ 平面 EFDC ； （Ⅱ）求二面角 E - BC - A 的余弦值．【2015，18】如图，四边形 ABCD 为菱形，∠ABC = 120A，E , F是平面 ABCD 同一侧的两点，BE ⊥平面 ABCD ，DF ⊥平面ABCD ， BE = 2DF ， AE ⊥ EC ．（I ）证明：平面 AEC ⊥平面 AFC ；（II ）求直线 AE 与直线 CF 所成角的余弦值．【2014，19】如图三棱柱 ABC - A 1B 1C 1 中，侧面 BB 1C 1C 为菱形， AB ⊥ B 1C ．(Ⅰ) 证明： AC = AB 1 ；（Ⅱ）若 AC ⊥ AB 1 ， ∠CBB 1 = 60 ，AB=BC ，求二面角A - A 1B 1 -C 1 的余弦值．【2013，18】如图，三棱柱ABC－A1B1C1 中，CA＝CB，AB＝AA1，∠BAA1＝60°．(1)证明：AB⊥A1C；(2)若平面ABC⊥平面AA1B1B，AB＝CB，求直线A1C 与平面BB1C1C 所成角的正弦值．1AA1，D 是棱AA1 的中点，DC1⊥BD．【2012，19】如图，直三棱柱ABC－A1B1C1 中，AC=BC=2（1）证明：DC1⊥BC；（2）求二面角A1－BD－C1 的大小．B1AB【2011，18】如图，四棱锥P-ABCD 中，底面ABCD 为平行四边形，∠DAB=60°,AB=2AD,PD⊥底面ABCD．(Ⅰ)证明：P A⊥BD；(Ⅱ)若PD=AD，求二面角A-PB-C 的余弦值．C2 2 2 2 2 22 28．解析几何一、选择题【2017，10】已知F 为抛物线 C ：y 2=4x 的焦点，过 F 作两条互相垂直的直线 l 1，l 2，直线 l 1 与 C 交于 A 、B 两点，直线 l 2 与C 交于D 、E 两点，则|AB |+|DE |的最小值为（）A ．16B ．14C ．12D ．10【2016，10】以抛物线 C 的顶点为圆心的圆交 C 于 A , B 两点，交 C 的准线于 D , E 两点，已知 AB = 4 2 ,DE = 2 5 ，则C 的焦点到准线的距离为（ ）A ．2B ．4C ．6D ．8【2016，5】已知方程x 2 m 2+ ny 2- 3m 2 - n= 1 表示双曲线，且该双曲线两焦点间的距离为 4 ，则 n 的 取值范围是（ ）A ． (-1,3)B ． (-1, 3)C ． (0,3)D ． (0, 3)x 2 【2015，5】已知 M ( x 0 , y 0 ) 是双曲线 C ： 2- y 2= 1上的一点，F 1 , F 2 是 C 的两个焦点，若 MF 1 ⋅ MF 2 < 0 ，则 y 0 的取值范围是（）A ． (- , )B ． (-, )C ． (-,D ． (-,3 36 63 33 3【2014，4】已知 F 是双曲线 C ：x 2 - my 2 = 3m (m > 0) 的一个焦点，则点 F 到 C 的一条渐近线的距离为A B ．3C ．D ． 3m【2014，10】已知抛物线 C ： y 2= 8x 的焦点为 F ，准线为 l ， P 是l 上一点，Q 是直线 PF 与C 的一个 交点，若 FP = 4FQ ，则| QF | =（）A ． 72B ． 5222C ．3D ．2x y 【2013，4】已知双曲线 C ： - a 2 b 2 =1 (a ＞0，b ＞0)的离心率为 ，则 C 的渐近线方程为( )．2A ．y ＝ ± 1 x 4B ．y ＝ ± 1 x 3 2 2C ．y ＝ ± 1 x 2D ．y ＝±x x y 【2013，10】已知椭圆E ： + a 2 b 2=1 (a ＞b ＞0)的右焦点为 F (3,0)，过点 F 的直线交 E 于 A ，B 两点．若 AB 的中点坐标为(1，－1)，则 E 的方程为()A ． x + y =1B ． x + y =1C ． x + y =1D ． x + y =145 3636 2727 1818 9x 2 y 2 3a【2012，4】设 F 1 、 F 2 是椭圆 E ： a 2 + b 2 （ a > b > 0 ）的左、右焦点，P 为直线 x = 上一点，2∆F 2 PF 1 是底角为 30°的等腰三角形，则 E 的离心率为（）A ． 12B ． 23C ． 34D ． 45【2012，8】等轴双曲线 C 的中心在原点，焦点在 x 轴上，C 与抛物线 y 2= 16x 的准线交于 A ，B 两点，| AB |=，则 C 的实轴长为（ ）A B ．C ．4 D ．8【2011，7】设直线 L 过双曲线 C 的一个焦点，且与 C 的一条对称轴垂直，L 与 C 交于 A ,B 两点， AB 为C 的实轴长的 2 倍，则 C 的离心率为（ ）A B C ．2 D ．3二、填空题【2017，15】已知双曲线 C ： x 2y 2-= 1 （a >0，b >0）的右顶点为 A ，以 A 为圆心，b 为半径作圆 A ，圆 A a 2 b 2与双曲线 C 的一条渐近线交于 M 、N 两点．若∠MAN =60°，则 C 的离心率为 ．x 2 【2015，14】一个圆经过椭圆 y 2+ = 1的三个顶点，且圆心在 x 轴的正半轴上，则该圆的标准方程为 ．16 4【2011，14】在平面直角坐标系 xOy 中，椭圆 C 的中心为原点，焦点 F 1 , F 2 在 x 轴上，离心率为 ．过2F 1 的直线 L 交 C 于 A , B 两点，且 ABF 2 的周长为 16，那么 C 的方程为．三、解答题【2017，20】已知椭圆 C ： x 2 y 2 + =1（a >b >0），四点 P （1,1），P （0,1），P （–1 ），P （1， ） a 2 b 2 1 2 3 42 2中恰有三点在椭圆C 上．（1）求 C 的方程；（2）设直线 l 不经过 P 2 点且与 C 相交于 A ，B 两点．若直线 P 2A 与直线 P 2B 的斜率 的和为–1，证明：l 过定点．【2016，20】设圆x2 +y2 + 2x -15 = 0 的圆心为A ，直线l 过点B(1,0) 且与x 轴不重合，l 交圆A 于C, D 两点，过B 作AC 的平行线交AD 于点E ．（Ⅰ）证明EA +EB 为定值，并写出点E 的轨迹方程；（Ⅱ）设点E 的轨迹为曲线C1 ，直线l 交C1 于M , N 两点，过B 且与l 垂直的直线与圆A 交于P,Q两点，求四边形MPNQ 面积的取值范围．x2【2015，20】在直角坐标系xOy 中，曲线C ：y =与直线l ：y =kx +a （a > 0 ）交于M , N 两点．4（Ⅰ）当k = 0 时，分别求C 在点M 和N 处的切线方程；（Ⅱ）在y 轴上是否存在点P ，使得当k 变动时，总有∠OPM =∠OPN ？说明理由．x 2 y 2 【2014，20】已知点 A （0，-2），椭圆 E ： + a 2 b 2直线 AF 的斜率为， O 为坐标原点．3= 1(a > b > 0) 的离心率为， F 是椭圆的焦点，(Ⅰ)求 E 的方程；（Ⅱ）设过点 A 的直线l 与 E 相交于 P , Q 两点，当 ∆OPQ 的面积最大时，求l 的方程．【2013，20】已知圆 M ：(x ＋1)2＋y 2＝1，圆 N ：(x －1)2＋y 2＝9，动圆 P 与圆 M 外切并且与圆 N 内切，圆 心 P 的轨迹为曲线 C ．(1)求 C 的方程；(2)l 是与圆 P ，圆 M 都相切的一条直线，l 与曲线 C 交于 A ，B 两点，当圆 P 的半径 最长时，求|AB |．【2012，20】设抛物线C：x2 =2py（p > 0 ）的焦点为F，准线为l ，A 为C 上一点，已知以F 为圆心，F A 为半径的圆F 交l 于B，D 两点．（1）若∠BFD=90°，△ABD 的面积为4 2 ，求p 的值及圆F 的方程；（2）若A，B，F 三点在同一直线m 上，直线n 与m 平行，且n 与C 只有一个公共点，求坐标原点到m ，n 距离的比值．【2011，20】在平面直角坐标系xOy 中，已知点A(0,-1)，B 点在直线y = -3 上，M 点满足MB / /OA ，MA⋅AB =MB ⋅BA ，M 点的轨迹为曲线C．（Ⅰ）求C 的方程；（Ⅱ）P 为C 上的动点，l 为C 在P 点处得切线，求O 点到l 距离的最小值．59．统计、概率分布列、计数原理一、选择题【2017，2】如图，正方形 ABCD 内的图形来自中国古代的太极图，正方形内切圆中的黑色部分和白色部 分关于正方形的中心成中心对称．在正方形内随机取一点，则此点取自黑色部分的概率是（）1 π 1 π A ．B ．C ．D ．4824【2017，6】(1 + 1+ x )6 展开式中 x 2 的系数为（ ） x 2A ．15B ．20C ．30D ．35【2016，4】某公司的班车在 7 : 30 ，8 : 00 ，8 : 30 发车，小明在 7 : 50 至8 : 30 之间到达发车站乘坐班车，且到达发车丫的时候是随机的，则他等车时间不超过 10 分钟的概率是（ ）A ．1 B ．1C ．2 D ．3 3234【2015，10】 (x 2 + x + y )5 的展开式中， x 5 y 2 的系数为（）A ．10B ．20C ．30D ．60【2015，4】投篮测试中，每人投 3 次，至少投中 2 次才能通过测试．已知某同学每次投篮投中的概率为 0．6， 且各次投篮是否投中相互独立，则该同学通过测试的概率为（ ）A ．0．648B ．0．432C ．0．36D ．0．312 【2014，5】4 位同学各自在周六、周日两天中任选一天参加公益活动，则周六、周日都有同学参加公益活 动的概率（ ）A ． 18 B ． 38 C ． 58 D ． 78【2013，3】为了解某地区的中小学生的视力情况，拟从该地区的中小学生中抽取部分学生进行调查，事 先已了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异，而男女生视力情况差异不大．在 下面的抽样方法中，最合理的抽样方法是( )A ．简单随机抽样B ．按性别分层抽样C ．按学段分层抽样D ．系统抽样 【2013，9】设 m 为正整数， ( x + y )2m 展开式的二项式系数的最大值为 a ， (x + y )2m +1展开式的二项式系 数的最大值为 b ．若 13a ＝7b ，则 m ＝( )A ．5B ．6C ．7D ．8 【2012，2】将 2 名教师，4 名学生分成 2 个小组，分别安排到甲、乙两地参加社会实践活动，每个小组由 1 名教师和 2 名学生组成，不同的安排方案共有（ ）A ．12 种B ．10 种C ．9 种D ．8 种【2011，8】 ⎛ x + a ⎫ ⎛2x - 1 ⎫的展开式中各项系数的和为 2，则该展开式中常数项为（ ） x ⎪ x ⎪ ⎝ ⎭ ⎝⎭ A ． -40B ． -20C ．20D ．40【2011，4】有 3 个兴趣小组，甲、乙两位同学各自参加其中一个小组，每位同学参加各个小组的可能性相同，则这两位同学参加同一个兴趣小组的概率为（）A ． 13二、填空题B ． 12C ． 23D ． 34【2016，14】 (2x +x )5 的展开式中， x 3 的系数是 ．（用数字填写答案）【2014，13】 (x - y )(x + y )8 的展开式中 x 2 y 7 的系数为 ．(用数字填写答案)【2012，15】某一部件由三个电子元件按下图方式连接而成，元件 1 或元件 2 正常工作，且元件 3 正常工作，则部件正常工作．设三个 电子元件的使用寿命（单位：小时）均服从正态分布 N （1000，502），且各个元件元件1元件2元件3 能否正常工作相互独立，那么该部件的使用寿命超过 1000 小时的概率为 ． 三、解答题【2017，19】为了监控某种零件的一条生产线的生产过程，检验员每天从该生产线上随机抽取16 个零件， 并测量其尺寸（单位：cm ）．根据长期生产经验，可以认为这条生产线正常状态下生产的零件的尺寸服从 正态分布N (μ,σ2)． （1）假设生产状态正常，记X 表示一天内抽取的 16 个零件中其尺寸在(μ–3σ,μ+3σ)之外的零件数，求P (X ≥1)及 X 的数学期望；（2）一天内抽检零件中，如果出现了尺寸在(μ–3σ,μ+3σ)之外的零件，就认为这条生产线在这一天的 生产过程可能出现了异常情况，需对当天的生产过程进行检查．（ⅰ）试说明上述监控生产过程方法的合理性；（ⅱ）下面是检验员在一天内抽取的16 个零件的尺寸：1 16经计算得 x = ∑ x i = 9.97 ，s ==≈ 0.212 ，其中 x i 为抽取 16 i =1的第i 个零件的尺寸，i =1,2, (16)用样本平均数x 作为 μ 的估计值 μˆ ，用样本标准差 s 作为 σ 的估计值σˆ ，利用估计值判断是否需对当 天的生产过程进行检查？剔除(μˆ - 3σˆ , μˆ + 3σˆ ) 之外的数据，用剩下的数据估计 μ 和 σ（精确到 0．01）． 附：若随机变量Z 服从正态分布 N (μ,σ2)，则 P (μ–3σ<Z <μ+3σ)=0．9974，0．997416≈0．9592≈ 0.09 ．【2016，19】某公司计划购买2 台机器，该种机器使用三年后即被淘汰．机器有一易损零件，在购进机器时，可以额外购买这种零件作为备件，每个200 元．在机器使用期间，如果备件不足再购买，则每个500 元．现需决策在购买机器时应同时购买几个易损零件，为此搜集并整理了100 台这种机器在三年使用期内更换的易损零件数，得下面柱状图：以这100 台机器更换的易损零件数的频率代替1 台机器更换的易损零件数发生的概率，记X 表示2 台机器三年内共需更换的易损零件数，n 表示购买2 台机器的同时购买的易损零件数．（Ⅰ）求X 的分布列；（Ⅱ）若要求P( X ≤n) ≥ 0.5 ，确定n 的最小值；（Ⅲ）以购买易损零件所需费用的期望值为决策依据，在n = 19 与n = 20 之中选其一，应选用哪个？8【2015，19】某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费 x （单位：千元）对年销售 量 y （单位：t ）和年利润 z （单位：千元）的影响，对近 8 年的年宣传费 x i 和年销售量 y i （i = 1, 2, , 8 ）数据作了初步处理，得到下面的散点图及一些统计量的值．1 8表中 w i =， w =∑ wii =1（Ⅰ）根据散点图判断， y = a + bx 与 y = c + y 关于年宣传费 x 的回归方程类型？（给出判断即可，不必说明理由）（Ⅱ）根据（Ⅰ）的判断结果及数据，建立 y 关于 x 的回归方程；（III ）已知这种产品的年利润 z 与 x ， y 的关系为 z = 0.2 y - x ，根据（Ⅱ）的结果回答下列问题：（i ）年宣传费 x =49 时，年销售量及年利润的预报值是多少？（ii ）年宣传费 x 为何值时，年利润的预报值最大？附：对于一组数据 (u 1 , v 1 ), (u 2 , v 2 ), , (u n , v n ) ，其回归直线 v = α + β u 的斜率和截距的最小二乘估计n∑ (ui- u )(v i - v )分别为 β = i =1n，α = v - β u ．∑i =1(u i- u )2【2014，18）】从某企业的某种产品中抽取500 件，测量这些产品的一项质量指标值，由测量结果得如下频率分布直方图：(Ⅰ)求这500 件产品质量指标值的样本平均数x 和样本方差s 2 （同一组数据用该区间的中点值作代表）；（Ⅱ）由频率分布直方图可以认为，这种产品的质量指标值Z 服从正态分布N(μ,δ2 ) ，其中μ近似为样本平均数x ，δ2 近似为样本方差s 2 ．(i)利用该正态分布，求P(187.8 <Z < 212.2) ；（ii）某用户从该企业购买了100 件这种产品，记X 表示这100 件产品中质量指标值为于区间（187．8,212．2）的产品件数，利用（i）的结果，求EX ．12．2．若Z ～N(μ,δ2 ) ，则P(μ-δ<Z <μ+δ) =0．6826，P(μ- 2δ<Z <μ+ 2δ) =0．9544．【2013，19】一批产品需要进行质量检验，检验方案是：先从这批产品中任取4 件作检验，这4 件产品中优质品的件数记为n．如果n＝3，再从这批产品中任取4 件作检验，若都为优质品，则这批产品通过检验；如果n＝4，再从这批产品中任取1 件作检验，若为优质品，则这批产品通过检验；其他情况下，这批产品都不能通过检验．假设这批产品的优质品率为50%，即取出的每件产品是优质品的概率都为1，且各件产品是否为优质2品相互独立．(1)求这批产品通过检验的概率；(2)已知每件产品的检验费用为100 元，且抽取的每件产品都需要检验，对这批产品作质量检验所需的费用记为X(单位：元)，求X 的分布列及数学期望．【2012，18】某花店每天以每枝5 元的价格从农场购进若干枝玫瑰花，然后以每枝10 元的价格出售，如果当天卖不完，剩下的玫瑰花作垃圾处理．（1）若花店一天购进16 枝玫瑰花，求当天的利润y（单位：元）关于当天需求量n（单位：枝，n N ）的函数解析式；（2）花店记录了100 天玫瑰花的日需求量（单位：枝），整理得下表：以100 天记录的各需求量的频率作为各需求量发生的概率．①若花店一天购进16 枝玫瑰花，X 表示当天的利润（单位：元），求X 的分布列、数学期望及方差；②若花店计划一天购进16 枝或17 枝玫瑰花，你认为应购进16 枝还是17 枝？请说明理由．⎨ ⎩ 【2011，19】某种产品的质量以其质量指标值衡量，质量指标值越大表明质量越好，且质量指标值大于或 等于 102 的产品为优质品，现用两种新配方（分别称为 A 配方和 B 配方）做试验，各生产了 100 件这种产 品，并测量了每件产品的质量指标值，得到下面试验结果： A 配方的频数分布表B 配方的频数分布表（Ⅰ）分别估计用 A 配方，B 配方生产的产品的优质品率；⎧-2, t < 94（Ⅱ）已知用 B 配方生成的一件产品的利润 y(单位：元)与其质量指标值 t 的关系式为y = ⎪2, 94 ≤ t < 102 ⎪4, t ≥ 102从用 B 配方生产的产品中任取一件，其利润记为 X （单位：元），求 X 的分布列及数学期望．（以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率）10．复数及其运算一、选择题【2017，3】设有下面四个命题1p 1 : 若复数 z 满足 ∈ R ，则 z ∈ R ； p 2 : 若复数 z 满足 z 2 ∈ R ，则z ∈ R ； z p 3 : 若复数 z 1 , z 2 满足 z 1 z 2 ∈ R ，则 z 1 = z 2 ； p 4 : 若复数 z ∈ R ，则 z ∈R ． 其中的真命题为（ ）A ． p 1 , p 3B ． p 1 , p 4C ． p 2 , p 3D ． p 2 , p 4【2016，2】设 (1 + i )x = 1 + yi ，其中 x , y 是实数，则 x + yi = （ ）A ．1B ． 2C ． 3D ． 2【2015，1】设复数 z 满足1 + z= i ，则| z | =（ ） 1 - zA ．1B C ．D ．2(1 + i )3【2014，2】(1 - i )2=（ ）A ．1 + iB ．1 - iC ． -1+ iD ．-1- i 【2013，2】若复数 z 满足(3－4i)z ＝|4＋3i|，则 z 的虚部为()．A ．－4B ． - 45C ．4D ． 45【2012，3】下面是关于复数 z = 22 -1 + i的四个命题：p 1 ：| z |= 2 ； p 2 ： z = 2i ； p 3 ： z 的共轭复数为1 + i ； p 4 ： z 的虚部为 -1．其中的真命题为（ ）A ． p 2 ， p 3B ． p 1 ， p 2C ． p 2 ， p 4D ． p 3 ， p 4【2011，1】复数2 + i的共轭复数是（ ） 1 - 2iA ． - 3 i5B ． 3 iC ． -i5D ．i11．程序框图一、选择题【2017，8】右面程序框图是为了求出满足3n - 2n >1000 的最小偶数n，那么在两个空白框中，可以分别填入A．A+1 B．A>1000 和n=n+2C．A ≤1000 和n=n+1 D．A ≤1000 和n=n+2【2017，8】【2016，9】【2015，9】【2016，9】执行右面的程序框图，如果输入的x = 0 ，y =1，n =1，则输出x, y 的值满足（）A．y =2x B．y =3x C．y =4x D．y =5x【2015，9】执行右面的程序框图，如果输入的t =0.01，则输出的n =（）A．5 B．6 C．7 D．8【2014，7】执行下图的程序框图，若输入的a,b, k 分别为1,2,3，则输出的M =（）A ．203B ．165C ．72D ．158【2013，5】执行下面的程序框图，如果输入的t∈[－1,3]，则输出的s 属于( )．A．[－3,4] B．[－5,2] C．[－4,3] D．[－2,5]【2012，6】如果执行右边和程序框图，输入正整数N （N ≥ 2 ）和实数a1 ，a2 ，…，a N ，输出A，B，则（）A．A +B 为a1 ，a2 ，…，a N 的和B．A +B为a ，a ，…，a 的算术平均数2 1 2 NC．A 和B 分别是a1 ，a2 ，…，a N 中最大的数和最小的数D．A 和B 分别是a1 ，a2 ，…，a N 中最小的数和最大的数【2013，5】【2012，6】【2011，3】【2011,3】执行右面的程序框图，如果输入的N 是6，那么输出的p 是（）A．120 B．720 C．1440 D．5040⎩12．坐标系与参数方程一、解答题⎧ x = 3cos θ ,【2017，22】（选修 4-4，坐标系与参数方程）在直角坐标系 xOy 中，曲线 C 的参数方程为 ⎨（θ ⎩ y = sin θ ,⎧ x = a + 4t ,为参数），直线 l 的参数方程为 ⎨ y = 1 - t , （ t 为参数）．（1）若 a = -1 ，求 C 与 l 的交点坐标；（2）若 C 上的点到 l 的距离的最大值为a ．⎧x = a cos t ,【2016，23】（选修 4－4：坐标系与参数方程）在直角坐标系 xOy 中，曲线 C 1 的参数方程为 ⎨⎩ y = 1 + a sin t ,(t 为参数， a > 0) ．在以坐标原点为极点， x 轴正半轴为极轴的极坐标系中，曲线C 2 : ρ = 4 c os θ ．（Ⅰ）说明 C 1 是哪一种曲线，并将 C 1 的方程化为极坐标方程；（Ⅱ）直线 C 3 的极坐标方程为θ = α 0 ，其中α 0 满足 tan α 0 = 2 ，若曲线 C 1 与 C 2 的公共点都在C 3 上， 求 a ．。
高考数学全国卷分类汇编(解析几何)
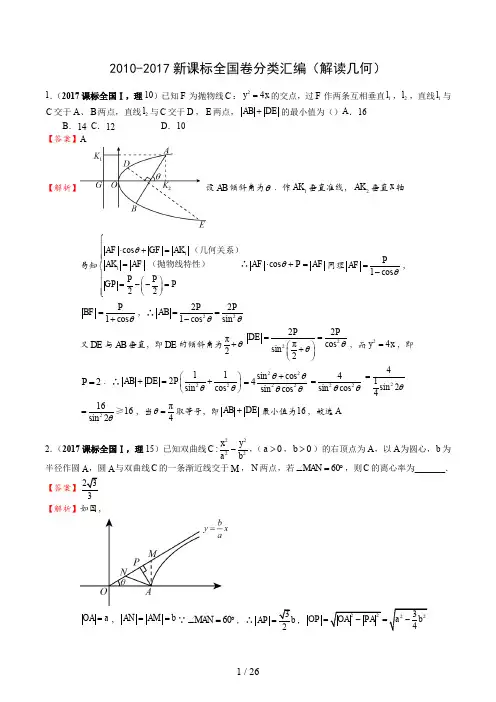
2010-2017新课标全国卷分类汇编（解读几何）1．（2017课标全国Ⅰ，理10）已知F 为抛物线C ：24y x =的交点，过F 作两条互相垂直1l ，2l ，直线1l 与C 交于A 、B 两点，直线2l 与C 交于D ，E 两点，AB DE +的最小值为（）A ．16B ．14C ．12D ．10【答案】A【解析】设AB 倾斜角为θ．作1AK 垂直准线，2AK 垂直x 轴易知11cos 22⎧⎪⋅+=⎪⎪=⎨⎪⎛⎫⎪=--= ⎪⎪⎝⎭⎩AF GF AK AK AF P P GP Pθ（几何关系）（抛物线特性）cos AF P AF θ⋅+=∴同理1cos PAF θ=-，1cos P BF θ=+，∴22221cos sin P PAB θθ==-又DE 与AB 垂直，即DE 的倾斜角为π2θ+2222πcos sin 2P PDE θθ==⎛⎫+ ⎪⎝⎭，而24y x =，即2P =．∴22112sin cos AB DE P θθ⎛⎫+=+ ⎪⎝⎭2222sin cos 4sin cos θθθθ+=224sin cos θθ=241sin 24=θ21616sin 2θ=≥，当π4θ=取等号，即AB DE +最小值为16，故选A2．（2017课标全国Ⅰ，理15）已知双曲线2222:x y C a b-，（0a >，0b >）的右顶点为A ，以A 为圆心，b 为半径作圆A ，圆A 与双曲线C 的一条渐近线交于M ，N 两点，若60MAN ∠=︒，则C 的离心率为_______．【解析】如图，OA a =，AN AM b ==∵60MAN ∠=︒，∴AP =，OP =∴tan AP OP θ==又∵tan b aθ=b a =，解得223a b =∴e ==3．（2017课标全国Ⅰ，理20）（12分）已知椭圆C ：22221x y a b+=()0a b >>，四点()111P ，，()201P ，，31P ⎛- ⎝⎭，41P ⎛ ⎝⎭中恰有三点在椭圆C 上．（1）求C 的方程；（2）设直线l 不经过2P 点且与C 相交于A 、B 两点，若直线2P A 与直线2P B 的斜率的和为1-，证明：l 过定点．【解析】（1）根据椭圆对称性，必过3P 、4P 又4P 横坐标为1，椭圆必不过1P ，所以过234P P P ，，三点 将()23011P P ⎛- ⎝⎭，，代入椭圆方程得222113141b ab ⎧=⎪⎪⎨⎪+=⎪⎩，解得24a =，21b = ∴椭圆C 的方程为：2214x y +=．（2）①当斜率不存在时，设()():A A l x m A m y B m y =-，，，，221121A A P A P B y y k k m m m----+=+==- 得2m =，此时l 过椭圆右顶点，不存在两个交点，故不满足． ②当斜率存在时，设()1l y kx b b =+≠∶，()()1122A x y B x y ，，，联立22440y kx bx y =+⎧⎨+-=⎩，整理得()222148440k x kbx b +++-=122814kb x x k -+=+，21224414b x x k -⋅=+，则22121211P A P By y k k x x --+=+()()21212112x kx b x x kx b x x x +-++-=222228888144414kb k kb kbk b k --++=-+()()()811411k b b b -==-+-，又1b ≠21b k ⇒=--，此时64k ∆=-，存在k 使得0∆>成立．∴直线l 的方程为21y kx k =--当2x =时，1y =-，所以l 过定点()21-，．4．（2017课标全国Ⅱ，理9）若双曲线)00(1:2222>>=-b a by a x C ，的一条渐近线被圆4)2(22=+-y x 所截得的弦长为2，则C 的离心率为A ．2B ．3C ．2D ．332 【答案】A【解读】由几何关系可得，双曲线()222210,0x y a b a b-=>>的渐近线方程为0bx ay ±=，圆心()2,0到渐近线距离为d =，则点()2,0到直线0b x a y +=的距离为2bd c=== 即2224()3c a c -=，整理可得224c a =，双曲线的离心率2e ===．故选A ． 【考点】 双曲线的离心率；直线与圆的位置关系，点到直线的距离公式【名师点睛】双曲线的离心率是双曲线最重要的几何性质，求双曲线的离心率(或离心率的取值范围)，常见有两种方法：①求出a ，c ，代入公式ce a=；②只需要根据一个条件得到关于a ，b ，c 的齐次式，结合b 2＝c 2－a 2转化为a ，c 的齐次式，然后等式(不等式)两边分别除以a 或a 2转化为关于e 的方程(不等式)，解方程(不等式)即可得e (e 的取值范围)．5．（2017课标全国Ⅱ，理16）已知F 是抛物线x y C 8:2=的焦点，M 是C 上一点，FM 的延长线交y 轴于点N .若M 为FN 的中点，则=FN . 【答案】6 【解读】试卷分析：如图所示，不妨设点M 位于第一象限，设抛物线的准线与x 轴交于点F'，作MB l ⊥与点B ，NA l ⊥与点A ，由抛物线的解读式可得准线方程为2x =-，则2,4A N F F '==，在直角梯形ANFF'中，中位线'32AN FF BM +==，由抛物线的定义有：3MF MB ==，结合题意，有3MN MF ==，故336FN FM NM =+=+=．【考点】抛物线的定义、梯形中位线在解读几何中的应用．【名师点睛】抛物线的定义是解决抛物线问题的基础，它能将两种距离(抛物线上的点到焦点的距离、抛物线上的点到准线的距离)进行等量转化．如果问题中涉及抛物线的焦点和准线，又能与距离联系起来，那么用抛物线定义就能解决问题．因此，涉及抛物线的焦半径、焦点弦问题，可以优先考虑利用抛物线的定义转化为点到准线的距离，这样就可以使问题简单化．6．（2017课标全国Ⅱ，理20）（12分）设O 为坐标原点，动点M 在椭圆12:22=+y x C 上，过M 作x 轴的垂线，垂足为N ，点P 满足= (1)求点P 的轨迹方程； (2)设点Q 在直线3-=x 上，且1=⋅. 证明：过点P 且垂直于OQ 的直线l 过C 的左焦点F .解：（1）设)(y x P ，，则)22(y x M ，，将点M 代入C 中得12222=+y x ，所以点P 的轨迹方程为222=+y x .（2）由题可知)01(，-F ，设)()3(n m P t Q ，，，-，则)1( )3(n m t ---=-=，，，， )3( )(n t m n m ---==，，，.由1=⋅得1322=-+--n tn m m ，由（1）有222=+n m ，则有033=-+tn m ，所以033 =-+=⋅tn m ，即过点P 且垂直于OQ 的直线l 过C 的左焦点F .7．（2017课标全国Ⅲ，理1）已知集合A={}22(,)1x y x y +=│，B={}(,)x y y x =│，则A ⋂B 中元素的个数为A ．3B ．2C ．1D ．0【答案】B【解读】A 表示圆221x y +=上所有点的集合，B 表示直线y x =上所有点的集合，故AB 表示两直线与圆的交点，由图可知交点的个数为2，即AB 元素的个数为2，故选B.8．（2017课标全国Ⅲ，理5）已知双曲线C 22221x y a b -= (a ＞0,b ＞0)的一条渐近线方程为y x =,且与椭圆221123x y +=有公共焦点，则C 的方程为A. 221810x y -=B. 22145x y -=C. 22154x y -=D. 22143x y -=【答案】B【解读】∵双曲线的一条渐近线方程为y，则b a =① 又∵椭圆221123x y +=与双曲线有公共焦点，易知3c =，则2229a b c +==②由①②解得2,a b =C 的方程为22145x y -=，故选B. 9．（2017课标全国Ⅲ，理10）已知椭圆C ：22221x y a b+=，（a >b >0）的左、右顶点分别为A 1，A 2，且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切，则C 的离心率为D.13【答案】A【解读】∵以12A A 为直径为圆与直线20bx ay ab -+=相切，∴圆心到直线距离d 等于半径，∴d a ==又∵0,0a b >>，则上式可化简为223a b = ∵222b ac =-，可得()2223a a c=-，即2223c a =∴c e a == A10．（2017课标全国Ⅲ，理12）在矩形ABCD 中，1AB =，2AD =，动点P 在以点C 为圆心且与BD 相切的圆上．若AP AB AD λμ=+，则λμ+的最大值为（） A ．3B．D ．2【答案】A【解读】由题意，画出右图．设BD 与C 切于点E ，连接CE ． 以A 为原点，AD 为x 轴正半轴， AB 为y 轴正半轴建立直角坐标系， 则C 点坐标为(2,1)． ∵||1CD =，||2BC =．∴BD = ∵BD 切C 于点E ． ∴CE ⊥BD ．∴CE 是Rt BCD △中斜边BD 上的高．()A O Dxy BP gCE12||||22||||||BCDBC CDSECBD BD⋅⋅⋅====△即C．∵P在C上．∴P点的轨迹方程为224(2)(1)5x y-+-=．设P点坐标00(,)x y，可以设出P点坐标满足的参数方程如下：21xyθθ⎧=⎪⎪⎨⎪=⎪⎩而00(,)AP x y=，(0,1)AB =，(2,0)AD =．∵(0,1)(2,0)(2,)AP AB ADλμλμμλ=+=+=∴112xμθ==+，1yλθ==+．两式相加得：112)2sin()3λμθθθϕθϕ+=+++=++=++≤(其中sinϕcosϕ=)当且仅当π2π2kθϕ=+-，k∈Z时，λμ+取得最大值3．11．（2017课标全国Ⅲ，理20）（12分）已知抛物线C：y2=2x，过点（2,0）的直线l交C与A,B 两点，圆M是以线段AB为直径的圆.（1）证明：坐标原点O在圆M上；（2）设圆M过点P（4，-2），求直线l与圆M的方程.解：（1）设()()11222A x,y,B x,y,l:x my=+由222x myy x=+⎧⎨=⎩可得212240则4y my,y y--==-又()22212121212==故=224y yy yx,x,x x=4因此OA 的斜率与OB 的斜率之积为1212-4==-14y y x x 所以OA ⊥OB故坐标原点O 在圆M 上.（2）由（1）可得()2121212+=2+=++4=24y y m,x x m y y m + 故圆心M 的坐标为()2+2，m m ，圆M 的半径r =由于圆M 过点P （4，-2），因此0AP BP =,故()()()()121244220x x y y --+++= 即()()121212124+2200x x x x y y y y -++++= 由（1）可得1212=-4，=4y y x x ，所以2210m m --=，解得11或2m m ==-.当m=1时，直线l 的方程为x-y-2=0，圆心M 的坐标为（3,1），圆M ，圆M 的方程为()()223110x y -+-=当12m =-时，直线l 的方程为240x y +-=，圆心M 的坐标为91，-42⎛⎫ ⎪⎝⎭，圆M 的半径为4，圆M 的方程为229185++4216x y ⎛⎫⎛⎫-= ⎪ ⎪⎝⎭⎝⎭12.（2016课标全国Ⅰ，理5）已知方程132222=--+nm y n m x 表示双曲线，且该双曲线两焦点间的距离为4，则n 的取值范围是（A ）)3,1(-（B ）)3,1(-（C ）)3,0(（D ）)3,0(【解读】：222213x y m n m n-=+-表示双曲线，则()()2230m n m n +->，∴223m n m -<<由双曲线性质知：()()222234c m n m n m =++-=，其中c 是半焦距，∴焦距2224c m =⋅=，解得1m =∴13n -<<，故选A ．13.（2016课标全国Ⅰ，理10）以抛物线C 的顶点为圆心的圆交C 于B A ,两点，交C 的准线于ED ,两点，已知24=AB ,52=DE ，则C 的焦点到准线的距离为|||M N MN y y =- （A ）2 （B ）4 （C ）6 （D ）8【解读】：以开口向右的抛物线为例来解答，其他开口同理设抛物线为22y px =()0p >，设圆的方程为222x y r +=，如图：设(0A x ，2pD ⎛- ⎝，点(0A x 在抛物线22y px =上，∴082px =……①；点2pD ⎛- ⎝在圆222x y r +=上，∴2252p r ⎛⎫+= ⎪⎝⎭……②；点(0A x 在圆222x y r +=上，∴2208x r +=……③；联立①②③解得：4p =， 焦点到准线的距离为4p =．故选B ．14.（2016课标全国Ⅰ，理20）（本小题满分12分）设圆015222=-++x y x 的圆心为A ，直线l 过点)0,1(B 且与x 轴不重合，l 交圆A 于D C ,两点，过B 作AC 的平行线交AD 于点E ．（Ⅰ）证明EB EA +为定值，并写出点E 的轨迹方程；（Ⅱ）设点E 的轨迹为曲线两点，求四边形MPNQ【解读】：⑴圆A 整理为(x BE AC Q ∥，则C =∠EBD D ∴=∠∠，则EB ⑵221:143x yC +=；设:l x 联立1l C 与椭圆：24x x =⎧⎪⎨⎪⎩圆心A 到PQ 距离d ==F所以||PQ==，()2212111||||2234MPNQmS MN PQm+⎡∴=⋅=⋅==⎣+15.（2016课标全国Ⅱ，理4）圆2228130x y x y+--+=的圆心到直线10ax y+-=的距离为1，则a=（）（A）43-（B）34-（C（D）216.（2016课标全国Ⅱ，理11）已知12,F F是双曲线2222:1x yEa b-=的左，右焦点，点M在E上，1MF与x轴垂直，211sin3MF F∠=,则E的离心率为（）（A（B）32（C（D）217.（2016课标全国Ⅱ，理20）（本小题满分12分）已知椭圆:E 2213x y t +=的焦点在x 轴上，A 是E 的左顶点，斜率为(0)k k >的直线交E 于,A M 两点，点N 在E 上，MA NA ⊥．（Ⅰ）当4,||||t AM AN ==时，求AMN ∆的面积；（Ⅱ）当2AM AN =时，求k 的取值范围．【答案】（Ⅰ）；（Ⅱ）.【解读】试卷分析：（Ⅰ）先求直线的方程，再求点的纵坐标，最后求的面积；（Ⅱ）设，，将直线的方程与椭圆方程组成方程组，消去，用表示，从而表示，同理用表示，再由求.试卷解读：（I ）设，则由题意知，当时，的方程为，.由已知及椭圆的对称性知，直线的倾斜角为.因此直线的方程为. 将代入得.解得或，所以.因此的面积.（II ）由题意，，.将直线的方程代入得. 由得，故.由题设，直线的方程为，故同理可得，由得，即.当时上式不成立，因此.等价于，即.由此得，或，解得.因此的取值范围是.考点：椭圆的性质，直线与椭圆的位置关系.18.（2016课标全国Ⅲ，理11）已知O为坐标原点，F是椭圆C：22221(0)x ya ba b+=>>的左焦点，,A B分别为C的左，右顶点.P为C上一点，且PF x⊥轴.过点A的直线l与线段PF交于点M，与y轴交于点E.若直线BM经过OE的中点，则C的离心率为（）（A）13（B）12（C）23（D）34【答案】A考点：椭圆方程与几何性质．【思路点拨】求解椭圆的离心率问题主要有三种方法：（1）直接求得,a c 的值，进而求得e 的值；（2）建立,,a b c 的齐次等式，求得ba 或转化为关于e 的等式求解；(3)通过特殊值或特殊位置，求出e ．19.（2016课标全国Ⅲ，理16）已知直线l ：30mx y m ++=与圆2212x y +=交于,A B 两点，过,A B 分别做l 的垂线与x 轴交于,C D 两点，若AB =||CD =__________________.【答案】4考点：直线与圆的位置关系．【技巧点拨】解决直线与圆的综合问题时，一方面，要注意运用解读几何的基本思想方法(即几何问题代数化)，把它转化为代数问题；另一方面，由于直线与圆和平面几何联系得非常紧密，因此，准确地作出图形，并充分挖掘几何图形中所隐含的条件，利用几何知识使问题较为简捷地得到解决．20.（2016课标全国Ⅲ，理20）（本小题满分12分）已知抛物线C ：22y x =的焦点为F ，平行于x 轴的两条直线12,l l 分别交C 于,A B 两点，交C 的准线于P Q ，两点．（I ）若F 在线段AB 上，R 是PQ 的中点，证明AR FQ ；（II ）若PQF ∆的面积是ABF ∆的面积的两倍，求AB 中点的轨迹方程.【答案】（Ⅰ）见解读；（Ⅱ）21y x =-．试卷解读：由题设)0,21(F .设b y l a y l ==:,:21，则0≠ab ，且)2,21(),,21(),,21(),,2(),0,2(22b a R b Q a P b b B a A +---.记过B A ,两点的直线为l ，则l 的方程为0)(2=++-ab y b a x . .....3分（Ⅰ）由于F 在线段AB 上，故01=+ab . 记AR 的斜率为1k ，FQ 的斜率为2k ，则222111k b a aba ab a b a a b a k =-=-==--=+-=，所以AR FQ . ......5分（Ⅱ）设l 与x 轴的交点为)0,(1x D ，则2,2121211b a S x a b FD a b S PQF ABF -=--=-=∆∆. 由题设可得221211b a x a b -=--，所以01=x （舍去），11=x . 设满足条件的AB 的中点为),(y x E . 当AB 与x 轴不垂直时，由DE ABk k =可得)1(12≠-=+x x yb a .而y ba =+2，所以)1(12≠-=x x y .当AB 与x 轴垂直时，E 与D 重合，所以，所求轨迹方程为12-=x y . ....12分考点：1、抛物线定义与几何性质；2、直线与抛物线位置关系；3、轨迹求法．【方法归纳】（1）解读几何中平行问题的证明主要是通过证明两条直线的斜率相等或转化为利用向量证明；（2）求轨迹的方法在高考中最常考的是直接法与代入法（相关点法），利用代入法求解时必须找准主动点与从动点．21.(2015课标全国Ⅰ，理5)已知00(,)M x y 是双曲线22:12x C y -=上的一点，12,F F 是C 的两个焦点，若120MF MF ⋅<,则0y 的取值范围是（A)((B)( (C)((D)( 答案：A解读：由条件知F1(－，0)，F2(，0)，＝(－－x0，－y0)，＝(－x0，－y0)，－3＜0.①又＝1，＝2+2.代入①得，∴－＜y0＜22.(2015课标全国Ⅰ，理14)一个圆经过椭圆221164x y+=的三个顶点，且圆心在x轴的正半轴上，则该圆的规范方程为答案：+y2＝解读：由条件知圆经过椭圆的三个顶点分别为(4，0)，(0，2)，(0，－2)，设圆心为(a，0)(a＞0)，所以＝4－a，解得a＝，故圆心为，此时半径r＝4－，因此该圆的规范方程是+y2＝23.(2015课标全国Ⅰ，理20)在直角坐标系xOy中，曲线2:4xC y=与直线:(0)l y kx a a=+>交于,M N两点。
2011-2017全国1卷分类汇编 立体几何
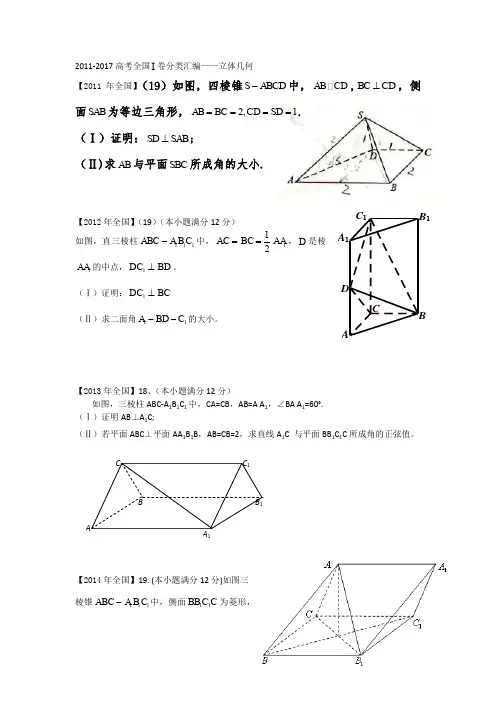
2011-2017高考全国I 卷分类汇编——立体几何【2011年全国】（19）如图，四棱锥S ABCD -中，AB CD ,BC CD ⊥，侧面SAB 为等边三角形，2,1AB BC CD SD ====. （Ⅰ）证明：SD SAB ⊥;（Ⅱ)求AB 与平面SBC 所成角的大小.【2012年全国】（19）（本小题满分12分） 如图，直三棱柱111ABC A B C -中，112AC BC AA ==，D 是棱1AA 的中点，1DC BD ⊥。
（Ⅰ）证明：1DC BC ⊥（Ⅱ）求二面角11A BD C --的大小。
【2013年全国】18、（本小题满分12分）如图，三棱柱ABC-A 1B 1C 1中，CA=CB ，AB=A A 1，∠BA A 1=60°. （Ⅰ）证明AB ⊥A【2014年全国】19. (本小题满分12分)如图三棱锥111ABC AB C -中，侧面11BB C C 为菱形，A 11AB B C ⊥.(Ⅰ) 证明：1AC AB =；（Ⅱ）若1AC AB ⊥，o160CBB ∠=，AB=Bc ，求二面角111A A B C --的余弦值.【2015年全国】（18）如图，，四边形ABCD 为菱形，∠ABC=120°，E ，F 是平面ABCD同一侧的两点，BE ⊥平面ABCD ，DF ⊥平面ABCD ，BE=2DF ，AE ⊥EC 。
（1）证明：平面AEC ⊥平面AFC（2）求直线AE 与直线CF 所成角的余弦值【2016年全国】（18）（本题满分为12分）如图，在已A ，B ，C ，D ，E ，F 为顶点的五面体中，面ABEF 为正方形，AF =2FD ，90AFD ∠=，且二面角D -AF -E 与二面角C -BE -F 都是60． （I ）证明；平面ABEF ⊥平面EFDC ； （II ）求二面角E -BC -A 的余弦值．【2017年全国】18．（12分）如图，在四棱锥P−ABCD 中，AB//CD ，且90BAP CDP ∠=∠=.（1）证明：平面PAB ⊥平面PAD ；（2）若PA =PD =AB =DC ，90APD ∠=，求二面角A −PB −C 的余弦值.。
9.解析几何——2011—2017年新课标全国卷理科数学分类真题解析(含答案)
=6.
椭圆的性质,容易排除点 P1(1,1)不在椭圆上,从而求出椭圆方程;(2)利用直线与椭圆 优解 依题意,抛物线 C:y2=8x 的焦点 F(2,0),准线 x=-2,因为 M 是 C 上一点,FM 的延
的方程得出根与系数的关系,从而使问题得解,在解题中要注意斜率不存在的情形.
长线交 y 轴于点 N,M 为 FN 的中点,则点 M 的横坐标为 1,所以|FN|=2|MF|=2[1-(-2)]=6.
第 1页 共 28页 ◎ 第 2页 共 28页
……○…………内…………○…………装…………○…………订…………○…………线…………○……… ※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
……○…………外…………○…………装…………○…………订…………○…………线…………○………
9-2
的斜率为 k,则 l1:y=k(x-1),l2:y=- (x-1),由
消去 y 得 k2x2-(2k2+4)x+k2=0,
(2)设直线 P2A 与直线 P2B 的斜率分别为 k1,k2. 如果 l 与 x 轴垂直,设 l:x=t,由题设知 t≠0,且|t|<2,得 A,B 的坐标分别为(t,
),(t,- ).
的距离 d=
,因为∠MAN=60°,圆的半径为 b,所以 b·sin 60°= ,即
,所
2018 课标Ⅱ卷(全国甲卷)
以 e=
.
2018 课标Ⅲ卷(全国丙卷)
20．已知椭圆 C: + =1(a>b>0),四点 P1(1,1),P2(0,1),P3(-1, ),P4(1, )中恰有三点在
2017 课标Ⅰ卷(全国乙卷) 10．已知 F 为抛物线 C:y2=4x 的焦点,过 F 作两条互相垂直的直线 l1,l2,直线 l1 与 C 交
2011年—2017年新课标全国1卷理科数学题型分类汇编(含答案)
2011 年—2017 年新课标高考全国Ⅰ卷 理科数学分类汇编（含答案）
说明：2017 年高考中，安徽、湖北、福建、湖南、山西、河北、江西、广东、河南等 9 个省份选择使 用新课标全国Ⅰ卷．2017 年，除了保留北京、天津、上海、江苏、浙江实行自主命题外（山东省语文、数 学卷最后一年使用） ，大陆其他省区全部使用全国卷． 研究发现，新课标全国卷的试卷结构和题型具有一定的稳定性和连续性．每个题型考查的知识点、 考查方法、考查角度、思维方法等相对固定．掌握了全国卷的各种题型，就把握住了全国卷命题的灵魂． 正所谓知己知彼，才能百战不殆，为了方便老师和同学们备考 2018 年高考，本人认真研究近 7 年新 课标高考全国Ⅰ卷理科数学和高考数学考试说明，将 2011 年—2017 年新课标全国Ⅰ卷进行了分类整理．
1
整理人，中山一中，朱欢
1．集合与常用逻辑用语
一、选择题 【2017，1】已知集合 A x x 1 ， B x 3
A． A
B {x | x 0}
B． A
BR
C． A
B {x | x 1}
B
【2016，1】设集合 A {x x 2 4 x 3 0} ， B {x 2 x 3 0} ，则 A A． (3, )
2011 年—2017 年新课标高考全国Ⅰ卷理科数学分类汇编
1．集合与常用逻辑用语 ................................................................................................................................. 2 2．函数与导数 ................................................................................................................................................. 3 3．三角函数、解三角形 ................................................................................................................................. 7 4．平面向量 ................................................................................................................................................... 10 5．数列 ........................................................................................................................................................... 11 6．不等式、推理与证明 ............................................................................................................................... 13 7．立体几何 ................................................................................................................................................... 14 8．解析几何 ................................................................................................................................................... 18 9．统计、概率分布列、计数原理 ............................................................................................................... 23 10．复数及其运算 ......................................................................................................................................... 30 11．程序框图 ................................................................................................................................................. 31 12．坐标系与参数方程 ................................................................................................................................. 33 13．不等式选讲 ............................................................................................................................................. 36
2011-2017全国1卷分类汇编 解析几何
2011-2017全国卷分类汇编——解析几何【2011年全国】（21）已知O 为坐标原点，F 为椭圆22:12y C x +=在y 轴正半轴上的焦点，过F 且斜率为l 与C 交与A 、B 两点，点P 满足0.OA OB OP ++=(Ⅰ)证明：点P 在C 上；（Ⅱ）设点P 关于点O 的对称点为Q ，证明：A 、P 、B 、Q 四点在同一圆上.【2012年全国】（20）（本小题满分12分）设抛物线2:2(0)C x py p =>的焦点为F ，准线为l ，A 为C 上一点，已知以F 为圆心，FA 为半径的圆F 交l 于,B D 两点。
（Ⅰ）若90BFD ∠=，ABD ∆的面积为求p 的值及圆F 的方程；（Ⅱ）若,,A B F 三点在同一直线m 上，直线n 与m 平行，且n 与C 只有一个公共点，求坐标原点到m ，n 距离的比值。
【2013年全国】(20)(本小题满分12分)已知圆M ：(x ＋1)2＋y 2=1，圆N ：(x －1)2＋y 2=9，动圆P 与圆M 外切并与圆N 内切，圆心P 的轨迹为曲线 C（Ⅰ）求C 的方程；（Ⅱ）l 是与圆P ，圆M 都相切的一条直线，l 与曲线C 交于A ，B 两点，当圆P 的半径最长时，求|AB|.【2014年全国】20. (本小题满分12分) 已知点A （0，-2），椭圆E ：22221(0)x y a b a b+=>>的离心率为2，F 是椭圆的焦点，直线AF 的斜率为3，O 为坐标原点. (Ⅰ)求E 的方程；（Ⅱ）设过点A 的直线l 与E 相交于,P Q 两点，当OPQ ∆的面积最大时，求l 的方程.【2015年全国】（20）（本小题满分12分）在直角坐标系xoy 中，曲线C ：y =24x 与直线y kx a =+(a ＞0)交与M ,N 两点， （Ⅰ）当k =0时，分别求C 在点M 和N 处的切线方程；（Ⅱ）y 轴上是否存在点P ，使得当k 变动时，总有∠OPM =∠OPN ？说明理由。
2011—2017年新课标全国卷123理科数学分类汇编——9.解析几何衷敬奎
2012年—2017年新课标全国卷Ⅰ理科数学试题分类汇编9．解析几何一、选择题【2017，10】已知F 为抛物线C ：y 2=4x 的焦点，过F 作两条互相垂直的直线l 1，l 2，直线l 1与C 交于A 、B 两点，直线l 2与C 交于D 、E 两点，则|AB |+|DE |的最小值为（ ）A ．16B ．14C ．12D ．10【2016，10】以抛物线C 的顶点为圆心的圆交C 于B A ,两点，交C 的准线于E D ,两点，已知24=AB ,52=DE ，则C 的焦点到准线的距离为（ ）A ．2B ．4C ．6D ．8【2016，5】已知方程132222=--+nm y n m x 表示双曲线，且该双曲线两焦点间的距离为4，则n 的取值范围是（ ） A ．)3,1(-B ．)3,1(-C ．)3,0(D ．)3,0(【2015，5】已知00(,)M x y 是双曲线C ：2212x y -=上的一点，12,F F 是C 的两个焦点，若120MF MF ⋅< ，则0y 的取值范围是（ ）A ．(33-B ．(,)66-C ．(33-D ．(33- 【2014，4】已知F 是双曲线C ：223(0)x my m m -=>的一个焦点，则点F 到C 的一条渐近线的距离为A B ．3 C D ．3m【2014，10】已知抛物线C ：28y x =的焦点为F ，准线为l ，P 是l 上一点，Q 是直线PF 与C 的一个交点，若4FP FQ =，则||QF =（ ）A ．72B ．52C ．3D ．2【2013，4】已知双曲线C ：2222=1x y a b -(a ＞0，b ＞0)的离心率为2，则C 的渐近线方程为( )．A ．y ＝14x ±B ．y ＝13x ±C ．y ＝12x ± D ．y ＝±x【2013，10】已知椭圆E ：2222=1x y a b+(a ＞b ＞0)的右焦点为F (3,0)，过点F 的直线交E 于A ，B 两点．若AB 的中点坐标为(1，－1)，则E 的方程为( )A ．22=14536x y + B ．22=13627x y + C ．22=12718x y + D ．22=1189x y + 【2012，4】设1F 、2F 是椭圆E ：2222x y a b+（0a b >>）的左、右焦点，P 为直线32ax =上一点，21F PF ∆是底角为30°的等腰三角形，则E 的离心率为（ ） A ．12 B ．23 C ．34 D ．45【2012，8】等轴双曲线C 的中心在原点，焦点在x 轴上，C 与抛物线216y x =的准线交于A ，B 两点，||AB =，则C 的实轴长为（ ）AB ．C ．4D ．8【2011，7】设直线L 过双曲线C 的一个焦点，且与C 的一条对称轴垂直，L 与C 交于A ,B 两点，AB 为C 的实轴长的2倍，则C 的离心率为（ ）A B C ．2 D ．3 二、填空题【2017，15】已知双曲线C ：22221x y a b-=（a >0，b >0）的右顶点为A ，以A 为圆心，b 为半径作圆A ，圆A 与双曲线C 的一条渐近线交于M 、N 两点．若∠MAN =60°，则C 的离心率为________．【2015，14】一个圆经过椭圆221164x y +=的三个顶点，且圆心在x 轴的正半轴上，则该圆的标准方程为 ．【2011，14】在平面直角坐标系xOy 中，椭圆C 的中心为原点，焦点12,F F 在x 轴上，离心率为2．过1F 的直线L 交C 于,A B 两点，且2ABF V 的周长为16，那么C 的方程为 ．三、解答题【2017，20】已知椭圆C ：2222=1x y a b +（a >b >0），四点P 1（1,1），P 2（0,1），P 3（–1，2 ），P 4（1，2）中恰有三点在椭圆C 上．（1）求C 的方程；（2）设直线l 不经过P 2点且与C 相交于A ，B 两点．若直线P 2A 与直线P 2B 的斜率的和为–1，证明：l 过定点．【2016，20】设圆015222=-++x y x 的圆心为A ，直线l 过点)0,1(B 且与x 轴不重合，l 交圆A 于D C ,两点，过B 作AC 的平行线交AD 于点E ．（Ⅰ）证明EB EA +为定值，并写出点E 的轨迹方程；（Ⅱ）设点E 的轨迹为曲线1C ，直线l 交1C 于N M ,两点，过B 且与l 垂直的直线与圆A 交于Q P ,两点，求四边形MPNQ 面积的取值范围．【2015，20】在直角坐标系xOy 中，曲线C ：24x y =与直线l ：y kx a =+（0a >）交于,M N 两点．（Ⅰ）当0k =时，分别求C 在点M 和N 处的切线方程；（Ⅱ）在y 轴上是否存在点P ，使得当k 变动时，总有OPM OPN ∠=∠？说明理由．【2014，20】已知点A （0，-2），椭圆E ：22221(0)x y a b a b +=>>，F 是椭圆的焦点，直线AF 的斜率为3，O 为坐标原点．(Ⅰ)求E 的方程；（Ⅱ）设过点A 的直线l 与E 相交于,P Q 两点，当OPQ ∆的面积最大时，求l 的方程．【2013，20】已知圆M ：(x ＋1)2＋y 2＝1，圆N ：(x －1)2＋y 2＝9，动圆P 与圆M 外切并且与圆N 内切，圆心P 的轨迹为曲线C ．(1)求C 的方程；(2)l 是与圆P ，圆M 都相切的一条直线，l 与曲线C 交于A ，B 两点，当圆P 的半径最长时，求|AB |．【2012，20】设抛物线C ：py x 22=（0>p ）的焦点为F ，准线为l ，A 为C 上一点，已知以F 为圆心，F A 为半径的圆F 交l 于B ，D 两点．（1）若∠BFD =90°，△ABD 的面积为24，求p 的值及圆F 的方程；（2）若A ，B ，F 三点在同一直线m 上，直线n 与m 平行，且n 与C 只有一个公共点，求坐标原点到m ，n 距离的比值．【2011，20】在平面直角坐标系xOy 中，已知点A(0,-1)，B 点在直线y = -3上，M 点满足//MB OA uuu r uu r， MA AB MB BA ⋅=⋅uuu r uu u r uuu r uu r，M 点的轨迹为曲线C ．（Ⅰ）求C 的方程；（Ⅱ）P 为C 上的动点，l 为C 在P 点处得切线，求O 点到l 距离的最小值．2012年—2017年新课标全国卷Ⅰ理科数学试题分类汇编9．解析几何（解析版）一、选择题【2017，10】已知F 为抛物线C ：y 2=4x 的焦点，过F 作两条互相垂直的直线l 1，l 2，直线l 1与C 交于A 、B 两点，直线l 2与C 交于D 、E 两点，则|AB |+|DE |的最小值为（ ）A ．16B ．14C ．12D ．10【解析】设AB 倾斜角为θ．作1AK 垂直准线，2AK 垂直x 轴，易知11cos 22⎧⎪⋅+=⎪⎪=⎨⎪⎛⎫⎪=--= ⎪⎪⎝⎭⎩AF GF AK AK AF P P GP Pθ（几何关系）（抛物线特性），cos AF P AF θ⋅+=∴，同理1cos P AF θ=-，1cos P BF θ=+，∴22221cos sin P PAB θθ==-， 又DE 与AB 垂直，即DE 的倾斜角为π2θ+，2222πcos sin 2P PDE θθ==⎛⎫+ ⎪⎝⎭，而24y x =，即2P =． ∴22112sin cos AB DE P θθ⎛⎫+=+ ⎪⎝⎭2222sin cos 4sin cos θθθθ+=224sin cos θθ=241sin 24=θ 21616sin 2θ=≥，当且仅当π4θ=取等号，即AB DE +最小值为16，故选A ； 【法二】依题意知：22sin PAB θ=，2222πcos sin 2P PDE θθ==⎛⎫+ ⎪⎝⎭，由柯西不等式知： 2222211(11)22816sin cos sin cos AB DE P P P θθθθ+⎛⎫+=+≥⋅== ⎪+⎝⎭，当且仅当π4θ=取等号，故选A ； 【2016，10】以抛物线C 的顶点为圆心的圆交C 于B A ,两点，交C 的准线于E D ,两点，已知24=AB ,52=DE ，则C 的焦点到准线的距离为（ ）A ．2B ．4C ．6D ．8 【解析】以开口向右的抛物线为例来解答，其他开口同理设抛物线为22y px =()0p >，设圆的方程为222x y r +=，如图：设(0,A x，2p D ⎛- ⎝，点(0,A x 在抛物线22y px =上，∴082px =……①；点2p D ⎛- ⎝在圆222x y r +=上，∴2252p r ⎛⎫+= ⎪⎝⎭……②；点(0A x 在圆222x y r +=上，∴2208x r +=……③；联立①②③解得：4p =，焦点到准线的距离为4p =．故选B ． 【2016，5】已知方程132222=--+nm y n m x 表示双曲线，且该双曲线两焦点间的距离为4，则n 的取值范围是（ ） A ．)3,1(-B ．)3,1(-C ．)3,0(D ．)3,0(【解析】222213x y m n m n-=+-表示双曲线，则()()2230m n m n +->，∴223m n m -<<由双曲线性质知：()()222234c m n m n m =++-=，其中c 是半焦距，∴焦距2224c m =⋅=，解得1m =∴13n -<<，故选A ．F【2015，5】已知00(,)M x y 是双曲线C ：2212x y -=上的一点，12,F F 是C 的两个焦点，若120MF MF ⋅< ，则0y 的取值范围是（ ）A．(33-B．(,)66- C．(33- D．(33- 解析：从120MF MF ⋅< 入手考虑，120MF MF ⋅=可得到以12FF 为直径的圆与C 的交点1234,,,M M M M （不妨设12,M M 在左支上，34,M M 在右支上），此时1112M F M F ⊥，1112M F M F -=-12F F =112111201211||22M F F S M F M F y F F ∆=⋅=⋅解得0||y =，则M 在双曲线的 12M M 或 34M M 上运动，0y∈(，故选A ．.【2014，4】已知F 是双曲线C ：223(0)x my m m -=>的一个焦点，则点F 到C 的一条渐近线的距离为 AB .3 CD .3m【解析】：由C ：223(0)x my m m -=>，得22133x y m -=，233,c m c =+设)F，一条渐近线y x =，即0x =，则点F 到C的一条渐近线的距离d =A. 【2013，4】已知双曲线C ：2222=1x y a b -(a ＞0，b ＞0)C 的渐近线方程为( )．A ．y ＝14x ±B ．y ＝13x ±C ．y ＝12x ± D ．y ＝±x解析：选C ，∵c e a ==，∴22222254c a b e a a +===，∴a 2＝4b 2，1=2b a ±，∴渐近线方程为12b y x x a =±±. 【2013，10】已知椭圆E ：2222=1x y a b+(a ＞b ＞0)的右焦点为F (3,0)，过点F 的直线交E 于A ，B 两点．若AB 的中点坐标为(1，－1)，则E 的方程为( )A ．22=14536x y + B ．22=13627x y + C ．22=12718x y + D ．22=1189x y + 解析：选D ，设A (x 1，y 1)，B (x 2，y 2)，∵A ，B 在椭圆上，∴2211222222221,1,x y a bx y a b ⎧+=⎪⎪⎨⎪+=⎪⎩①② ①－②，得1212121222=0x x x x y y y y a b (+)(-)(+)(-)+，即2121221212=y y y y b a x x x x (+)(-)-(+)(-)， ∵AB 的中点为(1，－1)，∴y 1＋y 2＝－2，x 1＋x 2＝2，而1212y y x x --＝k AB ＝011=312-(-)-，∴221=2b a . 又∵a 2－b 2＝9，∴a 2＝18，b 2＝9.∴椭圆E 的方程为22=1189x y +.故选D. 【2012，4】设1F 、2F 是椭圆E ：2222x y a b+（0a b >>）的左、右焦点，P 为直线32ax =上一点，21F PF ∆是底角为30°的等腰三角形，则E 的离心率为（ ）A ．12 B ．23 C ．34 D ．45【解析】如图所示，21F PF ∆是等腰三角形，212130F F P F PF ∠=∠=︒，212||||2F P F F c ==，260PF Q ∠=︒，230F PQ ∠=︒，2||F Q c =，又23||2aF Q c =-， 所以32a c c -=，解得34c a =，因此34c e a ==，故选择C ．【2012，8】等轴双曲线C 的中心在原点，焦点在x 轴上，C 与抛物线216y x =的准线交于A ，B两点，||AB =，则C 的实轴长为（ ）AB．C ．4D ．8【解析】设等轴双曲线C 的方程为22221x y a a-=，即222x y a -=（0a >），抛物线216y x =的准线方程为4x =-，联立方程2224x y a x ⎧-=⎨=-⎩，解得2216y a =-，因为||AB =，所以222||(2||)448AB y y ===，从而212y =，所以21612a -=，24a =，2a =，因此C 的实轴长为24a =，故选择C ．【2011，7】设直线L 过双曲线C 的一个焦点，且与C 的一条对称轴垂直，L 与C 交于A ,B 两点，AB 为C 的实轴长的2倍，则C 的离心率为（ ）ABC ．2D ．3解析：通径|AB|=222b a a=得2222222b a a c a =⇒-=，选B 二、填空题【2017，15】已知双曲线C ：22221x y a b-=（a >0，b >0）的右顶点为A ，以A 为圆心，b 为半径作圆A ，圆A 与双曲线C 的一条渐近线交于M 、N 两点．若∠MAN =60°，则C 的离心率为________．（15）【解析】如图，OA a =，AN AM b ==， ∵60MAN ∠=︒，∴AP =，OP =，∴tan AP OP θ==tan b a θ=b a =，解得223a b =，∴e = 【法二】如上图可知(,0)A a 到渐进线0bx ay -=的距离为abd AP c===， 1,60,cos cos302ab AP AMN a c AN AM b AMN AN b c e∠==∠=∴=====又，e ∴= 【法三】如图在等边三角形AMN ∆中,,AP FH b == 由OAP OFH ∆∆知2aa e cbc =⇒==； 【法四】如图，由等面积法可得，在三角形OAN 中，12223ab c c e a =⇒==；【法五】因为,AM b OA a ==且渐进线bxy a=可得三角形OAN 为 双曲线三角线（即三边分别为,,a b c ），有几何意义易得30MAP MOA ∠=∠=tan 33b MOA e a ∴∠====；【2015，14】一个圆经过椭圆221164x y +=的三个顶点，且圆心在x 轴的正半轴上，则该圆的标准方程为 . 解析：由椭圆的性质可知，圆只能经过短轴顶点和右顶点三个点(0,2),(0,2),(4,0)-；（方法一）设圆的半径为r ，则有222(4)2r r -+=，可得52r =，故所求圆的标准方程为22325()24x y -+=.（方法二）设圆的标准方程为222()(0)x a y r a -+=>，代入点(0,2),(4,0)，解方程组可得35,22a r ==半径为r ，故所求圆的标准方程为22325()24x y -+=.（方法三）设圆的一般方程为220x y Dx Ey F ++++=，代入点(0,2),(0,2),(4,0)-，解方程组可得3,0,4D E F =-==-,化为标准方程为22325()24x y -+=. 【2014，10】已知抛物线C ：28y x =的焦点为F ，准线为l ，P 是l 上一点，Q 是直线PF 与C 的一个交点，若4FP FQ =，则||QF =A .72B .52C .3D .2 【解析】选C ，过Q 作QM ⊥直线L 于M ，∵4FP FQ =∴34PQ PF =，又344QM PQ PF ==，∴3QM =，由抛物线定义知3QF QM == 【2011，14】在平面直角坐标系xOy 中，椭圆C 的中心为原点，焦点12,F F 在x．过1F 的直线L 交C 于,A B 两点，且2ABF V 的周长为16，那么C 的方程为 ．解析：由2416c a a ⎧=⎪⎨⎪=⎩得a=4.c=从而b=8,221168x y ∴+=为所求． 三、解答题【2017，20】已知椭圆C ：2222=1x y a b +（a >b >0），四点P 1（1,1），P 2（0,1），P 3（–1），P 4（1有三点在椭圆C 上．|MN （1）求C 的方程；（2）设直线l 不经过P 2点且与C 相交于A ，B 两点．若直线P 2A 与直线P 2B 的斜率的和为–1，证明：l 过定点．【解析】（1）根据椭圆对称性，必过3P 、4P ，又4P 横坐标为1，椭圆必不过1P ，所以过234P P P ，，三点，将()23011P P ⎛- ⎝⎭，，代入椭圆方程得：222113141b ab ⎧=⎪⎪⎨⎪+=⎪⎩，解得24a =，21b =， ∴椭圆C 的方程为：2214x y +=．（2）①当斜率不存在时，设()():A A l x m A m y B m y =-，，，，， 221121A A P A P B y y k k m m m----+=+==-，得2m =，此时l 过椭圆右顶点，不存在两个交点，故不满足． ②当斜率存在时，设()1l y kx b b =+≠∶，()()1122A x y B x y ，，，， 联立22440y kx b x y =+⎧⎨+-=⎩，整理得()222148440k x kbx b +++-=， 122814kb x x k -+=+，21224414b x x k -⋅=+，则22121211P A P By y k k x x --+=+()()21212112x kx b x x kx b x x x +-++-= 222228888144414kb k kb kbk b k--++=-+()()()811411k b b b -==-+-，又1b ≠，21b k ⇒=--，此时64k ∆=-， 存在k 使得0∆>成立．∴直线l 的方程为21y kx k =--，当2x =时，1y =-，所以l 过定点()21-，． 【2016，20】设圆015222=-++x y x 的圆心为A ，直线l 过点)0,1(B 且与x 轴不重合，l 交圆A 于D C ,两点，过B 作AC 的平行线交AD 于点E ．（Ⅰ）证明EB EA +为定值，并写出点E 的轨迹方程；四边形【解析】Q ∴⑵ 1C()2212111||||2234MPNQm S MN PQ m +⎡∴=⋅=⋅==⎣+ 【2015，20】在直角坐标系xOy 中，曲线C ：24x y =与直线l ：y kx a =+（0a >）交于,M N 两点.（Ⅰ）当0k =时，分别求C 在点M 和N 处的切线方程；（Ⅱ）在y 轴上是否存在点P ，使得当k 变动时，总有OPM OPN ∠=∠？说明理由.解：（Ⅰ）当0k =时，点)M a和()N a -，2xy '=，故x =y a x --0y a --=；同理，x =-y a x -=+0y a ++=.（Ⅱ）在y 轴上存在点P ，使得当k 变动时，总有OPM OPN ∠=∠.证明如下： 设(0,)P b 为符合题意的点，1122(,),(,)M x y N x y ，直线,PM PN 的斜率分别为12,k k .直线l 与曲线C 的方程联立可得2440x kx a --=，则12124,4x x k x x a +==-.1212121212122()()()y b y b kx x a b x x k a b k k x x x x a--+-+++=+==，当b a =-时，120k k +=，则直线,PM PN 的倾斜角互补，故OPM OPN ∠=∠，即(0,)P a -符合题意.【2014，20】已知点A （0，-2），椭圆E ：22221(0)x y a b a b +=>>，F 是椭圆的焦点，直线AF 的O 为坐标原点.(Ⅰ)求E 的方程；（Ⅱ）设过点A 的直线l 与E 相交于,P Q 两点，当OPQ ∆的面积最大时，求l 的方程. 【解析】：(Ⅰ) 设(),0F c，由条件知2c =c =又c a =， 所以a=2 ，2221b a c =-= ,故E 的方程2214x y +=. …….6分 （Ⅱ）依题意当l x ⊥轴不合题意，故设直线l ：2y kx =-，设()()1122,,,P x y Q x y将2y kx =-代入2214x y +=，得()221416120k x kx +-+=， 当216(43)0k ∆=->，即234k >时，1,2x =从而12214PQ x k =-=+，又点O 到直线PQ的距离d =，所以∆OPQ的面积12OPQ S d PQ ∆==t =，则0t >，244144OPQt S t t t∆==≤++， 当且仅当2t =，k =0∆>，所以当∆OPQ 的面积最大时，l的方程为：2y x =-或2y x =-. ……12分【2013，20】已知圆M ：(x ＋1)2＋y 2＝1，圆N ：(x －1)2＋y 2＝9，动圆P 与圆M 外切并且与圆N 内切，圆心P 的轨迹为曲线C .(1)求C 的方程；(2)l 是与圆P ，圆M 都相切的一条直线，l 与曲线C 交于A ，B 两点，当圆P 的半径最长时，求|AB |.解：由已知得圆M 的圆心为M (－1,0)，半径r 1＝1；圆N 的圆心为N (1,0)，半径r 2＝3.设圆P 的圆心为P (x ，y )，半径为R .(1)因为圆P 与圆M 外切并且与圆N 内切，所以|PM |＋|PN |＝(R ＋r 1)＋(r 2－R )＝r 1＋r 2＝4.由椭圆的定义可知，曲线C 是以M ，N 为左、右焦点，长半轴长为2(左顶点除外)，其方程为22=143x y +(x ≠－2)． (2)对于曲线C 上任意一点P (x ，y )，由于|PM |－|PN |＝2R －2≤2，所以R ≤2，当且仅当圆P 的圆心为(2,0)时，R ＝2.所以当圆P 的半径最长时，其方程为(x －2)2＋y 2＝4. 若l 的倾斜角为90°，则l 与y 轴重合，可得|AB |＝若l 的倾斜角不为90°，由r 1≠R 知l 不平行于x 轴，设l 与x 轴的交点为Q ，则1||||QP RQM r =，可求得Q (－4,0)，所以可设l ：y ＝k (x ＋4)．由l 与圆M=1，解得k＝4±. 当k＝4时，将4y x =22=143x y +，并整理得7x 2＋8x －8＝0，解得x 1,2＝47-±. 所以|AB |2118|7x x -=.当k =时，由图形的对称性可知|AB |＝187.综上，|AB |＝|AB |＝187.【2012，20】设抛物线C ：py x 22=（0>p ）的焦点为F ，准线为l ，A 为C 上一点，已知以F 为圆心，F A 为半径的圆F 交l 于B ，D 两点． （1）若∠BFD =90°，△ABD 的面积为24，求p 的值及圆F 的方程；（2）若A ，B ，F 三点在同一直线m 上，直线n 与m 平行，且n 与C 只有一个公共点，求坐标原点到m ，n 距离的比值． 【解析】（1）若∠BFD =90°，则△BFD 为等腰直角三角形，且|BD|=2p ，圆F的半径||r FA =， 又根据抛物线的定义可得点A 到准线l 的距离||d FA ==．因为△ABD 的面积为24，所以1||2BD d ⋅⋅=122p ⋅= 所以24p =，由0>p ，解得2p =．从而抛物线C 的方程为24x y =，圆F 的圆心F （0，1），半径||r FA == 因此圆F 的方程为22(1)8x y +-=． （2）若A ，B ，F 三点在同一直线m 上， 则AB 为圆F 的直径，∠ADB=90°， 根据抛物线的定义，得1||||||2AD FA AB ==，所以30ABD ∠=︒，从而直线m或当直线mm的方程为2p y x =+，原点O 到直线m的距离1pd =．依题意设直线n的方程为y x b =+，联立22y x b x py⎧=+⎪⎨⎪=⎩，得220x px pb -=， 因为直线n 与C 只有一个公共点，所以24803p pb ∆=+=，从而6pb =-． 所以直线n的方程为36p y x =-，原点O 到直线n的距离2pd =． 因此坐标原点到m ，n 距离的比值为12236p dpd ==．当直线m的斜率为m ，n 距离的比值也为3．【2011，20】在平面直角坐标系xOy 中，已知点A(0,-1)，B 点在直线y = -3上，M 点满足//MB OA uuu r uu r， MA AB MB BA ⋅=⋅uuu r uu u r uuu r uu r，M 点的轨迹为曲线C ．（Ⅰ）求C 的方程；（Ⅱ）P 为C 上的动点，l 为C 在P 点处得切线，求O 点到l 距离的最小值．解：（I ）设(),M x y ，由已知得(),3B x -，()0,1A -. 所以(),1,MA x y =--- ，()0,3,MB y =-- ，(),2AB x =-.再由题意可知()0MA MB AB +⋅= ，即()(),4,2,20x y x ---⋅=. 所以曲线C 的方程为2124y x =-.（II ）设()00,P x y 为曲线21:24C y x =-上一点，因为12y x '=，所以l 的斜率为012x .因此直线l 的方程为()00012y y x x x -=-，即2000220x x y y x -+-=.则O 点到l的距离d . 又200124y x =-，所以2014122x d +⎫=≥ 当00x =时取等号，所以O 点到l 的距离的最小值为2.2012年—2017年新课标全国卷ⅡⅢ理科数学试题分类汇编11．解析几何一、选择题（2017·9）若双曲线C :22221x y a b-=（0a >，0b >）的一条渐近线被圆()2224x y -+=所截得的弦长为2，则C的离心率为（ ）A ．2BCD （2016·4）圆2228130x y x y +--+=的圆心到直线10ax y +-=的距离为1，则a =（ ）A ．43-B ．34- C D ．2（2016·11）已知F 1，F 2是双曲线E ：22221x y a b-=的左，右焦点，点M 在E 上，M F 1与x 轴垂直，211sin 3MF F ∠=，则E 的离心率为（ ）A B ．32C D ．2（2015·7）过三点A (1, 3)，B (4, 2)，C (1, -7)的圆交于y 轴于M 、N 两点，则MN =（ ）A ．B ．8C ．D ．10 （2015·11）已知A ，B 为双曲线E 的左，右顶点，点M 在E 上，∆ABM 为等腰三角形，且顶角为120°，则E 的离心率为（ ）A B ．2 C D （2014·10）设F 为抛物线C :23y x =的焦点，过F 且倾斜角为30º的直线交C 于A , B 两点，O 为坐标原点，则△OAB 的面积为（ ）A B C ．6332 D ．94（2013·11）设抛物线2:2(0)C y px p =>的焦点为F ，点M 在C 上，||5MF =，若以MF 为直径的园过点(0,2)，则C 的方程为（ ）A .24y x =或28y x =B .22y x =或28y x =C .24y x =或216y x =D .22y x =或216y x = （2013·12）已知点(1,0)A -，(1,0)B ，(0,1)C ，直线(0)y ax b a =+>将ABC △分割为面积相等的两部分，则b 的取值范围是（ ）A .(0,1)B .1(1)2C .1(1]3D .11[,)32（2012·4）设F 1，F 2是椭圆E : 12222=+by a x )0(>>b a 的左右焦点，P 为直线23a x =上的一点，12PF F △是底角为30º的等腰三角形，则E 的离心率为（ ） A.21 B.32 C.43 D.54 （2012·8）等轴双曲线C 的中心在原点，焦点在x 轴上，C 与抛物线y 2=16x 的准线交于A ，B 两点，|AB |=34，则C 的实轴长为（ ） A.2 B. 22 C. 4 D. 8 （2011·7）设直线l 过双曲线C 的一个焦点，且与C 的一条对称轴垂直，l 与C 交于A , B 两点，|AB |为C 的实轴长的2倍，则C 的离心率为（ ）A B C ．2 D ．3 二、填空题（2017·16）已知F 是抛物线C :28y x =的焦点，M 是C 上一点，F M 的延长线交y 轴于点N ．若M 为F N 的中点，则F N = ．（2014·6）设点M (0x ,1)，若在圆O :221x y +=上存在点N ，使得∠OMN =45º，则0x 的取值范围是________.（2011·14）在平面直角坐标系xoy 中，椭圆C 的中心为原点，焦点F 1，F 2在x 过F 1的直线l交C 于A ，B 两点，且△ABF 2的周长为16，那么C 的方程为 . 三、解答题（2017·20）设O 为坐标原点，动点M 在椭圆C ：2212x y +=上，过M 做x 轴的垂线，垂足为N ，点P 满足NP = .（1）求点P 的轨迹方程； （2）设点Q 在直线x =-3上，且1OP PQ ⋅=.证明：过点P 且垂直于OQ 的直线l 过C 的左焦点F .（2016·20）已知椭圆E :2213x y t +=的焦点在x 轴上，A 是E 的左顶点，斜率为k (k >0)的直线交E 于A ，M 两点，点N 在E 上，MA ⊥NA .（Ⅰ）当t =4，|AM|=|AN|时，求△AMN 的面积； （Ⅱ）当2|AM|=|AN|时，求k 的取值范围.（2015·20）已知椭圆C ：2229x y m +=(m ＞0)，直线l 不过原点O 且不平行于坐标轴，l 与C 有两个交点A ，B ，线段AB 的中点为M .（Ⅰ）证明：直线OM 的斜率与l 的斜率的乘积为定值； （Ⅱ）若l 过点(,)3mm ，延长线段OM 与C 交于点P ，四边形OAPB 能否平行四边形？若能，求此时l 的斜率；若不能，说明理由．（2014·20）设F 1，F 2分别是椭圆()222210y x a b a b+=>>的左右焦点，M 是C 上一点且MF 2与x 轴垂直，直线MF 1与C 的另一个交点为N .（Ⅰ）若直线MN 的斜率为34，求C 的离心率；（Ⅱ）若直线MN 在y 轴上的截距为2，且15MN F N =，求a, b .（2013·20）平面直角坐标系xOy 中，过椭圆2222:1(0)x y M a b a b+=>>右焦点F 的直线0x y +=交M 于,A B 两点，P 为AB 的中点，且OP 的斜率为12.（Ⅰ）求M 的方程；（Ⅱ）,C D 为M 上的两点，若四边形ACBD 的对角线CD AB ⊥，求四边形ACBD 面积的最大值.（2012·20）设抛物线:C py x 22=)0(>p 的焦点为F ，准线为l ，A 为C 上的一点，已知以F 为圆心，F A 为半径的圆F 交l 于B ，D 两点. （Ⅰ）若∠BFD =90º，△ABD 面积为24，求p 的值及圆F 的方程； （Ⅱ）若A 、B 、F 三点在同一直线m 上，直线n 与m 平行，且n 与C 只有一个公共点，求坐标原点到m ，n 的距离的比值.（2011·20）在平面直角坐标系xOy 中，已知点A (0, -1)，B 点在直线y =-3上，M 点满足//MB OA u u u r u u r ， MA AB MB BA ⋅=⋅uuur uu u r uuu r uu r ，M 点的轨迹为曲线C . （Ⅰ）求C 的方程；（Ⅱ）P 为C 上的动点，l 为C 在P 点处得切线，求O 点到l 距离的最小值 .2012年—2017年新课标全国卷Ⅱ理科数学试题分类汇编11．解析几何（逐题解析版）一、选择题（2017·9）A 【解析】解法一：根据双曲线的标准方程可求得渐近线方程为by x a=±，根据直线与圆的位置关系可求得=2e =. 解法二：设渐进线的方程为y kx =∴=23k =；由于渐近线的斜率与离心率关系为221k e =-，解得2e =.（2016·4）A 解析：圆2228130x y x y +--+=化为标准方程为：()()22144x y -+-=，故圆心为()14，，1d ==，解得43a =-，故选A ．（2015·7）C 解析：由已知得，，所以k AB k CB =-1，所以AB ⊥CB ，即△ABC 为直角三角形，其外接圆圆心为(1, -2)，半径为5，所以外接圆方程为(x -1)2+(y +2)2=25，令x =0，得，所以，故选C.（2016·11）A 解析：离心率1221F F e MF MF =-，由正弦定理得122112sin 31sin sin 13F F Me MF MF F F ====---． 故选A ．（2015·11）D 解析：设双曲线方程为22221(0,0)x y a b a b-=>>，如图所示，|AB |=|BM |，∠ABM =120º，过点M 作MN ⊥x 轴，垂足为N ，在Rt △BMN 中，|BN |=a，||MN ，故点M的坐标为(2)M a ，代入双曲线方程得a 2 = b 2 = c 2 -a 2，即c 2 = 2a 2，所以e =故选D.（2014·10）D 解析：∵3(,0)4F ，∴设直线AB的方程为3)4y x =-，代入抛物线方程得：22190216x x -+=，设11(,)A x y 、22(,)B x y ，∴12212x x +=，12916x x ⋅=，由弦长公式得||12AB =，由点到直线的距离公式得：O 到直线AB 的距离0038d --==，∴13912284OABS ∆=⨯⨯=. 【另解】直线AB的方程3)4y x =-代入抛物线方程得：2490y --=，∴12y y +=，1294y y ⋅=-，∴139244OAB S ∆=⨯.（2013·11）C 解析：设点M 的坐标为(x 0，y 0)，由抛物线的定义，得|MF |＝x 0＋2p ＝5，则x 0＝5－2p.又点F 的坐标为(,0)2p ，所以以MF 为直径的圆的方程为220525()()224y x y -+-=.将x ＝0，y ＝2代入得2002404y y -+=，所以y 0＝4.由20y ＝2px 0，得162(5)2pp =-，解之得p ＝2，或p ＝8.所以C 的方程为y 2＝4x 或y 2＝16x . 故选C.（2013·12）B 解析：由题意知b ∈(0, 1)，当直线过点(-1, 0)时，要将△ABC 分割为面积相等的两部分，直线必须过点11(,)22，此时有-a +b =0且1122a b +=，解得13b =；当a =1时，直线y =ax +b 平行于直线AC ，要将△ABC 分割为面积相等的两部分，可求此时的1b =.（2012·4）C 解析：由题意可得，21F PF △是底角为30º的等腰三角形可得212PF F F =，即32()22ac c -=， 所以34c e a ==.（2012·8）C 解析：抛物线的准线方程是x =4，所以点A (-在222x y a -=上，将点A 代入得24a =，所以实轴长为24a =.（2011·7）B 解析：通径|AB |=222b a a=得2222222b a a c a =⇒-=，故选B.二、填空题 （2017·16）6【解析】∵ 点M 为线段NF 的中点，∴ 1M x =，∴ 23M MF x =+=，∴ 26NF MF ==． （2014·6）[1,1]-解析：由图可知点M 所在直线1y =与圆O 相切，又1ON =，由正弦定理得sin sin ON OMOMN ONM=∠∠，∴sin OMONM =∠，即OM ONM =∠，∵0O N M π≤∠≤，∴OM ≤，即≤011x -≤≤.【另解】过OA ⊥MN ，垂足为A ，因为在Rt △OMA 中，|OA|≤1，∠OMN =45º，所以||||s i n 4O A O M =o =||12OM ≤，解得||OM ≤M (x0, 1)，所以||OM =，解得011x -≤≤，故0x 的取值范围是[1,1]-.（2011·14）221168xy ∴+= 解析：由416c a a ⎧=⎪⎨⎪=⎩得a =4，c =b =8，221168x y ∴+=.三、解答题（2017·20）设O 为坐标原点，动点M 在椭圆C ：2212x y +=上，过M做x 轴的垂线，垂足为N ，点P 满足NP = .（1）求点P 的轨迹方程；（2）设点Q 在直线x =-3上，且1OP PQ ⋅=.证明：过点P 且垂直于OQ 的直线l 过C 的左焦点F .解析：（1）解法一：相关点法求轨迹：设()00,M x y ，()0,0N x ,(),P x y ，则：()0,NP x x y =-,()00,NM y = .又NP =,所以：())00,0,x x y y -=，则：00,x x y =.又()00,M x y 在椭圆C 上，所以：220012x y +=，所以：222x y+=. 解法二： 椭圆C 的参数方程为：sin x y θθ⎧=⎪⎨=⎪⎩（θ为参数）.设),sin M θθ，),0N θ,(),P x y ，则：(),NP x y θ= ,()0,sin NM θ=. 又NP=,所以：()),0,sin x y θθ=，则：,x y θθ==.则：222x y +=.（Ⅱ）解法一：设)Pθθ，()13,Q y -,()1,0F-,则)OP θθ=，()13,OQ y =-,()13,y PQ θθ=-，()1,PF θθ=-. 又1OP PQ ⋅=,所以：)()22113,y 2cos sin 2sin 1θθθθθθθθ⋅-=---=即：12s 2s i n 3θθ=-.那么：()()11,3,y 3sin 0PF OQ θθθθ⋅=-⋅-=+= .所以：PF OQ ⊥. 即过P 垂直于OQ 的直线l 过椭圆C 的左焦点F 。
2011-2017新课标全国卷1理科数学分类汇编
目录1、 集合与常用逻辑用语2、 函数及其性质3、 导函数及其应用4、 三角函数、解三角形5、 平面向量6、 数列7、 不等式、推理与证明 8、 立体几何 9、 解析几何10、 统计、概率分布列、计数原理 11、 复数及其运算 12、 程序框图13、 坐标系及参数方程 14、 不等式选讲2011—2017年新课标高考全国Ⅰ卷理科数学分类汇编1．集合与常用逻辑用语（含解析）一、选择题【2017，1】已知集合{}1A x x =<，{}31xB x =<，则（ ）A ．{|0}AB x x =< B ．A B =RC ．{|1}A B x x =>D ．A B =∅【2016，1】设集合}034{2<+-=x x x A ，}032{>-=x x B ，则A B =I （ ）A ．)23,3(--B ．)23,3(-C ．)23,1(D ．)3,23(【2015，3】设命题p ：n ∃∈N ，22n n >，则p ⌝为（ ）A ．n ∀∈N ，22n n >B ．n ∃∈N ，22n n ≤C ．n ∀∈N ，22n n ≤D ．n ∃∈N ，22n n = 【2014，1】已知集合A={x |2230x x --≥}，B={}22x x -≤<，则A B ⋂=( )A ．[-2,-1]B ．[-1,2）C ．[-1,1]D ．[1,2）【2013，1】已知集合A ＝{x |x 2－2x ＞0}，B ＝{x |x ，则( )A ．A ∩B ＝B ．A ∪B ＝RC ．B ⊆AD ．A ⊆B【2012，1】已知集合A={1，2，3，4，5}，B={（x ，y ）|x A ∈，y A ∈，x y A -∈}，则B 中包含元素的个数为（ ） A ．3 B ．6 C ．8 D ．101．集合与常用逻辑用语（解析版）一、选择题【2017，1】已知集合{}1A x x =<，{}31xB x =<，则（ ）A ．{|0}AB x x =< B ．A B =RC ．{|1}A B x x =>D ．A B =∅【解析】{}1A x x =<，{}{}310xB x x x =<=<，∴{}0A B x x =<，{}1A B x x =<，故选A【2016，1】设集合}034{2<+-=x x x A ，}032{>-=x x B ，则A B =I （ ）A ．)23,3(--B ．)23,3(-C ．)23,1(D ．)3,23(【解析】{}13A x x =<<，{}32302B x x x x ⎧⎫=->=>⎨⎬⎩⎭．故332A B x x ⎧⎫=<<⎨⎬⎩⎭I ．故选D ． 【2015，3】设命题p ：n ∃∈N ，22nn >，则p ⌝为（ ）A ．n ∀∈N ，22n n >B ．n ∃∈N ，22n n ≤C ．n ∀∈N ，22n n ≤D ．n ∃∈N ，22n n = 解析：命题p 含有存在性量词（特称命题），是真命题（如3n =时），则其否定（p ⌝）含有全称量词（全称命题），是假命题，故选C ．.【2014，1】已知集合A={x |2230x x --≥}，B={}22x x -≤<，则A B ⋂=( )A .[-2,-1]B .[-1,2）C .[-1,1]D .[1,2）【解析】∵{|13}A x x x =≤-≥或，B={}22x x -≤<，∴A B ⋂={}21x x -≤≤，选A.【2013，1】已知集合A ＝{x |x 2－2x ＞0}，B ＝{x |x ，则( )A ．A ∩B ＝B ．A ∪B ＝RC ．B ⊆AD ．A ⊆B解析：∵x (x －2)＞0，∴x ＜0或x ＞2，∴集合A 与B 可用图象表示为：由图象可以看出A ∪B ＝R ，故选B.【2012，1】已知集合A={1，2，3，4，5}，B={（x ，y ）|x A ∈，y A ∈，x y A -∈}，则B 中包含元素的个数为（ ）A ．3B ．6C ．8D ．10 【解析】由集合B 可知，x y >，因此B={（2，1），（3，2），（4，3），（5，4），（3，1），（4，2），（5，3），（4，1），（5，2），（5，1）}，B 的元素10个，所以选择D ．2．函数及其性质（含解析）一、选择题【2017，5】函数()f x 在(,)-∞+∞单调递减，且为奇函数．若(11)f =-，则满足21()1x f --≤≤的x 的取值范围是（ ）A ．[2,2]-B ． [1,1]-C ． [0,4]D ． [1,3]【2017，11】设,,x y z 为正数，且235x y z ==，则（ ）A ．2x <3y <5zB ．5z <2x <3yC ．3y <5z <2xD ．3y <2x <5z 【2016，7】函数xe x y -=22在]2,2[-的图像大致为（ ）A ．B ．C ．D ．【2016，8】若1>>b a ，10<<c ，则（ ）A ．c c b a <B ．c c ba ab <C ．c b c a a b log log <D ．c c b a log log <【2014，3】设函数()f x ，()g x 的定义域都为R ，且()f x 是奇函数，()g x 是偶函数，则下列结论正确的是（ ）A ．()f x ()g x 是偶函数B ．|()f x |()g x 是奇函数C ．()f x |()g x |是奇函数D ．|()f x ()g x |是奇函数【2013，11】已知函数f (x )＝220ln(1)0.x x x x x ⎧-+≤⎨+>⎩，，，若|f (x )|≥ax ，则a 的取值范围是( )A ．(－∞，0]B ．(－∞，1]C ．[－2,1]D ．[－2,0] 【2012，10】已知函数1()f x =，则()y f x =的图像大致为（ ）A ．B ．D ．【2011，12】函数11y x =-的图像与函数2sin (24)y x x π=-≤≤的图像所有交点的横坐标之和等于（ ）A ．2 B ．4 C ．6 D ．8【2011，2】下列函数中，既是偶函数又在+∞（0，）单调递增的函数是（ ）A ．3y x =B ．1y x =+C ．21y x =-+D ．2xy -=二、填空题【2015，13】若函数f (x )=x ln （x a =2．函数与导数（解析版）一、选择题【2017，5】函数()f x 在(,)-∞+∞单调递减，且为奇函数．若(11)f =-，则满足21()1x f --≤≤的x 的取值范围是（ ）A ．[2,2]-B ． [1,1]-C ． [0,4]D ． [1,3]【解析】因为()f x 为奇函数，所以()()111f f -=-=，于是()121f x --≤≤，等价于()()()121f f x f --≤≤，又()f x 在()-∞+∞，单调递减，121x ∴--≤≤，3x ∴1≤≤，故选D ． 【2017，11】设,,x y z 为正数，且235x y z ==，则（ ）A ．2x <3y <5zB ．5z <2x <3yC ．3y <5z <2xD ．3y <2x <5z【解析】取对数：ln 2ln3ln5x y ==．ln 33ln 22x y =>，∴23x y >，ln 2ln 5x z =，则ln55ln 22x z =<，∴25x z <∴325y x z <<，故选D ．【法二】取对数：5ln 3ln 2ln z y x ==，y x y x y x 3212ln 3ln 2ln 33ln 2323ln 2ln 32>⇒>==⇒=， z x z x z x 5212ln 5ln 2ln 55ln 2525ln 2ln 52<⇒<==⇒=，z x y 523<<∴，故选D ； 【2016，7】函数xe x y -=22在]2,2[-的图像大致为（ ）【解析】()22288 2.80f e =->->，排除A ；()22288 2.71f e =-<-<，排除B ；0x >时，()22xf x x e =-，()4x f x x e '=-，当10,4x ⎛⎫∈ ⎪⎝⎭时，()01404f x e '<⨯-= 因此()f x 在10,4⎛⎫⎪⎝⎭单调递减，排除C ；故选D ．【2016，8】若1>>b a ，10<<c ，则（ ）A ．c c b a <B ．c c ba ab <C ．c b c a a b log log <D ．c c b a log log <【解析】由于01c <<，∴函数c y x =在R 上单调递增，因此1c c a b a b >>⇔>，A 错误；由于110c -<-<，∴函数1c y x -=在()1,+∞上单调递减，∴111c c c c a b a b ba ab -->>⇔<⇔<，B 错误； 要比较log b a c 和log a b c ，只需比较ln ln a c b和ln ln b c a ，只需比较ln ln c b b 和ln ln ca a ，只需lnb b 和ln a a ， 构造函数()()ln 1f x x x x =>，则()'ln 110f x x =+>>，()f x 在()1,+∞上单调递增，因此()()110ln ln 0ln ln f a f b a a b b a a b b >>⇔>>⇔<，又由01c <<得ln 0c <， ∴ln ln log log ln ln a b c cb c a c a a b b<⇔<，C 正确； 要比较l o g a c 和log b c ，只需比较ln ln c a 和ln ln cb ，而函数ln y x =在()1,+∞上单调递增，故111ln ln 0ln ln a b a b a b >>⇔>>⇔<，又由01c <<得ln 0c <，∴ln ln log log ln ln a b c c c c a b>⇔>，D 错误；故选C ．【2014，3】设函数()f x ，()g x 的定义域都为R ，且()f x 是奇函数，()g x 是偶函数，则下列结论正确的是（ ）A .()f x ()g x 是偶函数B .|()f x |()g x 是奇函数C .()f x |()g x |是奇函数D .|()f x ()g x |是奇函数【解析】设()()()F x f x g x =，则()()()F x f x g x -=--，∵()f x 是奇函数，()g x 是偶函数，∴()()()()F x f x g x F x -=-=-，()F x 为奇函数，选C.【2013，11】已知函数f (x )＝220ln(1)0.x x x x x ⎧-+≤⎨+>⎩，，，若|f (x )|≥ax ，则a 的取值范围是( )．A ．(－∞，0]B ．(－∞，1]C ．[－2,1]D ．[－2,0] 解析：选D ，由y ＝|f (x )|的图象知：①当x ＞0时，y ＝ax 只有a ≤0时，才能满足|f (x )|≥ax ，可排除B ，C. ②当x ≤0时，y ＝|f (x )|＝|－x 2＋2x |＝x 2－2x . 故由|f (x )|≥ax 得x 2－2x ≥ax . 当x ＝0时，不等式为0≥0成立．当x ＜0时，不等式等价于x －2≤a ，∵x －2＜－2，∴a ≥－2. 综上可知：a ∈[－2,0]．【2012，10】已知函数1()ln(1)f xx x=+-，则()y f x=的图像大致为（）【解析】()y f x=的定义域为{|1x x>-且0}x≠，排除D；因为221(1)1'()[ln(1)](1)[ln(1)]xxf xx x x x x--+==+-++-，所以当(1,0)x∈-时，'()0f x<，()y f x=在（－1，0）上是减函数；当(0,)x∈+∞时，'()0f x>，()y f x=在(0,)+∞上是增函数．排除A、C，故选择B．【2011】(12)函数11yx=-的图像与函数2sin(24)y x xπ=-≤≤的图像所有交点的横坐标之和等于A．2 B．4 C．6 D．8解析：图像法求解．11yx=-的对称中心是（1,0）也是2sin(24)y x xπ=-≤≤的中心，24x-≤≤他们的图像在x=1的左侧有4个交点，则x=1右侧必有4个交点．不妨把他们的横坐标由小到大设为1,2345678,,,,,,x x x x x x x x，则182736452x x x x x x x x+=+=+=+=，所以选D【2011，2】下列函数中，既是偶函数又在+∞（0，）单调递增的函数是（）A．3y x=(B) 1y x=+C．21y x=-+(D) 2xy-=解析：由图像知选B二、填空题【2015，13】若函数f(x)=x ln（x a=解析：由函数f(x)=x ln（x()ln(g x x=为奇函数（(0)0g==）；由ln(ln(0x x++-+=（()()0g x g x+-=），得ln0a=，1a=，故填1.A．B．D．3．导数及其应用（含解析）一、选择题【2014，11】已知函数()f x =3231ax x -+，若()f x 存在唯一的零点0x ，且0x ＞0，则a 的取值范围为A ．（2，+∞） B ．（-∞，-2） C ．（1，+∞） D ．（-∞，-1） 【2012，12】设点P 在曲线12xy e =上，点Q 在曲线ln(2)y x =上，则||PQ 的最小值为（ ）A ．1ln 2-B ln 2)-C ．1ln 2+D ln 2)+【2011，9】由曲线y 2y x =-及y 轴所围成的图形的面积为（ ）A ．103 B ．4 C ．163D ．6 二、填空题【2017，16】如图，圆形纸片的圆心为O ，半径为5 cm ，该纸片上的等边三角形ABC 的中心为O ．D 、E 、F 为圆O 上的点，△DBC ，△ECA ，△F AB 分别是以BC ，CA ，AB 为底边的等腰三角形．沿虚线剪开后，分别以BC ， CA ，AB 为折痕折起△DBC ，△ECA ，△F AB ，使得D ，E ，F 重合，得到三棱锥．当△ABC ．的边长变化时，所得三棱锥体积（单位：cm 3）的最大值为_______．【2013，16】若函数f (x )＝(1－x 2)(x 2＋ax ＋b )的图像关于直线x ＝－2对称，则f (x )的最大值为__________． 三、解答题【2017，12】已知函数()()22xx f x aea e x =+--．（1）讨论()f x 的单调性；（2）若()f x 有两个零点，求a 的取值范围．【2016，12】已知函数2)1()2()(-+-=x a e x x f x 有两个零点． （Ⅰ）求a 的取值范围；（Ⅱ）设21,x x 是)(x f 的两个零点，证明：221<+x x ．【2015，12】已知函数31()4f x x ax =++，()ln g x x =-． （Ⅰ）当a 为何值时，x 轴为曲线()y f x =的切线；（Ⅱ）用min{,}m n 表示,m n 中的最小值，设函数min{),()(}()h x f x g x =（0x >），讨论()h x 零点的个数．【2014，21】设函数1(0ln x xbe f x ae x x-=+，曲线()y f x =在点（1，(1)f 处的切线为(1)2y e x =-+． (Ⅰ)求,a b ； （Ⅱ）证明：()1f x >．【2013，21】设函数f (x )＝x 2＋ax ＋b ，g (x )＝e x (cx ＋d )．若曲线y ＝f (x )和曲线y ＝g (x )都过点P (0,2)，且在点P 处有相同的切线y ＝4x ＋2．(1)求a ，b ，c ，d 的值；(2)若x ≥－2时，f (x )≤kg (x )，求k 的取值范围．【2012，21】已知函数)(x f 满足2121)0()1(')(x x f e f x f x +-=-． （1）求)(x f 的解析式及单调区间；（2）若b ax x x f ++≥221)(，求b a )1(+的最大值．【2011，21】已知函数ln ()1a x bf x x x=++，曲线()y f x =在点(1,(1))f 处的切线方程为230x y +-=． （Ⅰ）求a 、b 的值；（Ⅱ）如果当0x >，且1x ≠时，ln ()1x kf x x x>+-，求k 的取值范围．2．导数及其应用（解析版）一、选择题【2015，12】设函数()f x =(21)x e x ax a --+,其中1a <，若存在唯一的整数0x ，使得0()0f x <，则a 的取值范围是（ ）A ．3,12e ⎡⎫-⎪⎢⎣⎭ B ． 33,2e 4⎡⎫-⎪⎢⎣⎭ C ． 33,2e 4⎡⎫⎪⎢⎣⎭ D ． 3,12e ⎡⎫⎪⎢⎣⎭解析：设()g x =(21)x e x -，y ax a =-，由题知存在唯一的整数0x ，使得0()g x 在直线y ax a =-的下方.因为()(21)x g x e x '=+，所以当12x <-时，()g x '＜0，当12x >-时，()g x '＞0，所以当12x =-时，min [()]g x =122e --，当0x =时，(0)1g =-，(1)30g e =>，直线y ax a =-恒过（1,0）斜率且a ，故(0)1a g ->=-，且1(1)3g e a a --=-≥--，解得32e≤a ＜1，故选D ．. 作为选择题，该题也可先找到满足0()0f x <的整数0x ，由0x 的唯一性列不等式组求解.由(0)10f a =-+<得00x =.又0x 是唯一使()0f x <的整数，所以(1)0(1)0f f -≥⎧⎨≥⎩，解得32a e ≥，又1a <，且34a =时符合题意.故选D ．. 【2014，11】已知函数()f x =3231ax x -+，若()f x 存在唯一的零点0x ，且0x ＞0，则a 的取值范围为A .（2，+∞）B .（-∞，-2）C .（1，+∞）D .（-∞，-1）【解析1】：由已知0a ≠，2()36f x ax x '=-，令()0f x '=，得0x =或2x a=， 当0a >时，()22,0,()0;0,,()0;,,()0x f x x f x x f x a a ⎛⎫⎛⎫'''∈-∞>∈<∈+∞> ⎪ ⎪⎝⎭⎝⎭； 且(0)10f =>，()f x 有小于零的零点，不符合题意．当0a <时，()22,,()0;,0,()0;0,,()0x f x x f x x f x a a ⎛⎫⎛⎫'''∈-∞<∈>∈+∞< ⎪ ⎪⎝⎭⎝⎭要使()f x 有唯一的零点0x 且0x ＞0，只需2()0f a>，即24a >，2a <-．选B 【解析2】：由已知0a ≠，()f x =3231ax x -+有唯一的正零点，等价于3113a x x =- 有唯一的正零根，令1t x=，则问题又等价于33a t t =-+有唯一的正零根，即y a =与33y t t =-+有唯一的交点且交点在在y 轴右侧记3()3f t t t =-+，2()33f t t '=-+，由()0f t '=，1t =±，()(),1,()0;1,1,()0;t f t t f t ''∈-∞-<∈->，()1,,()0t f t '∈+∞<，要使33a t t =-+有唯一的正零根，只需(1)2a f <-=-，选B【2012，10】已知函数1()ln(1)f x x x=+-，则()y f x =的图像大致为（ ）【解析】()y f x =的定义域为{|1x x >-且0}x ≠，排除D ；因为221(1)1'()[ln(1)](1)[ln(1)]x x f x x x x x x --+==+-++-，所以当(1,0)x ∈-时，'()0f x <，()y f x =在（－1，0）上是减函数；当(0,)x ∈+∞时，'()0f x >，()y f x =在(0,)+∞上是增函数．排除A 、C ，故选择B ． 【2012，12】设点P 在曲线12xy e =上，点Q 在曲线ln(2)y x =上，则||PQ 的最小值为（ ） A ．1ln 2-B ln 2)-C ．1ln 2+D ln 2)+【解析】函数12xy e =与函数ln(2)y x =互为反函数，图象关于直线y x =对称． 问题转化为求曲线12xy e =上点P 到直线y x =的距离的最小值d ，则||PQ 的最小值为2d ．（用切线法）：设直线y x b =+与曲线12x y e =相切于点1(,)2t P t e ， 因为1'2x y e =，所以根据导数的几何意义，得112te =，ln 2t =，所以切点(ln 2,1)P ，从而1ln 2b =-，所以1ln 2y x =+- 因此曲线12xy e =上点P 到直线y x =的距离的最小值d 为直线 1ln 2y x =+-与直线y x =的距离，从而d =，所以min ||2ln2)PQ d =-，故选择B ． 【2011，9】由曲线y 2y x =-及y 轴所围成的图形的面积为（ ）A ．B ．D ．A ．103 B ．4 C ．163D ．6解析：用定积分求解432420021162)(2)|323s x dx x x x =+=-+=⎰，选C二、填空题【2017，16】如图，圆形纸片的圆心为O ，半径为5 cm ，该纸片上的等边三角形ABC 的中心为O ．D 、E 、F 为圆O 上的点，△DBC ，△ECA ，△F AB 分别是以BC ，CA ，AB 为底边的等腰三角形．沿虚线剪开后，分别以BC ， CA ，AB 为折痕折起△DBC ，△ECA ，△F AB ，使得D ，E ，F 重合，得到三棱锥．当△ABC 的边长变化时，所得三棱锥体积（单位：cm 3）的最大值为_______．【解析】由题，连接OD ，交BC 与点G ，由题，OD BC ⊥，OG =， 即OG 的长度与BC 的长度或成正比，设OG x =，则BC =，5DG x =-，三棱锥的高h =2132ABC S x =⋅=△，则213ABC V S h =⋅△令()452510f x x x =-，5(0,)2x ∈，()3410050f x x x '=-，令()0f x '>，即4320x x -<，2x <，则()()280f x f =≤，则45V =，∴体积最大值为3． 【2013，16】若函数f (x )＝(1－x 2)(x 2＋ax ＋b )的图像关于直线x ＝－2对称，则f (x )的最大值为__________． 解析：∵函数f (x )的图像关于直线x ＝－2对称，∴f (x )满足f (0)＝f (－4)，f (－1)＝f (－3)，即15164,0893,b a b a b =-(-+)⎧⎨=-(-+)⎩解得8,15.a b =⎧⎨=⎩∴f (x )＝－x 4－8x 3－14x 2＋8x ＋15. 由f ′(x )＝－4x 3－24x 2－28x ＋8＝0，得x 1＝－2x 2＝－2，x 3＝－2易知，f (x )在(－∞，－2上为增函数，在(－22)上为减函数，在(－2，－2上为增函数，在(－2∞)上为减函数．∴f (－2－＝[1－(－2－2][(－22＋8(－2＋15]＝(－8－－＝80－64＝16.f (－2)＝[1－(－2)2][(－2)2＋8×(－2)＋15]＝－3(4－16＋15)＝－9.f (－2＝[1－(－22][(－22＋8(－2＋15] ＝(－8＋＋＝80－64＝16. 故f (x )的最大值为16.三、解答题【2017，12】已知函数()()22xx f x aea e x =+--．（1）讨论()f x 的单调性；（2）若()f x 有两个零点，求a 的取值范围．【解析】（1）由于()()2e 2e x x f x a a x =+--，故()()()()22e 2e 1e 12e 1x x x xf x a a a '=+--=-+，①当0a ≤时，e 10x a -<，2e 10x +>．从而()0f x '<恒成立．()f x 在R 上单调递减； ②当0a >时，令()0f x '=，从而e 10x a -=，得ln x a =-．综上，当0a ≤ 当0a >时，()f x 在(,ln )a -∞-上单调递减，在(ln ,)a -+∞上单调递增（2）由（1）知，当0a ≤时，()f x 在R 上单调减，故()f x 在R 上至多一个零点，不满足条件． 当0a >时，()min 1ln 1ln f f a a a =-=-+．令()11ln g a a a=-+． 令()()11ln 0g a a a a =-+>，则()211'0g a a a=+>．从而()g a 在()0+∞，上单调增，而()10g =．故当01a <<时，()0g a <．当1a =时()0g a =．当1a >时()0g a >， 若1a >，则()min 11ln 0f a g a a=-+=>，故()0f x >恒成立，从而()f x 无零点，不满足条件． 若1a =，则min 11ln 0f a a=-+=，故()0f x =仅有一个实根ln 0x a =-=，不满足条件． 若01a <<，则min 11ln 0f a a =-+<，注意到ln 0a ->．()22110e e ea a f -=++->． 故()f x 在()1ln a --，上有一个实根，而又31ln 1ln ln a a a ⎛⎫->=- ⎪⎝⎭．且33ln 1ln 133ln(1)e e2ln 1a a f a a a a ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫-=⋅+--- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭()3333132ln 11ln 10a a a a a a ⎛⎫⎛⎫⎛⎫⎛⎫=-⋅-+---=---> ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭． 故()f x 在3ln ln 1a a ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭，上有一个实根． 又()f x 在()ln a -∞-，上单调减，在()ln a -+∞，单调增，故()f x 在R 上至多两个实根．又()f x 在()1ln a --，及3ln ln 1a a ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭，上均至少有一个实数根，故()f x 在R 上恰有两个实根．综上，01a <<．【法二】令()0f x =，则22x x xe x a e e +=+．再令0xt e =>，则22ln t t a t t +=+， 而()f x 有两个零点，则22ln t t a t t +=+有两解，即直线y a =与曲线22ln t t y t t+=+有两个交点； 令()22ln (0)t t g t t t t +=>+，则()()()()()2222211ln 2ln t t t t t g t t t t t +--+'==++， 令()1ln h t t t =--，则()110h t t'=--<，注意到()10h =，所以()g t 在()0,1上单调递增，在()1,+∞上单调递减，即()()max 11g t g ==；而0lim (),lim ()0t t g t g t →→+∞→-∞→，所以当()0,1t ∈时，()(),1g t ∈-∞；当()0,1t ∈时，()()0,1g t ∈， 所以，当22ln t ta t t+=+有两解时，a 的取值范围为()0,1．【2016，12】已知函数2)1()2()(-+-=x a e x x f x有两个零点．（Ⅰ）求a 的取值范围；（Ⅱ）设21,x x 是)(x f 的两个零点，证明：221<+x x ．【解析】：⑴ 由已知得：()()()()()'12112x x f x x e a x x e a =-+-=-+① 若0a =，那么()()0202x f x x e x =⇔-=⇔=，()f x 只有唯一的零点2x =，不合题意； ② 若0a >，那么20x x e a e +>>，所以当1x >时，()'0f x >，()f x 单调递增;当1x <时，()'0f x <，()f x 单调递减; 即：由于()20f a =>，()10f e =-<，则()()210f f <， 根据零点存在性定理，()f x 在()1,2上有且仅有一个零点． 而当1x <时，x e e <，210x -<-<，故()()()()()()()222212111x f x x e a x e x a x a x e x e =-+->-+-=-+--则()0f x =的两根11t +，21t =+， 12t t <，因为0a >，故当1x t <或2x t >时，()()2110a x e x e -+--> 因此，当1x <且1x t <时，()0f x >又()10f e =-<，根据零点存在性定理，()f x 在(),1-∞有且只有一个零点． 此时，()f x 在R 上有且只有两个零点，满足题意．③ 若02ea -<<，则()ln 2ln 1a e -<=，当()ln 2x a <-时，()1ln 210x a -<--<，()ln 2220a x e a e a -+<+=，即()()()'120x f x x e a =-+>，()f x 单调递增；当()ln 21a x -<<时，10x -<，()ln 2220ax e a e a -+>+=，即()()()'120x f x x e a =-+<，()f x 单调递减；当1x >时，10x ->，()ln 2220a x e a e a -+>+=，即()'0f x >，()f x 单调递增．即：()()()(){}22ln 22ln 22ln 21ln 2210f a a a a a a a -=---+--=--+<⎡⎤⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦⎣⎦故当1x ≤时，()f x 在()ln 2x a =-处取到最大值()ln 2f a -⎡⎤⎣⎦，那么()()ln 20f x f a -<⎡⎤⎣⎦≤恒成立，即()0f x =无解而当1x >时，()f x 单调递增，至多一个零点 此时()f x 在R 上至多一个零点，不合题意．④ 若2ea =-，那么()ln 21a -=当()1ln 2x a <=-时，10x -<，()ln 2220a x e a ea -+<+=，即()'0f x >，()f x 单调递增 当()1ln 2x a >=-时，10x ->，()ln 2220a x e a ea -+>+=，即()'0f x >，()f x 单调递增又()f x 在1x =处有意义，故()f x 在R 上单调递增，此时至多一个零点，不合题意．⑤ 若2ea <-，则()ln 21a ->当1x <时，10x -<，()ln 212220a x e a e a ea -+<+<+=，即()'0f x >，()f x 单调递增当()1ln 2x a <<-时，10x ->，()ln 2220a x e a ea -+<+=，即()'0f x <，()f x 单调递减当()ln 2x a >-时，()1ln 210x a ->-->，()ln 2220a x e a ea -+>+=，即()'0f x >，()f x 单调递增 即：0e -<恒成立，即()0f x =无解当()ln 2x a >-时，()f x 单调递增，至多一个零点,此时()f x 在R 上至多一个零点，不合题意． 综上所述，当且仅当0a >时符合题意，即a 的取值范围为()0,+∞． ⑵ 由已知得：()()120f x f x ==，不难发现11x ≠，21x ≠，故可整理得：()()()()121222122211x x x e x e a x x ---==--,()()()221xx e g x x -=-，则()()12g x g x = ()()()2321'1x x g x e x -+=-，当1x <时，()'0g x <，()g x 单调递减；当1x >时，()'0g x >，()g x 单调递增．设0m >，构造代数式： ()()111222*********m m m m m m m m g m g m e e e e m m m m +-----+-⎛⎫+--=-=+ ⎪+⎝⎭设()2111m m h m e m -=++，0m >,则()()2222'01m m h m e m =>+，故()h m 单调递增，有()()00h m h >=． 因此，对于任意的0m >，()()11g m g m +>-．由()()12g x g x =可知1x 、2x 不可能在()g x 的同一个单调区间上，不妨设12x x <，则必有121x x << 令110m x =->，则有()()()()()1111211112g x g x g x g x g x +->--⇔->=⎡⎤⎡⎤⎣⎦⎣⎦ 而121x ->，21x >，()g x 在()1,+∞上单调递增，因此：()()121222g x g x x x ->⇔-> 整理得：122x x +<．【2015，12】已知函数31()4f x x ax =++，()ln g x x =-. （Ⅰ）当a 为何值时，x 轴为曲线()y f x =的切线；（Ⅱ）用min{,}m n 表示,m n 中的最小值，设函数min{),()(}()h x f x g x =（0x >），讨论()h x 零点的个数.解：（Ⅰ）2()3f x x a '=+，若x 轴为曲线()y f x =的切线，则切点0(,0)x 满足00()0,()0f x f x '==，也就是2030x a +=且300104x ax ++=，解得012x =，34a =-，因此，当34a =-时，x 轴为曲线()y f x =的切线；（Ⅱ）当1x >时，()ln 0g x x =-<，函数()()()(min{}),h x f x g x g x ≤=没有零点； 当1x =时，若54a ≥-，则5(1)04f a =+≥，min{,(1)(1)(1)}(1)0h fg g ===，故1x =是()h x 的零点；当01x <<时，()ln 0g x x =->，以下讨论()y f x =在区间(0,1)上的零点的个数. 对于2()3f x x a '=+，因为2033x <<，所以令()0f x '=可得23a x =-，那么（i ）当3a ≤-或0a ≥时，()f x '没有零点（()0f x '<或()0f x '>），()y f x =在区间(0,1)上是单调函数，且15(0),(1)44f f a ==+，所以当3a ≤-时，()y f x =在区间(0,1)上有一个零点；当0a ≥时，()y f x =在区间(0,1)上没有零点；（ii ）当30a -<<时，()0f x '<（0x <<且()0f x '>1x <），所以x =最小值点，且14f =.显然，若0f >，即304a -<<时，()y f x =在区间(0,1)上没有零点；若0f =，即34a =-时，()y f x =在区间(0,1)上有1个零点；若0f <，即334a-<<-时，因为15(0),(1)44f f a ==+，所以若5344a -<<-，()y f x =在区间(0,1)上有2个零点；若534a -<≤-，()y f x =在区间(0,1)上有1个零点. 综上，当34a >-或54a <-时，()h x 有1个零点；当34a =-或54a =-时，()h x 有2个零点；当5344a -<<-时，()h x 有3个零点. 【2014，21】设函数1(0ln x xbe f x ae x x-=+，曲线()y f x =在点（1，(1)f 处的切线为(1)2y e x =-+.(Ⅰ)求,a b ； （Ⅱ）证明：()1f x >.【解析】(Ⅰ) 函数()f x 的定义域为()0,+∞，112()ln xx x x a b b f x ae x e e e x x x--'=+-+ 由题意可得(1)2,(1)f f e '==，故1,2a b == ……………6分（Ⅱ）由(Ⅰ)知，12()ln x xe f x e x x-=+，从而()1f x >等价于2ln xx x xe e ->-设函数()ln g x x x =，则()l n g x x x'=+，所以当10,x e ⎛⎫∈ ⎪⎝⎭时，()0g x '<，当1,x e ⎛⎫∈+∞ ⎪⎝⎭时，()0g x '>，故()g x 在10,e ⎛⎫ ⎪⎝⎭单调递减，在1,e ⎛⎫+∞ ⎪⎝⎭单调递增，从而()g x 在()0,+∞的最小值为11()g e e =-. 设函数2()xh x xe e-=-，则()()1xh x e x -'=-，所以当()0,1x ∈时，()0h x '>，当()1,x ∈+∞时，()0h x '<，故()h x 在()0,1单调递增，在()1,+∞单调递减，从而()h x ()g x 在()0,+∞的最小值1(1)h e=-. 综上：当0x >时，()()g x h x >，即()1f x >. ……………12分【2013，理21】设函数f (x )＝x 2＋ax ＋b ，g (x )＝e x (cx ＋d )．若曲线y ＝f (x )和曲线y ＝g (x )都过点P (0,2)，且在点P 处有相同的切线y ＝4x ＋2.(1)求a ，b ，c ，d 的值；(2)若x ≥－2时，f (x )≤kg (x )，求k 的取值范围． 解：(1)由已知得f (0)＝2，g (0)＝2，f ′(0)＝4，g ′(0)＝4.而f ′(x )＝2x ＋a ，g ′(x )＝e x (cx ＋d ＋c )，故b ＝2，d ＝2，a ＝4，d ＋c ＝4. 从而a ＝4，b ＝2，c ＝2，d ＝2.(2)由(1)知，f (x )＝x 2＋4x ＋2，g (x )＝2e x (x ＋1)．设函数F (x )＝kg (x )－f (x )＝2k e x (x ＋1)－x 2－4x －2，则F ′(x )＝2k e x (x ＋2)－2x －4＝2(x ＋2)(k e x －1)． 由题设可得F (0)≥0，即k ≥1. 令F ′(x )＝0得x 1＝－ln k ，x 2＝－2.①若1≤k ＜e 2，则－2＜x 1≤0.从而当x ∈(－2，x 1)时，F ′(x )＜0；当x ∈(x 1，＋∞)时，F ′(x )＞0.即F (x )在(－2，x 1)单调递减，在(x 1，＋∞)单调递增．故F (x )在[－2，＋∞)的最小值为F (x 1)．而F (x 1)＝2x 1＋2－21x －4x 1－2＝－x 1(x 1＋2)≥0. 故当x ≥－2时，F (x )≥0，即f (x )≤kg (x )恒成立． ②若k ＝e 2，则F ′(x )＝2e 2(x ＋2)(e x －e －2)．从而当x ＞－2时，F ′(x )＞0，即F (x )在(－2，＋∞)单调递增． 而F (－2)＝0，故当x ≥－2时，F (x )≥0，即f (x )≤kg (x )恒成立． ③若k ＞e 2，则F (－2)＝－2k e －2＋2＝－2e －2(k －e 2)＜0. 从而当x ≥－2时，f (x )≤kg (x )不可能恒成立． 综上，k 的取值范围是[1，e 2]． 【2012】21．（本小题满分12分）已知函数)(x f 满足2121)0()1(')(x x f e f x f x +-=-． （1）求)(x f 的解析式及单调区间；（2）若b ax x x f ++≥221)(，求b a )1(+的最大值．【解析】（1）因为2121)0()1(')(x x f e f x f x +-=-，所以1'()'(1)(0)x f x f e f x -=-+，所以1(0)'(1)'(1)'(1)(0)1f f ef f f ⎧=⋅⎪⎨⎪=-+⎩，解得(0)1f =，'(1)f e =． 所以)(x f 的解析式为21()2xf x e x x =-+，由此得'()1x f x e x =-+． 而'()1xf x e x =-+是R 上的增函数，且'(0)0f =，因此，当(0,)x ∈+∞时，'()'(0)0f x f >=，)(x f 在(0,)+∞上是增函数； 当(,0)x ∈-∞时，'()'(0)0f x f <=，)(x f 在(,0)-∞上是减函数． 综上所述，函数)(x f 的增区间为(0,)+∞，减区间为(,0)-∞．（2）由已知条件得(1)x e a x b -+≥． ①（i ）若10a +<，则对任意常数b ，当0x <，且11bx a -<+， 可得(1)x e a x b -+<，因此①式不成立． （ii ）若10a +=，则(1)0a b +=．（iii ）若10a +>，设()(1)x g x e a x =-+，则'()(1)x g x e a =-+．当(,ln(1))x a ∈-∞+，'()0g x <；当(ln(1),)x a ∈++∞，'()0g x > 从而()g x 在(,ln(1))a -∞+单调递减，在(ln(1),)a ++∞单调递增． 所以b ax x x f ++≥221)(等价于1(1)ln(1)b a a a ≤+-++． ② 因此22(1)(1)(1)ln(1)a b a a a +≤+-++．设22()(1)(1)ln(1)h a a a a =+-++，则'()(1)(12ln(1))h a a a =+-+． 所以()h a 在12(1,1)e --单调递增，在12(1,)e -+∞单调递减， 故()h a 在121a e =-在处取得最大值，从而()2e h a ≤，即(1)2e a b +≤． 当121a e =-，122e b =时，②式成立，故b ax x x f ++≥221)(．综合得，b a )1(+的最大值为2e．【2011，21】已知函数ln ()1a x bf x x x=++，曲线()y f x =在点(1,(1))f 处的切线方程为230x y +-=． （Ⅰ）求a 、b 的值；（Ⅱ）如果当0x >，且1x ≠时，ln ()1x kf x x x>+-，求k 的取值范围． （21）解：（I ）()()221ln 1x a x b x f x x x +⎛⎫- ⎪⎝⎭'=-+ 由于直线230x y +-=的斜率为12-，且过点()1,1，故()()11112f f =⎧⎪⎨'=-⎪⎩，即1122b ab =⎧⎪⎨-=-⎪⎩，解得1a =，1b =.（II ）由（I ）知()ln 11x f x x x =++，所以()()()2211ln 12ln 11k x x k f x x x x x x ⎛⎫--⎛⎫ ⎪-+=+ ⎪ ⎪--⎝⎭⎝⎭考虑函数()()()()2112ln 0k x h x x x x--=+>，则()()()22112k x xh x x -++'=（i ）设0k ≤，由()()()22211k x x h x x+--'=知，当1x ≠时，()0h x '<. 而()10h =，故当()0,1x ∈时，()0h x <，可得()2101h x x >-； 当()1,x ∈+∞时，()0h x <，可得()2101h x x >- 从而当0x >，且1x ≠时，()ln 01x k f x x x ⎛⎫-+> ⎪-⎝⎭，即()ln 1x k f x x x ⎛⎫>+ ⎪-⎝⎭.（ii ）设01k <<，由于当11,1x k ⎛⎫∈ ⎪-⎝⎭时，()()21120k x x -++>，故()0h x '>，而()10h =，故当11,1x k ⎛⎫∈ ⎪-⎝⎭时，()0h x >，可得()2101h x x <-，与题设矛盾. （iii ）设1k ≥，此时()0h x '>，而()10h =，故当()1,x ∈+∞时，()0h x >，得()2101h x x <-，与题设矛盾.综合得，k 的取值范围为(],0-∞.4．三角函数、解三角形一、选择题【2017，9】已知曲线C 1：y =cos x ，C 2：y =sin (2x +2π3)，则下面结正确的是（ ） A ．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C 2B ．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C 2C ．把C 1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C 2D ．把C 1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C 2【2016，12】已知函数)2,0)(sin()(πϕωϕω≤>+=x x f ，4π-=x 为)(x f 的零点，4π=x 为)(x f y =图像的对称轴，且)(x f 在)365,18(ππ单调，则ω的最大值为（ ）A ．11B ．9C ．7D ．5【2015，8】函数()f x =cos()x ωϕ+的部分图象如图所示，则()f x 的单调递减区间为（ ）A ．13(,),44k k k ππ-+∈Z B ．13(2,2),44k k k ππ-+∈Z C ．13(,),44k k k -+∈Z D ．13(2,2),44k k k -+∈Z【2015，2】sin 20cos10cos160sin10-=（ ）A ．BC ．12-D ．12【2014，6】如图，圆O 的半径为1，A 是圆上的定点，P 是圆上的动点，角x 的始边为射线OA ，终边为射线OP ，过点P 作直线OA 的垂线，垂足为M ，将点M 到直线OP 的距离表示为x 的函数()f x ，则y =()f x 在[0,π]上的图像大致为（ ）【2014，8】设(0,)2πα∈，(0,)2πβ∈，且1sin tan cos βαβ+=，则（ ） A ．32παβ-=B ．22παβ-=C ．32παβ+=D ．22παβ+=【2012，9】已知0ω>，函数()sin()4f x x πω=+在（2π，π）上单调递减，则ω的取值范围是（ ） A ．[12，54] B ．[12，34] C ．（0，12] D ．（0，2]【2011，5】已知角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线2y x =上，则cos 2θ=A ．45-B ．35-C ．35D ．45【2011，11】设函数()sin()cos()(0,)2f x x x πωϕωϕωϕ=+++><的最小正周期为π，且()()f x f x -=，则（ ）A ．()f x 在0,2π⎛⎫⎪⎝⎭单调递减 B ．()f x 在3,44ππ⎛⎫⎪⎝⎭单调递减 C ．()f x 在0,2π⎛⎫⎪⎝⎭单调递增 D ．()f x 在3,44ππ⎛⎫⎪⎝⎭单调递增 二、填空题【2015，16】在平面四边形ABCD 中，75A B C ∠=∠=∠=，2BC =，则AB 的取值范围是 ． 【2014，16】已知,,a b c 分别为ABC ∆的三个内角,,A B C 的对边，a =2，且(2)(sin sin )()sin b A B c b C +-=-，则ABC ∆面积的最大值为 ． 【2013，15】设当x ＝θ时，函数f (x )＝sin x －2cos x 取得最大值，则cos θ＝__________．【2011，16】在ABC V 中，60,B AC ==2AB BC +的最大值为 ． 三、解答题【2017，17】△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知△ABC 的面积为23sin a A（1）求sin B sin C ；（2）若6cos B cos C =1,a =3,求△ABC 的周长【2016，17】ABC ∆的内角C B A ,,的对边分别为c b a ,,，已知c A b B a C =+)cos cos (cos 2． （Ⅰ）求C ；（Ⅱ）若7=c ，ABC ∆的面积为233，求ABC ∆的周长．【2013，17】如图，在△ABC 中，∠ABC ＝90°，AB BC ＝1，P 为△ABC 内一点，∠BPC ＝90°．(1)若PB ＝12，求P A ；(2)若∠APB ＝150°，求tan ∠PBA ．【2012，17】已知a ，b ，c 分别为△ABC 三个内角A ，B ，C 的对边，cos sin 0a C C b c --=．（1）求A ；（2）若2a =，△ABC b ，c ．3．三角函数、解三角形（解析版）一、选择题【2017，9】已知曲线C 1：y =cos x ，C 2：y =sin (2x +2π3)，则下面结正确的是（ ） A ．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C 2B ．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C 2C ．把C 1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C 2D ．把C 1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C 2【解析】1:cos C y x =，22π:sin 23⎛⎫=+ ⎪⎝⎭C y x ，首先曲线1C 、2C 统一为一三角函数名，可将1:cos C y x =用诱导公式处理．πππcos cos sin 222⎛⎫⎛⎫==+-=+ ⎪ ⎪⎝⎭⎝⎭y x x x ．横坐标变换需将1=ω变成2=ω，即112πππsin sin 2sin 2224⎛⎫⎛⎫⎛⎫=+→=+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭C 上各坐短它原y x y x x 点横标缩来2ππsin 2sin 233⎛⎫⎛⎫−−→=+=+ ⎪ ⎪⎝⎭⎝⎭y x x ． 注意ω的系数，在右平移需将2=ω提到括号外面，这时π4+x 平移至π3+x ， 根据“左加右减”原则，“π4+x ”到“π3+x ”需加上π12，即再向左平移π12．故选D ； 【2016，12】已知函数)2,0)(sin()(πϕωϕω≤>+=x x f ，4π-=x 为)(x f 的零点，4π=x 为)(x f y =图像的对称轴，且)(x f 在)365,18(ππ单调，则ω的最大值为（ ）A ．11B ．9C ．7D ．5【解析】：由题意知：12π+π 4ππ+π+42k k ωϕωϕ⎧-=⎪⎪⎨⎪=⎪⎩则21k ω=+，其中k ∈Z ，()f x 在π5π,1836⎛⎫⎪⎝⎭单调，5π,123618122T ππω∴-=≤≤，接下来用排除法：若π11,4ωϕ==-，此时π()sin 114f x x ⎛⎫=- ⎪⎝⎭，()f x 在π3π,1844⎛⎫ ⎪⎝⎭递增，在3π5π,4436⎛⎫ ⎪⎝⎭递减，不满足()f x 在π5π,1836⎛⎫⎪⎝⎭单调；若π9,4ωϕ==，此时π()sin 94f x x ⎛⎫=+ ⎪⎝⎭，满足()f x 在π5π,1836⎛⎫⎪⎝⎭单调递减．故选B ．【2015，8】函数()f x =cos()x ωϕ+的部分图象如图所示，则()f x 的单调递减区间为（ ）A ．13(,),44k k k ππ-+∈Z B ．13(2,2),44k k k ππ-+∈ZC ．13(,),44k k k -+∈ZD ．13(2,2),44k k k -+∈Z解析：由五点作图知，1+4253+42πωϕπωϕ⎧=⎪⎪⎨⎪=⎪⎩，解得=ωπ，=4πϕ，所以()cos()4f x x ππ=+，令22,4k x k k πππππ<+<+∈Z ，解得124k -＜x ＜324k +，k ∈Z ，故单调减区间为（124k -，324k +），k ∈Z ，故选D ． 【2015，2】sin 20cos10cos160sin10-=（ ）A．2-B．2C ．12-D ．12解析：sin 20cos10cos160sin10sin 20cos10cos 20sin10sin30-=+=，选D ．. 【2014，6】如图，圆O 的半径为1，A 是圆上的定点，P 是圆上的动点，角x的始边为射线OA ，终边为射线OP ，过点P 作直线OA 的垂线，垂足为M ，将点M 到直线OP 的距离表示为x 的函数()f x ，则y =()f x 在[0,π]上的图像大致为（ ）【解析】：如图：过M 作MD ⊥OP 于Ｄ，则 PM=sin x ，OM=cos x ,在Rt OMP ∆中，MD=cos sin 1x x OM PM OP =cos sin x x =1sin 22x =，∴()f x 1sin 2(0)2x x π=≤≤，选B. 【2014，8】设(0,)2πα∈，(0,)2πβ∈，且1sin tan cos βαβ+=，则A .32παβ-=B .22παβ-=C .32παβ+=D .22παβ+=【解析】∵sin 1sin tan cos cos αβααβ+==，∴sin cos cos cos sin αβααβ=+ ()sin cos sin 2παβαα⎛⎫-==- ⎪⎝⎭，,02222ππππαβα-<-<<-<∴2παβα-=-，即22παβ-=，选B【2012，9】已知0ω>，函数()sin()4f x x πω=+在（2π，π）上单调递减，则ω的取值范围是（ ） A ．[12，54] B ．[12，34] C ．（0，12] D ．（0，2]【解析】因为0ω>，2x ππ<<，所以2444x ππππωωωπ⋅+<+<⋅+，因为函数()sin()4f x x πω=+在（2π，π）上单调递减，所以242342πππωππωπ⎧⋅+≥⎪⎪⎨⎪⋅+≤⎪⎩，解得1524ω≤≤，故选择A. 【2011，11】设函数()sin()cos()(0,)2f x x x πωϕωϕωϕ=+++><的最小正周期为π，且()()f x f x -=，则（ ） A ．()f x 在0,2π⎛⎫⎪⎝⎭单调递减 B ．()f x 在3,44ππ⎛⎫⎪⎝⎭单调递减 C ．()f x 在0,2π⎛⎫⎪⎝⎭单调递增 D ．()f x 在3,44ππ⎛⎫⎪⎝⎭单调递增 解析：())4f x x πωϕ=++，所以2ω=，又f(x)为偶函数，,424k k k z πππϕπϕπ∴+=+⇒=+∈，())2f x x x π∴=+=，选A.。
2011年新课标高考试题分类评析——解析几何
．
解析 几何 是 高 中数学 的 重要 内容 ， 是 学 习高 等 也
数 学 的基础 知 识 ， 当然 是 高考 命 题 的 热 点 之 一． 几 近
年 高考数 学 对解 析几何 的考 查 一直 占有 较 大 的 比例 ， 且题 型 、 题量 、 度均 保持 相 对 稳定 ． 难 向量 与 导数圆１ ＋ 一 南 ） 椭 ： 如
（ ＞ ６ ） 离 心率 为 ， ｎ ＞。 的 ｚ轴 被 曲线 ｃ ： ＝ｚ 一６ ｚ 截得 的线 段长 等 于 Ｃ 的长半轴 长． （ ）求 Ｃ ， ２的方程 ； １ 。Ｃ （ ）设 Ｃ ２ 。与 ｙ轴 的交 点为 Ｍ ， 坐标 原点 ０的直 过 线 ｚ与 Ｃ。相 交 于 点 Ａ， Ｂ， 直线 ＭＡ， ＭＢ分 别 与 Ｃ 相 交 于 点 Ｄ， ． Ｅ
示 一０或 — ｚ—ｍ＝０过 定点 （ ， ） 一０与 圆 一１ Ｏ ，
析 （ 由 意 ： ～２从 ６又 １ 题 知 ＝ ） ： 詈 ，而 ，
２ 一口 解 得 ａ ，—１故 Ｃ ， 的方 程分别 为 √ ， 一２６ ， Ｃ
等＋ 一１ ｙ ． ， ＝ｘ一１
（ ）① 由题 意 知 ， 线 ｌ的斜 率 存 在 ， 其方 程 ２ 直 设
ｋ ． ： 忌 ． ￣－ ｙ 一 Ｈ１
一 一
森
示两条 直 线是 解题 的关键．
生 ！ ± 兰± ± 一二 ！ 垒± 一～ ！ ＝ 兰 墨± ！
１１ 只 有 不 断 找 寻 机 会 的 人 才 会 度 时把 握 机 会
故 ＭＡ＿ Ｍ Ｂ， Ｍ Ｄ上 Ｍ Ｅ ｌ ＿ 即 ．
2017年普通高等学校招生全国统一考试(全国新课标Ⅰ卷)数学试题 (理科)解析版
得到曲线 C2
1
π
C．把 C1 上各点的横坐标缩短到原来的 倍，纵坐标不变，再把得到的曲线向右平移 个单位长度，
色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点，
则此点取自黑色部分的概率是（ ）
A． 1 4
B． π 8
C． 1 2
D． π 4
【答案】B
【解析】设正方形边长为 a ，则圆的半径为 a ，正方形的面积为 a2 ，圆的面 2
πa2
积为 .由图形的对称性可知，太极图中黑白部分面积相等，即各占圆面积的一半.由几何概型概率
一、选择题：本题共 12 小题，每小题 5 分，共 60 分。在每小题给出的四个选项中，只有一项是符合 题目要求的。
1．已知集合 A={x|x<1}，B={x| 3x 1 }，则（ ） A． A B {x | x 0} B． A B R C． A B {x | x 1} D． A B
4
的计算公式得，此点取自黑色部分的概率是
1 πa2 24
a2
π
，选 B.
8
秒杀解析：由题意可知，此点取自黑色部分的概率即为黑色部分面积占整个面积的比例，由图可知其
概率 p 满足 1 p 1 ，故选 B.
4
2
3．设有下面四个命题
p1
：若复数
z
满足
1 z
R
，则
z
R
；
p2 ：若复数 z 满足 z2 R ，则 z R ；
【答案】A
【解析】由 3x 1 可得 3x 30 ，则 x 0 ，即 B {x | x 0} ，所以 A B {x | x 1}{x | x 0} {x | x 0}， A B {x | x 1}{x | x 0} {x | x 1} ，故选 A.
高考数学全国卷分类汇编解析几何
-高考数学全国卷分类汇编(解析几何）————————————————————————————————作者：————————————————————————————————日期:20１0－2017新课标全国卷分类汇编（解析几何)1.（２0１7课标全国Ⅰ，理10）已知F 为抛物线C ：24y x =的交点,过F 作两条互相垂直1l ，2l ，直线1l 与C 交于A 、B 两点，直线2l 与C 交于D ，E 两点,AB DE +的最小值为（）A ．16B ．14 Ｃ．12ﻩＤ．10【答案】A 【解析】设AB 倾斜角为θ．作1AK 垂直准线，2AK 垂直x 轴ﻫ易知11cos 22⎧⎪⋅+=⎪⎪=⎨⎪⎛⎫⎪=--= ⎪⎪⎝⎭⎩AF GF AK AK AF P P GP Pθ（几何关系）（抛物线特性）ﻫcos AF P AF θ⋅+=∴ 同理1cos P AF θ=-,1cos P BF θ=+，∴22221cos sin P PAB θθ==-又DE 与AB 垂直，即DE 的倾斜角为π2θ+2222πcos sin 2P PDE θθ==⎛⎫+ ⎪⎝⎭，而24y x =，即2P =.ﻫ∴22112sin cos AB DE P θθ⎛⎫+=+ ⎪⎝⎭2222sin cos 4sin cos θθθθ+=224sin cos θθ=241sin 24=θﻫ21616sin 2θ=≥,当π4θ=取等号，即AB DE +最小值为16，故选A2．（2017课标全国Ⅰ,理15)已知双曲线2222:x y C a b-，(0a >，0b >)的右顶点为A ,以A 为圆心,b 为半径作圆A ,圆A 与双曲线C 的一条渐近线交于M ,N 两点,若60MAN ∠=︒，则C 的离心率为＿___＿__．【答案】233【解析】如图，OA a =，AN AM b ==ﻫ∵60MAN ∠=︒，∴32AP b =，222234OP OA PA a b =-=-∴2232tan 34b AP OP a b θ==-又∵tan b aθ=，∴223234bb a a b =-,解得223a b = ∴221231133b e a =+=+=3.(2017课标全国Ⅰ,理20）（１２分)已知椭圆C ：22221x y a b+=()0a b >>，四点()111P ，,()201P ，，3312P ⎛⎫- ⎪ ⎪⎝⎭，,4312P ⎛⎫⎪ ⎪⎝⎭，中恰有三点在椭圆C 上. (１)求C 的方程；（2）设直线l 不经过2P 点且与C 相交于A 、B 两点,若直线2P A 与直线2P B 的斜率的和为1-,证明：l 过定点．【解析】（1）根据椭圆对称性,必过3P 、4P 又4P 横坐标为1，椭圆必不过1P ，所以过234P P P ，，三点ﻫ将()2330112P P ⎛⎫- ⎪ ⎪⎝⎭，，，代入椭圆方程得 222113141b ab ⎧=⎪⎪⎨⎪+=⎪⎩，解得24a =,21b =ﻫ∴椭圆C 的方程为：2214x y +=．ﻫ(2)①当斜率不存在时，设()():A A l x m A m y B m y =-，，，，221121A A P A P B y y k k m m m----+=+==- 得2m =,此时l 过椭圆右顶点，不存在两个交点,故不满足． ②当斜率存在时,设()1l y kx b b =+≠∶,()()1122A x y B x y ，，，ﻫ联立22440y kx bx y =+⎧⎨+-=⎩，整理得()222148440k x kbx b +++-=ﻫ122814kb x x k -+=+,21224414b x x k -⋅=+,ﻫ则22121211P A P By y k k x x --+=+()()21212112x kx b x x kx b x x x +-++-=222228888144414kb k kb kbk b k --++=-+ﻫ()()()811411k b b b -==-+-，又1b ≠21b k ⇒=--，此时64k ∆=-,存在k 使得0∆>成立．∴直线l 的方程为21y kx k =--当2x =时,1y =-，所以l 过定点()21-，.4．(２017课标全国Ⅱ，理９)若双曲线)00(1:2222>>=-b a by a x C ，的一条渐近线被圆4)2(22=+-y x 所截得的弦长为2，则C 的离心率为 Ａ．2 Ｂ．3 C.2Ｄ.332【答案】A【解析】由几何关系可得,双曲线()222210,0x y a b a b-=>>的渐近线方程为0bx ay ±=，圆心()2,0到渐近线距离为22213d =-=，则点()2,0到直线0bx ay +=的距离为222023b a bd ca b +⨯===+， 即2224()3c a c -=,整理可得224c a =，双曲线的离心率2242c e a ===.故选A. 【考点】 双曲线的离心率；直线与圆的位置关系，点到直线的距离公式【名师点睛】双曲线的离心率是双曲线最重要的几何性质,求双曲线的离心率（或离心率的取值范围)，常见有两种方法:①求出a ,c ，代入公式ce a=；②只需要根据一个条件得到关于a ,b ，c 的齐次式，结合ｂ2=c 2－a ２转化为a ，c 的齐次式,然后等式(不等式）两边分别除以ａ或ａ2转化为关于e 的方程(不等式),解方程(不等式）即可得e (e 的取值范围）.5.(2017课标全国Ⅱ，理１6)已知F 是抛物线x y C 8:2=的焦点,M 是C 上一点，FM 的延长线交y 轴于点N .若M 为FN 的中点,则=FN ．【答案】6 【解析】试题分析：如图所示，不妨设点M 位于第一象限，设抛物线的准线与x 轴交于点F',作MB l ⊥与点B ,NA l ⊥与点A ，由抛物线的解析式可得准线方程为2x =-,则2,4AN FF'==，在直角梯形ANFF'中，中位线'32AN FF BM +==,由抛物线的定义有：3MF MB ==，结合题意，有3MN MF ==，故336FN FM NM =+=+=.【考点】抛物线的定义、梯形中位线在解析几何中的应用．【名师点睛】抛物线的定义是解决抛物线问题的基础,它能将两种距离(抛物线上的点到焦点的距离、抛物线上的点到准线的距离)进行等量转化.如果问题中涉及抛物线的焦点和准线，又能与距离联系起来，那么用抛物线定义就能解决问题．因此，涉及抛物线的焦半径、焦点弦问题,可以优先考虑利用抛物线的定义转化为点到准线的距离，这样就可以使问题简单化.6．(20１7课标全国Ⅱ,理2０)（１2分)设O 为坐标原点,动点M 在椭圆12:22=+y x C 上,过M作x 轴的垂线,垂足为N ,点P 满足NM NP 2=.（１）求点P 的轨迹方程;（2）设点Q 在直线3-=x 上,且1=⋅PQ OP ． 证明:过点P 且垂直于OQ 的直线l 过C 的左焦点F .解:(1)设)(y x P ，，则)22(y x M ，,将点M 代入C 中得12222=+y x ，所以点P 的轨迹方程为222=+y x ．（2)由题可知)01(，-F ,设)()3(n m P t Q ，，，-，则)1( )3(n m PF t OQ ---=-=，，，， )3( )(n t m PQ n m OP ---==，，，．由1=⋅OQ OP 得1322=-+--n tn m m ,由(1)有222=+n m ,则有033=-+tn m ，所以033 =-+=⋅tn m PF OQ ，即过点P 且垂直于OQ 的直线l 过C 的左焦点F .7.（201７课标全国Ⅲ，理１)已知集合Ａ={}22(,)1x y x y +=│ ，B ＝{}(,)x y y x =│,则A ⋂B 中元素的个数为A.3B.2 Ｃ．1 D ．０【答案】Ｂ【解析】A 表示圆221x y +=上所有点的集合,B 表示直线y x =上所有点的集合，故AB 表示两直线与圆的交点，由图可知交点的个数为2,即A B 元素的个数为2，故选B.8．(2017课标全国Ⅲ，理5）已知双曲线C 22221x y a b -= (a >0，ｂ>0)的一条渐近线方程为52y x =,且与椭圆221123x y += 有公共焦点，则Ｃ的方程为A. 221810x y -= Ｂ. 22145x y -= Ｃ. 22154x y -= D. 22143x y -=【答案】B【解析】∵双曲线的一条渐近线方程为52y x =,则52b a =① 又∵椭圆221123x y +=与双曲线有公共焦点，易知3c =,则2229a b c +==②由①②解得2,5a b ==,则双曲线C 的方程为22145x y -=,故选B. ９．（20１7课标全国Ⅲ,理10）已知椭圆C ：22221x y a b+=，(ａ>b >0)的左、右顶点分别为A 1，Ａ2，且以线段Ａ1Ａ２为直径的圆与直线20bx ay ab -+=相切，则C 的离心率为 Ａ．63 B.33 Ｃ．23Ｄ.13【答案】A【解析】∵以12A A 为直径为圆与直线20bx ay ab -+=相切，∴圆心到直线距离d 等于半径，∴222abd a a b==+又∵0,0a b >>，则上式可化简为223a b = ∵222b ac =-，可得()2223a a c=-，即2223c a =∴63c e a ==，故选A10．(201７课标全国Ⅲ，理12）在矩形ABCD 中,1AB =,2AD =，动点P 在以点C 为圆心且与BD 相切的圆上．若AP AB AD λμ=+,则λμ+的最大值为（） A ．３ﻩﻩB.22ﻩC.5ﻩ ﻩD ．２【答案】Ａ【解析】由题意，画出右图．设BD 与C 切于点E ,连接CE .以A 为原点，AD 为x 轴正半轴,AB 为y 轴正半轴建立直角坐标系， 则C 点坐标为(2,1)． ∵||1CD =，||2BC =. ∴22125BD =+=. ∵BD 切C 于点E ． ∴CE ⊥BD .∴CE 是Rt BCD △中斜边BD 上的高．12||||2222||5||||55BCD BC CD S EC BD BD ⋅⋅⋅====△即C 的半径为255． ∵P 在C 上.∴P 点的轨迹方程为224(2)(1)5x y -+-=. 设P 点坐标00(,)x y ，可以设出P 点坐标满足的参数方程如下:00225cos 5215sin 5x y θθ⎧=+⎪⎪⎨⎪=+⎪⎩而00(,)AP x y =,(0,1)AB =，(2,0)AD =. ∵(0,1)(2,0)(2,)AP AB AD λμλμμλ=+=+= ∴0151cos 25x μθ==+,0215sin 5y λθ==+． 两式相加得:222515sin 1cos 552552()()sin()552sin()3λμθθθϕθϕ+=+++=+++=++≤ (其中5sin 5ϕ=，25cos 5ϕ=) 当且仅当π2π2k θϕ=+-，k ∈Z 时，λμ+取得最大值3.１１.（2017课标全国Ⅲ，理2０)(１2分)已知抛物线C ：ｙ2=２x ，过点(2,0)的直线l 交C 与A ，B 两点,圆Ｍ是以线段ＡＢ为直径的圆．()A O DxyB PCE(1）证明：坐标原点Ｏ在圆M 上;(２)设圆M 过点P （４，-2）,求直线l 与圆Ｍ的方程． 解：（1）设()()11222A x ,y ,B x ,y ,l :x my =+由222x my y x =+⎧⎨=⎩可得212240则4y my ,y y --==- 又()22212121212==故=224y y y y x ,x ,x x =4因此OA 的斜率与OB 的斜率之积为1212-4==-14y y x x 所以OA ⊥O Ｂ故坐标原点Ｏ在圆M 上.(2)由（1)可得()2121212+=2+=++4=24y y m,x x m y y m + 故圆心M 的坐标为()2+2，m m ,圆Ｍ的半径()2222r m m =++由于圆Ｍ过点P （4,-2）,因此0AP BP =,故()()()()121244220x x y y --+++= 即()()121212124+2200x x x x y y y y -++++= 由(１）可得1212=-4，=4y y x x ，所以2210m m --=，解得11或2m m ==-.当m=1时,直线l 的方程为x-y-2=0,圆心M 的坐标为(3,1)，圆Ｍ的半径为10,圆Ｍ的方程为()()223110x y -+-=当12m =-时,直线l 的方程为240x y +-=，圆心M 的坐标为91，-42⎛⎫⎪⎝⎭，圆M 的半径为854，圆M 的方程为229185++4216x y ⎛⎫⎛⎫-= ⎪ ⎪⎝⎭⎝⎭12.(2016课标全国Ⅰ,理5)已知方程132222=--+nm y n m x 表示双曲线，且该双曲线两焦点间的距离为4,则n 的取值范围是(A ）)3,1(-ﻩﻩ（B ）)3,1(-(C ）)3,0( ﻩ(D))3,0(432112344224xEDABC【解析】：222213x y m n m n-=+-表示双曲线，则()()2230m n m n +->,∴223m n m -<<由双曲线性质知:()()222234c m n m n m =++-=,其中c 是半焦距,∴焦距2224c m =⋅=，解得1m =∴13n -<<，故选Ａ.13.（２０16课标全国Ⅰ，理１0）以抛物线C 的顶点为圆心的圆交C 于B A ,两点，交C 的准线于E D ,两点,已知24=AB ，52=DE ，则C 的焦点到准线的距离为（A ）2 ﻩ(B ）4 ﻩ(Ｃ）６ﻩﻩ （Ｄ）8【解析】：以开口向右的抛物线为例来解答，其他开口同理设抛物线为22y px =()0p >，设圆的方程为222x y r +=，如图：设()0,22A x ，,52pD ⎛⎫- ⎪⎝⎭,点()0,22A x 在抛物线22y px =上，∴082px =……①；点,52pD ⎛⎫- ⎪⎝⎭在圆222x y r +=上,∴2252p r ⎛⎫+= ⎪⎝⎭……②;点()0,22A x 在圆222x y r +=上，∴2208x r +=……③;联立①②③解得:4p =， 焦点到准线的距离为4p =.故选Ｂ.14.(2０1６课标全国Ⅰ,理２0)（本小题满分1２分)设圆015222=-++x y x 的圆心为A ，直线l 过点)0,1(B 且与x 轴不重合,l 交圆A 于D C ,两点，过B 作AC 的平行线交AD 于点E .(Ⅰ）证明EB EA +为定值，并写出点E 的轨迹方程; ﻩ(Ⅱ）设点E 的轨迹为曲线1C ,直线l 交1C 于N M ,两点，过B 且与l 垂直的直线与圆A 交于Q P ,两点,求四边形MPNQ 面积的取值范围.【解析】：⑴圆A 整理为()22116x y ++=,A 坐标()1,0-，如图,BE AC ∥，则C EBD =∠∠,由,AC AD D C ==则∠∠， EBD D ∴=∠∠，则EB ED=，4||AE EB AE ED AD AB ∴+=+==>根据椭圆定义为一个椭圆,方程为22143x y +=，(0y ≠);F4 32112344224xQPNMAB()()2222222363634121||1||13434M Nm m mMN m y y mm m+++=+-=+=++⑵221:143x yC+=ﻩ；设:1l x my=+，因为PQ l⊥，设():1PQ y m x=--,联立1l C与椭圆:221143x myx y=+⎧⎪⎨+=⎪⎩()2234690m y my++-=，则圆心A到PQ距离()22|11||2|11m mdm m---==++，所以2222224434||2||21611m mPQ AQ dm m+=-=-=++,())2222222121114342411||||2412,831223413431MPNQm m mS MN PQm m mm+++⎡∴=⋅=⋅⋅==∈⎣+++++15.（2０1６课标全国Ⅱ,理4)圆2228130x y x y+--+=的圆心到直线10ax y+-=的距离为1，则a=（）（A）43-（B）34-(C）3(D）２16.(２01６课标全国Ⅱ,理１１）已知12,F F是双曲线2222:1x yEa b-=的左,右焦点,点M在E上,1MF与x轴垂直,211sin3MF F∠=,则E的离心率为( )(A）2（B）32(C）3(Ｄ)２１７.（20１６课标全国Ⅱ，理20）(本小题满分１2分）已知椭圆:E 2213x y t +=的焦点在x 轴上，A 是E 的左顶点,斜率为(0)k k >的直线交E 于,A M 两点,点N 在E 上，MA NA ⊥．(Ⅰ）当4,||||t AM AN ==时,求AMN ∆的面积;(Ⅱ)当2AM AN =时，求k 的取值范围．【答案】（Ⅰ)；（Ⅱ).【解析】试题分析:（Ⅰ)先求直线的方程，再求点的纵坐标,最后求的面积;(Ⅱ）设，，将直线的方程与椭圆方程组成方程组,消去，用表示，从而表示,同理用表示，再由求.试题解析：(I)设，则由题意知，当时,的方程为,.由已知及椭圆的对称性知,直线的倾斜角为.因此直线的方程为.将代入得.解得或，所以.因此的面积．(ＩI)由题意，，.将直线的方程代入得.由得，故.由题设,直线的方程为,故同理可得，由得，即.当时上式不成立，因此.等价于,即.由此得，或，解得.因此的取值范围是．考点：椭圆的性质,直线与椭圆的位置关系.18.(2016课标全国Ⅲ，理11)已知O 为坐标原点，F 是椭圆C ：22221(0)x y a b a b +=>>的左焦点,,A B分别为C 的左，右顶点.P 为C 上一点，且PF x ⊥轴.过点A 的直线l 与线段PF 交于点M ,与y 轴交于点E ．若直线BM 经过OE 的中点,则C 的离心率为（ )（A ）13 ﻩﻩ（B ）12 ﻩ（C ）23 ﻩ（D)34【答案】A考点:椭圆方程与几何性质.【思路点拨】求解椭圆的离心率问题主要有三种方法:（1)直接求得,a c 的值，进而求得e 的值;(２)建立,,a b c 的齐次等式,求得ba 或转化为关于e 的等式求解；（3)通过特殊值或特殊位置，求出e .1９.(２０１6课标全国Ⅲ，理1６)已知直线l :330mx y m ++-=与圆2212x y +=交于,A B 两点，过,A B 分别做l 的垂线与x 轴交于,C D 两点,若23AB =,则||CD =_＿＿_＿_＿____＿____＿_.【答案】4考点:直线与圆的位置关系．【技巧点拨】解决直线与圆的综合问题时，一方面,要注意运用解析几何的基本思想方法（即几何问题代数化),把它转化为代数问题；另一方面,由于直线与圆和平面几何联系得非常紧密,因此，准确地作出图形，并充分挖掘几何图形中所隐含的条件,利用几何知识使问题较为简捷地得到解决.２0.(20１6课标全国Ⅲ，理20)(本小题满分12分）已知抛物线C :22y x =的焦点为F ,平行于x 轴的两条直线12,l l 分别交C 于,A B 两点,交C 的准线于P Q ，两点．（Ｉ)若F 在线段AB 上，R 是PQ 的中点，证明AR FQ ；（ＩI ）若PQF ∆的面积是ABF ∆的面积的两倍,求AB 中点的轨迹方程.【答案】(Ⅰ)见解析；（Ⅱ)21y x =-.试题解析:由题设)0,21(F .设b y l a y l ==:,:21，则0≠ab ，且)2,21(),,21(),,21(),,2(),0,2(22b a R b Q a P b b B a A +---.记过B A ,两点的直线为l ，则l 的方程为0)(2=++-ab y b a x ． .....3分 （Ⅰ）由于F 在线段AB 上，故01=+ab .记AR 的斜率为1k ，FQ 的斜率为2k ,则222111k b a ab a ab a b a a b a k =-=-==--=+-=，所以AR FQ . ．.．.．.5分（Ⅱ)设l 与x 轴的交点为)0,(1x D ，则2,2121211b a S x a b FD a b S PQF ABF -=--=-=∆∆. 由题设可得221211b a x a b -=--，所以01=x （舍去)，11=x . 设满足条件的AB 的中点为),(y x E ． 当AB 与x 轴不垂直时，由DE ABk k =可得)1(12≠-=+x x yb a .而y ba =+2,所以)1(12≠-=x x y .当AB 与x 轴垂直时，E 与D 重合，所以，所求轨迹方程为12-=x y . ...．１2分 考点:1、抛物线定义与几何性质;2、直线与抛物线位置关系；3、轨迹求法.【方法归纳】(１)解析几何中平行问题的证明主要是通过证明两条直线的斜率相等或转化为利用向量证明;（2）求轨迹的方法在高考中最常考的是直接法与代入法(相关点法）,利用代入法求解时必须找准主动点与从动点.2１.(2015课标全国Ⅰ,理5) 已知00(,)M x y 是双曲线22:12x C y -=上的一点,12,F F 是C 的两个焦点,若120MF MF ⋅<,则0y 的取值范围是（Ａ)33(,)33-(B) 33(,)66- (C) 2222(,)33- （D)2323(,)33-答案：A解析：由条件知F１(－，０),Ｆ2（，0),＝（－-x0,－y０)，＝（-x0,－y０)，－3<０．ﻩ①又＝1，＝2＋2.代入①得，∴-<y0<２2.(2015课标全国Ⅰ,理１4)一个圆经过椭圆221164x y+=的三个顶点，且圆心在x轴的正半轴上,则该圆的标准方程为答案:+y2＝解析:由条件知圆经过椭圆的三个顶点分别为（4,0),（0，2),(0，－2),设圆心为(ａ，0)（ａ>0)，所以=４－a，解得a=，故圆心为,此时半径ｒ＝4－,因此该圆的标准方程是+ｙ2=23.(2015课标全国Ⅰ,理20）在直角坐标系xOy中,曲线2:4xC y=与直线:(0)l y kx a a=+>交于,M N两点。
2011全国卷1理科数学试题及解析
2011年普通高等学校招生全国统一考试理科数学(全国卷Ⅰ)一、选择题:本大题共12小题,每小题5分,共60分、 1、复数212ii+-的共轭复数就是( ) A 、35i - B 、35i C 、i - D 、i 2、下列函数中,既就是偶函数又在+∞（0，）单调递增的函数就是( ) A 、3y x = B 、1y x =+ C 、21y x =-+ D 、2xy -=3、执行右面的程序框图,如果输入的N 就是6, 那么输出的p 就是( ) A 、120 B 、720 C 、1440 D 、50404、有3个兴趣小组,甲、乙两位同学各自参加其中一个小组,每位同学参加各个小组的可能性相同,则这两位同学参加同一个兴趣小组的概率为( ) A 、13 B 、12 C 、23 D 、345、已知角θ的顶点与原点重合,始边与x 轴的正半轴重合, 终边在直线2y x =上,则cos2θ=( ) A 、45-B 、35-C 、35D 、456、在一个几何体的三视图中,正视图与俯视图如右图所示, 则相应的俯视图可以为( )7、设直线L 过双曲线C 的一个焦点,且与C 的一条对称轴垂直,L 与C 交于 A ,B 两点,AB 为C 的实轴长的2倍,则C 的离心率为( )A B C 、2 D 、38、512a x x x x ⎛⎫⎛⎫+- ⎪⎪⎝⎭⎝⎭的展开式中各项系数的与为2,则该展开式中常数项为( )A 、-40B 、-20C 、20D 、409、由曲线y =,直线2y x =-及y 轴所围成的图形的面积为( )A 、103 B 、4 C 、163D 、6 10、已知a 与b 均为单位向量,其夹角为θ,有下列四个命题12:10,3P a b πθ⎡⎫+>⇔∈⎪⎢⎣⎭ 22:1,3P a b πθπ⎛⎤+>⇔∈⎥⎝⎦3:10,3P a b πθ⎡⎫->⇔∈⎪⎢⎣⎭ 4:1,3P a b πθπ⎛⎤->⇔∈ ⎥⎝⎦其中的真命题就是( )A 、14,P PB 、13,P PC 、23,P PD 、24,P P 11、设函数()sin()cos()(0,)2f x x x πωϕωϕωϕ=+++><的最小正周期为π,且()()f x f x -=,则( )A 、()f x 在0,2π⎛⎫ ⎪⎝⎭单调递减 B 、()f x 在3,44ππ⎛⎫⎪⎝⎭单调递减 C 、()f x 在0,2π⎛⎫ ⎪⎝⎭单调递增 D 、()f x 在3,44ππ⎛⎫⎪⎝⎭单调递增 12、函数11y x =-的图像与函数2sin (24)y x x π=-≤≤的图像所有交点的横坐标之与等于( ) A 、2 B 、 4 C 、6 D 、8二、填空题:本大题共4小题,每小题5分、13、若变量,x y 满足约束条件329,69,x y x y ≤+≤⎧⎨≤-≤⎩则2z x y =+的最小值为 、14、在平面直角坐标系xOy 中,椭圆C 的中心为原点,焦点12,F F 在x 轴上,离心率为2、过1F 的直线L 交C 于,A B 两点,且2ABF 的周长为16,那么C 的方程为 、15、已知矩形ABCD 的顶点都在半径为4的球O 的球面上,且6,AB BC ==,则棱锥O ABCD -的体积为 、16、在ABC 中,60,B AC ==则2AB BC +的最大值为 、三、解答题:解答应写出文字说明,证明过程或演算步骤、 17、(本小题满分12分)等比数列{}n a 的各项均为正数,且212326231,9.a a a a a +==(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)设 31323log log ......log ,n n b a a a =+++求数列1n b ⎧⎫⎨⎬⎩⎭的前n 项与、18、(本小题满分12分)如图,四棱锥P-ABCD 中,底面ABCD 为平行四边形,∠DAB=60°,AB=2AD ,PD ⊥底面ABCD 、(Ⅰ)证明:P A ⊥BD ;(Ⅱ)若PD =AD ,求二面角A-PB-C 的余弦值、某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品,现用两种新配方(分别称为A配方与B配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:(Ⅰ)分别估计用A配方,B配方生产的产品的优质品率;(Ⅱ)已知用B配方生成的一件产品的利润y(单位:元)与其质量指标值t的关系式为2,942,941024,102ty tt-<⎧⎪=≤<⎨⎪≥⎩, 从用B配方生产的产品中任取一件,其利润记为X(单位:元),求X的分布列及数学期望、(以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率)在平面直角坐标系xOy 中,已知点A(0,-1),B 点在直线y = -3上,M 点满足//MB OA , MA AB MB BA ⋅=⋅,M 点的轨迹为曲线C 、 (Ⅰ)求C 的方程;(Ⅱ)P 为C 上的动点,l 为C 在P 点处得切线,求O 点到l 距离的最小值、21、(本小题满分12分)已知函数ln ()1a x bf x x x=++,曲线()y f x =在点(1,(1))f 处的切线方程为230x y +-=、 (Ⅰ)求a 、b 的值;(Ⅱ)如果当0x >,且1x ≠时,ln ()1x kf x x x>+-,求k 的取值范围、请考生在第22、23、24题中任选一题做答,如果多做,则按所做的第一题记分、做答时请写清题号、 22、(本小题满分10分)选修4-1:几何证明选讲如图,D ,E 分别为ABC ∆的边AB ,AC 上的点,且不与ABC ∆的顶点重合、已知AE 的长为n ,AD ,AB 的长就是关于x 的方程2140x x mn -+=的两个根、(Ⅰ)证明:C ,B ,D ,E 四点共圆;(Ⅱ)若90A ∠=︒,且4,6m n ==,求C ,B ,D ,E 所在圆的半径、23、(本小题满分10分)选修4-4:坐标系与参数方程在直角坐标系xOy 中,曲线C 1的参数方程为2cos 22sin x y αα=⎧⎨=+⎩(α为参数)M 就是C 1上的动点,P 点满足2OP OM =,P 点的轨迹为曲线C 2 (Ⅰ)求C 2的方程(Ⅱ)在以O 为极点,x 轴的正半轴为极轴的极坐标系中,射线3πθ=与C 1的异于极点的交点为A ,与C 2的异于极点的交点为B ,求AB 、24、(本小题满分10分)选修4-5:不等式选讲设函数()3f x x a x =-+,其中0a >、 (Ⅰ)当1a =时,求不等式()32f x x ≥+的解集; (Ⅱ)若不等式()0f x ≤的解集为{}|1x x ≤- ,求a 的值、2011年普通高等学校招生全国统一考试理科数学试卷参考答案一、选择题(1)C (2)B (3)B (4)A (5)B (6)D (7)B (8)D (9)C (10)A (11)A (12)D 二、填空题(13)-6 (14)221168x y +=(15)三、解答题 (17)解:(Ⅰ)设数列{a n }的公比为q,由23269a a a =得32349a a =所以219q =。
新课标全国卷理科数学分类汇编立体几何
2011年—2017年新课标高考全国Ⅰ卷理科数学分类汇编（含答案）8．立体几何【2017，7】某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形，该多面体的各个面中有若干个是梯形，这些梯形的面积之和为（ ） A ．10 B ．12 C ．14 D ．16【2016，11】平面α过正方体1111D C B A ABCD -的顶点A ，//α平面11D CB ，αI 平面ABCD m =，I α平面n A ABB =11，则n m ,所成角的正弦值为（ ）（A ）23 （B ）22 （C ）33 （D ）31 【2016，6】如图，某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径．若该几何体的体积是328π，则它的表面积是（ ） （A ）π17 （B ）π18 （C ）π20 （D ）π28【2015，6】《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺.问：积及为米几何？”其意思为：“在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一），米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放的米约有（A ）14斛 （B ）22斛 （C ）36斛 （D ）66斛 【2015，11】圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体，该几何体三视图中的正视图和俯视图如图所示. 若该几何体的表面积为1620π+，则r =（ ）（A ）1 （B ）2 （C ）4 （D ）8【2014，12】如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的个条棱中，最长的棱的长度为A .62B .42C .6D .4【2013，6】如图，有一个水平放置的透明无盖的正方体容器，容器高8 cm ，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6 cm ，如果不计容器的厚度，则球的体积为( )．A ．500π3cm 3B ．866π3cm 3C ．1372π3cm 3D ．2048π3cm 3【2013，8】某几何体的三视图如图所示，则该几何体的体积为( )．A ．16＋8πB ．8＋8πC ．16＋16πD ．8＋16π【2012，7】如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为A ．6B ．9C ．12D ．15【2012，11】已知三棱锥S －ABC 的所有顶点都在球O 的球面上，△ABC 是边长为1的正三角形，SC 为球O 的直径，且SC =2，则此棱锥的体积为（ ） A ．26B ．36C ．23D ．22【2011，6】在一个几何体的三视图中，正视图和俯视图如右图所示，则相应的侧视图可以为（ ）二、填空题【2011，15】已知矩形ABCD 的顶点都在半径为4的球O 的球面上，且6,23AB BC ==,则棱锥O ABCD -的体积为 。
(含详解)2011-2017新课标1卷理科数学分类汇编(立体几何)(K12教育文档)
(含详解)2011-2017新课标1卷理科数学分类汇编(立体几何)(word版可编辑修改)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（(含详解)2011-2017新课标1卷理科数学分类汇编(立体几何)(word版可编辑修改)）的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为(含详解)2011-2017新课标1卷理科数学分类汇编(立体几何)(word版可编辑修改)的全部内容。
立体几何20177．某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2,俯视图为等腰直角三角形。
该多面体的各个面中有若干个是梯形，这些梯形的面积之和为A．10 B．12 C．14 D．1616．如图，圆形纸片的圆心为O，半径为5 cm,该纸片上的等边三角形ABC的中心为O.D、E、F 为圆O上的点，△DBC，△ECA，△FAB分别是以BC,CA，AB为底边的等腰三角形.沿虚线剪开后，分别以BC，CA,AB为折痕折起△DBC，△ECA，△FAB，使得D、E、F重合，得到三棱锥.当△ABC的边长变化时，所得三棱锥体积（单位：cm3)的最大值为_______.18.（12分）如图，在四棱锥P—ABCD中，AB//CD,且90BAP CDP∠=∠=。
（1）证明：平面PAB⊥平面PAD；（2）若PA=PD=AB=DC,90APD∠=，求二面角A-PB-C的余弦值.2016(6)如图，某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是283π，则它的表面积是（A）17π（B)18π（C)20π(D）28π(11）平面a过正方体ABCD—A1B1C1D1的顶点A,a//平面CB1D1,a⋂平面ABCD=m，a⋂平面ABB1A1=n，则m、n所成角的正弦值为（A)32（B)22(C）33(D)13（18）(本题满分为12分）如图，在以A，B,C，D,E，F为顶点的五面体中，面ABEF为正方形,AF=2FD，90AFD∠=，且二面角D-AF—E与二面角C-BE-F都是60．(I）证明：平面ABEF⊥EFDC；（II）求二面角E—BC—A的余弦值．20156、《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题:“今有委米依垣内角，下周八尺，高五尺,问”积及为米几何？"其意思为：“在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一），米堆底部的弧长为8尺,米堆的高为5尺，米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1。
2011—2017年新课标全国卷1理科数学分类汇编 三角函数、解三角形
4．三角函数、解三角形一、选择题【2017，9】已知曲线C 1：y =cos x ，C 2：y =sin (2x +2π3)，则下面结正确的是（ ） A ．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C 2B ．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C 2C ．把C 1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C 2D ．把C 1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C 2【2016，12】已知函数)2,0)(sin()(πϕωϕω≤>+=x x f ，4π-=x 为)(x f 的零点，4π=x 为)(x f y =图像的对称轴，且)(x f 在)365,18(ππ单调，则ω的最大值为（ ）A ．11B ．9C ．7D ．5【2015，8】函数()f x =cos()x ωϕ+的部分图象如图所示，则()f x 的单调递减区间为（ ）A ．13(,),44k k k ππ-+∈Z 错误!未找到引用源。
B ．13(2,2),44k k k ππ-+∈Z 错误!未找到引用源。
C ．13(,),44k k k -+∈ZD ．13(2,2),44k k k -+∈Z【2015，2】sin 20cos10cos160sin10-=（ ）A ．32-B ．32C ．12-D ．12【2014，6】如图，圆O 的半径为1，A 是圆上的定点，P 是圆上的动点，角x 的始边为射线OA ，终边为射线OP ，过点P 作直线OA 的垂线，垂足为M ，将点M 到直线OP 的距离表示为x 的函数()f x ，则y =()f x 在[0,π]上的图像大致为（ ）【2014，8】设(0,)2πα∈，(0,)2πβ∈，且1sin tan cos βαβ+=，则（ ） A ．32παβ-=B ．22παβ-=C ．32παβ+=D ．22παβ+=【2012，9】已知0ω>，函数()sin()4f x x πω=+在（2π，π）上单调递减，则ω的取值范围是（ ）A ．[12，54] B ．[12，34] C ．（0，12] D ．（0，2]【2011，5】已知角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线2y x =上，则cos2θ=A ．45-B ．35-C ．35D ．45【2011，11】设函数()sin()cos()(0,)2f x x x πωϕωϕωϕ=+++><的最小正周期为π，且()()f x f x -=，则（ ）A ．()f x 在0,2π⎛⎫⎪⎝⎭单调递减 B ．()f x 在3,44ππ⎛⎫⎪⎝⎭单调递减 C ．()f x 在0,2π⎛⎫⎪⎝⎭单调递增 D ．()f x 在3,44ππ⎛⎫⎪⎝⎭单调递增 二、填空题【2015，16】在平面四边形ABCD 中，75A B C ∠=∠=∠=，2BC =，则AB 的取值范围是 ． 【2014，16】已知,,a b c 分别为ABC ∆的三个内角,,A B C 的对边，a =2，且(2)(sin sin )()sin b A B c b C +-=-，则ABC ∆面积的最大值为 ． 【2013，15】设当x ＝θ时，函数f (x )＝sin x －2cos x 取得最大值，则cos θ＝__________． 【2011，16】在ABC 中，60,3B AC ==2AB BC +的最大值为 ． 三、解答题【2017，17】△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知△ABC 的面积为23sin a A（1）求sin B sin C ；（2）若6cos B cos C =1,a =3,求△ABC 的周长【2016，17】ABC ∆的内角C B A ,,的对边分别为c b a ,,，已知c A b B a C =+)cos cos (cos 2． （Ⅰ）求C ；（Ⅱ）若7=c ，ABC ∆的面积为233，求ABC ∆的周长．【2013，17】如图，在△ABC 中，∠ABC ＝90°，AB ，BC ＝1，P 为△ABC 内一点，∠BPC ＝90°．(1)若PB ＝12，求P A ；(2)若∠APB ＝150°，求tan ∠PBA ．【2012，17】已知a ，b ，c 分别为△ABC 三个内角A ，B ，C 的对边，cos sin 0a C C b c --=．（1）求A ；（2）若2a =，△ABC b ，c ．3．三角函数、解三角形（解析版）一、选择题【2017，9】已知曲线C 1：y =cos x ，C 2：y =sin (2x +2π3)，则下面结正确的是（ ） A ．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C 2B ．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C 2C ．把C 1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C 2D ．把C 1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C 2【解析】1:cos C y x =，22π:sin 23⎛⎫=+ ⎪⎝⎭C y x ，首先曲线1C 、2C 统一为一三角函数名，可将1:cos C y x =用诱导公式处理．πππcos cos sin 222⎛⎫⎛⎫==+-=+ ⎪ ⎪⎝⎭⎝⎭y x x x ．横坐标变换需将1=ω变成2=ω，即112πππsin sin 2sin 2224⎛⎫⎛⎫⎛⎫=+−−−−−−−−−→=+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭C 上各坐短它原y x y x x 点横标缩来2ππsin 2sin 233⎛⎫⎛⎫−−→=+=+ ⎪ ⎪⎝⎭⎝⎭y x x ． 注意ω的系数，在右平移需将2=ω提到括号外面，这时π4+x 平移至π3+x ， 根据“左加右减”原则，“π4+x ”到“π3+x ”需加上π12，即再向左平移π12．故选D ； 【2016，12】已知函数)2,0)(sin()(πϕωϕω≤>+=x x f ，4π-=x 为)(x f 的零点，4π=x 为)(x f y =图像的对称轴，且)(x f 在)365,18(ππ单调，则ω的最大值为（ ）A ．11B ．9C ．7D ．5【解析】：由题意知：12π+π 4ππ+π+42k k ωϕωϕ⎧-=⎪⎪⎨⎪=⎪⎩则21k ω=+，其中k ∈Z ，()f x 在π5π,1836⎛⎫⎪⎝⎭单调，5π,123618122T ππω∴-=≤≤，接下来用排除法：若π11,4ωϕ==-，此时π()sin 114f x x ⎛⎫=- ⎪⎝⎭，()f x 在π3π,1844⎛⎫ ⎪⎝⎭递增，在3π5π,4436⎛⎫ ⎪⎝⎭递减，不满足()f x 在π5π,1836⎛⎫⎪⎝⎭单调；若π9,4ωϕ==，此时π()sin 94f x x ⎛⎫=+ ⎪⎝⎭，满足()f x 在π5π,1836⎛⎫⎪⎝⎭单调递减．故选B ．【2015，8】函数()f x =cos()x ωϕ+的部分图象如图所示，则()f x 的单调递减区间为（ ）A ．13(,),44k k k ππ-+∈Z 错误!未找到引用源。
(2011-2017)高考试题新课标理科数学分类汇编(精校版)
§ 1 . 集合及其运算1 . （ 201 7 ·2 ）设集合，．若，则（）A ．B ．C ．D ．2 . （ 201 6 · 2 ）已知集合 A ={1 ， 2 ， 3} ， B ={ x |( x +1)( x - 2)<0 ，x ∈ Z } ，则（）A ． {1}B ． {1 ， 2}C ． {0 ， 1 ， 2 ， 3}D ． { - 1 ， 0 ， 1 ， 2 ， 3}3 . （ 2015· 1 ）已知集合 A = { - 2 ， - 1 ， 0 ， 2 } ， B = { x | ( x - 1 )( x +2 )< 0 } ，则A ∩ B = （）A ． { - 1 ， 0 }B ． {0 ， 1 }C ． { - 1 ， 0 ， 1 }D ． {0 ， 1 ， 2 }4 . （ 201 4 · 1 ）设集合 M = { 0, 1, 2 } ， N = ，则= （）A ． {1}B ． {2}C ． {0 ， 1}D ． {1 ， 2}5 . （ 201 3 · 1 ）已知集合 M = { x| ( x - 1) 2 < 4, x ∈ R } ， N = { - 1 ， 0 ， 1 ， 2 ，3 } ，则M ∩ N = （）A . { 0 , 1 , 2 }B . { - 1 , 0 , 1 , 2 }C . { - 1 , 0 , 2 , 3}D . {0 , 1 , 2 , 3}6 . （ 2012·1 ）已知集合 A ={1, 2, 3, 4, 5} ，B ={( x , y )| x ∈ A , y ∈ A , x - y ∈A } ，则B 中所含元素的个数为（）A. 3B. 6C. 8D. 10§ 2 . 复数计算1 . （ 201 7 · 1 ）（）A ．B ．C ．D ．2 . （ 201 6 · 1 ）已知在复平面内对应的点在第四象限，则实数m 的取值范围是 ( )A ．（ - 3 ， 1 ）B ．（ - 1 ， 3 ）C ．（ 1 ，+∞ ）D ．（ - ∞ ， - 3 ）3 . （ 2015· 2 ）若 a 为实数且 ( 2+ ai )( a - 2 i ) = -4 i ，则 a = （）A ． - 1B ． 0C ． 1D ． 24 . （ 201 4 · 2 ）设复数，在复平面内的对应点关于虚轴对称，，则（）A ． - 5B ． 5C ． - 4 + iD ． - 4 - i5 . （ 201 3 · 2 ）设复数满足，则（）A .B .C .D .6 . （ 2012·3 ）下面是关于复数的四个命题中，真命题为（）P 1 : | z |=2 ， P 2 : z 2 =2 i ， P 3 : z 的共轭复数为 1+ i ， P 4 : z 的虚部为- 1 .A. P 2 ， P 3B. P 1 ， P 2C. P 2 ， P 4D. P 3 ， P 47 . （ 201 1 · 1 ）复数的共轭复数是（）A ．B ．C ．D ．§ 3 . 简易逻辑1 . （ 201 7 · 7 ）甲、乙、丙、丁四位同学一起去问老师询问成语竞赛的成绩．老师说：你们四人中有2 位优秀， 2 位良好，我现在给甲看乙、丙的成绩，给乙看丙的成绩，给丁看甲的成绩．看后甲对大家说：我还是不知道我的成绩．根据以上信息，则（）A ．乙可以知道四人的成绩B ．丁可以知道四人的成绩C ．乙、丁可以知道对方的成绩D ．乙、丁可以知道自己的成绩2. （ 201 1 · 10 ）已知 a 与 b 均为单位向量，其夹角为θ，有下列四个命题中真命题是（）A ． P 1 ， P 4B ． P 1 ， P 3C ． P 2 ， P 3D ． P 2 ， P 43 . （ 201 6 · 15 ）有三张卡片，分别写有 1 和 2 ， 1 和 3 ， 2 和 3 . 甲，乙，丙三人各取走一张卡片，甲看了乙的卡片后说：“ 我与乙的卡片上相同的数字不是2 ” ，乙看了丙的卡片后说：“ 我与丙的卡片上相同的数字不是1 ” ，丙说：“ 我的卡片上的数字之和不是5 ” ，则甲的卡片上的数字是 .§ 4 . 平面向量1 . （ 201 7 · 12 ）已知△ ABC 是边长为 2 的等边三角形， P 为平面 ABC 内一点，则的最小值是（）A. B. C. D.2 . （ 201 6 ·3 ）已知向量，且，则 m = （）A ． - 8B ． - 6C ． 6D ． 83 . （ 2014 · 3 ）设向量满足，，则= （）A ． 1B ． 2C ． 3D ． 54 . （ 2015· 13 ）设向量 a ， b 不平行，向量与平行，则实数=____________ ．5 . （ 201 3 · 13 ）已知正方形的边长为 2 ，为的中点，则_______.6 . （ 2012·13 ）已知向量 a ， b 夹角为 45 º，且，，则 .§ 5 . 程序框图1 . （ 201 7 · 8 ）执行右面的程序框图，如果输入的 a = - 1 ，则输出的 S = （）A ． 2B ． 3C ． 4D ． 52 . （ 201 6 · 8 ）中国古代有计算多项式值的秦九韶算法，右图是实现该算法的程序框图．执行该程序框图，若输入的 x =2 ， n =2 ，依次输入的 a 为2 ， 2 ， 5 ，则输出的 s = （）A ． 7B ． 12C ． 17D ． 343 . （ 2015· 8 ）右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术” . 执行该程序框图，若输入 a ， b 分别为 14 ， 18 ，则输出的 a = （）A ． 0B ． 2C ． 4D ． 144 . （ 201 4 · 7 ）执行右面程序框图，如果输入的 x ， t 均为 2 ，则输出的 S = （）A ． 4B ． 5C ． 6D ． 75 . （ 201 3 ·6 ）执行右面的程序框图，如果输入的，那么输出的（）A .B .C .D .6 . （ 2012·6 ）如果执行右边的程序框图，输入正整数 N （ N ≥2 ）和实数 a 1 ， a 2 ，… ， a N ，输入 A 、 B ，则（）A. A + B 为 a 1 ， a 2 ，… ， a N 的和B. 为 a 1 ， a 2 ，… ， a N 的算术平均数C. A 和 B 分别是 a 1 ， a 2 ，… ， a N 中最大的数和最小的数D. A 和 B 分别是 a 1 ， a 2 ，… ， a N 中最小的数和最大的数7 . （ 201 1 · 3 ）执行右面的程序框图，如果输入的 N 是 6 ，那么输出的 p 是（）A ． 120B ． 720C ． 1440D ． 5040§ 6 . 线性规划1 . （ 201 7 · 5 ）设，满足约束条件，则的最小值是（）A ． - 15B ． - 9C ． 1D ． 92 . （ 201 4 · 9 ）设 x ， y 满足约束条件，则的最大值为（）A ． 10B ． 8C ． 3D ． 23 . （ 201 3 · 9 ）已知， x ， y 满足约束条件，若的最小值为 1 ，则 a = （）A .B .C . 1D . 24 . （ 2015· 14 ）若 x ， y 满足约束条件，则的最大值为_______ ．5 . （ 201 4 · 14 ）设 x ， y 满足约束条件，则的取值范围为 .6 . （ 201 1 · 13 ）若变量 x ， y 满足约束条件，则的最小值为 .§ 7 . ※二项式定理1 . （ 201 3 · 5 ）已知的展开式中的系数为 5 ，则（）A .B .C .D .2 . （ 201 1 · 8 ）的展开式中各项系数的和为 2 ，则该展开式中常数项为（）A ． - 40B ． - 20C ． 20D ． 403 . （ 2015· 15 ）的展开式中 x 的奇数次幂项的系数之和为 32 ，则 a =_______ ．4 . （ 201 4 · 13 ）的展开式中，的系数为 15 ，则 a =________.§ 8 . 数列1. （ 201 7 · 3 ）我国古代数学名著《算法统宗》中有如下问题：“ 远望巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯？” 意思是：一座 7 层塔共挂了 381 盏灯，且相邻两层中的下一层灯数是上一层灯数的 2 倍，则塔的顶层共有灯（）A ． 1 盏B ． 3 盏C ． 5 盏D ． 9 盏2 . （ 2015· 4 ）已知等比数列 { a n } 满足 a 1 =3 ， a 1 + a 3 + a 5 =21 ，则 a 3 + a5 + a 7 = （）A ． 21B ． 42C ． 63D ． 843 . （ 201 3 · 3 ）等比数列的前项和为，已知，，则（）A .B .C .D .4 . （ 2012·5 ）已知 { a n } 为等比数列， a 4 + a 7 = 2 ， a 5 a6 = - 8 ，则 a 1 +a 10 = （）A. 7B. 5C. - 5D. - 75 . （ 201 7 · 15 ）等差数列的前项和为，，，则．6 . （ 2015· 16 ）设 S n 是数列 { a n } 的前项和，且，，则 S n= ．7 . （ 201 3 · 16 ）等差数列的前项和为，已知，，则的最小值为 ___ _.8 . （ 2012·16 ）数列满足，则的前 60 项和为 .9 . （ 201 6 · 17 ） S n 为等差数列 { a n } 的前 n 项和，且 a 1 =1 ， S 7 =28 . 记 b n=[lg a n ] ，其中 [ x ] 表示不超过 x 的最大整数，如 [0.9]=0 ， [lg99]=1 .（Ⅰ）求 b 1 ， b 11 ， b 101 ；（Ⅱ）求数列 { b n } 的前 1 000 项和 .10 . （ 201 4 ·1 7 ）已知数列 { a n } 满足 a 1 =1 ， a n +1 =3 a n +1.（Ⅰ）证明是等比数列，并求 { a n } 的通项公式；（Ⅱ）证明：.11 . （ 201 1 · 17 ）等比数列的各项均为正数，且（Ⅰ）求数列的通项公式；（Ⅱ）设，求数列的前 n 项和 .§ 9 . 三角函数1 . （ 201 6 · 7 ）若将函数 y =2sin2 x 的图像向左平移个单位长度，则平移后图象的对称轴为（）A ．B ．C ．D ．2 . （ 201 6 · 9 ）若，则sin 2 α = （）A ．B ．C ．D ．3 . （ 2014 · 4 ）钝角三角形 ABC 的面积是， AB =1 ， BC = ，则 AC = （）A ． 5B ．C ． 2D ． 14 . （ 2012·9 ）已知，函数在单调递减，则的取值范围是（）A. B. C. D.5 . （ 201 1 · 5 ）已知角θ的顶点与原点重合，始边与 x 轴的正半轴重合，终边在直线 y =2 x 上，则 cos2 θ = （）A ．B ．C ．D ．6 . （ 201 1 · 11 ）设函数的最小正周期为，且，则（）A ．在单调递减B ．在单调递减C ．在单调递增D ．在单调递增7 . （ 201 7 · 14 ）函数（）的最大值是．8 . （ 201 6 · 13 ）△ ABC 的内角 A 、 B 、 C 的对边分别为 a 、 b 、 c ，若，， a = 1 ，则 b = .9 . （ 201 4 · 14 ）函数的最大值为 _________.10 . （ 201 3 · 15 ）设为第二象限角，若，则_________.1 1 . （ 201 1 · 16 ）在△ AB C 中，，则的最大值为 .1 2 . （ 201 7 · 17 ）的内角的对边分别为，已知．（ 1 ）求（ 2 ）若, 面积为 2 ，求1 3 . （ 2015· 17 ）在∆ ABC 中， D 是 BC 上的点， AD 平分∠ BAC ，∆ ABD 面积是∆ ADC 面积的2 倍．（Ⅰ）求；（Ⅱ）若 AD =1 ， DC = ，求 BD 和 AC 的长．1 4 . （ 201 3 · 17 ）在△ ABC 内角 A 、 B 、 C 的对边分别为 a ， b ， c ，已知a=bcosC+csinB .（Ⅰ）求 B ；（Ⅱ）若 b= 2 ，求△ ABC 面积的最大值 .1 5 . （ 2012 · 17 ）已知 a ， b ， c 分别为△ ABC 三个内角 A ， B ， C 的对边，.（Ⅰ）求 A ；（Ⅱ）若 a =2 ，△ ABC 的面积为，求 b ， c .§ 10 . 立体几何1 . （ 201 7 · 4 ）如图，网格纸上小正方形的边长为 1 ，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分所得，则该几何体的体积为（）A ． B ． C ． D ．2 . （ 201 7 · 10 ）已知直三棱柱中，，，，则异面直线与所成角的余弦值为（）A ．B ．C ．D ．3 . （ 201 6 · 6 ）右图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为（）A ．20 πB ．24 πC ．28 πD ．32 π4 . （ 2015· 6 ）一个正方体被一个平面截去一部分后，剩余部分的三视图如右图，则截去部分体积与剩余部分体积的比值为（）A ．B ．C ．D ．5 . （ 2015· 9 ）已知 A ， B 是球 O 的球面上两点，∠ AOB =90 º ，C 为该球面上的动点，若三棱锥 O - ABC 体积的最大值为 36 ，则球 O 的表面积为（）A ．36 πB ．64 πC ．144 πD ．256 π6 . （ 201 4 · 6 ）如图，网格纸上正方形小格的边长为 1 （表示 1cm ），图中粗线画出的是某零件的三视图，该零件由一个底面半径为 3cm ，高为 6cm 的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为（）A ．B ．C ．D ．7 . （ 201 4 · 11 ）直三棱柱 ABC - A 1 B 1 C 1 中，∠ BCA =90 º ， M ， N 分别是 A1 B 1 ， A 1 C 1 的中点， BC = CA = CC 1 ，则 BM 与 AN 所成的角的余弦值为（）A ．B ．C ．D ．8 . （ 201 3 · 4 ）已知为异面直线，平面，平面. 直线满足，，，，则（）A . α // β且 l // αB . 且C . 与相交，且交线垂直于D . 与相交，且交线平行于9 . （ 201 3 · 7 ）一个四面体的顶点在空间直角坐标系中的坐标分别是(1,0,1) ， (1,1,0) ， (0,1,1) ， (0,0,0) ，画该四面体三视图中的正视图时，以平面为投影面，则得到正视图可以为（）10 . （ 2012·7 ）如图，网格纸上小正方形的边长为 1 ，粗线画出的是某几何体的三视图，则此几何体的体积为（）A. 6B. 9C. 12D. 1811 . （ 2012·11 ）已知三棱锥 S - ABC 的所有顶点都在球 O 的球面上，△ ABC 是边长为 1 的正三角形， SC 为球 O 的直径，且 SC =2 ，则此棱锥的体积为（）A. B. C. D.12 . （ 201 1 · 6 ）在一个几何体的三视图中，正视图和俯视图如右图所示，则相应的侧视图可以为（）A. B. C. D.1 3 . （ 201 6 · 14 ）α、β是两个平面， m 、 n 是两条直线，有下列四个命题：（ 1 ）如果 m ⊥ n ， m ⊥ α ，n ∥ β ，那么α ⊥ β .（ 2 ）如果 m ⊥ α ，n ∥ α ，那么 m ⊥ n .（ 3 ）如果α ∥ β ， m α ，那么m ∥ β .（ 4 ）如果m ∥ n ，α ∥ β ，那么 m 与α 所成的角和 n 与β 所成的角相等 .其中正确的命题有 . ( 填写所有正确命题的编号 .)1 4 . （ 201 1 · 15 ）已知矩形 ABCD 的顶点都在半径为 4 的球 O 的球面上，且，则棱锥 O - ABCD 的体积为 .1 5 . （ 201 7 · 19 ）如图，四棱锥 P-ABCD 中，侧面 PAD 为等边三角形且垂直于底面三角形 BCD ， E 是 PD 的中点 .（ 1 ）证明：直线 CE // 平面 PAB（ 2 ）点 M 在棱 PC 上，且直线 BM 与底面 ABCD 所成锐角为 45 º，求二面角 M-AB-D 的余弦值 .1 6 . （ 201 6 · 19 ）（满分 12 分）如图，菱形 ABCD 的对角线 AC 与 BD 交于点O ， AB =5 ， AC =6 ，点 E ， F 分别在 AD ， CD 上， AE = CF = ， EF 交 BD 于点H . 将△ DEF 沿 EF 折到△ D ´ EF 的位置，.（Ⅰ）证明：平面 ABCD ；（Ⅱ）求二面角的正弦值 .1 7 . （ 2015· 19 ）如图，长方体 ABCD - A 1 B 1 C 1 D 1 中AB =16 ， BC =10 ， AA 1 =8 ，点 E ， F 分别在 A 1 B 1 ， D 1 C 1 上， A 1 E = D 1 F =4 ，过点 E ， F 的平面与此长方体的面相交，交线围成一个正方形 .（Ⅰ）在图中画出这个正方形（不必说出画法和理由）；（Ⅱ）求直线 AF 与平面所成角的正弦值 .1 8 . （ 201 4 · 18 ）如图，四棱锥 P - ABCD 中，底面 ABCD 为矩形， PA ⊥平面ABCD ， E 为 PD 的中点 .（Ⅰ）证明： PB // 平面 AEC ；（Ⅱ）设二面角 D - AE - C 为 60 º， AP =1 ， AD = ，求三棱锥 E - ACD 的体积 .19 . （ 201 3 · 18 ）如图，直三棱柱中，，分别是，的中点，.（Ⅰ）证明：// 平面；（Ⅱ）求二面角的正弦值 .2 0 . （ 201 2 · 19 ）如图，直三棱柱 ABC - A 1 B 1 C 1 中，， D 是棱 AA 1 的中点， DC 1 ⊥ BD .（Ⅰ）证明： DC 1 ⊥ BC ；（Ⅱ）求二面角 A 1 - BD - C 1 的大小 .21 . （ 201 1 · 18 ）如图，四棱锥 P - ABCD 中，底面ABCD 为平行四边形，∠ DAB =60° ， AB =2 AD ， PD ⊥底面 ABCD .（Ⅰ）证明： PA ⊥ BD ；（Ⅱ）若 PD = AD ，求二面角 A - PB - C 的余弦值 .§ 1 1 . 排列组合、概率统计1 . （ 201 7 · 6 ）安排 3 名志愿者完成 4 项工作，每人至少完成 1 项，每项工作由1 人完成，则不同的安排方式共有（）A ． 12 种B ． 18 种C ． 24 种D ． 36 种2 . （ 201 6 · 5 ）如图，小明从街道的 E 处出发，先到 F 处与小红会合，再一起到位于 G 处的老年公寓参加志愿者活动，则小明到老年公寓可以选择的最短路径条数为（）A ． 24B ． 18C ． 12D ． 93 . （ 201 6 · 10 ）从区间 [0 ， 1] 随机抽取 2 n 个数 x 1 ， x 2 ，… ， x n ， y 1 ，y 2 ，… ， y n ，构成 n 个数对，，… ，，其中两数的平方和小于 1 的数对共有 m 个，则用随机模拟的方法得到的圆周率π的近似值为（）A ．B ．C ．D ．4 . （ 2015· 3 ）根据下面给出的 2004 年至 2013 年我国二氧化硫年排放量（单位：万吨）柱形图，以下结论中不正确的是（）A ．逐年比较， 2008 年减少二氧化硫排放量的效果最显著 .B ． 2007 年我国治理二氧化硫排放显现成效 .C ． 2006 年以来我国二氧化硫年排放量呈减少趋势 .D ． 2006 年以来我国二氧化硫年排放量与年份正相关 .5 . （ 201 4 · 5 ）某地区空气质量监测资料表明，一天的空气质量为优良的概率是0.75 ，连续两天为优良的概率是 0.6 ，已知某天的空气质量为优良，则随后一天的空气质量为优良的概率是（）A ． 0.8B ． 0.75C ． 0.6D ． 0.456 . （ 2012·2 ）将 2 名教师， 4 名学生分成两个小组，分别安排到甲、乙两地参加社会实践活动，每个小组由一名教师和 2 名学生组成，不同的安排方案共有（）A. 12 种B. 10 种C. 9 种D. 8 种7 . （ 201 1 · 4 ）有 3 个兴趣小组，甲、乙两位同学各自参加其中一个小组，每位同学参加各个小组的可能性相同，则这两位同学参加同一个兴趣小组的概率为（）A ．B ．C ．D ．8 . （ 201 7 · 13 ）一批产品的二等品率为 0.02 ，从这批产品中每次随机取一件，有放回地抽取 100 次，表示抽到的二等品件数，则．9 . （ 201 3 · 14 ）从个正整数 1 ， 2 ，…， n 中任意取出两个不同的数，若取出的两数之和等于 5 的概率为，则 n= ________ .10 . （ 2012·15 ）某一部件由三个电子元件按下图方式连接而成，元件 1 或元件 2 正常工作，且元件 3 正常工作，则部件正常工作 . 设三个电子元件的使用寿命（单位：小时）服从正态分布 N (1000 ， 50 2 ) ，且各元件能否正常工作互相独立，那么该部件的使用寿命超过 1000 小时的概率为 .1 1 . （ 201 7 · 18 ）淡水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取 100 个网箱，测量各箱水产品的产量（单位： kg ）某频率直方图如下：（ 1 ）设两种养殖方法的箱产量相互独立，记 A 表示事件：旧养殖法的箱产量低于 50kg ，新养殖法的箱产量不低于 50kg ，估计 A 的概率；（ 2 ）填写下面列联表，并根据列联表判断是否有 99% 的把握认为箱产量与养殖方法有关：<50kg ≥ 50kg旧养殖法新养殖法（ 3 ）根据箱产量的频率分布直方图，求新养殖法箱产量的中位数的估计值（精确到 0.01 ）P ( K 2 ≥ k )0.050 0.010 0.001k 3.841 6.635 10.8281 2 . （ 201 6 · 18 ）某险种的基本保费为 a （单位：元），继续购买该险种的投保人称为续保人，续保人的本年度的保费与其上年度的出险次数的关联如下：上年度出险次数0 1 2 3 4 5保费0.85 a a 1.25 a 1.5 a 1.75 a 2 a设该险种一续保人一年内出险次数与相应概率如下：一年内出险次数0 1 2 3 4 5概率0.30 0.15 0.20 0.20 0.10 0. 05（Ⅰ）求一续保人本年度的保费高于基本保费的概率；（Ⅱ）若一续保人本年度的保费高于基本保费，求其保费比基本保费高出 60% 的概率；（Ⅲ）求续保人本年度的平均保费与基本保费的比值 .13 . （ 2015· 18 ）某公司为了解用户对其产品的满意度，从 A ， B 两地区分别随机调查了 20 个用户，得到用户对产品的满意度评分如下：A 地区6273819295857464537678869566977888827689B 地区7383625191465373648293486581745654766579（Ⅰ）根据两组数据完成两地区用户满意度评分的茎叶图，并通过茎叶图比较两地区满意度评分的平均值及分散程度（不要求计算出具体值，得出结论即可）；（Ⅱ）根据用户满意度评分，将用户的满意度从低到高分为三个等级：满意度评分低于 70 分70 分到 89 分不低于 90 分满意度等级不满意满意非常满意记事件 C ：“ A 地区用户的满意度等级高于 B 地区用户的满意度等级”，假设两地区用户的评价结果相互独立，根据所给数据，以事件发生的频率作为相应事件发生的概率，求 C 的概率．14 . （ 201 4 · 19 ）某地区 2007 年至 2013 年农村居民家庭纯收入 y （单位：千元）的数据如下表：年份2007 2008 2009 2010 2011 2012 2013年份代号 t 1 2 3 4 5 6 7人均纯收入 y 2.9 3.3 3.6 4.4 4.8 5.2 5.9（Ⅰ）求 y 关于 t 的线性回归方程；（Ⅱ）利用（Ⅰ）中的回归方程，分析 2007 年至 2013 年该地区农村居民家庭人均纯收入的变化情况，并预测该地区 2015 年农村居民家庭人均纯收入 .附：回归直线的斜率和截距的最小二乘法估计公式分别为：，.15 . （ 201 3 · 19 ）经销商经销某种农产品，在一个销售季度内，每售出 1 t 该产品获利润 500 元，未售出的产品，每 1 t 亏损 300 元 . 根据历史资料，得到销售季度内市场需求量的频率分布直方图，如有图所示 . 经销商为下一个销售季度购进了130 t 该农产品 . 以 x （单位： t ，100≤ x ≤150 ）表示下一个销售季度内的市场需求量， T （单位：元）表示下一个销售季度内经销该农产品的利润 .（Ⅰ）将 T 表示为 x 的函数；（Ⅱ）根据直方图估计利润 T 不少于 57000 元的概率；（Ⅲ）在直方图的需求量分组中，以各组的区间中点值代表该组的各个需求量落入该区间的频率作为需求量取该区间中点值的概率（例如：若x ∈ [100, 110) ，则取 x =105 ，且 x =105 的概率等于需求量落入 [100, 110) 的概率），求利润 T 的数学期望 .1 6 . （ 2012 · 18 ）某花店每天以每枝 5 元的价格从农场购进若干枝玫瑰花，然后以每枝 10 元的价格出售，如果当天卖不完，剩下的玫瑰花做垃圾处理 .（Ⅰ）若花店某天购进 16 枝玫瑰花，求当天的利润 y （单位：元）关于当天需求量 n （单位：枝，n ∈ N ）的函数解析式；（Ⅱ）花店记录了 100 天玫瑰花的日需求量（单位：枝），整理得下表：日需求量 n 14 15 16 17 18 19 20频数10 20 16 16 15 13 10以 100 天记录的各需求量的频率作为各需求量发生的概率 .（ i ）若花店一天购进 16 枝玫瑰花， X 表示当天的利润（单位：元），求 X 的分布列、数学期望及方差；（ ii ）若花店计划一天购进 16 枝或 17 枝玫瑰花，你认为应购进 16 枝还是 17 枝？请说明理由 .1 7 . （ 201 1 · 19 ）某种产品的质量以其质量指标值衡量，质量指标值越大表明质量越好，且质量指标值大于或等于 102 的产品为优质品，现用两种新配方（分别称为 A 配方和 B 配方）做试验，各生产了 100 件这种产品，并测量了每件产品的质量指标值，得到下面试验结果：A 配方的频数分布表指标值分组[90,94) [94,98) [98,102) [102,106) [106,110 ]频数8 20 42 22 8B 配方的频数分布表指标值分组[90,94) [94,98) [98,102) [102,106) [106,110 ]频数 4 12 42 32 10（Ⅰ）分别估计用 A 配方， B 配方生产的产品的优质品率；（Ⅱ）已知用 B 配方生成的一件产品的利润 y ( 单位：元 ) 与其质量指标值 t 的关系式为，从用 B 配方生产的产品中任取一件，其利润记为 X （单位：元），求 X 的分布列及数学期望 . （以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率）§ 1 2 . 解析几何1 . （ 201 7 · 9 ）若双曲线（，）的一条渐近线被圆所截得的弦长为 2 ，则的离心率为（）A ． 2B ．C ．D ．2 . （ 201 6 · 4 ）圆的圆心到直线的距离为 1 ，则a = （）A ．B ．C ．D ． 23 . （ 201 6 · 11 ）已知 F 1 ， F 2 是双曲线 E ：的左，右焦点，点 M 在E 上， MF 1 与 x 轴垂直，，则 E 的离心率为（）A ．B ．C ．D ． 24 . （ 2015· 7 ）过三点 A ( 1, 3 ) ， B ( 4, 2 ) ， C ( 1, - 7 ) 的圆交于 y 轴于 M 、 N 两点，则= （）A ．B ． 8C ．D ． 105 . （ 2015· 11 ）已知 A ， B 为双曲线 E 的左，右顶点，点 M 在 E 上，∆ ABM 为等腰三角形，且顶角为 120°，则 E 的离心率为（）A ．B ． 2C ．D ．6 . （ 201 4 · 10 ）设 F 为抛物线 C : 的焦点，过 F 且倾斜角为 30º的直线交C 于 A , B 两点， O 为坐标原点，则△ OAB 的面积为（）A ．B ．C ．D ．7 . （ 201 3 · 11 ）设抛物线的焦点为，点在上，，若以为直径的园过点，则的方程为（）A . 或B . 或C . 或D . 或8 . （ 201 3 · 12 ）已知点，，，直线将分割为面积相等的两部分，则的取值范围是（）A .B .C .D .9 . （ 2012·4 ）设 F 1 ， F 2 是椭圆 E : 的左右焦点， P 为直线上的一点，是底角为 30 º的等腰三角形，则 E 的离心率为（）A. B. C. D.10 . （ 2012·8 ）等轴双曲线 C 的中心在原点，焦点在 x 轴上， C 与抛物线 y 2=16 x 的准线交于 A ， B 两点， | AB |= ，则 C 的实轴长为（）A. B. C. 4 D. 811 . （ 201 1 · 7 ）设直线 l 过双曲线 C 的一个焦点，且与 C 的一条对称轴垂直， l与 C 交于 A , B 两点， | AB | 为 C 的实轴长的 2 倍，则 C 的离心率为（）A ．B ．C ． 2D ． 31 2. （ 201 7 · 16 ）已知 F 是抛物线 C : 的焦点， M 是 C 上一点， FM 的延长线交轴于点 N ．若 M 为 FN 的中点，则 | FN |= ．13 . （ 201 4 · 6 ）设点 M ( ,1) ，若在圆 O : 上存在点 N ，使得∠ OMN =45 º，则的取值范围 .1 4 . （ 201 1 · 14 ）在平面直角坐标系 xoy 中，椭圆 C 的中心为原点，焦点 F 1 ，F 2 在 x 轴上，离心率为. 过 F 1 的直线 l 交 C 于 A ， B 两点，且△ ABF 2 的周长为 16 ，那么 C 的方程为 .1 5 . （ 201 7 · 20 ）设 O 为坐标原点，动点 M 在椭圆 C ：上，过 M 做 x轴的垂线，垂足为 N ，点 P 满足.（ 1 ）求点 P 的轨迹方程；（ 2 ）设点 Q 在直线 x = - 3 上，且. 证明：过点 P 且垂直于 OQ 的直线 l过 C 的左焦点 F .1 6 . （ 201 6 · 20 ）已知椭圆 E : 的焦点在轴上， A 是 E 的左顶点，斜率为 k ( k >0) 的直线交 E 于 A ， M 两点，点 N 在 E 上， MA ⊥ NA .（Ⅰ）当 t =4 ， | AM | =| AN | 时，求△ AMN 的面积；（Ⅱ）当 2| AM | =| AN | 时，求 k 的取值范围 .17 . （ 2015· 20 ）已知椭圆 C ： ( m ＞ 0) ，直线 l 不过原点 O 且不平行于坐标轴， l 与 C 有两个交点 A ， B ，线段 AB 的中点为 M .（Ⅰ）证明：直线 OM 的斜率与 l 的斜率的乘积为定值；（Ⅱ）若 l 过点，延长线段 OM 与 C 交于点 P ，四边形 OAPB 能否平行四边形？若能，求此时 l 的斜率；若不能，说明理由．18 . （ 201 4 · 20 ）设 F 1 ， F 2 分别是椭圆的左右焦点， M是 C 上一点且 MF 2 与 x 轴垂直，直线 MF 1 与 C 的另一个交点为 N .（Ⅰ）若直线 MN 的斜率为，求 C 的离心率；（Ⅱ）若直线 MN 在 y 轴上的截距为 2 ，且，求 a, b .1 9 . （ 201 3 · 20 ）平面直角坐标系中，过椭圆右焦点的直线交于两点，为的中点，且的斜率为.（Ⅰ）求的方程；（Ⅱ）为上的两点，若四边形的对角线，求四边形面积的最大值 .20 . （ 201 2 · 20 ）设抛物线的焦点为 F ，准线为 l ， A 为 C上的一点，已知以 F 为圆心， FA 为半径的圆 F 交 l 于 B ， D 两点 .（Ⅰ）若∠ BFD =90 º ，△ AB D 面积为，求 p 的值及圆 F 的方程；（Ⅱ）若 A 、 B 、 F 三点在同一直线 m 上，直线 n 与 m 平行，且 n 与 C 只有一个公共点，求坐标原点到 m ， n 的距离的比值 .21 . （ 201 1 · 20 ）在平面直角坐标系 xOy 中，已知点 A (0, - 1) ， B 点在直线 y= - 3 上， M 点满足，， M 点的轨迹为曲线 C .（Ⅰ）求 C 的方程；（Ⅱ） P 为 C 上的动点， l 为 C 在 P 点处得切线，求 O 点到 l 距离的最小值 .§ 1 3 . 函数与导数1 . （ 201 7 · 11 ）若是函数的极值点，则的极小值为（）A. B. C. D.12 . （ 201 6 · 12 ）已知函数满足，若函数与图像的交点为，，… ，，则（）A ． 0B ． mC ． 2 mD ． 4 m3 . （ 2015· 5 ）设函数，则（）A ． 3B ． 6C ． 9D ． 124 . （ 2015· 10 ）如图，长方形 ABCD 的边 AB =2 ， BC =1 ，O 是 AB 的中点，点 P 沿着边 BC ， CD 与 DA 运动，记∠ BOP = x. 将动点 P 到 A ，B 两点距离之和表示为 x 的函数 f （ x ），则 f （ x ）的图像大致为（）A ．B ．C ．D ．5 . （ 2015· 12 ）设函数是奇函数的导函数，，当 x >0 时，，则使得 f ( x ) >0 成立的 x 的取值范围是（）A ．B ．C ．D ．6 . （ 201 4 · 8 ）设曲线 y = ax - ln( x +1) 在点 (0,0) 处的切线方程为 y =2 x ，则 a = （）A ． 0B ． 1C ． 2D ． 37 . （ 201 4 · 12 ）设函数，若存在的极值点满足，则 m 的取值范围是（）A ．B ．C ．D ．8 . （ 201 3 · 8 ）设，，，则（）A .B .C .D .9 . （ 201 3 · 10 ）已知函数，下列结论中错误的是（）A .B . 函数的图像是中心对称图形C . 若是的极小值点，则在区间单调递减D . 若是的极值点，则10 . （ 2012·10 ）已知函数，则的图像大致为（）A. B. C. D.11 . （ 2012·12 ）设点 P 在曲线上，点在曲线上，则的最小值为（）A. B. C. D.12 . （ 201 1 · 2 ）下列函数中，既是偶函数又在单调递增的函数是（）A ．B ．C ．D ．13 . （ 201 1 · 9 ）由曲线，直线及 y 轴所围成的图形的面积为（）A ．B ． 4C ．D ． 614 . （ 201 1 · 12 ）函数的图像与函数的图像所有交点的横坐标之和等于（）A ． 2B ． 4C ． 6D ． 81 5 ．（ 201 6 · 16 ）若直线 y = kx + b 是曲线 y = ln x +2 的切线，也是曲线 y = ln ( x + 1 ) 的切线，则 b = .1 6 . （ 201 4 · 15 ）已知偶函数 f ( x ) 在[0, + ∞ ) 单调递减， f (2)=0. 若 f ( x - 1)>0 ，则 x 的取值范围是 _________.17 . （ 201 7 · 21 ）已知函数，且.（ 1 ）求 a ；（ 2 ）证明：存在唯一的极大值点，且.18 . （ 201 6 · 21 ）（Ⅰ）讨论函数的单调性，并证明当>0 时，；（Ⅱ）证明：当时，函数有最小值 . 设 g ( x ) 的最小值为，求函数的值域 .19 . （ 2015· 21 ）设函数.（Ⅰ）证明： f ( x ) 在（ - ∞ ， 0 ）单调递减，在（ 0 ，+∞ ）单调递增；（Ⅱ）若对于任意 x 1 , ，x 2 ∈ [ - 1 ， 1] ，都有｜ f ( x 1 ) - f ( x 2 ) ｜≤ e - 1 ，求 m 的取值范围．20 . （ 201 4 · 21 ）已知函数.（Ⅰ）讨论的单调性；（Ⅱ）设，当时，，求的最大值；（Ⅲ）已知，估计 ln2 的近似值（精确到 0.001 ） .21 . （ 201 3 · 21 ）已知函数.（Ⅰ）设是的极值点，求，并讨论的单调性；（Ⅱ）当时，证明.22 . （ 201 2 · 21 ）已知函数.（Ⅰ）求的解析式及单调区间；（Ⅱ）若，求的最大值 .23 . （ 201 1 · 21 ）已知函数，曲线在点处的切线方程为.（Ⅰ）求 a 、 b 的值；（Ⅱ）如果当，且时，，求 k 的取值范围 .§ 1 4 . 几何证明选讲1 . （ 201 6 · 22 ）如图，在正方形 ABCD 中， E ， G 分别在边DA ， DC 上（不与端点重合），且 DE = DG ，过 D 点作 DF ⊥ CE ，垂足为 F . （Ⅰ）证明： B ， C ， G ， F 四点共圆；（Ⅱ）若 AB =1 ， E 为 DA 的中点，求四边形 BCGF 的面积 .2 . （ 201 5 · 22 ）如图， O 为等腰三角形 ABC 内一点，⊙ O 与△ ABC 的底边 BC 交于 M 、 N 两点，与底边上的高 AD 交于点 G ，且与 AB ， AC 分别相切于 E ， F 两点 .（Ⅰ）证明：EF ∥ BC ；（Ⅱ）若 AG 等于⊙ O 的半径，且 AE=MN= ，求四边形 EBCF 的面积 .3 . （ 2014 · 22 ）如图， P 是⊙ O 外一点， PA 是切线， A 为切点，割线 PBC 与⊙ O 相交于点 B 、 C ， PC =2 PA ， D 为 PC 的中点， AD 的延长线交⊙ O 于点 E .证明：（Ⅰ） BE = EC ；（Ⅱ） AD · DE = 2 PB 2 .4 . （ 201 3 · 22 ）如图，为外接圆的切线，的延长线交直线于点，，分别为弦与弦上的点，且， B 、 E 、 F 、 C 四点共圆 .（Ⅰ）证明：是外接圆的直径；（Ⅱ）若，求过 B 、 E 、 F 、 C 四点的圆的面积与外接圆面积的比值 .5 . （ 201 2 · 22 ）如图， D ， E 分别为△ ABC 边 AB ， AC 的中点，直线 DE 交于△ ABC 的外接圆于 F ， G 两点，若 CF // AB ，证明：（Ⅰ） CD = BC ；（Ⅱ）△ BCD ∽ △ GBD .6 . （ 201 1 · 22 ）如图， D ， E 分别为△ ABC 的边 AB ， AC 上的点，且不与△ ABC 的顶点重合 . 已知 AE 的长为 m ， AC 的长为 n ， AD ，AB 的长是关于 x 的方程 x 2 - 14 x + mn =0 的两个根 .（Ⅰ）证明： C 、 B 、 D 、 E 四点共圆；（Ⅱ）若∠ A =90 º ，且 m =4 ， n =6 ，求 C 、 B 、 D 、 E 所在圆的半径 .§ 1 5 . 坐标系与参数方程1 . （ 201 7 · 22 ）在直角坐标系 xo y 中，以坐标原点为极点， x 轴的正半轴为极轴建立极坐标系，曲线 C 1 的极坐标方程为．（ 1 ） M 为曲线 C 1 上的动点，点 P 在线段 OM 上，且满足，求点 P 的轨迹 C 2 的直角坐标方程；（ 2 ）设点 A 的极坐标为，点 B 在曲线 C 2 上，求△ OAB 面积的最大值．2 . （ 201 6 · 23 ）在直角坐标系 xOy 中，圆 C 的方程为.（Ⅰ）以坐标原点为极点， x 轴的正半轴为极轴建立极坐标系，求 C 的极坐标方程；（Ⅱ）直线 l 的参数方程是（ t 为参数）， l 与 C 交于 A ， B 两点，，求 l 的斜率 .3 . （ 201 5 · 23 ）在直角坐标系中，曲线 C 1 ：（ t 为参数，t ≠ 0 ）其中，在以 O 为极点， x 轴正半轴为极轴的极坐标系中，曲线 C 2 :， C 3 : .（Ⅰ）求 C 2 与 C 3 交点的直角坐标；（Ⅱ）若 C 1 与 C 2 相交于点 A ， C 1 与 C 3 相交于点 B ，求 | AB | 的最大值 .4 . （ 201 4 · 23 ）在直角坐标系 xoy 中，以坐标原点为极点， x 轴为极轴建立极坐标系，半圆 C 的极坐标方程为，.（Ⅰ）求 C 的参数方程；（Ⅱ）设点 D 在 C 上， C 在 D 处的切线与直线垂直，根据（Ⅰ）中你得到的参数方程，确定 D 的坐标 .5 . （ 201 3 · 23 ）已知动点 P ， Q 都在曲线上，对应参数分别为t= α 与t= 2 α ( 0< α <2 π ) ， M 为 PQ 的中点 .（Ⅰ）求 M 的轨迹的参数方程；（Ⅱ）将 M 到坐标原点的距离 d 表示为α 的函数，并判断 M 的轨迹是否过坐标原点 .6 . （ 201 2 · 23 ）已知曲线 C 1 的参数方程是（为参数），以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线 C 2 的极坐标方程是ρ = 2 .正方形 ABCD 的顶点都在 C 2 上，且 A ， B ， C ， D 依逆时针次序排列，点 A 的极坐标为.（Ⅰ）点 A ， B ， C ， D 的直角坐标；（Ⅱ）设 P 为 C 1 上任意一点，求 | PA | 2 + | PB | 2 + | PC | 2 + | PD | 2 的取值范围 .7 . （ 201 1 · 23 ）在直角坐标系 xOy 中，曲线 C 1 的参数方程为（为参数）， M 是 C 1 上的动点， P 点满足， P 点的轨迹为曲线 C 2 . （Ⅰ）求 C 2 的方程；（Ⅱ）在以 O 为极点， x 轴的正半轴为极轴的极坐标系中，射线与 C 1 的异于极点的交点为 A ，与 C 2 的异于极点的交点为 B ，求 | AB | .§ 1 6 . 不等式选讲1 . （ 201 7 · 23 ）已知，证明：（ 1 ）；（ 2 ）．2 . （ 201 6 · 24 ）已知函数， M 为不等式的解集 . （Ⅰ）求 M ；（Ⅱ）证明：当 a ，b ∈ M 时，.3 . （ 201 5 · 24 ）设 a ， b ， c ， d 均为正数，且，证明：（Ⅰ）若> ，则；（Ⅱ）是的充要条件 .4 . （ 201 4 · 24 ）设函数.（Ⅰ）证明：f ( x ) ≥ 2 ；（Ⅱ）若 f (3) < 5 ，求 a 的取值范围 .5 . （ 201 3 · 24 ）设均为正数，且.证明：（Ⅰ）；（Ⅱ）.6 . （ 201 2 · 24 ）已知函数 f ( x ) = | x + a | + | x - 2|.（Ⅰ）当 a = - 3 时，求不等式f ( x ) ≥ 3 的解集；（Ⅱ）若f ( x ) ≤ | x - 4 | 的解集包含 [1, 2] ，求 a 的取值范围 .7 . （ 201 1 · 24 ）设函数，其中.（Ⅰ）当时，求不等式的解集；（Ⅱ）若不等式的解集为，求 a 的值 .参考答案§ 1 . 集合及其运算1 ．【答案： C 】解析：由，得，所以，，故选 C.2. 【答案： C 】解析：，∴ ，∴ ，故选C ．3 . 【答案： A 】解析：由已知得，故，故选 A .4 ．【答案： D 】解析：∵ ，∴ .5 ．【答案： A 】解析：解不等式 ( x - 1) 2 < 4 ，得 - 1 < x < 3 ，即 M ＝ { x | - 1 < x < 3} ．而 N ＝ { - 1, 0, 1, 2, 3} ，所以M ∩ N ＝ {0, 1, 2} ，故选 A.6 ．【答案： D 】解析：要在 1 ， 2 ， 3 ， 4 ， 5 中选出两个，大的是 x ，小的是 y ，共种选法 .§ 2 . 复数计算1 ．【答案： D 】解析：，故选 D.2 ．【答案： A 】解析：∴ ，，∴ ，故选 A ．3 . 【答案： B 】解析：由已知得 4 a + ( a 2 - 4) i = - 4 i ，所以 4 a = 0 ， a 2 - 4 = - 4 ，解得 a =0 ，故选 B.4 ．【答案： A 】解析：∵ ，复数，在复平面内的对应点关于虚轴对称，∴ ，∴ .5 ．【答案： A 】解析：由 (1 - i ) · z =2 i ，得＝＝－ 1 ＋ i .6 ．【答案： C 】解析：经计算，复数的共轭复数为，的虚部为，综上可知 P 2 ， P 4 正确 .7 . 【答案： C 】解析：= 共轭复数为 C .§ 3 . 简易逻辑1 ．【答案： D 】解析：由甲的说法可知乙、丙一人优秀一人良好，则甲丁一人优秀一人良好，乙看到丙的结果则知道自己的结果，丁看到甲的结果则知道自己的结果，故选 D .2 . 【答案： A 】解析：由得.由得，故选 A .3 . 【答案： 1 和 3 】解析：由题意得：丙不拿（ 2 ， 3 ），若丙（ 1 ， 2 ），则乙（ 2 ， 3 ），甲（ 1 ， 3 ）满足；若丙（ 1 ， 3 ），则乙（ 2 ， 3 ），甲（ 1 ， 2 ）不满足，故，甲（ 1 ， 3 ） . § 4 . 平面向量1 ．【答案： B 】解析：以 B C 为 x 轴， BC 的垂直平分线 AD 为 y 轴， D 为坐标原点建立坐标系，则，设 P ( x ， y ) ，所以，所以当时，所求的最小值为，故 B.2. 【答案： D 】解析：，∵ ，∴ ，解得，故选 D ．3 ．【答案： A 】解析：两式相减得：. 故选 A .4 . 【答案：】解析：因为向量与平行，所以，则，所以．5 ．【答案： 2 】解析：以 AB 所在直线为 x 轴， AD 所在直线为 y 轴建立平面直角坐标系，则点 A的坐标为 (0,0) ，点 B 的坐标为 (2,0) ，点 D 的坐标为 (0,2) ，点 E 的坐标为 (1,2) ，则＝ (1,2) ，＝ ( - 2, 2) ，所以.6 ．【答案：】解析：因，即：，解得.§ 5 . 程序框图1 ．【答案： B 】解析：，故选 B .2. 【答案： C 】解析：第一次运算：，第二次运算：，第三次运算：，故选 C ．3 . 【答案： B 】解析：程序在执行过程中， a ， b 的值依次为 a =14 ， b =18 ， b =4 ， a =10 ， a =6 ， a =2 ， b =2 ，此时 a = b =2 程序结束，输出 a 的值为 2 ，故选 B ．4 ．【答案： D 】。
2011年—2017年新课标全国卷1理科数学分类汇编——1.集合与常用逻辑用语
2011 年—2017 年新课标高考全国Ⅰ卷理科数学分类汇编（含答案）1．集合与常用逻辑用语一、选择题【2017，1】已知集合A ={x x <1}，B ={x 3x <1}，则（）A．A B = {x | x <0}B．A B =R C．A B = {x | x >1}D．A B=∅【2016，1】设集合A = {x x2 - 4x + 3 <0}，B = {x 2x - 3 > 0} ，则A B =（）A．(-3,-3)2B．(-3,3)2C．(1,3)2D．(3,3)2【2015，3】设命题p ：∃n∈N，n2 > 2n ，则⌝p 为（）A．∀n ∈N ，n2 >2n B．∃n∈N，n2 ≤2n C．∀n ∈N ，n2 ≤2n D．∃n∈N ，n2 =2n【2014，1】已知集合A={ x | x2 - 2x - 3 ≥ 0 }，B= {x -2 ≤x < 2}，则A ⋂B =( )A ．[-2,-1]B ．[-1,2）C ．[-1,1]D ．[1,2）【2013，1】已知集合A＝{x|x2－2x＞0}，B＝{x|－x＜，则( )A．A∩B＝ B．A∪B＝R C．B ⊆A D．A ⊆B【2012，1】已知集合A={1，2，3，4，5}，B={（x ，y ）| x∈A，y ∈A ，x -y ∈A }，则B 中包含元素的个数为（）A．3 B．6 C．8 D．101．集合与常用逻辑用语（解析版）一、选择题【2017，1】已知集合A = {x x < 1}， B = {x 3x < 1}，则（ ）A ． AB = {x | x < 0} B ． A B = RC ． A B = {x | x > 1}D ． A B =∅【解析】 A = {x x < 1} ， B = {x 3x < 1} = {x x < 0} ，∴ A B = {x x < 0} ， A B = {x x < 1} ，故选A【2016，1】设集合 A = {x x 2 - 4x + 3 < 0} ， B = {x 2x - 3 > 0} ，则 A B = （）A ． (-3,- 3)2B ． (-3, 3)2C ． (1, 3)2D ． ( 3,3)2⎫【解析】 A = {x 1 < x < 3} ， B = {x 2x - 3 > 0} = ⎧x x > 3 ⎫ ．故A B = ⎧x 3< x < 3 ．故选 D ． ⎨ 2 ⎬ ⎨ 2 ⎬ ⎩ ⎭ ⎩ ⎭【2015，3】设命题 p ： ∃n ∈ N ， n 2 > 2n ，则 ⌝p 为（）A ．∀n ∈ N ， n 2 > 2nB ．∃n ∈ N ， n 2 ≤ 2nC ．∀n ∈ N ， n 2 ≤ 2nD ．∃n ∈ N ， n 2 = 2n解析：命题 p 含有存在性量词（特称命题），是真命题（如 n = 3 时），则其否定（ ⌝p ）含有全称量词（全称命题），是假命题，故选 C ．.【2014，1】已知集合 A={ x | x 2- 2x - 3 ≥ 0 }，B= {x -2 ≤ x < 2}，则 A ⋂ B =()A .[-2,-1]B .[-1,2）C .[-1,1]D .[1,2）【解析】∵ A = {x | x ≤ -1或x ≥ 3}，B= {x -2 ≤ x < 2}，∴ A ⋂ B = {x -2 ≤ x ≤ 1}，选 A.【2013，1】已知集合 A ＝{x |x 2－2x ＞0}，B ＝{x |－x ＜，则()A ．A ∩B ＝B ．A ∪B ＝RC ．B ⊆ AD ．A ⊆ B解析：∵x (x －2)＞0，∴x ＜0 或 x ＞2，∴集合 A 与 B 可用图象表示为：由图象可以看出 A ∪B ＝R ，故选 B.【2012，1】已知集合 A={1，2，3，4，5}，B={（ x ， y ）| x ∈ A ， y ∈ A ， x - y ∈ A }，则 B 中包含元 素的个数为（ ）A ．3B ．6C ．8D ．10 【解析】由集合 B 可知， x > y ，因此 B={（2，1），（3，2），（4，3），（5，4），（3，1），（4，2），（5，3），（4，1），（5，2），（5，1）}，B 的元素 10 个，所以选择 D ．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
9．解析几何（含解析）一、选择题【2017，10】已知F 为抛物线C ：y 2=4x 的焦点，过F 作两条互相垂直的直线l 1，l 2，直线l 1与C 交于A 、B 两点，直线l 2与C 交于D 、E 两点，则|AB |+|DE |的最小值为（ ） A ．16 B ．14 C ．12 D ．10【2016，10】以抛物线C 的顶点为圆心的圆交C 于B A ,两点，交C 的准线于E D ,两点，已知24=AB ,52=DE ，则C 的焦点到准线的距离为（ ）A ．2B ．4C ．6D ．8【2016，5】已知方程132222=--+nm y n m x 表示双曲线，且该双曲线两焦点间的距离为4，则n 的取值范围是（ ） A ．)3,1(-B ．)3,1(-C ．)3,0(D ．)3,0(【2015，5】已知00(,)M x y 是双曲线C ：2212x y -=上的一点，12,F F 是C 的两个焦点，若120MF MF ⋅<，则0y 的取值范围是（ ）A ．(B ．(C ．(D ．( 【2014，4】已知F 是双曲线C ：223(0)x my m m -=>的一个焦点，则点F 到C 的一条渐近线的距离为A B ．3 C D ．3m【2014，10】已知抛物线C ：28y x =的焦点为F ，准线为l ，P 是l 上一点，Q 是直线PF 与C 的一个交点，若4FP FQ =，则||QF =（ ）A ．72 B ．52C ．3D ．2【2013，4】已知双曲线C ：2222=1x y a b-(a ＞0，b ＞0)的离心率为2，则C 的渐近线方程为( )．A ．y ＝14x ±B ．y ＝13x ±C ．y ＝12x ± D ．y ＝±x【2013，10】已知椭圆E ：2222=1x y a b+(a ＞b ＞0)的右焦点为F (3,0)，过点F 的直线交E 于A ，B 两点．若AB 的中点坐标为(1，－1)，则E 的方程为( )A ．22=14536x y + B ．22=13627x y + C ．22=12718x y + D ．22=1189x y +【2012，4】设1F 、2F 是椭圆E ：2222x y a b +（0a b >>）的左、右焦点，P 为直线32ax =上一点，21F PF ∆是底角为30°的等腰三角形，则E 的离心率为（ ）A ．12 B ．23 C ．34 D ．45【2012，8】等轴双曲线C 的中心在原点，焦点在x 轴上，C 与抛物线216y x =的准线交于A ，B 两点，||AB =，则C 的实轴长为（ ）AB ．C ．4D ．8【2011，7】设直线L 过双曲线C 的一个焦点，且与C 的一条对称轴垂直，L 与C 交于A ,B 两点，AB 为C 的实轴长的2倍，则C 的离心率为（ ）A B C ．2 D ．3 二、填空题【2017，15】已知双曲线C ：22221x y a b-=（a >0，b >0）的右顶点为A ，以A 为圆心，b 为半径作圆A ，圆A与双曲线C 的一条渐近线交于M 、N 两点．若∠MAN =60°，则C 的离心率为________．【2015，14】一个圆经过椭圆221164x y +=的三个顶点，且圆心在x 轴的正半轴上，则该圆的标准方程为 ．【2011，14】在平面直角坐标系xOy 中，椭圆C 的中心为原点，焦点12,F F 在x 轴上，离心率为2．过1F 的直线L 交C 于,A B 两点，且2ABF 的周长为16，那么C 的方程为 ．三、解答题【2017，20】已知椭圆C ：2222=1x y a b +（a >b >0），四点P 1（1,1），P 2（0,1），P 3（–1），P 4（1）中恰有三点在椭圆C 上．（1）求C 的方程；（2）设直线l 不经过P 2点且与C 相交于A ，B 两点．若直线P 2A 与直线P 2B 的斜率的和为–1，证明：l 过定点．【2016，20】设圆015222=-++x y x 的圆心为A ，直线l 过点)0,1(B 且与x 轴不重合，l 交圆A 于D C ,两点，过B 作AC 的平行线交AD 于点E ． （Ⅰ）证明EB EA +为定值，并写出点E 的轨迹方程；（Ⅱ）设点E 的轨迹为曲线1C ，直线l 交1C 于N M ,两点，过B 且与l 垂直的直线与圆A 交于Q P ,两点，求四边形MPNQ 面积的取值范围．【2015，20】在直角坐标系xOy 中，曲线C ：24x y =与直线l ：y kx a =+（0a >）交于,M N 两点．（Ⅰ）当0k =时，分别求C 在点M 和N 处的切线方程；（Ⅱ）在y 轴上是否存在点P ，使得当k 变动时，总有OPM OPN ∠=∠？说明理由．【2014，20】已知点A （0，-2），椭圆E ：22221(0)x y a b a b+=>>的离心率为2，F 是椭圆的焦点，直线AF ，O 为坐标原点． (Ⅰ)求E 的方程；（Ⅱ）设过点A 的直线l 与E 相交于,P Q 两点，当OPQ ∆的面积最大时，求l 的方程．【2013，20】已知圆M ：(x ＋1)2＋y 2＝1，圆N ：(x －1)2＋y 2＝9，动圆P 与圆M 外切并且与圆N 内切，圆心P 的轨迹为曲线C ．(1)求C 的方程；(2)l 是与圆P ，圆M 都相切的一条直线，l 与曲线C 交于A ，B 两点，当圆P 的半径最长时，求|AB |．【2012，20】设抛物线C ：py x 22=（0>p ）的焦点为F ，准线为l ，A 为C 上一点，已知以F 为圆心，F A 为半径的圆F 交l 于B ，D 两点．（1）若∠BFD =90°，△ABD 的面积为24，求p 的值及圆F 的方程；（2）若A ，B ，F 三点在同一直线m 上，直线n 与m 平行，且n 与C 只有一个公共点，求坐标原点到m ，n 距离的比值．【2011，20】在平面直角坐标系xOy 中，已知点A(0,-1)，B 点在直线y = -3上，M 点满足//MB OA ，MA AB MB BA ⋅=⋅，M 点的轨迹为曲线C ．（Ⅰ）求C 的方程；（Ⅱ）P 为C 上的动点，l 为C 在P 点处得切线，求O 点到l 距离的最小值．9．解析几何（解析版）一、选择题【2017，10】已知F 为抛物线C ：y 2=4x 的焦点，过F 作两条互相垂直的直线l 1，l 2，直线l 1与C 交于A 、B 两点，直线l 2与C 交于D 、E 两点，则|AB |+|DE |的最小值为（ ） A ．16 B ．14 C ．12 D ．10【解析】设AB 倾斜角为θ．作1AK 垂直准线，2AK 垂直x 轴，易知11cos 22⎧⎪⋅+=⎪⎪=⎨⎪⎛⎫⎪=--= ⎪⎪⎝⎭⎩AF GF AK AK AF P P GP Pθ（几何关系）（抛物线特性），cos AF P AF θ⋅+=∴，同理1cos P AF θ=-，1cos P BF θ=+，∴22221cos sin P PAB θθ==-， 又DE 与AB 垂直，即DE 的倾斜角为π2θ+， 2222πcos sin 2P PDE θθ==⎛⎫+ ⎪⎝⎭，而24y x =，即2P =． ∴22112sin cos AB DE P θθ⎛⎫+=+ ⎪⎝⎭2222sin cos 4sin cos θθθθ+=224sin cos θθ=241sin 24=θ 21616sin 2θ=≥，当且仅当π4θ=取等号，即AB DE +最小值为16，故选A ；【法二】依题意知：22sin PAB θ=，2222πcos sin 2P PDE θθ==⎛⎫+ ⎪⎝⎭，由柯西不等式知： 2222211(11)22816sin cos sin cos AB DE P P P θθθθ+⎛⎫+=+≥⋅== ⎪+⎝⎭，当且仅当π4θ=取等号，故选A ； 【2016，10】以抛物线C 的顶点为圆心的圆交C 于B A ,两点，交C 的准线于E D ,两点，已知24=AB ,52=DE ，则C 的焦点到准线的距离为（ ）A ．2B ．4C ．6D ．8【解析】以开口向右的抛物线为例来解答，其他开口同理设抛物线为22y px =()0p >，设圆的方程为222x y r +=，如图：设(0,22A x ，52p D ⎛- ⎝，点(0,22A x 在抛物线22y px =上，∴082px =……①；点52p D ⎛- ⎝在圆222x y r +=上，F∴2252p r ⎛⎫+= ⎪⎝⎭……②；点(0A x 在圆222x y r +=上，∴2208x r +=……③；联立①②③解得：4p =，焦点到准线的距离为4p =．故选B ． 【2016，5】已知方程132222=--+nm y n m x 表示双曲线，且该双曲线两焦点间的距离为4，则n 的取值范围是（ ） A ．)3,1(-B ．)3,1(-C ．)3,0(D ．)3,0(【解析】222213x y m n m n-=+-表示双曲线，则()()2230m n m n +->，∴223m n m -<<由双曲线性质知：()()222234c m n m n m =++-=，其中c 是半焦距，∴焦距2224c m =⋅=，解得1m = ∴13n -<<，故选A ．【2015，5】已知00(,)M x y 是双曲线C ：2212x y -=上的一点，12,F F 是C 的两个焦点，若120MF MF ⋅<，则0y 的取值范围是（ ）A ．(B ．(C ．(,33-D ．( 解析：从120MF MF ⋅<入手考虑，120MF MF ⋅=可得到以12FF 为直径的圆与C 的交点1234,,,M M M M （不妨设12,M M 在左支上，34,M M 在右支上），此时1112M F M F ⊥，1112M F M F -=-12F F =112111201211||22M F F S M F M F y F F ∆=⋅=⋅解得0||3y =，则M 在双曲线的12M M 或34M M 上运动，0y ∈(，故选A ．. 【2014，4】已知F 是双曲线C ：223(0)x my m m -=>的一个焦点，则点F 到C 的一条渐近线的距离为A B .3 C D .3m【解析】：由C ：223(0)x my m m -=>，得22133x y m -=，233,c m c =+=设)F，一条渐近线y x =，即0x =，则点F 到C 的一条渐近线的距离d =A.【2013，4】已知双曲线C ：2222=1x y a b-(a ＞0，b ＞0)的离心率为52，则C 的渐近线方程为( )．A ．y ＝14x ±B ．y ＝13x ±C ．y ＝12x ± D ．y ＝±x解析：选C ，∵5c e a ==，∴22222254c a b e a a +===，∴a 2＝4b 2，1=2b a ±，∴渐近线方程为12b y x x a =±±.【2013，10】已知椭圆E ：2222=1x y a b+(a ＞b ＞0)的右焦点为F (3,0)，过点F 的直线交E 于A ，B 两点．若AB 的中点坐标为(1，－1)，则E 的方程为( )A ．22=14536x y + B ．22=13627x y + C ．22=12718x y + D ．22=1189x y + 解析：选D ，设A (x 1，y 1)，B (x 2，y 2)，∵A ，B 在椭圆上，∴2211222222221,1,x y a b x y a b ⎧+=⎪⎪⎨⎪+=⎪⎩①②①－②，得1212121222=0x x x x y y y y a b (+)(-)(+)(-)+，即2121221212=y y y y b a x x x x (+)(-)-(+)(-)， ∵AB 的中点为(1，－1)，∴y 1＋y 2＝－2，x 1＋x 2＝2，而1212y y x x --＝k AB ＝011=312-(-)-，∴221=2b a .又∵a 2－b 2＝9，∴a 2＝18，b 2＝9.∴椭圆E 的方程为22=1189x y +.故选D. 【2012，4】设1F 、2F 是椭圆E ：2222x y a b +（0a b >>）的左、右焦点，P 为直线32ax =上一点，21F PF ∆是底角为30°的等腰三角形，则E 的离心率为（ ）A ．12 B ．23 C ．34 D ．45【解析】如图所示，21F PF ∆是等腰三角形，212130F F P F PF ∠=∠=︒，212||||2F P F F c ==，260PF Q ∠=︒，230F PQ ∠=︒，2||F Q c =，又23||2aF Q c =-， 所以32a c c -=，解得34c a =，因此34c e a ==，故选择C ．【2012，8】等轴双曲线C 的中心在原点，焦点在x 轴上，C 与抛物线216y x =的准线交于A ，B 两点，||43AB =，则C 的实轴长为（ ）A ．2B ．22C ．4D ．8【解析】设等轴双曲线C 的方程为22221x y a a-=，即222x y a -=（0a >），抛物线216y x =的准线方程为4x =-，联立方程2224x y a x ⎧-=⎨=-⎩，解得2216y a =-，因为||43AB =，所以222||(2||)448AB y y ===，从而212y =， 所以21612a -=，24a =，2a =，因此C 的实轴长为24a =，故选择C ．【2011，7】设直线L 过双曲线C 的一个焦点，且与C 的一条对称轴垂直，L 与C 交于A ,B 两点，AB 为C 的实轴长的2倍，则C 的离心率为（ ）A 2B 3C ．2D ．3解析：通径|AB|=222b a a=得2222222b a a c a =⇒-=，选B 二、填空题【2017，15】已知双曲线C ：22221x y a b-=（a >0，b >0）的右顶点为A ，以A 为圆心，b 为半径作圆A ，圆A与双曲线C 的一条渐近线交于M 、N 两点．若∠MAN =60°，则C 的离心率为________．（15）【解析】如图，OA a =，AN AM b ==， ∵60MAN ∠=︒，∴3AP =，222234OP OA PA a b =-=-，∴2232tan 34AP OP a b θ==-，又∵tan b a θ=，∴223234b a a b =-，解得223a b =，∴22123113b e a =+=+=；【法二】如上图可知(,0)A a 到渐进线0bx ay -=的距离为22abd AP ca b ===+， 1,60,cos cos302ab AP AMN a c AN AM b AMN AN b c e∠==∠=∴=====又，233e ∴=； 【法三】如图在等边三角形AMN ∆中3,,2AP b FH b ==由OAP OFH∆∆知32323baaec b c=⇒==；【法四】如图，由等面积法可得，在三角形OAN中，13232223ab cc b ea=⇒==；【法五】因为,AM b OA a==且渐进线bxya=可得三角形OAN为双曲线三角线（即三边分别为,,a b c），有几何意义易得30MAP MOA∠=∠=2323tan,133b bMOA ea a⎛⎫∴∠===+=⎪⎝⎭；【2015，14】一个圆经过椭圆221164x y+=的三个顶点，且圆心在x轴的正半轴上，则该圆的标准方程为 .解析：由椭圆的性质可知，圆只能经过短轴顶点和右顶点三个点(0,2),(0,2),(4,0)-；（方法一）设圆的半径为r，则有222(4)2r r-+=，可得52r=，故所求圆的标准方程为22325()24x y-+=.（方法二）设圆的标准方程为222()(0)x a y r a-+=>，代入点(0,2),(4,0)，解方程组可得35,22a r==半径为r，故所求圆的标准方程为22325()24x y-+=.（方法三）设圆的一般方程为220x y Dx Ey F++++=，代入点(0,2),(0,2),(4,0)-，解方程组可得3,0,4D E F=-==-,化为标准方程为22325()24x y-+=.【2014，10】已知抛物线C：28y x=的焦点为F，准线为l，P是l上一点，Q是直线PF与C的一个交点，若4FP FQ =，则||QF =A .72B .52C .3D .2 【解析】选C ，过Q 作QM ⊥直线L 于M ，∵4FP FQ =∴34PQ PF =，又344QM PQ PF ==，∴3QM =，由抛物线定义知3QF QM == 【2011，14】在平面直角坐标系xOy 中，椭圆C 的中心为原点，焦点12,F F 在x轴上，离心率为2．过1F 的直线L 交C 于,A B 两点，且2ABF 的周长为16，那么C 的方程为 ．解析：由416c a a ⎧=⎪⎨⎪=⎩得a=4.c=,从而b=8,221168x y ∴+=为所求． 三、解答题【2017，20】已知椭圆C ：2222=1x y a b +（a >b >0），四点P 1（1,1），P 2（0,1），P 3（–12 ），P 4（12）中恰有三点在椭圆C 上．（1）求C 的方程；（2）设直线l 不经过P 2点且与C 相交于A ，B 两点．若直线P 2A 与直线P 2B 的斜率的和为–1，证明：l 过定点．【解析】（1）根据椭圆对称性，必过3P 、4P ，又4P 横坐标为1，椭圆必不过1P ，所以过234P P P ，，三点，将()23011P P ⎛- ⎝⎭，，代入椭圆方程得：222113141b ab ⎧=⎪⎪⎨⎪+=⎪⎩，解得24a =，21b =， ∴椭圆C 的方程为：2214x y +=．（2）①当斜率不存在时，设()():A A l x m A m y B m y =-，，，，， 221121A A P A P B y y k k m m m----+=+==-，得2m =，此时l 过椭圆右顶点，不存在两个交点，故不满足． ②当斜率存在时，设()1l y kx b b =+≠∶，()()1122A x y B x y ，，，， 联立22440y kx b x y =+⎧⎨+-=⎩，整理得()222148440k x kbx b +++-=，|||M N MN y y =-122814kb x x k -+=+，21224414b x x k -⋅=+，则22121211P A P B y y k k x x --+=+()()21212112x kx b x x kx b x x x +-++-= 222228888144414kb k kb kbk b k --++=-+()()()811411k b b b -==-+-，又1b ≠，21b k ⇒=--，此时64k ∆=-， 存在k 使得0∆>成立．∴直线l 的方程为21y kx k =--，当2x =时，1y =-，所以l 过定点()21-，． 【2016，20】设圆015222=-++x y x 的圆心为A ，直线l 过点)0,1(B 且与x 轴不重合，l 交圆A 于D C ,两点，过B 作AC 的平行线交AD 于点E ． （Ⅰ）证明EB EA +为定值，并写出点E 的轨迹方程；（Ⅱ）设点E 的轨迹为曲线1C ，直线l 交1C 于N M ,两点，过B 且与l 垂直的直线与圆A 交于Q P ,两点，求四边形MPNQ【解析】：⑴ 圆A 整理为(1x +BE AC ∥，则C =∠EBD D ∴=∠∠，则EB =⑵ 221:143x y C +=；设:l x 联立l 与椭圆圆心A 到所以||PQ =()2212111||||2234MPNQm S MN PQ m +⎡∴=⋅=⋅==⎣+ 【2015，20】在直角坐标系xOy 中，曲线C ：24x y =与直线l ：y kx a =+（0a >）交于,M N 两点.（Ⅰ）当0k =时，分别求C 在点M 和N 处的切线方程；（Ⅱ）在y 轴上是否存在点P ，使得当k 变动时，总有OPM OPN ∠=∠？说明理由. 解：（Ⅰ）当0k =时，点(2,)M a a 和(2,)N a a -，2xy '=，故2x a =处的导数值为a ，切线方程为(2)y a a x a -=-，即0ax y a --=；同理，2x a =-处的导数值为a -，切线方程为(2)y a a x a -=-+，即0ax y a ++=.（Ⅱ）在y 轴上存在点P ，使得当k 变动时，总有OPM OPN ∠=∠.证明如下： 设(0,)P b 为符合题意的点，1122(,),(,)M x y N x y ，直线,PM PN 的斜率分别为12,k k . 直线l 与曲线C 的方程联立可得2440x kx a --=，则12124,4x x k x x a +==-.1212121212122()()()y b y b kx x a b x x k a b k k x x x x a--+-+++=+==，当b a =-时，120k k +=，则直线,PM PN 的倾斜角互补，故OPM OPN ∠=∠，即(0,)P a -符合题意.【2014，20】已知点A （0，-2），椭圆E ：22221(0)x y a b a b+=>>的离心率为32，F 是椭圆的焦点，直线AF 的斜率为233，O 为坐标原点. (Ⅰ)求E 的方程；（Ⅱ）设过点A 的直线l 与E 相交于,P Q 两点，当OPQ ∆的面积最大时，求l 的方程. 【解析】：(Ⅰ) 设(),0F c ，由条件知2233c =，得3c = 又3c a =， 所以a=2，2221b a c =-= ,故E 的方程2214x y +=. …….6分 （Ⅱ）依题意当l x ⊥轴不合题意，故设直线l ：2y kx =-，设()()1122,,,P x y Q x y将2y kx =-代入2214x y +=，得()221416120k x kx +-+=， 当216(43)0k ∆=->，即234k >时，21,22824314k k x k±-=+ 从而2221241431k k PQ k x +-=+-=，又点O 到直线PQ 的距离21d k =+，所以∆OPQ的面积221443214OPQk S d PQ k ∆-==+ ，设243k t -=，则0t >，244144OPQ t S t t t∆==≤++， 当且仅当2t =，7k =±等号成立，且满足0∆>， 所以当∆OPQ 的面积最大时，l 的方程为：72y x =- 或72y x =--. ……12分 【2013，20】已知圆M ：(x ＋1)2＋y 2＝1，圆N ：(x －1)2＋y 2＝9，动圆P 与圆M 外切并且与圆N 内切，圆心P 的轨迹为曲线C .(1)求C 的方程；(2)l 是与圆P ，圆M 都相切的一条直线，l 与曲线C 交于A ，B 两点，当圆P 的半径最长时，求|AB |.解：由已知得圆M 的圆心为M (－1,0)，半径r 1＝1；圆N 的圆心为N (1,0)，半径r 2＝3.设圆P 的圆心为P (x ，y )，半径为R .(1)因为圆P 与圆M 外切并且与圆N 内切，所以|PM |＋|PN |＝(R ＋r 1)＋(r 2－R )＝r 1＋r 2＝4.由椭圆的定义可知，曲线C 是以M ，N 为左、右焦点，长半轴长为2，短半轴长为3的椭圆(左顶点除外)，其方程为22=143x y +(x ≠－2)． (2)对于曲线C 上任意一点P (x ，y )，由于|PM |－|PN |＝2R －2≤2，所以R ≤2，当且仅当圆P 的圆心为(2,0)时，R ＝2.所以当圆P 的半径最长时，其方程为(x －2)2＋y 2＝4.若l 的倾斜角为90°，则l 与y 轴重合，可得|AB |＝23.若l 的倾斜角不为90°，由r 1≠R 知l 不平行于x 轴，设l 与x 轴的交点为Q ，则1||||QP RQM r =，可求得Q (－4,0)，所以可设l ：y ＝k (x ＋4)．由l 与圆M 相切得2=11k +，解得k ＝2±. 当k ＝24时，将224y x =+代入22=143x y +，并整理得7x 2＋8x －8＝0，解得x 1,2＝4627-±. 所以|AB |＝221181||7k x x +-=.当2k =-时，由图形的对称性可知|AB |＝187.综上，|AB |＝23或|AB |＝187.【2012，20】设抛物线C ：py x 22=（0>p ）的焦点为F ，准线为l ，A 为C 上一点，已知以F 为圆心，F A 为半径的圆F 交l 于B ，D 两点．（1）若∠BFD =90°，△ABD 的面积为24，求p 的值及圆F 的方程；（2）若A ，B ，F 三点在同一直线m 上，直线n 与m 平行，且n 与C 只有一个公共点，求坐标原点到m ，n 距离的比值． 【解析】（1）若∠BFD =90°，则△BFD 为等腰直角三角形，且|BD|=2p ，圆F 的半径||2r FA p ==，又根据抛物线的定义可得点A 到准线l 的距离||2d FA p ==．因为△ABD 的面积为24， 所以1||422BD d ⋅⋅=，即122422p p ⋅⋅=， 所以24p =，由0>p ，解得2p =． 从而抛物线C 的方程为24x y =，圆F 的圆心F （0，1），半径||22r FA ==， 因此圆F 的方程为22(1)8x y +-=． （2）若A ，B ，F 三点在同一直线m 上， 则AB 为圆F 的直径，∠ADB=90°， 根据抛物线的定义，得1||||||2AD FA AB ==，所以30ABD ∠=︒，从而直线m 的斜率为3或3-． 当直线m 的斜率为33时，直线m 的方程为332py x =+，原点O 到直线m 的距离12231()3pd =+．依题意设直线n 的方程为33y x b =+，联立2332y x b x py⎧=+⎪⎨⎪=⎩，得223203x px pb --=， 因为直线n 与C 只有一个公共点，所以24803p pb ∆=+=，从而6pb =-． 所以直线n 的方程为336py x =-，原点O 到直线n 的距离22631()3pd =+．因此坐标原点到m ，n 距离的比值为12236p dpd ==．当直线m 的斜率为3-时，由图形的对称性可知，坐标原点到m ，n 距离的比值也为3． 【2011，20】在平面直角坐标系xOy 中，已知点A(0,-1)，B 点在直线y = -3上，M 点满足//MB OA ，MA AB MB BA ⋅=⋅，M 点的轨迹为曲线C ．（Ⅰ）求C 的方程；（Ⅱ）P 为C 上的动点，l 为C 在P 点处得切线，求O 点到l 距离的最小值． 解：（I ）设(),M x y ，由已知得(),3B x -，()0,1A -. 所以(),1,MA x y =---，()0,3,MB y =--，(),2AB x =-.再由题意可知()0MA MB AB +⋅=，即()(),4,2,20x y x ---⋅=. 所以曲线C 的方程为2124y x =-. （II ）设()00,P x y 为曲线21:24C y x =-上一点，因为12y x '=，所以l 的斜率为012x . 因此直线l 的方程为()00012y y x x x -=-，即2000220x x y y x -+-=. 则O 点到l的距离d =. 又200124y x =-，所以2014122x d +⎫==≥ 当00x =时取等号，所以O 点到l 的距离的最小值为2.。