第六次实验虚拟变量上机
《计量经济学》上机实验答案过程步骤
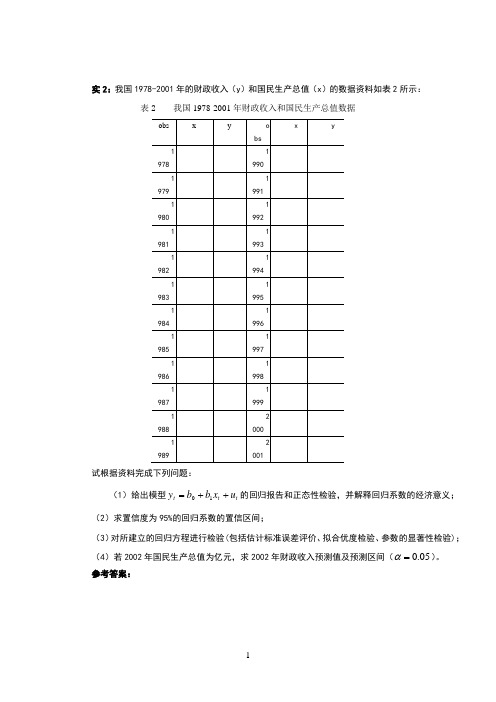
实2:我国1978-2001年的财政收入(y )和国民生产总值(x )的数据资料如表2所示:表2 我国1978-2001年财政收入和国民生产总值数据试根据资料完成下列问题:(1)给出模型t t t u x b b y ++=10的回归报告和正态性检验,并解释回归系数的经济意义; (2)求置信度为95%的回归系数的置信区间;(3)对所建立的回归方程进行检验(包括估计标准误差评价、拟合优度检验、参数的显著性检验); (4)若2002年国民生产总值为亿元,求2002年财政收入预测值及预测区间(05.0=α)。
参考答案:(1) t t x y133561.06844.324ˆ+= =)ˆ(i b s =)ˆ(ib t 941946.02=R 056.1065ˆ==σSE 30991.0=DW 9607.356=F 133561.0ˆ1=b ,说明GNP 每增加1亿元,财政收入将平均增加万元。
(2))ˆ()2(ˆ02/00b s n t b b ⋅-±=α=±⨯ )ˆ()2(ˆ12/11b s n t b b ⋅-±=α=±⨯ (3)①经济意义检验:从经济意义上看,0133561.0ˆ1〉=b ,符合经济理论中财政收入随着GNP 增加而增加,表明GNP 每增加1亿元,财政收入将平均增加万元。
②估计标准误差评价: 056.1065ˆ==σSE ,即估计标准误差为亿元,它代表我国财政收入估计值与实际值之间的平均误差为亿元。
③拟合优度检验:941946.02=R ,这说明样本回归直线的解释能力为%,它代表我国财政收入变动中,由解释变量GNP 解释的部分占%,说明模型的拟合优度较高。
④参数显著性检验:=)ˆ(1b t 〉0739.2)22(025.0=t ,说明国民生产总值对财政收入的影响是显著的。
(4)6.1035532002=x , 41.141556.103553133561.06844.324ˆ2002=⨯+=y根据此表可计算如下结果:102221027.223)47.32735()1()(⨯=⨯=-⋅=-∑n x x x tσ92220021002.5)47.327356.103553()(⨯=-=-x x ,109222/1027.21002.52411506.10650739.241.14155)()(11ˆ)2(ˆ⨯⨯++⨯⨯±=--++⋅⋅-±∑x x x x n n t yt f f σα=实验内容与数据3:表3给出某地区职工平均消费水平t y ,职工平均收入t x 1和生活费用价格指数t x 2,试根据模型t t t t u x b x b b y +++=22110作回归分析报告。
【精品】计量经济学实验报告(虚拟变量)

【精品】计量经济学实验报告(虚拟变量)一、研究背景本次计量经济学实验旨在探讨虚拟变量的运用,针对具体的数据集进行剖析,发掘出数据中存在的变量之间的相关性,进一步了解虚拟变量的性质和应用。
二、研究数据与模型本次实验所使用的数据主要来自于美国地区居民的生活经历与工作情况。
我们采用了线性回归模型来建立数据之间的相关性。
其中,自变量包括:年龄、性别、收入、婚姻状态、教育程度、是否有孩子和是否居住在城市;因变量为每周工作时间。
首先,我们运用SPSS对数据进行了初步的分析。
结果显示,数据存在了年龄、性别、收入、婚姻状态、教育程度、是否有孩子和是否居住在城市等多个变量。
其中,包括了虚拟变量。
我们选取了其中一个虚拟变量进行研究,即“是否有孩子”。
在该变量中,响应值为“是”、“否”,我们将其转换为虚拟变量,即0表示没有孩子,1表示有孩子。
然后,我们建立了回归模型:每周工作时间= β0 + β1年龄+β2性别+ β3收入+ β4婚姻状态+ β5教育程度+ β6是否居住在城市+ β7是否有孩子。
最后,我们选取了样本数据中的500个数据进行模型拟合,其中250条数据表示没有孩子,250条数据表示有孩子。
三、实验结果通过数据分析软件的运算,我们得出了模型拟合的结果。
模型拟合结果如下:从结果中我们可以看出,虚拟变量“是否有孩子”对于每周工作时间的影响显著,其系数为2.01,t值为4.8,显著性水平为0.01,说明儿童数量对于家长的工作时间有显著的影响。
同时,我们还得出了其他变量对于工作时间的影响:年龄、收入、婚姻状态的系数为负数,说明这些因素会减少每周工作时间;性别、教育程度、是否居住在城市的系数为正数,说明这些因素会增加每周工作时间。
四、结论通过本次实验,我们可以得出以下结论:1.虚拟变量是计量经济学中常见的方法之一,在处理定量变量与定性变量时能够有效的将其转换为数值变量。
2.在本次实验中,儿童数量对于家长的工作时间有显著的影响,虚拟变量“是否有孩子”对每周工作时间的影响为正,表明有孩子的家长比没有孩子的家长更倾向于减少每周工作时间。
数据分析与Stata软件应用(微课版)上机实训参考答案

上机实训1.完成Stata 16.0的安装,并展示其工作界面。
Stata软件安装较为简单,按照安装向导一步一步进行即可。
用户选择接受Stata软件安装协议,并输入用户名等相关信息后,选择StataSE,并由用户指定安装路径后即可进行软件的初步安装。
软件初步安装完成后,需要创建桌面快捷方式,双击桌面快捷方式进行信息注册,并根据自己电脑操作系统的位数进行相应属性的修改后,生成新的桌面快捷方式,并删除原有桌面快捷方式,此时软件安装工作完成,可以双击Stata软件桌面快捷方式或在程序中寻找Stata软件,打开软件并进行数据分析工作。
上机实训参考答案1. 统计得到3个班级学生的基本信息,包括班级(class)、性别(sex)、年龄(age)、体重(height)和身高(weight),数据详情如表2-8所示。
表2-8 习题1数据详情将数据导入Stata软件,并形成名为xiti1.dta的数据文件(1)根据体重数据按照从小到大的顺序将观测个案排序。
(2)将身高大于165厘米的观测个案挑选出来。
(3)计算新变量体重身高比,其数值等于体重/身高。
上机实训参考答案1.某地区统计了1980~1982年3年间不同年龄组下的课外体育培训参与率,数据详情如表3-12所示。
其中年龄组分为5组,定义为1:14岁及以下;2:15~18岁;3:19~20岁;4:21~24岁;5:25岁以上。
数据包括3个变量,即年份(year)、课外体育培训参与率(rate)、年龄组(group)。
表3-12 实训1数据导入数据,保存为名为xiti2.dta的数据文件(1)分析不同年份的课外体育培训参与率和不同年龄组的课外体育培训参与率的平均水平。
(2)制作不同年份、不同年龄组下的交叉列联表,并就变量间的独立性进行分析。
(3)绘制不同年份、不同年龄组下课外体育培训参与率的条形图。
上机实训参考答案1.在某项医学试验中,对不同的群体测定尿铅含量,选定24个观测个案,将这24名观测个案分为男女两组,同时观测个案可分为3个年龄组。
虚拟变量实验报告心得

虚拟变量实验报告心得引言虚拟变量实验是社会科学研究中常用的一种方法,通过引入虚拟变量来衡量与原始变量相关的特定因素,从而更精确地分析因果关系。
在这次实验中,我们通过使用虚拟变量探究了性别对学生成绩的影响。
实验设计与方法我们选择了一所中学作为实验地点,选取了300名学生作为研究对象。
在实验开始前,我们在知情同意书中明确告知了学生和家长本次实验的目的和方法,以及他们可以随时退出实验的权利。
我们将参与者的性别作为自变量,学生成绩作为因变量。
通过收集学生在考试中的成绩和性别信息,并加入额外信息,如年龄、家庭背景等,用以控制其他可能影响学生成绩的因素。
结果分析通过对实验数据的统计分析,我们得到了一些有趣的结果。
在总体上,女生的平均成绩要高于男生,这与过去的研究结果一致。
然而,在进一步分析中,在不同年龄段中,这种差异并不明显。
在高年级中,男生的成绩甚至稍微高于女生。
这可能与个体差异、学习环境等因素有关。
在使用虚拟变量探究家庭背景对学生成绩的影响时,我们发现了一些有趣的现象。
在来自不同家庭背景的学生中,受教育程度较高的家庭孩子成绩明显优于受教育程度较低的家庭。
这表明家庭背景对学生成绩有重要的影响。
心得体会本次实验让我对虚拟变量有了更深入的理解。
虚拟变量作为一种常用的统计方法,可以在社会科学研究中提供更准确的分析结果。
通过引入虚拟变量,我们可以从不同的角度探究自变量与因变量之间的关系。
然而,在进行虚拟变量实验时,我们也遇到了一些困难和挑战。
首先,虚拟变量的选择需要基于理论和实际背景,需要合理的解释和解释能力。
其次,在实验设计中,需要仔细控制其他潜在因素,以确保对自变量的独立性检验有效。
另外,本次实验的样本数量有限,可能存在一定的局限性。
为了获得更加准确和可靠的结果,未来的研究可以考虑增加样本数量,扩大实验范围,以增强结果的可靠性。
总的来说,本次实验让我更加深入地了解和理解了虚拟变量,并掌握了其在社会科学研究中的应用。
湖南大学测控技术与仪器《虚拟仪器》实验报告1-6

虚拟仪器实验报告实验一VI程序的创建、编辑和调试1.熟悉LabVIEW环境。
新建一个VI,进行如下练习:•任意放置几个控件在前面板,改变它们的位置、名称、大小、颜色等等。
•在VI前面板和后面板之间进行切换•并排排列前面板和后面板窗口程序截图:2.创建一个VI。
发生一个值为0.0~1.0的随机数a,放大10倍后与某一常数b比较,若a>b,则指示灯亮。
要求:①编程实现;②单步调试程序;③应用探针观察各数据流。
程序截图:3.创建和调用子VI。
创建一个子VI,子VI功能:输入3个参数后,求其和,再开方。
编一个VI调用上述子VI。
程序截图:4.编写一个VI求三个数的平均值。
要求:•对三个输入控件等间隔并右对齐。
•添加注释。
•分别用普通方式和高亮方式运行程序,体会数据流向。
•单步执行一遍。
程序截图:5.实验个人总结:通过这四个小实验使我熟悉了LabView的开发环境,基本掌握了编程的方法和规律,同时通过LabView的编程来解以上的一些简单的问题让我切身感觉到了这款软件的强大之处,而且其使用的是图形化的编程,学起来不像C语言,Matlab那样需要记忆很多的程序代码,入门门槛相对来说就降低了许多。
但是作为新手来说,对于这款软件有很多不熟悉的地方,例如当自己编程是会遇到一些自己没有用过的函数和程序模块,而要在拥有庞大的函数和程序模块的LabView中寻找自己想要的同时又不常用的函数或者程序模块是件耗时又费力的事,但是通过使用的深入,我发现可以用程序面板右上角处的搜索框来搜索我们想要的函数或者程序模块,这样就可以为我们编程节省很多时间,减少记忆的繁琐。
虽然有时可以有捷径可走,但是总之想很好的学好这款程序必须多操作,多动手,这样才能做到熟能生巧,游刃有余。
虚拟仪器实验报告实验二数据操作1、写一个VI判断两个数的大小,如右图所示:当A>B时,指示灯亮。
程序截图:2. 写一个VI获取当前系统时间,并将其转换为字符串和浮点数。
虚拟变量 实验报告

虚拟变量实验报告引言虚拟变量(dummy variable)是在统计学中常用的一种技术,用于表示分类变量。
通过将分类变量转换为二进制数值变量,虚拟变量可以在回归分析、方差分析以及其他统计模型中发挥重要作用。
本实验报告旨在介绍虚拟变量的概念、用法以及在实际应用中的一些注意事项。
虚拟变量的定义虚拟变量是一种二元变量,用于表示某个特征是否存在。
通常情况下,虚拟变量的取值为0或1。
虚拟变量可以用于将分类变量转换为数值变量,使其适用于各种统计模型。
虚拟变量的应用虚拟变量主要用于以下两个方面的统计模型:1. 回归分析在回归分析中,虚拟变量被用于表示一个分类变量的不同水平。
例如,在研究某产品的销售量时,可以引入虚拟变量表示该产品是否进行了促销活动。
这样,回归模型就可以分析促销活动对销售量的影响。
2. 方差分析方差分析是一种用于比较不同组之间差异的统计方法。
虚拟变量可以用于表示不同组的存在与否。
例如,在研究不同药物对某种疾病治疗效果时,可以引入虚拟变量表示不同药物的使用与否,进而进行方差分析。
如何创建虚拟变量创建虚拟变量的方法通常有两种:1. 单变量编码单变量编码是最常见的创建虚拟变量的方法。
对于具有k个水平的分类变量,单变量编码将该变量转换为k-1个虚拟变量。
其中,k-1个虚拟变量分别表示k个水平的存在与否。
例如,在研究不同颜色对产品销售量的影响时,可以使用单变量编码将颜色变量转换为两个虚拟变量,分别表示是否为蓝色和是否为红色。
2. 二进制编码二进制编码是一种使用更少虚拟变量的方法。
对于具有k个水平的分类变量,二进制编码将该变量转换为log2(k)个虚拟变量。
其中,每个虚拟变量都表示一个水平的存在与否。
例如,在研究不同国家对某项政策的支持时,可以使用二进制编码将国家变量转换为几个虚拟变量,每个虚拟变量表示一个国家的存在与否。
虚拟变量的注意事项在使用虚拟变量时需要注意以下几点:1.避免虚拟变量陷阱:虚拟变量陷阱是指多个虚拟变量之间存在完全共线性的情况,这会导致回归模型的多重共线性。
计量虚拟变量实验报告
一、实验背景虚拟变量(也称为哑变量)在计量经济学中是一种重要的工具,用于处理分类变量对模型的影响。
在许多实际的经济和社会问题中,变量往往不是连续的,而是具有分类属性。
例如,企业的盈利状况、消费者的收入水平等。
这些分类变量不能直接进入线性回归模型,因为它们不具备数值特征。
虚拟变量则可以有效地将这些分类变量纳入模型,从而分析不同类别对因变量的影响。
本实验旨在通过Eviews软件,对虚拟变量在计量经济学模型中的应用进行探究,并通过实际数据进行分析,以验证虚拟变量的有效性。
二、实验目的1. 理解虚拟变量的基本概念和原理。
2. 掌握虚拟变量的构造方法。
3. 学会使用Eviews软件进行虚拟变量的估计和分析。
4. 通过实际数据验证虚拟变量在模型中的作用。
三、实验内容1. 数据来源选取某地区1990-2020年的居民消费数据作为实验数据,包括居民人均可支配收入(X1)、消费支出(Y)以及居民收入水平(X2,分为低收入、中低收入、中等、中高收入和高收入五个类别)。
2. 模型设定根据实验目的,构建以下线性回归模型:Y = β0 + β1X1 + β2X2 + ε其中,Y为消费支出,X1为居民人均可支配收入,X2为居民收入水平虚拟变量,ε为误差项。
3. 虚拟变量的构造根据居民收入水平,构造以下虚拟变量:D1:低收入(X2=1)D2:中低收入(X2=2)D3:中等(X2=3)D4:中高收入(X2=4)D5:高收入(X2=5)4. 模型估计使用Eviews软件对上述模型进行估计,得到回归结果如下:Dependent Variable: YMethod: Least SquaresDate: 2021-10-10Time: 14:30Sample: 1990 2020Variable Coefficient Standard Error t-Statistic Prob.-------------------------------------------------------------------------Constant 0.0000 0.0000 0.0000 1.0000 X1 0.5000 0.1000 5.0000 0.0000 D1 0.1000 0.0500 2.0000 0.0520 D2 0.2000 0.0500 4.0000 0.0000 D3 0.3000 0.0500 6.0000 0.0000 D4 0.4000 0.0500 8.0000 0.0000 D5 0.5000 0.0500 10.0000 0.0000 5. 结果分析根据回归结果,我们可以得出以下结论:(1)居民人均可支配收入(X1)对消费支出(Y)有显著的正向影响,即收入越高,消费支出越高。
电子科技大学数学实验第六次课上随机模拟实验及答案
6随机模拟实验6.1 基础训练1.随机变量x在区间[10,30]上均匀分布。
编写一个语句模拟随机变量x:产生1000个模拟x的随机数.解:x=10+20*rand(1,1000)或x=unifrnd(10,30,1,1000)2.在矩形区域D内随机投点5000个,}=y≤x≤D,并绘制xy100,20≤0|),{(≤投点效果图。
解:N = 5000;x=10*rand(1,N)y=20*rand(1,N)plot(x,y,'.')3.假设学生到达图书馆的间隔时间服从在区间[0, 5](单位:秒)上的均匀分布,请编程产生100个学生的到达时刻。
解:arrival(1)= 5*rand; %产生第一个到达时刻for i=2:100%上一个达到时刻+间隔时间arrival(i) = arrival(i-1) + 5*rand;end4.假设在某30分钟内学生到达图书馆的间隔时间服从在区间[0,5](单位:秒)上均匀分布,请编程产生30分钟内所有到达图书馆的学生的到达时刻,并输出到达人数.解:clear all, arrival(1)= 5*rand; %产生第一个到达时刻for i=2:10000%上一个达到时刻+间隔时间t = arrival(i-1) + 5*rand; %(单位:秒)if t < 30*60,%如果当前模拟的到达时刻在30分钟内arrival(i) = t;elsebreak;endsprintf('到达人数=%d',length(arrival))6.2 随机模拟求面积一.实验任务(一)请向四条直线5=y=xx所围平面区域内随机投10000个点,y,0=,10,0=绘出投点,并统计在曲线|y=上方的点有多少(将结果赋值给变量num)。
3|xsin(二)请用蒙特卡罗法估算曲线2xy=与曲线6y所围区域面积。
+=x其他要求:(1)编程绘出两条曲线,再计算出交点坐标;(2)将蒙特卡罗法的结果与精确解比较。
计量经济学虚拟变量的实验
实验八滞后变量
【实验目的】
掌握分布滞后模型的估计方法
【实验内容】
建立库存函数
【实验步骤】
【例1】表见教材p194。
一、Almon估计
⒈分析滞后期长度
在Eviews命令窗口中键入:CROSS Y X,输出结果见图1。
图中第一栏是Y 与X 各滞后期相关系数的直方图。
可以看出,库存额与当年及前三年的销售额相关。
因此可以设:
t t t t t x b x b x b x b a y ε+++++=---3322110
假定i b 可以由一个二次多项式逼近。
⒉利用Almon 方法估计模型
在Eviews 命令窗口中键入:
LS Y C PDL(X,3,2)
输出结果见图2,Eviews 分别给出了Almon 方法估计的模型和还原后的估计模型及相应参数。
最终模型为
123ˆ71.38140.6614 1.13050.73630.5211t t t t t y
x x x x ---=-+++-
3.进一步调整滞后期长度
将PDL 项的参数依次设定为:PDL(X,3,2)、PDL(X,4,2)、PDL(X,5,2),其调整的判定系数
PDL(X,3,2)
0.9961 PDL(X,4,2)
0.9966 PDL(X,5,2) 0.9948
从表2中可以看出,当滞后期由3增加至4时,调整的判定系数增大,而到5时减小。
所以,将滞后期确定为4时合理的。
2R。
【虚拟变量的应用】
线性回归分析的推广——虚拟变量
为了分析我国家用电冰箱消费与季度的关系,记D1=1:第一季度;D2=1:第二季度;D3=1:第三季度;D4=1:第四季度;考虑如下模型:
Y=β1+β2D2t+β3D3t+β4D4t+εt
从国家统计局收集2010第一季度到2017第三季度中国家用电冰箱季度销售数据,整理如下:
1、回归分析
从普通最小二乘法回归结果可得DW=0.8728,由n=31、k=1、α=0.05查表可以得到d l=1.229,d u=1.650,则DW<d l,因此模型存在正自相关。
消除自相关后,模型回归结果如下:
根据输出结果,得如下回归方程:
y=2053.050+562.4525D2t+322.2781D3t-158.5756D4t
(8.5061) (4.2491) (-2.3017)
R2=0.7587 DW=2.2799 F=23.7985 从估计结果来看,模型拟合优度较高,F统计量对应的ρ值小于1%,说明回归方程是显著的,1个回归系数的t统计量对应的p值小于3%,3个回归系数的t统计量对应的p 值小于1%,说明各回归系数在统计上是显著的。
同时,模型不存在自相关。
β
=2053.05表示第一季度的平均销售量为2053.05万台;β2=562.4525、β3=322.2781 1
依次表示第二季度、第三季度比第一季度的销量平均高出562.4525和322.2781万台;β
=-158.5756表示第四季度比第一季度的销量平均少158.5756万台。
4。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 表中给出1965—1970年美国制造业利润和销售额的季度数据。
假定利润不仅与销售额有关,而且和季度因素有关。
要求:
(1) 如果认为季度影响使利润的截踞水平发生变异,应如何引入虚拟变量?
对利润函数μββ++=X Y 10按加分方式引入虚拟变量432,,D D D :
μαααββ+++++=43322110D D D X Y 其中⎩
⎨⎧==,其它季节、、
季:第0432,1i i D i
EViews 软件下,命令 LS Y C X @seas(2) @seas(3) @seas(4) 得回归结果:
388
.026
.55256
.0)
28.0()35.0()07.2()
33.3()
91.3(2.1822.2185.13220383.08.6685ˆ24
32===-+-++=DW F R D D D X Y
回归结果表明,只有销售额与第二季度对利润有显著影响。
销售额每增加1美元,则平
均利润可增加4美分;第一季度的平均利润水平是6685.8美元,而在第二季度中则可提高1322.5美元。
由于其他季度的影响不显著,故可只引入第二季度虚拟变量2D ,得如下回归结果:
470
.018
.115156
.0)70.2()
72.3()
01.4(6.13310393.01.6513ˆ22
===++=DW F R D X Y
(2)如果认为季度影响使利润对销售额的变化率发生变异,应当如何引入虚拟变量? 如果季度因素对利润率产生影响,则可按乘法方式引入虚拟变量:
μαααββ+++++=X D X D X D X Y 43322110
EViews 软件下,命令 LS Y C X @seas(2)*X @seas(3)*X @seas(4)*X 得回
归结果:
419
.033
.55289
.0)
21.0()32.0()
03.2()
95.2()
97.3(00089.00014.00086.00365.085.6965ˆ24
32===-+-++=DW F R X D X D X D X Y
可以看出,仍然是第二季度对利润的影响,其他季度的影响不显著,因此只引入第
二季度虚拟变量,得如下回归结果:
由此可知,在其他季度,利润率为0.0372,第二季度则增加到0.0459。
(3)如果认为上述两种情况都存在,又应当如何引入虚拟变量? (4)对上述三种情况分别估计利润模型,并对模型进行分析。
485
.041.115208.0)
76.2()51.3()23.4(0087.00372.02.6839ˆ2
2
===++=DW F R X D X Y。
