3_2动量守恒定律
合集下载
第3章动量守恒定律_物理学

K K 两小球质量分别为m1和m2, 碰前速度为v1 和 v 2 , K K 碰后速度为 u1和 u 2 。
根据动量守恒定律得 K K K K m1v1 + m2 v 2 = m1u1 + m2 u 2 ⑴
根据能量守恒定律得
1 2 2 2 2 1 1 m1v12 + 1 m v = m u + m u 2 2 2 2 2 1 1 2 2
⑵ ⑶ ⑷ ⑸ ⑹
若碰撞为正碰,则有
m1v1 + m2 v 2 = m1u1 + m2 u 2
⑵式除以⑶得
v1 - v 2 = u 2 - u1
m1 - m2 2m 2 )v1 + ( )v 2 由⑶、⑷解得 u1 = ( m1 + m2 m1 + m2 m2 - m1 2m1 u2 = ( )v1 + ( )v 2 m1 + m2 m1 + m2
⎫ = − F d t m v m v ∫t0 ∑ ix ∑ i ix ∑ i i 0 x ⎪ ⎪ t ⎪ ∫t0 ∑ Fiy dt = ∑ mi viy − ∑ mi vi 0 y ⎬ ⎪ t ⎪ = − F d t m v m v ∫t0 ∑ iz ∑ i iz ∑ i i 0 z ⎪ ⎭
t
此式表明,外力矢量和在某一方向的冲量等于在 该方向上质点系动量分量的增量。
0
此式表示,在运动过程中,作用于质点的合力 在一段时间内的冲量等于质点动量的增量。这个结 论称为动量定理。 K K K F 为恒力时 I = F (t - t 0 ) K F 为变力,且作用时间很短时,可用平均值来代替 t K K K K ∫t F d t I = F (t - t 0 ) F= t − t0
基础物理 第三章 动量与角动量 3-2

Fn
地
动量不守恒。因为 Fn作用,即 F外 0。
03_02_动量守恒定律 —— 动量与角动量
7/11
例题03 一辆装煤车以的速率v 3 m / s 从煤斗下面通过, 每秒落入车厢的煤 。如果车厢的速率保持不变, m 500 kg 应该用多大的牵引力拉车厢?(不计车厢与钢轨之间的摩擦) t 时刻煤车和已经落入煤车煤的质量为m,速率v dt 时间内落入煤车的煤的质量dm
1/11
对两个质点分别应用牛顿第二定律得到
dp F1 f 1 dt dp F2 f ' 2 dt f f '
—— 两个质点相互作用内力是一对作用与反作用力
d —— 两式相加 F1 F2 ( p1 p2 ) dt
03_02_动量守恒定律 —— 动量与角动量
dp F dt
2/11
dp F dt F F1 F2 —— 两个质点构成的系统受到的外力
p p1 p2 ——
两个质点构成的系统总的动量
Fdt dp
—— 两个质点系统的动量定理
03_02_动量守恒定律 —— 动量与角动量
3/11
i t0 i i
—— 积分形式
4/11
03_02_动量守恒定律 —— 动量与角动量
2. 动量守恒定律
如果 Fi 0
i
d d Fi pi mi vi dt i dt i i mivi C —— 质点系动量守恒定律
i
if Fx 0
直角坐标系中 if F 0 y
3.2 动量守恒定律 1.质点系的动量定理
多个质点构成的系统 —— 质点系 外力 —— 来自系统以外对系统 内所有质点的作用力 内力 —— 系统内质点之间的相 互作用力 —— 两个质点构成的系统
地
动量不守恒。因为 Fn作用,即 F外 0。
03_02_动量守恒定律 —— 动量与角动量
7/11
例题03 一辆装煤车以的速率v 3 m / s 从煤斗下面通过, 每秒落入车厢的煤 。如果车厢的速率保持不变, m 500 kg 应该用多大的牵引力拉车厢?(不计车厢与钢轨之间的摩擦) t 时刻煤车和已经落入煤车煤的质量为m,速率v dt 时间内落入煤车的煤的质量dm
1/11
对两个质点分别应用牛顿第二定律得到
dp F1 f 1 dt dp F2 f ' 2 dt f f '
—— 两个质点相互作用内力是一对作用与反作用力
d —— 两式相加 F1 F2 ( p1 p2 ) dt
03_02_动量守恒定律 —— 动量与角动量
dp F dt
2/11
dp F dt F F1 F2 —— 两个质点构成的系统受到的外力
p p1 p2 ——
两个质点构成的系统总的动量
Fdt dp
—— 两个质点系统的动量定理
03_02_动量守恒定律 —— 动量与角动量
3/11
i t0 i i
—— 积分形式
4/11
03_02_动量守恒定律 —— 动量与角动量
2. 动量守恒定律
如果 Fi 0
i
d d Fi pi mi vi dt i dt i i mivi C —— 质点系动量守恒定律
i
if Fx 0
直角坐标系中 if F 0 y
3.2 动量守恒定律 1.质点系的动量定理
多个质点构成的系统 —— 质点系 外力 —— 来自系统以外对系统 内所有质点的作用力 内力 —— 系统内质点之间的相 互作用力 —— 两个质点构成的系统
大学物理之3-2动量守恒定律

实验器材与步骤
• 实验器材:滑块、气垫导轨、挡光板、光电门、天平、砝 码、小车等。
实验器材与步骤
实验步骤 1. 将滑块放置在气垫导轨上,调整挡光板的位置,使滑块能够顺利通过光电门。
2. 使用天平测量滑块和小车的质量,并记录下来。
实验器材与步骤
01
3. 将小车从静止状态释放,使其与滑块发生碰撞。
04 动量守恒定律的推导与证 明
推导过程
01
牛顿第二定律:物体受到的合外 力等于其质量与加速度的乘积。
02
定义动量为物体的质量与速度的 乘积,即$p=mv$。
根据牛顿第二定律,物体受到的 合外力等于其动量的变化率,即 $frac{dp}{dt}=ma$。
03
当合外力为零时,动量守恒,即 $frac{dp}{dt}=0$。
02
4. 使用光电门测量小车和滑块碰撞前后的速度,并记录下来。
5. 根据测量数据计算系统在碰撞前后的动量变化,验证动量守
03
恒定律。
实验结果与结论
实验结果
通过测量和计算,发现系统在碰撞前后的动量变化符合动量守恒定律。
实验结论
实验验证了动量守恒定律的正确性,加深了对动量守恒定律的理解。同时,实验过程中需要注意控制 实验条件,保证测量数据的准确性和可靠性。
能量守恒定律
在某些条件下,动量守恒定律和能量守恒定律可以 结合起来使用,如碰撞过程中动能和动量的关系。
角动量守恒定律
当系统受到的力矩为零时,系统的角动量保 持不变,与动量守恒定律一起描述了机械运 动的守恒规律。
在现代物理学中的应用
01
基本粒子
在研究基本粒子的相互作用和演 化过程中,动量守恒定律是重要 的理论基础。
3-2质心运动定理、角动量守恒
L
O
●
rA r
●
A α m
●
v
证明: 不受外力,质点将做 匀速直线运动。 m在某一时刻经过A点时, 其对固定点O的角动量为
L rA mv rAmvsin r m v
固定点O到轨迹直线的垂直距离只有一 个值,所以角动量的大小恒定。 而角动量的方向恒垂直于固定点O和运动 轨迹所决定的平面。 所以m对任意固定点的角动量矢量保持不变。
力矩的大小:
力矩的方向: 角动量定理:
M r F rF sin
也由右螺旋法则确定。
dL M dt
质点所受的合外力矩等于它的角动量对时间的 变化率。 M 注意:定理中的力矩和角 动量是对惯性系中地同一 固定点而言的。
o
●
r
F
r
α
m
§3.7 角动量守恒定律
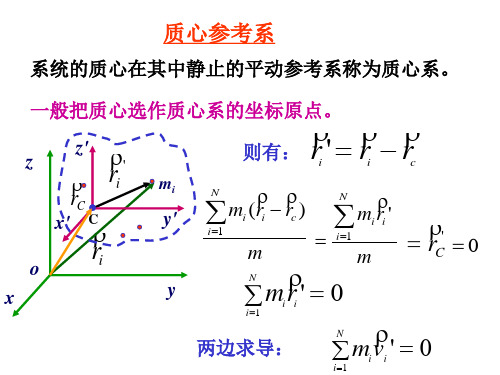
给上式两边同时乘以系统质量m
rC
mi ri
i
则:
mvc mi vi p
dvc dp p mvc 两边求导得: m mac dt dt dp F m a c dt
——质心运动定理
i
不管物体的质量如何分布,也不管外力作用在 物体的什么位置上,质心的运动就象是物体的质量 全部都集中于此,而且所有外力也都集中于此的一 个质点的运动一样。 实际上在质心位置处可能既无质量,又未受力。
i 1
m
' rC
0
两边求导:
'0 mv i i
N i 1
z
z'
x'
o
rC
' ri
第三章-动量守恒定律

cos d
R
2、求半径为 R 、顶角为 2 的均匀扇形薄板的质
心?
习题3-8
3、求质量均匀分布的半球体的质心?
解:
建立坐标系
计算 C z
dz z
由对称性可知,质心在 z 轴上 根据质心定义式 zC
设球体的体密度为
zdm dm
dm ( R 2 z 2 )dz
v10 v1 v2 v20 v10 v20 v2 v1
碰前相互接近的速度 = 碰后相互离开的速度
m1 m2 时 v1 v20 , v2 v10 m1 m2 2m1 v v , v v10 v20 0 时 1 10 2 m1 m2 m1 m2
根据质点动量定理:
t I Fdt p p0 mv mv0 0 mv0
根据平均冲力定义: F I mv0 t t m(v0 ) mv0 F t t
根据质点动能定理: mgh 1 mv 2 0
F
h
mg
m 2 gh F 3.1105 N t
2
v0 2 gh
方向向上
§ 3-2 质点系动量定理和质心运动定理
一、质点系动量定理
1、两个质点构成的质点系
研究对象 受力分析 内力:
F2
f12
2
f 21
F1
1
外力:
运动特点
t0 :
t:
分别对 应用质点动量定理
i
动量守恒定律
当外力矢量和为零时,质点系的总动量保持不变。
说明
分量守恒
动量守恒定律

定义:动量守恒定 律是物理学中的基 本定律之一,它描 述了系统中物体动 量的变化与作用力 的关系。
适用范围:适用于 宏观和微观领域, 包括经典力学、相 对论和量子力学等 领域。
地位:是物理学中 的基石之一,对于 理解物质运动规律 和解决实际问题具 有重要意义。
作用:在科学研究 、工程技术和日常 生活中有着广泛的 应用,如航天器发 射、碰撞、爆炸等 领域。
物理科学研究: 推动物理学理论 的发展与完善
05
动量守恒定律的局限性和未来发展方向
动量守恒定律的局限性
适用范围有限:只适用于封闭系统,且不受外力作用 忽略微观粒子间的相互作用:无法考虑微观粒子间的相互作用对动 量的影响 忽略量子效应:无法解释微观粒子的量子效应对动量的影响
无法解释宇宙膨胀现象:无法解释宇宙大尺度上的动量守恒问题
动量守恒定律的数学表达式
p=mv m1v1+m2v2=m1v3+m2v4 Δp1=-Δp2 Δp=0
动量守恒定律的适用范围
宏观低速:适用于宏观低速的物体运动,不适用于微观高速的物体运动。 孤立系统:适用于孤立系统,即系统不受外界作用力或外界作用力可忽略不计的情况。 不考虑相对论效应:在经典力学中,动量守恒定律适用于不考虑相对论效应的情况。 弹性碰撞:适用于弹性碰撞,即碰撞过程中能量损失很小的情况。
火箭升空
碰撞问题
定义:两个或 多个物体在空 间中相互碰撞, 动量守恒定律
的应用。
实例:汽车碰 撞、子弹射击 目标、行星碰
撞等。
计算方法:利 用动量守恒定 律计算碰撞前 后的速度和能
量。
结论:动量守 恒定律在碰撞 问题中具有广 泛的应用,可 以帮助我们理 解物体的运动 规律和预测物 体的运动行为。
第8章第三节动量守恒定律

栏目 导引
即时应用 2.质量为M的小车,以速度v0在光 滑水平地面上前进,上面站着一个质量为m的
人,问:当人以相对车的速度u向后水平跳出
后,车速为多大?
栏目 导引
解析:选取人和车的整体为研究对象,系统 所受合外力为零,动量守恒.以地面为参考 系,以小车前进的方向为正方向,根据动量 守恒定律有:(M+m)v0=Mv-m(u-v),解 m 得 v=v0+ u. M+m m 答案:v0+ u M+m
的动量守恒.
总之,在确定使用动量守恒定律时,一定要 仔细分析守恒条件,明确研究对象,是哪一
个系统哪一个过程动量守恒.
栏目 导引
即时应用 1.如图8-3-1所示,气球与绳梯 的质量为M,气球的绳梯上站着一个质量为m 的人,原来整个系统处于静止状态,若空气 阻力不计,当人沿绳梯向上爬时,对于整个 系统来说动量是否守恒?为什么?
不变.若同时放开,那么作用后系统的总动
量就等于放手前的总动量,即为零;若两手 先后放开,那么两手都放开后的总动量也是
守恒的,但不为零.
栏目 导引
【答案】
ACD (1)系统动量守恒,除系统不
【思维升华】
受外力或所受外力之和为零之外,若系统在 极短时间内所受外力远比系统内相互作用力 小(如碰撞、爆炸),因而外力可忽略时,系统
水平桌面上以v1=30 cm/s的速率向右运动,恰
遇上质量为m2=50 g的小球以v2=10 cm/s的速
率向左运动,碰撞后,小球m2恰好停止,则 碰后小球m1的速度大小、方向如何?
栏目 导引
解析:设向右为正方向,则各速度为:v1=30 cm/s,v2=-10 cm/s,v2′=0. 由两球组成的系统满足动量守恒定律条件, 由动量守恒定律列方程 m1v1+m2v2=m1v1′+m2v2′,
动量守恒定律 (共30张PPT)

系统之外与系统发生相互作用的 其他物体统称为外界。
碰撞 系统Leabharlann 重力势能属于地面附近 的物体与地球组成的系统。
弹簧具有的弹性势能 属于构成它的许多小小 的物质单元(这些物质单 元之间有弹力的作用)组 成的系统。
研究炸弹的爆炸时,它的 所有碎片及产生的燃气也要作 为一个系统来。
2、内力:属于同一个系统内,它们之间的力。 系统以外的物体施加的力,叫做外力。
解得:v共=88.2m/s正值,方向不变。
解: ①以子弹木块系统为研究对象,取右为正方向。
②碰撞前子弹的动量P子=mv,木块的动量P2=0
碰撞后不粘一起,P'子=mv',P'木=Mv'木
③列表带入公式:系统初动量=系统末动量
碰撞前
碰撞后
物块1 物块2 = 物块1 物块2
mv 0
mv' Mv'木
所以:mv=mv'+Mv'木
解:动量问题只与初末状态有关。
①以第一节车厢和把剩余车厢看为整体的系统为研究
对象,取右为正方向。
②碰撞前的动量P=mv,剩余车厢的动量P余=0
碰撞后粘一起,P共=(m+15m)v共
③列表带入公式:系统初动量=系统末动量
碰撞前
碰撞后
物块1 物块2 = 物块1 物块2
mv 0
(m+15m) v共
所以:mv=(m+15m)v共
解得:v'B=7.4m/s
带数据得:5×9+4×6=5v'1+4×10 正值,方向不变。
3、质量是10g的子弹,以300m/s的速度射入质量是24g、静止在光滑水平桌面上的木 块,并留在木块中。子弹留在木块中以后,木块运动的速度是多大?如果子弹把木块 打穿,子弹穿过后的速度为100ms,这时木块的速度又是多大?
碰撞 系统Leabharlann 重力势能属于地面附近 的物体与地球组成的系统。
弹簧具有的弹性势能 属于构成它的许多小小 的物质单元(这些物质单 元之间有弹力的作用)组 成的系统。
研究炸弹的爆炸时,它的 所有碎片及产生的燃气也要作 为一个系统来。
2、内力:属于同一个系统内,它们之间的力。 系统以外的物体施加的力,叫做外力。
解得:v共=88.2m/s正值,方向不变。
解: ①以子弹木块系统为研究对象,取右为正方向。
②碰撞前子弹的动量P子=mv,木块的动量P2=0
碰撞后不粘一起,P'子=mv',P'木=Mv'木
③列表带入公式:系统初动量=系统末动量
碰撞前
碰撞后
物块1 物块2 = 物块1 物块2
mv 0
mv' Mv'木
所以:mv=mv'+Mv'木
解:动量问题只与初末状态有关。
①以第一节车厢和把剩余车厢看为整体的系统为研究
对象,取右为正方向。
②碰撞前的动量P=mv,剩余车厢的动量P余=0
碰撞后粘一起,P共=(m+15m)v共
③列表带入公式:系统初动量=系统末动量
碰撞前
碰撞后
物块1 物块2 = 物块1 物块2
mv 0
(m+15m) v共
所以:mv=(m+15m)v共
解得:v'B=7.4m/s
带数据得:5×9+4×6=5v'1+4×10 正值,方向不变。
3、质量是10g的子弹,以300m/s的速度射入质量是24g、静止在光滑水平桌面上的木 块,并留在木块中。子弹留在木块中以后,木块运动的速度是多大?如果子弹把木块 打穿,子弹穿过后的速度为100ms,这时木块的速度又是多大?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
v ex v ex 2)守恒条件 合外力为零 F = ∑ Fi = 0 )
Fxex = 0 , F F
ex y
p x = ∑ mi vix = C x p y = ∑ mi viy = C y p z = ∑ mi viz = C z
= 0, = 0,
ex z
4) 动量守恒定律只在惯性参考系中成立 是自 ) 动量守恒定律只在惯性参考系中成立, 惯性参考系中成立 然界最普遍, 然界最普遍,最基本的定律之一 .
3 – 2 动量守恒定律
第三章动量守恒定律和能量守恒定律
例如在碰撞, 打击, 爆炸等问题中. 认为系统动量守恒 . 例如在碰撞 打击 爆炸等问题中 3)若某一方向合外力为零 则此方向动量守恒 . ) 某一方向合外力为零, 方向动量守恒 方向合外力为零
i v ex v in 当 F << F 时,可 略去外力的作用, 近似地 略去外力的作用
因dm的喷射,火箭总质量M在减少,减少量为−dM, 的喷射,火箭总质量 在减少,减少量为− , 的喷射 在减少 故有dm = −dM。于是上式变为 故有 。
0 = [(M + dM )(v + dv ) (−dM )(v + dv − u)] Mv + − = Mdv + udM
积分得 0 =
v M
火箭在运行时生成的炽热气体高速向后喷 火箭在运行时生成的炽热气体高速向后喷 使火箭主体获得向前的动量。 射, 使火箭主体获得向前的动量。若将火 箭的总质量M分成两部分 火箭主体质量 箭的总质量 分成两部分, 分成两部分 M−dm ;将被喷射的物质质量 。 − 将被喷射的物质质量dm。 时刻, 尚未被喷出, 在t 时刻 dm尚未被喷出 火箭总质量相 尚未被喷出 对于地面的速度为v,动量为Mv; 对于地面的速度为 ,动量为 ;在t+dt 时刻, 被以相对于火箭的速度(称为喷射 时刻 dm被以相对于火箭的速度 称为喷射 被以相对于火箭的速度 速度) 喷出 喷出, 速度 u喷出 火箭主体则以 v+dv的速度相 的速度相 对于地面运行。 对于地面运行。
5
3 – 2 动量守恒定律
第三章动量守恒定律和能量守恒定律
将火箭主体和喷射物质视为一个系统, 将火箭主体和喷射物质视为一个系统 并忽略作用于 系统的仅有的外力,即火箭所受重力Mg, 那么根据动量 系统的仅有的外力,即火箭所受重力 守恒定律, 方向的分量式应有 守恒定律,在z方向的分量式应有
0 = [ M − dm )v + dv ) (dm )v + dv − u) − Mv ( ( + ( ]
∫ dv
0
+ u∫
dM
M0
M0 = v − u ln M M
6
3 – 2 量守恒定律
第三章动量守恒定律和能量守恒定律
火箭主体在其质量从M 火箭主体在其质量从 0变到 M0 v = u ln M时所达到的速度为 时所达到的速度为 M 火箭的速度决定于喷射速度和质量比 0/M)的自然 火箭的速度决定于喷射速度和质量比(M 的自然 质量比
对数。化学燃烧过程所达到的喷射速度理论值为 5×103m·s-1 , 而实际能达到的只是此值的一半左右 。 × 而实际能达到的只是此值的一半左右。 提高火箭速度的潜力在于提高质量比(M0/M)。 提高火箭速度的潜力在于提高质量比 。 是火箭尚未发射时的质量, 在(M0/M)中, M0是火箭尚未发射时的质量 包括负 中 火箭外壳等结构及全部燃料质量, 是负载及外 载 、 火箭外壳等结构及全部燃料质量 M是负载及外 壳 等 质 量 。 要 使 火 箭 主 体 超 过 第 一 宇 宙 速 度 (7.9 km⋅s−1),用以发射人造地球卫星 质量比要高达 左 ⋅ ,用以发射人造地球卫星, 质量比要高达55左 右。大质量比困难, 一般采用多级火箭来实现。 大质量比困难 一般采用多级火箭来实现。
水平方向上 动量守恒
mv v' = − cos θ M
3 – 2 动量守恒定律
第三章动量守恒定律和能量守恒定律
运载火箭在运行时, 自身携带的燃料(液态氢 液态氢) 例 2 运载火箭在运行时 自身携带的燃料 液态氢 在氧化剂(液态氧 的作用下急剧燃烧, 液态氧)的作用下急剧燃烧 在氧化剂 液态氧 的作用下急剧燃烧 生成炽热气体并 相对火箭以高速u向后喷射 向后喷射, 相对火箭以高速 向后喷射,致使火箭主体获得向前 的动量。火箭总重量为M0,火箭主体重量为M, 的动量。火箭总重量为 ,火箭主体重量为 ,求火 箭最后能达到的速度。 箭最后能达到的速度。
3 – 2 动量守恒定律 第三章动量守恒定律和能量守恒定律 v v ex t v v 质点系动量定理 I = ∫ ∑ Fi d t = ∑ p i − ∑ p i 0
t0 i i i
动量守恒定律
v ex v ex 若质点系所受的合外力为零 若质点系所受的合外力为零 F = ∑ Fi = 0
则系统的总动量守恒,即 则系统的总动量守恒, 守恒
7
理论值 umt = 5 × 103 m ⋅ s −1
实际值 ump ≈ umt / 2
多级火箭技术
3 – 2 动量守恒定律
第三章动量守恒定律和能量守恒定律
运载火箭技术反映了当代科技水平的综合技术, 运载火箭技术反映了当代科技水平的综合技术, 但其动力学原理仍是动量定理和动量守恒定律。 但其动力学原理仍是动量定理和动量守恒定律。
v p=
∑
v pi
i
保持不变 . 保持不变
v ex 力的瞬时作用规律 F
v iv v v dp ex = , F = 0, P = C dt
1)系统的动量守恒是指系统的总动量不变,系 )系统的动量守恒是指系统的总动量不变, 总动量不变 统内任一物体的动量是可变的, 各物体的动量必相 统内任一物体的动量是可变的 各物体的动量必相 对于同一惯性参考 同一惯性参考系 对于同一惯性参考系 .
3 – 2 动量守恒定律
第三章动量守恒定律和能量守恒定律
如图所示, 大炮在发射时炮身会发生反冲现象。 例 1 如图所示 大炮在发射时炮身会发生反冲现象。 设炮身的仰角为θ, 炮弹和炮身的质量分别为m和 设炮身的仰角为 炮弹和炮身的质量分别为 和M, 炮 弹在离开炮口时的速率为v, 弹在离开炮口时的速率为 若忽略炮身反冲时与地面的 摩擦力, 求炮身的反冲速率。 摩擦力 求炮身的反冲速率。
