第二节洛必达LHospital法则
第二节L’Hospital 法 则

注:对于 ∞ − ∞ 型的极限,可转通过适 当的变型,化为 0 ∞ 或 型不定型极限。 0 ∞
2011-12-11
L’Hospital法则运用举例 法则运用举例10 法则运用举例
例 求极限: 求极限:
ax+1 + bx+1 + c lim x→0 a +b+c
1 lim (cot x − ) x→0 x ∞ −∞ cos x 1 x cos x − sin x 解:原式 = lim ( − ) = lim x → 0 sin x x→0 x x sin x 0 sin x ~ x x cos x − sin x 0 x sin x = lim = lim =0 2 x→0 x→0 x 2x
例 求极限: 求极限:
2 1 − cos x 1 1 = lim = lim1 = 2 L . H 3 x →0 x 3 x →0 3 注:用等价无穷小代换,化其它函数为幂函数,简化运算
0 0
x2 1− cos x 似)
tan x ~ x
− x csc x − x ⋅ tan x 解: ) = lim (2 = lim L . H x → +0 x → +0 sin 2 x cot x
x + sin x sin x 反例: lim = lim 1 + =1 x →∞ x →∞ x x f ′( x ) 1 + cos x 但是 lim = lim 却∃ / x → ∞ g ′( x ) x→∞ 1
2011-12-11
3. L’Hospital法则运用举例 法则运用举例1 法则运用举例
先代入,以简化运算过程。
l'hospital法则

l'hospital法则如果当x→a(或x→∞)时,两个函数f(x)与F()都趋于0或∞,那么极限limx→a(x→∞)f(x)F(x)可能存在,也可能不存在. 通常把这种极限叫做未定式,并分别简记为 00或∞∞.在极限是未定式的条件下,通过分子分母同时分别求导再求极限来确定未定式的值的方法称为洛必达(L’Hospital)法则洛必达法则的两个定理:对于x→a时的未定式00(亦即x→∞时的未定式∞∞)的情形,有以下定理:定理一:设 (1)当x→a时,函数f(x)及F(x)都趋向于0; (2)在点a的某去心邻域内,f′(x)及F′(x)都存在,且F′(x)≠0; (3)limx→af′(x)F′(x)存在(或为无穷大),则limx→af(x)F(x)=limx→af′(x)F′(x)对于x→∞时的未定式00(亦即x→a时的未定式∞∞)的情形,有以下定理:定理二:设 (1)当x→∞时,函数f(x)及F(x)都趋向于0; (2)当|x|>N时,f′(x)与F′(x)都存在,且F′(x)≠0; (3)limx→af′(x)F′(x)存在(或为无穷大),则limx→af(x)F(x)=limx→af′(x)F′(x)其他还有一些0⋅∞、∞−∞、00、i∞、∞0型的未定式,也可以通过00或∞∞型的未定式来计算.下面举一些例子: 1、求limx→0+xnlnx(n>0).解:这是 0⋅∞未定式.因为xnlnx=lnx1xn当 x→0+时,上式右端是未定式∞∞,应用洛必达法则,得limx→0+xnlnx=limx→0+(−xnn)=02、求limx→π2(secx−tanx).解:这是∞−∞型.因为secx−tanx=1−sinxcosx, 当 x→π2时,上式右端是未定式 00,应用洛必达法则,得limx→π2(secx−tanx)=limx→π2−cosx−sinx=03、求limx→x+xx解这是 00未定式.设 y=xx,取对数得lny=xlnx当 x→0+时,上式右端是未定式 0⋅∞.应用洛必达法则得limx→x+lny=limx→x+(xlnx)=limx→x+lnx1x=0因为 y=elny,而 limy=limelny=limelimlny(x→0+),所以limx→x+xx=limx→x+y=e0=1。
洛必达(L Hospital)法则

1 ⎧ 1 x ⎪ (1 + x ) x ] , 当x > 0 ⎪[ 三、讨论函数 f ( x ) = ⎨ , e ⎪ −1 ⎪ 当x ≤ 0 ⎩e 2 ,
在点x = 0处 的连续性.
2007年8月
南京航空航天大学 理学院 数学系 马儒宁
例10 解
2007年8月
求 lim x
x →1 x →1
1 1− x
. =e
ln x x →11− x lim
( 1∞ )
=e
1 lim x x → 1 −1
原式 = lim e
1 ln x 1− x
= e −1 .
15
南京航空航天大学 理学院 数学系 马儒宁
例11 求 lim+ (cot x )
0 型 0 ∞ 型 ∞
令y = f 取对数
g
0⋅∞ 型
f ⋅g= f 1g
2007年8月
南京航空航天大学 理学院 数学系 马儒宁
21ቤተ መጻሕፍቲ ባይዱ
思考题
f ( x) f ′( x ) 设 lim 是不定型极限,如果 的极 g( x ) g ′( x ) f ( x) 限不存在,是否 的极限也一定不存在? g( x )
3 x2 − 3 6x 3 解 原式 = lim 2 = lim = . 1 x→ 3 x − 2 x − 1 x →1 6 x − 2 2
2007年8月 南京航空航天大学 理学院 数学系 马儒宁 7
ln sin ax . 例3 求 lim x → 0 ln sin bx
∞ ( ) ∞
a cos ax ⋅ sin bx cos bx 解 原式 = lim = lim = 1. x → 0 b cos bx ⋅ sin ax x → 0 cos ax
第二节 L'Hospital法则

第二节 L’Hospital 法则这一节我们通过Cauchy 中值定理来得到一个求极限的法则——L ’Hospital 法则。
并利用它来求一些所谓不定型的极限.定理 6.11 设0)(lim =→x f ax ,0)(lim =→x g ax ,且)(x f ,)(x g 在a 的某个去心邻域中可导,若)()(limx g x f ax ''→ 存在(可以是有限数或∞),则)()(lim)()(lim x g x f x g x f a x a x ''=→→. 证 由于)(x f ,)(x g 在a 的某个去心邻域中可导,所以可假设0)()(==a g a f ,这样,)(x f ,)(x g 就都在a 点连续了.故由Cauchy 中值定理得到)()()()()()()()(ξξg f a g x g a f x f x g x f ''=--=, (ξ介于x 与a 之间) 当a x →时,a →ξ.而当a →ξ时,)()(lim x g x f a x ''→存在,所以)()(lim)()(lim )()(limx g x f g f x g x f a x a ax ''=''=→→→ξξξ. 注 6.2 (1).若0)(lim =→x f ax ,0)(lim =→x g ax ,我们称)()(limx g x f ax →为0型的未定式. (2).若)()(limx g x f ax ''→不存在,不能说)()(lim x g x f a x →也不存在.我们容易知道xx x x 1sinlim2π→是00型的未定式,且其极限为0.但是()11cos1sin 2lim1sin lim 020x x x x x x x x -=''⎪⎭⎫ ⎝⎛→→不存在,所以用L ’Hospital 法则不能证明极限不存在.以下用L ’Hospital 法则计算几个极限.例6.6 求ππ-→x xx sin lim. 解 当π→x 时,x sin 与π-x 的极限都是0,所以此极限是0型的未定式,可以考虑用L ’Hospital 法则.11cos lim sin lim-==-→→xx x x x πππ. 例6.7 求30sin limxxx x -→. 解:此极限是0型的未定式,考虑用L ’Hospital 法则.616sin lim 3cos 1lim sin lim 02030==-=-→→→x x x x x x x x x x . 这里连续用了两次L ’Hospital 法则.类似地,若将定理中的a x →换为∞→x 可以得到同样的结论.看下面的例子:例6.8 求.1sin )11ln(lim⎪⎭⎫⎝⎛+∞→x x x . 111cos 1111lim 1sin )11ln(lim22=-⋅-⋅+=⎪⎭⎫⎝⎛+∞→∞→xx x x x x x x .若将定理中的0)(lim =→x f ax ,0)(lim =→x g ax 换为∞=→)(lim x f ax ,∞=→)(lim x g ax ,也可以有类似的L ’Hospital 法则.此时我们称)()(limx g x f ax →为∞∞的不定式.也就是下面的定理. 定理6.12 设∞=→)(lim x f ax ,∞=→)(lim x g ax ,且)(x f ,)(x g 在a 的某个去心邻域中可导,若)()(limx g x f ax ''→ 存在(可以是有限数或∞),则)()(lim)()(lim x g x f x g x f a x a x ''=→→. 证 (略).进一步,我们可以得到定理6.13 设∞=→)(lim x g ax ,且)(x f ,)(x g 在a 的某个去心邻域中可导,若)()(lim x g x f ax ''→ 存在(可以是有限数或∞),则)()(lim)()(limx g x f x g x f a x ax ''=→→ 证 (略).例6.9 求λ-→x xx ln lim0,()0>λ.解 此极限为∞∞的不定式.用L ’Hospital 法则可以得到 0lim 1lim ln lim 0100=-=-=→--→-→λλλλλx x x x x x x x . 即对于任意的()0>λ,有0ln lim 0=→x x x λ.我们也可以将上面定理中的a x →也可以换为∞→x .例6.10 设,N n ∈+∈R λ,求||lim x nx ex λ∞→.解 这是∞∞型的未定式,所以可以考虑用L ’Hospital 法则. 0!lim lim lim 1====+∞→-+∞→+∞→xn x x n x x n x e n e nx e x λλλλλ.... 当-∞→x 时,有||||||)1(lim lim x nn x x n x ex e x λλ-=∞→∞→, ||||x n ex λ是无穷小,n)1(-是有界量,所以原式=0.例6.11 当1>a ,N n ∈时,求x nx ax +∞→lim 。
3-2第二节洛必达L’Hospital法则

系
高
等 数 学
.例如 当x→∞时,
x sin x 是, x cos x
型不定式
电 子 教
显然有.
lim x sin x 1 x x cos x
案
但是如果用洛必达法则,则得不出结果
lim x sin x lim (x sin x) lim 1 cos x lim (1 cos x)
子
教 案
在区间[a,x]或[x,a]上应用柯西中值定理
f (x) f (a) f ( ) , ( [a, x]) g(x) g(a) g ( )
武
x a, a
汉
科
技 学 院
lim f (x) lim f ( ) lim f (x) A
数 理
xa g(x) x g ( ) xa g (x)
ln cos x
exp[lim x0
x2
]
武 汉
exp[lim tgx ] exp[ 1 1]
x0 2 x
2
科
技 学
e1/ 2 1
院 数
e
理 系
(tgx) sec2 x
高
等 数
(3) lim (1 1 ) x lim e x ln(11/ x)
x0
院
数
理
系
高 等 数
例1 求下列极限
(1 x)a 1
(1) lim
;
学
x0
x
1
(2) lim n(e n 1) n
电 子
解: (1)是0/0型的,用洛必达法则,得到
教 案
lim (1 x)a 1 lim a(1 x)a1 a(1 0)a1 a
4-2洛必达法则1211

例
tan x ∞ . ( ) 求 lim π ∞ x → tan 3 x
2
sin x ⋅ cos 3 x 原式 = lim π x → cos x ⋅ sin 3 x
2
sec2 x 解 原式 = lim π 3 sec 2 3 x x→
2
cos 3 x 0 = −lim ( ) π cos x 0 x→
15
二、其它未定式
1. 0 ⋅ ∞, ∞ − ∞型未定式
0 ∞ 型 关键 将其化为洛必达法则可解决的 , 0 ∞ ∞ 1 0⋅ ∞ 型 0⋅ ∞ ⇒ ⋅ ∞ ⇒ 或 0⋅ ∞ ⇒0⋅ 1 ⇒ 0 ⋅ 0 ∞ ∞ 0
求 lim x − 2e x . ( 0 ⋅ ∞ ) 例
x → +∞
ex ∞ ex ∞ 解 原式 = lim 2 ( ) = lim ( ) x → +∞ 2 x ∞ x → +∞ x ∞ ex = lim = +∞ . x → +∞ 2 16
例 求 lim x(
x → +∞
π
2
− arctan x ). ( ∞⋅ 0 )
π
解 原式 = lim 2
x → +∞
− arctan x
1 x 1 − 2 2 x = lim 1 + x = lim 2 =1 x → +∞ 1 x → +∞ 1 + x − 2 x
0 ( ) 0
17
∞−∞ 型
1 1 0 0− 0 ∞− ∞⇒ − ⇒ ⇒ 0 0 0⋅ 0 0
∞ ln sin ax 例 求 lim ( ) . x→0 ln sin bx → ∞ a cos ax ⋅ sin bx a sin bx 解 原式 = lim = lim x →0 b cos bx ⋅ sin ax x →0 b sin ax
洛必达法则洛必达法则

洛必达法则洛必达法则洛必达法则洛必达法则(L'Hospital法则),是在一定条件下通过分子分母分别求导再求极限来确定未定式值的方法。
设(1)当x→a时,函数f(x)及F(x)都趋于零;(2)在点a的去心邻域内,f'(x)及F'(x)都存在且F'(x)≠0;(3)当x→a时lim f'(x)/F'(x)存在(或为无穷大),那么x→a时 lim f(x)/F(x)=lim f'(x)/F'(x)。
再设(1)当x→∞时,函数f(x)及F(x)都趋于零;(2)当|x|>N时f'(x)及F'(x)都存在,且F'(x)≠0;(3)当x→∞时lim f'(x)/F'(x)存在(或为无穷大),那么x→∞时 lim f(x)/F(x)=lim f'(x)/F'(x)。
利用洛必达法则求未定式的极限是微分学中的重点之一,在解题中应注意:①在着手求极限以前,首先要检查是否满足0/0或∞/∞型未定式,否则滥用洛必达法则会出错。
当不存在时(不包括∞情形),就不能用洛必达法则,这时称洛必达法则不适用,应从另外途径求极限。
比如利用泰勒公式求解。
②若条件符合,洛必达法则可连续多次使用,直到求出极限为止。
③洛必达法则是求未定式极限的有效工具,但是如果仅用洛必达法则,往往计算会十分繁琐,因此一定要与其他方法相结合,比如及时将非零极限的乘积因子分离出来以简化计算、乘积因子用等价量替换等等. 泰勒公式(T aylor's formula)泰勒中值定理:若函数f(x)在开区间(a,b)有直到n+1阶的导数,则当函数在此区间内时,可以展开为一个关于(x-x.)多项式和一个余项的和:f(x)=f(x.)+f'(x.)(x-x.)+f''(x.)/2!*(x-x.)^2,+f'''(x.)/3!*(x-x.)^3+……+f(n)(x.) /n!*(x-x.)^n+Rn其中Rn=f(n+1)(ξ)/(n+1)!*(x-x.)^(n+1),这里ξ在x和x.之间,该余项称为拉格朗日型的余项。
4-2洛比达法则
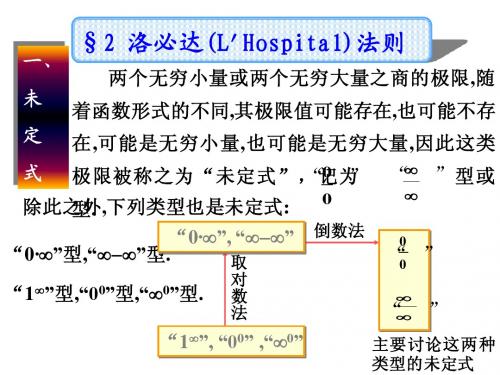
∞ “ ” 型或 ∞
除此之外,下列类型也是未定式 除此之外 下列类型也是未定式: 型. 下列类型也是未定式 ∞−∞” “0·∞”, “∞−∞ ∞ 取 ∞−∞ ∞−∞”型 “0·∞”型,“∞−∞ 型. ∞ 型 ∞−∞ 对 “1∞”型,“00”型,“∞0”型. 型 型 ∞ 型
数 法
0 “ 0
∞ “ ∞
2
极
又如
失效之二 循环
x→ +∞
lim
x 1+ x2
1+ x2 x = lim = lim x→ x→ +∞ +∞ x 1+ x2
解:原极限= lim 原极限
1 1+(1/ x )
2
x→ +∞
=1
春风得意洛 春风得意洛必塔 一招遍摘极限花 可叹英雄亦失手 莫忘前章有妙法
练习
x +sinx lim x→ x −sinx ∞
sinx co 3x s −3sin3x = lim lim = − lim =3 x→ / 2sin3x x→ / 2 ⋅ co x x→ / 2 −sinx π π π s
lnx lim α (α > 0) 例7.求 求 ∞ x→ +∞ x “∞ ”型. 1/ x 1 原极限= 解:原极限 lim 0 α−1 = lim α= x→ α +∞ x x→ α +∞ x ex ex ex 原极限= 例8.计算 lim 2 解:原极限 lim 计算 = lim = +∞ x→ x +∞ x→ 2x x→ +∞ +∞ 2
2 等价无穷小) 等价无穷小 ta 2 x (等价无穷小 n x = lim = lim 0 1− o x→ 1−c s x x→ 1 0 → x2 2 lnx +1− x 例4.计算极限 lim 计算极限
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x? 0?
x? 0?
(3) lim (1 ? 1 ) x
x? 0?
x
x ) 1/ x 2 ;
系理数院学技科汉武
解:(1) 令y=xx, 则 lny=xlnx, 再取极限, 得到
ln x
1/ x
lim ln y ? lim
? lim
x? 0?
x? 0? 1 / x
x? 0? ? 1 / x 2
? lim x ? 0 x? 0?
? lim ln y ? 0 x? 0?
? lim y ? e 0 ? 1 ? x? 0?
lim x x ? 1
x? 0?
案教子电学数等高
也可以
( 1 ) lim x x ? lim e x ln x
x? 0?
x? 0?
? exp[
lim ( x ln x )]
x? 0?
? exp[
lim
1/ x ] ? e 0 ? 1
x ? 0 ? ? 1/ x 2
(2) lim(cos x? 0
x ) 1/ x 2 ? lim
1 ln cos x
e x2
x? 0
ln cos x
? exp[lim x? 0
x2
]
? tgx
? exp[lim
] ? exp[
x? 0 2 x
? 1 ? 1] 2
系理数院学技科汉武
? e ? 1/ 2 ?
在区间[a,x] 或[x,a] 上应用柯西中值定理
f ( x ) ? f ( a ) ? f ?(? ) , (? ? [ a , x ]) g ( x ) ? g ( a ) g ?(? )
x ? a,? ? a
系理数院学技科汉武
? lim f ( x) ? lim f ?(? ) ? lim f ?( x) ? A x? a g ( x) x? ? g ?(? ) x? a g ?( x)
sec 2 x
?
x?
?0
2
型)
? lim ?
cos 2 x ( ?
x ? ? /2 ?
x?
?0
2
型)
2 cos x ( ? sin x )
? lim ?
1
x?
?0
2
? - l i m sin 2 x ? 0 x? ? ? 0 2
系理数院学技科汉武
案教子电学数等高
(2) 对于其他的形式可以通过恒等变形,化为基本型.可使
案教子电学数等高
定理1又称为洛必达法则 洛必达法则是求不定式极限的一个有效方法.掌握这 个法则没有什么困难,但是需要注意以下问题:
(1) 只有不定式极限问题才能够运用洛必达法则,非不定 式极限要用四则运算或其他方法.对于不定式极限,若 干次运用罗比达法则以后如果已经化为非不定式,就 不能继续运用洛必达法则,否则就会出现错误.
(2) lim (ctgx ? csc x ) ? lim ( cos x ? 1 )
x? 0
x? 0 sin x sin x
cos x ? 1
? sin x
? lim
? lim
? 0.
x ? 0 sin x
x ? 0 cos x
系理数院学技科汉武
案教子电学数等高
例5 求下列极限:
(1 ) lim x x ; (2) lim (cos
则 lim f (x) ? lim f ?(x) ? A x? a g (x) x? a g?( x)
案教子电学数等高
例3
求函数
lim ln(? / 2? x) x? ? ?0 tgx
的极限
2
解:
l i m ln ( ? / 2 ? x ) ( ?
x? ? ? 0
tg x
?
2
型)
? lim ?
1 /( ? / 2 ? x ) ( ?
案教子电学数等高
第二节 洛必达(L' Hospital)法则
洛必达法则是求0/0, ∞/ ∞, 0* ∞, ∞- ∞, 1 ∞, 00 , ∞0类型
极限的有力工具.
系理数院学技科汉武
定理1 (0/0型) 假设
(1) lim f (x) ? 0, lim g(x) ? 0;
x? a
x? a
(2)函数f (x), g(x)在点a的某邻域内都可导 , 且g?(x) ? 0;
系理数院学技科汉武
案教子电学数等高
例1 求下列极限
(1) lim (1 ? x ) a ? 1 ;
x? 0
x
1
( 2 ) lim n ( e n ? 1) n ??
解: (1)是0/0型的,用洛必达法则,得到
lim
(1 ?
x)a
?1 ?
lim
a (1 ?
x)a?1
?
a (1 ?
0)a?1 ?
a
x? 0
f ?(x)
(3) lim
? A,
x? a g ?( x)
则 lim f (x) ? lim f ?(x) ? A x? a g ( x) x? a g ?( x)
案教子电学数等高
证明: 我们补充定义f(a)=g(a)=0,有
f (x) ?
f (x) ? f (a)
g (x) g (x) ? g (a)
x
解:
sin x ? x cos x ? 1 1 ? sin x
lim
x? 0
x3
? lim x? 0
3x2
? lim 3 x? 0 2x
? ? 1 lim sin x ? ? 1
6 x? 0 x
6
解此0/0型,连用三次洛必达法则可得到结果。在使用
系理数院学技科汉武
洛必达法则时,必须要检查是否是0/0型的。在计算中常
1
e
( tgx ) ? ? sec 2 x
案教子电学数等高
( 3) lim (1 ? 1 ) x ? lim e x ln( 1? 1 / x )
犯的错误是没有满足0/0的条件。
案教子电学数等高
定理2
? (
ห้องสมุดไป่ตู้
型)
设:
?
(1)lim f ( x) ? ? ,lim g( x) ? ?;
x? a
x? a
(2) 函数f(x)与g(x)在点a的某邻域内(点a可以除外)都可
导,且g'(x)≠0
f ?( x)
(3) lim
?A
x? a g ?( x )
系理数院学技科汉武
x
x? 0
1
系理数院学技科汉武
(2)是∞0型的,可以化为0/0型.
1
1
lim
1
n(e n
? 1)
?
lim
en
?1
?
lim
ex
? 1(y
?
1/ x)
n ??
n ??
1
x?? 1 / x
n
?
ey lim
?1 ?
ey lim
?1
y? 0 y
y? 0 1
案教子电学数等高
例2
求极限
lim
x? 0
sin
x? x3
用洛必达法则求极限.
例4 求下列极限 (1) lim x a ln x; (2) lim (ctgx ? csc x).
x? 0
x? 0
解:(1) lim x? 0
xa
ln
x
?
lim
x? 0
ln x x?a
?
lim
x? 0
?
1/ x ax ? ( a ?1)
? ? 1 lim x a ? 0 a x? 0
