小学期数学建模大作业 西安交通大学
西安交大少年班历届考试题目

西安交大少年班历届考试题目和有关事项50[ 标签:西安,交大,少年班]西安交大少年班历届语文、数学、英语、物理考过什么题目,面试内容一般是什么考试时有什么注意事项等等知道多少,回答多少,多多益善!谢了!Kaka 回答:2 人气:116 解决时间:2009-02-07 11:55满意答案好评率:87%1.一矩形分成四个小矩形,在每个小矩形内种四种不同的花,相邻小矩形种的种类不同,共有__种不同的种法。
(2008年西安交通大学少年班数学试题)2.在三角形ABC中,BE为AC边的中线,D、F为BC的三等分点。
BE与AD、AF 分别相交于点M、N,求BM:MN:NE。
(2006年西安交通大学少年班数学试题)面试内容包括科普知识、人生、社会、心理等综合内容。
2006交大面试题,希望对大家有用1、假如你知道你在学校所学的知识到了社会工作时全都没有用,你作何感想2、有一家国有企业和微软同时邀请你,你去哪一家3、请对近日国内外大事举一例,并解读。
4、你对医保有什么看法你认为国家应采取什么措施5、所有老师中你最喜欢与最不喜欢的是怎样的老师不喜欢的老师的课,你会上得好吗6、根据四个英语单词twins,identilal,doctor,fun编一个故事。
7、就社会上的学术造假发表你的看法8、和别的考生相比,你有何优势9、网络黑客算不算创新10、高校自主招生,我们考察的是什么11、分析烟酒奶粉等出现造假现象的原因,并提三条解决意见。
12、谈谈应试教育和素质教育的关系。
13、给我介绍一个你的朋友。
二、考生认为最难的问题1、山西省会在哪里2、你对雷锋怎么看3、交大的校训是什么4、昨天的新闻有些什么内容5、步行器电机功率是多少6、你的综合能力体面在哪些方面7、你知道国家的十一五规划吗8、你对上海房屋规划中的房屋间隔问题了解吗9、你是否知道矛盾论请运用矛盾论解题。
10、如果你在政府部门身居要职,有公司因第一次审批不合格,就暗中塞钱给你,你又因结婚、搬家等事急着用钱,反之,现在不收钱,这个企业也会把质量搞好,但要等个把月,你的选择是11、有人觉得探月计划劳民伤财,不适合中国国情,你怎么看简述三条理由。
2014西南交大数学建模期末大作业

2014西南交大数学建模期末大作业2014数学建模课程大作业题目:物流装载优化问题组别:队员1 队员2 队员3 姓名学号学院专业电话Email乘用车物流装载优化模型【摘要】本文对乘用车物流计划问题进行建模,结合枚举法、约束解除、动态寻优的方法对题目所给的三个装载问题进行求解。
我们记用1-1型货运车每层装运的I型乘用轿车的数量为a1,用1-2型货运车每层装运的I型乘用车的数量为a2;用1-1型货运车每层装运的II型乘用车的数量为b1,用1-2型货运车每层装运的II型乘用车的数量为b2;用1-1型货运车每层装运的III型乘用车的数量为c1,用1-2型货运车每层装运的III型乘用车的数量为c2。
对于问题一,只需要考虑I型车和II型车,来寻找最优装载方案;对于问题二,是对问题一的扩展,我们需要考虑到由于III型车的高度问题,它只能装在1-1和1-2型货运车的下层;对于问题三,这是问题一和问题二的结合,所以结合前两问的寻找最优解的方法和得到的结论来寻找问题三的最优装载方案。
本文详细介绍了寻找装载方案最优解的方法;以及对于所给的问题一、二、三,使用所给方法得到的最优装载方案的过程和结果。
关键词:物流最优化动态规划整数规划§1问题的重述一、问题背景众所周知,我国已经成为了世界第二大经济体,国民生活水平和人均GDP 也在大幅提高。
家用轿车已经日渐成为国人出行代步的重要工具,国内汽车消费增长趋势明显,乘用车市场需求旺盛。
1、整车物流的概述整车物流是指按照客户订单对整车快速配送的全过程。
随着我国汽车工业的高速发展,整车物流量,特别是乘用车的整车物流量迅速增长。
乘用轿车生产厂家根据全国客户的购车订单,向物流公司下达运输乘用车到全国各地的任务,物流公司则根据下达的任务制定运输计划并配送这批乘用车。
为此,物流公司首先要从他们当时可以调用的“货运车”中选择出若干辆货运车,进而给出其中每一辆货运车上乘用轿车的装载方案和目的地,以保证运输任务的完成。
西安交大数学建模实验报告

数学建模实验报告1,存货问题(一)问题描述某企业对于某种材料的月需求量为随机变量,具有如下表概率分布:每次订货费为500元,每月每吨保管费为50元,每月每吨货物缺货费为1500元,每吨材料的购价为1000元。
该企业欲采用周期性盘点的),(S s 策略来控制库存量,求最佳的s ,S 值。
(注:),(S s 策略指的是若发现存货量少于s 时立即订货,将存货补充到S ,使得经济效益最佳。
)(二)问题分析随机产生每个月需求量的概率,取遍每一个S 和s 的值,将每种S ,s 的组合对应的每月平均花费保存在数组money 里,筛选数组,选出其中费用最小值,并求出对应的S 和s 。
模拟400个月的生产情况。
(三)程序代码clear;clc;need=0; remain=0; cost=0; mincostavg=inf; forsl=30:10:70 forsh=80:10:140 fornum=1:100000m=rand; if m<=0.1 need=50;elseif m<=0.3 need=60;elseif m<=0.45 need=70;elseif m<=0.7 need=80;elseif m<=0.75 need=90;elseif m<=0.85 need=100;elseif m<=0.95need=110;elseneed=120;endif remain<slcost=cost+(sh-remain)*1000+500;ifsh<needcost=cost+(need-sh)*1500;remain=0;elsecost=cost+(sh-need)*50;remain=sh-need;endelseif remain<needcost=cost+(need-remain)*1500;remain=0;elsecost=cost+(remain-need)*50;remain=remain-need;endendendcostavg=cost/100000;ifcostavg<mincostavgmincostavg=costavg;propersl=sl;propersh=sh;endfprintf('s=%d, S=%d\nMonthly average cost=%.1f\n',sl,sh,costavg);cost=0;endendfprintf('\nWhen s=%d, S=%d\nThe least monthly average cost=%.1f\n',propersl,propersh,mincostavg);(四)运行结果s=30, S=80Monthly average cost=85466.9s=30, S=90Monthly average cost=87007.6Monthly average cost=87114.2 s=30, S=110Monthly average cost=87951.0 s=30, S=120Monthly average cost=86778.9 s=30, S=130Monthly average cost=86411.8 s=30, S=140Monthly average cost=86374.8 s=40, S=80Monthly average cost=83707.2 s=40, S=90Monthly average cost=84026.6 s=40, S=100Monthly average cost=85089.1 s=40, S=110Monthly average cost=85386.0 s=40, S=120Monthly average cost=86294.0 s=40, S=130Monthly average cost=85148.0 s=40, S=140Monthly average cost=84992.9 s=50, S=80Monthly average cost=83693.0 s=50, S=90Monthly average cost=82548.0 s=50, S=100Monthly average cost=82730.9 s=50, S=110Monthly average cost=83873.1 s=50, S=120Monthly average cost=84029.5 s=50, S=130Monthly average cost=84908.4 s=50, S=140Monthly average cost=84134.1 s=60, S=80Monthly average cost=83615.9 s=60, S=90Monthly average cost=82503.9 s=60, S=100Monthly average cost=81677.0Monthly average cost=81905.5s=60, S=120Monthly average cost=82946.0s=60, S=130Monthly average cost=83449.2s=60, S=140Monthly average cost=83871.3s=70, S=80Monthly average cost=83522.6s=70, S=90Monthly average cost=82525.8s=70, S=100Monthly average cost=81627.9s=70, S=110Monthly average cost=81323.3s=70, S=120Monthly average cost=82005.5s=70, S=130Monthly average cost=82601.6s=70, S=140Monthly average cost=82858.3When s=70, S=110The least monthly average cost=81323.3(五)结果分析用计算机模拟的结果和用数学分析的结果有一定的差异,由于计算机模拟时一般情况都是要简化模型的,所以在一定程度上会有所差异,我们可以考虑能不能通过改进算法来消除该差异,但对于一般的生产要求亦可以满足。
西安交通大学02-08数学建模期末试题

高等数学(下册)期末考试汇编(2008-7-8)一、解答下列各题 1. 设)cos(y x e z xy +=,求yzx z ∂∂∂∂,. 2. 求曲线3222,,x t y t z t ===在1=t 处的切线与法平面方程。
3. 求曲面32=+-xy e z z 在点)0,2,1(处的法线方程。
4. 求微分方程x e y y y 236--=-'-''的通解. 5. 设),(y x f 连续,交换积分次序⎰⎰⎰⎰-+xx y y x f xy y x f x202110d ),(d d ),(d 2.6. 设有一物体,它是由曲面22y x z +=和228y x z --=所围成,已知它在任意的点),,(z y x 处的密度z =ρ,求此物体的质量.7. 设L 是从点)0,1(A 到点)2,1(-B 的直线段,求第一型曲线积分⎰+Ls y x d )(.8. 计算第一型曲面积分⎰⎰∑++2)124(d y x s,其中∑是平面1648=++z y x 在第一卦限的部分.9. 设222z y x u ++=在椭球面1222222=++c z b y a x 点),,(0000z y x M 处沿外法线方向的方向导数.10. (注意:学习《工科数学分析》的做(1),其余的做(2))(1) 设函数⎰-=22d )(x x xyy ye x F ,求)(x F '. (2) 函数),(y x z z =由方程)(bz y az x -=-ϕ所确定,其中)(u ϕ有连续导数,b a ,为不全为零的常数,计算yz b x z a∂∂+∂∂. 二、求函数),(2x y x f x z =的偏导数22,xzx z ∂∂∂∂,其中f 具有二阶连续偏导数.三、计算第二型曲面积分⎰⎰∑∧++∧+∧+=y x z xx z x z y z x I d d )(d d d d )2(2,其中∑是曲面222y x z +-=在xoy 面上方部分,方向取上侧.四、若曲线积分⎰-+=Ly x x x y I d )3(d 33,其中L 为圆周)0(222>=+R R y x ,方向取正向,求R为何值时,I 有最大值.五、(注意:学习《工科数学分析》的做(1),其余的做(2))(1)求微分方程组x t x ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=542452222d d 的通解. (2)已知x xx x x x x e e xe y e xe y e xe y --++=+=+=23221,,是x x xe e y a y a y 221-=+'+''的特解,求21,a a 以及该方程的通解. 六、设)(x f 具有二阶连续的导数,试求)(x f 使得曲线积分⎰⋂'++-+=ABkx y x f x y x kf x f k e I d )(d )]()()1(['与积分路径无关.七、设D 为4,1,4,====xy xy x y x y 所围成的区域,F 是一元函数,且)()()()()(v f u f vu f v F u F +='+',其中)(x f 为正的连续函数,计算⎰∂+⎪⎭⎫⎝⎛-D y y xy F x x y xF d )(d ,其中D ∂为D 的边界曲线,方向为正向.(2007-7-8)一、解答下列各题(每小题6分,共60分)1.设cos(),y u u z xy x x y∂∂=∂∂求和. 2.求曲线2,,31x t y t z t ==-=-在对应于1t =处的切线和法平面方程。
数学建模校内赛

6) 不考虑天气等自然因素的影响。 7) 假设每次导弹发射时间均为 0。 8) 假设敌机始终在距离地面高度为 H 公里处飞行。 9) 导弹和敌机的速度已经确定即为迅速飞行。
三、符号说明
(2.5)
c11 c12 C c21 c22 c 31 c32
而
(2.6)
fi f f x1 i y1 i z1 x y z c11 x1 c12 y1 c13 z1 fi fi fi xs c21 x2 c22 y2 c23 z2 x2 y2 z2 y z c x c y c z x 31 3 32 3 33 3 f f f i x3 i y3 i z3 y z x
(x i , yi , zi ) ,距离为 ri , i 1,2,3 .定位目标飞行物的坐标为 S ( x, y, z ) 。
必须首先找到距离误差和坐标误差与最终的定位误差 x 之间的关系。为此, 在假设由每组测量数据可以得到目标的一个存在误差的方位的前提下, 首先进行 以下推导: 易知各测量站测得的目标距离:
fi f y y i i ci 2 i 1, 2,3 y yi ri ,
fi f z zi i ci 3 i 1, 2,3 z zi ri ,
因此有 式 2.5 中
(2.4)
r C x sx
f1 x c13 f c23 2 x c33 f 3 x f1 y f 2 y f3 y f1 z f 2 z f3 z
西交大经济数学建模作业及答案

−14%i
= 7200∑ e−14%i ≈ 38756 > 35000
i =1
所以买车比租车合算。
5 、 一商家销售某种商品的价格满足关系
p = 7 − 0.2 x (万元/吨), x 为销售量(单位:吨);商
品的成本函数是 C=3x+1(万元)。 (1) 若每销售一吨商品,政府要征税 t(万元),求 该商家获最大利润时商品的销售量; (2) t 为何值时,政府税收总额最大。
令 得
y = 1− (
则
dy = − aky (1 − y ) dt y (0) = y0
y 0 e − kat y= 1 − y 0 (1 − e − kat )
x0 a y0 = 1 − ( ) xm
解得
所以
y0 e− kat 1 − y0 x a ( ) = 1− = xm 1 − y0 (1 − e− kat ) 1 − y0 (1 − e− kat )
(1)利润L(x)= Px − C − T
令
= (7 − 0.2 x) x − 3 x − tx − 1 = (4 − t ) x − 0.2 x 2 − 1
T' = 0 ⇒ t = 2
5 (2) T = tx = 10t − t 2 2
5 L' ( x ) = 0, L'' ( x ) < 0 ⇒ x = 10 − t 2
损益阵为
收益值 (元)
需求10台 需求10台 10
需求20台 需求20台 20
需求30台 需求30台 30
选择10台 选择10台 10 选择20台 选择20台 20 选择30台 选择30台 30
西安交通大学数学建模上机实验报告
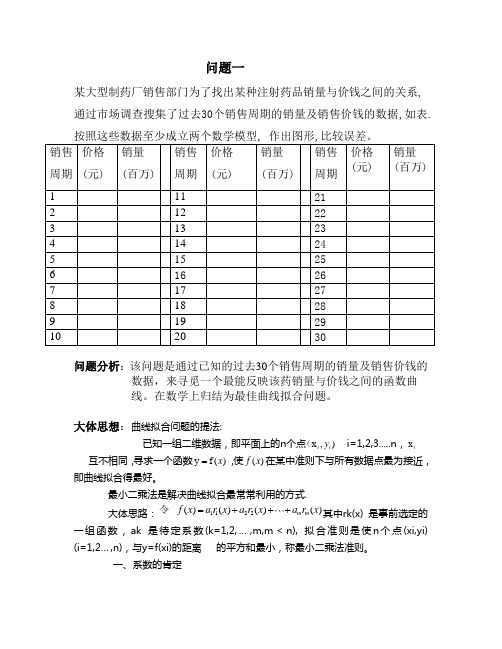
问题一某大型制药厂销售部门为了找出某种注射药品销量与价钱之间的关系,通过市场调查搜集了过去30个销售周期的销量及销售价钱的数据,如表.按照这些数据至少成立两个数学模型, 作出图形,比较误差。
问题分析:该问题是通过已知的过去30个销售周期的销量及销售价钱的 数据,来寻觅一个最能反映该药销量与价钱之间的函数曲 线。
在数学上归结为最佳曲线拟合问题。
大体思想:曲线拟合问题的提法:已知一组二维数据,即平面上的n 个点),x i i y ( i=1,2,3.....n ,i x 互不相同,寻求一个函数)(f y x =,使)(x f 在某中准则下与所有数据点最为接近,即曲线拟合得最好。
最小二乘法是解决曲线拟合最常常利用的方式.大体思路:1122 ()()()()m m f x a r x a r x a r x =+++令其中rk(x) 是事前选定的一组函数,ak 是待定系数(k=1,2,…,m,m <n), 拟合准则是使n 个点(xi,yi) (i=1,2…,n),与y=f(xi)的距离 的平方和最小,称最小二乘法准则。
一、系数的肯定22111 (,,)[()]n nm ii i i i J a a f x y δ====-∑∑记求m a a ,,1 使得使J 达到最小.0 (1,,)kJ k m a ∂==∂ 取得关于 m a a ,,1 的线性方程组:11111()[()]0 ()[()]0nmi k k i i i k n mm i k k i i i k r x a r x y r x a r x y ====⎧-=⎪⎪⎪⎨⎪⎪-=⎪⎩∑∑∑∑ 1 ,,().m a a f x 解出,即得散点图: 程序: x=[,,,,,,,,,,,,,,,,,,,,,,,,,,,,,]; y=[,,,,,,,,,,,,,,,,,,,,,,,,,,,,,]; plot(x,y,'r.')通过观察,结合实际情形。
2011年西安交通大学建模夏令营第二轮模拟赛A题

2011西安交通大学数学建模夏令营第三轮模拟竞赛题目A题:重构被人类影响的海洋生态系统考虑如图1所示的一个狭窄通道区域,它位于陆地A和陆地B之间,这里过去长满了珊瑚礁并且支撑了一个巨大的生物种群。
由于商业化遮目鱼养殖的引入,这一区域的生物多样性戏剧性地减少。
曾经这里生活着大量的珊瑚,但现在海域底部大部分都被淤泥所覆盖。
自从珊瑚被埋葬以后, 由于过度的捕捞和缺少野生鱼的栖息地,现在已经很少有野生鱼出没了。
然而鱼是当地居民的重要食物来源, 寻找新的方法来使得自然生态系统继续繁荣是关系到人民生活的重要事情,也就需要建立一个混养系统来代替现有的遮目鱼单养系统。
理想情况下的混养方案是多种生物混养在一起,一些生物的排泄物恰好是另外一些生物的食物,这不仅会减少鱼养殖中向周围水体排放的富营养物质,同时也通过利用养鱼产生的大量副产品(贻贝,海带等)来增加农民的收入。
就建模的目的而言,生物多样性环境中的主要动物生物体可细分为肉食性鱼类、草食性鱼类、软体动物、甲壳类动物、棘皮动物和藻类。
根据供养种类,有初级生产者(光合作用生产者)、滤食性动物(株浮游生物,有机颗粒,部分水中微生物)、沉积性动物(吃泥土和消化其中的有机分子和养分)、食草动物(吃初级生产者)和捕食性动物(如食肉动物)。
在海洋中的食肉动物除了吃食草动物或小一些的肉食动物以外,它们也吃滤食性动物和沉积性动物。
大多数动物的生长效率只有10-20%,所以他们摄入的80-90%的食物最终会以不同的形式释放出来,有些作为热量散发出来,有些是排泄物。
在这一生物多样性的环境中,珊瑚的作用主要是划分空间,并通过让大量生物各自在一个狭小空间内获得适宜生存的环境,来使物种能够集中共存。
珊瑚还可以进行一定的滤食,这有助于水的净化。
一个海域支持珊瑚生存的能力,取决于许多因素,其中最重要的是水质。
例如在该区域,当每毫升海水中含有50万至100万微生物,以及每升海水中含有0.25ug叶绿素(大量浮游植物的替代物)时,珊瑚就能够生存繁殖。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一次作业一、问题得叙述,问题得分析叙述:对于由连续曲线所围成得平面区域能否做到以下几点: 1 用平行于某定直线得直线二等分该区域; 2 用垂直于某定直线得直线二等分该区域; 3 用相互垂直得两条直线四等分该区域 分析:问题简化为对三个题目得证明已知平面上一条没有交叉点得封闭曲线(形状不定),设有一定直线L过某点P 0且与x轴得正向夹角为a二、问题求解 <1>:证明作一平行于L得直线l,l过点p 且将曲线所围图形分为两部分,其面积分别记为,、若=(发生得概率较小),则得到直线a 得斜率,即可得定直线L ;若,设,且L 得斜率为t anα将直线l 按逆时针方向旋转,面积,连续地依赖斜率变化而变化,记为(k),(k),设,如图17-3,17—4所示.PS 1(a)S 2(a)a 0xl图17-3 旋转成a 角laPS 1(a 0+180°)S 2(a 0+180°)a 0xl图17-4 旋转180°后a 0+180°令)则有函数上连续,且在端点异号:=(k 1)-(k1)根据闭区间上连续函数得零点定理必存在一斜率使=0,即。
过曲线内p 做直线l,取斜率为则直线L 过定点P 0且斜率为,所以解得某定直线L 与其平行得任意直线l 平分改闭合区域。
由上述知1得证<2〉:证明同理有定直线L,垂直于L得直线为b,其斜率为K3=-1/tanα。
同理可得存在这样得一条直线b,所以2得证.<3〉:证明由<1>,<2>可知,对平面上任意得封闭区域,在任意方向上都存在直线将其面积等分如下图两种连续移动都可以满足介值定理,通过平移得方法很容易证明,在任意一个方向上都可以先找到一条直线a使其平分封闭区域得面积,然后可以作直线b,垂直于L且可以平分该封闭区域得面积此时Ⅰ+Ⅱ=Ⅲ+Ⅳ=Ⅰ+Ⅳ=Ⅱ+Ⅲ,从而Ⅰ=Ⅲ,Ⅱ=Ⅳ,若求得Ⅰ=Ⅱ,则命题得证;设Ⅰ逆时针调节直线a,b,直到a与b得初始位置重合如下图;在调整得过程中,Ⅰ= Ⅱ, Ⅱ=Ⅰ,于就是根据介值定理,必然存在某一时刻Ⅰ=Ⅱ,所以〈3>得证第二次作业1.题目:2.题目分析:(1)y k=C k+Z K+g;(2)C K=b y k-1;(3)Z K=α(Ck—C k-1);3.模型求解:有题目分析得CK=b yk—1,Z K=α(C k—C k—1)= αb(yk—1-y k-2)将CK,ZK代入y k 得y k+1=by k +αb(yk—y k-1)+g;一个特解为;特征方程为λ2—。
(αb+b)λ+αb=0;假设α=10,g=5,y1 =12,y2=15、775讨论:(1)若方程有两个实根解得:λ1= b/2 + (a*b)/2—(b*(b -4*a + 2*a*b+a^2*b))^(1/2)/2λ2=b/2 +(a*b)/2+(b*(b— 4*a +2*a*b+ a^2*b))^(1/2)/2所以yk =C1 λ1k+ C2λ2k+=C1[b/2 +(a*b)/2 - (b*(b-4*a +2*a*b + a^2*b))^(1/2)/2]k+ C2[b/2+ (a*b)/2- (b*(b -4*a + 2*a*b+ a^2*b))^(1/2)/2]k+取b=0、5有解得原方程得解为:(2)方程有一个解△=0;b=;λ=解得原方程为(3)△<0原方程无解程序x=1:20;y1=10+4、3508、^x+1、4192、^x;y2=(12-3、3266、*x)、*1、8182、^x;plot(x,y1,’g、','markersize’,25)hold on;plot(x,y2,’r、’,’markersize',25)legend('Á½¸öʵ¸ù’,'Ò»¸öʵ¸ù')grid;第三次作业P、172 实验二最短电缆长度问题设有九个节点,它们得坐标分别为a(0,15),b(5,20),c(16,24),d(20,20),e(33,25),f(23,11), g(35,7), h(25,0), i(10,3)任意两个节点之间得距离为:问:怎样连接电缆,使每个节点都连通,且所用得总电缆得长度为最短、问题分析:本题研究得就是一个最优化问题。
问题中给出了9个节点坐标,需要从复杂得连接方案中选出最短得电缆连接路线.要设计方案求最短电缆长度,可先求出任意两点间得距离,然后在构造边权矩阵,用prim算法求电缆线得最优连通方案。
符号说明:W:任意两点之间得距离矩阵X:节点得横坐标Y:节点得纵坐标解:先计算出任意两点间得距离;W=[];X =[0516 2033 23 35 25 10];Y=[152024 20 25 11 7 0 3];N=length(X);for i=1:Nfor j=1:NW=[W;(abs(X(i)-X(j))+abs(Y(i)—Y(j)))]endendW’输出结果截图为:a b c d e fgh iw(I,j)a 43 43 40b 0 22c 7de 0 24 20 33 21f 0 1613 29g 0 17 29h0 18i 0用prim算法求电缆线得最优连通方案;运行结果截图为:分析结果可知:最小生成树得边集合为{(1,2),(2,3),(3,4),(4,6),(6,8),(6,7),(3,5),(8,9)}即用prime算法求出得最优电缆连接方案为:{(a,b),(b,c),(c,d),(d,f),(f,h),(f,g),(c,e),(h,i)}。
第四次作业一、问题引入:假设某地人口总数保持不变,每年有A%得农村人口流入城镇,有B%得城镇人口流入农村,但人口得流动性始终保持在5%以下,并且农村人口流入城镇比例大于城镇流入农村人口,即(B<A〈5).试讨论至少四组不同得A、B值,得到该地得城镇人口与农村人口得分布得最终状态。
二、问题分析:ﻩ关于人口迁移问题:这个人口得变化可以由矩阵乘法来确定。
假设初始时有30%生活在城市,70%生活在农村。
令c=,=则1年后,城市与农村人口比例可由表示,一般得,n年后,城市与农村人口比例可由表示.三、编辑程序运行:利用所建模型,用Matlab计算第i年人口得关系式假设A=4,B=2,令i得值逐渐增大,求得:, ,,,研究本问题中当时间无限长时农村人口以及城镇人口得极限状况.因为=,所以当n趋向于无穷时讨论A、B不同取值对最终结果得影响。
A B 城市人口所占比例农村人口所占比例11、50、51/43/422、50、51/6 5/632、51、53/85/843、50、51/8 7/853、51、53/10 7/1063、52、55/127/1274、50、51/109/1084、51、51/43/494、52、50、3571 0、64291 04、53、57/16 9/16第五次作业一、问题得叙述,问题得分析叙述:房屋管理部门想在房顶得边檐安装一个檐槽, 其目得就是为了雨天出入方便。
从屋脊到屋檐得房顶可瞧成就是一个a米长,b米宽得矩形平面,房顶与水平方向得倾斜角度一般在20~50ba现有一公司想承接这项业务,允诺:提供一种新型得檐槽,包括一个横截面为半圆形(半径为dcm)得水槽与一个竖直得排水管(直径为lcm),不论天气情况如何,这种檐槽都能排掉房顶得雨水。
b a房管部门犹豫,考虑公司得承诺能否实现。
请您建立数学模型,论证这个方案得可行性。
也可结合实际中进行水槽得设计. 分析:水槽得容量能否足以排出雨水得问题,简化为水箱得流入流出问题。
从房项上流下得雨水量就是流入量;顺垂直于房顶得排水管排出得就是流出量。
水槽能否在没有溢出得情况下将全部雨水排出,即就就是要研究水槽中水得深度与时间得函数关系。
假设:(1)雨水垂直下落并且直接落在房顶上;(2)落在房顶上得雨水全部迅速流入水槽中; (3)落在房顶上得雨没有溅到外面去;(4)在排水系统中不存在一些预料不到得障碍,象落在房顶上得杂物、树叶等; (5)假设在水槽中已有雨水深0、05m ; 模型建立:根据速度平衡原理,对于房顶排水系统水槽中水得容量得变化率=雨水得流入速度 - 排水管流出得速度。
分别就是单位时间流入水槽与从水槽流出得雨水量得体积。
表示单位时间里落在水平面上雨水得深度,房顶得面积 水流实际受雨得水平面积,房顶上雨水得流速 流入水槽得速度应就是在铅垂方向得分量排水管得流出速度应与水槽中水得深度有关。
根据能量守恒原理水槽中水得体积为 , h求解与分析:将表中得数据代入(7)式,用mat lab 解得由假设(1)若。
先讨论水槽得深度趋于一个低于0。
075m得稳定值,即时。
将代入上述模型,得到 h(t)= 899209、148v^2当h(t)<=0、075时,解得v<= 0、00028802由此得到,当v<= 0。
00028802m/s时,水不溢出;当v>0。
00028802 m/s时,水溢出。
下面,用matlab对这一结论进一步分析。
不妨取v=0、0002、0、000288 分别代入方程(*)求其数值解,并作出图形:编写a、m 文件:function hp=a(t,h1)hp=(1、374038*0、0002-0、001449*sqrt(h1))/sqrt(0、15*h1-h1^2);function hp=b(t,h2)hp=(1、374038*0、0003-0、001449*sqrt(h2))/sqrt(0、15*h2—h 2^2);执行matlab程序:>>[t,h1]=ode45('a’,[0,60],0、01);>> plot(t,h1)〉> [t,h2]=ode45(’b',[0,60],0、01);plot(t,h2)我国气象部门规定24 h降水量在200mm以上(约0、000 002m/s)得雨为特大暴雨。
对于这种情形,v>0.00028802 m/s 即24 h降水量在24884。
9mm 以上得强降雨机率几乎为0,因此,这个公司得承诺就是能兑现得。
(2)若为周期函数,不妨设为正弦函数,即:这表明下雨过程就是在60s内发生得一个短促得强阵雨过程,最大得降雨强度就是0、00001m/s,由方程(*)得到如下微分方程:运用matlab求数值解:编写shuicao、m 文件:functionf=shuicao(t,h)f=(0、000412*sin(pi*t/60)-0、001449*sqrt(h))/sqrt(0、15*h-h^2);执行matlab程序:>>[t,h]=ode45('shuicao',[0,60],0、01);〉>plot(t,h)从图中可以瞧出,h(t)得最大值不会超过0.075m,因此,对于第(2)种情况,水槽得水也不会溢出,这个公司得承诺就是能兑现得。
