数学建模大作业
数学建模_大作业1
数学建模大作业姓名1：赵成宏学号：201003728姓名2：吴怡功学号：201003738姓名3：蒲宁宁学号：201004133专业：车辆工程2013年5 月28 日直升机运输公司问题一家运输公司正考虑用直升机从某城市的一摩天大楼运送人员。
你被聘为顾问，现在要确定需要多少架飞机。
按照建模过程仔细分析，建模。
为了简化问题，可以考虑升机运输公司问题。
基本假设如下：假设运载的直升机为统一型号; 假设每架飞机每次载人数相同；假设飞机运送的人员时互不影响；假定人员上了飞机就安全，因此最后一次运输时，只考虑上飞机所花时间。
1、按照数学建模的全过程对本题建立模型，并选用合理的数据进行计算（模型求解）; 2、本问题是否可以抽象为优化模型;除了考虑建立优化模型之外，是否可以采用更简单的方法建立模型。
注意考虑假设条件。
甚至基于不同的假设建立多个模型。
归纳起来，有以下假设：（H1）所有飞机的飞行高度度均为10 000m ，飞行速度均为800km/h 。
(H2)飞机飞行方向角调整幅度不超过6，调整可以立即实现；(H3)飞机不碰撞的标准是任意两架飞机之间的距离大于8km; (H4)刚到达边界的飞机与其他飞机的距离均大于60km; (H5)最多考虑N 架飞机;(H6)不必考虑飞机离开本区域以后的状况. 为方便以后的讨论，我们引进如下记号: D 为飞行管理区域的边长;S 为飞行管理区域取直角坐标系使其为[0,D ]×[0，D]; v 为飞机飞行速度，v=800km/h;（x 0i ，y i）第i 架飞机的初始位置;（)(),(t t y x ii ）为第i 架飞机在t 时刻的位置;θ0i为第i 架飞机的原飞行方向角，即飞行方向与x 轴夹角，0≤θ≤2π;θi ∆第i 架飞机的方向角调整，-6π≤i θ∆≤6π; i θ﹦i 0i θθ∆+为第i 架飞机调整后的飞行方向角;一、两架飞机不碰撞的条件1、两架飞机距离大于8km 的条件设第i 架和第j 架飞机的初始位置为（0i 0i y x ，），（0j 0j y x ，）,飞行方向角分别为错误！未找到引用源。
数学建模案例作业
数学建模案例作业作业1 商人过河问题三名商人各带一个随从乘船渡河，一只小船只能容纳二人，由他们自己划行（六个人都会划船）。
随从们密谋，无论何时，一旦随从的人数比商人多，就杀人越货。
但是如何乘船渡河的决定权掌握在商人手中。
商人们怎样才能安全渡河？示意图如下： 随从：商人： 一、状态变量一次决策),(k k k y x S = 3,2,1=k 表示第k 次渡河时，此岸的商人数，随从数. 最初 )3,3(0=S 且为整数）3,0(≤≤k k y x)}0,0(),1,0(),2,0(),3,0(),0,1(),1,1(),2,1(),3,1(),0,2(),1,2(),2,2(),3,2(),0,3(),1,3(),2,3(),3,3{(=S要安全过河，需保证彼岸此岸都安全，及随从数不能大于商人数，所以安全的情况有10种，即)}0,0(),1,0(),2,0(),3,0(),1,1(),2,2(),0,3(),1,3(),2,3(),3,3{(=S ② 二、决策变量设),(k k k v u d =2,0(≤≤k k v u 且)21≤+≤k k v u 表示第k 次渡河时，船上的商人数和随从数 )}1,0(),0,1(),2,0(),1,1(),0,2{(=D与状态变量相结合，安全的情况有三种，即 )}1,0(),2,0(),1,1{((=D ③ 三、状态转移方程奇数次（此案到彼岸）k k k d S S -=+1 偶数次（彼岸到此案）k k k d S S +=+1 即k k k k d S S )1(1-+=+ ① 数学建模：由①确定的转移方程下，经过n 次决策，将初始状态转移到最终状态)0,0(=n S . 每次的决策取自③式，每次到达的状态在②中. 图解法：①从右上角移到左下角，每次最多移两步；②奇数次渡河往左下方，偶数次渡河往右下方。
建立平面直角坐标系如图：n S 过河方案：从A 点)3,3(0=S 出发到D 点)0,0(=n S 结束① 小船一次最多能载两人，所以每次最多移动两个格子② 由此岸即彼岸时人员减少，即奇数遍时向左下方行走；有彼岸及此岸时人员增加，即偶数遍时向右上方行走。
数学建模期末大作业
数学建模承诺书
我们仔细阅读了数学建模作业的对应规则。
我们完全明白，在开始做题后不能以任何方式（包括电话、电子邮件、网上咨询等）与队外的任何人研究、讨论与赛题有关的问题。
我们知道，抄袭别人的成果是违反规则的。
如果引用别人的成果或其他公开的资料（包括网上查到的资料），必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺，严格遵守规则，以保证公正、公平性。
如有违反规则的行为，我们将受到严肃处理。
我们选择的题号是（A/B/C/D题）： D
参赛队员：
1. 专业年级软件工程姓名段永春学号201410413112 成绩
2. 专业年级软件工程姓名殷福贵学号201410413113 成绩
3. 专业年级软件工程姓名高培富学号201410413107 成绩
日期： 2015 年 6 月 15 日。
数学建模第四套
徐州工程学院个性化教育数学建模（大作业）试卷班级 学号 姓名 得分1、某农场饲养的某种动物所能达到的最大年龄为15岁，将其分成三个年龄组：第一组，0~5岁；第二组，6~10岁；第三组，11~15岁。
动物从第二年龄组开始繁衍后代，经过长期统计，第二组和第三组的繁殖率分别为4和3，第一年龄和第二年龄组的动物能顺利进入下一个年龄组的存活率分别为1/2和1/4。
假设农场现有三个年龄段的动物各100头，问15年后农场三个年龄段的动物各有多少头？解：由于年龄分为五岁一段，所以时间周期取5年。
设(k)i x 表示第k 个时间周期，第i 组年龄阶段动物的数量。
因为某一时间周期第二年龄组和第三年龄组的动物数量是由上一周期上一年龄组存活下来的动物的数量决定的，所以有(k)(k 1)(k)(k 1)213211,22x x x x --== 又因为某一时间周期，第一年龄组的动物数量是由上一时间周期各个年龄组出生的动物数量决定的，所以有(k)(k 1)(k 1)12343x x x --=+由此得到递推关系式： (k)(k 1)(k 1)123(k)(k 1)21(k)(k 1)32431214x x x x x x x ----⎧=+⎪⎪⎪=⎨⎪⎪=⎪⎩ 用矩阵表示为： (k)(k 1)11(k)(k 1)22(k)(k 1)3304310021004x x x x x x ---⎡⎤⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦即(k)(k 1)x Lx -=，其中(n)043100100,10021001004L x ⎡⎤⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦则有()()()(3)(2)(1)(0)1437.5137.587.5x Lx L Lx L L Lx ⎡⎤⎢⎥====⎢⎥⎢⎥⎣⎦计算过程代码如下： >> x0=[100;100;100];>> L=[0,4,3;1/2,0,0;0,1/4,0]; >> x1=L*x0; >> x2=L*x1; >> x3=L*x2x3 =1.0e+03 * 1.4375 0.1375 0.0875结果分析：由于动物的数量不可能出现小数，所以根据实际，15年后农场饲养动物的数量2、深洞的估算： 假如你站在洞口且身上仅带着一只具有跑秒功能的计算器，你出于好奇心想用扔下一块石头听回声的方法来估计洞的深度，假定你捡到一块质量是1KG 的 石头，并准确的测定出听到回声的时间T=5S ，就下面给定情况，分析这一问题，给出相应的数学模型，并估计洞深。
数学建模通识课大作业题目
数学建模通识课大作业题目注意事项:(1) 大型作业由学生组队完成,每队不超过3人；(2) 在17个题目中任选一题完成；(3) 答卷包括问题复述、建模假设与建立、模型求解与计算等部分组成，引用别人的成果或其他公开的资料(包括网上查到的资料) 必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出；(4) 答卷必须具有原创性，如发现抄袭和雷同，成绩计0分；(5) 答卷以电子版的形式发给各任课老师指定的邮箱，交卷截止时间为2012年12月20日晚上9：30。
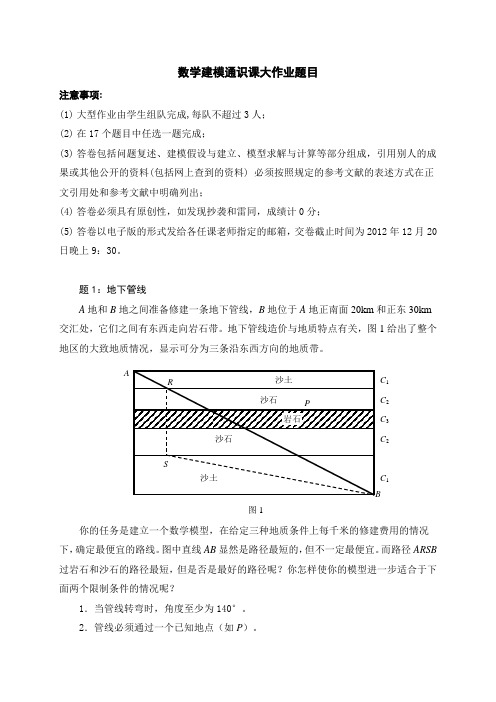
题1：地下管线A 地和B 地之间准备修建一条地下管线，B 地位于A 地正南面20km 和正东30km 交汇处，它们之间有东西走向岩石带。
地下管线造价与地质特点有关，图1给出了整个地区的大致地质情况，显示可分为三条沿东西方向的地质带。
你的任务是建立一个数学模型，在给定三种地质条件上每千米的修建费用的情况下，确定最便宜的路线。
图中直线AB 显然是路径最短的，但不一定最便宜。
而路径ARSB 过岩石和沙石的路径最短，但是否是最好的路径呢？你怎样使你的模型进一步适合于下面两个限制条件的情况呢？1．当管线转弯时，角度至少为140°。
2．管线必须通过一个已知地点（如P ）。
AC 1 C 1C 2 C 2C 3 图1题2：电子游戏中的数学近年来，随着电子游戏的日益普及，电子游戏业已成为横跨信息技术和文化的重要产业。
对电子游戏中的一些数学问题进行研究，成为数学界和相关人士的一个热门话题。
在某电子游戏中，玩家每次下注一元，由机器随机分配给玩家五张扑克牌，然后允许玩家有一次换牌的机会，即可以放弃其中的某几张牌，放弃的牌留下的空缺由机器在剩下的47张牌中再次随机分配。
玩家的奖金依据其最后所持有的牌型而定。
下面是一份典型的奖金分配表：牌型奖金（元）同花大顺（10到A）800同花顺50四张相同点数的牌25满堂红（三张同点加一对）8同花 5顺子 4三张相同点数的牌 3两对 2一对高分对（J及以上） 1其它0在上表中，玩家的牌型属于某一类型且不属于任何更高的类型，则赢得该牌型相应的奖金。
数学建模 大作业1
N
（ 1, 2 ,..... N )= i 的极小值。通常表示为 i 1
N
min F（ 1, 2 ,..... N )= i , i 1
s.t. rij2 (t)＞64 ，t tij ，i，j=1,2，….N,i≠j
i
6
，i=1,2，….N.
由于在这个及消化问题中目标函数可约束条件关于变量 1, 2 ,..... N 均为非 线性的，因此上述方程组是一个有约束的非线性的规划模型。
数学建模大作业
姓名 1：廉文秀 学号：200904745 姓名 2：沙吾列 学号：200903952 姓名 3：索海娟 学号：200903951 专业：车辆工程 班级：094 指导老师：张仲荣
2012 年 5 月 22 日
升机运输公司问题
一家运输公司正考虑用直升机从某城市的一摩天大楼运送人员。你被聘为顾 问，现在要确定需要多少架飞机。按照建模过程仔细分析，建模。为了简化问题， 可以考虑升机运输公司问题。 基本假设如下：
由于约束条件 ri2j (t)>64, t t ij ，i，j=1,2，…N，i j
有较强的非线性，特别是 tij 的表达式比较复杂，我们可以将问题进一步简化。注
(t)=vtcos
+
x
0 j
(t)=vtsin
+
y
0 j
若记时刻 t 他们距离为 (t),则他们之间距离的平方为
ri2j （t）=（xi（t）-xj(t)）2+（yi(t)-yj（t））2
经简单计算可得
ri2j （ t ） =v2 [(cos i -cos j )2+(sin i -sin j )2] t2
i
架飞机的方向角调整，-
数学建模期末大作业
数学建模期末大作业论文题目：A题美好的一天组长：何曦（2014112739）组员：李颖（2014112747）张楚良（2014112740）班级：交通工程三班指导老师：陈崇双美好的一天摘要关键字：Dijkstra算法多目标规划有向赋权图 MATLAB SPSS1 问题的重述Hello！大家好，我是没头脑,住在西南宇宙大学巨偏远的新校区（节点22）。
明天我一个外地同学来找我玩，TA叫不高兴，是个镁铝\帅锅，期待ing。
我想陪TA在城里转转，当然是去些不怎么花钱的地方啦~~。
目前想到的有林湾步行街(节点76)、郫郫公园（节点91），大川博物院（节点72）。
交通嘛，只坐公交车好了,反正公交比较发达，你能想出来的路线都有车啊。
另外，进城顺便办两件事，去老校区财务处一趟（节点50），还要去新东方（节点34）找我们宿舍老三，他抽奖中了两张电影票，我要霸占过来明晚吃了饭跟TA一起看。
电影院嘛，TASHIWODE电影院（节点54）不错，比较便宜哈。
我攒了很久的钱，订了明晚开心面馆（节点63）的烛光晚餐，额哈哈，为了TA，破费一下也是可以的哈。
哦，对了，老三说了，他明天一整天都上课，只有中午休息的时候能接见我给我票。
我主要是想请教一下各位大神：1）明天我应该怎么安排路线才能够让花在坐车上的时间最少？2）考虑到可能堵车啊，TA比较没耐心啊，因为TA叫不高兴嘛。
尤其是堵车啊，等车啊，这种事，万一影响了气氛就悲剧了。
我感觉路口越密的地方越容易堵，如果考虑这个，又应该怎么安排路线呢？3）我们城比较挫啊，连地图也没有，Z老师搞地图测绘的，他有地图，跟他要他不给，只给了我一个破表格（见附件，一个文件有两页啊），说“你自己画吧”。
帮我画一张地图吧，最好能标明我们要去的那几个地方和比较省时的路线啊，拜托了~2 问题的分析2.1 对问题一的分析问题一要求安排路线使得坐车花费的时间最少。
对于问题一，假设公交车的速度维持不变，要使花费的时间最少，则将问题转化为对最短路径的求解。
数学建模大作业
兰州交通大学数学建模大作业学院：机电工程学院班级：车辆093学号：200903812 姓名：刘键学号：200903813 姓名：杨海斌学号：200903814 姓名：彭福泰学号：200903815 姓名：程二永学号：200903816 姓名：屈辉高速公路问题1 实验案例 (2)1.1 高速公路问题(简化) (2)1.1.1 问题分析 (3)1.1.2 变量说明 (3)1.1.3 模型假设 (3)1.1.4 模型建立 (3)1.1.5 模型求解 (4)1.1.6 求解模型的程序 (4)1实验案例1.1 高速公路问题(简化)A城和B城之间准备建一条高速公路，B城位于A城正南20公里和正东30公里交汇处，它们之间有东西走向连绵起伏的山脉。
公路造价与地形特点有关，图4.2.4给出了整个地区的大致地貌情况，显示可分为三条沿东西方向的地形带。
你的任务是建立一个数学模型，在给定三种地形上每公里的建造费用的情况下，确定最便宜的路线。
图中直线AB显然是路径最短的，但不一定最便宜。
而路径ARSB过山地的路段最短，但是否是最好的路径呢？AB图8.2 高速公路修建地段1.1.1 问题分析在建设高速公路时，总是希望建造费用最小。
如果要建造的起点、终点在同一地貌中，那么最佳路线则是两点间连接的线段，这样费用则最省。
因此本问题是一个典型的最优化问题，以建造费用最小为目标，需要做出的决策则是确定在各个地貌交界处的汇合点。
1.1.2 变量说明i x ：在第i 个汇合点上的横坐标（以左下角为直角坐标原点），i ＝1，2，…，4；x 5＝30（指目的地B 点的横坐标）x=[x 1，x 2，x 3，x 4]Tl i ：第i 段南北方向的长度（i ＝1，2， (5)S i ：在第i 段上地所建公路的长度（i ＝1，2， (5)由问题分析可知，()()()()25425524324423223322122221211x x l S x x l S x x l S x x l S x l S -+=-+=-+=-+=+=C 1：平原每公里的造价（单位：万元/公里）C 2：高地每公里的造价（单位：万元/公里） C 3：高山每公里的造价（单位：万元/公里）1.1.3 模型假设1、 假设在相同地貌中修建高速公路，建造费用与公路长度成正比；2、 假设在相同地貌中修建高速公路在一条直线上。
《数学建模》作业
要求1、选题要求，学号是1号的选A组第1题，2号选A组第2题，以此类推，15号选A组第15题，16号回头选A组第1题。
如果对上面的题目把握不大或不敢兴趣的，可以在B组题目中任选一题。
2、答卷论文内容包括：摘要（100——300字，含研究的问题、建模的方法及模型、模型解法和主要结果），问题分析与假设，符号说明，问题分析，模型建立，计算方法设计和实现（框图及计算机输出的计算结果），结果的分析和检验，优缺点和改进方向等。
用软件求解的，请在附件中附上算法程序。
3、论文（答卷）用白色A4纸，上下左右各留出2.5厘米的页边距。
4、第一页为封面（自己下载），写上学号、姓名、第二页为论文标题和摘要，从第三页开始是论文正文。
论文从第二页开始编写页码，页码必须位于每页页脚中部，用阿拉伯数字从“1”开始连续编号。
5、论文题目用3号黑体字、一级标题用4号黑体字，并居中。
论文中其他汉字一律采用小4号宋体字，行距用单倍行距。
6、引用别人的成果或其他公开的资料(包括网上查到的资料) 必须按照规定的参考文献的表述方式在正文引用处和参考文献中均明确列出。
正文引用处用方括号标示参考文献的编号，如[1][3]等；引用书籍还必须指出页码。
参考文献按正文中的引用次序列出，其中书籍的表述方式为：[编号] 作者．书名[M]．出版地：出版社，出版年参考文献中期刊杂志论文的表述方式为：[编号] 作者．论文名[J]．杂志名，卷期号：起止页码，出版年参考文献中网上资源的表述方式为：[编号] 作者．资源标题．网址，访问时间（年月日）。
论文提交：2015年5月（本学期第11周）论文打印装订成册上交注：2015年5月（本学期第11,12周）答辩大作业题目A组1、生产计划高校现有一笔资金100万元，现有4个投资项目可供投资。
项目A：从第一年到底四年年初需要投资，并于次年年末回收本利115%。
项目B：从第三年年初需要投资，并于第5年末才回收本利135%，但是规定最大投资总额不超过40万元。
数学建模大作业习题答案
数学建模大作业习题答案数学建模大作业习题答案作为一门应用数学课程，数学建模在现代科学研究和工程技术中具有重要的地位和作用。
通过数学建模，我们可以将实际问题转化为数学模型，从而利用数学方法进行分析和求解。
在数学建模的学习过程中，我们经常会遇到一些习题，下面我将为大家提供一些数学建模大作业题目的答案，希望能对大家的学习有所帮助。
1. 题目：某城市的交通拥堵问题解答：针对这个问题，我们可以采用图论的方法进行建模和求解。
首先，我们将城市的道路网络抽象为一个图，图的节点表示交叉口，边表示道路。
然后，我们可以给每条边赋予一个权重，表示道路的通行能力。
接着，我们可以使用最短路径算法，比如Dijkstra算法，来计算从一个交叉口到另一个交叉口的最短路径，从而找到最优的交通路线。
此外，我们还可以使用最小生成树算法，比如Prim算法，来构建一个最小的道路网络，以减少交通拥堵。
2. 题目：某工厂的生产调度问题解答：对于这个问题，我们可以采用线性规划的方法进行建模和求解。
首先，我们可以将工厂的生产任务抽象为一个线性规划模型，其中目标函数表示最大化生产效益，约束条件表示生产能力、物料供应和市场需求等方面的限制。
然后，我们可以使用线性规划求解器，比如Simplex算法或内点法，来求解这个线性规划模型，得到最优的生产调度方案。
此外，我们还可以引入一些启发式算法，比如遗传算法或模拟退火算法，来寻找更好的解决方案。
3. 题目：某股票的价格预测问题解答：对于这个问题，我们可以采用时间序列分析的方法进行建模和求解。
首先，我们可以将股票的价格序列抽象为一个时间序列模型，比如ARIMA模型。
然后，我们可以使用历史数据来拟合这个时间序列模型，并进行参数估计。
接着，我们可以利用这个时间序列模型来预测未来的股票价格。
此外，我们还可以引入其他的预测方法，比如神经网络或支持向量机，来提高预测的准确性。
通过以上的例子，我们可以看到，在数学建模的过程中，我们需要将实际问题抽象为数学模型，然后利用数学方法进行分析和求解。
数学建模大作业书写格式
题目成绩：组员：1．姓名：专业学号星期第讲2．姓名：专业学号星期第讲3．姓名：专业学号星期第讲请认真核对个人信息，乱填者，扣分摘要（写出你建模的大致思路、方法及主要结果，不得低于200字）关键词：（写出你论文中用到的主要关键词，一般五个左右）（摘要和关键词单独一页）1 问题重述（写出问题的具体内容，本部分可省略）2 条件假设（写出你对模型的基本假设条件，要合情合理）3 符号说明（对模型中出现的变量进行符号约定）4 问题分析（围绕问题对题目涉及的背景、内容等进行深入分析；若有多个问题，请逐题分析）5 模型建立（建立相应的数学模型；若有多个问题，请逐题建立各类数学模型）6 模型求解（给出你求解模型的算法、流程图等，给出具体计算结果）7 模型检验与评价（对模型的结果进行合理性评价，评价你建立的模型的优劣性）8 参考文献（例如：[1] 何仰赞，温增银. 电力系统分析（第三版）. 武汉：华中科技大学出版社，2003.[2] 范金城，梅长林. 数据分析. 北京：科学出版社，2002.[3] 郑君里，应启珩，杨为理. 信号与系统（第二版）. 北京：高等教育出版社，2000.）9 附录（程序流程图、源代码及其他要说明的；本部分可以省略）排版要求：1.论文（答卷）用白色A4纸，上下左右各留出2.5厘米的页边距。
2.论文第一页为论文题目和组员相关资料；论文摘要和关键词写在论文第二页上，从第三页开始是论文正文。
3.论文一级标题用4号黑体字，并居中。
论文中其他汉字一律采用小4号宋体字，行距及字间距用单倍行距。
4.提请大家注意：摘要应该是一份简明扼要的详细摘要（包括关键词），在整篇论文评阅中占有重要权重，请认真书写。
5.引用别人的成果或其他公开的资料(包括网上查到的资料) 必须按照规定的参考文献的表述方式在正文引用处和参考文献中均明确列出。
6.若需要输入数学符号或公式，请使用mathtype编辑器。
数学建模作业完整版
数学建模作业HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】《数学建模》作业学号姓名工作量 100 %专业所属学院指导教师二〇一七年六月数学建模作业第一部分：请在以下两题中任选一题完成（20 分）。
1、（马王堆一号墓入葬年代的测定建模问题）湖南省长沙市马王堆一号墓于 1972 年 8 月发掘出土，其时测得出土的木炭标本中碳-14 平均原子蜕变数为次/分钟，而新烧成的同种木材的木炭标本中碳-14（C-14）原子蜕变数为次/分钟. 又知碳-14 的半衰期为 5730 年，试推断该一号墓入葬的大致年代。
问题分析：放射性元素衰变的速度是不受环境影响的，它总是和该元素当前的量成正比，运用碳—14测定文物或化石年代的方法是基于下面的理由：（1）宇宙射线不断轰击大气层，使大气层中产生碳—14而同时碳—14又在不断衰变，从而大气层中碳—14含量处于动态平衡中，且其含量自古至今基本上是不变的；（2）碳—14被动植物体所吸收，所以活着的生物体由于不断的新陈代谢，体内的碳—14也处于动态平衡中，其含量在物体中所占的百分比自古至今都是一样的；（3）动植物的尸体由于停止了从环境中摄取碳—14，从而其体内碳—14含量将由于衰变的不断减少，碳定年代法就是根据碳—14的减少量来判断物体的大致死亡时间。
模型建立设t 时刻生物体中碳—14的含量为x （t ），放射性物质的半衰期（即放射性物质的原子数衰减一半所需的时间）为T ，生物体死亡时间为t0，则由放射性物质衰变规律得数学模型⎪⎩⎪⎨⎧=-=,)(,00x t x x dtdx λ ① 其中0>λ称为衰变系数，由放射性物质所决定，x 0为生物体在死亡时刻t 0时的碳—14含量。
模型求解对所得的一阶线性微分方程模型①采用同变量分离法求解，得 e x t t x t )(00)(--=λ??由于T t t =-0时，有 0021)()(x T t x t x =+=??代入上式，有 T e T 2ln ,212==-λ????? 所以得 ? T t t e x t x )(2ln 00)(--= ②这就是生物体中碳—14的含量随时间衰变的规律，由之易解得 )()(ln 2ln 00t x t x T t t =- ③ 将所得的数学模型的一般解应用于本例，此时以T=5730,37.380=x (新木炭标准中碳—14原子蜕变数)，X(1972)=（出土的木炭标本中碳—14原子蜕变数） 代入到③式,得 ?209578.2937.38ln 2ln 57300≈=-t t 年 于是得??1232095197220950-=-=-≈t t 年结果表明,马王堆墓入葬年代大约在公元前123年左右的西汉中期，该结论与马王堆出土文物的考证结果相一致。
数学建模作业
数学建模作业一、钓鱼问题1、试验问题某度假村建了一个鱼塘，该鱼塘的平均深度为6米，鱼塘平面图见图1，度假村的经理打算在钓鱼季节来临之前将鱼放入鱼塘，投放的鱼数按每3m³有一条鱼的比例投放。
如果一张钓鱼证可以钓鱼20条，而要求钓鱼季节结束时所剩的鱼是开始的25％，试问最多可以卖出多少钓鱼证？图表 1符号说明S:鱼塘水面面积，单位是㎡；V:鱼塘体积，单位是m³；M:可以卖出的最多的钓鱼证数，单位为个；H:鱼塘的深度单位为米。
2、问题分析由于是人工建造的鱼塘，考虑到经济原因，不妨设整个鱼塘是以鱼塘水面面积为底，高为6米的柱体，于是鱼塘的体积等于水面面积乘以高，即V=SH，问题归结为怎样计算鱼塘平面面积，因为鱼塘面积的边界曲线没有给出，而只给了一组数据，因此要求算出鱼塘面积的边界曲线，然后用定积分算出面积。
有一组数据来计算定积分可以用数值积分，由于数据点的间隔较大，计算结果的误差会较大，因此应该先利用这组数据鱼塘水面边界的近似曲线。
由于鱼塘水面便捷具有对称性，这里只考虑在第一象限中的边界问题，并采用曲线拟合的方法求鱼塘边界。
3、问题求解观察这组数据，发现它具有二次函数的形状，可以采用二次或三次拟合函数求拟合曲线，一旦求出拟合曲线f(x),则可以求出鱼塘面积的近似值，并得到鱼塘体积的近似值，求出鱼塘体积V之后，根据题目要求，最多可以卖出去的鱼证满足关系式，因此有卖出去的最多鱼证数为。
用数学软件求解，键入命令In[1]:=Clear[x,v,s]In[2]:=d={{0,0},{5,260},{10,400},{15,500}，{20,570}，{25,580}，{30，550}，{35，,40}，{40,270}，{45,0}}In[3]:=q=Listplot[d,PlotStyle->PointSize[0.025]]输出图形见图2.Out[3]=-Graphics-In[4]:=p2=Fit[d,{1,x,xˆ2},x]Out[4]=3.81818+51.7333x-1.13939x²In[5]:=p21=plot[p2,{x,0,45}]输出图形见图3Out[5]=-Graphics-In[6]:=Show[q,p21]输出图形见图4.Out[6]=-Graphics-In[7]=p3=Fit[d,{1,x,xˆ2,xˆ3},x]Out[7]=17.8182+46.6111x-0.83939x²-0.0044444x³In[9]:=show[q,p31]输出图形见图5Out[9]=-Graphics-In[10]:=s=2*Integrate[p3,{x,0,45}] Out[10]=35885.5 In[11]:=v=s*6Out[12]=215313In[13]:=m=(1-0.250*v/60Out[13]=2691.41即可以卖出钓鱼证的最多个数为2691个二、追击曲线问题1、问题介绍一敌舰在某海域内沿正北方向航行时，我方战舰恰位于敌舰的正西方1n mile （海里）处。
数学建模大作业题目
(1) 用起泡法对10个数由小到大排序. 即将相邻两个数比较,将小的调到前头. （10个数字自己选择，方法要一般）(2)有一个45⨯矩阵,编程求出其绝对值最大值及其所处的位置. （用abs 函数求绝对值）(3)编程求201!n n =∑ （ 分别用for 和while 循环）(4)一球从100米高度自由落下,每次落地后反跳回原高度的一半,再落下. 求它在第10次落地时,共经过多少米?第10次反弹有多高? (5)有一函数2(,)sin 2f x y x xy y =++,写一程序,输入自变量的值,输出函数值，并画出其图像，加上图例和注释. （区间自理） (6) 建立一个脚本M 文件将向量a,b 的值互换。
(7) 某商场对顾客所购买的商品实行打折销售，标准如下(商品价格用price 来表示)： price<200 没有折扣; 200≤price<500 3%折扣; 500≤price<1000 5%折扣; 1000≤price<2500 8%折扣; 2500≤price<5000 10%折扣;5000≤price 14%折扣;输入所售商品的价格，求其实际销售价格。
(用input 函数) (8) 已知y ，22221111123y n=++++,当n=100时，求y 的值。
(9)画出分段函数2221y 1 122 1 2x x x x x x x ⎧<⎪=-≤<⎨⎪-+≥⎩的图像，并求分段函数在任意几点的函数值。
(用hold on 函数)(10) 给定5阶方阵，求方阵的行列式、特征值、迹、上三角元素的和。
(11) 输入40个数字，按照从小到大的顺序排列输出。
(12) 把当前窗口分成四个区域，在每个区域中分别用不同的颜色和线形画sin ;tan y x y x==，x y e =和31y x x =++的图像。
（区间自理）(13) 对于,AXB YA B==，如果⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=753467294A ，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=282637B ，，求解X,Y ;(14) 如果⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=753467294A ，242679836B ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,求1122,*,.*,,,,T A B A B A B AB A B A A ---。
数学建模(合)大作业
学生实验报告实验时间：2017 学年第 2 学期专业班级：信息与计算科学1502班____ （学号）：庞云杰（20155653）_______2017年 03月21日通过N(t)=N0e rt其中r=0.0202（1/年），N0 =6.0450（百万）；我们可以预测美国2010,2020,2030,2040,2050年的人口；通过计算，我们可以得出2010年 514.28（百万）2020年629.39（百万） 2030年770.26（百万） 2040年942.66（百万）2050年1153.65（百万）误差分析利用指数增长模型预测美国人口变化状况，其预测结果与真实值比较，相对误差在1%-55%之间，预测模型明显不可靠。
模型2利用MATLAB进行曲线拟合，首先在平面上绘出已知数据的分布图，通过直观观察，猜测人口随时间的变化规律，再用函数拟合的方法确定其中的未知参数，从而估计出2010 2020 2030 2040 2050年的美国人口。
利用MATLAB作出美国人口统计数据的连线图如图1。
1美国人口统计数据连线图2建模方法2拟合效果图由图1可以发现美国人口的变化规律曲线近似为一条指数函数曲线，因此我们假设美国的人口满足函数关系x=f（t）, f(t)=ea+bt，a, b为待定常数，根据最小二乘拟合的原理，a, b是函数的最小值点。
其中xi是ti时刻美国的人口数。
利用MATLAB中的曲线拟合程序“curvefit”，编制的程序如下：首先创建指数函数的函数M——文件用最小二乘拟合求上述函数中待定常数，以及检验拟合效果的图形绘制程序m-function, fun1.mfunction f=fun1(a,t)f=exp(a(1)*x + a(2));t=1790:10:2000;图3误差分析观察误差和图像，模型2对过去的统计数据吻合得较好，但也存在问题，即人口是呈指数规律无止境地增长，此时人口的自然增长率随人口的增长而增长，这不可能。
数学建模大作业_操场追及问题
2
由于小明室友从中心开始追小明，因此初始条件为 我们发现，由于没有小明的位置与时间的关系，因此我们无法求出上述微分方程的 解。因此，接下来我们应该尝试建立 X 与 Y 关于时间的表达式。 引入椭圆的参变量方程， 给出 X 和 Y 关于参变量 的表达式：X a cos , Y b sin . 而 得： ，由于小明速度为 1，因此在时间 t 内小明走过的弧长为 t ，依据弧长公式可
图1
图2
3
36.5 400 ，模仿椭圆的概念， c a 2 b2 36.5 85 36.5 长轴 a 短轴 b 36.5 .可以计算出离心率为 e 0.89 ， 79 ， a a 2 查阅椭圆周长计算公式 ， 将以上两式联立方程组可以求得建模后椭圆 长轴及短轴的值。解得 a 79.35, b 36.18.
参考《田径场地设施标准手册 1999》 ，我们得到 400m 跑道的设计标准如下：大多数 适宜的 400 米椭圆跑道被建成弯道半径为 35.00m 到 38.00m 之间，最好的是 36.50m ， 国际田联建议所有新造的跑道应该按后者的规定建造，并被称之为“400 米标准跑道” ， 图 1 给出了实际的 400m 跑道设计图，图 2 是根据标准手册简化的 400m 跑道图。
1
一、问题重述
小明在平面上沿 400 周长的操场（可考虑为椭圆）以恒定的速率 v=1 跑步。 他的室友从操场中心出发，以恒定速率 w 跑向小明，室友的跑步的方向始终指向小 明。讨论 w 大约为多大时，室友能追上小明，做出轨迹图，并讨论追上的时间。
二、问题分析
本题是一个追及问题，追及问题的三个要素是路程、速度和时间，在此题中时间为 未知量，速度大小的给出方式常规，因此此题的关键就在于速度方向的模型化。 为解决此问题，我们提出了两个模型，第一个为从实际跑道中抽象化的椭圆轨道模 型，第二个为实际 400m 跑道模型。 在一个模型中，我们采取了速度分解的方法。将系统置于平面直角坐标系中，设出 小明和他室友的位置坐标，连线方向即为舍友下一时刻的运动方向，也即速度的方向， 通过在水平和竖直两个方向的分解，可以得出室友横坐标与纵坐标随着时间变化的微分 方程。此微分方程包含小明的位置坐标，方程右侧并不是显含时间的，为解决这个问题 引入参变量 ，根据椭圆的参数方程将小明的位置坐标表示成 的函数，并依据弧长公 式将 表示成 t 的函数进而建立起完整的微分方程组，最后用 Matlab 进行数值模拟。 第二个模型利用了第一个模型速度分解的理论，唯一不同的是在给出小明位置坐标 时直接写出了位置与时间的显式分段表达式，进而建立了完整的微分方程组，并最终给 出了追及轨迹及数值结果。
小学期数学建模大作业 西安交通大学
第一次作业一、问题的叙述，问题的分析叙述:对于由连续曲线所围成的平面区域能否做到以下几点: 1 用平行于某定直线的直线二等分该区域; 2 用垂直于某定直线的直线二等分该区域; 3 用相互垂直的两条直线四等分该区域 分析:问题简化为对三个题目的证明已知平面上一条没有交叉点的封闭曲线（形状不定），设有一定直线L 过某点P 0且与x 轴的正向夹角为a二、问题求解 〈1>：证明作一平行于L 的直线l ，l 过点p 且将曲线所围图形分为两部分，其面积分别记为，。
若=（发生的概率较小），则得到直线a 的斜率，即可得定直线L;若,设，且L 的斜率为tanα将直线l 按逆时针方向旋转，面积，连续地依赖斜率变化而变化，记为（k ），（k ），设，如图17—3,17-4所示。
PS 1(a)S 2(a)a 0xl图17-3 旋转成a 角laPS 1（a 0+180°）S 2（a 0+180°）a 0xl图17-4 旋转180°后a 0+180°令)则有函数上连续,且在端点异号：=(k1）—（k1）根据闭区间上连续函数的零点定理必存在一斜率使=0,即。
过曲线内p 做直线l ，取斜率为则直线L 过定点P 0且斜率为,所以解得某定直线L 与其平行的任意直线l 平分改闭合区域。
由上述知1得证〈2〉:证明同理有定直线L，垂直于L的直线为b，其斜率为K3=—1/tanα。
同理可得存在这样的一条直线b，所以2得证。
〈3>:证明由<1〉，〈2>可知,对平面上任意的封闭区域，在任意方向上都存在直线将其面积等分如下图两种连续移动都可以满足介值定理，通过平移的方法很容易证明，在任意一个方向上都可以先找到一条直线a使其平分封闭区域的面积，然后可以作直线b，垂直于L且可以平分该封闭区域的面积此时Ⅰ+Ⅱ=Ⅲ+Ⅳ=Ⅰ+Ⅳ=Ⅱ+Ⅲ，从而Ⅰ=Ⅲ, Ⅱ=Ⅳ，若求得Ⅰ=Ⅱ,则命题得证；设Ⅰ逆时针调节直线a，b，直到a与b的初始位置重合如下图;在调整的过程中, Ⅰ= Ⅱ, Ⅱ=Ⅰ,于是根据介值定理，必然存在某一时刻Ⅰ=Ⅱ,所以<3〉得证第二次作业1.题目:2.题目分析：(1)y k=C k+Z K+g；(2)C K=b y k-1；(3)Z K=α（C k -C k-1)；3.模型求解：有题目分析得C K=b y k-1，Z K=α（C k -C k-1）= αb（y k-1 -y k—2 ）将C K,Z K代入y k 得y k+1=by k +αb(y k—y k—1 ）+g;一个特解为；特征方程为λ2—（αb+b)λ+αb=0；假设α=10,g=5，y1 =12,y2=15。
数学建模大作业题目
A 题：图书馆购书计划的制定现代化图书馆馆藏图书，主要目的不是为了收藏而是为了使用。
除了国家图书馆等特大型的图书馆以外，一般图书馆都有特定的服务群体，办馆宗旨就是要尽量好地为这些特定群体服务，提高馆藏资源的利用率、读者文献信息需求的满足率以及对图书馆服务功能的满意率。
图书馆每年用于购书的经费是有限的，如何合理分配使用，以便使有限的购书经费最大限度地发挥其特定的经济效益是图书馆工作的重要环节之一。
以学校图书馆为例，要实现办馆效益，必须做到入藏文献合乎本校教师、学生（有时也兼顾社会）的需求，使图书馆藏书结构（学科结构、文种结构、文献类型结构等）满足本校教学科研的要求，以求藏书体系与本校专业设置相适应。
所购图书要能够真实地反映读者的实际需要，使读者结构和藏书结构尽量吻合，以便减少读者借不到图书的现象，即降低读者被借的比率、增加满足率。
文献只有在流通中才能传播信息，产生效益。
文献资料得不到利用，购置文献资料所耗费的资金就体现不出其价值。
因此，图书馆在增加藏书规模的同时，要千方百计地把文献提供给读者，以增加图书的出借次数、出借时间以及在借图书的数量等，力求使有限的价值投入获得最大的办馆效益。
设某普通高校现有十个系：计算机科学与技术系，在校学生960 人，信息科学与工程系，在校学生900 人，信息与计算科学系，在校学生280 人，生物与制药工程系，在校学生1500 人，机电工程系，在校学生1440 人，建筑工程系，在校生960 人，外语系，在校学生720 人，法律系，在校学生460 人，新闻系，在校学生642 人，经济与管理系，在校学生2400 人。
此外，该校目前还有“药物分子设计及生物化工”和“土木建筑工程”2 个重点学科；“外国语言学及应用语言学”重点扶植学科以及“计算机科学与技术”、“市场营销”2 个重点专业。
该校图书馆每学年都要投入大量资金购置图书，图书覆盖全院各学科专业、具有较完整的中外文文献资源。
数学建模大作业.
《数学实验》报告实验名称数学建模与 MATLAB 学院材料学院专业班级材料 1014姓名徐萌孔德成戴思雨学号 41071046 41030400 410303992012年 6月一、问题的提出。
传染病是当今世界最严重的疾病之一, 2009年 4月 26日世界卫生组织以确认, 美国和墨西哥发生了甲型 H1N1流感, 随后疫情迅速蔓延, 截止 8月中旬, 全球感染人数约 5万人。
因此,运用传染病的数学模型来描述传染病甲型 H1N1流感的传播过程, 分析受感染人数的变化规律, 探索制止甲型 H1N1蔓延的手段是值得关注的。
二、模型的建立。
考查中国内地疫情变化,在疾病传播期间不考虑人口的出生率和死亡率, 人口总数不变, 为常量。
中国的疫情研究发现易感染人数多为 20~50岁的青壮年, 故保守估计在此传染病系统的人数 N=50000人。
甲型 HINI 流感的传播途径是与病源的直接接触, 患者与健康者接触时, 都使健康者感染病变. 故将人群分为 3类:健康者(易感染者人群、患者 (已被感染人群、治愈者 (研究期间 6月 14日~8 月 14日间中国内地感染病毒死亡人数为 0, 故此处不考虑死亡者 . 三者在总人数中的比例分别为 :s(t,i(t,r(t且 s(t+i(t+r(t=1,io,So分别为患者人数, 健康人数的比例初始值.设每个患者每日感染健康者的平均人数为日感染率,记为λj ,则λj=j日新增病例数 /(j-1日(累计确诊人数 -累计出院人数 ;每日被治愈的患者人数占其总数的比例为日治愈率,记为μj ,则Μj=j日被治愈的人数 /j日累计确诊病人数 ;定义整个传染期内每个患者有效接触的平均人数为接触数σ,由 s(t+i(t+r(t=1可知, 对于病愈免疫的治愈者而言应有dr/dt=μi, 因此考虑 SIR 传染模型,该模型的方程为2λsi-μi;λsi (1三、模型的求解1、数值运算由于在方程 (1中无法求出 s(t和 i(t的解析解,故先做数值运算.据来自中国卫生部网站公布的 2009年 6月 14日~8月 14日的疫情数据 (见表1[包括日累计确诊病例、日累计治愈病例等. 其中缺失的部分数据, 将以通过给定的数据拟合得到 .表 1疫情原始数据日期新增病例确诊病例累计治愈累计新增治愈数6月 14日 20 185 736月 15日 41 226 86 136月 16日 11 237 97 11 6月 17日 27 264 114 17 6月 18日 33 297 135 21 6月 19日 31 328 160 25 6月 20日 28 356 185 25 6月 21日 58 414 199 14 6月 22日 27 441 227 28 6月 23日 49 490 251 24 6月 24日 38 528 275 24 6月 25日 42 570 321 46 6月 26日 48 618 338 17 6月 27日 60 678 373 35 6月 28日 51 729 401 28 6月 29日 37 766 445 44 6月 30日 44 810 496 51 7月 1日 56 866 554 58 7月 2日 49 915 612 58 7月 3日 45 960 660 48 7月 4日 40 1000 704 4437月 5日 40 1040 749 45 7月 6日 57 1097 793 44 7月 7日 54 1151 870 77 7月 8日 36 1187 927 57 7月 9日 36 1223 985 58 7月 10日 40 1263 1035 50 7月 11日 39 1302 1085 50 7月 12日 26 1328 1110 25 7月 13日 26 1354 1134 24 7月 14日 45 1399 1166 32 7月 15日 45 1444 1197 31 7月 16日 41 1485 1230 33 7月 17日 52 1537 1263 33 7月 18日 44 1581 1293 30 7月 19日 44 1625 1323 30 7月 20日 43 1668 1355 32 7月 21日 52 1720 1404 49 7月 22日 52 1772 1454 50 7月 23日 38 1810 1529 75 7月 24日 42 1852 1604 75 7月 25日 26 1878 1663 59 7月 26日 26 1904 1722 59 7月 27日 26 1930 1781 59 7月 28日 37 1967 1817 36 7月 29日 36 2003 1853 36 7月 30日 43 2046 1883 30 7月 31日 44 2090 1912 29 8月 1日 20 2110 1937 25 8月 2日 21 2131 1962 25 8月 3日 21 2152 1988 26 8月 4日 29 2181 2031 43 8月 5日 29 2210 2074 43 8月 6日 27 2237 2098 24 8月 7日 27 2264 2122 24 8月 8日 28 2292 2137 15 8月 9日 28 2320 2152 15 8月 10日 28 2348 2167 15 8月 11日 38 2386 2203 36 8月 12日 39 2425 2240 37 8月 13日 57 2482 2261 21 8月 14日 55 2537 2283 22注:2009年疫情效据见文献 [8]4以 6月 15日为基日,当日累计确诊病例 226例,累计出院者 86例,故s(0=(50000-226+86/50000=0.9972;I(0=(226-86/50000=0.0028;在研究期间,平均日感染率λ和平均日治愈率μ由每天相应数据平均求得. 设计程序为:新增病例 A 确诊病例累计 B 治愈累计 C 新增治愈数 D>>A=[41 11 27 33 31 28 58 27 49 38 42 48 60 51 37 44 56 49 45 40 40 57 54 36 3640 39 26 26 45 45 41 52 44 44 43 52 52 38 42 26 26 26 37 36 43 44 20 21 21 29 29 27 27 28 28 28 38 39 57 55]>>B=[226 237 264 297 328 356 414 441 490 528 570 618 678 729 766 810 866 915 9601000 1040 1097 1151 1187 1223 1263 1302 1328 1354 1399 1444 1485 1537 1581 1625 1668 1720 1772 1810 1852 1878 1904 1930 1967 2003 2046 2090 2110 2131 2152 2181 2210 2237 2264 2292 2320 2348 2386 2425 2482 2537]>>C=[86 97 114 135 160 185 199 227 251 275 321 338 373 401 445 496 554 612 660704 749 793 870 927 985 1035 1085 1110 1134 1166 1197 1230 1263 1293 1323 1355 1404 1454 1529 1604 1663 1722 1781 1817 1853 1883 1912 1937 1962 1988 2031 2074 2098 2122 2137 2152 2167 2203 2240 2261 2283]>>D=[13 11 17 21 25 25 14 28 24 24 46 17 35 28 44 51 58 58 48 44 45 44 77 57 5850 50 25 24 32 31 33 33 30 30 32 49 50 75 75 59 59 59 36 36 30 29 25 25 26 43 43 24 24 15 15 15 36 37 21 22]>>E=A./(B-C %日感染率>>e=sum(E/61 %平均日感染率>>F=D./(B-C %日治愈率>>f=sum(F/61 %平均日治愈率运行结果:A =Columns 1 through 1641 11 27 33 31 28 58 27 49 38 42 48 60 51 37 44Columns 17 through 3256 49 45 40 40 57 54 36 36 40 39 26 26 45 45 41552 44 44 43 52 52 38 42 26 26 26 37 36 43 44 20 Columns 49 through 6121 21 29 29 27 27 28 28 28 38 39 57 55B =Columns 1 through 8226 237 264 297 328 356 414 441Columns 9 through 16490 528 570 618 678 729 766 810 Columns 17 through 24866 915 960 1000 1040 1097 1151 1187 Columns 25 through 321223 1263 1302 1328 1354 1399 1444 1485 Columns 33 through 40 1537 1581 1625 1668 1720 1772 1810 1852 Columns 41 through 48 1878 1904 1930 1967 2003 2046 2090 2110 Columns 49 through 56 2131 2152 2181 2210 2237 2264 2292 2320 Columns 57 through 61 2348 2386 2425 2482 2537C =Columns 1 through 886 97 114 135 160 185 199 227 Columns 9 through 16251 275 321 338 373 401 445 496 Columns 17 through 24554 612 660 704 749 793 870 927 Columns 25 through 32985 1035 1085 1110 1134 1166 1197 1230 Columns 33 through 40 1263 1293 1323 1355 1404 1454 1529 1604 Columns 41 through 48 1663 1722 1781 1817 1853 1883 1912 1937 Columns 49 through 56 1962 1988 2031 2074 2098 2122 2137 2152 Columns 57 through 61 2167 2203 2240 2261 2283D =Columns 1 through 1613 11 17 21 25 25 14 28 24 24 46 17 35 28 44 5158 58 48 44 45 44 77 57 58 50 50 25 24 32 31 33Columns 33 through 4833 30 30 32 49 50 75 75 59 59 59 36 36 30 29 25Columns 49 through 6125 26 43 43 24 24 15 15 15 36 37 21 22e =0.173970451885603 %平均日感染率λ=0.173970451885603 f =0.164030384929960 %平均日治愈率μ=0.164030384929960 接触数:σ=λ/μ=0.173970451885603/0.164030384929960=1.060598936958463 可得模型方程为:;然后用 Matlab 软件编程,解常微分方程做出患者人数比例 i(t--时间 t/d关图, 健康者比例 s(t--时间 t/d关系图 ,患者人数比例 i-健康者比例 s 图。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
兰州交通大学数学建模大作业学院：机电工程学院班级：车辆093学号：********* 姓名：刘键学号：********* 姓名：杨海斌学号：********* 姓名：彭福泰学号：********* 姓名：程二永学号：********* 姓名：屈辉高速公路问题1 实验案例 (2)1.1 高速公路问题(简化) (2)1.1.1 问题分析 (3)1.1.2 变量说明 (3)1.1.3 模型假设 (3)1.1.4 模型建立 (3)1.1.5 模型求解 (4)1.1.6 求解模型的程序 (4)1实验案例1.1 高速公路问题(简化)A城和B城之间准备建一条高速公路，B城位于A城正南20公里和正东30公里交汇处，它们之间有东西走向连绵起伏的山脉。
公路造价与地形特点有关，图4.2.4给出了整个地区的大致地貌情况，显示可分为三条沿东西方向的地形带。
你的任务是建立一个数学模型，在给定三种地形上每公里的建造费用的情况下，确定最便宜的路线。
图中直线AB显然是路径最短的，但不一定最便宜。
而路径ARSB过山地的路段最短，但是否是最好的路径呢？AB图8.2 高速公路修建地段1.1.1 问题分析在建设高速公路时，总是希望建造费用最小。
如果要建造的起点、终点在同一地貌中，那么最佳路线则是两点间连接的线段，这样费用则最省。
因此本问题是一个典型的最优化问题，以建造费用最小为目标，需要做出的决策则是确定在各个地貌交界处的汇合点。
1.1.2 变量说明i x ：在第i 个汇合点上的横坐标（以左下角为直角坐标原点），i ＝1，2，…，4；x 5＝30（指目的地B 点的横坐标）x=[x 1，x 2，x 3，x 4]Tl i ：第i 段南北方向的长度（i ＝1，2， (5)S i ：在第i 段上地所建公路的长度（i ＝1，2， (5)由问题分析可知， ()()()()25425524324423223322122221211x x l S x x l S x x l S x x l S x l S -+=-+=-+=-+=+=C 1：平原每公里的造价（单位：万元/公里）C 2：高地每公里的造价（单位：万元/公里）C 3：高山每公里的造价（单位：万元/公里） 1.1.3 模型假设1、 假设在相同地貌中修建高速公路，建造费用与公路长度成正比；2、 假设在相同地貌中修建高速公路在一条直线上。
在理论上，可以使得建造费用最少，当然实际中一般达不到。
1.1.4 模型建立在A 城与B 城之间建造一条高速公路的问题可以转化为下面的非线性规划模型。
优化目标是在A 城与B 城之间建造高速公路的费用。
()4,3,2,1300..)(min 5142332211=≤≤++++=i x t s S C S C S C S C S C x f i1.1.5模型求解这里采用Matlab编程求解。
模型求解时，分别取C i(i=1,2,3)如下。
平原每公里的造价C1＝400万元/公里；高地每公里的造价C2＝800万元/公里；高山每公里的造价C3＝1200万元/公里。
输入主程序model_p97.m，运行结果如下：model_p97optans =2.2584e+004len =38.9350ans =12.1731 14.3323 15.6677 17.8269求解程序见附录。
注：实际建模时必须查找资料来确定参数或者题目给定有数据）6.模型结果及分析通过求解可知，为了使得建造费用最小。
建造地点的选择宜采取下列结果。
x1=12.1731，x2=14.3233，x3=15.6677，x4=17.8269建造总费用为2.2584亿元。
总长度为38.9350公里1.1.6求解模型的程序（1）求解主程序model_p97function x=model_p97 %数学建模教材 P97 高速公路clear allglobal C LC=[400 800 1200];L=[4 4 4 4 4];x=fmincon('objfun_97',[1,1,1,1],[],[],[],[],zeros(1,4),ones(1,4)* 30,'mycon_p97');optans=objfun_97(x)C=ones(3,1);len = objfun_97(x)（2）模型中描述目标函数的Matlab程序objfun_97.mfunction obj=objfun_97(x)global C Lobj=C(1)*sqrt(L(1)^2+x(1)^2) + C(2)*sqrt(L(2)^2+(x(2)-x(1))^2) + ... C(3)*sqrt(L(3)^2+(x(3)-x(2))^2)C(2)*sqrt(L(4)^2+(x(4)-x(3))^2)+C(1)*sqrt(L(5)^2+(...30-x(4))^2); （3）模型中描述约束条件的Matlab函数mycon_p97.mfunction [c,ceq]=mycon_p97(x)c(1)=x(1)-x(2);c(2)=x(2)-x(3);c(3)=x(3)-x(4);c(4)=x(4)-30;ceq=[];综合实验：施肥效果分析【问题提出】施肥效果分析（1992年全国大学生数学模型联赛题A）某地区作物生长所需的营养素主要是氮（N）、钾（K）、磷（P）。
某作物研究所在某地区对土豆与生菜做了一定数量的实验，实验数据如下列表所示，其中ha表示公顷，t表示吨，kg表示公斤。
当一个营养素的施肥量变化时，总将另两个营养素的施肥量保持在第七个水平上，如对土豆产量关于N的施肥量做实验时，P与K的施肥量分别取为196kg／ha与372kg／ha。
试分析施肥量与产量之间关系，并对所得结果从应用价值与如何改进等方面做出估计。
土豆：N P K生菜：N P K数据拟合方法[1]在数学建模问题中常常有着重要的应用。
根据实验数据来求出实际问题中变量之间的经验公式[1～2],然后再根据经验公式来讨论模型的最优解,是许多数学建模问题中的一种重要方法。
下面就利用这种方法来讨论一个数学建模问题[3～4]。
某地区作物生长所需的营养素主要是氮(N)、磷(P)、钾(K)。
某作物研究所在该地区对土豆与生菜做了一定数量的实验,实验数据可参见文献[3],其中ha表示公顷,t表示吨,kg表示公斤。
当一个营养素的施肥量变化时,总将另两个营养素的施肥量保持在第七个水平上,如对土豆产量关于N的施肥量做实验时,P与K的施肥量分别取为196kg/ha与372kg/ha。
我们来分析施肥量与产量之间的关系,并对所得结果从应用价值与如何改进等方面作出估价。
首先,将题中的数据用MA TLAB软件[5]作出图形:从图上可看出,N、P、K的取值范围不一样,可以将它们的取值范围转化成区间[0,1],这样它们的变化范围就都一样了。
转化后的数据图形如下:1模型的建立及求解要分析施肥量与产量之间的关系,首先要建立施肥量与产量之间的函数关系。
可以用数据拟合的方法来建立这种函数关系。
这又需要确定拟合的函数的形式,即所谓经验公式。
施肥量与产量之间的函数可以是每一种肥料的施用量与产量的关系,也可以是三种肥料共同的施用量与产量的关系。
按一般常识,N、P、K是作物生长的三种基本肥料要素,它们用量的多少将直接影响农作物的产量。
这种对作物产量的“影响”通常是这三种肥料的共同影响,而不应是单一某一种肥料对作物产量的“影响”。
但每一种肥料的用量对于不同的作物产量的影响效果又有不同。
例如,N肥的施用量对有些农作物产量的影响是:当N肥施用量较少时,随着N肥用量的增加,农作物的产量会增加,到一定用量后产量达到最大,然后,当N肥用量继续增加时,农作物的产量反而会降低。
这从上面的土豆和生菜产量与N肥用量的数据图上也可以看到这样的规律。
而在一定的范围内,P肥和K肥的用量对农作物产量的影响将随着其用量的增加而一直增加,只是当P肥和K肥的用量较少时,随着其用量的增加,农作物产量增加较快,而当P肥和K肥的用量较多时,随着其用量的增加,农作物产量增加不大。
从上面的土豆和生菜产量与P肥或K肥用量的数据图上可以看到这样的规律。
具有这种特点的函数关系在数学上用二次多项式就能较好地反映出来。
当然也可以考虑用分段函数来描述。
为简单起见,下面在拟合这些函数时都用二次多项式。
在实验数据中,K肥料施用量与生菜产量的实验数据波动性较大,这种产量与肥料的施用量的关系在农作物中是很少出现的现象。
如果从数据图形的整体来看,其实K肥料施用量与生菜产量的实验数据的特点还是与上面所说的情况相似的,其波动性可看作是实验误差。
要利用实验数据来拟合出这些函数关系,显然,如果实验数据越多、数据分布越合理,则拟合的效果就越好。
这样拟合出来的函数,其所反映出来的规律就越符合实际情况。
例如,应当给出充分多的数据,且这些数据应当是在N、P、K三种肥料的不同用量下的产量数据。
又比如,应该有这样的数据:当N、P、K三种肥料中某两种肥料限制在不同的固定值时,相应地,第三种肥料取不同值时的产量数据,这样才有可能反映出N、P、K 三种肥料在对农作物产量的共同影响时的相互影响的规律。
但事实上,这里所给出的实验数据非常有限,而且很不均匀,所以用现有的数据来拟合N、P、K的施用量与产量之间的函数关系,并根据这些函数的性质所推断出的施肥量与产量之间的关系,其可信性是有限的。
另外,拟合每一种肥料的施用量与产量的函数时,其余两种肥料的用量都是限制在一个数值上的,其结果通常也只能得到,当相应的另两肥料的用量在所限制的数值下的情况。
虽然我们得到的结果可能有一定的局限性,但这里所用到的方法却是处理这类问题的常用方法,从建立模型的角度来说,还是值得讨论的。
如果要想得到更精确的结果,只需要有更多的产量施肥量实验数据,再用本文中给出的模型讨论即可。
用这些函数来讨论施肥效果产量与施肥量的函数关系,有两种方式,一种是对三种肥料施用量与产量分别来拟合相应的函数,这需要拟合三个函数,每个函数都是一元函数,这种做法可以使拟合的效果较好。
另一种是考虑三种肥料共同对产量的影响,这只需要拟合出一个函数,这是一个三元函数,且由于数据量偏少且不均匀等的原因,拟合效果要差一些,但这是讨论肥料施用量与产量的全局最优解所必须的。
下面分别来讨论。
1.1模型1对三种肥料的用量与土豆和生菜产量分别拟合相应的函数讨论一种肥料的用量与产量的关系时,其它两种肥料的用量都固定在第7种水平,三种肥料的用量分别是:土豆n07=0.5499,p07=k07=0.5714;生菜n17=0.57149,p17=0.5708,k17=0.5714。
先考虑土豆与每一种肥料用量的函数关系,我们利用所给数据来拟合这些函数关系。