matlab 作业
matlab作业

上机实践练习五实验五:MATLAB 数据可视化实验目的:掌握MATLAB 二维、三维图形绘制,掌握图形属性的设置和图形修饰;掌握图像文件的读取和显示。
学时:2学时实验内容:(1)二维图形绘制。
(2)隐函数绘图(2) 三维曲线和三维曲面绘制。
(3) 图像文件的读取和显示。
1.写出实现下列图形的M文件。
t=[0:0.1:pi];y1=sin(2*t);y2=cos(3*t);plot(t,y1,'b-o');hold onplot(t,y2,'k:o');xlabel('ʱ¼ä')ylabel('·ùÖµ')text(1,sin(2*1),'\fontsize{16}\leftarrowsin(2t) ');text(2.4,cos(3*(2.4)),'\fontsize{16}cos(3t)\rightarrow ',... 'HorizontalAlignment','right')2. 将窗口分割成4个区域,并且在[]0,2π区间上绘制1sin 2,6y x π⎛⎫=+⎪⎝⎭()224cos 3,y x =()3cos y x =,()35sin 1y x =+四条曲线,并且给每一个图形添加标题和标注。
clearx=0:pi/10:2*pi; y1=sin(2.*x+pi/6); y2=4.*cos(3.*x.^2); y3=cos(x); y4=5.*sin(x+1); subplot(2,2,1); plot(x,y1); title('y1');text(1,sin(2*1+pi/6),'sin(2*x+pi/6)') subplot(2,2,2); plot(x,y2)title('y2');text(2,4.*cos(3*2^2),'4*cos(3*x^2)') subplot(2,2,3); plot(x,y3)title('y3');text(2,cos(2),'cos(x)')subplot(2,2,4);plot(x,y4)title('y4');text(2,5.*sin(3),'5*sin(x+1)')3.已知y1=x2,y2=cos(2x),y3=y1*y2,其中x为取值-2π~2π的等差数列(每次增加0.02π),完成下列操作(1)在同一坐标系下用不同的颜色和线型绘制三条曲线,给三条曲线添加图例。
MATLAB课程作业

注意:11月15日是交作业的最后期限。
(交word和MATLAB程序清单,word以“班级-学号-姓名”命名,每个MATLAB程序以”zuoye_题号”命名后,放在一个文件夹下(文件夹命名为“作业程序”),如zuoye_1_1.m),将word和“作业程序”文件夹放在一个文件夹(文件夹以“班级-学号-姓名”)交到班长处,班长统一交到教学办公室。
第一部分程序设计1.1、用MA TLAB可以识别的格式输入下面两个矩阵:(1) 矩阵A的维数;(2) 矩阵A中的元素a41的值;(3) 修改矩阵A的元素,使a41 =3.0;(4) 矩阵A中最后2行和最后3列交汇形成的子矩阵的值。
(5)求出A和B的乘积矩阵C,并将C矩阵的右下角2X 3子矩阵赋给D矩阵。
1.2、已知111121111,131,111214A B⎡⎤⎡⎤⎢⎥⎢⎥=-=-⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦求(1)AB-2A,(2)A*B,(3)A﹒*B,(4) AB-BA 1.3、解线性方程:1.4、解方程组:1.5、用MA TLAB语言实现下面的分段函数:1.6、已知x=[1 2 3 ],y=[4 5 6 ],试计算z=x.*y 、x.\y 和x./y.1.7、分别用for 和while 循环语句编写程序,求出1.8、 已知在平面坐标中两点(x 1, y 1)和(x 2, y 2)之间的距离计算公式为 ()()222121y y x x L -+-=(1) 利用命令文件的形式,编写求解该距离的M 文件dis1.m ;(2) 利用函数文件的形式,编写求解该距离的M 文件dis2.m ;(3) 给定两点坐标的值(2,3)和(8, -5),试分别调用命令文件dis1.m 和函数文件dis2.m 求解该两点间距离的值。
1.9、求解方程x 5+6x 3一3x 2=10的5个根,并将其位置用五角星符号标记在复平面上,要求横纵坐标袖的刻度等长,注明虚轴和实轴,在title 位置上写㈩方程。
matlab作业

实验三某厂利用a、b、c三种原料生产A、B、C三种产品,已知生产每种产品在消耗原料方面的各项技术条件和单位产品的利润,以及可利用的各种原料的量,是制定适当的生产规划使得该厂的总利润最大。
对于这个问题,可先将该问题转化为数学模型。
Z=2x1+4x2+3x3X1+3x2+2x3<=802x1+x2+2x3<=403x1+4x2+2x3<=60X1,x2,x3>=0据此可以画出图形,可依靠图形来求出Z的最大值。
c=[-2 -4 -3]A=[1 3 2;2 1 2;3 4 2]b=[60 40 80]lb=[0 0 0][x,f,exitflag,output]=linprog(c,A,b,[],[],lb,[])将上述程序输入matlab。
就可得出结果。
结果如下:x =4.000012.000010.0000f =-86.0000exitflag =1output =iterations: 7cgiterations: 0algorithm: 'lipsol'由上述结果可以知道当A、B、C分别生产4,12,10 公斤时,总利润最大,可达到86。
某工厂生产甲、乙、丙三种产品,单位产品所需工时分别为2、3、1个;单位产品所需原料分别为3、1、5公斤;单位产品利润分别为2、3、5元。
工厂每天可利用的工时为12个,可供应的原料为15公斤。
为使总利润为最大,试确定日生产计划和最大利润。
对于这个问题,可先将该问题转化为数学模型。
Z=2x+3y+5z2x+3y+z<=123x+y+5z<=15据此可以画出图形,可依靠图形来求出Z的最大值。
c=[-2 -3 -5]A=[2 3 1;3 1 5]b=[12;15]lb=[0 0 0][x,Z,exitflag,output]=linprog(c,A,b,[],[],lb,[])将上述程序输入matlab。
就可得出结果。
MATLAB期末大作业

MATLAB期末⼤作业学号:姓名:《Matlab/Simulink在数学计算与仿真中的应⽤》⼤作业1.假设地球和⽕星绕太阳运转的半径分别为r和2r,利⽤comet指令动画显⽰从地球到⽕星的转移轨迹(r可以任意取值,要求实时显⽰探测器、太阳、地球和⽕星的位置)。
解函数function comet(varargin)[ax,args,nargs] = axescheck(varargin{:});error(nargchk(1,3,nargs,'struct'));% Parse the rest of the inputsif nargs < 2, x = args{1}; y = x; x = 1:length(y); endif nargs == 2, [x,y] = deal(args{:}); endif nargs < 3, p = 0.10; endif nargs == 3, [x,y,p] = deal(args{:}); endif ~isscalar(p) || ~isreal(p) || p < 0 || p >= 1error('MATLAB:comet:InvalidP', ...'The input ''p'' must be a real scalar between 0 and 1.'); End指令 %particle_motiont = 0:5:16013;r1=6.7e6;%随便给定参数%---------------------------r2=2*r1;g=9.8;R=6.378e6;m=g*R^2;%内轨道v_inner=sqrt(m/r1);w_inner=v_inner/r1;x_inter=r1*cos(w_inner*t);y_inter=r1*sin(w_inner*t);%外轨道v_outer=sqrt(m/r2);w_outer=v_outer/r2;x_outer=r2*cos(w_outer*t);y_outer=r2*sin(w_outer*t);%控制器转移轨道a=(r1+r2)/2;E=-m/(2*a);V_near=sqrt(m*(2/r1-2/(r1+r2)));%转移轨道在近地点的速度V_far=sqrt(m*(2/r2-2/(r1+r2)));%转移轨道在远地点的速度h=r1*V_near;%由于在近地点的速度垂直于位置失量, h是转移轨道的⽐动量矩e=sqrt(1+2*E*h^2/m^2);%e为椭圆轨迹的偏⼼率TOF=pi*sqrt(a^3/m);%转移轨道是椭圆的⼀半及飞⾏时间是周期的⼀半(开普勒第三定律) w=pi/TOF;%椭圆轨迹的⾓速度c=a*e;b=sqrt(a^2-c^2);x_ellipse=a*cos(w*t)-0.5*r1;y_ellipse=b*sin(w*t);%动画显⽰运动轨迹x=[x_inter;x_outer;x_ellipse]';y=[y_inter;y_outer;y_ellipse]';comet(x,y)%---------------------------动态图像如下:2.利⽤两种不同途径求解边值问题dfdxf gdgdxf g f g=+=-+==34430001,,(),()的解.途径⼀:指令syms f g[f,g]=dsolve('Df=3*f+4*g,Dg=-4*f+3*g','f(0)=0,g(0)=1'); disp('f=');disp(f)disp('g=');disp(g)结果(Matlab 7.8版本)f=i/(2*exp(t*(4*i - 3))) - (i*exp(t*(4*i + 3)))/2g=exp(t*(4*i + 3))/2 + 1/(2*exp(t*(4*i - 3)))(Matlab 6.5版本)f=exp(3*t)*sin(4*t)g=exp(3*t)*cos(4*t)>>途径⼆:%problem2function dy=problem2(t,y)dy = zeros(2,1);dy(1) = 3*y(1)+4*y(2);dy(2) = -4*y(1)+3*y(2);[t,y] = ode45('problem2',[0 2],[0 1]);plot(t,y(:,1),'r',t,y(:,2),'b');图23.假设著名的Lorenz 模型的状态⽅程表⽰为-+-=+-=+-=)()()()()()()()()()()()(322133223211t x t x t x t x t x t x t x t x t x t x t x t x σρρβ其中,设28,10,3/8===σρβ。
Matlab大作业

Matlab的基本操作一、使用函数实现对下列矩阵的左旋和右旋以及反转已知答案:如图:矩阵如图矩阵的左旋如图一矩阵的右旋如图二矩阵的左右反转如图三矩阵的上下反转如图四二、已知A=[8 9 5 ] B=[-1 3 -2][36 -7 11] [2 0 3][21 -8 5] [-3 1 9 ]计算:1)A+5*B;2)A*B和A.*B3)A^3和A.^34)A/B和B\A5)[A,B]答案:A=[8 9 5;36 -7 11;21 -8 5];B=[-1 3 -2;2 0 3;-3 1 9];A+5*BA*BA.*BA^3A.^3A/BA\B[A,B]程序运行结果如下:第二章、Matlab程序设计一、已知S=1+2+22+23+…+263求S的值答案:代码如下:ClearClcs=0,j=2for i=1:63s=s+j^iends程序运行结果如下:二、第三章、Matlab绘图一、在同一坐标系中画出下列函数的图像:x2,-x2,xsin(x)在[0,2π]上的函数图像程序代码如下:clearclcx=0:pi/100:2*pi;y1=x.^2;y2=-x.^2;y3=x.*sin(x);title('同一坐标下的函数图像')plot(x,y1,':',x,y2,'h',x,y3,'--')程序运行结果如下:二、绘制极坐标图像:程序代码如下:clearclcx=0:0.01:2*pi;y=2*cos(2*(x-pi/8));title('极坐标图像')xlabel('x')ylabel('y')polar(x,y)程序运行结果如下:第四章、Matlab符号运算一、求函数y=e-x2 的傅立叶变换及其逆变换程序代码如下:clearclcsyms x t;y=exp(-x^2);Ft=fourier(y,x,t)fx=ifourier(Ft,t,x)程序运行结果如下:二、求下列极限值:答案:1、程序代码:clearclcsyms x;s1=sin(2*x)/sin(5*x);limit(s1,x,0)s2=(1+1/x)^(2*x);limit(s2,x,inf)程序运行结果如下:第五章、Matlab数值运算一、建立一个3*4阶随机矩阵,求矩阵的最大值、最小值、方差和标准差、极差、协方差,和自相关阵程序代码如下:clearclcA=rand(3,4)B=var(A)C=std(A)D=range(A)E=cov(A)F=corrcoef(A)程序运行结果如下:二、求函数f(x)=x3-2x+1在x=[-1 1]之间的极小值和x=-1附近的零点程序代码如下:clearclc[x,y]=fminbnd('x.^3-2.*x+1',-1,1)[x,y]=fzero('x.^3-2.*x+1',-1)程序运行结果如下:第六章、Matlab图形用户界面一、建立一个具有三个输入框的窗口对话框程序代码如下:clearclcprompt={'姓名','年龄','班级'};DTitle='注册学生信息';line[1;1;1];def{'乔阳','18','100412105'};info=inputdlg(prompt,DTitle,line,def,'ON')程序运行结果如下:二、设计一个表现下载进度的进度条程序代码如下:clearclch = waitbar(0,'正在下载,请稍等……');for i=1:1000waitbar(i/10000,h)endclose(h)程序运行结果如下:第七章、Matlab Simulink 仿真一、仿真信号x(t)=sin(t)sin(10t)的波形仿真步骤:1.建立模型窗口:生成无标题(intitled)的模型窗口;2.添加信号源模块(sine)、输出模块(scope)、数学模块(Dot product)3.设置模块参数:如下图:4.编辑模块即将各个模块连接起来。
matlab1-8章课后作业

MATLAB基础教程1~8章作业Matlab第一章1.阐述Matlab的功能Matlab作为一种高级计算软件,是进行算法开发、数据可视化、数据分析以及数值计算的交互式应用开发环境,已被广泛应用于不同领域。
Matlab的基本功能包括:数学计算功能、图形化显示功能、M语言编程功能、编译功能、图形用户界面开发功能、Simulink建模仿真功能、自动代码生成功能。
Matlab第二章1.创建double的变量,并进行计算。
(1)a=87,b=190,计算a+b、a-b、a*b。
(2)创建uint8 类型的变量,数值与(1)中相同,进行相同的计算。
>> a=87,b=190a =87b =190>> a+bans =277>> a-bans =-103>> a*bans =16530>> c=uint8(87), d=uint8(190)c =87d =190>> c+dans =255>> c-dans =>> c*dans =2552.计算(1)sin(60)(2)e^3(3)cos(3π/4)>> sind(60)ans =0.8660>> exp(3)ans =20.0855>> cos(3*pi/4)ans =-0.70713.设u=2,v=3,计算:(1)(2)(3)>> u=2;>> v=3;>> 4*u*v/log(v)ans =21.8457>> (exp(u)+v)^2/(v^2-u)ans =15.4189>> sqrt(u-3*v)/(u*v)ans =0 + 0.4410i4.计算如下表达式:(1)(2)>> (3-5*i)*(4+2*i)ans =22.0000 -14.0000i>> sin(2-8*i)ans =1.3553e+003 +6.2026e+002i5.判断下面语句的运算结果。
MATLAB作业4-1
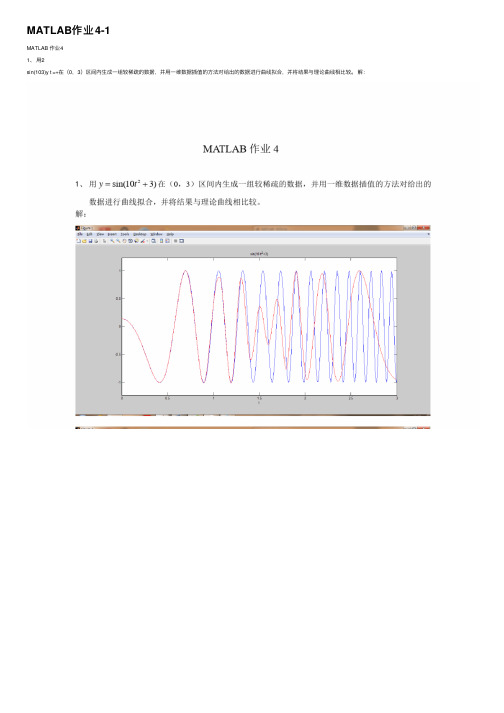
MATLAB作业4-1MATLAB 作业41、⽤2sin(103)y t =+在(0,3)区间内⽣成⼀组较稀疏的数据,并⽤⼀维数据插值的⽅法对给出的数据进⾏曲线拟合,并将结果与理论曲线相⽐较。
解:2、⽤242231(,)sin()3x y f x y e xy x y x y--=++原型函数⽣成⼀组⽹络数据或随机数据,分别拟合出曲⾯,并和原曲⾯进⾏⽐较。
解:⽹格数据:随机数据:x∈-区间内的光滑函数曲线,⽐较各种插值算法3、假设已知⼀组数据,试⽤插值⽅法绘制出(2,4.9)>> x=[-2,-1.7,-1.4,-1.1,-0.8,-0.5,-0.2,0.1,0.4,0.7,1,1.3,...1.6,1.9,2.2,2.5,2.8,3.1,3.4,3.7,4,4.3,4.6,4.9];y=[0.10289,0.11741,0.13158,0.14483,0.15656,0.16622,0.17332,...0.1775,0.17853,0.17635,0.17109,0.16302,0.15255,0.1402,...0.12655,0.11219,0.09768,0.08353,0.07019,0.05786,0.04687,...0.03729,0.02914,0.02236];解:x y在(0.1,0.1)~(1.1,1.1)区域内的点进⾏插值,并⽤三维曲⾯4、假设已知实测数据由下表给出,试对(,)>> [x,y]=meshgrid(0.1:0.1:1.1);z=[0.83041,0.82727,0.82406,0.82098,0.81824,0.8161,0.81481,0.81463,0.81579,0.81853,0.82304 ;0.83172,0.83249,0.83584,0.84201,0.85125,0.86376,0.87975,0.89935,0.92263,0.94959,0.9801; 0.83587,0.84345,0.85631,0.87466,0.89867,0.9284,0.96377,1.0045,1.0502,1.1,1.1529;0.84286,0.86013,0.88537,0.91865,0.95985,1.0086,1.0642,1.1253,1.1904,1.257,1.3222;0.85268,0.88251,0.92286,0.97346,1.0336,1.1019,1.1764,1.254,1.3308,1.4017,1.4605;0.86532,0.91049,0.96847,1.0383,1.118,1.2046,1.2937,1.3793,1.4539,1.5086,1.5335;0.88078,0.94396,1.0217,1.1118,1.2102,1.311,1.4063,1.4859,1.5377,1.5484,1.5052;0.89904,0.98276,1.082,1.1922,1.3061,1.4138,1.5021,1.5555,1.5573,1.4915,1.346;0.92006,1.0266,1.1482,1.2768,1.4005,1.5034,1.5661,1.5678,1.4889,1.3156,1.0454;0.94381,1.0752,1.2191,1.3624,1.4866,1.5684,1.5821,1.5032,1.315,1.0155,0.62477;0.97023,1.1279,1.2929,1.4448,1.5564,1.5964,1.5341,1.3473,1.0321,0.61268,0.14763];解:5、习题3和4给出的数据分别为⼀元数据和⼆元数据,试⽤分段三次样条函数和B样条函数对其进⾏拟合。
MATLAB作业

MATLAB作业⼀、必答题:1. MATLAB系统由那些部分组成?答:MATLAB系统主要由开发环境、MATLAB语⾔、MATLAB数学函数库、图形功能和应⽤程序接⼝五个部分组成。
2. 如何启动M⽂件编辑/调试器?答:在操作界⾯上选择“建⽴新⽂件”或“打开⽂件”操作时,M⽂件编辑/调试器将被启动。
在命令窗⼝中键⼊“edit”命令也可以启动M⽂件编辑/调试器。
3. 存储在⼯作空间中的数组能编辑吗?如何操作?答:存储在⼯作空间的数组可以通过数组编辑器进⾏编辑:在⼯作空间浏览器中双击要编辑的数组名打开数组编辑器,再选中要修改的数据单元,输⼊修改内容即可。
4. 在MATLAB中有⼏种获得帮助的途径?答:在MATLAB中有多种获得帮助的途径:(1)帮助浏览器:选择view菜单中的Help菜单项或选择Help菜单中的MATLAB Help菜单项可以打开帮助浏览器;(2)help命令:在命令窗⼝键⼊“help” 命令可以列出帮助主题,键⼊“help 函数名”可以得到指定函数的在线帮助信息;(3)lookfor命令:在命令窗⼝键⼊“lookfor 关键词”可以搜索出⼀系列与给定关键词相关的命令和函数(4)模糊查询:输⼊命令的前⼏个字母,然后按Tab键,就可以列出所有以这⼏个字母开始的命令和函数。
5. 有⼏种建⽴矩阵的⽅法?各有什么优点?答:(1)以直接列出元素的形式输⼊;(2)通过语句和函数产⽣;(3).在m⽂件中创建矩阵;(4)从外部的数据⽂件中装⼊。
6. 命令⽂件与函数⽂件的主要区别是什么?答:命令⽂件: M⽂件中最简单的⼀种,不需输出输⼊参数,⽤M ⽂件可以控制⼯作空间的所有数据。
运⾏过程中产⽣的变量都是全局变量。
运⾏⼀个命令⽂件等价于从命令窗⼝中顺序运⾏⽂件⾥的命令,程序不需要预先定义,只要依次将命令编辑在命令⽂件中即可。
函数⽂件:如果M⽂件的第⼀个可执⾏⾏以function开始,便是函数⽂件,每⼀个函数⽂件定义⼀个函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一
1、熟悉MATLAB的窗口结构(命令窗口、历史命令窗口、工作区窗口、当前目录
窗口)
2、掌握命令窗口中基本命令的使用
3、在命令窗口中,给定圆的半径r,求得圆的周长c和面积s,并查看工作区窗
口的变化
4、将r,c,s变量保存到磁盘文件abc.mat中,并删除内存变量r,c,s,查看工作
区窗口的变化
5、将abc.mat文件中变量装入内存,查看工作区窗口的变化
6、将历史命令窗口中的命令再装入命令窗口中使用
7、改变当前目录,查看当前目录窗口的变化
8、掌握命令窗口中
cd,quit,help,date,dir,ls,what,who,clocl,fix(clock),format,save,loa d,clc,clear等命令的使用
9、注意各种MATLAB版本的差别
实验二
1、在命令窗口中,输入长方形的长和宽,求长方形的周长和面积
2、输入三角形的三条边(要满足构成三角形的条件),求三角形的周长和面积
3、掌握MATLAB中各标准函数的使用(sin,cos,sind,fix,mod,…)
4、用fprintf输出各种类型的数据(如fprintf('a=%d\n',123)
a=123
>> fprintf('b=%f\n',123.456)
b=123.456000
>> fprintf('c=%c\n','A')
c=A……)
实验三
1、在编辑窗口中:输入学生成绩,输出该成绩的等级。
等级规定如下:[90,
100]为A等,[80,90)为B等,[70,80)为C等,[60,70)为D等,[0,60)为E等。
要求用if和 switch两种方法实现。
2、商场购物,100件以下,不优惠,100~199件95折,200~399件90折,400~799
件85折,800~1499件80折,1500件以上,75折。
输入所购货物的单价、件数,求实际付款数目。
要求用if和 switch两种方法实现(在编辑窗口中实现)。
实验四
1、求两个正整数的最大公约数和最小公倍数(在编辑窗口中实现,命令窗口中
调用)。
2、求100~300内所有素数(在编辑窗口中实现,命令窗口中调用)。
实验五
1、用函数文件求两个正整数的最大公约数和最小公倍数(在编辑窗口中实现,
命令窗口中调用)。
2、用函数文件求100~300内所有素数(在编辑窗口中实现,命令窗口中调用)。
3、给定一个班的人数和成绩,用函数文件求该班的最高分、最低分和平均分。
实验六
1、自己给定矩阵,实现两矩阵的加、减、乘、除运算
2、用函数文件输出任意行的杨辉三角形
3、自己给定矩阵,实现矩阵的点乘和点除
试验七
1、给定一个行向量,个数自定,用循环的嵌套和函数文件实现该行向量的从小
到大的排列
2、一个学生数据包含:学号、姓名、性别、年龄、成绩,输入一个班若干个学
生数据,将学生数据按成绩从高到低重新排列。
3、自己设定多项式,求多项式的根和多项式的值。
实验八
1、用红色画出y=sin(x)在[-pi,pi]中的图像
2、在同一坐标中,用蓝色画出y=x3+2x2-4x+5的图像
3、在同一坐标中,用黄色画出y=e x的图像
试验九
在第1个子窗口用极坐标画图显示r=0.5(1+cos(θ)),其中θ∈[0,2π];在第2个子窗口作填充图,填充坐标矢量为X=[0 0.2 0.8 1 0.5 0],Y=[1 0 0 1 1.8 1],填充颜色为蓝色;在第3个子窗口作双y轴图y1=sin(t),t∈[0,4π],y2=20*cos(t);在第4个子窗口显示相图x=sin(t),y=cos(t).如图所示。
试验十
1、在区间x=0: π/100:2*π内,在同一幅图上同时绘制曲线
,,并对图形加上一些说明,得到如下所示的图形。
2、在第1个子窗口用半对数坐标同时画出曲线y1=6+log(x)+x和y2=x+5,x∈[0,10],在第2个子窗口用极坐标画图显示r=cos(6θ),其中θ∈[0,2π];在第3个子窗口画出如图所示曲线y=sin(x),x∈[0,2π];在第4个子窗口显示三维离散数据图x=exp(t),y=t,z=exp(t), t∈[0,5].如图所示。
实验十一
1.对x’=-2x(t)+u(t)进行仿真,其中信号u是阶跃波信号。
建模所需模块如下:
Gain 增益模块-2
Integator积分模块
Add 相加
Step 阶跃波
Scope 示波器
Out1 输出变量到工作空间
建立的模型框图如下
代码见e15_1.mdl
可以在命令窗口输入:plot(tout,yout);并与仿真结果比较。
2.GUI编程
在第一个窗口中设置一个列表框,里面有内容:张三、李四、王五、赵六(分四行)。
若双击某行,则弹出第二个窗口,显示选中的内容,按返回按钮,则回到第一个窗口。
代码见mainfig.fig,mainfig.m, nextfig.fig, nextfig.m 或main1fig.fig,main1.m,nextfig1.fig,nextfig1.m
实验十二
设计一个GUI界面如下:
输入姓名,选中性别,选中民族,点击提交按钮,将选中的内容在静态文本框中显示。
代码见zhuce.fig,zhuce.m
实验十三
1、对于给定的一元函数y=f(x) 的n+1个节点值yi=f(xi) (i=0,1,2,…,n)。
试用Lagrange 公式求其插值多项式。
数据如下: 计算f(0.596)和f(0.99)的值。
(提示:f(0.596)≈0.625732,f(0.99)≈1.05423 )
2、用三次Lagrange 公式和Newton 公式求插值多项式,此多项式在x 0=1,x 1=3,x 2=6,x 3=7处的函
数值与f(x)=x 2
相同。
最后求出在x=1.5、2.5、5.5处的近似值。
实验十四
1、 用复合梯形(取n=2,4,8,16)和MATLAB 函数文件求
⎰
10
dx e x 的近似值
2、 用复合辛铺森(取n=2,4,8,16)和MATLAB 函数文件求 ⎰
1
dx e x 的近似值
3、 将上述求得的近似值与真值进行比较 。
试验十五
1、用二分法求方程x 2-x-1=0的正根,使误差小于0.05,用MATLAB 编程实现。
2、求方程x 3-x 2-1=0在x 0=1.5附近的一个根,请自己选择至少两个收敛的迭代公式,用MATLAB 编程实现。
3、用牛顿法求f(x)=x 3-3x-1=0在x 0=2附近的根,用MATLAB 编程实现。
试验十六
1、用gauss 消去法和LU 分解求下列方程组的解
x 0.4
0.55
0.65
0.80
0.95 1.05 y
0.41075 0.57815 0.69675 0.90
1.00
1.25382
4 2 -3 -1 2 1 0 0 0 0 x1
5 8
6 -5 -3 6 5 0 1 0 0 x2 12 4 2 -2 -1 3 2 -1 0 3 1 x3 3 0 -2 1 5 -1 3 -1 1 9 4 x4 2 -4 2 6 -1 6
7 -3 3 2 3 x5 3
8 6 -8 5 7 17 2 6 -3 5 x6 46 0 2 -1 3 -4 2 5 3 0 1 x7 13 16 10 -11 -
9 17 34 2 -1 2 2 x8 38 4 6 2 -7 13 9 2 0 12 4 x9 19 0 0 -1 8 -3 -24 -8 6 3 -1 x10 -21
=
×
真解为x *
=(1,-1,0,1,2,0,3,1,-1,1)’
2、用雅可比迭代和高斯-塞德尔迭代求下列方程组的解
4 2 -3 -1 2 1 0 0 0 0 x1
5 8
6 -5 -3 6 5 0 1 0 0 x2 12 4 2 -2 -1 3 2 -1 0 3 1 x3 3 0 -2 1 5 -1 3 -1 1 9 4 x4 2 -4 2 6 -1 6
7 -3 3 2 3 x5 3
8 6 -8 5 7 17 2 6 -3 5 x6 46 0 2 -1 3 -4 2 5 3 0 1 x7 13 16 10 -11 -
9 17 34 2 -1 2 2 x8 38 4 6 2 -7 13 9 2 0 12 4 x9 19 0 0 -1 8 -3 -24 -8 6 3 -1 x10 -21
=
×
真解为x *=(1,-1,0,1,2,0,3,1,-1,1)。
