初中九年级数学专题复习教案:动态几何之定值问题探讨
初三中考复习专题:定值问题

初三数学讲义 专题探究:定值类问题教学过程:一、教学衔接(课前环节)1、回收上次课的教案,了解家长的反馈意见;2、检查学生的作业,及时指点3、捕捉学生的思想动态和了解学生的本周学校的学习内容二、知识点解析在几何问题中,当一些几何元素按照一定的规律在确定的范围内变化时,与它相关另一些几何元素的某些量或其数量关系保持不变,这种几何问题称之为几何定值问题. 定值问题由于所求证的问题不明确、具体,而使人难已下手,给问题解决带来困难.近年来,该类问题在各省市中考试题中频频出现,为便于广大师生复习教学,现对其归类例析.一、线段长度为定值例1如图,在半径为6,圆心角为90°的扇形OAB 的弧AB 上,有一个动点P ,PH ⊥OA ,垂足为H ,△OPH 的重心为G 。
(1)当点P 在弧AB 上运动时,线段GO 、GP 、GH 中,有无长度保持不变的线段?如果有,请指出这样的线段,并求出相应的长度;(2)设PH =,GP =,求关于的函数解析式,并写出函数的定义域; (3)如果△PGH 是等腰三角形,试求出线段PH 的长。
分析:解决此题时,首先要根据线段GH 的特征,添出辅助线,找出与其有关的长度为定值的线段间的联系,从而获得问题的解决.图一BOAGPHE二、线段长度为定值例 在给定的梯形ABCD 中,AD ∥BC ,E 是AB 边上的动点,点1O 、2O 分别是AED ∆和BEC ∆的外心。
求证:21O O 的长为一定值。
变式练习 如图,在ABC ∆中,A ∠与底边BC 为一定值,BD ⊥AC ,CE ⊥AB ,D 、E 为垂足,连结DE 。
求证:DE 为定长。
三、角的度数为定值例 如图,定长的弦ST 在一个以AB 为直径的半圆上滑动,M 是ST 的中点,P 是S 对AB 作垂线的垂足。
求证:不管ST 滑到什么位置,SPM ∠是一定角。
ACB DEEDABCPM A O BS T例题.(2010广东广州,24,14分)如图,⊙O 的半径为1,点P 是⊙O 上一点,弦AB 垂直平分线段OP ,点D 是 APB 上任一点(与端点A 、B 不重合),DE ⊥AB 于点E ,以点D 为圆心、DE 长为半径作⊙D ,分别过点A 、B 作⊙D 的切线,两条切线相交于点C .(1)求弦AB 的长;(2)判断∠ACB 是否为定值,若是,求出∠ACB 的大小;否则,请说明理由; (3)记△ABC 的面积为S ,若2SDE =43,求△ABC 的周长.四、面积为定值例. 如图7(1),正方形ABCD 的对角线相交于点O ,O 是正方形A'B'C'O 的一个顶点,如果两个正方形的边长为a,求证:正方形A'B'C'O 绕点O 无论怎样转动,两个正方形重叠部分的面积总是一个定值.CP DOBAEFE 图10图9C'B'A'C'B'A'OBDBDAC C A真题练习1.(2011•广州)已知关于x的二次函数y=ax2+bx+c(a>0)的图象经过点C(0,1),且与x轴交于不同的两点A、B,点A的坐标是(1,0)(1)求c的值;(2)求a的取值范围;(3)该二次函数的图象与直线y=1交于C、D两点,设A、B、C、D四点构成的四边形的对角线相交于点P,记△PCD的面积为S1,△PAB的面积为S2,当0<a<1时,求证:S1-S2为常数,并求出该常数.2.(2011•河北)如图,在平面直角坐标系中,点P从原点O出发,沿x轴向右以毎秒1个单位长的速度运动t秒(t>0),抛物线y=x2+bx+c经过点O和点P,已知矩形ABCD的三个顶点为 A(1,0),B(1,-5),D(4,0).(1)求c,b(用含t的代数式表示):(2)当4<t<5时,设抛物线分别与线段AB,CD交于点M,N.①在点P的运动过程中,你认为∠AMP的大小是否会变化?若变化,说明理由;若不变,求出∠AMP 的值;②求△MPN的面积S与t的函数关系式,并求t为何值时,要S=218错误!未找到引用源。
中考复习专题:动态几何之定值问题探讨
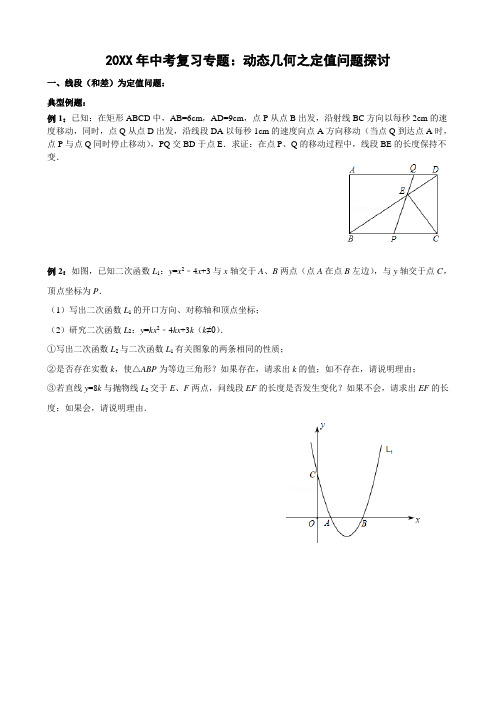
20XX年中考复习专题:动态几何之定值问题探讨一、线段(和差)为定值问题:典型例题:例1:已知:在矩形ABCD中,AB=6cm,AD=9cm,点P从点B出发,沿射线BC方向以每秒2cm的速度移动,同时,点Q从点D出发,沿线段DA以每秒1cm的速度向点A方向移动(当点Q到达点A时,点P与点Q同时停止移动),PQ交BD于点E.求证:在点P、Q的移动过程中,线段BE的长度保持不变.例2:如图,已知二次函数L1:y=x2﹣4x+3与x轴交于A、B两点(点A在点B左边),与y轴交于点C,顶点坐标为P.(1)写出二次函数L1的开口方向、对称轴和顶点坐标;(2)研究二次函数L2:y=kx2﹣4kx+3k(k≠0).①写出二次函数L2与二次函数L1有关图象的两条相同的性质;②是否存在实数k,使△ABP为等边三角形?如果存在,请求出k的值;如不存在,请说明理由;③若直线y=8k与抛物线L2交于E、F两点,问线段EF的长度是否发生变化?如果不会,请求出EF的长度;如果会,请说明理由.练习题:1.如图,Rt△ABC中,∠A=30°,BC=10cm,点Q在线段BC上从B向C运动,点P在线段BA上从B向A 运动.Q、P两点同时出发,运动的速度相同,当点Q到达点C时,两点都停止运动.作PM⊥PQ交CA 于点M,过点P分别作BC、CA的垂线,垂足分别为E、F.(1)求证:△PQE∽△PMF;(2)当点P、Q运动时,请猜想线段PM与MA的大小有怎样的关系?并证明你的猜想;(3)设BP=x,△PEM的面积为y,求y关于x的函数关系式,当x为何值时,y有最大值,并将这个值求出来.2、已知正方形ABCD,点P是对角线AC所在直线上的动点,点E在DC边所在直线上,且随着点P的运动而运动,PE=PD总成立.(1)如图(1),当点P在对角线AC上时,请你通过测量、观察,猜想PE与PB有怎样的关系?(直接写出结论不必证明);(2)如图(2),当点P运动到CA的延长线上时,(1)中猜想的结论是否成立?如果成立,请给出证明;如果不成立,请说明理由;(3)如图(3),当点P运动到CA的反向延长线上时,请你利用图(3)画出满足条件的图形,并判断此时PE与PB有怎样的关系?(直接写出结论不必证明)(1)(2) (3)3、如图,梯形ABCD中,AD∥BC,BC=20cm,AD=10cm,现有两个动点P、Q分别从B、D两点同时..出发,点P以每秒2cm的速度沿BC向终点C移动,点Q以每秒1cm的速度沿DA向终点A移动,线段PQ与BD相交于点E,过E作EF∥BC交CD于点F,射线QF交BC的延长线于点H,设动点P、Q移动的时间为t(单位:秒,0<t<10).(1)当t为何值时,四边形PCDQ为平行四边形?(2)在P、Q移动的过程中,线段PH的长是否发生改变?如果不变,求出线段PH的长;如果改变,请说明理由.4、已知:A、B、C不在同一直线上.(1)若点A、B、C均在半径为R的⊙O上,i)如图一,当∠A=45°时,R=1,求∠BOC的度数和BC的长度;ii)如图二,当∠A为锐角时,求证sin∠A= BC2R;(2).若定长线段....BC的两个端点分别在∠MAN的两边AM、AN(B、C均与点A不重合)滑动,如图三,当∠MAN=60°,BC=2时,分别作BP⊥AM,CP⊥AN,交点为点P,试探索:在整个滑动过程中,P、A 两点的距离是否保持不变?请说明理由.二、面积(和差)为定值问题:典型例题:例1:如图,在梯形ABCD中,AD∥BC,E、F分别是AB、DC边的中点,AB=4,∠B=60°,(1)求点E到BC边的距离;(2)点P为线段EF上的一个动点,过P作PM⊥BC,垂足为M,过点M作MN∥AB交线段AD于点N,连接PN、探究:当点P在线段EF上运动时,△PMN的面积是否发生变化?若不变,请求出△PMN的面积;若变化,请说明理由.例2:如图,在平面直角坐标系x O y中,矩形AOCD的顶点A的坐标是(0,4),现有两动点P、Q,点P 从点O出发沿线段OC(不包括端点O,C)以每秒2个单位长度的速度,匀速向点C运动,点Q从点C 出发沿线段CD(不包括端点C,D)以每秒1个单位长度的速度匀速向点D运动.点P,Q同时出发,同2.时停止,设运动时间为t秒,当t=2秒时PQ=5(1)求点D的坐标,并直接写出t的取值范围;(2)连接AQ并延长交x轴于点E,把AE沿AD翻折交CD延长线于点F,连接EF,则△AEF的面积S是否随t的变化而变化?若变化,求出S与t的函数关系式;若不变化,求出S的值.(3)在(2)的条件下,t为何值时,四边形APQF是梯形?练习题:1.如图1,在△ABC 中,AB=AC=5,BC=6,D 、E 分别是AB 、AC 的中点,F 、G 为BC 上的两点,FG=3,线段DG ,EF 的交点为O ,当线段FG 在线段BC 上移动时,三角形FGO 的面积与四边ADOE 的面积之和恒为定值,则这个定值是 .2.如图2,在矩形ABCD 中,AD=5,AB=4,点E 、G 、H 、F 分别在AB 、BC 、CD 、AD 上,且AF=CG=2,BE=DH=1,点P 是直线EF 、GH 之间任意一点,连接PE 、PF 、PG 、PH ,则△PEF 和△PGH 的面积和等于 _________ .图1 图23.如图所示,四边形OABC 是矩形.点A 、C 的坐标分别为(30-,),(0,1),点D 是线段BC 上的动点(与端点B 、C 不重含),过点D 作直线12y x b =+交折线OAB 于点E 。
中考数学解法探究专题 :探究动态几何定值问题

中考数学解法探究专题动态几何定值问题考题研究:数学因运动而充满活力,数学因变化而精彩纷呈。
动态题是近年来中考的的一个热点问题,以运动的观点探究几何图形的变化规律问题,称之为动态几何问题,随之产生的动态几何试题就是研究在几何图形的运动中,伴随着出现一定的图形位置、数量关系的“变”与“不变”性的试题,就其运动对象而言,有点动、线动、面动三大类,就其运动形式而言,有轴对称(翻折)、平移、旋转(中心对称、滚动)等,就问题类型而言,有函数关系和图象问题、面积问题、最值问题、和差问题、定值问题和存在性问题等。
解这类题目要“以静制动”,即把动态问题,变为静态问题来解,而静态问题又是动态问题的特殊情况。
以动态几何问题为基架而精心设计的考题,可谓璀璨夺目、精彩四射。
解题攻略:动态几何形成的定值和恒等问题是动态几何中的常见问题,其考点包括线段(和差)为定值问题;角度(和差)为定值问题;面积(和差)为定值问题;其它定值问题。
解答动态几何定值问题的方法,一般有两种:第一种是分两步完成:先探求定值. 它要用题中固有的几何量表示.再证明它能成立.探求的方法,常用特殊位置定值法,即把动点放在特殊的位置,找出定值的表达式,然后写出证明.第二种是采用综合法,直接写出证明.解题思路:在中考中,动态几何形成的定值和恒等问题命题形式主要为解答题。
在中考压轴题中,动态几何之定值(恒等)问题的重点是线段(和差)为定值问题,问题的难点在于准确应用适当的定理和方法进行探究。
例题解析1.如图,直角△ABC中,∠A为直角,AB=6,AC=8.点P,Q,R分别在AB,BC,CA边上同时开始作匀速运动,2秒后三个点同时停止运动,点P由点A出发以每秒3个单位的速度向点B运动,点Q由点B出发以每秒5个单位的速度向点C运动,点R由点C出发以每秒4个单位的速度向点A运动,在运动过程中:(1)求证:△APR,△BPQ,△CQR的面积相等;(2)求△PQR面积的最小值;(3)用t(秒)(0≤t≤2)表示运动时间,是否存在t,使∠PQR=90°?若存在,请直接写出t的值;若不存在,请说明理由.【考点】KY:三角形综合题.【分析】(1)先利用锐角三角函数表示出QE=4t,QD=3(2﹣t),再由运动得出AP=3t,CR=4t,BP=3(2﹣t),AR=4(2﹣t),最后用三角形的面积公式即可得出结论;=18(t﹣1)2+6,即可得出结(2)借助(1)得出的结论,利用面积差得出S△PQR论;(3)先判断出∠DQR=∠EQP,用此两角的正切值建立方程求解即可.【解答】解:(1)如图,在Rt△ABC中,AB=6,AC=8,根据勾股定理得,BC=10,sin∠B===,sin∠C=,过点Q作QE⊥AB于E,在Rt△BQE中,BQ=5t,∴sin∠B==,∴QE=4t,过点Q作QD⊥AC于D,在Rt△CDQ中,CQ=BC﹣BQ=10﹣5t,∴QD=CQ•sin∠C=(10﹣5t)=3(2﹣t),由运动知,AP=3t,CR=4t,∴BP=AB﹣AP=6﹣3t=3(2﹣t),AR=AC﹣CR=8﹣4t=4(2﹣t),=AP•AR=×3t×4(2﹣t)=6t(2﹣t),∴S△APRS△BPQ=BP•QE=×3(2﹣t)×4t=6t(2﹣t),S△CQR=CR•QD=×4t×3(2﹣t)=6t(2﹣t),=S△BPQ=S△CQR,∴S△APR∴△APR,△BPQ,△CQR的面积相等;=S△BPQ=S△CQR=6t(2﹣t),(2)由(1)知,S△APR∵AB=6,AC=8,=S△ABC﹣(S△APR+S△BPQ+S△CQR)∴S△PQR=×6×8﹣3×6t(2﹣t)=24﹣18(2t﹣t2)=18(t﹣1)2+6,∵0≤t≤2,=6;∴当t=1时,S△PQR最小(3)存在,由(1)知,QE=4t,QD=3(2﹣t),AP=3t,CR=4t,AR=4(2﹣t),∴BP=AB﹣AP=6﹣3t=3(2﹣t),AR=AC﹣CR=8﹣4t=4(2﹣t),过点Q作QD⊥AC于D,作QE⊥AB于E,∵∠A=90°,∴四边形APQD是矩形,∴AE=DQ=3(2﹣t),AD=QE=4t,∴DR=|AD﹣AR|=|4t﹣4(2﹣t)|=|4(2t﹣2)|,PE=|AP﹣AE|=|3t﹣3(2﹣t)|=|3(2t﹣2)|∵∠DQE=90°,∠PQR=90°,∴∠DQR=∠EQP,∴tan∠DQR=tan∠EQP,在Rt△DQR中,tan∠DQR==,在Rt△EQP中,tan∠EQP==,∴,∴16t=9(2﹣t),∴t=.2.已知,点O是等边△ABC内的任一点,连接OA,OB,OC.(1)如图1,已知∠AOB=150°,∠BOC=120°,将△BOC绕点C按顺时针方向旋转60°得△ADC.①∠DAO的度数是90°②用等式表示线段OA,OB,OC之间的数量关系,并证明;(2)设∠AOB=α,∠BOC=β.①当α,β满足什么关系时,OA+OB+OC有最小值?请在图2中画出符合条件的图形,并说明理由;②若等边△ABC的边长为1,直接写出OA+OB+OC的最小值.【考点】KY:三角形综合题.【分析】(1)①根据旋转变换的性质、四边形内角和为360°计算即可;②连接OD,根据勾股定理解答;(2)①将△AOC绕点C按顺时针方向旋转60°得△A′O′C,连接OO′,根据等边三角形的性质解答;②根据等边三角形的性质计算.【解答】解:(1)①∵∠AOB=150°,∠BOC=120°,∴∠AOC=90°,由旋转的性质可知,∠OCD=60°,∠ADC=∠BOC=120°,∴∠DAO=360°﹣60°﹣90°﹣120°=90°,故答案为:90°;②线段OA,OB,OC之间的数量关系是OA2+OB2=OC2.如图1,连接OD.∵△BOC绕点C按顺时针方向旋转60°得△ADC,∴△ADC≌△BOC,∠OCD=60°.∴CD=OC,∠ADC=∠BOC=120°,AD=OB.∴△OCD是等边三角形,∴OC=OD=CD,∠COD=∠CDO=60°,∵∠AOB=150°,∠BOC=120°,∴∠AOC=90°,∴∠AOD=30°,∠ADO=60°.∴∠DAO=90°.在Rt△ADO中,∠DAO=90°,∴OA2+AD2=OD2.∴OA2+OB2=OC2.(2)①如图2,当α=β=120°时,OA+OB+OC有最小值.作图如图2,如图2,将△AOC绕点C按顺时针方向旋转60°得△A′O′C,连接OO′.∴△A′O′C≌△AOC,∠OCO′=∠ACA′=60°.∴O′C=OC,O′A′=OA,A′C=BC,∠A′O′C=∠AOC.∴△OC O′是等边三角形.∴OC=O′C=OO′,∠COO′=∠CO′O=60°.∵∠AOB=∠BOC=120°,∴∠AOC=∠A′O′C=120°.∴∠BOO′=∠OO′A′=180°.∴四点B,O,O′,A′共线.∴OA+OB+OC=O′A′+OB+OO′=BA′时值最小;②当等边△ABC的边长为1时,OA+OB+OC的最小值A′B=.3.两个直角边为6的全等的等腰Rt△AOB和Rt△CED中,按图1所示的位置放置,A与C重合,O与E重合.(Ⅰ)求图1中,A,B,D三点的坐标;(Ⅱ)Rt△AOB固定不动,Rt△CED沿x轴以每秒2个单位长的速度向右运动,当D点运动到与B点重合时停止,设运动x秒后Rt△AOB和Rt△CED的重叠部分面积为y,求y与x之间的函数关系式;(Ⅲ)当Rt△CED以(Ⅱ)中的速度和方向运动,运动时间x=4秒时Rt△CED运动到如图2所示的位置,求点G的坐标.【考点】KY:三角形综合题.【分析】(1)Rt△AOB≌Rt△CED且直角边为6,所以有A(0,6),B(6,0),D(﹣6,0),(2)Rt△CED沿x轴以每秒2个单位长的速度向右运动,且DE=6,所以在运动过程中有两种情况,即D点仍停留在y轴左侧和D在y轴右侧,需分情况讨论.在第一种情况中,重合部分为两个全等的直角梯形,在第二种情况中,重合部分为一个等腰直角三角形,面积易求出.(3)当运动时间为4秒时,即为(2)中第二种情况,此时G(4,2).【解答】解:(1)因为两个直角边为6的全等的等腰Rt△AOB和Rt△CED中,可得:A(0,6),B(6,0),D(﹣6,0).(2)当0≤x<3时,位置如图A所示,作GH⊥DB,垂足为H,可知:OE=2x,EH=x,DO=6﹣2x,DH=6﹣x,=2(S△GHD﹣S△IOD)∴y=2S梯形IOHG=2[(6﹣x)2﹣(6﹣2x)2]=2(x2+6x)=﹣3x2+12x当3≤x≤6时,位置如图B所示.可知:DB=12﹣2x=(DB)2= [(12﹣2x)]2=x2﹣12x+36∴y=S△DGB∴y与x的函数关系式为:y=;(3)图B中,作GH⊥OE,垂足为H,当x=4时,OE=2x=8,DB=12﹣2x=4,∴GH=DH=DB=2,OH=6﹣HB=6﹣DB=6﹣2=4∴G(4,2).4.如图1,等边△ABC中,BC=4,点P从点B出发,沿BC方向运动到点C,点P关于直线AB、AC的对称点分别为点M、N,连接MN.【发现】当点P与点B重合时,线段MN的长是4.当AP的长最小时,线段MN的长是6;【探究】如图2,设PB=x,MN2=y,连接PM、PN,分别交AB,AC于点D,E.(1)用含x的代数式表示PM=x,PN=(4﹣x);(2)求y关于x的函数关系式,并写出y的取值范围;(3)当点P在直线BC上的什么位置时,线段MN=3(直接写出答案)【拓展】如图3,求线段MN的中点K经过的路线长.【应用】如图4,在等腰△ABC中,∠BAC=30°,AB=AC,BC=2,点P、Q、R分别为边BC、AB、AC上(均不与端点重合)的动点,则△PQR周长的最小值是2+.(可能用到的数值:sin75°=,cos75°=,tan75°=2+)【考点】KY:三角形综合题.【分析】【发现】当点P为BC的中点时,MN最短,求出此时MN的长度,当点P与点B(或C)重合时,BN(或CM)最长,求出此时BN的长度;【探究】(1)解直角三角形即可得到结论;(2)如图2,分别过点M,N作直线BC的垂线MF,NG,垂足分别是F,G,过点M作MH⊥NG垂足为H.解直角三角形得到MF=x,PF=x,NG=(4﹣x),PG=(4﹣x),根据勾股定理即可得到结论;(3)由MN=3,得到MN2=63,把y=63时代入3(x﹣2)2+36=63,即可得到结论;【拓展】如图3,分别过点M,N作直线BC的垂线MF,NG,垂足分别是F,G,连接MG,过MN的中点K,作KT⊥BC于点T,交MG于点S.由MF∥KT∥NG,且点K为MN的中点,得到KS是△MNG的中位线,ST是△GMF的中位线,由【探究】中的过程可知,若设PB=x,则有PC=4﹣x,MF=x,NG=(4﹣x),根据三角形的中位线的性质即可得到结论;【应用】过BC的中点P作AB,AC的对称点M,N,连接MN交AB与Q,交AC 于R,则此时△PQR周长最小,根据三角形和四边形的内角和得到∠B=∠C=75°,∠MPN=150°,得到MN∥BC,PQ=PB=1,同理PR=PC=1,解直角三角形得到QR=2×PQ=,于是得到结论.【解答】解:【发现】当AP的长最小时,AP⊥BC,即点P为BC的中点时,此时E、F分别为AB、AC的中点,∴PE=AC,PF=AB,EF=BC,∴MN=ME+EF+FN=PE+EF+PF=6;当点P和点B重合时,此时G(H)为AB(AC)的中点,∴CG=2BH=2,BN=4;故答案为:4,6;【探究】(1)PM=2PD=2×PB=x,PN=2PE=2×PC=2×(4﹣x)=(4﹣x);故答案为:x,(4﹣x);(2)如图2,分别过点M,N作直线BC的垂线MF,NG,垂足分别是F,G,过点M作MH⊥NG垂足为H.∵在Rt△PMF中,∠MPF=30°,PM=x,∴MF=x,PF=x,同理,在Rt△PNG中,∠NPG=30°,PN=(4﹣x),∴NG=(4﹣x),PG=(4﹣x),∵四边形MFGH是矩形,则有NH=NG﹣HG=NG﹣MF=(4﹣x)﹣x=(2﹣x),MH=FG=PF+PG=x+(4﹣x)=6,∴在Rt△MNH中,由勾股定理得,MN2=NH2+MH2=3(x﹣2)2+36,则y=3(x﹣2)2+36,x=0或4时,y最大值=48,∵0≤x≤4,且当x=2时,y最小值=36;当∴36≤y≤48;(3)∵MN=3,MN2=63,∴当y=63时,即3(x﹣2)2+36=63,∴x=5或﹣1,∴当点P在B点右侧距离为5,或者在点P在B点左侧距离为1的位置处,均有线段MN=3;【拓展】如图3,分别过点M,N作直线BC的垂线MF,NG,垂足分别是F,G,连接MG,过MN的中点K,作KT⊥BC于点T,交MG于点S.∵MF∥KT∥NG,且点K为MN的中点,∴KS是△MNG的中位线,ST是△GMF的中位线,由【探究】中的过程可知,若设PB=x,则有PC=4﹣x,MF=x,NG=(4﹣x),由三角形中位线性质可得,ST=MF=x,KS=NG=(4﹣x),∴KT=ST+KS=x+(4﹣x)=,因此,在点P运动过程中,MN的中点K到BC边距离始终等于定值,且为等边△ABC高的一半,所以MN的中点K经过的路线恰为等边△ABC的中位线,其路线长为2.【应用】过BC的中点P作AB,AC的对称点M,N,连接MN交AB与Q,交AC 于R,则此时△PQR周长最小,∵∠BAC=30°,∴∠B=∠C=75°,∠MPN=150°,∴∠M=∠N=15°,∴∠MQB=∠PQB=∠B=75°,∴MN∥BC,PQ=PB=1,同理PR=PC=1,∵AP⊥BC,∴AP⊥MN.∵∠PQR=180°﹣75°﹣75°=30°,∴QR=2×PQ=,∴△PQR周长的最小值是2+.故答案为:2+.5.在学习三角形中位线的性质时,小亮对课本给出的解决办法进行了认真思考:课本研究三角形中位线性质的方法已知:如图①,已知△ABC中,D,E分别是AB,AC两边中点.求证:DE∥BC,DE=BC.证明:延长DE至点F,使EF=DE,连接FC.…则△ADE≌△CFE.∴…请你利用小亮的发现解决下列问题:(1)如图③,AD是△ABC的中线,BE交AC于点E,交AD于点F,且AE=EF,求证:AC=BF.请你帮助小亮写出辅助线作法并完成论证过程:(2)解决问题:如图⑤,在△ABC中,∠B=45°,AB=10,BC=8,DE是△ABC的中位线.过点D,E作DF∥EG,分别交BC于点F,G,过点A作MN∥BC,分别与FD,GE的延长线交于点M,N,则四边形MFGN周长的最小值是8+10.【考点】KY:三角形综合题.【分析】(1)先判断出△BDF≌△CDM,得出MC=BF,再判断出AC=MC,即可得出结论(2)先判断出四边形DEGF,DENM,FGNM是平行四边形,即:MN=FG=DE=4再判断出平行四边形FGNM是矩形时,四边形MFGN的周长最小,最后用锐角三角函数求出MF=GN=5,求和即可得出结论【解答】证明:(1)如图1,延长AD至点M,使MD=FD,连接MC,在△BDF和△CDM中,BD=CD,∠BDF=∠CDM,DF=DM.∴△BDF≌△CDM(SAS).∴MC=BF,∠M=∠BFM.∵EA=EF,∴∠EAF=∠EFA.∵∠AFE=∠BFM,∴∠M=∠MAC.∴AC=MC.∴BF=AC.(2)如图2,在△ABC中,∠B=45°,AB=10,BC=8,∵DE是△ABC的中位线.∴DE=BC=4,DE∥BC∵DF∥EG,MN∥BC,∴四边形DEGF,DENM,FGNM是平行四边形,∴MN=FG=DE=4,∴要四边形MFGN周长的最小只有MF=NG最小,即:MF⊥BC,∴平行四边形FGNM是矩形,过点A作AP⊥BC于P,∴AP=MF=NG,在Rt△ABP中,∠B=45°,AB=10,∴AP=5,∴MF=NG=5,即四边形MFGN周长的最小值是8+10.故答案为:8+10.6.如图,将△OAB放在平面直角坐标系中,O为原点,点A(2,4),点B(6,0)在边OB上有一动点P,过P作PC∥OA交AB于C,连接AP.(Ⅰ)求△OAB的面积;(Ⅱ)若设OP=x,△APC的面积为y,试用含x的式子表示y;=S△OAB的点P存在,求当m取得最小值时,点P的坐标(Ⅲ)若有满足S△APC(直接写出结果即可).【考点】KY:三角形综合题.【分析】(1)先确定出AD和OB的长,最后用三角形的面积公式即可;(2)先设出C的坐标,进而表示出BC,再用相似三角形的性质即可得出CE,最后用三角形的面积的差即可得出结论;(3)借助(1)(2)得出结论,先确定出y的最大值,即可判断出m的最小值,进而求出点P的坐标.【解答】解:(1)如图1,过点A作AD⊥x轴于D,∵A(2,4),∴AD=4,∵B(6,0),∴OB=6,=OB×AD=×6×4=12,∴S△OAB(2)如图2,过点A作AD⊥x轴于D,过点C作CE⊥x轴,∵A(2,4),B(6,0),∴直线AB的解析式为y=﹣x+6,设C(a,﹣a+6)(0<a<6),在Rt△ABD中,AD=4,BD=OB﹣OD=6﹣2=4,∴tan∠OBA==1,在Rt△BCE中,tan∠OBA==1,∴BE=CE=﹣a+6,∴BC=BE=(﹣a+6),∵A(2,4),B(6,0),∴AB=4,∵PC∥OA,∴△BPC∽△BOA,∴,∵OP=x,OB=6,∴BP=6﹣x,∴,∴a=2+x,∴CE=﹣a+6=﹣2﹣x+6=4﹣x,=S△OAB﹣S△OAP﹣S△BPC=12﹣x×4﹣(6﹣x)×(4﹣x)=﹣x2+2x ∴y=S△ACP(0<x<6),=y=﹣x2+2x=﹣(x﹣3)2+3,(3)由(2)知,S△ACP当x=3时,y最大=3=12,由(1)知,S△AOB=S△OAB,∵S△APC∴的最大值为3,∴m的最小值为4,∴m最小时,P(3,0).7.【探索发现】如图①,是一张直角三角形纸片,∠B=60°,小明想从中剪出一个以∠B为内角且面积最大的矩形,经过多次操作发现,当沿着中位线DE、EF剪下时,所得的矩形的面积最大,随后,他通过证明验证了其正确性,并得出:矩形的最大面积与原三角形面积的比值为.【拓展应用】如图②,在△ABC中,BC=a,BC边上的高AD=h,矩形PQMN的顶点P、N分别(用在边AB、AC上,顶点Q、M在边BC上,则矩形PQMN面积的最大值为.含a,h的代数式表示)【灵活应用】如图③,有一块“缺角矩形”ABCDE,AB=32,BC=40,AE=20,CD=16,小明从中剪出了一个面积最大的矩形(∠B为所剪出矩形的内角),求该矩形的面积.【实际应用】如图④,现有一块四边形的木板余料ABCD,经测量AB=50cm,BC=108cm,CD=60cm,且tanB=tanC=,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积.【考点】LO:四边形综合题.【分析】【探索发现】:由中位线知EF=BC、ED=AB、由=可得;【拓展应用】:由△APN∽△ABC知=,可得PN=a﹣PQ,设PQ=x,由S矩=PQ•PN═﹣(x﹣)2+,据此可得;形PQMN【灵活应用】:添加如图1辅助线,取BF中点I,FG的中点K,由矩形性质知AE=EH=20、CD=DH=16,分别证△AEF≌△HED、△CDG≌△HDE得AF=DH=16、CG=HE=20,从而判断出中位线IK的两端点在线段AB和DE上,利用【探索发现】结论解答即可;【实际应用】:延长BA、CD交于点E,过点E作EH⊥BC于点H,由tanB=tanC 知EB=EC、BH=CH=54,EH=BH=72,继而求得BE=CE=90,可判断中位线PQ的两端点在线段AB、CD上,利用【拓展应用】结论解答可得.【解答】解:【探索发现】∵EF、ED为△ABC中位线,∴ED∥AB,EF∥BC,EF=BC,ED=AB,又∠B=90°,∴四边形FEDB是矩形,则===,故答案为:;【拓展应用】∵PN∥BC,∴△APN∽△ABC,∴=,即=,∴PN=a﹣PQ,设PQ=x,=PQ•PN=x(a﹣x)=﹣x2+ax=﹣(x﹣)2+,则S矩形PQMN∴当PQ=时,S最大值为,矩形PQMN故答案为:;【灵活应用】如图1,延长BA、DE交于点F,延长BC、ED交于点G,延长AE、CD交于点H,取BF中点I,FG的中点K,由题意知四边形ABCH是矩形,∵AB=32,BC=40,AE=20,CD=16,∴EH=20、DH=16,∴AE=EH、CD=DH,在△AEF和△HED中,∵,∴△AEF≌△HED(ASA),∴AF=DH=16,同理△CDG≌△HDE,∴CG=HE=20,∴BI==24,∵BI=24<32,∴中位线IK的两端点在线段AB和DE上,过点K作KL⊥BC于点L,由【探索发现】知矩形的最大面积为×BG•BF=×(40+20)×(32+16)=720,答:该矩形的面积为720;【实际应用】如图2,延长BA、CD交于点E,过点E作EH⊥BC于点H,∵tanB=tanC=,∴∠B=∠C,∴EB=EC,∵BC=108cm,且EH⊥BC,∴BH=CH=BC=54cm,∵tanB==,∴EH=BH=×54=72cm,在Rt△BHE中,BE==90cm,∵AB=50cm,∴AE=40cm,∴BE的中点Q在线段AB上,∵CD=60cm,∴ED=30cm,∴CE 的中点P 在线段CD 上,∴中位线PQ 的两端点在线段AB 、CD 上,由【拓展应用】知,矩形PQMN 的最大面积为BC•EH=1944cm 2, 答:该矩形的面积为1944cm 2.8.问题呈现:如图1,点E 、F 、G 、H 分别在矩形ABCD 的边AB 、BC 、CD 、DA 上,AE=DG ,求证:2S 四边形EFGH =S 矩形ABCD .(S 表示面积)实验探究:某数学实验小组发现:若图1中AH ≠BF ,点G 在CD 上移动时,上述结论会发生变化,分别过点E 、G 作BC 边的平行线,再分别过点F 、H 作AB 边的平行线,四条平行线分别相交于点A 1、B 1、C 1、D 1,得到矩形A 1B 1C 1D 1. 如图2,当AH >BF 时,若将点G 向点C 靠近(DG >AE ),经过探索,发现:2S四边形EFGH=S 矩形ABCD +S.如图3,当AH >BF 时,若将点G 向点D 靠近(DG <AE ),请探索S 四边形EFGH 、S 矩形ABCD与S 之间的数量关系,并说明理由.迁移应用:请直接应用“实验探究”中发现的结论解答下列问题:(1)如图4,点E 、F 、G 、H 分别是面积为25的正方形ABCD 各边上的点,已知AH >BF ,AE >DG ,S 四边形EFGH =11,HF=,求EG 的长.(2)如图5,在矩形ABCD 中,AB=3,AD=5,点E 、H 分别在边AB 、AD 上,BE=1,DH=2,点F 、G 分别是边BC 、CD 上的动点,且FG=,连接EF 、HG ,请直接写出四边形EFGH 面积的最大值.【考点】LO:四边形综合题.=S矩形AEGD,同理S△EGF=S矩形BEGC,由此可【分析】问题呈现:只要证明S△HGE=S△HGE+S△EFG=S矩形BEGC;得S四边形EFGH=S矩形ABCD﹣.根据=,实验探究:结论:2S四边形EFGH=,=,=,即可证明;迁移应用:(1)利用探究的结论即可解决问题.(2)分两种情形探究即可解决问题.【解答】问题呈现:证明:如图1中,∵四边形ABCD是矩形,∴AB∥CD,∠A=90°,∵AE=DG,∴四边形AEGD是矩形,=S矩形AEGD,∴S△HGE=S矩形BEGC,同理S△EGF=S△HGE+S△EFG=S矩形BEGC.∴S四边形EFGH=S矩形ABCD﹣.实验探究:结论:2S四边形EFGH理由:∵=,=,=,=,=+++﹣,∴S四边形EFGH=2+2+2+2﹣2,∴2S四边形EFGH=S矩形ABCD﹣.∴2S四边形EFGH迁移应用:解:(1)如图4中,=S矩形ABCD﹣.∵2S四边形EFGH∴=25﹣2×11=3=A1B1•A1D1,∵正方形的面积为25,∴边长为5,∵A1D12=HF2﹣52=29﹣25=4,∴A1D1=2,A1B1=,∴EG2=A1B12+52=,∴EG=.=S矩形ABCD+.(2)∵2S四边形EFGH∴四边形A1B1C1D1面积最大时,矩形EFGH的面积最大.①如图5﹣1中,当G与C重合时,四边形A1B1C1D1面积最大时,矩形EFGH的面积最大.此时矩形A1B1C1D1面积=1•(﹣2)=②如图5﹣2中,当G与D重合时,四边形A1B1C1D1面积最大时,矩形EFGH的面积最大.此时矩形A1B1C1D1面积=2•1=2,∵2>﹣2,∴矩形EFGH的面积最大值=.9.如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A的坐标为(6,0),点B的坐标为(0,8),点C的坐标为(﹣2,4),点M,N分别为四边形OABC边上的动点,动点M从点O开始,以每秒1个单位长度的速度沿O→A→B路线向中点B匀速运动,动点N从O点开始,以每秒两个单位长度的速度沿O→C→B→A路线向终点A匀速运动,点M,N同时从O点出发,当其中一点到达终点后,另一点也随之停止运动,设动点运动的时间t秒(t>0),△OMN的面积为S.(1)填空:AB的长是10,BC的长是6;(2)当t=3时,求S的值;(3)当3<t<6时,设点N的纵坐标为y,求y与t的函数关系式;(4)若S=,请直接写出此时t的值.【考点】LO:四边形综合题.【分析】(1)利用勾股定理即可解决问题;(2)如图1中,作CE⊥x轴于E.连接CM.当t=3时,点N与C重合,OM=3,易求△OMN的面积;(3)如图2中,当3<t<6时,点N在线段BC上,BN=12﹣2t,作NG⊥OB于G,CF⊥OB于F.则F(0,4).由GN∥CF,推出=,即=,可得BG=8﹣t,由此即可解决问题;(4)分三种情形①当点N在边长上,点M在OA上时.②如图3中,当M、N 在线段AB上,相遇之前.作OE⊥AB于E,则OE==,列出方程即可解决问题.③同法当M、N在线段AB上,相遇之后,列出方程即可;【解答】解:(1)在Rt△AOB中,∵∠AOB=90°,OA=6,OB=8,∴AB===10.BC==6,故答案为10,6.学科网(2)如图1中,作CE⊥x轴于E.连接CM.∵C(﹣2,4),∴CE=4OE=2,在Rt△COE中,OC===6,当t=3时,点N与C重合,OM=3,=•OM•CE=×3×4=6,∴S△ONM即S=6.(3)如图2中,当3<t<6时,点N在线段BC上,BN=12﹣2t,作NG⊥OB于G,CF⊥OB于F.则F(0,4).∵OF=4,OB=8,∴BF=8﹣4=4,∵GN∥CF,∴=,即=,∴BG=8﹣t,∴y=OB﹣BG=8﹣(8﹣t)=t.(4)①当点N在边长上,点M在OA上时,•t•t=,解得t=(负根已经舍弃).②如图3中,当M、N在线段AB上,相遇之前.作OE ⊥AB 于E ,则OE==,由题意 [10﹣(2t ﹣12)﹣(t ﹣6)]• =,解得t=8,同法当M 、N 在线段AB 上,相遇之后. 由题意•[(2t ﹣12)+(t ﹣6)﹣10]• =,解得t=,综上所述,若S=,此时t 的值8s 或s 或s .10.已知:Rt △EFP 和矩形ABCD 如图①摆放(点P 与点B 重合),点F ,B (P ),C 在同一直线上,AB=EF=6cm ,BC=FP=8cm ,∠EFP=90°,如图②,△EFP 从图①的位置出发,沿BC 方向匀速运动,速度为1cm/s ,EP 与AB 交于点G ;同时,点Q 从点C 出发,沿CD 方向匀速运动,速度为1cm/s .过点Q 作QM ⊥BD ,垂足为H ,交AD 于点M ,连接AF ,FQ ,当点Q 停止运动时,△EFQ 也停止运动.设运动时间为t (s )(0<t <6),解答下列问题: (1)当t 为何值时,PQ ∥BD ?(2)设五边形AFPQM 的面积为y (cm 2),求y 与t 之间的函数关系式; (3)在运动过程中,是否存在某一时刻t ,使S 五边形AFPQM :S 矩形ABCD =9:8?若存在,求出t 的值;若不存在,请说明理由.(4)在运动过程中,是否存在某一时刻t ,使点M 在线段PG 的垂直平分线上?若存在,求出t 的值;若不存在,请说明理由.【考点】LO:四边形综合题.【分析】(1)如图1中,当PQ∥BD时,=,可得=,解方程即可;=S梯形AFCD﹣S△DMQ﹣S△PQC,由此计算即(2)如图2中,当0<t<6时,S五边形AFPQM可解决问题;(3)假设存在,根据题意列出方程即可解决问题;(4)如图3中,连接MG、MP,作MK⊥BC于K.利用勾股定理,根据MG=MP,列出方程即可解决问题;【解答】解:(1)如图1中,当PQ∥BD时,=,∴=,∴t=,∴t=s时,PQ∥BD.(2)如图2中,当0<t <6时,S 五边形AFPQM =S 梯形AFCD ﹣S △DMQ ﹣S △PQC=(8+8﹣t +8)•6﹣•(6﹣t )•(6﹣t )﹣•(8﹣t )•t =t 2﹣t +.(3)如图2中,假设存在,则有(t 2﹣t +.):48=9:8,解得t=2或18(舍弃),∴t=2s 时,S 五边形AFPQM :S 矩形ABCD =9:8.(4)存在.理由:如图3中,连接MG 、MP ,作MK ⊥BC 于K .易知:AG=6﹣t .DQ=6﹣t ,DM=KC=(6﹣t ),PK=8﹣t ﹣(6﹣t ),MK=CD=6, ∵点M 在PG 的垂直平分线上, ∴MG=MP ,∴AG 2+AM 2=PK 2+MK 2,∴(6﹣t )2+[8﹣(6﹣t )]2=62+[8﹣t ﹣(6﹣t )]2,解得t=或0(舍弃),∴t=s时,点M在线段PG的垂直平分线上11.如图,已知四边形ABCD为正方形,AB=2,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.(1)求证:矩形DEFG是正方形;(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由;(3)设AE=x,四边形DEFG的面积为S,求出S与x的函数关系式.【考点】LO:四边形综合题.【分析】(1)作出辅助线,得到EN=EM,然后判断∠DEN=∠FEM,得到△DEM ≌△FEM,则有DE=EF即可;(2)同(1)的方法判断出△ADE≌△CDG得到CG=AE,即:CE+CG=CE+AE=AC=4;(3)由正方形的性质得到∠DAE=45°,表示出AM=EM,再表示出DM,再用勾股定理求出DE2.【解答】解:(1)如图,作EM⊥BC,EN⊥CD∴∠MEN=90°,∵点E是正方形ABCD对角线上的点,∴EM=EN,∵∠DEF=90°,∴∠DEN=∠MEF,在△DEM和△FEM中,,∴△DEM≌△FEM,∴EF=DE,∵四边形DEFG是矩形,∴矩形DEFG是正方形;(2)CE+CG的值是定值,定值为4,∵正方形DEFG和正方形ABCD,∴DE=DG,AD=DC,∵∠CDG+∠CDE=∠ADE+∠CDE=90°,∴∠CDG=∠ADE,∴△ADE≌△CDG,∴AE=CG.∴CE+CG=CE+AE=AC=AB=×2=4,(3)如图,∵正方形ABCD中,AB=2,∴AC=4,过点E作EM⊥AD,∴∠DAE=45°,∵AE=x,∴AM=EM=x,在Rt△DME中,DM=AD﹣AM=2﹣x,EM=x,根据勾股定理得,DE2=DM2+EM2=(2﹣x)2+(x)2=x2﹣4x+8,∵四边形DEFG为正方形,=DE2=x2﹣4x+8.∴S=S正方形DEFG12.如图,在平行四边形ABCD中,AB=4,∠A=45°,∠ADB=90°,点E从点B 出发,以每秒1个单位的速度向终点D运动.点G在射线BD上,且EG=2BE(点G在E上方),以EG为对角线作正方形EFGH,设点E的运动时间为t(秒).(1)用含t的代数式表示DG的长;(2)求点H落在AD上时t的值;(3)设正方形EFGH与平行四边形ABCD的重叠部分图形的面积为S,求S与t 之间的函数关系式;(4)连结FH,直接写出运动过程中线段FH扫过的图形面积.【考点】LO:四边形综合题.【分析】(1)由于点E在射线BD上移动,所以点G有两种情况:①点G在线段BD上,②点G在BD的延长线上;(2)正方形EFGH与平行四边形ABCD的重叠部分图形共有三种情况,需要分别计算出点H在AD上、点G与点D重合、点E与D重合所对应的t值;(3)线段FH扫过的图形为△BHF,所以当点E与点D重合时,计算出△BHF的面积即可.【解答】解:(1)由题意知:△ABD是等腰直角三角形,∴AD=BD,由勾股定理可知:BD=4,当点G在线段BD上时,DG=4﹣3t,当点G在线段BD的延长线上时,DG=3t﹣4;(2)在等腰直角△DHE中,DE=4﹣t∴DH=DE=4﹣t,在等腰直角△DHG中,DG=3t﹣4,∴DH=DG=3t﹣4∴4﹣t=3t﹣4∴t=2;(3)当点G与点D重合时,此时,BE+EG=BD∴t+2t=4∴t=,当点H在AD上时,由(2)可知:t=2,当点E与D重合时,此时,BE=BD=4∴t=4,如图2,当0≤t≤时,此时,HE=EG=t,∴S=HE2=2t2,如图3,当时,此时,HE=GE=t,DE=4﹣t,DG=3t﹣4正方形EFGH的面积为:HE2=2t2,∴S=2t2﹣(3t﹣4)2﹣ [+t][t﹣] =t2+10t﹣4,如图4,当2<t≤4时,此时,DE=4﹣t,∴S=+(4﹣t)2=t2﹣6t+12,(4)当点E到达点D时,连接BH,BF,∴线段FH扫过的图形为△BHF,此时,GD=HF=8,BD=4,∴△BHF的面积为:×8×8=32.13.如图所示,在平面直角坐标系中xOy中,抛物线y=ax2﹣2ax﹣3a(a<0)与x轴交于A,B两点(点A在点B的左侧),经过点A的直线l:y=kx+b与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=4AC.(1)求A、B两点的坐标及抛物线的对称轴;(2)求直线l的函数表达式(其中k、b用含a的式子表示);(3)点E是直线l上方的抛物线上的动点,若△ACE的面积的最大值为,求a 的值;(4)设P是抛物线对称轴上的一点,点Q在抛物线上,以点A、D、P、Q为顶点的四边形能否成为矩形?若能,求出点P的坐标;若不能,请说明理由.学科网【考点】HF:二次函数综合题.【分析】(1)解方程即可得到结论;(2)根据直线l:y=kx+b过A(﹣1,0),得到直线l:y=kx+k,解方程得到点D 的横坐标为4,求得k=a,得到直线l的函数表达式为y=ax+a;(3)过E作EF∥y轴交直线l于F,设E(x,ax2﹣2ax﹣3a),得到F(x,ax+a),求出EF=ax2﹣3ax﹣4a,根据三角形的面积公式列方程即可得到结论;(4)令ax2﹣2ax﹣3a=ax+a,即ax2﹣3ax﹣4a=0,得到D(4,5a),设P(1,m),①若AD是矩形ADPQ的一条边,②若AD是矩形APDQ的对角线,列方程即可得到结论.【解答】解:(1)当y=0时,ax2﹣2ax﹣3a=0,解得:x1=﹣1,x2=3,∴A(﹣1,0),B(3,0),对称轴为直线x==1;(2)∵直线l:y=kx+b过A(﹣1,0),∴0=﹣k+b,即k=b,∴直线l:y=kx+k,∵抛物线与直线l交于点A,D,∴ax2﹣2ax﹣3a=kx+k,即ax2﹣(2a+k)x﹣3a﹣k=0,∵CD=4AC,∴点D的横坐标为4,∴﹣3﹣=﹣1×4,∴k=a,∴直线l的函数表达式为y=ax+a;(3)过E作EF∥y轴交直线l于F,设E(x,ax2﹣2ax﹣3a),则F(x,ax+a),EF=ax2﹣2ax﹣3a﹣ax﹣a=ax2﹣3ax﹣4a,=S△AFE﹣S△CEF=(ax2﹣3ax﹣4a)(x+1)﹣(ax2﹣3ax﹣4a)x=(ax2∴S△ACE﹣3ax﹣4a)=a(x﹣)2﹣a,∴△ACE的面积的最大值=﹣a,∵△ACE的面积的最大值为,∴﹣a=,解得a=﹣;(4)以点A、D、P、Q为顶点的四边形能成为矩形,令ax2﹣2ax﹣3a=ax+a,即ax2﹣3ax﹣4a=0,解得:x1=1,x2=4,∴D(4,5a),∵抛物线的对称轴为直线x=1,设P(1,m),①若AD是矩形ADPQ的一条边,则易得Q(﹣4,21a),m=21a+5a=26a,则P(1,26a),∵四边形ADPQ是矩形,∴∠ADP=90°,∴AD2+PD2=AP2,∴52+(5a)2+32+(26﹣5a)2=22+(26a)2,即a2=,∵a<0,∴a=﹣,∴P(1,﹣);②若AD是矩形APDQ的对角线,则易得Q(2,﹣3a),m=5a﹣(﹣3a)=8a,则P(1,8a),∵四边形APDQ是矩形,∴∠APD=90°,∴AP2+PD2=AD2,∴(﹣1﹣1)2+(8a)2+(1﹣4)+(8a﹣5a)2=52+(5a)2,即a2=,∵a<0,∴a=﹣,∴P(1,﹣4),综上所述,点A、D、P、Q为顶点的四边形能成为矩形,点P(1,﹣)或(1,﹣4).14.如图,直线y=﹣x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣x2+bx+c经过点A,B.(1)求点B的坐标和抛物线的解析式;(2)M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.①点M在线段OA上运动,若以B,P,N为顶点的三角形与△APM相似,求点M的坐标;②点M在x轴上自由运动,若三个点M,P,N中恰有一点是其它两点所连线段的中点(三点重合除外),则称M,P,N三点为“共谐点”.请直接写出使得M,P,N三点成为“共谐点”的m的值.【考点】HF:二次函数综合题.【分析】(1)把A点坐标代入直线解析式可求得c,则可求得B点坐标,由A、B的坐标,利用待定系数法可求得抛物线解析式;(2)①由M点坐标可表示P、N的坐标,从而可表示出MA、MP、PN、PB的长,分∠NBP=90°和∠BNP=90°两种情况,分别利用相似三角形的性质可得到关于m 的方程,可求得m的值;②用m可表示出M、P、N的坐标,由题意可知有P为线段MN的中点、M为线段PN的中点或N为线段PM的中点,可分别得到关于m的方程,可求得m的值.【解答】解:(1)∵y=﹣x+c与x轴交于点A(3,0),与y轴交于点B,∴0=﹣2+c,解得c=2,∴B(0,2),∵抛物线y=﹣x2+bx+c经过点A,B,∴,解得,∴抛物线解析式为y=﹣x2+x+2;(2)①由(1)可知直线解析式为y=﹣x+2,∵M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N,∴P(m,﹣m+2),N(m,﹣m2+m+2),∴PM=﹣m+2,AM=3﹣m,PN=﹣m2+m+2﹣(﹣m+2)=﹣m2+4m,∵△BPN和△APM相似,且∠BPN=∠APM,∴∠BNP=∠AMP=90°或∠NBP=∠AMP=90°,当∠BNP=90°时,则有BN⊥MN,∴BN=OM=m,∴=,即=,解得m=0(舍去)或m=2.5,∴M(2.5,0);当∠NBP=90°时,则有=,∵A(3,0),B(0,2),P(m,﹣m+2),∴BP==m,AP==(3﹣m),∴=,解得m=0(舍去)或m=,∴M(,0);综上可知当以B,P,N为顶点的三角形与△APM相似时,点M的坐标为(2.5,0)或(,0);②由①可知M(m,0),P(m,﹣m+2),N(m,﹣m2+m+2),∵M,P,N三点为“共谐点”,∴有P为线段MN的中点、M为线段PN的中点或N为线段PM的中点,当P为线段MN的中点时,则有2(﹣m+2)=﹣m2+m+2,解得m=3(三点重合,舍去)或m=;当M为线段PN的中点时,则有﹣m+2+(﹣m2+m+2)=0,解得m=3(舍去)或m=﹣1;当N为线段PM的中点时,则有﹣m+2=2(﹣m2+m+2),解得m=3(舍去)或m=﹣;综上可知当M,P,N三点成为“共谐点”时m的值为或﹣1或﹣.15.如图,抛物线y=ax2+bx﹣a﹣b(a<0,a、b为常数)与x轴交于A、C两点,与y轴交于B点,直线AB的函数关系式为y=x+.(1)求该抛物线的函数关系式与C点坐标;(2)已知点M(m,0)是线段OA上的一个动点,过点M作x轴的垂线l分别与直线AB和抛物线交于D、E两点,当m为何值时,△BDE恰好是以DE为底边的等腰三角形?(3)在(2)问条件下,当△BDE恰好是以DE为底边的等腰三角形时,动点M 相应位置记为点M′,将OM′绕原点O顺时针旋转得到ON(旋转角在0°到90°之间);i:探究:线段OB上是否存在定点P(P不与O、B重合),无论ON如何旋转,始终保持不变,若存在,试求出P点坐标;若不存在,请说明理由;ii:试求出此旋转过程中,(NA+NB)的最小值.【考点】HF:二次函数综合题.【分析】(1)根据已知条件得到B(0,),A(﹣6,0),解方程组得到抛物线的函数关系式为:y=﹣x2﹣x+,于是得到C(1,0);(2)由点M(m,0),过点M作x轴的垂线l分别与直线AB和抛物线交于D、E两点,得到D(m,m+),当DE为底时,作BG⊥DE于G,根据等腰三角形的性质得到EG=GD=ED,GM=OB=,列方程即可得到结论;(3)i:根据已知条件得到ON=OM′=4,OB=,由∠NOP=∠BON,特殊的当△NOP∽△BON时,根据相似三角形的性质得到=,于是得到结论;ii:根据题意得到N在以O为圆心,4为半径的半圆上,由(i)知,=,得到NP=NB,于是得到(NA+NB)的最小值=NA+NP,此时N,A,P三点共线,根据勾股定理得到结论.。
初中九年级数学专题复习教案:动态几何之定值问题探讨

【2013年中考攻略】专题3:动态几何之定值问题探讨 动态题是近年来中考的的一个热点问题,动态包括点动、线动和面动三大类,解这类题目要“以静制动”,即把动态问题,变为静态问题来解,而静态问题又是动态问题的特殊情况。
常见的题型包括最值问题、面积问题、和差问题、定值问题和存在性问题等。
前面我们已经对最值问题、面积问题、和差问题进行了探讨,本专题对定值问题进行探讨。
结合2011年和2012年全国各地中考的实例,我们从三方面进行动态几何之定值问题的探讨:(1)线段(和差)为定值问题;(2)面积(和差)为定值问题;(3)其它定值问题。
一、线段(和差)为定值问题:典型例题:例1:(2012黑龙江绥化8分)如图,点E 是矩形ABCD 的对角线BD 上的一点,且BE=BC ,AB=3,BC=4,点P 为直线EC 上的一点,且PQ ⊥BC 于点Q ,PR ⊥BD 于点R .(1)如图1,当点P 为线段EC 中点时,易证:PR+PQ= 512(不需证明). (2)如图2,当点P 为线段EC 上的任意一点(不与点E 、点C 重合)时,其它条件不变,则(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由.(3)如图3,当点P 为线段EC 延长线上的任意一点时,其它条件不变,则PR 与PQ 之间又具有怎样的数量关系?请直接写出你的猜想.【答案】解:(2)图2中结论PR +PQ=125仍成立。
证明如下: 连接BP ,过C 点作CK ⊥BD 于点K 。
∵四边形ABCD 为矩形,∴∠BCD=90°。
又∵CD=AB=3,BC=4,∴2 2 22BD CD BC 345=+=+=。
∵S △BCD =12BC•CD=12BD•CK ,∴3×4=5CK ,∴CK=125。
∵S△BCE=12BE•CK,S△BEP=12PR•BE,S△BCP=12PQ•BC,且S△BCE=S△BEP+S△BCP,∴12BE•CK=12PR•BE+12PQ•BC。
2020年中考数学动态几何题中的“定值型”问题赏析精品版

特殊的位置,探得定值,如果需要的话再考虑证明;或直接推理、计算,并在计算中消去变
量,从而得到定值 。以下以 2010 年中考题为例说明具体的求解策略
一、长度定值
例 1.( 2010 山东聊城)如图,点 P 是矩形 ABCD 的边 AD 的一个动点,矩形的两条边 AB、
BC 的长分别为 3 和 4,那么点 P 到矩形的两条对角线 AC 和 BD 的距离之和是 (
点 D 是线段 BC 上的动点(与端点 线 OAB 于点 E.
B、C 不重合),过点 D 作直线 y =- 1 x + b 交折 2
( 1)略 ( 2)当点 E 在线段 OA 上时,若矩形 OABC 关于直线 DE 的对称图形为四边形 O1A1B1C1,
试探究 O1A1B1C1 与矩形 OABC 的重叠部分的面积是否发生变化,若不变,求出该 重叠部分的面积;若改变,请说明理由 .
y
C
D
B
O
EA
x
思路点拨:(2)重叠部分是一个平行四边形, 由于这个平行四边形上下边上的高不变, 因此
决定重叠部分面积是否变化的因素就是看这个平行四边形落在
OA 边上的线段长度是否变
化.
解:( 1)略
( 2)如图 3,设 O1A1 与 CB 相交于点 M ,OA 与 C1 B1 相交于点 N,则矩形 O1A 1B 1C1 与矩 形 OABC 的重叠部分的面积即为四边形 DNEM 的面积。
解:( 1)如图 4, OE=5, r 2 ,CH =2
( 2)略 ( 3)如图 6,连接 AK ,AM,延长 AM ,
与圆交于点 G,连接 TG,则 GTA 90 2 4 90
3 4 , 2 3 90 由于 BKO 3 90 ,故, BKO 2 ; 而 BKO 1,故 1 2 在 AMK 和 NMA 中, 1 2 ; AMK NMA
动点与定值问题初三

动点与定值问题初三一、动点与定值问题解析动点与定值问题是一种常见的数学问题,主要考察学生的空间思维能力和代数运算能力。
这类问题通常涉及到几何图形中的动点和定点,通过给定的条件和关系,求出动点的轨迹或定值。
解决动点与定值问题的关键在于理解问题的几何背景和代数关系。
首先,要明确动点和定点的位置关系,以及它们之间的距离、角度等关系。
其次,要运用代数方法,将几何关系转化为代数方程或不等式,通过求解方程或不等式得到答案。
二、例题讲解例题1:在直角坐标系中,点A的坐标为(0,1),点B的坐标为(2,0),点C的坐标为(4,3)。
若点P是x轴上的一个动点,当△PAB的周长最小时,求点P的坐标。
分析:首先,我们可以通过平移的方式找到点P的位置。
由于点A和点B关于x轴对称,我们可以将点A关于x轴的对称点设为点P,这样△PAB的周长最小。
解:设点P的坐标为(x,0)。
由于点A和点B关于x轴对称,因此,我们有:AP = BP根据点到点的距离公式,我们可以得到:AP = √(x^2 + 1)BP = √((x-2)^2 + 1)因为AP=BP,所以:x^2 + 1 = (x-2)^2 + 1解这个方程,我们得到:x = 1所以,当△PAB的周长最小时,点P的坐标为(1,0)。
例题2:在矩形ABCD中,AB=2, BC=4, 点E是BC的中点。
将△ABE沿AE折起,使得AB=BE=2, 求二面角B-AE-D的平面角的余弦值。
分析:首先,我们需要找到二面角B-AE-D的平面角所在的三角形。
通过观察和计算,我们可以发现平面角所在的三角形是△BAE。
因此,我们需要求出△BAE 的三边长度,然后利用余弦定理求出余弦值。
解:由于AB=BE=2,AE=2√2(根据勾股定理)。
我们可以得到△BAE的三边长度分别为2、2√2、4。
根据余弦定理,我们可以得到:cos∠BAE = (AB^2 + AE^2 - BE^2) / (2 ×AB ×AE)= (4 + 8 - 4) / (2 ×2 ×2√2)= √2/2所以,二面角B-AE-D的平面角的余弦值为√2/2。
初中数学总复习《动态几何之存在性问题探讨》学生版 讲义

教师辅导讲义学员姓名:辅导课目:数学年级:九年级学科教师:汪老师授课日期及时段课题初中数学总复习——动态几何——存在性问题探讨学习目标教学内容初中数学总复习——动态几何——存在性问题探讨动态题是近年来中考的的一个热点问题,动态包括点动、线动和面动三大类,解这类题目要“以静制动”,即把动态问题,变为静态问题来解,而静态问题又是动态问题的特殊情况。
常见的题型包括最值问题、面积问题、和差问题、定值问题和存在性问题等。
结合2012年全国各地中考的实例,我们从七方面进行动态几何之存在性问题的探讨:(1)等腰(边)三角形存在问题;(2)直角三角形存在问题;(3)平行四边形存在问题;(4)矩形、菱形、正方形存在问题;(5)梯形存在问题;(6)全等、相似三角形存在问题;(7)其它存在问题。
【一、等腰(边)三角形存在问题:】例1、(2012广西崇左10分)如图所示,抛物线c=2(a≠0)的顶点坐标为点A(-2,3),y++axbx且抛物线c=2与y轴交于点B(0,2).+bxaxy+(1)求该抛物线的解析式;(2)是否在x轴上存在点P使△P AB为等腰三角形,若存在,请求出点P的坐标;若不存在,请说明理由(3)若点P是x轴上任意一点,则当PA-PB最大时,求点P的坐标.例2、(2012山东临沂13分)如图,点A在x轴上,OA=4,将线段OA绕点O顺时针旋转120°至OB的位置.(1)求点B的坐标;(2)求经过点A.O、B的抛物线的解析式;(3)在此抛物线的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,说明理由.例3、(2012福建龙岩14分)在平面直角坐标系xoy中,一块含60°角的三角板作如图摆放,斜边AB在x轴上,直角顶点C在y轴正半轴上,已知点A(-1,0).(1)请直接写出点B、C的坐标:B(,)、C(,);并求经过A、B、C三点的抛物线解析式;(2)现有与上述三角板完全一样的三角板DEF(其中∠EDF=90°,∠DEF=60°),把顶点E放在线段AB上(点E是不与A、B两点重合的动点),并使ED所在直线经过点C.此时,EF所在直线与(1)中的抛物线交于第一象限的点M.①设AE=x,当x为何值时,△OCE∽△OBC;②在①的条件下探究:抛物线的对称轴上是否存在点P使△PEM是等腰三角形,若存在,请求点P的坐标;若不存在,请说明理由.【二、直角三角形存在问题:】例1、(2012山东枣庄10分)在平面直角坐标系中,现将一块等腰直角三角板ABC 放在第二象限,斜靠在两坐标轴上,点C 为 (-1,0) .如图所示,B 点在抛物线y =12x 2+12x -2图象上,过点B 作BD ⊥x 轴,垂 足为D ,且B 点横坐标为-3.(1)求证:△BDC ≌△COA ; (2)求BC 所在直线的函数关系式;(3)抛物线的对称轴上是否存在点P ,使△ACP 是以AC 为直角边的直角三角形?若存在,求出所有点 P 的坐标;若不存在,请说明理由.例2、(2012内蒙古赤峰12分)如图,抛物线2y x bx 5=--与x 轴交于A .B 两点(点A 在点B 的左侧), 与y 轴交于点C ,点C 与点F 关于抛物线的对称轴对称,直线AF 交y 轴于点E ,|OC |:|OA |=5:1.(1)求抛物线的解析式; (2)求直线AF 的解析式;(3)在直线AF 上是否存在点P ,使△CFP 是直角三角形?若存在,求出P 点坐标;若不存在,说明理由.例3、(2012重庆市12分)已知:如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=2,BC=6,AB=3.E为BC边上一点,以BE为边作正方形BEFG,使正方形BEFG和梯形ABCD在BC的同侧.(1)当正方形的顶点F恰好落在对角线AC上时,求BE的长;(2)将(1)问中的正方形BEFG沿BC向右平移,记平移中的正方形BEFC为正方形B′EFG,当点E与点C重合时停止平移.设平移的距离为t,正方形B′EFG的边EF与AC交于点M,连接B′D,B′M,DM,是否存在这样的t,使△B′DM是直角三角形?若存在,求出t的值;若不存在,请说明理由;(3)在(2)问的平移过程中,设正方形B′EFG与△ADC重叠部分的面积为S,请直接写出S与t之间的函数关系式以及自变量t的取值范围.【三、平行四边形存在问题:】例1、(2012山西省14分)综合与实践:如图,在平面直角坐标系中,抛物线y=﹣x2+2x+3与x轴交于A.B 两点,与y轴交于点C,点D是该抛物线的顶点.(1)求直线AC的解析式及B.D两点的坐标;(2)点P是x轴上一个动点,过P作直线l∥AC交抛物线于点Q,试探究:随着P点的运动,在抛物线上是否存在点Q,使以点A.P、Q、C为顶点的四边形是平行四边形?若存在,请直接写出符合条件的点Q的坐标;若不存在,请说明理由.(3)请在直线AC上找一点M,使△BDM的周长最小,求出M点的坐标.例2、(2012黑龙江黑河、齐齐哈尔、大兴安岭、鸡西10分)如图,在平面直角坐标系中,已知Rt△AOB的两条直角边0A、08分别在y轴和x轴上,并且OA、OB的长分别是方程x2—7x+12=0的两根(OA<0B),动点P从点A开始在线段AO上以每秒l个单位长度的速度向点O运动;同时,动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动,设点P、Q运动的时间为t秒.(1) 求A、B两点的坐标。
专题19:动态几何之定值问题探讨.docx

动态题是近年來中考的的一个热点问题,动态包括点动、线动和面动三大类,解这类题目要“以静制动”,即把动态问题,变为静态问题來解,而静态问题又是动态问题的特殊情况。
常见的题型包括最值问题、而积问题、和差问题、定值问题和存在性问题等。
前面我们已经对最值问题、面积问题、和差问题进 行了探讨,本专题对定值问题进行探讨。
结合2011年和2012年全国各地中考的实例,我们从三方而进行动态几何之定值问题的探讨:(1)线段(和差)为定值问题;(2)面积(和差)为定值问题;(3)具它定值问题。
一、线段(和差)为定值问题:典型例题:例1: (2012黑龙江绥化8分)如图,点E 是矩形ABCD 的对角线BD ±的一点,且BE=BC, AB=3, BC=4, 点P 为直线EC±的一点,且PQ 丄BC 于点Q, PR 丄BD 于点R.12(1) ill 图1,当点P 为线段EC 中点时,易证:PR+PQ 二一(不需证明). 5(2) 如图2,当点P 为线段EC±的任意一点(不与点E 、点C 重合)时,其它条件不变,则(I )中的 结论是否仍然成立?若成立,请给予证明;若不成立,请说明理山.(3)如图3,当点P 为线段EC 延长线上的任意一点时,其它条件不变,则PR 与PQ 之间又具有怎样的【2013年中考攻略】 专题19:动态几何之定值问题探讨【答案】解(2)图2中结论PR+PQ=y仍成立。
证明如下:连接BP,过(:点作CK丄BD于点K。
V四边形ABCD为矩形,・•・ZBCD=90°。
又•・• CD=AB=3, BC=4, BD = VcD2+BC2 = ^32 +42 = 5。
I S ABCD= - BC・CD= - BD・CK, Z. 3x4=5CK, Z. CK=—。
2 2 5边),与y 轴交于点C.(1) 写出二次函数L|的开口方向、对称轴和顶点坐标;(2) 研究二次函数 L2: y=kx 2 - 4kx+3k (k#)).① 写出二次函数L 2与二次函数Li 有关图彖的两条相同的性质;② 是否存在实数k,使AABP 为等边三角形?如果存在,请求出k 的值;如不存在,请说明理山;③ 若直线y=8k 与抛物线L2交于E 、F 两点,问线段EF 的长度是否发生变化?如果不会,请求出EF 的长 度;如果会,请说明理山.【答案】解(1) J 抛物线y = X 2-4X + 3 = (X -2)2-1,V S ABCE = — BE ・CK, S ABH >= — PR ・BE, S ABCP = — PQ ・BC, JIL S ABCE 二S/\BEP +S Z \BCP , 2 2 2・•・-BE ・CK= - PR ・BE+ - PQ ・BC 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【2013年中考攻略】专题3:动态几何之定值问题探讨 动态题是近年来中考的的一个热点问题,动态包括点动、线动和面动三大类,解这类题目要“以静制动”,即把动态问题,变为静态问题来解,而静态问题又是动态问题的特殊情况。
常见的题型包括最值问题、面积问题、和差问题、定值问题和存在性问题等。
前面我们已经对最值问题、面积问题、和差问题进行了探讨,本专题对定值问题进行探讨。
结合2011年和2012年全国各地中考的实例,我们从三方面进行动态几何之定值问题的探讨:(1)线段(和差)为定值问题;(2)面积(和差)为定值问题;(3)其它定值问题。
一、线段(和差)为定值问题:典型例题:例1:(2012黑龙江绥化8分)如图,点E 是矩形ABCD 的对角线BD 上的一点,且BE=BC ,AB=3,BC=4,点P 为直线EC 上的一点,且PQ ⊥BC 于点Q ,PR ⊥BD 于点R .(1)如图1,当点P 为线段EC 中点时,易证:PR+PQ= 512(不需证明). (2)如图2,当点P 为线段EC 上的任意一点(不与点E 、点C 重合)时,其它条件不变,则(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由.(3)如图3,当点P 为线段EC 延长线上的任意一点时,其它条件不变,则PR 与PQ 之间又具有怎样的数量关系?请直接写出你的猜想.【答案】解:(2)图2中结论PR +PQ=125仍成立。
证明如下: 连接BP ,过C 点作CK ⊥BD 于点K 。
∵四边形ABCD 为矩形,∴∠BCD=90°。
又∵CD=AB=3,BC=4,∴BD 5===。
∵S △BCD =12BC•CD=12BD•CK ,∴3×4=5CK ,∴CK=125。
∵S△BCE=12BE•CK,S△BEP=12PR•BE,S△BCP=12PQ•BC,且S△BCE=S△BEP+S△BCP,∴12BE•CK=12PR•BE+12PQ•BC。
又∵BE=BC,∴12CK=12PR+12PQ。
∴CK=PR+PQ。
又∵CK=125,∴PR+PQ=125。
(3)图3中的结论是PR-PQ=125.【考点】矩形的性质,三角形的面积,勾股定理。
【分析】(2)连接BP,过C点作CK⊥BD于点K.根据矩形的性质及勾股定理求出BD的长,根据三角形面积相等可求出CK的长,最后通过等量代换即可证明。
(3)图3中的结论是PR-PQ=125 。
连接BP,S△BPE-S△BCP=S△BEC,S△BEC 是固定值,BE=BC 为两个底,PR,PQ 分别为高,从而PR-PQ=125。
例2:(2012江西省10分)如图,已知二次函数L1:y=x2﹣4x+3与x轴交于A.B两点(点A在点B左边),与y轴交于点C.(1)写出二次函数L1的开口方向、对称轴和顶点坐标;(2)研究二次函数L2:y=kx2﹣4kx+3k(k≠0).①写出二次函数L2与二次函数L1有关图象的两条相同的性质;②是否存在实数k,使△ABP为等边三角形?如果存在,请求出k的值;如不存在,请说明理由;③若直线y=8k与抛物线L2交于E、F两点,问线段EF的长度是否发生变化?如果不会,请求出EF的长度;如果会,请说明理由.【答案】解:(1)∵抛物线()22y x 4x 3x 21=-+=--,∴二次函数L 1的开口向上,对称轴是直线x=2,顶点坐标(2,﹣1)。
(2)①二次函数L 2与L 1有关图象的两条相同的性质:对称轴为x=2;都经过A (1,0),B (3,0)两点。
②存在实数k ,使△ABP 为等边三角形.∵()22y kx 4kx 3k k x 2k =-+=--,∴顶点P (2,-k ).∵A (1,0),B (3,0),∴AB=2要使△ABP 为等边三角形,必满足|-k|=,∴。
③线段EF 的长度不会发生变化。
∵直线y=8k 与抛物线L 2交于E 、F 两点,∴kx 2﹣4kx+3k=8k ,∵k ≠0,∴x 2﹣4x+3=8。
解得:x 1=﹣1,x 2=5。
∴EF=x 2﹣x 1=6。
∴线段EF 的长度不会发生变化。
【考点】二次函数综合题,二次函数的性质,等边三角形的性质,解直角三角形。
【分析】(1)抛物线y=ax 2+bx+c 中:a 的值决定了抛物线的开口方向,a >0时,抛物线的开口向上;a <0时,抛物线的开口向下。
抛物线的对称轴方程和顶点坐标,可化为顶点式或用公式求解。
(2)①新函数是由原函数的各项系数同时乘以k 所得,因此从二次函数的图象与解析式的系数的关系入手进行分析。
②当△ABP 为等边三角形时,P 点必为函数的顶点,首先表示出P 点纵坐标,倍,由此确定k 的值。
③联立直线和抛物线L2的解析式,先求出点E、F的坐标,从而可表示出EF的长,若该长度为定值,则线段EF的长不会发生变化。
例3:(2012山东德州12分)如图所示,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.(1)求证:∠APB=∠BPH;(2)当点P在边AD上移动时,△PDH的周长是否发生变化?并证明你的结论;(3)设AP为x,四边形EFGP的面积为S,求出S与x的函数关系式,试问S是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.【答案】解:(1)如图1,∵PE=BE,∴∠EBP=∠EPB.又∵∠EPH=∠EBC=90°,∴∠EPH﹣∠EPB=∠EBC﹣∠EBP,即∠PBC=∠BPH。
又∵AD∥BC,∴∠APB=∠PBC。
∴∠APB=∠BPH。
(2)△PHD的周长不变为定值8。
证明如下:如图2,过B作BQ⊥PH,垂足为Q。
由(1)知∠APB=∠BPH,又∵∠A=∠BQP=90°,BP=BP,∴△ABP≌△QBP(AAS)。
∴AP=QP,AB=BQ。
又∵AB=BC,∴BC=BQ。
又∵∠C=∠BQH=90°,BH=BH,∴△BCH≌△BQH(HL)。
∴CH=QH。
∴△PHD的周长为:PD+DH+PH=AP+PD+DH+HC=AD+CD=8。
(3)如图3,过F作FM⊥AB,垂足为M,则FM=BC=AB。
又∵EF 为折痕,∴EF ⊥BP 。
∴∠EFM+∠MEF=∠ABP+∠BEF=90°。
∴∠EFM=∠ABP 。
又∵∠A=∠EMF=90°,AB=ME ,∴△EFM ≌△BPA (ASA )。
∴EM=AP=x .∴在Rt △APE 中,(4﹣BE )2+x 2=BE 2,即2x BE 2+8=。
∴2x CF BE EM 2+x 8=-=-。
又∵四边形PEFG 与四边形BEFC 全等, ∴()()22211x 11S BE CF BC=4+x 4=x 2x+8=x 2+622422⎛⎫=⋅+⋅⋅-⋅-- ⎪ ⎪⎝⎭。
∵1042<<,∴当x=2时,S 有最小值6。
【考点】翻折变换(折叠问题),正方形的性质,折叠的性质,全等三角形的判定和性质,勾股定理,二次函数的最值。
【分析】(1)根据翻折变换的性质得出∠PBC=∠BPH ,进而利用平行线的性质得出∠APB=∠PBC 即可得出答案。
(2)先由AAS 证明△ABP ≌△QBP ,从而由HL 得出△BCH ≌△BQH ,即可得CH=QH 。
因此,△PDH 的周长=PD+DH+PH=AP+PD+DH+HC=AD+CD=8为定值。
(3)利用已知得出△EFM ≌△BPA ,从而利用在Rt △APE 中,(4﹣BE )2+x 2=BE 2,利用二次函数的最值求出即可。
例4:(2012福建泉州12分)已知:A 、B 、C 不在同一直线上.(1)若点A 、B 、C 均在半径为R 的⊙O 上,i )如图一,当∠A=45°时,R=1,求∠BOC 的度数和BC 的长度;ii )如图二,当∠A 为锐角时,求证sin ∠A= BC 2R; (2).若定长线段....BC 的两个端点分别在∠MAN 的两边AM 、AN (B 、C 均与点A 不重合)滑动,如图三,当∠MAN=60°,BC=2时,分别作BP ⊥AM ,CP ⊥AN ,交点为点P ,试探索:在整个滑动过程中,P 、A 两点的距离是否保持不变?请说明理由.【答案】解:(1)i )∵∠A=45°,∴∠BOC=90°(同弧所对的圆周角等于其所对的圆心角的一半)。
又∵R=1,∴由勾股定理可知ii )证明:连接BO 并延长,交圆于点E ,连接EC 。
可知EC ⊥BC (直径所对的圆周角为90°),且∠E=∠A (同弧所对的圆周角相等)。
故sin ∠A=sin ∠A=BC BC BE 2R=。
(2)保持不变。
理由如下:如图,连接AP ,取AP 的中点K ,连接BK 、CK ,在Rt △APC 中,CK=12AP=AK=PK 。
同理得:BK=AK=PK 。
∴CK=BK=AK=PK 。
∴点A 、B 、P 、C 都在⊙K 上。
∴由(1)ii )sin ∠A=BC 2R 可知sin60°=BC AP 。
∴AP=BC sin60=︒(为定值)。
【考点】三角形的外接圆与外心,圆周角定理,勾股定理,锐角三角函数定义,特殊角的三角函数值,直角三角形中线性质。
【分析】(1)i )根据圆周角定理得出∠BOC=2∠A=90°,再利用勾股定理得出BC 的长;ii )作直径CE ,则∠E=∠A ,CE=2R ,利用sin ∠A=sin ∠E=BC BC BE 2R = ,得出即可。
(2)首先证明点A 、B 、P 、C 都在⊙K 上,再利用sin ∠A=BC 2R ,得出AP=BC sin60︒ (定值)即可。
例5:(2012山东潍坊11分)如图,已知抛物线与坐标轴分别交于A(-2,O)、B(2,0)、C(0,-l)三点,过坐标原点O 的直线y=kx 与抛物线交于M 、N 两点.分别过点C 、D(0,-2)作平行于x 轴的直线1l 、2l .(1)求抛物线对应二次函数的解析式;(2)求证以ON 为直径的圆与直线1l 相切;(3)求线段MN 的长(用k 表示),并证明M 、N 两点到直线2l 的距离之和等于线段MN 的长.【答案】解:(1)设抛物线对应二次函数的解析式为y=ax 2+bx +c ,则4a 2b+c=04a+2b+c=0c=1-⎧⎪⎨⎪-⎩ 解得1a=4b=0c=1⎧⎪⎪⎨⎪-⎪⎩。
∴抛物线对应二次函数的解析式 所以21y=x 14-。
(2)设M(x 1,y 1),N(x 2,y 2),因为点M 、N 在抛物线上,∴22112211y =x 1y =x 144--,,∴x 22=4(y 2+1)。
