江苏省南京市六校联合体2017-2018学年高二下学期期末考试数学(理)试卷
江苏省南京市金陵中学2017-2018学年高二下学期期末考试数学试题含答案

金陵中学2017-2018学年度第二学期期末考试高二数学试卷数学I一、填空题:本大题共14小题,每小题5分,共70分.请把答案填在答题卡相应位置上.1.设集合,,则 .2.已知复数,其中是虚数单位,则的值是 .3.某校共有教师200人,男学生1200人,女学生1000人.现用分层抽样的方法从所有师生中抽取一个容量为的样本,已知从女学生中抽取的人数为50人,那么的值为 .4.如图是一算法的伪代码,则输出值为 .5.如图,在长方体中, ,,则三棱锥的体积为 .6.在平面直角坐标系中,若双曲线的一条渐近线方程为,则实数的值为 .7.设各项均为正数的等比数列的前项和为,若,则数列的通项公式为 .8.将一颗均匀的骰子连续抛掷2次,向上的点数依次记为,则“”的概率是 .9.若实数满足条件则的取值范围为 .10.在平面直角坐标系中,已知,,两曲线与在区间上交点为.若两曲线在点处的切线与轴分别相交于两点,则线段的为 .11.如图,在平面四边形中, 是对角线的中点,且,. 若,则的值为 .12.若对满足的任意正实数,都有,则实数的取值范围为 .13.在平面直角坐标系中,记椭圆的左右焦点分别为,若该椭圆上恰好有6个不同的点,使得为等腰三角形,则该椭圆的离心率的取值范围是 .14.对于任意的实数,记为中的最小值.设函数,,函数,若在恰有一个零点,则实数的取值范围是 .二、解答题:本大题共6小题,共计90分.解答时应写出文字说明、证明过程.15.在平面直角坐标系中,设向量,.(1)当时,求的值;(2)若,且.求的值.16.如图,在四棱锥中,底面是矩形,平面平面,,点在棱上, ,点是棱的中点,求证:(1) 平面;(2) 平面.17.如图,在一个水平面内,河流的两岸平行,河宽1(单位:千米)村庄和供电站恰位于一个边长为2(单位:千米)的等边三角形的三个顶点处,且位于河流的两岸,村庄侧的河岸所在直线恰经过的中点.现欲在河岸上之间取一点,分别修建电缆和,.设,记电缆总长度为 (单位:千米).(1)求的解析式;(2)当为多大时,电缆的总长度最小,并求出最小值.18.如图,在平面直角坐标系中,已知椭圆的离心率为,且过点.设为椭圆的右焦点, 为椭圆上关于原点对称的两点,连结并延长,分别交椭圆于两点.(1)求椭圆的标准方程;(2)设直线的斜率分别为,是否存在实数,使得?若存在,求出实数的值;若不存在,请说明理由.19.设数列的前项的和为,且满足,对,都有 (其中常数),数列满足.(1)求证:数列是等比数列;(2)若,求的值;(3)若,使得,记,求数列的前项的和.20.在平面直角坐标系中,已知函数的图像与直线相切,其中是自然对数的底数.(1)求实数的值;(2)设函数在区间内有两个极值点.①求实数的取值范围;②设函数的极大值和极小值的差为,求实数的取值范围 .高二数学Ⅱ(附加题)21.已知矩阵,.(1)求;(2)在平面直角坐标系中,求直线在对应的变换作用下所得直线的方程.22.在直角坐标系中,以原点为极点,以轴的非负半轴为极轴,取与直角坐标系相同的长度单位,建立极坐标系.设曲线的参数方程为,(为参数, ),直线的极坐标方程为.(1)写出曲线的普通方程和直线的直角坐标方程;(2)求曲线上的点到直线的最大距离.23.假定某篮球运动员每次投篮命中率均为.现有3次投篮机会,并规定连续两次投篮均不中即终止投篮,已知该运动员不放弃任何一次投篮机会,且恰好用完3次投篮机会的概率是.(1)求的值;(2)设该运动员投篮命中次数为,求的概率分布及数学期望.24.如图,已知正四棱柱的底面边长为2,侧棱长为3, ,垂足为,交于点.(1)求证: ⊥平面;(2)记直线与平面所成的角,求的值.试卷答案一、填空题.1. 2. 3. 4.5. 6. 7. 8.9. 10. 11. 12.13. 14. 或二、解答题.15. 解(1)当时,,,所以.(2),若.则,即.因为,所以,所以,所以.16.证明(1)因为在中, ,所以点是棱的中点.又点是棱的中点,所以是的中位线,所以.因为底面是矩形,以,所以.又平面, 平面,所以平面.(2)因为平面平面, 平面,平面平面,所以平面.又平面,所以.因为,, ,平面,平面, 所以平面.17.解(1)易得垂直平分,则,,,于是,因为在之间,所以,故,.(2) ,,令,得,故当,,递减,当,,递增,所以,当时, .答:当时, 最小值为.18.解(1)设椭圆的方程为,,由题意知解得所以椭圆的方程为.(2)设,则,,又,所以直线的方程为.由消去,得.因为是该方程的一个解,所以点的横坐标. 又点在直线上,所以,从而点的坐标为同理,点的坐标为,所以,即存在,使得.19.(1)证明:因为,都有,所以两式相减得,即,当时,所以,又因为,所以,所以数列是常数列, ,所以是以2为首项, 为公比的等比数列.(2)由(1)得.所以.(3)由(1)得.. 因为,所以当时, ,当时,.因此数列的前项的和.20. (1)设直线与函数相切于点,函数在点处的切线方程为: ,,把代入上式得.所以,实数的值为.(2)①由(1)知,设函数在区间内有两个极值点,令,则,设,因为,故只需,所以, .②因为,所以,由,得,且..设,,令,,(在上单调递减,从而,所以,实数的取值范围是.高二数学Ⅱ(附加题)21. 解(1)由题知,所以,根据逆矩阵公式,得.(2)设由上的任意一点在作用下得到上对应点.由,即解得,因为,所以,即.即直线的方程为.22.解(1)由得,由,得,即.(2)在上任取一点,则点到直线的距离为,,当,即时,.23. 解(1)设事件:“恰用完3次投篮机会”,则其对立事件:“前两次投篮均不中”, 依题意, ,解得.(2)依题意, 的所有可能值为,且,,,故.的概率分布列为:数学期望.24.解(1)如图,以为坐标原点,分别以直线所在直线为轴, 轴, 轴,建立空间直角坐标系,易得,设,则,因为,所以,解得,即,又,,所以,所以, 且,所以,又,所以平面.(2) ,,,设平面的一个法向量,则即令,则,即,.。
江苏省南京市六校联合体2017-2018学年高二下学期期末考试数学(理)含答案

10.若 (2 x 2 ) 6 a0 a1x 2 a2 x4
a5x10 a6 x12 ,
则 a0 a2 a4 a6 = ▲ . 11.已知 m∈ R,设命题 P: x R, mx2 mx 1 0 ;
命题 Q:函数 f ( x) x3 3x2 m 1 只有一个零点 . 则使“ P Q”为假命题的实数 m 的取值范围为 ▲ .
三年级抽 10 人 .已知该校高二年级共有学生 300 人,则该校学生总数为
▲.
7.函数 y f ( x) 在点 P (1,m) 处切线方程为 x y 6 0 ,则 f (1) f (1) = ▲ .
8.若 (2 x
1 x2
)n
的展开式中所有二项式系数和为
64,则展开式中的常数项是
▲.
9.根据如图所示的伪代码可知 ,输出的结果为 ▲ .
1 ) 2018 7 .
1000
18.(本小题满分 16 分)
某抛掷骰子游戏中,规定游戏者可以有三次机会抛掷一颗骰子,若游戏者在前两次抛掷中至
少成功一次才可以进行第三次抛掷,其中抛掷骰子不成功得
0 分,第 1 次成功得 3 分,第 2
次成功得 3 分,第 3 次成功得 4 分 .游戏规则如下:抛掷 1 枚骰子,第 1 次抛掷骰子向上的点
12.有编号分别为 1, 2, 3, 4, 5 的 5 个黑色小球和编号分别为
i←1 S← 0 While i< 8
S←3i+S i← i+ 2 End While Print S
第 9题 1, 2, 3, 4, 5 的 5 个白色
小球,若选取的 4 个小球中既有 1 号球又有白色小球,则有
▲ 种不同的选法 .
q p 的最大值为 ▲ .
江苏省南京市六校联合体2017-2018学年高二下学期期末考试英语含答案

南京市六校联合体高二期末试卷英语第一部分听力 (共两节,满分20分)第一节 (共5小题;每小题1分,满分5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. Who is the man looing for?A. Tami.B. Dr. Mawell.C. Alison Simpson.2. What will the woman probably do?A. Call the airline soon.B. Stay at home for a while.C. Leave for the airport before lunch.3. What does the man thin of his current boo?A. It’s eciting.B. It’s relain g.C. It’s long.4. When does the man hope to see the woman?A. This afternoon.B. Tomorrow night.C. Tomorrow afternoon.5. What does the man mean?A. He didn’t put in any sugar.B. He added some natural flavors.C. He also thins the coffee tastes strange.第二节 (共15小题;每小题1分,满分15分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
每段对话或独白读两遍。
听第6段材料,回答第6、7题。
江苏省南京市六校联合体2017-2018学年高二下学期期末考试英语含答案

南京市六校联合体高二期末试卷英语第一部分听力 (共两节,满分20分)第一节 (共5小题;每小题1分,满分5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. Who is the man looing for?A. Tami.B. Dr. Mawell.C. Alison Simpson.2. What will the woman probably do?A. Call the airline soon.B. Stay at home for a while.C. Leave for the airport before lunch.3. What does the man thin of his current boo?A. It’s eciting.B. It’s relaing.C. It’s long.4. When does the man hope to see the woman?A. This afternoon.B. Tomorrow night.C. Tomorrow afternoon.5. What does the man mean?A. He didn’t put in any sugar.B. He added some natural flavors.C. He also thins the coffee tastes strange.第二节 (共15小题;每小题1分,满分15分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
每段对话或独白读两遍。
听第6段材料,回答第6、7题。
2017-2018学年江苏省南京市金陵中学高二第二学期期末考试数学试题-解析版
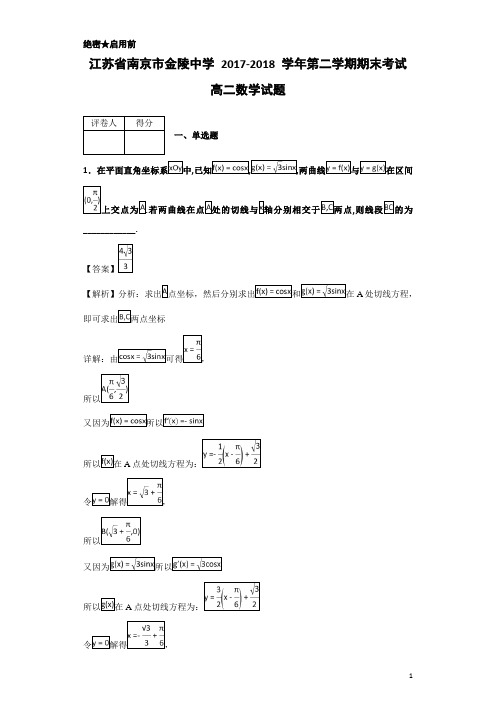
绝密★启用前江苏省南京市金陵中学2017-2018 学年第二学期期末考试高二数学试题一、单选题1,,____________.【解析】分析:求出A处切线方程,又因为A又因为A所以线段BC的长度为点睛:熟练记忆导函数公式是解导数题的前提条件,导数的几何意义是在曲线上某一点处的导数就等于该点处切线斜率,是解决曲线切线的关键,要灵活掌握.第II卷(非选择题)请点击修改第II卷的文字说明二、填空题2,【答案】{2,4,6,8}详解:A集合和B集合“加”起来的元素,重复的元点睛:在求集合并集时要注意集合的互异性.3,____________.【答案】5【解析】分析:先将复数z右边化为.4.某校共有教师200人,男学生1200人,女学生1000人.现用分层抽样的方法从所有师,已知从女学生中抽取的人数为50人,____________.【答案】120【解析】分析:根据分层抽样的原则先算出总体中女学生的比例,再根据抽取到女学生的人数计算样本容量n详解:因为共有教师200人,男学生1200人,女学生1000人女学生中抽取的人数为50人所以n=120点睛:分层抽样的实质为按比例抽,所以在计算时要算出各层所占比例再乘以样本容量即为该层所抽取的个数.5.如图是一算法的伪代码,则输出值为____________.【答案】4【解析】分析:按照循环体执行,直到跳出循环详解:第一次循环后:S=7,n=6;第二次循环后:S=13,n=5;第三次循环后:S=18,n=4;所以输出值为4点睛:程序题目在分析的时候一定要注意结束条件,逐次执行程序即可.6.如图,,为____________.【答案】3,=33点睛:在求解三棱锥体积问题时,如果所求椎体高不好确定时,往往要通过等体积转化,找到合适的高所对应的椎体进行计算,体现了数学中的转化与化归思想,要深刻体会.7,____________.x的值为x轴上,又因为该双曲线一条渐近线方程为所以的值为点睛:双曲线渐近线方程:当焦点在x y轴上时为8.,若则数列的通【解析】分析:根据基本量直接计算点睛:在等比数列问题中的未知量为首项和公比,求解这两个未知量需要两个方程,所以如果已知条件可以构造出来两个方程,则一定可以解出首项和公比,进而可以解决其他问题,因此基本量求解是这类问题的基本解法.9.将一颗均匀的骰子连续抛掷2次,则的概率是____________.【解析】分析:骰子连续抛掷2次共有366种详解:一颗均匀的骰子连续抛掷2次,(3,1),(4,1),(5,1),(6,1),(5,2),(6,2)6种点睛:古典概型概率要准确求出总的事件个数和基本事件个数,然后根据概率公式.10____________.A点处取得最小值,在C点处取得最大值所以的取值范围为点睛:点睛:线性规划要能够准确画出可行域,尤其是判断每一个不等式代表的是直线的左侧还是右侧时不能出错,常用带点方法判断比较准确。
【配套K12】江苏省南京市六校联合体2017-2018学年高二数学下学期期末考试试题 理

南京市六校联合体高二期末试卷 数学(理科) 2018.6参考公式:方差2211()n i i s x x n ==-∑一、填空题:本大题共14小题,每小题5分,共70分.请把答案直接填写在答题卡相应位置上......... 1.设i 为虚数单位,复数2iz i+=,则z 的模||z = ▲ . 2.一根木棍长为5米,若将其任意锯为两段,则锯成的两段木棍的长度都大于2米的概率为 ▲ . 3.命题“若0a =,则复数(,)z a bi a b R =+∈为纯虚数”的逆命题...是 ▲ 命题.(填“真”或“假”)4.已知一组数据为2,3,4,5,6,则这组数据的方差为 ▲ .5.将一颗骰子抛掷两次,用m 表示向上点数之和,则10m ≥的概率为 ▲ .6.用分层抽样的方法从某校学生中抽取1个容量为45的样本,其中高一年级抽20人,高三年级抽10人.已知该校高二年级共有学生300人,则该校学生总数为 ▲ . 7.函数()y f x =在点(1,)P m 处切线方程为60x y +-=,则(1)(1)f f '+= ▲ . 8.若21(2)nx x-的展开式中所有二项式系数和为64,则展开式中的常数项是 ▲ . 9.根据如图所示的伪代码可知,输出的结果为 ▲ . 10.若2624101201256(2)x a a x a x a x a x +=+++++,则0246a a a a +++= ▲ .11.已知m ∈R,设命题P :2,10x R mx mx ∀∈++>; 命题Q :函数32()31f x x x m =-+-只有一个零点. 则使“P ∨Q ”为假命题的实数m 的取值范围为 ▲ .12.有编号分别为1,2,3,4,5的5个黑色小球和编号分别为1,2,3,4,5的5个白色小球,若选取的4个小球中既有1号球又有白色小球,则有 ▲ 种不同的选法.ABDO(第16题)E B 1A 1CC 1D 1 13.观察下列等式:请你归纳出一般性结论 ▲ .14.乒乓球比赛,三局二胜制.任一局甲胜的概率是(01)p p <<,甲赢得比赛的概率是q ,则q p -的最大值为 ▲ .二、解答题:本大题共6小题,共计90分。
江苏省南京市金陵中学2017-2018学年高二下学期期末考试数学试题含答案

金陵中学2017-2018学年度第二学期期末考试高二数学试卷数学I一、填空题:本大题共14小题,每小题5分,共70分.请把答案填在答题卡相应位置上. 1.设集合{2,4}A =,{2,6,8}B =,则AB = .2.已知复数2(12i)z =-,其中i 是虚数单位,则||z 的值是 .3.某校共有教师200人,男学生1200人,女学生1000人.现用分层抽样的方法从所有师生中抽取一个容量为n 的样本,已知从女学生中抽取的人数为50人,那么n 的值为 .4.如图是一算法的伪代码,则输出值为 .5.如图,在长方体1111ABCD A B C D -中, 3cm AB AD ==,12cm AA =,则三棱锥111A AB D -的体积为 .6.在平面直角坐标系xOy 中,若双曲线2221(0)x y m m-=>的一条渐近线方程为30x y +=,则实数m 的值为 .7.设各项均为正数的等比数列{}n a 的前n 项和为n S ,若52378,13a a S -==,则数列{}n a 的通项公式为n a = .8.将一颗均匀的骰子连续抛掷2次,向上的点数依次记为,m n ,则“2m n >”的概率是 .9.若实数,x y 满足条件14,23,x y x y -≤+≤⎧⎨≤-≤⎩则42z x y =-的取值范围为 .10.在平面直角坐标系xOy 中,已知()cos f x x =,()3sin g x x =,两曲线()y f x =与()y g x =在区间(0,)2π上交点为A .若两曲线在点A 处的切线与x 轴分别相交于,B C 两点,则线段BC 的为 .11.如图,在平面四边形ABCD 中, O 是对角线AC 的中点,且10OB =,6OD =. 若28DA DC ⋅=-,则BA BC ⋅的值为 .12.若对满足64x y xy ++=的任意正实数,x y ,都有22210x xy y ax ay ++--+≥,则实数a 的取值范围为 .13.在平面直角坐标系xOy 中,记椭圆22221(0)x y a b a b+=>>的左右焦点分别为12,F F ,若该椭圆上恰好有6个不同的点P ,使得12F F P ∆为等腰三角形,则该椭圆的离心率的取值范围是 .14.对于任意的实数,m n ,记min{,}m n 为,m n 中的最小值.设函数21()4f x x a x=++,()ln g x x =-,函数()min{(),()}h x f x g x =,若()h x 在(0,)+∞恰有一个零点,则实数a 的取值范围是 .二、解答题:本大题共6小题,共计90分.解答时应写出文字说明、证明过程.15.在平面直角坐标系xOy 中,设向量(sin ,1)m x =-,2(3cos ,cos )n x x =.(1)当3x π=时,求m n ⋅的值;(2)若[0,]4x π∈,且3132m n ⋅=-.求cos2x 的值. 16.如图,在四棱锥P ABCD -中,底面ABCD 是矩形,平面PAD ⊥平面ABCD ,AP AD =,点M 在棱PD 上, AM PD ⊥,点N 是棱PC 的中点,求证:(1) MN ∥平面PAB ; (2) AM ⊥平面PCD .17.如图,在一个水平面内,河流的两岸平行,河宽1(单位:千米)村庄,A B 和供电站C 恰位于一个边长为2(单位:千米)的等边三角形的三个顶点处,且,A C 位于河流的两岸,村庄A 侧的河岸所在直线恰经过BC 的中点D .现欲在河岸上,A D 之间取一点E ,分别修建电缆CE 和EA ,EB .设DCE θ∠=,记电缆总长度为()f θ (单位:千米).(1)求()f θ的解析式;(2)当DCE ∠为多大时,电缆的总长度()f θ最小,并求出最小值.18.如图,在平面直角坐标系xOy 中,已知椭圆22221(0)x y a b a b+=>>的离心率为3,且过点1(3,)2.设F 为椭圆的右焦点, ,A B 为椭圆上关于原点对称的两点,连结,AF BF 并延长,分别交椭圆于,C D 两点.(1)求椭圆的标准方程;(2)设直线,AB CD 的斜率分别为12,k k ,是否存在实数m ,使得21k mk =?若存在,求出实数m 的值;若不存在,请说明理由.19.设数列{}n a 的前n 项的和为n S ,且满足12a =,对*n N ∀∈,都有1(1)2n n a p S +=-+ (其中常数1p >),数列{}n b 满足2121log ()n n b a a a n=.(1)求证:数列{}n a 是等比数列; (2)若220172p =,求2018b 的值;(3)若*k N ∃∈,使得2212k p +=,记3||2n n c b =-,求数列{}n c 的前2(1)k +项的和. 20.在平面直角坐标系xOy 中,已知函数()1n (R)f x c x c =∈的图像与直线2y x e=相切,其中e 是自然对数的底数.(1)求实数c 的值; (2)设函数()()a h x ax g x x =--在区间1(,e)e内有两个极值点. ①求实数a 的取值范围;②设函数()h x 的极大值和极小值的差为M ,求实数M 的取值范围 .高二数学Ⅱ(附加题)21.已知矩阵 2 11 3M -⎡⎤=⎢⎥⎣⎦, 1 12 1N ⎡⎤=⎢⎥-⎣⎦. (1)求1()MN -;(2)在平面直角坐标系xOy 中,求直线:210L x y +-=在M 对应的变换T 作用下所得直线L '的方程.22.在直角坐标系xOy 中,以原点O 为极点,以x 轴的非负半轴为极轴,取与直角坐标系xOy相同的长度单位,建立极坐标系.设曲线C 的参数方程为sin x y θθ⎧=⎪⎨=⎪⎩,(θ为参数,[0,2]θπ∈),直线l 的极坐标方程为cos()4p πθ-=(1)写出曲线C 的普通方程和直线l 的直角坐标方程;(2)求曲线C 上的点到直线l 的最大距离.23.假定某篮球运动员每次投篮命中率均为(01)p p <<.现有3次投篮机会,并规定连续两次投篮均不中即终止投篮,已知该运动员不放弃任何一次投篮机会,且恰好用完3次投篮机会的概率是2125. (1)求p 的值;(2)设该运动员投篮命中次数为X ,求X 的概率分布及数学期望()E X .24.如图,已知正四棱柱1111ABCD A B C D -的底面边长为2,侧棱长为3, 1AE A B ⊥,垂足为F ,AE 交1B B 于点E .(1)求证: 1D B ⊥平面AEC ;(2)记直线AE 与平面1ACD 所成的角θ,求sin θ的值.试卷答案一、填空题. 1. {2,4,6,8} 2. 5 3. 120 4. 45. 37. 31n-8.169. [5,13] 11. 36 12. 10(,]3-∞ 13. 111(,)(,1)32214. 5{|4a a <-或3}4a >- 二、解答题.15. 解(1)当3x π=时,1]m =-,1]4n =, 所以311442m n ⋅=-=.(2) 2cos cos m n x x x ⋅=-112cos222x x =-- 1sin[2]62x π=--,若12m n ⋅=-.则11sin[2]622x π--=-,即sin[2]6x π-=. 因为[0,]4x π∈,所以2663x πππ-≤-≤,所以cos[2]6x π-= 所以cos2cos[[2]]66x x ππ=-+cos[2]6x π=--1sin[2]62x π-⨯132326-=⨯-⨯=.16.证明(1)因为在PAD ∆中, ,AP AD AM PD =⊥, 所以点M 是棱PD 的中点. 又点N 是棱PC 的中点, 所以MN 是PDC ∆的中位线, 所以MN DC ∥. 因为底面ABCD 是矩形, 以AB DC ∥, 所以MN AB ∥.又AB ⊂平面PAB , MN ⊄平面PAB ,所以MN ∥平面PAB . (2)因为平面PAD ⊥平面ABCD , CD ⊂平面ABCD , 平面PAD平面,ABCD AD CD AD =⊥,所以CD ⊥平面PAD .又AM ⊂平面PAD ,所以CD AM ⊥. 因为CD AD ⊥,CD AM ⊥, CD PD D =,CD ⊂平面PCD ,PD ⊂平面PCD ,所以AM ⊥平面PCD .17.解(1)易得AD 垂直平分BC ,1CD BD ==则1cos CE EB θ==,tan ED θ=,tan AE θ=,于是11()cos cos f θθθ=++2sin tan cos θθθ-=+因为E 在CD 之间,所以03πθ<<,故2sin ()cos f θθθ-=+,03πθ<<.(2) 22cos (2sin )(sin )()cos f θθθθθ----=,03πθ<<, 令()0f θ=,得1sin ,26πθθ==, 故当06πθ<<,()0f θ<,()f θ递减,当sin 62ππθ<<,()0f θ>,()f θ递增,所以,当6πθ=时, min ()()6f f πθ==122-+=答:当6DCE π∠=时, ()f θ最小值为18.解(1)设椭圆的方程为22221(0)x y a b a b+=>>,c =,由题意知22311,4c a a b ⎧=⎪⎪⎨⎪+=⎪⎩ 解得2,1,a b =⎧⎨=⎩所以椭圆的方程为2214x y +=. (2)设00(,)A x y ,则00(,)B x y --,010y k x =,又F , 所以直线AF的方程为y x =-.由221,4y x x y ⎧=-⎪⎪⎨⎪+=⎪⎩消去y ,得2200(7)x x --20070x -+=.因为0x x =是该方程的一个解,所以点C的横坐标C x =又点(,)C C C x y在直线y x =-上,所以C C y x =-=C的坐标为 同理,点D的坐标为,所以2k =101472y k x ==, 即存在7m =,使得217k k =.19.(1)证明:因为*n N ∀∈,都有1(1)2n n a p S +=-+,21(1)2n n a p S ++=-+所以两式相减得211(1)n n n a a p a +++-=-, 即21n n a pa ++=,当1n =时211(1)2a p a pa =-+=,所以*1,()n n a pa n N +=∈,又因为1p >,所以11n nn n a a p p++=, 所以数列{}n na p是常数列, 112,2n n n n a a a p p p p -===, 所以{}n a 是以2为首项, p 为公比的等比数列.(2)由(1)得12n n a p -=.2121log ()n n b a a a n==(1)221log (2)n n np n -=1(1)()2017n n n n -+所以20182b =.(3)由(1)得12n n a p -=.2121log ()n n b a a a n==(1)221log (2)n n n p n -=(1)2121log (22)n n n k n -+1121n k -=++.因为322322(21)n n k b k ---=+, 所以当11n k ≤≤+时, 32n n c b =-,当2n k ≥+时,32n n c b =-. 因此数列{}n c 的前2(21)k +项的和22k T +121()k b b b +=-++++2222()k k k b b b ++++++0121k k +++=-++(1)(2)2+121k k k k ++++++ (1)221k k k +=-++2(1)(22)(1)22121k k k k k k ++++=++. 20. (1)设直线2y x e =与函数()1n f x c x =相切于点00(,1n )P x c x ,函数()1n f x c x =在点00(,1n )P x c x 处的切线方程为: 0001()c y c nx x x x -=-,02c x e=, 把0,0x y ==代入上式得0,2x e c ==. 所以,实数c 的值为2. (2)①由(1)知()21n ah x ax x x=--, 设函数()h x 在区间1(,e)e内有两个极值点1212,()x x x x <,令22()a a h x a x x x'=+--2220ax x ax -+==, 则220ax x a -+=,设2()2m x ax x a =-+,因为121x x =,故只需0,20,()0,am e ∆>⎧⎪⎪>⎨⎪>⎪⎩,所以, 2211e a e <<+.②因为121x x =,所以,121()()M f x f x ax =-=1221221n (21n )a ax ax x x x ----- 11121n a ax x x =---1111(21n )a ax x x -- 21112221n aax x x =--由21120ax x a -+=,得12121x a x =+,且111x e<<. 12111211222121x x x M x x x +=-+222111211121n 4(1n )12x x x x --=-+. 设21x t =,211t e <<,令11()4(1n )+12t t t t ϕ-=-, 221()4()(+1)2t t t ϕ'=-222(1)0(1)t t t --=<+, ()t ϕ(在21(,1)e 上单调递减,从而21(1)()()t e ϕϕϕ<<, 所以,实数M 的取值范围是28(0,)1e +. 高二数学Ⅱ(附加题)21. 解(1)由题知 2 11 3MN -⎡⎤=⎢⎥⎣⎦ 1 10 32 17 2⎡⎤⎡⎤=⎢⎥⎢⎥--⎣⎦⎣⎦,所以0 3)2l 7 det(2MN ⎡⎤==-⎢⎥-⎣⎦, 根据逆矩阵公式,得121 217)1 03(MN -⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦.(2)设由L 上的任意一点(,)P x y '''在T 作用下得到L '上对应点(,)p x y .由 2 11 3x x y y '-⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎣⎦,即2,3'x y x x y y ''-=⎧⎨''+=⎩解得3+72'7x y x y x y ⎧'=⎪⎪⎨-⎪=⎪⎩, 因为210x y ''+-=,所以3221077x y y x +-⨯+-=, 即5470x y +-=.即直线L 的方程为5470x y +-=. 22.解(1)由,sin ,x y θθ⎧=⎪⎨=⎪⎩得22:13x C y +=,由cos ()4p πθθ-=cos sin 4p p θθ+=,即:40l x y +-=.(2)在22:13xC y+=上任取一点(3cos,sin)Pθθ(02)θπ≤≤,则点P到直线l的距离为|3cos sin4|2dθθ+-=|2sin()4|32πθ+-=,02θπ≤≤,当sin()13πθ+=-,即76πθ=时,max32d=.23. 解(1)设事件A:“恰用完3次投篮机会”,则其对立事件A:“前两次投篮均不中”, 依题意, ()1()P A P A=-2211(1)25p=--=,解得35p=.(2)依题意, X的所有可能值为0,1,2,3,且24(0)(1)25P X p==-=,2(1)(1)P X p p==-24(1)(1)125p p p+--=,327(3)125P X p===,故(2)1(0)P X P X==-=54(1)(3)125P X P X-=-==.X的概率分布列为:数学期望24()2125E X=+⨯54272133125125125+⨯=.24.解(1)如图,以D为坐标原点,分别以直线1,,DA DC DD所在直线为x轴, y轴, z轴,建立空间直角坐标系D xyz-,易得1(0,2,3)A B=-,设BE a=,则(0,2,)AE a=,因为1A B AE⊥,所以1(0,2,3)AB AE⋅=- (0,2,)430a a⋅=-=,解得43a=,即4(0,2,)3AE=,又1(2,2,3)D B=-,(2,2,0)AC=-,所以1(2,23)D B AE⋅=-4(0,2,)03⋅=,所以1D B AE⊥,且1(2,2,3)(2,2,0)0D B AC⋅=-⋅-=,所以1D B AC⊥,又AE AC A=,所以1D B⊥平面AEC.(2)4(0,2,)3AE=,1(2,0,3)D A=-,1(0,2,3)DC=-,设平面1ACD的一个法向量(,,)n x y z=,则110,0,D A nD C n⎧⋅=⎪⎨⋅=⎪⎩即230,230,x zy z-=⎧⎨-=⎩令0z=,则3x y==,即(3,3,2)n=,sin|cos,AEθ=<|||||AE nnAE n⋅>=⋅22222423=2342+()3+3+23⨯⨯=⨯286=.。
江苏省南京市六校联合体2017_2018学年高二物理下学期期末考试试题201807020157

南京市六校联合体高二期末考试物理试题第一部分 必做题考试时间 100分钟 总分 120分一、单项选择题:(本题共 4小题,每小题 3分,共 12分,每小题只有一个选项符合题意.)1.下列说法中不符合物理史实的是( )A .汤姆孙提出了原子的“西瓜模型”B . 粒子的散射实验表明原子核具有复杂结构C .玻尔第一次将量子观念引入原子领域,成功地解释了氢原子光谱的实验规律D .密立根通过著名的“油滴实验”精确测定了电子电荷2.下列叙述中正确的是( )A .随着温度的升高,辐射强度的极大值向频率较低的方向移动B .根据玻尔理论,在氢原子中,量子数 n 越大,则电子的轨道半径越小,能量越小C .γ 射线是高速电子流,能穿越几毫米厚的铝板D .光电效应和康普顿效应显示了光的粒子性3.用波长为 的光照射锌板,电子逸出锌板表面的最大初动能为 E .已知普朗克常量为 h ,k真空中的光速为 c ,能使锌产生光电效应的单色光的最大波长为( ) hc hc hc E kA .B .C .D . hc Ehc E hc k khc E hc k 4.如图,交流电源的电动势有效值与直流电源的电动势相等,两电源的内阻均可忽略,三个 灯泡是完全相同的,分别与定值电阻、电感器和电容器相接.当 S 接 1时三个灯泡的亮度相同, 那么 S 接 2时 ( )A .三个灯泡亮度相同B .甲灯比乙灯亮,丙灯不亮C .甲灯比乙灯暗,丙灯不亮D .甲灯和乙灯亮度相同,丙灯不亮二、多项选择题:(共 3小题,每小题 4分,选对部分得 2分,多选或错选不得分,共 12分.)5.氡 222是一种天然放射性气体,被吸入后,会对人的呼吸系统造成辐射损伤.它是世界卫 生组织公布的主要环境致癌物质之一.下列说法正确的是( )A .氡 222衰变成钋 218,其衰变方程为Rn Po 0e 28262 21884 1B .氡 222衰变成钋 218,其衰变方程为Rn Po 4He 28262 21884 2C .已知氡 222的半衰期是 3.8天,经过 19天 32g 的 222Rn 衰变后还剩 1g86D .已知氡 222的半衰期是 3.8天,经过 15.2天 32g 的 222Rn 衰变后还剩 1g86- 1 -6.如图所示是研究光电效应的电路,阴极K和阳极A是密封在真空玻璃管中的两个电极,K在受到光照时能够发射光电子.阳极A吸收阴极K发出的光电子,在电路中形成电流.如果用单色光a照射阴极K,电流表的指针发生偏转;用单色光b照射光电管阴极K时,电流表的指针不发生偏转.下列说法正确的是()A.a光的波长一定小于b光的波长B.只增加a光的强度可能使通过电流表的电流增大C.只增加a光的强度可使逸出的电子最大初动能变大D.用单色光a照射阴极K,当电源的正、负极对调时,电流表的读数可能减为零7.如图所示的交流电路中,理想变压器原线圈输入电压有效值为U1且保持不变,输入功率为P1,输出功率为P2,输出电压有效值为U2,各交流电表均为理想电表.当滑动变阻器R的滑动头向下移动时()A.灯L变亮R1B.各个电表读数均变大C.因为U1及原副线圈匝数比不变,所以U2不变D.P 变大,且始终有P =P1 12 ~U1U2VL AR三、填空题:(共3小题,每空2分,共12分.请将解答填写在答题卡相应的位置.)8.氦原子的一个核外电子被电离,形成类氢结构的氦离子.如图所示氦离子能级的示意图.现有一群氦离子处于n=3能级,当它们跃迁时最多能辐射出种能量的光子,辐射出的光子中能量的最大值为eV.n ∞4 3E-3.4eV -6.0eV2-13.6eV1-54.4eVE19.已知氢原子的基态能量为E1(E1<0),量子数为n的激发态的能量为,大量处于n=4激发n2态的氢原子跃迁时,发出多个能量不同的光子,其中频率最大的光子的频率为.电子质量为m,基态氢原子中的电子吸收一频率为ν的光子被电离后,电子速度大小为_______(普朗克常量为h).10.历史上美国宇航局曾经完成了用“深度撞击”号探测器释放的撞击器“击中”坦普尔1号彗星的实验.探测器上所携带的重达400kg的彗“星撞击器将”以1.0×104m/s的速度径直撞向彗星的彗核部分撞,击彗星“后撞击器融”化消失这,次撞击使该彗星自身的运行速度出现 1.0×10-7m/s的改变.已知普朗克常量h=6.6×10-34J·s.则:- 2 -(1)撞击前彗星“撞击器”对应物质波波长为;(2)根据题中相关信息数据估算出彗星的质量为 . 四、计算题:(本题共 4小题,共计 44分.解答请写出必要的文字说明、方程式和重要的演 算步骤.只写出最后答案的不能得分.有数值计算的题,答案中必须明确写出数值和单位.) (8分)11.蹦床运动有"空中芭蕾"之称,某质量 m =45kg 的运动员从空中 h 1=1.25m 落下,接 着又能弹起 h 2=1.8m 高度,此次人与蹦床接触时间 t =0.40s ,取 g =10m/s 2,求:(1)运动员与蹦床接触时间内,所受重力的冲量大小 I ;(2)运动员与蹦床接触时间内,受到蹦床平均弹力的大小 F .(9分)12.如图所示,水平 U 形光滑框架,宽度为 l =1m ,电阻忽略不计,导体棒 ab 的质量 m = 0.2kg ,电阻 R = 0.5Ω,匀强磁场的磁感应强度 B = 1T ,方向垂直框架向上.现用 F =6N 的 恒定外力由静止开始向右拉 ab 棒,求:(1)当 ab 棒的速度达到 2m/s 时,ab 棒产生的感应电流的大小和方向;(2)当 ab 棒的速度达到 2m/s 时,ab 棒的加速度大小;(3)ab 棒运动的最大速度.(12分)13.如图所示为一交流发电机的原理示意图,已知矩形线圈 abcd 的面积 S=0.1m 2, 匝数 N =100,线圈的总电阻 r =1Ω,线圈两端通过电刷 E 、F 与阻值 R =9Ω 的定值电阻连接.线 2 圈在磁感强度 T 的匀强磁场中绕垂直于磁场的转轴OO' B 10 b O '匀速转动,转速 n =1200r/min .不计电路中的其它电阻.求:(1)线圈中感应电动势的最大值 E m ;(2)图中电压表的示数 U ;N a c S (3)线圈转动一圈过程中电阻 R 上产生的热量 Q .F V d R O E(15分)14.随着科技进步,无线充电已悄然走入人们的生活.图甲为兴趣小组制作的无线 充电装置中的受电线圈示意图,已知线圈匝数 n =100,电阻 r =1Ω,面积 S 1.5103 m 2 ,外 接电阻 R =3Ω.线圈处在平行于线圈轴线的匀强磁场中,磁场的磁感应强度随时间变化如图乙B /×10-2T- 3 -R2R1234 5 6 t/×10-2s所示.求:(1)t=0.01s时线圈中的感应电动势E;(2)0~0.02s内通过电阻R的电荷量q;(3)0~0.03s内电阻R上产生的热量Q R.第二部分:选做题(选修3-3)一、单项选择题:(本题共4小题,每小题3分,共12分,每小题只有一个选项符合题意.)1.下列对理想气体的理解,正确的是()A.实际气体任何情况下都可以视作理想气体B.理想气体实际上并不存在,只是一种理想模型C.理想气体的热力学温度T与分子的平均动能成反比EkD.一定质量的某种理想气体,体积减小时,分子的密集程度也将减小2.关于扩散现象和布朗运动,下列说法中正确的是()A.液体中的扩散现象是由于液体的对流形成的B.在显微镜下可以观察到煤油中小粒灰尘的布朗运动,这说明煤油分子在做无规则运动C.在扩散现象中,温度越高,扩散得越快D.布朗运动就是液体分子的无规则运动3.某种气体的摩尔质量为M mol,摩尔体积为V mol,每个分子的质量和体积分别为m和V0,阿伏加德罗常数为N A.下列关系式中正确的是()MA.B.N A =N A molmm MmolVV VmolC.D.00NA NA V mol4.当氢气和氧气温度相同时,下述说法中正确的是()A.两种气体分子的平均动能相等- 4 -B.氢气分子的平均速率等于氧气分子的平均速率C.两种气体分子热运动的总动能相等D.质量相等的氢气和氧气,温度相同,不考虑分子间的势能,则两者内能相等二、多项选择题:(每小题4分,选对部分得2分,多选或错选不得分,共8分.)两5.分子间的作用力F与分子间距离r的关系如图中曲线所示,曲线与r轴交点的横坐标为r F0>,0为斥力,F<0为引力.若将甲分子固定在坐标原点O乙,分子从图中a点处由静止释放在,它向甲分子靠近的过程中,下列说法正确的是()A.乙分子将一直做加速运动B.在r>r0阶段,乙分子做加速运动C.当乙分子到达r0位置时,其加速度最大D.在r>r0阶段,两分子的势能一直减小6.如图所示,一导热性能良好的金属气缸静放在水平面上,活塞与气缸壁间的摩擦不计。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
南京市六校联合体高二期末试卷 数学(理科) 2018.6参考公式:方差2211()ni i s x x n ==-∑一、填空题:本大题共14小题,每小题5分,共70分.请把答案直接填写在答.题卡相应位置上........ 1.设i 为虚数单位,复数2iz i+=,则z 的模||z = ▲ . 2.一根木棍长为5米,若将其任意锯为两段,则锯成的两段木棍的长度都大于2米的概率为 ▲ .3.命题“若0a =,则复数(,)z a bi a b R =+∈为纯虚数”的逆命题...是 ▲ 命题.(填“真”或“假”)4.已知一组数据为2,3,4,5,6,则这组数据的方差为 ▲ .5.将一颗骰子抛掷两次,用m 表示向上点数之和,则10m ≥的概率为 ▲ .6.用分层抽样的方法从某校学生中抽取1个容量为45的样本,其中高一年级抽20人,高三年级抽10人.已知该校高二年级共有学生300人,则该校学生总数为 ▲ . 7.函数()y f x =在点(1,)P m 处切线方程为60x y +-=,则(1)(1)f f '+= ▲ . 8.若21(2)nx x -的展开式中所有二项式系数和为64,则展开式中的常数项是 ▲ . 9.根据如图所示的伪代码可知,输出的结果为 ▲.10.若2624101201256(2)x a a x a x a x a x +=+++++,则0246a a a a +++= ▲ .11.已知m ∈R ,设命题P :2,10x R mx mx ∀∈++>; 命题Q :函数32()31f x x x m =-+-只有一个零点. 则使“P ∨Q ”为假命题的实数m 的取值范围为 ▲ .12.有编号分别为1,2,3,4,5的5个黑色小球和编号分别为1,2,3,4,5的5个白色小球,若选取的4个小球中既有1号球又有白色小球,则有 ▲ 种不同的选法.13.观察下列等式:请你归纳出一般性结论 ▲ .14.乒乓球比赛,三局二胜制.任一局甲胜的概率是(01)p p <<,甲赢得比赛的概率是q ,则q p -的最大值为 ▲ .二、解答题:本大题共6小题,共计90分。
请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤。
15.(本小题满分14分)在平面直角坐标系xoy 中,以O 为极点,Ox 为极轴建立极坐标系,曲线C 的极坐标方程是2sin ρθ=,直线l 的参数方程是12,1x t y t =+⎧⎨=-⎩(t 为参数).求直线l 被曲线C 截得的弦长.16.(本小题满分14分)在棱长为1的正方体1111ABCD A B C D -中,O 是AC 的中点,E 是线段D 1O 上一点,且D 1E =λEO . (1)若λ=1,求异面直线DE 与CD 1所成角的余弦值; (2)若平面CDE ⊥平面CD 1O ,求λ的值.17.(本小题满分14分)已知()()23*012312nn n x a a x a x a xa x n N +=++++∈,(1)求()3122312222nnn a a a a s =-+-++-的值; (2)若87a a >且89a a >,求n 的值; (3)求证:20181(1)71000+>.18.(本小题满分16分)某抛掷骰子游戏中,规定游戏者可以有三次机会抛掷一颗骰子,若游戏者在前两次抛掷中至少成功一次才可以进行第三次抛掷,其中抛掷骰子不成功得0分,第1次成功得3分,第2次成功得3分,第3次成功得4分.游戏规则如下:抛掷1枚骰子,第1次抛掷骰子向上的点数为奇数则记为成功,第2次抛掷骰子向上的点数为3的倍数则记为成功,第3次抛掷骰子向上的点数为6则记为成功.用随机变量ξ表示该游戏者所得分数. (1)求该游戏者有机会抛掷第3次骰子的概率; (2)求随机变量ξ的分布列和数学期望.19.(本小题满分16分) 已知函数322()f x x mx m =++(1)若()f x 在区间[1,)+∞上是单调递增函数,求实数m 的取值范围; (2)若()()g x f x nx =+在1x =处有极值10,求m n +的值;(3)若对任意的12,[1,1]x x ∈-,有12|()()|2f x f x -≤恒成立,求实数m 的取值范围.20.(本小题满分16分)把圆分成(3)n n ≥个扇形,设用4种颜色给这些扇形染色,每个扇形恰染一种颜色,并且要求相邻扇形的颜色互不相同,设共有()f n 种方法.(1)写出(3)f ,(4)f 的值;(2)猜想()f n (3)n ≥,并用数学归纳法证明。
南京市六校联合体高二期末试卷数学(理科)参考答案一、填空题2.15. 3. 真 4.2 5.166. 9007.48.2409.48 10.365 11.45m ≤≤ 12.13613.222222(7)(74)(75)(71)(72)(76)k k k k k k ++++=+++++k z ∈二、解答题15.曲线C 的直角坐标方程是22(1)1x y +-=…………4分 直线l 的普通方程是230x y +-=…………………8分圆心C 到直线l的距离5d =……………………11分14分 16.解(1以1,,DA DC DD 为单位正交基底建立如图所示的空间直角坐标系D xyz -.则A (1,0,0),()11022O ,,,()010C ,,,D 1(0,0,1), E ()111442,,, 于是()111442DE =,,,()1011CD =-,,.由cos 1DE CD 〈〉,=11||||DECD DE CD ⋅⋅=. 所以异面直线AE 与CD 1. ………6分 (2)设平面CD 1O 的向量为m =(x 1,y 1,z 1),由m ·CO =0,m ·1CD =0得 11111100x y y z ⎧-=⎪⎨⎪-+=⎩,,取x 1=1,得y 1=z 1=1,即m =(1,1,1) . ………8分由D 1E =λEO ,则E 12(1)2(1)1λλλλλ⎛⎫ ⎪+++⎝⎭,,,DE =12(1)2(1)1λλλλλ⎛⎫ ⎪+++⎝⎭,,.10分又设平面CDE 的法向量为n =(x 2,y 2,z 2),由n ·CD =0,n ·DE =0.得 2222002(1)2(1)1y x y z λλλλλ=⎧⎪⎨++=⎪+++⎩,, 取x 2=2,得z 2=-λ,即n =(-2,0,λ) .12分 因为平面CDE ⊥平面CD 1F ,所以m ·n =0,得λ=2. ……14分17(1)令12x =-,则()31202312222n nna a a a a -+-++-=0,又01a = 所以1S =-………………………………………………………………4分(2)由887788992222n nn nC C C C ⎧>⎪⎨>⎪⎩,解得11252n n >⎧⎪⎨<⎪⎩,所以12n = ………………9分(3)20181(1)1000+2341234201820182018201811114211227100010001000100033C C C C ⎛⎫⎛⎫⎛⎫>++++>++++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭………………………………………………………………14分 18.⑴该游戏者抛掷骰子成功的概率分别为211=p 、312=p 、316p =,该游戏者有机会抛掷第3次骰子为事件A .则1212122()(1)(1)3=-+-+=P A p p p p p p ; 答:该游戏者有机会抛掷第3次骰子的概率为23………………………………6分 (2)由题意可知,ξ的可能取值为0、3、6、7、10,31)1)(1()0(21=--==p p P ξ, 123123555(3)(1)(1)(1)(1)183612P p p p p p p ξ==--+--=+=, 1235(6)(1)36P p p p ξ==-=, 123123211(7)(1)(1)363612P p p p p p p ξ==-+-=+=, 1231(10)36P p p p ξ===, 所以ξ的分布列为………………………………………………14分所以ξ的数学期望155115303671031236123618E ξ=⨯+⨯+⨯+⨯+⨯=…………………16分 19解:(1) f '(x )=3x 2+2mx ,由f (x )在区间[1,+∞)上是单调递增函数得,当x ≥1时,3x 2+2mx ≥0恒成立,即m ≥-32x 恒成立,解得m ≥-32;………………………………4分(2)2()32g x x mx n '=++,由题(1)03(1)103g m g n '==-⎧⎧⇒⎨⎨==⎩⎩或411m n =⎧⎨=-⎩当33m n =-⎧⎨=⎩时,()0g x '≥,()g x 无极值,舍去.所以7m n +=-…………………………8分(没有舍扣2分)(3)由对任意的x 1,x 2∈[-1,1],有| f (x 1)-f (x 2)|≤2恒成立,得f max (x )-f min (x )≤2.且| f (1)-f (0)|≤2,| f (-1)-f (0)|≤2,解得m ∈[-1,1],…………10分 ①当m =0时,f '(x )≥0,f (x )在[-1,1]上单调递增,f max (x )-f min (x )= | f (1)-f (-1)|≤2成立.……………………………11分②当m ∈(0,1]时,令f '(x )<0,得x ∈(-23m ,0),则f (x )在(-23m ,0)上单调递减;同理f (x )在(-1,-23m ),(0,1)上单调递增,f (-23m )= 427m 3+m 2,f (1)= m 2+m +1,下面比较这两者的大小,令h (m )=f (-23m )-f (1)= 427m 3-m -1,m ∈[0,1],h '(m )= 49m 2-1<0,则h (m )在(0,1] 上为减函数,h (m )≤h (0)=-1<0,故f (-23m )<f (1),又f (-1)= m -1+m 2≤m 2=f (0),仅当m =1时取等号.所以f max (x )-f min (x )= f (1)-f (-1)=2成立.③同理当m ∈[-1 ,0)时,f max (x )-f min (x )= f (1)-f (-1)=2成立. 综上得m ∈[-1 ,1].…………………………16分 20.解:(1)(3)24,(4)84f f ==…………2+4=6分(2).当4n ≥时,首先,对于第1个扇形1a ,有4种不同的染法,由于第2个扇形2a 的颜色与1a 的颜色不同,所以,对于2a 有3种不同的染法,类似地,对扇形3a ,…,1n a -均有3种染法.对于扇形n a ,用与1n a -不同的3种颜色染色,但是,这样也包括了它与扇形1a 颜色相同的情况,而扇形1a 与扇形n a 颜色相同的不同染色方法数就是(1)f n -,于是可得1()43(1)n f n f n -=⨯--…………………………10分猜想()3(1)3n n f n =+-⋅…………………………12分① 当3n =时,左边(3)24f =,右边333(1)324+-⋅=,所以等式成立 ② 假设(3)n k k =≥时,()3(1)3k k f k =+-⋅,则1n k =+时,(1)43()433(1)3k k k k f k f k +=⨯-=⨯---⋅113(1)3k k ++=+-⋅ 即1n k =+时,等式也成立综上()3(1)3n n f n =+-⋅(3)n ≥…………………………16分。
