5.2.2平行线的判定导学案
山西省阳泉市七年级数学下册5.2.2平行线的判定导学案(新版)新人教版

平行线的判定自主学习、课前诊断一、温故知新1. 在同一平面内,的两条直线叫做平行线。
2.如图有_____对同位角,分别是______________________.有___对内错角,分别是________.有___对同旁内角,分别是_______________.二、设问导读:1、问题解决阅读课本P12-14完成下列问题:问题1:结合课本图5.2-8,思考如何利用“同位角相等,两直线平行”去证明“内错角相等,两直线平行”和“同旁内角互补,两直线平行”?问题2:总结直线平行的条件:如图如果∠3=,理由是 __如果∠6=,那么,理由是____ ______如果∠2+ ∠4= ____ 或________,那么a∥b,理由是__ __________三、自学检测:1. 直线a,b被直线c所截,现给出下列四个条件:•①∠1=∠5;②∠1=∠7;③∠2+∠3=180°;④∠4=∠7.其中能说明a∥b的条件序号为( ) A.①② B.①③C.①④D.③④2.∠B=60_______.导入新课二、交流展示学用结合、提高能力一、巩固训练:1. 完成推理,填写推理依据:(1)∵∠1=∠A (已知)∴__________( )(2)∵∠1=∠D (已知)∴__________2(1)当∠2=_____时,a ∥b;(2)当∠3=_____时,a ∥b;(3)当∠4=_____时,a ∥b;3 如图判定AB ∥CE 的理由是( )A .∠B=∠ACEB .∠A=∠ECDC .∠B=∠ACBD .∠A=∠ACE4.如图,∵AC ⊥AB ,BD ⊥AB (已知)∴∠CAB =90°,∠______=90°( )∴∠CAB =∠______( )∵∠CAE =∠DBF (已知)∴∠BAE =∠______∴_____∥_____( )二、当堂检测1.如图所示,在下列条件中,不能判断L1∥L2的是().A .∠1=∠3B .∠2=∠3C .∠4+∠5=180°D.∠2+∠4=180°2.如图,由∠1=∠21 C DB A EF2 可确定____∥______.由∠3=∠4可确定____∥______.3.如图所示,已知∠1=120°,∠2=60°.试说明a 与b 的关系?三、拓展延伸:如图,已知BE 平分∠ABC ,CF 平分∠BCD ,∠1=∠2,判断AB 与CD 是否平行,并请说明理由。
人教版七年级数学下册 第5章 5.2.2 平行线的判定 导学案

5.2 平行线及其判定5.2.2 平行线的判定一、新课导入1.导入课题:上节课我们学习了平行线的概念和画法,这节课我们来研究如何判定两条直线是不是平行线(板书课题).2.学习目标:(1)学会并记住平行线的判定方法1、2、3.(2)能运用平行线的判定方法进行简单的推理论证.3.学习重、难点:重点:平行线的判定方法1、2、3.难点:运用平行线的判定方法进行简单的推理论证.二、分层学习1.自学指导:(1)自学内容:课本P12至P13的内容.(2)自学时间:10分钟.(3)自学要求:阅读教材,重点处做好圈点,遇到疑难相互研讨.(4)自学参考提纲:①a.观察P12“思考”中用直尺和三角尺画平行线示意图,可以发现,在画平行线时,三角尺在移动时紧靠直尺,并且三角尺的角的大小不变,又在移动前、后,三角尺的角恰好是直线AB、CD被EF所截形成的一对同位角,这说明:如果∠DEF=∠BGF,那么AB∥CD.b.这一事实揭示的就是平行线的判定方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行,简称为同位角相等,两直线平行.用符号语言表述是:如图1,若∠1=∠2,则a∥b.c.在课本图5.2-7中,你能说出木工用图中的角尺画平行线的道理吗?②a.在图1中,∠2与∠3是一对内错角.b.若∠3=∠2,能得到直线a∥b吗?分析:若能由∠3=∠2转化为∠1=∠2,那么由判定方法1,就可得a∥b,你能写出推理过程吗?c.由②可得到平行线的判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行,简称为内错角相等,两直线平行.③a.在图1中,∠2与∠4是一对同旁内角.b.若∠2+∠4=180°,能得到直线a∥b吗?分析:若能由∠2+∠4=180°转化为∠1=∠2(或∠3=∠2),那么由判定方法1(或判定方法2),就可得a∥b,你能写出推理过程吗?c.由②可得到平行线的判定方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行,简称为同旁内角互补,两直线平行.2.自学:同学们可结合自学指导进行自学.3.助学:(1)师助生:①明了学情:教师巡视课堂,关注学生在自学中遇到的疑难问题.②差异指导:对个别学习有困难的学生进行点拨引导.(2)生助生:小组相互交流学习,纠正认知偏差.4.强化:(1)判定方法1、2、3及其几何表述.(2)练习:课本P15“复习巩固”的第1、2题.1.自学指导:(1)自学内容:课本P14例题.(2)自学时间:4分钟.(3)自学要求:阅读教材,重点处做好圈点,有疑点处做上记号.(4)自学参考提纲:①仔细体会,揣摩例题的几何推理过程,你能仿照它用别的方法说明b∥c 吗?②本例的结论也可作为平行线的一种判定方法,简述为:在同一平面内,垂直于同一条直线的两直线平行.③如图2,BE是AB的延长线.a.由∠CBE=∠A可以判定哪两条直线平行?根据是什么?答案:BC∥AD.根据是同位角相等,两直线平行.b.由∠CBE=∠C可以判定哪两条直线平行?根据是什么?答案:AB∥CD.根据是内错角相等,两直线平行.④如图3,这是小明同学自己制作的英语抄写纸的一部分,其中的横线互相平行吗?你有多少种判别方法?答案:平行.理由不唯一.2.自学:同学们可结合自学指导进行自学.3.助学:(1)师助生:①明了学情:关注学生完成自学参考提纲的进度、存在的问题及疑点.②差异指导:对个别学习有困难或认知不足的学生进行点拨引导.(2)生助生:小组内学生相互交流,取长补短.4.强化:(1)判断两条直线平行的方法:①平行公理的推论:如果两条直线都与第三条直线平行,这两条直线也互相平行.②平行线判定方法1,即同位角相等,两直线平行.③平行线判定方法2,即内错角相等,两直线平行.④平行线判定方法3,即同旁内角互补,两直线平行.⑤在同一平面内,垂直于同一条直线的两条直线互相平行.(2)练习:课本P14“练习”第2题.三、评价1.学生学习的自我评价:各小组针对学习收获和存在的困惑进行总结交流.2.教师对学生的评价:(1)表现性评价:对学生在学习过程中的态度、方法和成效进行点评.(2)纸笔评价:课堂评价检测.3.教师的自我评价(教学反思):本节课通过“问题情境—合作探究—建立模型—求解—应用”的基本过程,使学生体会到了数学知识之间的内在联系;通过对问题的探究,获得了一些研究问题的方法和经验;发展了思维能力,加深了对相关知识的理解,通过获得成功的体验和克服困难的经历,增强了学生学习数学、应用数学的自信心.(时间:12分钟满分:100分)一、基础巩固(70分)1.(20分)如图,直线a,b,c被直线l所截,量得∠1=∠2=∠3.(1)若∠1=∠2,则a∥b,理由是同位角相等,两直线平行.(2)若∠1=∠3,则a∥c,理由是内错角相等,两直线平行.(3)直线a,b,c互相平行吗?为什么?解:平行,∵b∥a,c∥a,∴b∥c,∴a∥b∥c.第1题图第2题图第3题图第4题图2.(10分)如图,根据图中所给条件:(1)互相平行的直线有a∥b,c∥d;(2)互相垂直的直线有e⊥b,e⊥a.3.(10分)如图,如果∠3=∠7或∠4=∠8或∠2=∠6或∠1=∠5,那么a∥b,理由是同位角相等,两直线平行;如果∠5=∠3或∠2=∠8,那么a∥b,理由是内错角相等,两直线平行;如果∠2+∠5=180°或∠3+∠8=180°,那么a∥b,理由是同旁内角互补,两直线平行.4.(10分)如图,如果∠2=∠6,那么AD∥BC,如果∠3+∠4+∠5+∠6=180°, 那么AD∥BC;如果∠9 =∠DAB,那么AD∥BC;如果∠9=∠3+∠4,那么AB∥CD.5.(20分)如图,直线a,b被直线c所截,现给出下列四个条件:①∠1=∠5;②∠1=∠7;③∠4=∠7;④∠2+∠3=180°.其中能说明a∥b的条件序号为(A)A.①②B.①③C.①④D.③④二、综合应用(20分)6.如图,当∠1=∠3时,直线a,b平行吗?当∠2+∠3=180°时,直线a,b 平行吗?为什么?解:∵∠1=∠3,∠3=∠4,∴∠1=∠4,∴a∥b(同位角相等,两直线平行).∵∠3=∠4,∠2=∠5,∠2+∠3=180°,∴∠4+∠5=180°,∴a∥b(同旁内角互补,两直线平行).三、拓展延伸(10分)7.如图所示,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,则a与c平行吗?为什么?解:∵∠1=∠2,∴a∥b(内错角相等,两直线平行).∵∠3+∠4=180°,∴b∥c(同旁内角互补,两直线平行).又∵a∥b,∴a∥c(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).。
七年级数学下册5.2.2 第1课时 平行线的判定导学案

第五章 相交线与平行线5.2 平行线及其判定5.2.2 平行线的判定 第1课时 平行线的判定学习目标:1.掌握平行线的三种判定方法,能运用平行线的判定方法解决问题.2.通过独立思考,小组探究,理解角与线的位置关系之间的联系,体会数形结合思想.3.激情投入,善于发现问题和提出问题,感受学习数学的乐趣. 重点:三种判定方法判定两直线平行.难点:根据平行线的判定方法进行简单的推理.一、知识链接1.在同一平面内, 的两条直线叫做平行线.2.过已知直线外一点能且只能画 条直线与这条直线垂直,能且只能画 条直线与这条直线平行.3.同位角、内错角、同旁内角的定义是怎样叙述的?4.怎样用三角板和直尺作已知直线的平行线?二、新知预习1.试利用三角板和直尺,经过直线外一点P 画出已知直线AB 的平行线CD ,由此你会发现什么?2.同位角 ,两直线平行. 三、自学自测1.如图,三角形ABC 中,∠A=70°,∠BED=70°,可以判断 ∥ .根据是 .由∠B=48°,∠FDC=48°,可以判断 ∥ .根据是 .第1题图 第2题图2.如图,用直尺和三角板作直线AB ,CD ,从图中可知,直线AB 与直线CD 的位置关系为 .四、我的疑惑___________________________________________________________________________自主学习教学备注【自学指导提示】学生在课前完成自主学习部分一、要点探究探究点1:利用同位角判定两条直线平行画一画:用三角尺和直尺画平行线的步骤有哪些?思考:(1)画图过程中,什么角始终保持相等? (2)直线a ,b 位置关系如何? (3)由上面的操作过程,你能发现判定两直线平行的方法吗? 总结归纳:判定方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行. 简单说成:同位角相等,两直线平行.应用格式: ∵∠1=∠2(已知)a ∥b (同位角相等,两直线平行)做一做:下图中若∠1=55°,∠2=55°,直线AB 、CD 平行吗?为什么?探究点2:利用内错角、同旁内角判定两条直线平行 问题1:如图,由∠3=∠2,可推出a//b 吗?如何推出?总结归纳:判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行. 简单说成:内错角相等,两直线平行.应用格式: ∵∠3=∠2(已知)a ∥b (内错角相等,两直线平行) 问题2:如图,如果∠1+∠2=180°,你能判定a//b 吗?总结归纳:判定方法3简单说成:同旁内角互补,两直线平行.课堂探究教学备注 配套PPT 讲授1.情景引入 (见幻灯片3)2.探究点1新知讲授(见幻灯片5-13)3.探究点2新知讲授(见幻灯片14-23)应用格式:∵∠1+∠2=180°(已知),∴a∥b(同旁内角互补,两直线平行)典例精析例1.根据条件完成填空.①∵∠2 = ∠6(已知)∴___∥___(___________________________)②∵∠3 = ∠5(已知)∴___∥___(___________________________)③∵∠4 +___=180°(已知)∴___∥___(___________________________)例2.如图,已知∠MCA= ∠A,∠DEC= ∠B,那么DE∥MN吗?为什么?针对训练1.根据条件完成填空.①∵∠1 =_____(已知)∴AB∥CE(___________________________)②∵∠1 +_____=180°(已知)∴CD∥BF( ___________________________)③∵∠1 +∠5 =180°(已知)∴_____∥_____(___________________________)④∵∠4 +_____=180°(已知)∴CE∥AB(___________________________)2.如图,直线AB、CD、EF、MN相交,若∠2=∠5,找出图中与∠2 互补的角.二、课堂小结文字叙述符号语言图形相等,两直线平行∵ (已知),∴a∥b相等,∵ (已知),教学备注配套PPT讲授3.探究点2新知讲授(见幻灯片14-23)两直线平行 ∴a ∥b互补, 两直线平行∵ (已知)∴a ∥b1.如图,可以确定AB ∥CE 的条件是( )A.∠2=∠BB. ∠1=∠AC. ∠3=∠BD. ∠3=∠A第1题图 第2题图2.如图,已知∠1=30°,∠2或∠3满足条件 ,则a//b.3.如图.(1)从∠1=∠4,可以推出 ∥ ,理由是 .(2)从∠ABC +∠ =180°,可以推出AB ∥CD ,理由是 .(3)从∠ =∠ ,可以推出AD ∥BC , 理由是 . (4)从∠5=∠ ,可以推出AB ∥CD ,理由是 .4.如图,已知∠1= ∠3,AC 平分∠DAB ,你能判断哪两条直线平行?请说明理由?当堂检测教学备注 配套PPT 讲授 4.课堂小结5.当堂检测 (见幻灯片24-28)。
2019-2020学年七年级数学下册《5.2.2 平行线的判定》导学案1(新版)新人教版.doc

2019-2020学年七年级数学下册《5.2.2 平行线的判定》导学案1(新版)新人教版学习目标掌握平行线的判定:“同位角相等,两直线平行”,并能用其解决实际问题。
(1)同一平面内,两条直线有几种位置关系?各是什么?(2)直线AB和直线CD被直线EF所截,指出图中的同位角,内错角,同旁内角。
二、探究新知画一画:如图,请你用一把直尺和一个三角板,作出过点P与直线l平行的直线b,试着画一画。
.Pl量一量:在上图中任选一对同位角,用量角器度量这两个角,并比较它们的大小。
试一试:用同样的方法另作平行线,在度量任意一对同位角,得到的结果一样吗?议一议:通过以上的操作,你能说出两条直线被第三条直线所截,如何判定这两条直线平行呢?平行线的判定1:简单说成:几何语言叙述为:如图,E三、学以致用1、如图,下列说法正确的是( )A 、若∠1=∠2,则c ︱︱ d ;B 、若∠1=∠3,则c ︱︱ d;C 、若∠1=∠4,则c ︱︱ d ;D 、若∠2=∠3,则c ︱︱ d.2、如图,已知直线321,,l l l 被直线l所截,,723,722,721︒=∠︒=∠︒=∠那么直线321,,l l l 有怎样的位置关系?为什么?(2题图) (1题图)3、如图,已知∠1=,60,120︒=∠︒C 判断直线AB 与CD 是否平行?请说出理由。
四、畅谈收获(1) 本节课你学到了什么?(2)下节课你想探究什么知识?A B CD F 1 2 311 12131 2 34 a bc d ABC D E1。
5.2.2 平行线的判定——导学案

5.2.2 平行线的判定——导学案(1案2课)班级:姓名:学号:学习目标:1.借助用直尺和三角板画平行线的过程,得出两直线平行的判定方法一“同位角相等,两直线平行”,进而推导出方法二“内错角相等,两直线平行”与方法三“同旁内角互补,两直线平行”。
2.理解掌握平行线的判定方法,并能运用它判定两直线的平行关系.3.培养识图能力,推理能力和有条理表达能力,发展空间观念。
学习重点:两直线平行的判定方法。
学习难点:运用判定方法来证明两直线的平行关系。
一、准备:1.如果a∥b ,b∥c ,那么__ ____,理由是________ _______________.2.如下图,已知四条直线AB、AC、DE、FG及所标示各角,请填空:①∠1与∠2是直线__ ___和直线_ ___被直线___ __所截而成的______角;②∠3与∠2是直线___ __和直线__ __被直线____ _所截而成的______角;③∠5与∠6是直线___ __和直线__ __被直线___ __所截而成的______角;④∠4与∠7是直线___ __和直线____ 被直线_____ 所截而成的______角;⑤∠8与∠2是直线_____ 和直线___ _被直线____ _所截而成的______角.3.仔细观察,下列图中有平行线吗?第2题图第3题图相信自己的眼睛吗?你该怎样说明这些直线是否平行呢?二、探究活动:1、思考·归纳①在实际生活中,都有哪些地方可以见到平行线?如: 铁轨、……(请同学们举出更多例子)[认识] :判定两条直线是否平行,在实际生活中具有极其重要的应用价值。
②什么是平行线?答:[我们可以利用这个定义来判定两条直线是否平行!]③还记得画平行线的方法吗?画画看[利用直尺和三角尺]任意画右边直线的平行线:C E 1 3 42 D F G④ 在作平行线的过程中,两种工具一静一动,这其中的道理你能明白吗?静的直尺是在固定一条直线;动的三角尺能确保一对_________相等.(图中的三线八角形成的条件是什么?P6)[归纳]既然这就是作平行线的方法,那由此作出来的就一定是平行线.因此,我们就得出一种判定平行线的方法:[判定方法1] 两条直线被第三条直线所截,若同位角相等,则这两条直线平行.简述为:_____________________________________2、例题·交流 例1、如图,直线AB 与CD 被直线EF 所截, ∠1=50°, ∠2=50°.问:AB 与CD 平行吗? 证明: 例1——数学走近生活:木工用右图中的角尺画CD 、EF ,CD 、EF 平行吗?为什么?答:三、初步训练:1.如右图,已知∠C=60°,则当∠ABE=________时,可判定__ _∥_ __(理由是: )2.根据下图填空:①例: ∵∠A=∠1∴AB ∥DC (同位角相等,两直线平行)②∵∠2=∠4 ∴____∥____( 同位角相等,两直线平行 ) ③∵∠3=______ ∴____∥BC( )④∵∠A=______ ∴____∥EF( )⑤∵AG ∥EF,BC ∥EF∴____∥____ ( )A B C DE1 2 CC E 1 3 4 2D FG 3.在第2题图中, ∠A 与∠3是一对__________,其形成条件是( ). 如果知道∠A=∠3,也能判定AB ∥DC.证明过程如下: ∵∠1=∠3( )∠A=∠3(已知)∴∠A=∠1(等量代换) ∴AB ∥DC( )[归纳]由此我们可以得出两直线平行的判定方法2: 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简述为:______________________________________4.(与第3题类似地) 在第2题图中, ∠A 与∠4是一对_____________,其形成条件是( ).如果知道∠A+∠4=180°,也能判定AB ∥DC.证明过程如下:∵∠1+∠4=180°( )∠A+∠4=180°(已知)∴∠A=∠1(等量代换)∴AB ∥DC( )[归纳]平行线的判定方法3: 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简述为:_______________________________________四、能力提升:1.如图,推理填空:① ∵∠1=∠2 ∴____∥____( ) ② ∵∠A=∠3∴____∥____( )③ ∵∠A+∠ABC=180° ∴____∥____( )2. 如图,已知∠1=030,∠B=060,AB ⊥AC.①求证:AD ∥BC② 由已知条件,你能证明AB ∥DC 吗? 答:____________③ 添加一个条件:_________________,结合已知条件,求证:AB ∥DC.321D C B A 1D CB A五、课堂小结:位置关系数量关系平行线判定示意图判定六、当堂检测:1如图⑦,∠D=∠EFC,那么()A.AD∥BC B.AB∥CD C.EF∥BC D.AD∥EF2、如图⑧,判定AB∥EC的理由是()A.∠B=∠ACE B.∠A=∠ECD C.∠B=∠ACB D.∠A=∠ACE 3、如图⑨,下列推理正确的是()A.∵∠1=∠3,∴a∥b B.∵∠1=∠2,∴a∥bC.∵∠1=∠2,∴c∥d D.∵∠1=∠5,∴c∥d4、已知,如图∠1+∠2=180°,填空。
七年级下册《5.2.2 平行线的判定》教案、导学案、同步练习

《5.2.2平行线的判定》教案一第一课时【教学目标】:经历探索两直线平行条件的过程,理解两直线平行的条件. 【重点】:探索两直线平行的条件【难点】:理解“同位角相等,两条直线平行” 【教学过程】 一、情景导入.装修工人正在向墙上钉木条,如果木条b 与墙壁边缘垂直,那么木条a 与墙壁边缘所夹角为多少度时,才能使木条a 与木条b 平行?要解决这个问题,就要弄清楚平行的判定。
二、直线平行的条件以前我们学过用直尺和三角尺画平行线,如图(课本P13图5.2-5)在三角板移动的过程中,什么没有变?三角板经过点P 的边与靠在直尺上的边所成的角没有变。
简化图5.2-5,得图3.图3∠1与∠2是三角板经过点P 的边与靠在直尺上的边所成的角移动前后的位置,显然∠1与∠2是同位角并且它们相等,由此我们可以知道什么?两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行. 简单地说:同位角相等,两条直线平行. 符号语言:∵∠1=∠2∴AB ∥CD.如图(课本P145.2-7),你能说出木工用图中这种叫做角尺的工具画平行线的道理吗?用角尺画平行线,实际上是画出了两个直角,根据“同位角相等,两条直线D C BA平行.”,可知这样画出的就是平行线。
如图,(1)如果∠2=∠3,能得出a ∥b 吗?(2)如果∠2+∠4=1800,能得出a ∥b 吗?你能用文字语言概括上面的结论吗?两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行. 简单地说:内错角相等,两直线平行. 符号语言:∵∠2=∠3∴a ∥b.(2)∵∠4+∠2=180°,∠4+∠1=180°(已知) ∴∠2=∠1(同角的补角相等) ∴a ∥b.(同位角相等,两条直线平行) 你能用文字语言概括上面的结论吗?两条直线被第三条直线所截,如果同旁内角互补,那么两条直线平行. 简单地说:同旁内角互补,两直线平行. 符号语言:∵∠4+∠2=180°∴a ∥b. 四、课堂练习1、课本P15练习1,补充(3)由∠A+∠ABC =1800可以判断哪两条直线平行?依据是什么?2、课本P162题。
5.2.2平行线的判定导学案

c P ba4321c b a 21 5.2.2平行线的判定 学习目标:1、使学生掌握平行线的四种判定方法,并初步运用它们进行简单的推理论证。
2、初步学会简单的论证和推理,认识几何证明的必要性和证明过程的严密性。
重点:在观察实验的基础上进行公理的概括与定理的推导 难点:定理形成过程中的逻辑推理及其书面表达。
预习案 1、预习疑难: 。
2、填空:经过直线外一点,_____ ___与这条直线平行. 探究案 (一)平行线判定方法1: 1、观察思考:过点P 画直线CD ∥AB 的过程,三角尺起了什么作用?2、判定方法1应用格式: 1=∠2(已知) ∴AB ∥CD (同位角相等,两直线平行) 应用:木工师傅使用角尺画平行线,有什么道理? (二)平行线判定方法2、3: 1、 思考:教材判定方法2应用格式: 2=∠3(已知) ∴a ∥b (内错角相等,两直线平行) 2、将上题中条件改变为∠2+∠4=180°,能得到a ∥b 吗?(试写出推理过程) 判定方法应用格式:∵∠2+∠4=180°(已知)a ∥b (同旁内角互补,两直线平行) (三)数学思想:教材15页探究。
【反馈提高】(一)例 教材15页(二)练一练:教材15页练习1、2、3 (三)总结直线平行的条件 (1) (2)方法1:若a ∥b ,b ∥c ,则a ∥c 。
即两条直线都与第三条直线平行,这两条直线也互相平行。
方法2:如图1,若∠1=∠3,则a ∥c 。
即 。
方法3:如图1,若 。
方法4:如图1, 若 。
方法5:如图2,若a ⊥b ,a ⊥c,则b ∥c 。
即在同一平面内,垂直于同一条直线的两条直线互相平行。
训练案 (一)选择题:1.如图1所示,下列条件中,能判断AB ∥CD 的是( )A.∠BAD=∠BCDB.∠1=∠2;C.∠3=∠4D.∠BAC=∠ACD(1) (2) (3) (4) 2.如图2所示,如果∠D=∠EFC,那么( ) A.AD ∥BC B.EF ∥BC C.AB ∥DC D.AD ∥EF8765c b a 34123.下列说法错误的是( )A.同位角不一定相等B.内错角都相等C.同旁内角可能相等D.同旁内角互补,两直线平行4.(2000.江苏)如图5,直线a,b 被直线c 所截,现给出下列四个条件:•①∠1=∠-5;②∠1=∠7;③∠2+∠3=180°;④∠4=∠7.其中能说明a ∥b 的条件序号为( )(5) A.①② B.①③ C.①④ D.③④ (二)填空题:1.如图3,如果∠3=∠7,或____ __,那么______,理由是_____ _____;如果∠5=∠3,或___ ____,那么________, 理由是____ __________;如果∠2+ ∠5= ______ 或者______,那么a ∥b,理由是___ _____.2.如图4,若∠2=∠6,则______∥______,如果∠3+∠4+∠5+∠6=180°,那么____∥_______,如果∠9=_____,那么AD ∥BC;如果∠9=_____,那么AB ∥CD.3.在同一平面内,若直线a,b,c 满足a ⊥b,a ⊥c,则b 与c 的位置关系是______.4.如图所示,BE 是AB 的延长线,量得∠CBE=∠A=∠C.(1)由∠CBE=∠A 可以判断______∥______,根据是_________.(2)由∠CBE=∠C 可以判断______∥______,根据是_________.本节课你的收获 。
5.2.2《平行线的判定》导学案
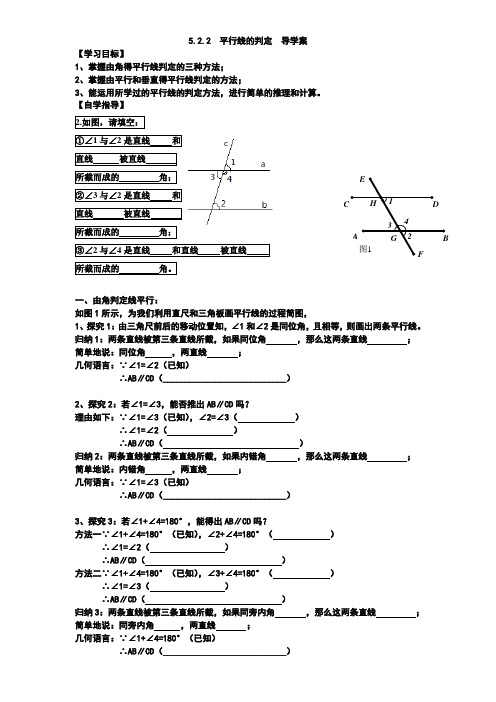
5.2.2 平行线的判定 导学案【学习目标】1、掌握由角得平行线判定的三种方法;2、掌握由平行和垂直得平行线判定的方法;3、能运用所学过的平行线的判定方法,进行简单的推理和计算。
【自学指导】 2.如图,请填空:①∠1与∠2是直线 和 直线 被直线 所截而成的 角; ②∠3与∠2是直线 和 直线 被直线 所截而成的 角;③∠2与∠4是直线 和直线 被直线 所截而成的 角。
一、由角判定线平行:如图1所示,为我们利用直尺和三角板画平行线的过程简图,1、探究1:由三角尺前后的移动位置知,∠1和∠2是同位角,且相等,则画出两条平行线。
归纳1:两条直线被第三条直线所截,如果同位角 ,那么这两条直线 ; 简单地说:同位角 ,两直线 ; 几何语言:∵∠1=∠2(已知)∴AB ∥CD (____________________________)2、探究2:若∠1=∠3,能否推出AB ∥CD 吗? 理由如下:∵∠1=∠3(已知),∠2=∠3( ) ∴∠1=∠2( )∴AB ∥CD ( )归纳2:两条直线被第三条直线所截,如果内错角 ,那么这两条直线 ; 简单地说:内错角 ,两直线 ; 几何语言:∵∠1=∠3(已知)∴AB ∥CD (____________________________)3、探究3:若∠1+∠4=180°,能得出AB ∥CD 吗? 方法一∵∠1+∠4=180°(已知),∠2+∠4=180°( ) ∴∠1=∠2( )∴AB ∥CD ( ) 方法二∵∠1+∠4=180°(已知),∠3+∠4=180°( ) ∴∠1=∠3( )∴AB ∥CD ( )归纳3:两条直线被第三条直线所截,如果同旁内角 ,那么这两条直线 ;简单地说:同旁内角 ,两直线 ; 几何语言:∵∠1+∠4=180°(已知)∴AB ∥CD (____________________________)4321图1G HCDABE F【练习1】1、如图4所示,可以判定直线a ∥b 的条件有 (至少写三个); 2.如图5所示,下列条件不能判定a ∥b 的是( )A.∠1=∠2B. ∠1=∠3C. ∠1+∠4=180°D. ∠2+∠4=180° 3.如图6所示,直线a 、b 都与直线c 相交,下列条件①∠1=∠2; ②∠3=∠6;③∠4+∠7=180°④∠5=∠8,其中能判断a ∥b 的条件有 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.如图2,若∠2=∠6,则______∥_______,如果∠3+∠4+∠5+∠6=180°,那么____∥_______,如果∠9=_____,那么AD∥BC,如果∠9=_____,那么AB∥CD。
5.如图3所示,下列条件中,不能判定AB∥CD的是( )
A. AB∥EF,CD∥EF
B.∠5=∠A
难点预设:直线平行的判定方法的应用。
学习过程
一、自学指导
认真阅读教材第14页思考到第15页的内容,完成下述问题。
1.判定方法2简称为_______ _______________________。
如图,符号语言描述:
∵∠1=∠2(已知)
∴AB∥CD()
2.判定方法3简称为__________ _____________________。
如图,符号语言描述:
∵∠1+∠2=180°(已知)
∴AB∥CD()
二、合作交流
针对“自学指导”部分的提问部分,请各小组讨论得出结论,并推选一名学生展示结果。对于仍然不理解的地方,再全班解决。
三、达标检测
1.继续完成教材15页例题(用符号语言描述)。
2.如图1,如果∠3=∠7,或____ __,那么______,理由是____;如果∠5=∠3,或________,那么________,理由是___ ___________;如果∠2+∠5= ______,或者_______,那么a∥b,理由是__________。
武汉市先锋中学初一数学导学案70522
主备人:授课人:授课时间:年月日第周
班级:姓名:检测评型
新授
学习目标
1、经历观察、想像、推理、交流等活动,发展空间观念、推理能力和表达能力;
2、经历探究直线平行条件的过程,掌握直线平行的条件,领悟数学思想方法。
重点难点
教学重点:探索并掌握直线平行的判定方法。
C.∠ABC+∠BCD=180°
D.∠2=∠3
图3
四、拓展延伸
如图,已知直线AB、BC、CD、DA相交于A、B、C、D四点,∠2+∠3=180°,求证:AB∥CD。
解:∵∠2=∠4,∠3=∠5()
∠2+∠3=180°(已知)
∴∠4+∠5=180°()
∴AB∥CD()
五、课堂收获与困惑点
备注(教师复备
或学生笔记)
