管理运筹学(本科)(参考答案)学习版.doc
管理运筹学答案.docx
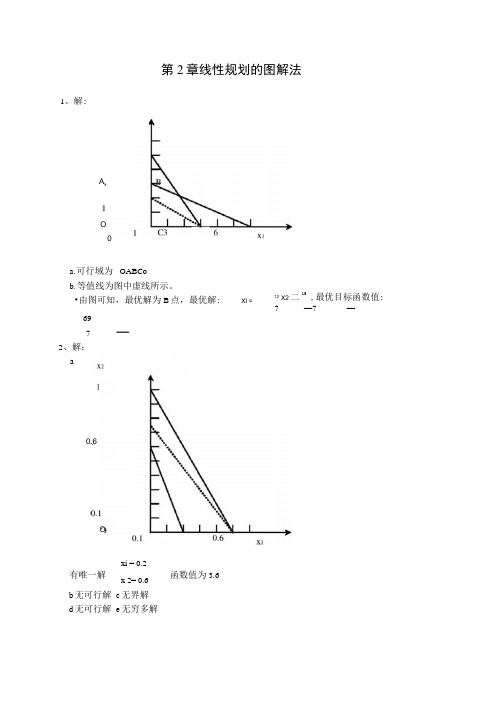
第2章线性规划的图解法1、解:12X2二15,最优目标函数值:7 —7—b 无可行解c 无界解d 无可行解e 无穷多解AO 0a. 可行域为b. 等值线为图中虚线所示。
OABCo69 0.6O72、解:axi = 0.2有唯一解x 2= 0.6函数值为3.6•由图可知,最优解为B 点,最优解:Xl =3、解:a 标准形式: max f = 3xi + 2 x 2 + Osi + 0 s 2 + Os 39 xi + 2 x 2 + si = 30 3xi + 2 x 2+ s 2= 13 2 xi+ 2x2 +S3 =9 X1 , X 2, Si , S 2, S3> 0max f = - xr+ 2 X2- 2 X2- Osi 一 0s2—3xi + 5 x 2— 5 x 2•+ si = 70 2 xr- 5 x‘2+ 5 x'2'= 50 3xr+ 2 x 2— 2 x T — S 2= 30 xr, X*2, X 21, Si , S 2> 03xi + 4 x 2 + si = 9 5 xi + 2 x 2+ s 2= 8 xi, x 2, si, s 2> 0f 有唯一解X2 =3函数值为—834、解:标准形式: max z = 10X 】 + 5X 2+0SI + 0S 2SI = 2, S2 = 0b 标准形式:max f = -4 xi - 6 X3- Osi - 0s23xi - x 2 - si = 6 XI + 2 X 2+ S 2= 10 7 xi - 6 x 2= 4 X1 , X 2, Si , S 2> 0c 标准形式:min f = 1 lxi + 8 x 2 + Osi + Os 2+ Os310 xi + 2 x 2- si = 20 3xi + 3x 2— s 2= 18 4XI + 9X 2-S3=36Xl,X2,Sl,S2,S3>0Si = 0, S2= 0, S3= 13 6、解:b 1 < ci< 3c 2 < C2 < 6xi = 6X2= 4e xi 丘[4,8] x 2= 16 - 2 xif 变化。
管理运筹学(第二版)课后习题参考答案

《管理运筹学》(第二版)课后习题参考答案第1章 线性规划(复习思考题)1.什么是线性规划?线性规划的三要素是什么?答:线性规划(Linear Programming ,LP )是运筹学中最成熟的一个分支,并且是应用最广泛的一个运筹学分支。
线性规划属于规划论中的静态规划,是一种重要的优化工具,能够解决有限资源的最佳分配问题。
建立线性规划问题要具备三要素:决策变量、约束条件、目标函数。
决策变量是决策问题待定的量值,取值一般为非负;约束条件是指决策变量取值时受到的各种资源条件的限制,保障决策方案的可行性;目标函数是决策者希望实现的目标,为决策变量的线性函数表达式,有的目标要实现极大值,有的则要求极小值。
2.求解线性规划问题时可能出现几种结果,哪种结果说明建模时有错误? 答:(1)唯一最优解:只有一个最优点; (2)多重最优解:无穷多个最优解;(3)无界解:可行域无界,目标值无限增大; (4)没有可行解:线性规划问题的可行域是空集。
当无界解和没有可行解时,可能是建模时有错。
3.什么是线性规划的标准型?松弛变量和剩余变量的管理含义是什么?答:线性规划的标准型是:目标函数极大化,约束条件为等式,右端常数项0≥i b ,决策变量满足非负性。
如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业来说不是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明“≥”型约束的左边取值大于右边规划值,出现剩余量。
4.试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关系。
答:可行解:满足约束条件0≥=X b AX ,的解,称为可行解。
基可行解:满足非负性约束的基解,称为基可行解。
可行基:对应于基可行解的基,称为可行基。
最优解:使目标函数最优的可行解,称为最优解。
最优基:最优解对应的基矩阵,称为最优基。
它们的相互关系如右图所示:5.用表格单纯形法求解如下线性规划。
s .t . ⎪⎩⎪⎨⎧≥≤++≤++0,,86238321321321x x x x x x x x x解:标准化 32124max x x x Z ++=s .t . ⎪⎩⎪⎨⎧≥=+++=+++0,,,,862385432153214321x x x x x x x x x x x x x 列出单纯形表故最优解为T X )6,0,2,0,0(*=,即2,0,0321===x x x ,此时最优值为4*)(=X Z . 6.表1—15中给出了求极大化问题的单纯形表,问表中d c c a a ,,,,2121为何值及变量属于哪一类型时有:(1)表中解为唯一最优解;(2)表中解为无穷多最优解之一;(3)下一步迭代将以1x 代替基变量5x ;(4)该线性规划问题具有无界解;(5)该线性规划问题无可行解。
管理运筹学课后习题答案

管理运筹学课后习题答案管理运筹学课后习题答案一、线性规划线性规划是管理运筹学中的一种重要方法,它通过建立数学模型,寻找最优解来解决实际问题。
下面我们来讨论一些常见的线性规划习题。
1. 一家工厂生产两种产品A和B,每单位产品A需要3小时的加工时间和2小时的装配时间,每单位产品B需要2小时的加工时间和4小时的装配时间。
工厂每天有8小时的加工时间和10小时的装配时间。
已知产品A的利润为300元,产品B的利润为400元。
如何安排生产,使得利润最大化?解答:设生产产品A的数量为x,生产产品B的数量为y。
根据题目中的条件,可以得到以下线性规划模型:目标函数:max 300x + 400y约束条件:3x + 2y ≤ 82x + 4y ≤ 10x, y ≥ 0通过求解上述线性规划模型,可以得到最优解,即生产4个产品A和1个产品B时,利润最大化,为2000元。
2. 一家超市有两种品牌的洗衣液,品牌A和品牌B。
品牌A每瓶售价20元,每瓶利润为5元;品牌B每瓶售价25元,每瓶利润为7元。
超市每天销售洗衣液的总利润不能超过100元,并且每天至少要销售10瓶洗衣液。
如何安排销售,使得利润最大化?解答:设销售品牌A的瓶数为x,销售品牌B的瓶数为y。
根据题目中的条件,可以得到以下线性规划模型:目标函数:max 5x + 7y约束条件:20x + 25y ≤ 100x + y ≥ 10x, y ≥ 0通过求解上述线性规划模型,可以得到最优解,即销售5瓶品牌A和5瓶品牌B时,利润最大化,为60元。
二、排队论排队论是管理运筹学中研究排队系统的一种方法,它通过数学模型和概率统计来分析和优化排队系统。
下面我们来讨论一些常见的排队论习题。
1. 一家银行有两个窗口,每个窗口的服务时间服从指数分布,平均服务时间分别为3分钟和4分钟。
顾客到达的间隔时间也服从指数分布,平均间隔时间为2分钟。
如果顾客到达时,两个窗口都有空闲,顾客会随机选择一个窗口进行服务。
管理运筹学(本科)(参考答案)

上交作业课程题目可以打印,答案必须手写,否则该门成绩0分。
管理运筹学 作业题一、名词解释(每题3分,共15分)1. 可行解:满足某线性规划所有的约束条件(指全部前约束条件和后约束条件)的任意一组决策变量的取值,都称为该线性规划的一个可行解,所有可行解构成的集合称为该线性规划的可行域(类似函数的定义域),记为K 。
2. 最优解:使某线性规划的目标函数达到最优值(最大值或最小值)的任一可行解,都称为该线性规划的一个最优解。
线性规划的最优解不一定唯一,若其有多个最优解,则所有最优解所构成的集合称为该线性规划的最优解域。
3. 状态:指每个阶段开始时所处的自然状态或客观条件。
4. 决策树:决策树(Decision Tree )是在已知各种情况发生概率的基础上,通过构成决策树来求取净现值的期望值大于等于零的概率,评价项目风险,判断其可行性的决策分析方法,是直观运用概率分析的一种图解法。
由于这种决策分支画成图形很像一棵树的枝干,故称决策树。
5. 最大最小准则:最大最小准则又称小中取大法或悲观法。
为不确定型决策的决策准则之一,其决策的原则是“小中取大”。
这种决策方法的思想是对事物抱有悲观和保守的态度,在各种最坏的可能结果中选择最好的。
决策时从决策表中各方案对各个状态的结果选出最小值,即在表的最右列,再从该列中选出最大者。
这种方法的基本态度是悲观与保守。
其基本思路是首先找出最不利情况下的最大收益。
二、 简答题(每题6分,共24分) 1. 简述单纯形法的基本步骤。
答:(1)把一般线形规划模型转换成标准型;(2)确定初始基可行解;(3)利用检验数j σ对初始基可行解进行最优性检验,若0≤j σ ,则求得最优解,否则,进行基变换;(4)基变换找新的可行基,通过确定入基变量和出基变量,求得新的基本可行解;(5)重复步骤(3)、(4)直至0≤j σ,求得最优解为止。
2. 简述动态规划的基本方程。
答:对于n 阶段的动态规划问题,在求子过程上的最优指标函数时,k 子过程与k+1过程有如下递推关系:对于可加性指标函数,基本方程可以写为n k s f x s r s f k k k k k s D x k k opt k k k ,,2,1)}(),({)(11)( =+=++∈终端条件:f n+1 (s n+1) = 0对于可乘性指标函数,基本方程可以写为n k s f x s r s f k k k k k s D x k k opt k k k ,,2,1)}(),({)(11)( =⨯=++∈终端条件:f n+1 (s n+1) = 13. 简述破圈法求最小生成树的步骤。
管理运筹学课后习题答案
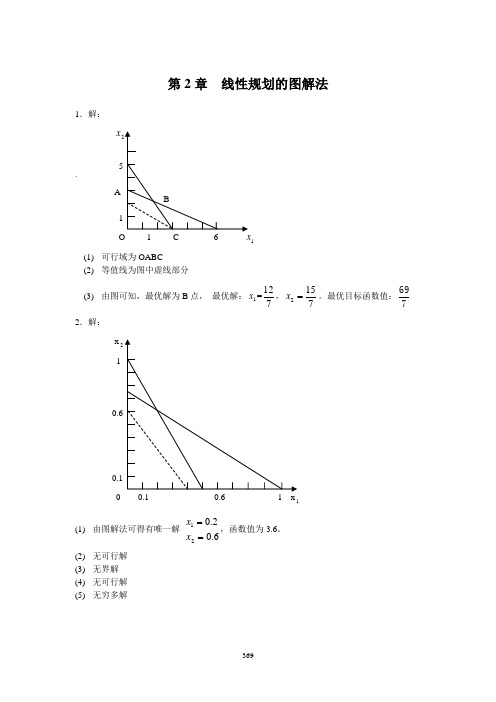
第2章 线性规划的图解法1.解:x`A 1 (1) 可行域为OABC(2) 等值线为图中虚线部分(3) 由图可知,最优解为B 点, 最优解:1x =712,7152=x 。
最优目标函数值:7692.解: x 2 10 1(1) 由图解法可得有唯一解 6.02.021==x x ,函数值为3.6。
(2) 无可行解 (3) 无界解 (4) 无可行解 (5)无穷多解(6) 有唯一解 3832021==x x ,函数值为392。
3.解:(1). 标准形式:3212100023m ax s s s x x f ++++=,,,,9221323302932121321221121≥=++=++=++s s s x x s x x s x x s x x(2). 标准形式:21210064m in s s x x f +++=,,,46710263212121221121≥=-=++=--s s x x x x s x x s x x(3). 标准形式:21''2'2'10022m in s s x x x f +++-=,,,,30223505527055321''2'2'12''2'2'1''2'2'11''2'21≥=--+=+-=+-+-s s x x x s x x x x x x s x x x4.解:标准形式:212100510m ax s s x x z +++=,,,8259432121221121≥=++=++s s x x s x x s x x松弛变量(0,0) 最优解为 1x =1,x 2=3/2.标准形式:32121000811m in s s s x x f ++++=,,,,369418332021032121321221121≥=-+=-+=-+s s s x x s x x s x x s x x剩余变量(0.0.13) 最优解为 x 1=1,x 2=5.6.解:(1) 最优解为 x 1=3,x 2=7. (2) 311<<c (3) 622<<c (4)4621==x x(5) 最优解为 x 1=8,x 2=0. (6) 不变化。
《管理运筹学》课后习题答案59页word
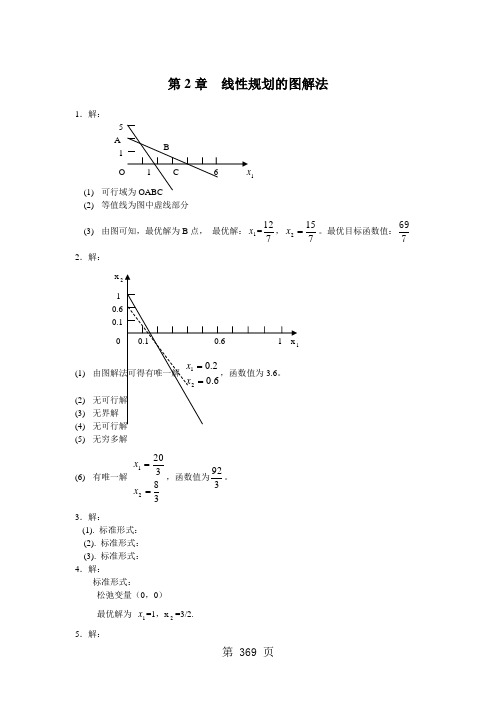
第2章 线性规划的图解法1.解: 5 A 11 (1) (2) 等值线为图中虚线部分(3) 由图可知,最优解为B 点, 最优解:1x =712,7152=x 。
最优目标函数值:7692.解: x 2 1 0(1) (2) (3) 无界解 (4) (5)无穷多解(6) 有唯一解 3832021==x x ,函数值为392。
3.解:(1). 标准形式: (2). 标准形式:(3). 标准形式: 4.解:标准形式:松弛变量(0,0) 最优解为 1x =1,x 2=3/2. 5.解:标准形式:剩余变量(0.0.13) 最优解为 x 1=1,x 2=5. 6.解:(1) 最优解为 x 1=3,x 2=7. (2) 最优解为 x 1=8,x 2=0. (3) 不变化。
因为当斜率31121-≤-≤-c c ,最优解不变,变化后斜率为1,所以最优解不变. 7.解:模型:(1) 1501=x ,702=x ,即目标函数最优值是103000 (2) 2,4有剩余,分别是330,15,均为松弛变量. (3) 50,0,200,0。
(4) 在[]500,0变化,最优解不变。
在400到正无穷变化,最优解不变. (5) 因为143045021-≤-=-c c ,所以原来的最优产品组合不变. 8.解:(1) 模型:b a x x f 38min +=基金a,b 分别为4000,10000,回报率为60000。
(2) 模型变为:b a x x z 45max +=推导出:180001=x 30002=x ,故基金a 投资90万,基金b 投资30万。
第3章 线性规划问题的计算机求解1.解:(1) 1501=x ,702=x 。
目标函数最优值103000。
(2) 1,3车间的加工工时已使用完;2,4车间的加工工时没用完;没用完的加工工时数为2车间330小时,4车间15小时. (3) 50,0,200,0含义:1车间每增加1工时,总利润增加50元;3车间每增加1工时,总利润增加200元;2车间与4车间每增加一个工时,总利润不增加。
《管理运筹学》复习题及参考答案

《管理运筹学》复习题及参考答案一、选择题1. 管理运筹学的研究对象是()A. 生产过程B. 管理活动C. 经济活动D. 运筹问题参考答案:D2. 以下哪个不属于管理运筹学的基本方法?()A. 线性规划B. 整数规划C. 非线性规划D. 人力资源规划参考答案:D3. 在线性规划中,约束条件是()A. 等式B. 不等式C. 方程组D. 矩阵参考答案:B4. 以下哪种方法不属于线性规划的对偶问题求解方法?()A. 单纯形法B. 对偶单纯形法C. 拉格朗日乘数法D. 牛顿法参考答案:D5. 在目标规划中,以下哪个不是目标约束的类型?()A. 等式约束B. 不等式约束C. 目标函数约束D. 线性约束参考答案:C二、填空题1. 管理运筹学的核心思想是______。
参考答案:最优化2. 在线性规划中,最优解存在的条件是______。
参考答案:可行性、有界性3. 整数规划的求解方法主要有______和______。
参考答案:分支定界法、动态规划法4. 在目标规划中,目标函数的求解方法有______、______和______。
参考答案:单纯形法、拉格朗日乘数法、动态规划法5. 非线性规划问题可以分为______、______和______。
参考答案:无约束非线性规划、约束非线性规划、非线性规划的对偶问题三、判断题1. 管理运筹学的研究对象是管理活动。
()参考答案:正确2. 在线性规划中,最优解一定存在。
()参考答案:错误3. 整数规划的求解方法比线性规划复杂。
()参考答案:正确4. 目标规划的求解方法与线性规划相同。
()参考答案:错误5. 非线性规划问题一定比线性规划问题复杂。
()参考答案:错误四、计算题1. 某工厂生产甲、乙两种产品,甲产品每件利润为10元,乙产品每件利润为8元。
生产甲产品每件需消耗2小时机器工作时间,3小时人工工作时间;生产乙产品每件需消耗1小时机器工作时间,2小时人工工作时间。
工厂每周最多可利用机器工作时间100小时,人工工作时间150小时。
管理运筹学(本科)(参考答案)学习版.doc

上交作业课程题目可以打印,答案必须手写,否则该门成绩0分。
管理运筹学 作业题一、名词解释(每题3分,共15分)1. 可行解:满足某线性规划所有的约束条件(指全部前约束条件和后约束条件)的任意一组决策变量的取值,都称为该线性规划的一个可行解,所有可行解构成的集合称为该线性规划的可行域(类似函数的定义域),记为K 。
2. 最优解:使某线性规划的目标函数达到最优值(最大值或最小值)的任一可行解,都称为该线性规划的一个最优解。
线性规划的最优解不一定唯一,若其有多个最优解,则所有最优解所构成的集合称为该线性规划的最优解域。
3. 状态:指每个阶段开始时所处的自然状态或客观条件。
4. 决策树:决策树(Decision Tree )是在已知各种情况发生概率的基础上,通过构成决策树来求取净现值的期望值大于等于零的概率,评价项目风险,判断其可行性的决策分析方法,是直观运用概率分析的一种图解法。
由于这种决策分支画成图形很像一棵树的枝干,故称决策树。
5. 最大最小准则:最大最小准则又称小中取大法或悲观法。
为不确定型决策的决策准则之一,其决策的原则是“小中取大”。
这种决策方法的思想是对事物抱有悲观和保守的态度,在各种最坏的可能结果中选择最好的。
决策时从决策表中各方案对各个状态的结果选出最小值,即在表的最右列,再从该列中选出最大者。
这种方法的基本态度是悲观与保守。
其基本思路是首先找出最不利情况下的最大收益。
二、 简答题(每题6分,共24分) 1. 简述单纯形法的基本步骤。
答:(1)把一般线形规划模型转换成标准型;(2)确定初始基可行解;(3)利用检验数j σ对初始基可行解进行最优性检验,若0≤j σ ,则求得最优解,否则,进行基变换;(4)基变换找新的可行基,通过确定入基变量和出基变量,求得新的基本可行解;(5)重复步骤(3)、(4)直至0≤j σ,求得最优解为止。
2. 简述动态规划的基本方程。
答:对于n 阶段的动态规划问题,在求子过程上的最优指标函数时,k 子过程与k+1过程有如下递推关系:对于可加性指标函数,基本方程可以写为n k s f x s r s f k k k k k s D x k k opt k k k ,,2,1)}(),({)(11)( =+=++∈终端条件:f n+1 (s n+1) = 0对于可乘性指标函数,基本方程可以写为n k s f x s r s f k k k k k s D x k k opt k k k ,,2,1)}(),({)(11)( =⨯=++∈终端条件:f n+1 (s n+1) = 13. 简述破圈法求最小生成树的步骤。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上交作业课程题目可以打印,答案必须手写,否则该门成绩0分。
管理运筹学 作业题
一、名词解释(每题3分,共15分)
1. 可行解:满足某线性规划所有的约束条件(指全部前约束条件和后约束条件)的任意一
组决策变量的取值,都称为该线性规划的一个可行解,所有可行解构成的集合称为该线性规划的可行域(类似函数的定义域),记为K 。
2. 最优解:使某线性规划的目标函数达到最优值(最大值或最小值)的任一可行解,都称
为该线性规划的一个最优解。
线性规划的最优解不一定唯一,若其有多个最优解,则所有最优解所构成的集合称为该线性规划的最优解域。
3. 状态:指每个阶段开始时所处的自然状态或客观条件。
4. 决策树:决策树(Decision Tree )是在已知各种情况发生概率的基础上,通过构成决策
树来求取净现值的期望值大于等于零的概率,评价项目风险,判断其可行性的决策分析方法,是直观运用概率分析的一种图解法。
由于这种决策分支画成图形很像一棵树的枝干,故称决策树。
5. 最大最小准则:最大最小准则又称小中取大法或悲观法。
为不确定型决策的决策准则之
一,其决策的原则是“小中取大”。
这种决策方法的思想是对事物抱有悲观和保守的态度,在各种最坏的可能结果中选择最好的。
决策时从决策表中各方案对各个状态的结果选出最小值,即在表的最右列,再从该列中选出最大者。
这种方法的基本态度是悲观与保守。
其基本思路是首先找出最不利情况下的最大收益。
二、 简答题(每题6分,共24分) 1. 简述单纯形法的基本步骤。
答:(1)把一般线形规划模型转换成标准型;(2)确定初始基可行解;(3)利用检验数j σ对初始基可行解进行最优性检验,若0≤j σ ,则求得最优解,否则,进行基变换;(4)基变换找新的可行基,通过确定入基变量和出基变量,求得新的基本可行解;(5)重复步骤(3)、(4)直至0≤j σ,求得最优解为止。
2. 简述动态规划的基本方程。
答:对于n 阶段的动态规划问题,在求子过程上的最优指标函数时,k 子过程与k+1过程有如下递推关系:
对于可加性指标函数,基本方程可以写为
n k s f x s r s f k k k k k s D x k k opt k k k ,,2,1)}(),({)(11)
( =+=++∈
终端条件:f n+1 (s n+1) = 0
对于可乘性指标函数,基本方程可以写为
n k s f x s r s f k k k k k s D x k k opt k k k ,,2,1)}
(),({)(11)
( =⨯=++∈
终端条件:f n+1 (s n+1) = 1
3. 简述破圈法求最小生成树的步骤。
答:第1 步: 令i=1, E0=Φ, G0=G;第2 步: 取边ei ∈E ( Gi- 1) 即E\Ei- 1, 令Ei =Ei- 1∪{ei}, 使得Gi= G [E\Ei] 连通, 且W ( ei) 权尽可能大; 第3 步: 若i<e- n+1, 令i=i+1, 返回第2 步,否则, Gi= G [E\Ei] 把Ei 中的边全部删除, 即是所求的最小支撑树。
4. 如何找计划网络图的关键路线?
答:关键线路就是由总时差为0的工作所组成的、各工作总的持续时间最长的线路。
(1)利用关键工作确定关键线路。
总时差最小的工作为关键工作。
将这些关键工作相连,并保证相邻两项关键工作之间的时间间隔为零而构成的线路就是关键线路。
(2)利用相邻两项工作之间的时间间隔确定关键线路。
从网络计划的终点节点开始,逆着箭线方向依次找出相邻两项工作之间时间间隔为零的线路就是关键线路。
三、计算题(1题13分,2、3、4题16分,共61分)
1. 利用单纯形法求下列线形规划问题的最优解
21x x 2z m ax +=
t s . ⎪⎪⎩
⎪⎪⎨⎧≥≤+≤+0x ,x 24x 2x 615x 5x 3212
121
解:(1)加入松弛变量43,x x 得到该线形规划问题的标准型
212m ax x x z +=
⎪⎩⎪
⎨⎧≥=++=++0,,,242615
534
321421321x x x x x x x x x x
最优解T
X )0,0,4/3,4/15(*
=,4/33*
=Z
2. 某工厂要用三种原料A 、B 、C 加工成三种不同规格的产品甲、乙、丙。
已知三种产品中A 、B 、C 原料的规格要求及三种产品的销售价格,见表1。
同时已知三种原料成本和各种原料的月供应量,如表2所示。
问:该厂应如何安排生产,使其利润为最大?试建立这个问题的数学模型。
表1
表2
解:设xij 为生产i 种面包所使用的j 种原材料数,i=1,2,3分别代表甲、乙、
丙,j=1,2,3分别代表A 、B 、C 。
其数学模型为:
max z=(3.40-0.50)(x11+x12+x13)+(2.85-0.40)(x21+x22+x23)+(2.25-0.30) (x31+x32+x33)-2.00(x11+x21+x31)-1.50(x12+x22+x32)-1.00(x13+x23+x33)
3. 某公司拟将某种设备5台,分配给所属的甲、乙、丙三个工厂,各工厂获得此设备后,预测可创造的利润如表3所示。
问这5台设备应如何分配给这3个工厂,使得所创造的总利润最大?
工厂
盈利
甲厂乙厂丙厂设备台数
0 0 0 0
1 3 5 4
2 7 10 6
3 9 11 11
4 12 11 12
5 13 11 12 解:
4. 某电信公司准备在甲、乙两地沿路架设一条光缆线,下图给出了甲乙两地间的交通图,权数表示两地间公路的长度,利用Dijkstra算法分析如何架设使其光缆线路最短?(单位:公里)。
v 2
3
5 2
7
5
3
1
5
1
2
v 1
甲地
v 6
乙地
v 5
v v 4。
