浙大博弈论考试题目
博弈期末考试题及答案

博弈期末考试题及答案一、选择题(每题2分,共20分)1. 博弈论中的“纳什均衡”是由哪位数学家提出的?A. 约翰·冯·诺伊曼B. 约翰·纳什C. 保罗·萨缪尔森D. 托马斯·谢林2. 以下哪个不是博弈论中的基本概念?A. 策略B. 收益C. 风险D. 均衡3. 在零和博弈中,一个玩家的损失等于另一个玩家的收益,那么这种博弈的总收益是:A. 正数B. 零C. 负数D. 无法确定4. 囚徒困境中,如果两个囚犯都选择背叛对方,那么:A. 他们都会受到最轻的惩罚B. 他们都会受到最重的惩罚C. 一个受到轻罚,另一个受到重罚D. 一个受到重罚,另一个获得释放5. 以下哪个是博弈论中的动态博弈?A. 石头剪刀布B. 囚徒困境C. 拍卖博弈D. 猎鹿博弈...(此处省略其他选择题)二、简答题(每题10分,共30分)1. 简述博弈论中的完全信息博弈和不完全信息博弈的区别。
2. 解释什么是“混合策略纳什均衡”,并给出一个例子。
3. 描述“公共品博弈”中的囚徒困境现象。
三、计算题(每题15分,共30分)1. 假设有两个玩家A和B,他们可以选择策略X或Y。
收益矩阵如下所示:| | X | Y |||||| X | 3,3 | 2,5 || Y | 5,2 | 4,4 |请计算并找出所有可能的纳什均衡。
2. 考虑一个重复博弈,其中两个玩家在每一轮中可以选择合作或背叛。
如果双方合作,他们各自获得收益R。
如果一方背叛而另一方合作,背叛者获得收益T,合作者获得收益S。
如果双方都背叛,他们各自获得收益P。
已知2R > T + S > R > P。
请证明在无限重复博弈中,存在一个策略组合,使得双方的长期收益都高于单次博弈的背叛收益。
四、论述题(20分)1. 论述博弈论在经济学中的应用,并给出两个具体的例子。
博弈期末考试题答案一、选择题答案1. B2. C3. B4. B5. D...(此处省略其他选择题答案)二、简答题答案1. 完全信息博弈是指所有玩家都完全知道博弈的结构和其他玩家的收益函数,而不完全信息博弈是指至少有一个玩家对博弈的结构或其它玩家的收益函数不完全了解。
博弈论期末考试试题及答案

博弈论期末考试试题及答案# 博弈论期末考试试题及答案一、选择题(每题2分,共20分)1. 博弈论中,参与者在没有沟通的情况下进行决策,这种博弈被称为:A. 完全信息博弈B. 不完全信息博弈C. 零和博弈D. 非零和博弈答案:B2. 纳什均衡是博弈论中的一个概念,它描述了一种什么样的状态?A. 所有参与者都获得最大收益的状态B. 至少有一个参与者能获得更大收益的状态C. 没有参与者能通过单方面改变策略来获得更大收益的状态D. 所有参与者都获得相同收益的状态答案:C3. 以下哪个不是博弈论中的策略类型?A. 纯策略B. 混合策略C. 随机策略D. 确定性策略答案:D4. 博弈论中的囚徒困境指的是:A. 参与者合作可以获得最优结果B. 参与者背叛可以获得最优结果C. 参与者合作可以获得次优结果,但背叛可以获得最优结果D. 参与者背叛可以获得次优结果,但合作可以获得最优结果答案:C5. 以下哪个不是博弈论中的基本概念?A. 参与者B. 策略C. 收益D. 概率答案:D...二、简答题(每题10分,共30分)1. 解释什么是博弈论,并给出一个实际生活中的例子。
答案:博弈论是研究具有冲突和合作特征的决策者之间互动的数学理论。
在实际生活中,博弈论的一个例子是拍卖。
在拍卖中,买家(参与者)需要决定出价(策略)以赢得商品(收益),同时考虑其他买家的出价策略。
2. 描述纳什均衡的概念,并解释为什么它在博弈论中如此重要。
答案:纳什均衡是指在非合作博弈中,每个参与者选择自己的最优策略,并且考虑到其他参与者的策略选择时,没有参与者能通过单方面改变策略来获得更大的收益。
纳什均衡在博弈论中非常重要,因为它提供了一种预测参与者行为的方法,即在均衡状态下,参与者没有动机去改变他们的策略。
3. 什么是完全信息博弈和不完全信息博弈?它们之间有什么区别?答案:完全信息博弈是指所有参与者都完全知道博弈的结构和其他参与者的收益函数。
而不完全信息博弈是指至少有一个参与者对博弈的结构或其它参与者的收益函数不完全了解。
浙江大学经济学院博士生博弈论课程习题及答案

纳什均衡1.在下表所示的战略式博弈中,找出重复删除劣战略的占优均衡表1.1首先,找出S2的劣战略。
对于S2,M策略严格劣于R策略,所以M为严格劣策略。
删除后M再找出S1的劣战略,显然对于S1而言,M策略和D策略严格劣于U策略,所以M和D为严格劣策略。
删除M与D后找占优均衡为(U,L)即,(4,3)。
2.求解下表所示的战略博弈式的所有的纯战略纳什均衡表1.2首先看S1选择X策略。
如果S2同样选择X策略,那么S3一定选择Y策略;同样,如果S3选择Y策略,S2也一定会选择X策略,因此(X,X,Y)是一个纳什均衡;如果S2选择Y策略,那么S3一定选择X策略;同样,如果S3选择X策略,S2也一定会选择Y策略,因此,(X,Y,X)是一个纳什均衡。
其次看S1选择Y策略。
如果S2选择X策略,S3一定选择X策略;同样,如果S3选择X策略,S2也一定会选择X策略,因此(Y,X,X)是一个纳什么均衡。
如果S2选择Y策略,S3选择Y策略是理性的,如果S3选择X,S2将选择X,这样(Y,Y,X)将不是一个纳什均衡;同样,如果S3选择Y策略,S2也一定会选择Y策略,因此(Y,Y,Y)是一个纳什均衡。
所以该博弈式的纯战略纳什均衡有4个:(X,X,Y)(X,Y,X)(Y,X,X)(Y,Y,Y)。
3.(投票博弈)假定有三个参与人(1、2和3)要在三个项目(A、B和C)中选中一个。
三人同时投票,不允许弃权,因此,每个参与人的战略空间Si={A,B,C}。
得票最多的项目被选中,如果没有任何项目得到多数票,项目A被选中。
参与人的支付函数如下:U1(A)=U2(B)=U3(C)=2U1(B)=U2(C)=U3(A)=1U1(C)=U2(A)=U3(B)=0求解以上博弈的所有纯战略纳什均衡。
由上,ABC策略是无差异的,但均衡策略只能是参与人3选择A 策略,因此(A ,A ,A )是一个纳什均衡。
如果参与人2选择B 策略,参与人3选择AB 策略是差异的,但均衡策略只能是其选择A ,因此(A ,B ,A )是一个纳什均衡。
大学博弈论试题及答案

大学博弈论试题及答案一、选择题(每题2分,共20分)1. 在博弈论中,非合作博弈是指:A. 参与者之间可以达成协议B. 参与者之间不能达成协议C. 参与者之间必须达成协议D. 参与者之间只能通过合作达到目标答案:B2. 纳什均衡是博弈论中的一个概念,它描述了一种情况,即:A. 所有参与者都处于最优策略B. 至少有一个参与者处于非最优策略C. 所有参与者都处于非最优策略D. 至少有一个参与者可以单方面改变策略以获得更好的结果答案:A3. 囚徒困境中,如果两个参与者都选择合作,那么:A. 他们都将获得最大收益B. 他们都将获得最小收益C. 他们都将获得中等收益D. 他们中的一个将获得最大收益,另一个获得最小收益答案:C4. 零和博弈是指:A. 一个参与者的收益等于另一个参与者的损失B. 参与者的总收益为零C. 参与者的总损失为零D. 参与者的总收益和总损失相等答案:B5. 在博弈论中,策略是指:A. 参与者的行动计划B. 参与者的收益C. 参与者的损失D. 参与者的支付结构答案:A6. 博弈论中的“混合策略”是指:A. 参与者随机选择策略B. 参与者总是选择相同的策略C. 参与者的策略是固定的D. 参与者的策略是预先确定的答案:A7. 博弈论中的“支配策略”是指:A. 无论对手选择什么策略,都是最优的策略B. 只有在特定情况下才是最优的策略C. 只有在对手选择特定策略时才是最优的策略D. 参与者总是选择的策略答案:A8. 博弈论中的“重复博弈”是指:A. 博弈只进行一次B. 博弈进行多次,但每次都是独立的C. 博弈进行多次,且参与者的记忆会影响后续决策D. 博弈进行多次,但参与者不能记住之前的决策答案:C9. 在博弈论中,如果一个策略在任何情况下都不是最优的,那么这个策略被称为:A. 支配策略B. 支配策略的反面C. 支配策略的替代D. 非支配策略答案:B10. 博弈论中的“共同知识”是指:A. 所有参与者都知道的信息B. 只有部分参与者知道的信息C. 参与者之间的秘密D. 参与者之间共享的信念答案:A二、填空题(每题2分,共20分)1. 在博弈论中,如果一个策略在任何情况下都不是最优的,那么这个策略被称为________。
博弈论十五道题以及答案

博弈论十五道题以及答案1.博弈理论在哪些方面扩展了传统的新古典经济学?2.法律和信誉是维持市场有序运行的两个基本机制。
请结合重复博弈理论谈谈信誉机制发生作用的几个条件。
3.经济发展史表明,在本来不认识的人之间建立相互之间的信任关系是经济发展的关键。
为什么?4.在传统社会中,即使没有法律,村民之间也可以建立起高度的信任。
请结合博弈理论解释其原因。
5.在旅游地很容易出现假货,而在居民小区的便利店则很少出现假货,请结合博弈论的相关理论进行解释。
6.你如何理解“Credible threats or promises about future behavior can influence current behavior”这句话的?7.有效的法律制度对经济发展具有什么作用?请结合博弈理论谈谈你的理解。
8.试用博弈理论解释家族企业为什么难以实行制度化管理?9.固定资产投资为什么可以作为一种可置信的承诺?10.以汽车保险为例谈谈因为信息不对称所可能产生的道德风险问题,并提出一种解决道德风险的方案。
11.以公司为例,谈谈所有者与经营者的分离可能产生的道德风险问题。
12.在波纳佩岛上,谁能种出特别大的山药,谁的社会地位就高,谁就能赢得人们的尊敬并可担任公共职务。
请结合信号传递模型谈谈波纳佩岛上的这种奇异风俗。
13.一位男生在女朋友过生日时送给女朋友三百元人民币,他的女朋友往往感觉受到了侮辱。
而他女朋友可能会欣然接受父母亲的现金礼物。
请解释其中可能的原因。
14.<圣经>(旧约)中记载了两个母亲争夺一个孩子的故事。
一次,两个女人为争夺一个婴儿争扯到所罗门王殿前,她们都说婴儿是自己的,请所罗门王作主。
所罗门王稍加思考后作出决定:将婴儿一刀劈为两段,两位妇人各得一半。
这时,其中一位妇人立即要求所罗门王将婴儿判给对方,并说婴儿不是自己的,应完整归还给另一位妇人,千万别将婴儿劈成两半。
听罢这位妇人的求诉,所罗门王立即作出最终裁决——婴儿是这位请求不杀婴儿的妇人的,应归于她。
博弈论试题及答案

博弈论试题及答案【正文】博弈论试题及答案一、选择题1.博弈论是研究:A. 地理分布B. 人类视力C. 决策制定D. 古典文学答案:C2.下列哪个不是博弈论中常见的概念?A. 纳什均衡B. 优势策略C. 输家效应D. 零和博弈答案:C3.描述纳什均衡的最佳方式是:A. 所有参与者都达到最佳策略B. 至少有一个参与者达到最佳策略C. 所有参与者都达到次优策略D. 至少有一个参与者达到次优策略答案:A4.下列哪个案例体现了零和博弈的情况?A. 两国签订贸易协定B. 赌徒在赌博中争夺赌注C. 两家公司合作推出新产品D. 好友一起玩棋盘游戏答案:B5.下列哪个不是博弈论的应用之一?A. 经济决策B. 政治博弈C. 生物进化D. 音乐创作答案:D二、填空题1.博弈论最早由_____________等人于20世纪40年代提出。
答案:冯·诺依曼(John von Neumann)2.博弈论是研究参与者间的_____________和_____________的学科。
答案:互动行为;决策制定3.零和博弈是指参与者的利益总和恒为_____________。
答案:零4.博弈论中的最佳策略指的是在其他参与者采取某个策略时,使某一参与者的_____________最大化的策略。
答案:利益5.斯坦福大学的_____________教授以其对博弈论的突出贡献而获得2005年诺贝尔经济学奖。
答案:约翰·纳什(John Nash)三、简答题1.简要解释博弈论中的纳什均衡。
答:纳什均衡是博弈论中的一个重要概念,指的是在参与者选择自己最佳策略的情况下,不存在任何一个参与者可以通过单独改变自己的策略来获得更好收益的状态。
简言之,纳什均衡是一种理性选择下的稳定状态。
2.举例说明博弈论在实际生活中的应用。
答:博弈论在经济学、政治学、生物学等领域中都有广泛应用。
例如,在贸易谈判中,两个国家之间的博弈就是典型的博弈论应用。
博弈论考试题及答案

博弈论考试题及答案一、选择题(每题2分,共20分)1. 博弈论中的“囚徒困境”是指什么?A. 两个囚犯相互合作B. 两个囚犯相互背叛C. 两个囚犯中一个合作一个背叛D. 两个囚犯相互猜疑答案:B2. 以下哪个不是博弈论中的基本概念?A. 策略B. 收益C. 公平D. 纳什均衡答案:C3. 在零和博弈中,一个玩家的损失等于另一个玩家的收益,这意味着:A. 总收益为零B. 总收益为正C. 总收益为负D. 总收益不确定答案:A4. 博弈论中的“混合策略”是指:A. 玩家随机选择策略B. 玩家固定选择一种策略C. 玩家根据对手的策略选择策略D. 玩家不使用策略答案:A5. 以下哪个是博弈论中的“完全信息”博弈?A. 拍卖博弈B. 石头剪刀布C. 桥牌D. 信息不对称博弈答案:C6. 博弈论中的“重复博弈”指的是:A. 博弈只进行一次B. 博弈进行多次C. 博弈进行无限次D. 博弈进行有限次但次数未知答案:B7. 以下哪个是博弈论中的“动态博弈”?A. 零和博弈B. 非零和博弈C. 同时博弈D. 顺序博弈答案:D8. 在博弈论中,如果一个策略组合是纳什均衡,那么:A. 每个玩家都有动机单方面改变策略B. 每个玩家都满足于当前策略C. 至少有一个玩家不满意当前策略D. 所有玩家都不满意当前策略答案:B9. 博弈论中的“合作博弈”是指:A. 玩家之间可以形成联盟B. 玩家之间不能形成联盟C. 玩家之间只能通过竞争来获得收益D. 玩家之间只能通过合作来获得收益答案:A10. 以下哪个是博弈论中的“公共知识”?A. 每个玩家的收益函数B. 每个玩家的策略选择C. 每个玩家的偏好D. 每个玩家的个人信息答案:A二、简答题(每题10分,共30分)1. 简述博弈论中的“纳什均衡”概念。
答案:纳什均衡是指在一个博弈中,每个玩家都选择了自己的最优策略,并且没有玩家能够通过单方面改变策略来提高自己的收益。
在纳什均衡状态下,每个玩家的策略是对其他玩家策略的最优反应。
浙江大学经济学院博士生博弈论课程习题及答案
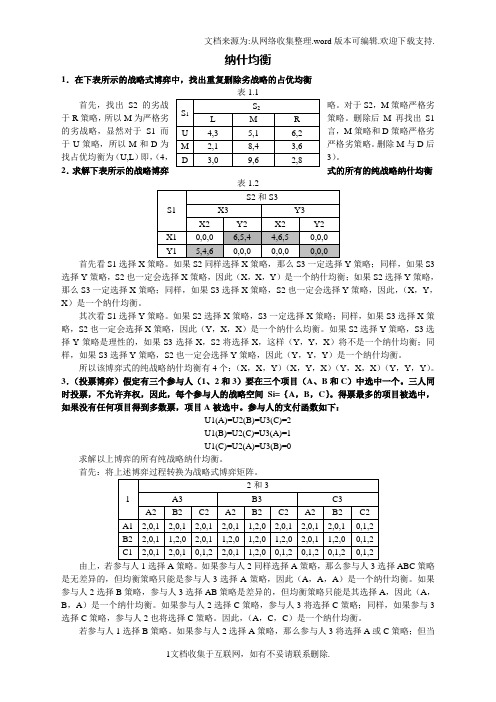
纳什均衡1.在下表所示的战略式博弈中,找出重复删除劣战略的占优均衡表1.1于R策略,所以M为严格劣策略。
删除后M再找出S1的劣战略,显然对于S1而言,M策略和D策略严格劣于U策略,所以M和D为严格劣策略。
删除M与D后找占优均衡为(U,L)即,(4,3)。
2.求解下表所示的战略博弈式的所有的纯战略纳什均衡表1.2首先看S1选择X策略。
如果S2同样选择X策略,那么S3一定选择Y策略;同样,如果S3选择Y策略,S2也一定会选择X策略,因此(X,X,Y)是一个纳什均衡;如果S2选择Y策略,那么S3一定选择X策略;同样,如果S3选择X策略,S2也一定会选择Y策略,因此,(X,Y,X)是一个纳什均衡。
其次看S1选择Y策略。
如果S2选择X策略,S3一定选择X策略;同样,如果S3选择X策略,S2也一定会选择X策略,因此(Y,X,X)是一个纳什么均衡。
如果S2选择Y策略,S3选择Y策略是理性的,如果S3选择X,S2将选择X,这样(Y,Y,X)将不是一个纳什均衡;同样,如果S3选择Y策略,S2也一定会选择Y策略,因此(Y,Y,Y)是一个纳什均衡。
所以该博弈式的纯战略纳什均衡有4个:(X,X,Y)(X,Y,X)(Y,X,X)(Y,Y,Y)。
3.(投票博弈)假定有三个参与人(1、2和3)要在三个项目(A、B和C)中选中一个。
三人同时投票,不允许弃权,因此,每个参与人的战略空间Si={A,B,C}。
得票最多的项目被选中,如果没有任何项目得到多数票,项目A被选中。
参与人的支付函数如下:U1(A)=U2(B)=U3(C)=2U1(B)=U2(C)=U3(A)=1U1(C)=U2(A)=U3(B)=0求解以上博弈的所有纯战略纳什均衡。
由上,若参与人1选择A策略。
如果参与人2同样选择A策略,那么参与人3选择ABC策略是无差异的,但均衡策略只能是参与人3选择A策略,因此(A,A,A)是一个纳什均衡。
如果参与人2选择B策略,参与人3选择AB策略是差异的,但均衡策略只能是其选择A,因此(A,B,A)是一个纳什均衡。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
博弈论考试1、完全信息静态博弈1“老师点名和学生逃课”的案例构建如下模型:老师点名不点名学生逃课a1,b1 a2,b2不逃课a3,b3 a4,b4结果:(1)老师每次点名,学生每次不逃课a3> a1 ,b3> b4 ,a2< a4 ,b2< b1(2)老师每次不点名,学生每次不逃课a4> a2 , b4> b3 , a1< a3 , b1< b2(3)老师有时候点名,学生有时候逃课a1< a3 , a2> a4 , b1> b2 , b3< b4(4)老师每次不点名,学生每次逃课a2> a4 , b2> b1 , a3< a1 , b3< b42市场占有者和想进入市场者构建模型:占有者默认斗争进入者进入(40,50)(-10,0)不进入(0,300)(0,300)没有占优战略均衡,也没有重复剔除的占优均衡。
结果:(1)占有者默认,进入者进入时,占有者会损失部分利益(2)占有者斗争,进入者进入,则占有者利益变0,而进入者为负,两败俱伤,因而占有者“斗争”是弱劣战略。
(3)占优者默认,进入者不进入,则占有者获得全部市场(4)(斗争,不进入时,占有者仍获得全部市场。
综上存在两个纳什均衡,(进入,默认)和(不进入,斗争)3应试教育和素质教育学生应试教育素质教育学校应试教育(0,0)(0,-1)素质教育(-1,0)(1,1)(1)假设学校和学生都采取应试教育为(0,0),那么若他们都转向素质教育达到最优结局(1,1),(2)但如果单方面采取素质教育,另一方为应试教育,其支付就变为-1,比如如果学校重视应试成绩,而学生重视素质教育,学生单方面受损,为-1 (3)若学校注重素质教育,而学生只注重成绩,学校的策略难以推行,支付为-1.此博弈中存在两个纳什均衡,即(应试,应试)和(素质,素质),虽然(素质,素质)是最优纳什均衡,但一方采取素质教育存在风险:另一方为应试时,支付变为-1;若采取应试没有变为-1的风险,那么最终结局为(应试,应试)。
4两个人合作开发一项产品假设项目开发成功每人收益为4,失败时收益为0,偷懒者的机会成本为1参与人2努力偷懒参与人1 努力9/16 3/8偷懒3/8 1/4(1)双方都努力的期望收益W=9/16*4-1=(2)自己偷懒对方努力:W=3/8*4=(3)自己努力,对方偷懒:3/8*4-1=(4)双方偷懒:W=1/4*4=1所以此博弈的收益矩阵分布为:努力偷懒努力偷懒1/1由此可见,偷懒成了最优策略5公共物品的供给问题(基础设施的建设)B建设不建设A 建设3,3 2,4不建设4,2 1,1当两者都建设时,是(3,3)当A建设,B不建设时,(2,4),B的利益大,A损失了部分利益当两者都不建设时,(1,1),是弱劣战略当A不建设,B建设时,(4,2)B损失了部分利益但是人们都是为了追求人类利益最大化的,最终会造成(不建设,不建设)的困境,也是典型的多劳不多得。
6中国政府于电信企业的博弈政府采用的策略不激励激励电信企业维持原状6,6 7,5技术改进5,9 8,7无论电信企业采取何种战略,“不激励”都是政府的占优策略。
(1)有纳什均衡(维持原状,不激励)是非合作博弈(2)电信维持原状,政府激励时,(7,5)政府损失部分利益(3)电信改进,政府不采取时,(5,9)电信有损失我们可以看出实际上(8,7)是最优战略,但他们都从“个体理性”出发,追求个人利益最大化,而得到了不好的结果。
2、过犹不及(1)竞技体育运动员B c指损失,a指收益激进(概率为q) 平和运动员A 激进a-c,a-c 2a,0平和0,2a a,a当a>c,采用激进—激进纯战略纳什均衡当a<c(先动优势),P=a/c同时出招,a-c<0时,W(A激进)=(a-c)*q+2a(1-q)为期望收益W(A平和)=0*q+a(1-q)当两者相等时,得出q=a/c 当a增加时,q增加;c增加时,q下降W(A平和)=a(1-q)=a(1-a/c)画图,当a增加时,可得出c/2是一个临界点,当>c/2时,太过于激进,收益反而下降,所以运动员在竞争时,尽力是好的,但过度激进,比如服用兴奋剂,反而会使运动生涯过早的结束。
(2)卖假烟卖假烟者A限量过量卖假烟者B 限量a,a 0,2a过量2a,0 a-c,a-cC指损失,a指卖假烟的收益,分析照上面,当P=a/c时为均衡点现在山寨是很流行的,卖假烟在一定程度上不能认为是违法行为的,有时可以缓解经济压力、充面子等,当然这只限于假烟的销量控制在一定范围内,如果过量造成假烟泛滥,则会使市场变得混乱,收益反而会下降,而贩卖假烟本身也可能因此坐牢,这是危害社会和个人的事情。
(3)腾讯QQ和360之间的竞争QQ(退)和平相处过度竞争(进)PA 360 和平相处PB 0,0 2,0过度竞争2,0 -3,-3E(B退)=P(A进)*0+P(A退)*0 E(B进)=P(A进)*-3+ P(A退)*-2当两者相等时,得出P(A进)= P(A退)=P(B进)= P(B退)=两者都选择和平共处时是(0,0),然而当它们都为自己的利益而过度竞争,相互斗争时,收益反而下降,它们的用户大量减少,这是双方都受损的情况,因而过度反而是不对的。
(4)对美国“”事件的态度官员A鹰鸽官员B 鹰2,2 10,0鸽0,10 5,5最好的是自己选择鹰战略,对方选择鸽战略鸽派立足美国自身做出反思,主张从自身寻找消除恐怖主义的途径,在国际关系中奉行多边合作,促进美国发展;但鹰派相反,更加强硬,主张先发制人消除威胁,如伊拉克战争等。
可鹰派的行为并未使自身安全,他们的盟友如英国、埃及惨遭打击,他们的过激行为反而阻碍了美国前进。
“租值消散”理论指无主的、没有归属的收入,在竞争下会消散,在边际上会下降为0,如公海没有业主,钓鱼不收费,他的边际租值为0.中国巨额的土地红利往往会带来巨大的竞争竞争人A a指土地红利合作竞争c指过度竞争带来的损失竞争人B 合作a,a 0,2a 分析可照上面竞争2a,0 a-c,a-c他们都是对自身利益最大化的追求,因而选择(竞争,竞争)概率很大,当过度竞争时,往往会造成贪污腐败,土地减产,价值下跌,暗箱操作等不良问题,反而使自己的投入得不到回报对于中国土地红利,我个人认为中国国民消费过于保守,投资理念始终停留在对国有银行的存款利息,从根本上让房产投资者土地升值。
我想正是因为它的巨大红利才会造成对土地竞争者的泛滥,供小于求,使得总收益下降,只有少部分获利,贫富差距拉大,妨碍了土地的整合和规模经济,而同时土地红利会造成资源的过度使用甚至是浪费。
3、石头、剪子、布假设A、B两人玩“石头、剪子、布”的游戏,A是说准备出石头的人,但是这并不可信。
因此两个人所出的仍然是随机的,可作如下标准式收益矩阵。
既然A说会出石头,他认为B受其影响极可能出“布”,则自己最好出“剪刀”,理性个人B预料到A会这么想,因此出“石头”最有利,并且A出布的可能性很小;况且如果他真的出石头,而自己再出剪刀岂不是自投罗网,显得“很没面子”,所以出剪刀的可能性最小。
如果我是A,实际上我会出“布”,因为根据以上分析,B最可能出石头,而我出“布”的胜算最大,我认为言语在利益对立的博弈中能起作用。
例子:抛硬币。
甲乙可自行绝对所抛出的硬币为正面还是反面,若方向相同,则甲胜;若方向相反,则乙胜。
收益矩阵如图所示:1/2,与甲不说时相同。
但实际上,言语对参与者而言打了一场心理战,甲认为乙会受影响而出“反”,他实际上很可能出“反”,乙也会意识到这点,因此他出“正”的概率反而会比“反”大。
所以我认为言语能在利益对立的博弈中起作用。
同样正如“石头、剪子、布”的游戏,A说会出石头,同样A、B两人因为这句话而打起了心理战。
4、“万元陷阱”“万元陷阱”是竞拍者利用人们对巨大利益追求的心理而从中获利的手段,(参与者都是自愿的),一旦参与者选择参与,多人竞争会使他们的喊价不断工作,组后则是鹬蚌相争,渔人得利。
参与者如果想要赢利,应该把握以下准则:1确定投入的极限及预先的约定,譬如投资多少钱或是多少时间?2要坚持到底(止损原则)3自己打定注意,不必看别人4保持良好的心态5别指望能以很低的价格买入6不要随波逐流,有自己的主见和底线。
7尽快传递“势在必得”的信号8合作,与他人共享,打倒其余的竞拍者。
具体事例:1如现实生活中购买彩票,抽奖活动,赌马,赌球,股票等,这些都是所谓的“万元陷阱”。
这些活动利用了人们追求巨大利益的心理,他们为此都不断投入精力去做,但最终不一定会有等价的回报,他们通常有两种动机:经济上和人际关系上。
想赢回自己的损失,有时却会导致更大的损失,而另一方面为了挽回失败的面子,证明自己。
2学校设立的期末奖项评比,也可看作是“万元陷阱”,为此学生想得奖来证明自己的能力,要付出很大的精力来学习,但是奖项是有限的、困难的,最终不一定会有所收获。
3企业的年终奖金评比,企业为了调动员工们的工作积极性,以年终奖来诱惑他们,员工们就陷入一种“万元陷阱”中,将不断投入精力去争取。
因此止损策略是十分重要的,它既要求我们不要无止境地把精力投放在某件事上,反而会得不偿失;又同时要求我们学会坚持到底,在确定极限后,不轻易更改,这样你就能获得最后的胜利,因此它教会我们有张有弛。
同时跟谁博弈比“怎么博弈”更加重要,“万元陷阱”中更理性的一方恰恰是损失更大的一方,虽然自己理性地选择,但是对象是属于“不理性”的,那么你最终反而会失利。
在选择竞争对手时,也要兼顾他与自己的比较,同样不能过于理性,有时要打定注意,坚持到底。
5、征税博弈理解:首先做一个关于征税博弈的收益树状图A百姓养鱼不养鱼重税 B B政府(-2,10)(4,4) (0,0) (0,0)轻税若政府事后违约,百姓即使养鱼仍收重税,那么百姓的实际收益反而下降,这是因为政府是强势的一方,没有关在笼子里,所以认为能建立有效的机制,把他们关在笼子里,才能增加百姓收入,建立和谐社会。
建一个收益矩阵甲养鱼不养鱼乙养鱼2,2 0,1不养鱼1,0 5,5此时有两个均衡点,但在都不养鱼的时候,是革命胜利的收益,但如果(不养鱼,不养鱼),可能会有损失的风险,往往会达成(养鱼,养鱼)的均衡,这样就革命失败了,没有完成把统治者关进笼子里的想法。
囚徒困境 A认罪不认罪B 认罪10年,10年0,20不认罪20,0 1,1他们都是从自我利益出发,A会想假定B认罪,他不认罪要判20年,B不认罪,他不认罪要判1年,综上认罪比不认罪要好,他们两人都这么想,结果得到一个相对较劣的结果。
在希望把统治者关进笼子里时,不同的人都从自己的利益出发,不愿直接和统治者相抗衡,想等其他人革命而暗中得利,但每个人都是这么想的,因而无法实现把统治者关进笼子里的愿望。
