28.2 解直角三角形2(仰角、俯角)[
2015年人教版28.2_解直角三角形(二)(三)提高训练(含答案)

28.2 解直角三角形(二)1.如图1,在△ABC中,∠C=90°,点D在BC上,CD=3,AD=BC,且cos∠ADC=3/5,则BD的长是( ) A.4 B.3 C.2 D.1a图1 图2图3 图42,图2在离地面高度5 m处引拉线固定电线杆,拉线与地面成60°角,则AC=____,AD=____.(用根号表示)3.如图3,初三年级某同学要测量校园内的旗杆AB的高度.在地面上C点用测角仪测得旗杆顶A 点的仰角为∠AFE=60°,再沿着直线BC后退8米到D,在D点又测得旗杆顶A的仰角∠AGE=45°.已知测角仪的高度为1.6米,求旗杆AB的高度.(3的近似值取1.7,结果保留1位小数)4.如图4,在比水面高2 m的A地,观测河对岸有一直立树BC的顶部B的仰角为30°,它在水中的倒影B′C顶部B′的俯角是45°,求树高BC.(结果保留根号)5.如图5,两建筑物的水平距离为a米,从A点测得D点的俯角为α,测得C点的俯角为β,则较低建筑物CD的高度为( ) A.a B.atanα C.a(s inα-cosα) D.a(tanβ-tanα)图5 图6 图7 图86.有人说,数学家就是不用爬树或把树砍倒就能够知道树高的人.小敏想知道校园内一棵大树的高度(如图6),他测得CB=10米,∠ACB=50°,请你帮他算出树高AB,约为________________米.(注:①树垂直于地面;②供选用数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.2)7.如图7,塔AB和楼CD的水平距离为80米,从楼顶C处及楼底D处测得塔顶A的仰角分别是45°和60°.求塔高与楼高.(精确到0.01米)(参考数据2=1.414 21,3=1.732 05)8.如图8,某船向正东方向航行,在A处望见某岛C在北偏东60°方向,前进6海里到B点,测得该岛在北偏东30°方向.已知该岛周围6海里内有暗礁,若该船继续向东航行,有无触礁危险?请说明理由.(参考数据:3≈1.732)9.如图9,武当山风景管理区,为提高游客到某景点的安全性,决定将到达该景点的步行台阶进行改善,把倾角由44°减至32°,已知原台阶AB的长为5米(BC所在地面为水平面).(1)改善后的台阶会加长多少?(2)改善后的台阶多占多长一段地面?(精确到0.01米)(sin44°= 0.6946 ,sin32°)= 0.5299, tan32° = 0.6248)图910.如图10,某海关缉私艇巡逻到达A处时接到情报,在A处北偏西60°方向的B处发现一艘可疑船只正以24海里/时的速度向正东方向前进,上级命令要对可疑船只进行检查,该艇立即沿北偏西45°的方向快速前进,经过1个小时的航行,恰好在C处截住可疑船只,求该艇的速度.(结果保留整数,6=2.449,3=1.732,2=1.414)图1028.2 解直角三角形(三)一、课前预习 (5分钟训练)1.在下列情况下,可解的直角三角形是( ) A.已知b=3,∠C=90° B.已知∠C=90°,∠B=46°C.已知a=3,b=6,∠C=90°D.已知∠B=15°,∠A=65°2.如图1,用测倾仪测得校园内旗杆顶点A 的仰角α=45°,仪器高CD =1.2 m ,测倾仪底部中心位置D 到旗杆根部B 的距离DB=9.8 m ,这时旗杆AB 的高为________ m.3.有一大坝其横截面为一等腰梯形,它的上底为6 m ,下底为10 m ,高为32 m,则坡角为_______. 二、课中强化(10分钟训练)1树被风折断,折断部分与地面夹角为30°,树尖着地处与树根的距离是35米,则原树高是____ m. 2.一等腰三角形顶角为100°,底边长为12,则它的面积是______________ (tan40° = 0.8391). 3.如图2,在Rt △ABC 中,∠C=90°,AD 平分∠CAB,CD=3,BD=32,求AB 及∠B.4.如图3,已知线段AB 、CD 分别表示甲、乙两幢楼的高,AB ⊥BD ,CD ⊥BD ,从甲楼顶部A 处测得乙楼顶部C 的仰角α=30°,测得乙楼底部D 的俯角β=60°,已知甲楼高AB=24 m , 求乙楼CD 的高.三、课后巩固(30分钟训练)1.菱形ABCD 的对角线AC 长为10 cm,∠BAC=30°,那么AD 为( ) A.3310B.33C.3315 D.32.Rt △ABC 中,∠C=90°,CD 是斜边AB 上的中线,BC=4,CD=3,则∠A≈_________. sinA≈0.666 73.如图4所示,为了测量河流某一段的宽度,在河北岸选了一点A ,在河南岸选相距200米的B 、C 两点,分别测得∠ABC=60°,∠ACB=45°.求这段河的宽度.(精确到0.1米)4.如图4,高速公路路基的横断面为梯形,高为4 m ,上底宽为16 m ,路基两边斜坡的坡度分别为i=1∶1,i′=1∶2,求路基下底宽.图45.为缓解“停车难”问题,某单位拟建造地下停车库,建筑设计师提供了该地下停车库的设计示意图(图5).按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,为标明限高,请你根据该图计算CE.(精确到0.1 m )(,,)图56.如图6,某校九年级3班的学习小组进行测量小山高度的实验活动.部分同学在山脚下点A 测得山腰上一点D 的仰角为30°,并测得AD 的长度为180米;另一部分同学在山顶点B 测得山脚点A 的俯角为45°,山腰点D 的俯角为60°,请你帮助他们计算出小山的高度BC.(计算过程和结果不取近似值)图628.2 解直角三角形(二)参考答案1.如图1,在△ABC 中,∠C=90°,点D 在BC 上,CD=3,AD=BC,且cos ∠ADC=53,则BD 的长是()图1A.4B.3C.2D.1解析:求BD 需求BC,而BC=AD,在Rt △ADC 中,已知一角一边,可求出AD. 在Rt △ADC 中,CD=3,且cos ∠ADC=53,∴AD=5,∴BC=AD=5.∴BD=2. 答案:C2.如图2,在离地面高度 5 m 处引拉线固定电线杆,拉线与地面成60°角,则AC=______,AD=__________.(用根号表示)图2解析:在Rt △ABD 中,∠A=60°,CD=5,∴AC=331060sin =︒CD ,AD=33560tan =︒CD .答案:33103353.如图3,初三年级某同学要测量校园内的旗杆AB 的高度.在地面上C 点用测角仪测得旗杆顶A 点的仰角为∠AFE=60°,再沿着直线BC 后退8米到D ,在D 点又测得旗杆顶A 的仰角∠AGE=45°.已知测角仪的高度为1.6米,求旗杆AB 的高度.(3的近似值取1.7,结果保留1位小数)图3解:设EF 为x 米, 在Rt △AEF 中,∠AFE=60°, ∴AE=EF·tan60°=3x ,在Rt △AGE 中,∠AGE=45°, ∴AE=GE·tan45°=GE=8+x. ∴3x=8+x.解之,得x=4+43.∴AE=12+43≈18.8.∴AB=20.4(米). 答:旗杆AB 高20.4米.4.如图4,在比水面高2 m 的A 地,观测河对岸有一直立树BC 的顶部B 的仰角为30°,它在水中的倒影B′C 顶部B′的俯角是45°,求树高BC.(结果保留根号)图4解Rt △AEB 与Rt △AEB′,得AE 与BE 、EB′的关系,解关于x 的方程可求得答案. 解:设树高BC=x(m),过A 作AE ⊥BC 于E ,在Rt △ABE 中,BE=x -2,∠BAE=30°,cot ∠BAE=BEAE,∴AE=BE·cot ∠BAE=(x -2)·3=3 (x -2).∵∠B′AE=45°,AE ⊥BC. ∴B′E=AE=3(x -2).又∵B′E=B′C+EC=BC+AD=x+2, ∴3(x -2)=x+2.∴x=(4+23)(m).答:树高BC 为(4+23) m.5.如图5,两建筑物的水平距离为a 米,从A 点测得D 点的俯角为α,测得C 点的俯角为β,则较低建筑物CD 的高度为()图5A.aB.atanαC.a(sinα-cosα)D.a(tanβ-tanα) 解析:过D 点作AB 的垂线交AB 于E 点,在 Rt △ADE 中,∠ADE=α,DE=a, ∴AE=a·tanα.在Rt △ABC 中,∠ACB=β,BC=a, ∴AB=a·tan β.∴CD=AB -AE=a·tan β-a·tan α. 答案:D6.有人说,数学家就是不用爬树或把树砍倒就能够知道树高的人.小敏想知道校园内一棵大树的高度(如图6),他测得CB=10米,∠ACB=50°,请你帮他算出树高AB,约为________________米. (注:①树垂直于地面;②供选用数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.2)图6解析:AB=BC·tanC=12(米). 答案:127.如图7,塔AB 和楼CD 的水平距离为80米,从楼顶C 处及楼底D 处测得塔顶A 的仰角分别是45°和60°.求塔高与楼高.(精确到0.01米)(参考数据2=1.414 21,3=1.732 05)图7解:在Rt △ABD 中,BD=80米,∠BDA=60°,∴AB=BD·tan60°=803≈138.56(米). Rt △AEC 中,EC=BD=80,∠ACE=45°, ∴AE=CE=80(米).∴CD=AB -AE≈58.56(米).答:塔高与楼高分别为138.56米、58.56米.8.如图8,某船向正东方向航行,在A 处望见某岛C 在北偏东60°方向,前进6海里到B 点,测得该岛在北偏东30°方向.已知该岛周围6海里内有暗礁,若该船继续向东航行,有无触礁危险?请说明理由.(参考数据:3≈1.732)图8解:继续向东行驶,有触礁的危险. 过点C 作CD 垂直AB 的延长线于D,∵∠CAB=30°,∠CBD=60°,∴∠BCD=30°. 设CD 的长为x,则tan ∠CBD=BDxBD CD =,∴BD=33x. ∴tan ∠CAB=tan30°=x x AD CD 33633+==.∴x=33.∴x≈5.2<6.∴继续向东行驶,有触礁的危险.9.如图9,武当山风景管理区,为提高游客到某景点的安全性,决定将到达该景点的步行台阶进行改善,把倾角由44°减至32°,已知原台阶AB 的长为5米(BC 所在地面为水平面). (1)改善后的台阶会加长多少?(精确到0.01米) (2)改善后的台阶多占多长一段地面?(精确到0.01米)图9解:(1)如图,在Rt △ABC 中,AC=AB·sin44°=5sin 44°≈3.473. 在Rt △ACD 中,AD=︒=︒32sin 473.332sin AC ≈6.554.∴AD -AB=6.554-5≈1.55.即改善后的台阶会加长1.55米, (2)如图,在Rt △ABC 中, BC=ABcos44°=5cos44°≈3.597. 在Rt △ACD 中,CD=︒=︒32tan 473.332tan AC ≈5.558,∴BD=CD -BC=5.558-3.597≈1.96,即改善后的台阶多占1.96米长的一段地面.10.如图10,某海关缉私艇巡逻到达A 处时接到情报,在A 处北偏西60°方向的B 处发现一艘可疑船只正以24海里/时的速度向正东方向前进,上级命令要对可疑船只进行检查,该艇立即沿北偏西45°的方向快速前进,经过1个小时的航行,恰好在C 处截住可疑船只,求该艇的速度.(结果保留整数,6=2.449,3=1.732,2=1.414)图10解:设OA 的长为x ,由于点C 在点A 的北偏西45°的方向上,∴OC=OA=x.根据题意,得tan30°=312243324=⇒+==⇒+x xxx x x +12.AC 2=x 2+x 2⇒AC=22x x +,∴AC≈46(海里).答:该艇的速度是46海里/时.28.2 解直角三角形(三)参考答案一、课前预习 (5分钟训练)1.在下列情况下,可解的直角三角形是( )A.已知b=3,∠C=90°B.已知∠C=90°,∠B=46°C.已知a=3,b=6,∠C=90°D.已知∠B=15°,∠A=65°解析:一般地,已知两边、已知一个锐角一边、已知一个锐角和两个边的关系或已知三边的关系的直角三角形可解.∴C 正确. 答案:C2.如图-1,用测倾仪测得校园内旗杆顶点A 的仰角α=45°,仪器高CD =1.2 m ,测倾仪底部中心位置D 到旗杆根部B 的距离DB=9.8 m ,这时旗杆AB 的高为________ m.图1解:过C 点作AB的垂线,垂足为E点,在Rt △ACE 中,∠ACE=α=45°,BD=9.8,∴AE=9.8.∴AB=AE+CD=11(m). 答案:113.有一大坝其横截面为一等腰梯形,它的上底为6 m ,下底为10 m ,高为32m,则坡角为_______.解:设坡角为α,则坡度=tanα=3)610(2132=-,∴坡角为60°.答案:60°二、课中强化(10分钟训练)1.有一棵树被风折断,折断部分与地面夹角为30°,树尖着地处与树根的距离是35米,则原树高是_______________ m.解析:如图,在Rt △ABC 中,∠A=30°,∠C=90°,AC=35,∴AB=AACcos =10,BC=AC·tanA=5.∴原树高为15米.答案:152.一等腰三角形顶角为100°,底边长为12,则它的面积是_________________.解析:如图所示,作CD ⊥A B ,在Rt △ADC 中,得AD=6,∠ACD=50°,∴CD≈5.03,∴面积为30.18.答案:30.183.如图28-2-3-2,在Rt △ABC 中,∠C=90°,AD 平分∠CAB,CD=3,BD=32,求AB 及∠B.图2解:过D 点作DE ⊥AB 于E 点,设AC=x ,则AE=x.在Rt △BED 中,得到BE=3,又由AB 2=AC 2+BC 2,得(3+x )2=x 2+27,解得x=3,AB=6, sinB=21,∴∠B=30°.4.如图3,已知线段AB 、CD 分别表示甲、乙两幢楼的高,AB ⊥BD ,CD ⊥BD ,从甲楼顶部A 处测得乙楼顶部C 的仰角α=30°,测得乙楼底部D 的俯角β=60°,已知甲楼高AB=24 m ,求乙楼CD 的高.图3解:过点A 作AE ⊥CD ,在Rt △ABD 中,∠ADB=β,AB=24,∴BD=38.在Rt △AEC中,∠CAE=α,BD=38,∴CE=8.∴CD=CE+AB=32(米).三、课后巩固(30分钟训练)1.菱形ABCD 的对角线AC 长为10 cm,∠BAC=30°,那么AD 为( )A.3310 B.33 C.3315 D.3解析:如图,∵AC ⊥BD,∴AD=331030cos 5=︒. 答案:A2.在Rt △ABC 中,∠C=90°,CD 是斜边AB 上的中线,BC=4,CD=3,则∠A≈_________.解析:由CD=3,得AB=6,∴sinA≈0.666 7.∴∠A≈41.8°. 答案:41.8°3.如图4所示,为了测量河流某一段的宽度,在河北岸选了一点A ,在河南岸选相距200米的B 、C 两点,分别测得∠ABC=60°,∠ACB=45°.求这段河的宽度.(精确到0.1米) 解:过A 作BC 的垂线,垂足为D. 在Rt △ADB 中,∠B=60°, ∴∠BAD=30°.∴BD=AD·tan30°=33AD. 在Rt △ADC 中,∠C=45°,∴CD=AD. 又∵BC=200,∴BD+CD=33AD+AD=200. ∴AD=331200≈126.8(米).答:这段河宽约为126.8米.4.如图4,高速公路路基的横断面为梯形,高为4 m ,上底宽为16 m ,路基两边斜坡的坡度分别为i=1∶1,i′=1∶2,求路基下底宽.图4解:作高AE 、DF ,则BE=4,CF=8. ∴CB=28(米).5.为缓解“停车难”问题,某单位拟建造地下停车库,建筑设计师提供了该地下停车库的设计示意图(图5).按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,为标明限高,请你根据该图计算CE.(精确到0.1 m )图5解:在Rt △ABD 中,AB=9,∠BAD=18°, ∴BD≈2.9.∴CD=2.4.在Rt △CDE 中,∠DCE=18°, ∴CE≈2.3(米). 答:略.6.如图6,某校九年级3班的学习小组进行测量小山高度的实验活动.部分同学在山脚下点A 测得山腰上一点D 的仰角为30°,并测得AD 的长度为180米;另一部分同学在山顶点B 测得山脚点A 的俯角为45°,山腰点D 的俯角为60°,请你帮助他们计算出小山的高度BC.(计算过程和结果不取近似值)图6解:如图,作DE ⊥AC 于E,DF ⊥BC 于F,设山高为x 米,在Rt △ADE 中,DE=90,AE=390,∴DF=x-390,BF=x-90.在Rt △BFD 中,DF ∶BF=tan30°, ∴x=90+390(米).。
三角函数应用举例(1)仰角俯角
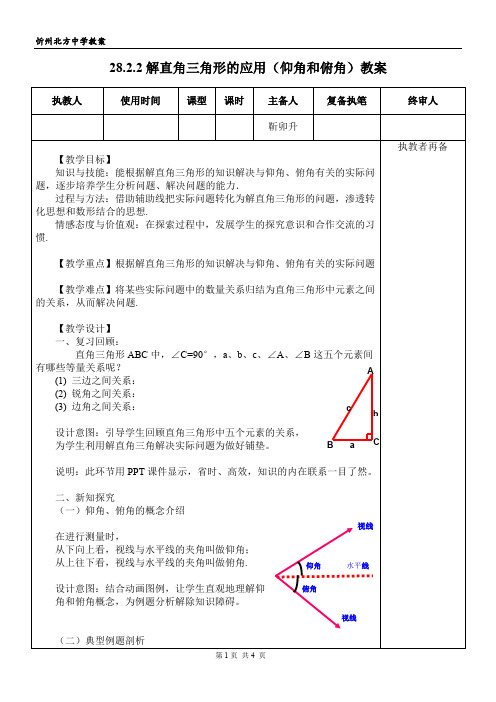
28.2.2解直角三角形的应用(仰角和俯角)教案
中,
D
设计意图:通过分析题意,引导学生构造直角三角形,把已知条件转化到两个直角三角形里,根据已知的边角条件,恰当地选择锐角三角函数关系,解决实际问题,让学生初步认识到解直角三角形在实际问题中的应用;同时通过
一方面让学生进一步认识到解直角三角形在实际问题中的应用,另一方面,让学生意识到通过设未知数,建立方程也是解决实际问题时常用到
处,看另一栋楼楼顶的俯角为30°,看这
BC有多高?
A
E
尽管实际问题的背景发生了变化,
C E。
人教版九年级下册数学 28.2.2解直角三角形的应用举例 例5 航海——方位角(共18张PPT)

险区。这渔船如果继续向东追赶鱼群,有没有进入危险 将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
方位角
区的可能? (3)边角之间的关系:
某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向
的速度沿西偏北30°方向前进,乙船以每小时15千米的速度沿东北 方向前进,甲船航行2小时到达C处,此时甲船发现渔具丢在乙船上, 于是甲船快速(匀速)沿北偏东75°的方向追赶,结果两船在B处 相遇。 (1)甲船从C处追赶上乙船用了多长时间? (2)甲船追赶乙船的速度北是每小时多少千米?
B
D
C 75°
45°
西走60米到达C点,测得点B在点C的北偏东60°方向。 这渔船如果继续向东追赶鱼群,有没有进入危险区的可能?
C
为有效开发海洋资源,保护海洋权益,我国对南海诸岛
2解直角三角形的应用举例
北 为有效开发海洋资源,保护海洋权益,我国对南海诸岛
进行了全面调查,一测量船在A岛测得B岛2解直角三角形的应用举例 航海问题——方位角
北 M东
B
A
D
N
解直角三角形的依据
(1)三边之间的关系: (2)锐角之间的关系:
(3)边角之间的关系:
B
c a
A
bC
仰角俯角
A
?
E 34
F
18
D
10米
B
方位角
北
C
西
O
B
东
南
利用锐角三角函数解决航海问题
如图,一艘海伦位于灯塔P的北偏东65°方向,距离灯 塔80海里的A处,它沿正南方向航行一段时间后,到达 位于灯塔P的南偏东34°方向的B处。这时,B处距离 灯塔P有多远?(结果取整数)(cos25°=0.9063, sin34°=0.5291, )
28.2解直角三角形(方向角及坡比问题)2014年3月18日

解: (1 ) 过点 A 作 AD 垂直于
BC ,垂足为
D
ABC
30
0
, AB 160 米
AD 80 米 100 米 ,
在 Rt ABD 中,解得
所以受噪声影响。
以点 A 为圆心, 100 米长为半径画圆弧分别
线段 EF 为受影响的路段 .
交 BC 于 E , F 两点
1 8 .4
沿水库拦河坝的背水坡将坝顶加宽2 米,坡度由原来的1:2改为1:2.5, 已知坝高6米,坝长50米。 (1)求加宽部分横断面AFEB (2)完成这一工程需要多少方土?
F
2
A D
6Leabharlann EBNM
1.在解直角三角形及应用时经常接触到 的一些概念(方位角;坡度、坡角等)
2.实际问题向数学模型的转化
sin B PC PB
65° P
A C
34°
PB
PC sin B
72.8 sin 34
72.8 0.559
B
130.23
当海轮到达位于灯塔P的南偏东34°方向时,它距离灯塔P大约130.23海里.
气象台发布的卫星云图显示,代号为W的台风在某海岛(设为 点O)的南偏东45°方向的B点生成,测得 O B 1 0 0 6 k m . 台 风中心从点B以40km/h的速度向正北方向移动,经5h后到达海 面上的点C处.因受气旋影响,台风中心从点C开始以30km/h 的速度向北偏西60°方向继续移动.以O为原点建立如图12所示 的直角坐标系. (1)台风中心生成点B的坐标为 ,台风中心转折点C的 坐标为 ;(结果保留根号) (2)已知距台风中心20km的范围内均会受到台风的侵袭.如 果某城市(设为A点)位于点O的正北方向且处于台风中心的移 动路线上,那么台风从生成到最初侵袭该城要经过多长时间? 北
解直角三角形的应用(仰角和俯角问题)

计算角度证结果:检 查计算结果是 否满足三角形 内角和为180
度的条件
添加标题
确定已知条件:已知三角形的边长和角度
添加标题
利用正弦定理:sin/ = sinB/b = sinC/c
添加标题
利用余弦定理:cos = (b^2 + c^2 - ^2) / (2bc)
正弦定理:在直角三角形中 任意一边的长度等于其对角 的正弦值乘以斜边的长度
余弦定理:在直角三角形中 任意两边长度的平方和等于 斜边的平方
正切定理:在直角三角形中 任意一边的长度等于其对角 的正切值乘以斜边的长度
余切定理:在直角三角形中 任意两边长度的平方差等于 斜边的平方
正割定理:在直角三角形中 任意一边的长度等于其对角 的正割值乘以斜边的长度
确保测量工具的 准确性和稳定性
避免在危险区域 进行测量如高空、
高压电等
遵守操作规程确 保人身安全
做好防护措施如 佩戴安全帽、手
套等
及时清理现场避 免杂物影响测量
结果
遇到突发情况及 时停止操作并寻
求帮助
仰角和俯角为0度:此时三角形退化为直线无法求解
仰角和俯角为90度:此时三角形退化为直角三角形可以直接求解
全站仪等
测量误差:注 意测量误差对 仰角和俯角测 量结果的影响
测量环境:注 意测量环境的 影响如温度、 湿度、风速等
测量方法:注 意测量方法的 选择如直接测 量、间接测量
等
测量误差:测量工具的精度、测量人员的操作水平等
计算误差:计算过程中的舍入误差、公式使用错误等
环境误差:温度、湿度、光照等环境因素对测量结果的影响
添加文档副标题
目录
01.
02.
人教版数学九年级下册28.2解直角三角形-仰角、俯角问题教案

另外,小组讨论和实践活动环节,学生的参与度很高,他们积极讨论,热烈交流,这让我很欣慰。但我也观察到,有些小组在分享成果时表达不够清晰,这可能是他们在整理思路和语言表达上还存在不足。在以后的教学中,我需要加强对学生表达能力的训练,鼓励他们更加自信、条理清晰地表达自己的观点。
(1)通过实际情境引入仰角、俯角的概念;
(2)掌握正切函数的定义,并应用于仰角、俯角问题的求解;
(3)通过例题讲解和练习,让学生熟练运用解直角三角形的方法解决实际生活中的仰角、俯角问题。
二、核心素养目标
1.培养学生运用数学知识解决实际问题的能力,提高数学建模素养;
2.通过对正切函数的运用,增强学生的数学运算和数据分析能力;
五、教学反思
在今天的课程中,我们探讨了解直角三角形中的仰角、俯角问题。我发现学生们在理解仰角、俯角概念上并没有太大困难,他们对于这些新知识充满了好奇。但在实际应用上,特别是在构建直角三角形模型和运用正切函数时,部分学生遇到了一些挑战。
首先,我注意到在案例分析环节,有些学生在确定直角三角形的边长和角度时显得犹豫不决。这说明他们对于如何将实际问题转化为数学模型还不够熟练。在未来的教学中,我需要提供更多的实际例子,让学生有更多的机会去练习和体会这一过程。
(二)新课讲授(用时10分钟)
1.理论介绍:首先,我们要了解仰角与俯角的基本概念。仰角是我们从水平线向上看时,视线与水平线所形成的角;俯角则是我们从水平线向下看时,视线与水平线所形成的角。它们在测量、建筑等领域有着广泛的应用。
人教初中数学九年级下册28-2 解直角三角形及其应用(教学设计)

师:尝试写出∠A 的三角函数。
生:∠A 的正弦值:sin A=∠A 所对的边斜边= ac∠A 的余弦值:cos A= ∠A 所邻的边斜边= bc∠A 的正切值:tan A=∠A 所对的边邻边= ab师:将 30°、45°、60°角的正弦值、余弦值和正切值填入下表:生:变式1-1 在Rt △ABC 中,∠C =90°,a = 30, b = 20,根据条件解直角三角形.变式1-2 在△ABC 中,∠C =90∘, AB =6, cosA =13,则AC 等于( )A .18B .2C .12D .118变式1-3在Rt △ABC 中,斜边AB 的长为m ,∠A =35°,则直角边BC 的长是( ) A .msin35° B .mcos35° C .m sin35°D .mcos35°变式1-4 如图,在Rt △ABC 中,∠C=90°,∠B=35° ,b=20,解这个直角三角形(结果保留小数点后一位). 变式1-5 如图,太阳光线与水平线成70°角,窗子高AB =2米, 要在窗子外面上方0.2米的点D 处安装水平遮阳板DC ,使光线不 能直接射入室内,则遮阳板DC 的长度至少是( ) A .2tan70°米 B .2sin70°米 C .2.2tan70°米 D .2.2cos70°米平线下方的叫做俯角。
指南或指北的方向线与目标方向线构成小于900的角,叫做方位角. 师:尝试说出A,B关于坐标原点O的位置?生:点A位于点O北偏东30°位置,点B位于点O南偏西45°位置[多媒体展示]热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高(结果精确到0.1m)。
九年级数学下册28.2《仰角、俯角》教案(新版)新人教版

仰角、俯角1.理解解直角三角形在实际问题中的应用(1)解决实际问题时,关键是根据题意抽象出其几何模型,然后再通过解决几何模型的问题得到实际问题的答案.(2)与斜三角形有关的问题,往往通过作一边上的高,把其转化为的问题.2.掌握与测量有关的几个概念如图,在测量时,视线与水平线所成的角中,视线在水平线的角叫仰角,在水平线的角叫俯角.重点一:解直角三角形解决简单实际问题利用解直角三角形解决实际问题的步骤:(1)将实际问题抽象为数学问题;(2)画出平面图形,转化为三角形的问题;1. 如图所示,A、B两点在河的两岸,要测量这两点之间的距离,测量者在与A同侧的河岸边选定一点C,测出AC=a米,∠A=90°,∠C=40°,则AB等于( )(A)asin 40°米(B)acos 40°米(C)atan 40°米(D)米2. 如图是某水库大坝横断面示意图.其中CD、AB分别表示水库上下底面的水平线,∠ABC=120°,BC的长是50 m,则水库大坝的高度h是( )(A)25 m (B)25 m (C)25 m (D) m3.某学校的校门是伸缩门,伸缩门中的每一行菱形有20个,每个菱形边长为30厘米.校门关闭时,每个菱形的锐角度数为60°(如图1),校门打开时,每个菱形的锐角度数从60°缩小为10°(如图2).问校门打开了多少米?(结果精确到1米,参考数据:sin 5°≈0.0872,cos 5°≈0.9962,sin 10°≈0.1736,cos 10°≈0.9848)重点二:有关仰角、俯角的测量问题4. (2013绵阳改编)如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底点G为BC的中点,则矮建筑物的高CD为( )(A)20米(B)10米 (C)15米(D)5米5. 如图所示,从热气球C处测得地面A、B两点的俯角分别为30°、45°,如果此时热气球C处的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是( )(A)200米(B)200米 (C)220米(D)100(+1)米6.(2014昆明)如图,在数学实践课中,小明为了测量学校旗杆CD的高度,在地面A处放置高度为1.5米的测角仪AB,测得旗杆顶端D的仰角为32°,AC=22米,求旗杆CD的高度(结果精确到0.1米,参考数据:sin 32°≈0.53,cos 32°≈0.85,tan 32°≈0.62).7. (2013遵义改编)某中学在创建“特色校园”的活动中,将该校的办学理念做成宣传牌(AB),放置在教学楼的顶部(如图所示).小明在操场上的点D处,用1米高的测角仪CD,从点C测得宣传牌的底部B的仰角为37°,然后向教学楼方向走了4米到达点F处,又从点E测得宣传牌的顶部A的仰角为45°.已知教学楼高BM=17米,且点A,B,M在同一直线上,求宣传牌AB的高度(结果精确到0.1米,参考数据:≈1.73,sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75).A层(基础)1. 在“测量旗杆的高度”的数学课题学习中,某学习小组测得太阳光线与水平面的夹角为27°,此时旗杆在水平地面上的影子的长度为24米,则旗杆的高度约为( )(A)24米(B)20米(C)16米 (D)12米2. 在一次数学活动中,李明利用一根拴有小锤的细线和一个半圆形量角器制作了一个测角仪,去测量学校内一座假山的高度CD.如图所示,已知李明距假山的水平距离BD为12 m,他的眼睛距地面的高度为1.6 m,李明的视线经过量角器零刻度线OA和假山的最高点C,此时,铅垂线OE经过量角器的60°刻度线,则假山的高度为( )(A)(4+1.6) m (B)(12+1.6) m (C)(4+1.6) m (D)4 m3. (2013山西)如图,某地修建高速公路,要从B地向C地修一座隧道(B,C在同一水平面上),为了测量B,C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升100 m到达A处,在A处观察B地的俯角为30°,则B,C两地之间的距离为( )(A)100 m (B)50 m (C)50 m (D) m4. 如图所示,某风景区为了方便游人参观,计划在主峰A处架设一条缆车线路到另一山峰C处,若在A处测得C处的俯角为30°,两山峰的底部B、D相距900 m,则缆车线路AC的长为( )(A)300 m (B)600 m (C)900 m (D)1800 m5.如图甲、乙两楼的楼间距AC为10米,某人在甲楼楼底A处测得乙楼的楼顶B的仰角为60°,在乙楼的楼底C处测得甲楼的楼顶D的仰角为45°,则甲楼比乙楼矮米.6. 如图所示,将45°的∠AOB按下面的方式放置在一把刻度尺上:顶点O与尺下沿的端点重合,OA与尺下沿重合,OB与尺上沿的交点B在尺上的读数恰为2 cm.若按相同的方式将37°的∠AOC放置在该刻度尺上,则OC与尺上沿的交点C在尺上的读数约为cm.(结果精确到0.1 cm,参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)7. 如图所示,从热气球C上测得两建筑物A、B底部的俯角分别为30°和60°.如果这时气球的高度CD 为90米,且点A、D、B在同一直线上,建筑物A、B间的距离为米.8. (2013十堰)如图,在小山的东侧A点有一个热气球,由于受西风的影响,以30米/分的速度沿与地面成75°角的方向飞行,25分钟后到达C处,此时热气球上的人测得小山西侧B点的俯角为30°,则小山东西两侧A、B两点间的距离为米.9. 某煤矿发生瓦斯爆炸,该地救援队立即赶赴现场进行救援,救援队利用生命探测仪在地面A、B两个探测点探测到C处有生命迹象.已知A、B两点相距4米,探测线与地面的夹角分别是30°和45°,试确定生命所在点C的深度(精确到0.1米,参考数据:≈1.41,≈1.73).10. (2013包头)如图,一根长 6米的木棒(AB),斜靠在与地面(OM)垂直的墙(ON)上,与地面的倾斜角(∠ABO)为60°.当木棒A端沿墙下滑至点A'时,B端沿地面向右滑行至点B'.(1)求OB的长;(2)当AA'=1米时,求BB'的长.教后反思:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P
答案: 答案: (200 3 + 200) 米
45° ° 30° °
O
B
400米 米
A合作与探究ຫໍສະໝຸດ 米的大楼AB上 例2:如图,直升飞机在高为200米的大楼 上 如图,直升飞机在高为 米的大楼 点处, 方P点处,从大楼的顶部和底部测得飞机的仰 点处 角为30° 角为 °和45°,求飞机的高度 ° 求飞机的高度PO .
P C
30° °
A
200米 米
45° °
O
B
2、在山脚C处测得山顶 的仰角为 °。问 、在山脚 处测得山顶 的仰角为45° 处测得山顶A的仰角为 题如下: 题如下: 1)沿着水平地面向前 米到达D点 )沿着水平地面向前300米到达 点,在D点 米到达 点 测得山顶A的仰角为 的仰角为60 求山高AB。 测得山顶 的仰角为 0 , 求山高 。
∴ AB = OA − OB = (450 3 − 450)(m) O 大桥的长AB为 答:大桥的长 为 (450 3 − 450)m.
B
A
合作与探究
变题1 如图,直升飞机在长 变题1:如图,直升飞机在长400米的跨江大桥 米的跨江大桥 AB的上方 点处,且A、B、O三点在一条直线 的上方P点处 的上方 点处, 、 、 三点在一条直线 在大桥的两端测得飞机的仰角分别为30° 上,在大桥的两端测得飞机的仰角分别为 ° 求飞机的高度PO . 和45 °,求飞机的高度
在进行观察或测量时, 在进行观察或测量时,
仰角和俯角
从下向上看,视线与水平线的夹角叫做仰角; 从下向上看,视线与水平线的夹角叫做仰角; 仰角 从上往下看,视线与水平线的夹角叫做俯角 俯角. 从上往下看,视线与水平线的夹角叫做俯角 铅 垂 线 视线 仰角 水平线 俯角 视线
1、如图,为了测量电线杆的高度AB,在离 、如图,为了测量电线杆的高度 , 电线杆22.7米的 处,用高 米的C处 用高1.20米的测角仪 电线杆 米的 米的测角仪 CD测得电线杆顶端 的仰角 =22°,求电 测得电线杆顶端B的仰角 测得电线杆顶端 的仰角a= ° 线杆AB的高.(精确到 的高.(精确到0.1米 线杆 的高.(精确到 米)
太阳光线
A
30° °
60° °
B
10
C
D
地面
热气球的探测器显 示,从热气球看一栋高 从热气球看一栋高 楼顶部的仰角为30° 楼顶部的仰角为 °, 看这栋高楼底部的俯 角为60° 热气球与高 角为 °,热气球与高 楼的水平距离为120m, 楼的水平距离为 这栋高楼有多高? 这栋高楼有多高
B
α=30° ° 120 D β=60° °
北 30° ° 东 A
西
O 45° ° B 南
海中有一个小岛A,它的周围8海里范围内有暗礁 海里范围内有暗礁, 例4.海中有一个小岛 ,它的周围 海里范围内有暗礁, 海中有一个小岛 渔船跟踪鱼群由西向东航行,在B点测得小岛 在北偏 渔船跟踪鱼群由西向东航行, 点测得小岛A在北偏 点测得小岛 海里到达D点 这时测得小岛A 东60°方向上,航行 海里到达 点,这时测得小岛 °方向上,航行12海里到达 在北偏东30°方向上, 在北偏东 °方向上,如果渔船不改变航线继续向东 航行,有没有触礁的危险? 航行,有没有触礁的危险?
A
C
合作与探究
变题2 如图,直升飞机在高为 米的大楼AB 变题2:如图,直升飞机在高为200米的大楼 米的大楼 左侧P点处 测得大楼的顶部仰角为45° 测得 点处, 左侧 点处,测得大楼的顶部仰角为 °,测得 大楼底部俯角为30° 大楼底部俯角为 °,求飞机与大楼之间的水 A 平距离. 平距离
P
45° ° 30° °
A
45° °
60° °
C 300 D
B
如图,太阳光与地面成60度角, 60度角 例3: 如图,太阳光与地面成60度角,一棵倾斜的大 AB与地面成30度角 与地面成30度角, 树AB与地面成30度角,这时测得大树在地面上的影 长为10m,请你求出大树的高. 的长 10m,请你求出大树的高 长为10m,请你求出大树的高. AB的长
P
30° °
A
200米 米
答案: 答案: (100 3 + 300) 米
O
45° °
B
L U D
合作与探究
米的大楼AB上 例2:如图,直升飞机在高为200米的大楼 上 如图,直升飞机在高为 米的大楼 点处, 方P点处,从大楼的顶部和底部测得飞机的仰 点处 角为30° 角为 °和45°,求飞机的高度 ° 求飞机的高度PO .
P
A
B
P α
450
归纳与提高
β
450 45° ° 30° ° 30° ° 45° °
P
O P
B C
30° °
60° °
A
B
O
A
A
P
45° ° 45° ° 30° ° 30° °
200 米 200米
D
45° °
45° 200米 ° 200米
O
B
O
B
更上一层楼
3.学生小王帮在测绘局工作的爸爸买了一些仪器后与同学 学生小王帮在测绘局工作的爸爸买了一些仪器后与同学 在环西文化广场休息,看到濠河对岸的电视塔, 在环西文化广场休息,看到濠河对岸的电视塔,他想用手 中的测角仪和卷尺不过河测出电视塔空中塔楼的高度.现已 中的测角仪和卷尺不过河测出电视塔空中塔楼的高度 现已 测出∠ 测出∠ADB=40°,由于不能过河,因此无法知道 的长 ° 由于不能过河,因此无法知道BD的长 于是他向前走50米到达 处测得∠ 米到达C处测得 度,于是他向前走 米到达 处测得∠ACB=55°,但他们 ° 在计算中碰到了困难,请大家一起想想办法, 在计算中碰到了困难,请大家一起想想办法,求出电视塔 21 7 塔楼AB的高 塔楼 的高. tan 40° ≈ , tan 55° ≈ ) 参考数据: (参考数据: 答案:空中塔楼 高 答案:空中塔楼AB高 约为105米 约为 米
200米 米 D
答案: 答案: (300 − 100 3 ) 米
O B
3.国外船只,除特许外,不得进入我国海洋100海里 海洋100 3.国外船只,除特许外,不得进入我国海洋100海里 国外船只 以内的区域,如图, 是我们的观察站, 以内的区域,如图,设A、B是我们的观察站,A和B 之间的距离为157.73海里,海岸线是过A、B的一条 之间的距离为157.73海里,海岸线是过A 距离为157.73海里 直线,一外国船只在P 点测得∠ 直线,一外国船只在P点,在A点测得∠BAP=450,同 时在B点测得∠ 时在B点测得∠ABP=600,问此时是否要向外国船只 发出警告,令其退出我国海域. 发出警告,令其退出我国海域.
=220 1.20 22.7
合作与探究
【例1】如图,直升飞机在跨江大桥AB的上方 如图,直升飞机在跨江大桥 的上方P 的上方 点处,此时飞机离地面的高度PO=450米,且A、 点处,此时飞机离地面的高度 米 、 B、O三点在一条直线上,测得大桥两端的俯角 三点在一条直线上, 、 三点在一条直线上 分别为α=30°,β=45°,求大桥的长AB . 分别为 ° ° 求大桥的长
A
30° °
60° °
B
12
D
F
解:由题意得,在Rt△PAO与Rt△PBO中 由题意得, △ 与 △ 中
∠PAO = 30°, ∠PBO = 45° PO PO Q = tan 30 °, = tan 45 ° P OA OB
α
β
∴ OA =
450 = 450 3, 450米 米 tan 30°
450 OB = = 450 tan 45°
25 5
A
濠 河
55° ° 40° °
B
C 50m D
方位角
指南或指北的方向线与目标方向线构成小于 900的角 叫做方位角 的角,叫做方位角 叫做方位角. 如图: 的北偏东30° 如图:点A在O的北偏东 ° 在 的北偏东 在点O的南偏西 点B在点 的南偏西 °(西南方向) 在点 的南偏西45° 西南方向)
利用解直角三角形的知识解决实际问题的 利用解直角三角形的知识解决实际问题的 解直角三角形的知识解决实际问题 一般过程是: 一般过程是
1.将实际问题抽象为数学问题 将实际问题抽象为数学问题; 将实际问题抽象为数学问题 (画出平面图形 转化为解直角三角形的问题 画出平面图形,转化为解直角三角形的问题 画出平面图形 转化为解直角三角形的问题) 2.根据条件的特点 适当选用锐角三角函数等去解直角三角形 根据条件的特点,适当选用锐角三角函数等去解直角三角形 根据条件的特点 适当选用锐角三角函数等去解直角三角形; 3.得到数学问题的答案 得到数学问题的答案; 得到数学问题的答案 4.得到实际问题的答案 得到实际问题的答案. 得到实际问题的答案
