第10章__动态规划_(管理运筹学_第三版_课件__共17章_韩伯棠) (3)
合集下载
管理运筹学课件第10章 存贮论共31页文档
经济订货量 Q * 2 k D h
Q* 210010000408 12
T C *2 1 0 0 1 2 1 0 0 0 0 4 8 9 9
最小总成本 TC* 2khD
订货间隔期 t TQ* T 2k
D
hD
订货次数
n
D Q*
hD 2k
t 1408 0.0408(年) 10000
04.12.2019
课件
25
由①C(Q)≤C(Q+1)：
Q
h (Q d)P (d)s (dQ )P (d)kQ
d0
dQ 1
Q 1
≤ h (Q 1 d )P (d ) s (d Q 1 )P (d ) k (Q 1 )
d 0
d Q 2
04.12.2019
课件
24
10.3.2 模型Ⅵ：需求是离散的随机存贮模型
若不考虑订货成本，总成本可描述为以下三项：
总成本=存储成本+缺货成本+采购成本
对订货量 q，需求量r，单位缺货成本s，单位存货成本h，
单位采购成本k，需求的概率分布P(d) 。
q
当q≤d时，因积压而产生损失 h(q d)P(d)
04.12.2019
课件
4
10.1.1 存贮系统
04.12.2019
课件
5
10.1.2 存贮策略
目标库存Q0
安全库存S
04.12.2019
Q1
Q2
L t1 t
L t1+t 2t
课件
6
10.1.2 存贮策略
目标库存Q0
订货点R
《管理运筹学》第4版课后习题解析(韩伯棠)
7
《管理运筹学》第四版课后习题解析
韩伯棠
（2）模型变为 max z 5 xA 4 xB
50 xA 100 xB ≤ 1 200 000 100 xB ≥ 300 000 xA , xB ≥ 0
推导出 x1 18 000 ， x2 3 000 ，故基金 A 投资 90 万元，基金 B 投资 30 万元。
第 2 章 线性规划的图解法
1．解： （1）可行域为 OABC。 （2）等值线为图中虚线部分。 （3）由图 2-1 可知，最优解为 B 点，最优解 x1 =
12 15 69 ， x2 ；最优目标函数值 。 7 7 7
图 2-1 2．解： （1）如图 2-2 所示，由图解法可知有唯一解
8
《管理运筹学》第四版课后习题解析
韩伯棠
第 3 章 线性规划问题的计算机求解
1．解： ⑴甲、乙两种柜的日产量是分别是 4 和 8，这时最大利润是 2720 ⑵每多生产一件乙柜，可以使总利润提高 13.333 元 ⑶常数项的上下限是指常数项在指定的范围内变化时， 与其对应的约束条件的对偶价格不变。 比如油漆时间变为 100，因为 100 在 40 和 160 之间，所以其对偶价格不变仍为 13.333 ⑷不变，因为还在 120 和 480 之间。 2．解： ⑴不是，因为上面得到的最优解不为整数解，而本题需要的是整数解 ⑵最优解为 (4，8) 3 ．解： ⑴农用车有 12 辆剩余 ⑵大于 300 ⑶每增加一辆大卡车，总运费降低 192 元 4．解： 计算机得出的解不为整数解，平移取点得整数最优解为(10，8) 5．解： 圆桌和衣柜的生产件数分别是 350 和 100 件，这时最大利润是 3100 元 相差值为 0 代表，不需要对相应的目标系数进行改进就可以生产该产品。 最优解不变，因为 C1 允许增加量 20-6=14；C2 允许减少量为 10-3=7，所有允许增加百分比 和允许减少百分比之和（7.5-6）/14+（10-9）/7〈100%，所以最优解不变。 6．解： （1） x1 150 ， x2 70 ；目标函数最优值 103 000。 （2）1、3 车间的加工工时数已使用完；2、4 车间的加工工时数没用完；没用完的加工工时 数为 2 车间 330 小时，4 车间 15 小时。 （3）50，0，200，0。 含义：1 车间每增加 1 工时，总利润增加 50 元；3 车间每增加 1 工时，总利润增加 200 元； 2 车间与 4 车间每增加一个工时，总利润不增加。 （4）3 车间，因为增加的利润最大。 （5）在 400 到正无穷的范围内变化，最优产品的组合不变。 （6）不变，因为在 0,500 的范围内。 （7）所谓的上限和下限值指当约束条件的右边值在给定范围内变化时，约束条件 1 的右边 值在 200,440 变化，对偶价格仍为 50（同理解释其他约束条件） 。 （8）总利润增加了 100×50=5 000，最优产品组合不变。 （9）不能，因为对偶价格发生变化。
《管理运筹学》第四版课后习题解析
韩伯棠
（2）模型变为 max z 5 xA 4 xB
50 xA 100 xB ≤ 1 200 000 100 xB ≥ 300 000 xA , xB ≥ 0
推导出 x1 18 000 ， x2 3 000 ，故基金 A 投资 90 万元，基金 B 投资 30 万元。
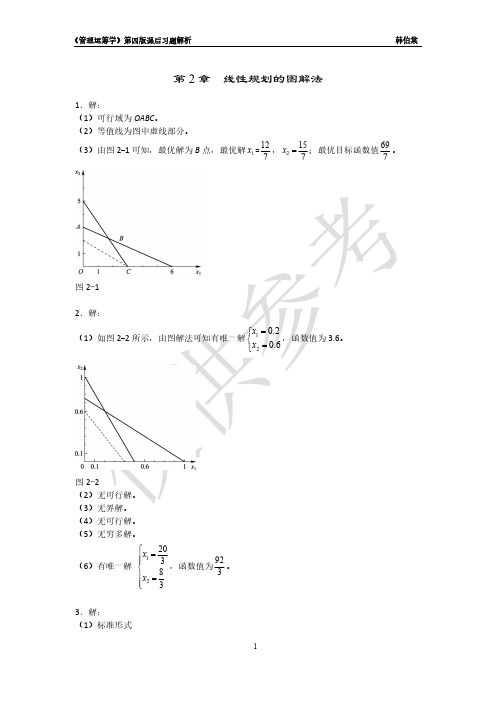
第 2 章 线性规划的图解法
1．解： （1）可行域为 OABC。 （2）等值线为图中虚线部分。 （3）由图 2-1 可知，最优解为 B 点，最优解 x1 =
12 15 69 ， x2 ；最优目标函数值 。 7 7 7
图 2-1 2．解： （1）如图 2-2 所示，由图解法可知有唯一解
8
《管理运筹学》第四版课后习题解析
韩伯棠
第 3 章 线性规划问题的计算机求解
1．解： ⑴甲、乙两种柜的日产量是分别是 4 和 8，这时最大利润是 2720 ⑵每多生产一件乙柜，可以使总利润提高 13.333 元 ⑶常数项的上下限是指常数项在指定的范围内变化时， 与其对应的约束条件的对偶价格不变。 比如油漆时间变为 100，因为 100 在 40 和 160 之间，所以其对偶价格不变仍为 13.333 ⑷不变，因为还在 120 和 480 之间。 2．解： ⑴不是，因为上面得到的最优解不为整数解，而本题需要的是整数解 ⑵最优解为 (4，8) 3 ．解： ⑴农用车有 12 辆剩余 ⑵大于 300 ⑶每增加一辆大卡车，总运费降低 192 元 4．解： 计算机得出的解不为整数解，平移取点得整数最优解为(10，8) 5．解： 圆桌和衣柜的生产件数分别是 350 和 100 件，这时最大利润是 3100 元 相差值为 0 代表，不需要对相应的目标系数进行改进就可以生产该产品。 最优解不变，因为 C1 允许增加量 20-6=14；C2 允许减少量为 10-3=7，所有允许增加百分比 和允许减少百分比之和（7.5-6）/14+（10-9）/7〈100%，所以最优解不变。 6．解： （1） x1 150 ， x2 70 ；目标函数最优值 103 000。 （2）1、3 车间的加工工时数已使用完；2、4 车间的加工工时数没用完；没用完的加工工时 数为 2 车间 330 小时，4 车间 15 小时。 （3）50，0，200，0。 含义：1 车间每增加 1 工时，总利润增加 50 元；3 车间每增加 1 工时，总利润增加 200 元； 2 车间与 4 车间每增加一个工时，总利润不增加。 （4）3 车间，因为增加的利润最大。 （5）在 400 到正无穷的范围内变化，最优产品的组合不变。 （6）不变，因为在 0,500 的范围内。 （7）所谓的上限和下限值指当约束条件的右边值在给定范围内变化时，约束条件 1 的右边 值在 200,440 变化，对偶价格仍为 50（同理解释其他约束条件） 。 （8）总利润增加了 100×50=5 000，最优产品组合不变。 （9）不能，因为对偶价格发生变化。
管理运筹学 第3版 韩伯棠 高教社 课后答案
（1） 、满足对职工需求的条件下，如何安排临时工的班次，使得临时工成本最小。 （2） 、这时付给临时工的工资总额是多少，一共需要安排多少临时工班次。请用剩余变量来说明应该安排一些临时
6
工的 3 小时工作时间的班次，可使得总成本更小。 （3） 、如果临时工每班工作时间可以是 3 小时，也可以是 4 小时，那么如何安排临时工的班次，使得临时工总成本 最小。这样比（1）节省多少费用，这时要安排多少临时工班次。 解题如下： (1)临时工的工作时间为 4 小时，正式工的工作时间也是 4 小时，则第五个小时需要新招人员，临时工只要招用，无 论工作多长时间，都按照 4 小时给予工资。每位临时工招用以后，就需要支付 16 元工资。从上午 11 时到晚上 10 时共计 11 个班次，则设 Xi(i =1,2,…,11)个班次招用的临时工数量，如下为最小成本： minf＝16（X1+X2+X3+X4+X5+X6+X7+X8+X9+X10+X11) 两位正式工一个在 11－15 点上班，在 15－16 点休息，然后在 16－20 点上班。另外一个在 13－17 点上班，在 17 －18 点休息，18－22 点上班。则各项约束条件如下： X1+1>=9 X1+X2+1>=9 X1+X2+X3+2>=9 X1+X2+X3+X4+2>=3 X2+X3+X4+X5+1>=3 X3+X4+X5+X6+2>=3 X4+X5+X6+X7+2>=6 X5+X6+X7+X8+1>=12 X6+X7+X8+X9+2>=12 X7+X8+X9+X10+1>=7 X8+X9+X10+X11+1>=7 Xi>=0(i＝1,2,…,11) 运用计算机解题，结果输出如下; **********************最优解如下************************* 目标函数最优值为 : 320 变量 最优解 -------------x1 8 x2 0 x3 1 x4 0 x5 1 x6 4 x7 0 x8 6 x9 0 x10 0 x11 0 目标函数最优值为 : 320 这时候临时工的安排为： 变量 班次 临时工班次 -------------x1 8 x2 0 x3 1 x4 0
管理运筹学课后答案-----韩伯裳
第2章 线性规划的图解法1．解：x`A 1 (1) 可行域为OABC(2) 等值线为图中虚线部分(3) 由图可知，最优解为B 点， 最优解：1x =712，7152=x 。
最优目标函数值：7692．解： x 2 10 1(1) 由图解法可得有唯一解 6.02.021==x x ，函数值为3.6。
(2) 无可行解 (3) 无界解 (4) 无可行解 (5)无穷多解(6) 有唯一解 3832021==x x ，函数值为392。
3．解：(1). 标准形式：3212100023m ax s s s x x f ++++=,,,,9221323302932121321221121≥=++=++=++s s s x x s x x s x x s x x(2). 标准形式：21210064m in s s x x f +++=,,,46710263212121221121≥=-=++=--s s x x x x s x x s x x(3). 标准形式：21''2'2'10022m in s s x x x f +++-=,,,,30223505527055321''2'2'12''2'2'1''2'2'11''2'21≥=--+=+-=+-+-s s x x x s x x x x x x s x x x4．解：标准形式：212100510m ax s s x x z +++=,,,8259432121221121≥=++=++s s x x s x x s x x松弛变量（0，0） 最优解为 1x =1，x 2=3/2.标准形式：32121000811m in s s s x x f ++++=,,,,369418332021032121321221121≥=-+=-+=-+s s s x x s x x s x x s x x剩余变量（0.0.13） 最优解为 x 1=1，x 2=5.6．解：(1) 最优解为 x 1=3，x 2=7. (2) 311<<c (3) 622<<c (4)4621==x x(5) 最优解为 x 1=8，x 2=0. (6) 不变化。
《管理运筹学》第三版习题答案（韩伯棠教授）
第 2 章 线性规划的图解法11a.可行域为 OABC 。
b.等值线为图中虚线所示。
12c.由图可知，最优解为 B 点，最优解： x 1 = 769 。
7 2、解：15 x 2 =7， 最优目标函数值：a x 210.60.1O1有唯一解x 1 = 0.2函数值为 3.6x 2 = 0.6b 无可行解c 无界解d 无可行解e 无穷多解1 2 2 1 2f 有唯一解20 x 1 =3 8函数值为 92 33、解：a 标准形式：b 标准形式：c 标准形式：x 2 = 3max fmax f= 3x 1 + 2 x 2 + 0s 1 + 0s 2 + 0s 3 9 x 1 + 2x 2 + s 1 = 303x 1 + 2 x 2 + s 2 = 13 2 x 1 + 2x 2 + s 3 = 9 x 1 , x 2 , s 1 , s 2 , s 3 ≥= −4 x 1 − 6x 3 − 0s 1 − 0s 23x 1 − x 2 − s 1 =6x 1 + 2x 2 + s 2 = 10 7 x 1 − 6 x 2 = 4x 1 , x 2 , s 1 , s 2 ≥max f = −x ' + 2x ' − 2 x ''− 0s − 0s'''− 3x 1 + 5x 2 − 5x 2 + s 1 = 70 2 x ' − 5x ' + 5x '' = 50122' ' ''3x 1 + 2 x 2 − 2x 2 − s 2 = 30'' ''4 、解：x 1 , x 2, x 2, s 1 , s 2 ≥ 0标准形式： max z = 10 x 1 + 5x 2 + 0s 1 + 0s 23x 1 + 4 x 2 + s 1 = 9 5x 1 + 2 x 2 + s 2 = 8 x 1 , x 2 , s 1 , s 2 ≥ 0s 1 = 2, s 2 = 0标准形式： min f = 11x 1 + 8x 2 + 0s 1 + 0s 2 + 0s 310 x 1 + 2x 2 − s 1 = 203x 1 + 3x 2 − s 2 = 18 4 x 1 + 9x 2 − s 3 = 36 x 1 , x 2 , s 1 , s 2 , s 3 ≥ 0s 1 = 0, s 2 = 0, s 3 = 136 、解：b 1 ≤c 1 ≤ 3c 2 ≤ c 2 ≤ 6d x 1 = 6 x 2 = 4e x 1 ∈ [4,8]x 2 = 16 − 2x 1f 变化。
运筹学课件--动态规划
J 表示留在左岸的仆人人数
初始状态s1是T(3,3)
结束状态sn是 T(0,0)
可达状态有哪些?(3,J) (2,2) (1,1) (0,J) J 3 2 1 0
2013-6-9
A
1
运筹学课件
2
3
I
阶段指标——每阶段选定决策xk后所产生的效益，记
vk= vk(Sk， xk)。
指标函数——各阶段的总效益，记相应于Pkn的指标函数
2013-6-9 运筹学课件
动态规划模型的分类： 以“时间”角度可分成：
离散型和连续型。
从信息确定与否可分成：
确定型和随机型。
从目标函数的个数可分成： 单目标型和多目标型。
2013-6-9 运筹学课件
8.2基本概念与方程
1.基本概念
阶段（Stage）——分步求解的过程，用阶段变量k表示，k=1，，n 状态（State）——每阶段初可能的情形或位置，用状态变 量Sk表示。 按状态的取值是离散或连续，将动态规划问题分为
当 k 3，f Max f v
3 0
3 3
3
4
Max 3x 5s 13.6(0.9s 0.2x )
0
3 3
3
3
3
3
Max 0.28x 17.24s
0
3 3
3
3
x s , f 17.52s ,即第3年初将全部完好机器都 投入高负荷。
指标函数vkn=
v
5
表示第k至5年的总产量；
1
递推公式：f Max f v
6
f 0, k 5, ,1
2013-6-9
运筹学课件
初始状态s1是T(3,3)
结束状态sn是 T(0,0)
可达状态有哪些?(3,J) (2,2) (1,1) (0,J) J 3 2 1 0
2013-6-9
A
1
运筹学课件
2
3
I
阶段指标——每阶段选定决策xk后所产生的效益，记
vk= vk(Sk， xk)。
指标函数——各阶段的总效益，记相应于Pkn的指标函数
2013-6-9 运筹学课件
动态规划模型的分类： 以“时间”角度可分成：
离散型和连续型。
从信息确定与否可分成：
确定型和随机型。
从目标函数的个数可分成： 单目标型和多目标型。
2013-6-9 运筹学课件
8.2基本概念与方程
1.基本概念
阶段（Stage）——分步求解的过程，用阶段变量k表示，k=1，，n 状态（State）——每阶段初可能的情形或位置，用状态变 量Sk表示。 按状态的取值是离散或连续，将动态规划问题分为
当 k 3，f Max f v
3 0
3 3
3
4
Max 3x 5s 13.6(0.9s 0.2x )
0
3 3
3
3
3
3
Max 0.28x 17.24s
0
3 3
3
3
x s , f 17.52s ,即第3年初将全部完好机器都 投入高负荷。
指标函数vkn=
v
5
表示第k至5年的总产量；
1
递推公式：f Max f v
6
f 0, k 5, ,1
2013-6-9
运筹学课件
管理运筹学 全套课件
Ⅰ
Ⅱ
设备
1
1 300台时
原料A
2
1 400Kg
原料B
0
1 250Kg
已知Ⅰ 、Ⅱ两种产品每单位分别可以获利50元、100 元，问工厂应该如何安排生产才能使工厂获利最多。
线性规划模型
设置变量：生产Ⅰ 产品x1个， Ⅱ产品 x2个
目标函数是利润最大化：
maxz 50x1 100x2
资源是有限的，第一个限制是设备台时 的限制：
角顶：设k为凸集，x∈k，如果不能用不同的 两点x1,x2∈k线性表出x，则称x为k的一个角 顶。
角顶可行解和角顶不可行解：既是角顶解又是 可行解的解称为角顶可行解，是角顶解而不是 可行解的解称为角顶不可行解。
图解法的几点启示
线性规划的可行域必定为凸集。 线性规划的最优解必定在顶点取得。 如果有多个最优解，那么至少有两个相
4x1 3x2
4x1 3x2
线性规划的图解法
从图中可以得到： x1=200,x2=600,z=2600
最优解为：生产200辆大轿车，生产600 辆载重汽车，可获利润2600千元。
钢材和工时全部用完，座椅剩余200套。
几个概念
凸集：设k是n维欧氏空间中的一个点集，在集 合中任意取两点x1,x2∈k。如果这两点连线上 的一切点都落在k中，则称k为凸集。
线性规划模型
建模型如下：设大轿车数量为x1,载重汽 车数量为x2。
m ax z 4 x1 3x2
2 x1 2 x2 1 6 0 0
s.t.5x1x1420.50x2 2 5 0 0
x1, x2 0
s.t.是subject to 的简写，表示受限制于。
线性规划模型
某工厂在计划期间内生产Ⅰ 、Ⅱ两种产品，已知生 产单位产品所需的设备台时及A、B两种原材料的消 耗，如下表所示：
管理运筹学全套ppt课件
线性规划模型
设置变量：生产Ⅰ 产品x1个， Ⅱ产品 x2个
目标函数是利润最大化：
maz x5x 0 110x20
资源是有限的，第一个限制是设备台时 的限制：
x1x2 300
采用PP管及配件：根据给水设计图配置好PP管及配件，用管件在 管材垂 直角切 断管材 ，边剪 边旋转 ，以保 证切口 面的圆 度，保 持熔接 部位干 净无污 物
线性规划模型
建模型如下：设生产Ⅰ 产品x1件, Ⅱ产品 x2件。
max z 50 x1 100 x 2 (1)
x1 x 2 300
s
.t
.
2 x
x1 x 2 2 250
400 (2)
x1 , x 2 0
采用PP管及配件：根据给水设计图配置好PP管及配件，用管件在 管材垂 直角切 断管材 ，边剪 边旋转 ，以保 证切口 面的圆 度，保 持熔接 部位干 净无污 物
线性规划模型
第二个限制是原材料A的限制： 2x1x2 400
第三个限制是原材料B的限制：
x2 250
显然，产量不可能为负数：
x1,x2 0
采用PP管及配件：根据给水设计图配置好PP管及配件，用管件在 管材垂 直角切 断管材 ，边剪 边旋转 ，以保 证切口 面的圆 度，保 持熔接 部位干 净无污 物
采用PP管及配件：根据给水设计图配置好PP管及配件，用管件在 管材垂 直角切 断管材 ，边剪 边旋转 ，以保 证切口 面的圆 度，保 持熔接 部位干 净无污 物
考核方法
平时成绩占20%，每位同学的初始成绩都 是60分（按100分为满分计算）。
每次作业交上加1分，不交不加不减，拷 贝别人作业一次扣2分。
运筹学的体系和发展历史
二次世界大战中，英美科学家研究如何 有效运用雷达，研究船队遇到袭击如何 减少损失，以及如何使用深水炸弹等紧 迫问题。
设置变量：生产Ⅰ 产品x1个， Ⅱ产品 x2个
目标函数是利润最大化：
maz x5x 0 110x20
资源是有限的，第一个限制是设备台时 的限制：
x1x2 300
采用PP管及配件：根据给水设计图配置好PP管及配件，用管件在 管材垂 直角切 断管材 ，边剪 边旋转 ，以保 证切口 面的圆 度，保 持熔接 部位干 净无污 物
线性规划模型
建模型如下：设生产Ⅰ 产品x1件, Ⅱ产品 x2件。
max z 50 x1 100 x 2 (1)
x1 x 2 300
s
.t
.
2 x
x1 x 2 2 250
400 (2)
x1 , x 2 0
采用PP管及配件：根据给水设计图配置好PP管及配件，用管件在 管材垂 直角切 断管材 ，边剪 边旋转 ，以保 证切口 面的圆 度，保 持熔接 部位干 净无污 物
线性规划模型
第二个限制是原材料A的限制： 2x1x2 400
第三个限制是原材料B的限制：
x2 250
显然，产量不可能为负数：
x1,x2 0
采用PP管及配件：根据给水设计图配置好PP管及配件，用管件在 管材垂 直角切 断管材 ，边剪 边旋转 ，以保 证切口 面的圆 度，保 持熔接 部位干 净无污 物
采用PP管及配件：根据给水设计图配置好PP管及配件，用管件在 管材垂 直角切 断管材 ，边剪 边旋转 ，以保 证切口 面的圆 度，保 持熔接 部位干 净无污 物
考核方法
平时成绩占20%，每位同学的初始成绩都 是60分（按100分为满分计算）。
每次作业交上加1分，不交不加不减，拷 贝别人作业一次扣2分。
运筹学的体系和发展历史
二次世界大战中，英美科学家研究如何 有效运用雷达，研究船队遇到袭击如何 减少损失，以及如何使用深水炸弹等紧 迫问题。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
解 题
max
0x3 s3
8x3
5(s3
x3 )
13.6s4
max
0x3 s3
8
x3
5(s3
x3
)
13.6[0.7
x3
0.9(
s3
x3
)]
阶 段
max
0x3 s3
17.52
x3
17.24(
s3
x3
)
(逆序 解法）
同样的，f3 (s3 ) 是x3的线性单调增函数，
s1=1000， s2 0.7x1* 0.9(s1 x1* ) 0.9s1 900
s3 0.7x2* 0.9(s2 x2* ) 0.9s2 810 s4 0.7x3* 0.9(s3 x3* ) 0.7s3 729 s5 0.7x4* 0.9(s4 x4* ) 0.7s4 656
二、离散随机性动态规划
随机型的动态规划是指状态的转移律是不确定的，即 对给定的状态和决策，下一阶段的到达状态是具有确定概率 分布的随机变量，这个概率分布由本阶段的状态和决策完全 确定。随机型动态规划的基本结构如下图：
管理运筹学
16
图中：1、N表示第k+1阶段可能的状态数 能达 2、到p下1、一p2个、状…态pN的为概给率定。状态sk和决策xk的前提下，可 函数值3、。ci为从k阶段状态sk转移到k+1 阶段状态为i时的指标
如
不
结
合 格
论
阶
第2阶段试制3件产品
段 如 不 合 格
第3个阶段试制5件产品
管理运筹学
22
随机采购问题
例8 某公司打算在5周内采购一批原料，未来5周内的原料的价 格有三种，这些价格的出现概率可以估计，如下表。该部 分由于生产需要，必须在5周内采购这批原料。如果第一周 价格很高，可以等到第2周；同样的，第2周如果仍对价格 不满意，可以等到第3周；类似地，未来几周都可能选择购 买或者等待，但必须保证第5周时采购了该原料。试问该选 择哪种采购方案，才能使得采购费用最小？
过程的演变方式为确定性时，这种动态规划 问题就称为连续确定性动态规划问题。
管理运筹学
3
机器负荷分配问题
一种机器能在高低两种不同的负荷状态下工作。设机 器在高负荷下生产时，产量函数为P1=8u1，其中u1为在高 负荷状态下生产的机器数目，年完好率为a=0.7，即到年底 有70％的机器保持完好。在低负荷下生产时，产量函数为 P2=5u2，其中u2为在低负荷状态下生产的机器数目，年完 好率为b=0.9。设开始生产时共有1000台完好的机器，请 问每年应该如何把完好机器分配给高、低两种负荷下生产， 才能使得5年内生产的产品总产量最高。
f5(s5)
max
0x5 s5
8x5
5(s5
x5 )
f6 (s6 )
解 题 阶 段
max 0x5 s5
8x5
5(s5
x5 ) 0
max 0x5 s5
8x5
5(s5
x5 )
(逆序解 法）
因为f5(s5)是x5的线性单调增函数， 故有x5* =s5，
管理运筹学
4
1、阶段 ：分为5个阶段，每个阶段为1年。
2、状态变量sk： 设状态变量sk表示在第k阶段初拥有的完好机
器数目； k=1,2,3,4,5。
建
3、决策变量xk：决策变量xk表示第k阶段中分配给高负荷状态
模
下生产的机器数目；k=1,2,3,4,5。
阶
显然sk-xk为分配给低负荷状态下生产的机器数目。
4
s4
1000 900 810 567
23.72s1＝23720 20.75s2 17.5s3 13.6s4
5
s5
397
8s5
6
---
278
0
解得前两年应把年初完好机器完全投入低负荷生产，后三年
应把年初完好机器完全投入高负荷生产,才能使5年内生产的产
品总产量最高。
管理运筹学
上面所讨论的最优策略过程，初始端状态 s1=1000台是固定的，终点状态s6没有要求。这种情 况下得到最优决策称为初始端固定终点自由的最优 策略。
管理运筹学第十章：
动态规划应用（2）
小组成员：吴侃、朱优胜 潘建凤、杨婷 刘素琴、廖玉丹
管理运筹学
1
1、阶段
2、状态
3、决策
解 建模阶段 4、最优函数
题
5、状态转移方程
思 路
6、基本方程
解题阶段 逆序解法（例：第三 第二 第一）
结论阶段 即：列出最优解的结果
管理运筹学
2
一、连续确定性动态规划 对于状态变量和决策变量只取连续值，
望费用最小？
管理运筹学
18
1、阶段：三次试制当作三个阶段（k=1,2,3）
建
2、状态变量sk：表示第k次试制前是否已经生
模
产出合格品
阶
段
3、决策变量xk：表示第k次生产的产品件数
4、最优函数fk(sk)：表示从状态sk、决策xk出 发的第k阶段以后的最小期望费用。故有fk(0) ＝0。
管理运筹学
19
5(s1
x1)
f 2 (s2 )
max
0 x1 s1
8x1
5(s1
x1)
20.8s2
解 题 阶
max8
0 x1 s1
x1
5(
s1
x1
)
20.8[0.7
x1
0.9(
s1
x1
)
max 0 x1 s1
1.15x1
23.72s1
段
(逆序解 法）
5、状态转移方程：
p(sk1 1) 0.6xk
p(sk1 0) 1 0.6xk
建
模
6、基本方程：
阶 段
fk (1)
min xk
{c(
xk
)
(1
0.6
xk
)
f
k
1
(0)
0.6
xk
f k 1 (1)}
min xk
{c( xk
)
0.6 xk
f k1 (1)}
7、 C(xk)：表示第k阶段的费用，第k阶段的 费用包括制造成本和装配费用：
题
因此有：f5(s5)=s5，
ห้องสมุดไป่ตู้
阶
即：f5(500)=500；
段
f5(600)=600； f5(700)=700。
(逆序解法）
管理运筹学
25
第四阶段：如第4周购买，则需花费s4；如果不 买，则必须在第5周购买。在第5周采购的费用 的期望值为：s4E 0.3 f5 (500) 0.3 f5 (600) 0.4 f5 (700)
管理运筹学
可见，为了使终点完好的机器数量增加到500 台，需要安排前四年中全部完好机器都要投入低负 荷生产，且在第5年，也只能全部投入高负荷。
相应的最优指标为 f1(s1)=29.4s1-7500＝21900。
可以看到，因为增加了附加条件，总产量f1(s1) 要比终点自由情况下的产量要低。
管理运筹学
C
(
xk
)
2 0
xk
xk 0 xk 0
管理运筹学
20
x3
K
0
= s3
3
00
C(x3)+20× 0.6x3
1
2
3
4
5
6
f3(s3 x3*
)
—————0 0
1 20 15 11.2 9.32 8.59 8.56 8.93 8.56 5
解
x2
C(x2)+8.56× 0.6x2
题 阶
K
0
max
0x4 s4
8x4
5(s4
x4
)
18.5s5
7500
max
0x4 s4
21.7s4
0.7 x4
7500
容易解得 x4* 0 ，f4(s4)=21.7s4-7500。
管理运筹学
依次类推，得
x3* x2* x1* 0
f3(s3)=24.5s3-7500 f2(s2)=27.1s2-7500 f1(s1)=29.4s1-7500 再采用顺序方法递推计算各年的状态，有
显然，由于固定了终点的状态，x5的取值受到了 约束。因此有
f5 (s5 ) max8(4.5s5 2500) 5(s5 4.5s5 2500)
18.5s5 7500
类似的，
f4 (s4 )
max
0x4 s4
8x4
5(s4
x4 )
f5 (s5 )
如果终点附加一定的条件，则问题就称为“终 端固定问题”。例如，规定在第5年度结束时仍要 保持500台机器完好（而不是278台），应如何安排 生产才能使得总产量最大？
下面来分析：
根据终点条件有
s6 0.7x5 0.9(s5 x5 ) 500
可得
x5 4.5s5 2500
管理运筹学
1
2
3
4
5