2018初一数学几何图形初步单元测试1(供参考)
七年级几何图形初步单元测试卷(含答案解析)
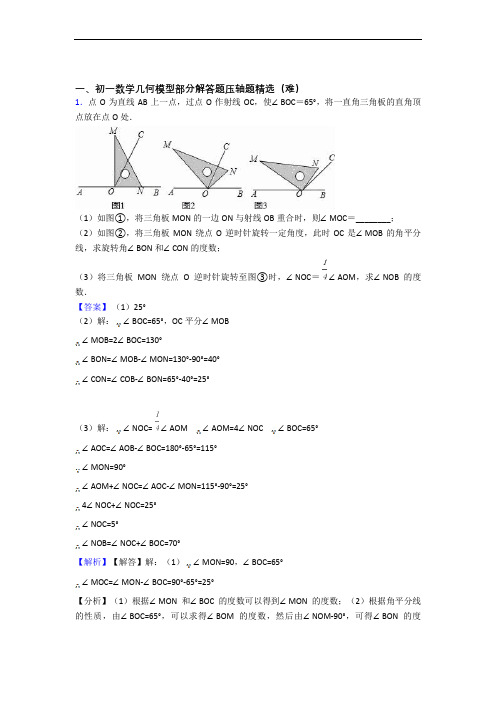
一、初一数学几何模型部分解答题压轴题精选（难）1．点O为直线AB上一点，过点O作射线OC，使∠BOC＝65°，将一直角三角板的直角顶点放在点O处．（1）如图①，将三角板MON的一边ON与射线OB重合时，则∠MOC＝________；（2）如图②，将三角板MON绕点O逆时针旋转一定角度，此时OC是∠MOB的角平分线，求旋转角∠BON和∠CON的度数；（3）将三角板MON绕点O逆时针旋转至图③时，∠NOC＝∠AOM，求∠NOB的度数．【答案】（1）25°（2）解：∠BOC=65°，OC平分∠MOB∠MOB=2∠BOC=130°∠BON=∠MOB-∠MON=130°-90°=40°∠CON=∠COB-∠BON=65°-40°=25°（3）解：∠NOC= ∠AOM ∠AOM=4∠NOC ∠BOC=65°∠AOC=∠AOB-∠BOC=180°-65°=115°∠MON=90°∠AOM+∠NOC=∠AOC-∠MON=115°-90°=25°4∠NOC+∠NOC=25°∠NOC=5°∠NOB=∠NOC+∠BOC=70°【解析】【解答】解：（1）∠MON=90，∠BOC=65°∠MOC=∠MON-∠BOC=90°-65°=25°【分析】（1）根据∠MON和∠BOC的度数可以得到∠MON的度数；（2）根据角平分线的性质，由∠BOC=65°，可以求得∠BOM的度数，然后由∠NOM-90°，可得∠BON的度数，从而得解；（3）由∠BOC=65°，∠NOM=90°，∠NOC= ∠AOM，从而可求得∠NOC的度数，然后由∠BOC=65°，从而得解.2．如图，直线m与直线n互相垂直，垂足为O,A、B两点同时从点O出发，点A沿直线m向左运动，点B沿直线n向上运动.（1）若∠BAO和∠ABO的平分线相交于点P，在点A、B的运动过程中，∠APB的大小是否会发生变化？若不发生变化，请求出其值；若发生变化，请说明理由；（2）若△ABO的两个外角的平分线AQ、BQ相交于点Q，AP的延长线交QB的延长线于点C，在点A、B的运动过程中，∠Q和∠C的大小是否会发生变化？若不发生变化，请求出∠Q和∠C的度数；若发生变化，请说明理由.【答案】（1）解：不变化.理由：∵AP和BP分别是∠BAO和∠ABO的平分线，∠AOB=90°，∴∠APB=180°（∠OAB+∠ABO）=180° ×90°=135°（2）解：都不变.理由：∵AQ和BQ分别是∠BAO的邻补角和∠ABO的邻补角的平分线，AP和BP分别是∠BAO和∠ABO的平分线，∴∠CAQ=∠QBP=90°，又∠APB=135°，∴∠Q=45°，∴∠C=45°【解析】【分析】根据角平分线定义和三角形内角和定理得到∠APB=180° −（∠OAB+∠ABO）；根据邻补角的平分线互相垂直，得到∠CAQ=∠QBP=90°，由∠APB的度数，求出∠Q和∠C的度数.3．已知AM∥CN，点B为平面内一点，AB⊥BC于B．（1）如图1，直接写出∠A和∠C之间的数量关系________；（2）如图2，过点B作BD⊥AM于点D，求证：∠ABD=∠C；（3）如图3，在（2）问的条件下，点E、F在DM上，连接BE、BF、CF，BF平分∠DBC，BE平分∠ABD，若∠FCB+∠NCF=180°，∠BFC=3∠DBE，求∠EBC的度数．【答案】（1）∠A+∠C=90°；（2）解：如图2，过点B作BG∥DM，∵BD⊥AM，∴DB⊥BG，即∠ABD+∠ABG=90°，又∵AB⊥BC，∴∠CBG+∠ABG=90°，∴∠ABD=∠CBG，∵AM∥CN，∴∠C=∠CBG，∴∠ABD=∠C；（3）解：如图3，过点B作BG∥DM，∵BF平分∠DBC，BE平分∠ABD，∴∠DBF=∠CBF，∠DBE=∠ABE，由（2）可得∠ABD=∠CBG，∴∠ABF=∠GBF，设∠DBE=α，∠ABF=β，则∠ABE=α，∠ABD=2α=∠CBG，∠GBF=β=∠AFB，∠BFC=3∠DBE=3α，∴∠AFC=3α+β，∵∠AFC+∠NCF=180°，∠FCB+∠NCF=180°，∴∠FCB=∠AFC=3α+β，△BCF中，由∠CBF+∠BFC+∠BCF=180°，可得（2α+β）+3α+（3α+β）=180°，①由AB⊥BC，可得β+β+2α=90°，②由①②联立方程组，解得α=15°，∴∠ABE=15°，∴∠EBC=∠ABE+∠ABC=15°+90°=105°．【解析】【分析】（1）根据平行线的性质以及直角三角形的性质进行证明即可；（2）先过点B作BG∥DM，根据同角的余角相等，得出∠ABD=∠CBG，再根据平行线的性质，得出∠C=∠CBG，即可得到∠ABD=∠C；（3）先过点B作BG∥DM，根据角平分线的定义，得出∠ABF=∠GBF，再设∠DBE=α，∠ABF=β，根据∠CBF+∠BFC+∠BCF=180°，可得（2α+β）+3α+（3α+β）=180°，根据AB⊥BC，可得β+β+2α=90°，最后解方程组即可得到∠ABE=15°，进而得出∠EBC=∠ABE+∠ABC=15°+90°=105°．4．综合题（1）ⅰ问题引入如图①，在△ABC中，点O是∠ABC和∠ACB平分线的交点，若∠A＝α，则∠BOC＝________（用α表示）；ⅱ拓展研究如图②，∠CBO＝∠ABC，∠BCO＝∠ACB，∠A＝α，试求∠BOC的度数________（用α表示）.ⅲ归纳猜想若BO、CO分别是△ABC的∠ABC、∠ACB的n等分线，它们交于点O，∠CBO＝∠ABC，∠BCO＝∠ACB，∠A＝α，则∠BOC＝________（用α表示）.（2）类比探索ⅰ特例思考如图③，∠CBO＝∠DBC，∠BCO＝∠ECB，∠A＝α，求∠BOC的度数________（用α表示）.ⅱ一般猜想若BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线，它们交于点O，∠CBO＝∠DBC，∠BCO＝∠ECB，∠A＝α，请猜想∠BOC＝________（用α表示）.【答案】（1）90°＋∠α；120°＋∠α；（2）120°－∠α； .【解析】【解答】（1）ⅰ90°＋∠α；ⅱ如图②，∵∠CBO＝∠ABC，∠BCO＝∠ACB，∠A＝α，∴∠BOC＝180°－（∠ABC＋∠ACB）＝180°－（180°－∠A）＝180°－（180°－∠α）＝180°－60°＋∠α＝120°＋∠α；ⅲ；（ 2 ）ⅰ如图③，∵∠CBO＝∠DBC，∠BCO＝∠ECB，∠A＝α，∴∠BOC＝180°－（∠DBC＋∠ECB）＝180°－ [360°－（∠ABC＋∠ACB）]＝180°－ [360°－（180°－∠A）]＝180°－（180°＋∠α）＝180°－60°－∠α＝120°－∠α.；ⅱ .【分析】（1）ⅰ根据角平分线的定义，可得出∠CBO=∠ABC，∠OCB=∠ACB，可得出∠CBO+∠OCB=（180°-∠A），再在△COB中，利用三角形内角和定理得出∠BOC=180°-（∠CBO+∠OCB），即可得出结果；ⅱ根据∠CBO=∠ABC，∠OCB=∠ACB，可得出∠CBO+∠OCB=（180°-∠A），再在△COB中，利用三角形内角和定理得出∠BOC=180°-（∠CBO+∠OCB），即可得出结果；ⅲ根据∠CBO=∠ABC，∠OCB=∠ACB，可得出∠CBO+∠OCB=（180°-∠A），再在△COB中，利用三角形内角和定理得出∠BOC=180°-（∠CBO+∠OCB），即可得出结果。
2018-2019学年七年级上册几何图形初步单元过关试卷含答案解析
【答案】152°； 62°.
【解析】
试题分析：∵ ∠AOC+∠COD=180°，∠AOC=28°，∴ ∠COD=152°. ∵ OC 是∠AOB 的平分线，
∠AOC=28°，
∴ ∠AOB=2∠AOC=2×28°=56°，∴ ∠BOD=180°－ ∠AOB=180°－56°=124°.∵ OE 是∠BOD 的平分线，
．
4
【答案】两点之间线段最短． 【解析】
考点：线段的性质：两点之间线段最短．
2．若一个角的补角是这个角 2 倍，则这个角度数为
度．
【答案】60°．
【解析】
试题分析：设这个角为 x°，则这个角的补角为 2x°，所以 x+2x=180°，解得 x=60°，即这个角的度数
为 60°．
考点：补角的定义．
3．已知点 P 是线段 AB 的中点，若 PB=8cm，则 AB= cm．
考点：探求规律问题.
6．若∠α 与∠β 互为补角，则下列式子成立的是（ ）
A．α-β= 90°
B．α+β=90°
C．α-β=180°
D．α+β=180°
【答案】D．
【解析】
试题分析：∵∠α 与∠β 互为补角，∴α+β=180°，
2
故选 D．
考点：余角和补角．
7．如图，点 O 在直线 AB 上，射线 OC 平分∠DOB．若∠COB=35°，则∠AOD 等于（
A.8 cm 【答案】D． 【解析】
B.12 cm
C.14 cm
D. 10 cm
考点：两点间距离．
5．往返于 A、B 两地的客车，中途停三个站，在客车正常营运中，不同的票价有（
）
A.10 种 B.4 种 C.3 种 D.5 种
人教版七年级上册数学《第四章几何图形初步》单元测试题(含解析)
人教版七年级上册数学《第四章几何图形初步》单元测试题（含解析）一．选择题（共10小题）1．如图所示的四种物体中，哪种物体最接近于圆柱（）A．B．C．D．2．下列几何体的截面分别是（）A．圆、平行四边形、三角形、圆B．圆、长方形、三角形、圆C．圆、长方形、长方形、三角形D．圆、长方形、三角形、三角形3．如图是我国南海地区图，图中的点分别代表三亚市，永兴岛，黄岩岛，渚碧礁，弹丸礁和曾母暗沙，该地区图上两个点之间距离最短的是（）A．三亚﹣﹣永兴岛B．永兴岛﹣﹣黄岩岛C．黄岩岛﹣﹣弹丸礁D．渚碧礁﹣﹣曾母暗山4．如图，图中共有线段（）第 1 页共31 页A．7条B．8条C．9条D．10条5．如图，C为线段AB上一点，D为线段BC的中点，AB=20，AD=14，则AC的长为（）A．10B．8C．7D．66．如图，∠AOB是平角，∠AOC=50°，∠BOD=60°，OM平分∠BOD，ON平分∠AOC，则∠MON的度数是（）A．135°B．155°C．125°D．145°7．将长方形纸片按如图所示的方式折叠，BC、BD为折痕．若∠ABC=25°，则∠DBE的度数为（）A．50°B．65°C．45°D．60°8．将一块长为a米，宽为b米的矩形空地建成一个矩形花园，要求在花园中修两条入口宽均为x米的小道，其中一条小道两边分别经过矩形一组对角顶点，剩余的地方种植花草，现有从左至右三种设计方案如图所示，种植花草的面积分别为S1，S2和S3，则它们的大小关系为（）第 2 页共31 页A．S3＜S1＜S2B．S1＜S2＜S3C．S2＜S1＜S3D．S1=S2=S39．下列七个图形中是正方体的平面展开图的有（）A．1个B．2个C．3个D．4个10．如图是一个棱长为1的正方体的展开图，点A，B，C是展开后小正方形的顶点，连接AB，BC，则∠ABC的大小是（）A．60°B．50°C．45°D．30°二．填空题（共8小题）11．下面的几何体中，属于柱体的有个．12．如图，是正方体的一个平面展开图，在这个正方体中，与“爱”字所在面相对的面上的汉字是第 3 页共31 页13．如果线段AB=10，点C、D在直线AB上，BC=6，D是AC的中点，则A、D 两点间的距离是．14．已知线段MN=16cm，点P为任意一点，那么线段MP与NP和的最小值是cm．15．如图，若∠3：∠2=2：5，且∠2﹣∠1=12°，∠3等于．16．如图，点B、O、D在同一直线上，且OB平分∠AOC，若∠COD=150°，则∠AOC的度数是．17．如图，一纸片沿直线AB折成的V字形图案，已知图中∠1=62°，则∠2的度数=．18．如图，A、O、B在一直线上，∠1=∠2，则与∠1互补的角是．若∠1=28°32′35″，则∠1的补角=．三．解答题（共7小题）19．太阳可以近似地看成球体，已知太阳的半经为6.96×108m，太阳的体积大约是多少？（球的体积的计算公式是V=πr3，π取3.14）第 4 页共31 页20．已知一个长方体的长为1cm，宽为1cm，高为2cm，请求出：（1）长方体有条棱，个面；（2）长方体所有棱长的和；（3）长方体的表面积．21．如图所示，若剪下来折叠能拼成一个正方体盒子，请你想象一下，能否在空格中填上适当的数，使相对的两个面上的数互为相反数？22．如图，点B、C把线段MN分成三部分，其比是MB：BC：CN=2：3：4，P 是MN的中点，且MN=18cm，求PC的长．23．如图，∠AOB是平角，∠DOE=90°，OC平分∠DOB．（1）若∠AOE=32°，求∠BOC的度数；（2）若OD是∠AOC的角平分线，求∠AOE的度数．24．以直线AB上点O为端点作射线OC，使∠BOC=60°，将直角△DOE的直角顶点放在点O处．（1）如图1，若直角△DOE的边OD放在射线OB上，则∠COE=；（2）如图2，将直角△DOE绕点O按逆时针方向转动，使得OE平分∠AOC，说第 5 页共31 页明OD所在射线是∠BOC的平分线；（3）如图3，将直角△DOE绕点O按逆时针方向转动，使得∠COD=∠AOE．求∠BOD的度数．25．探索性问题：已知A，B在数轴上分别表示m，n．（1）填表：（2）若A，B两点的距离为d，则d与m，n有何数量关系．（3）在数轴上整数点P到4和﹣5的距离之和为9，求出满足条件的所有这些整数的和．第 6 页共31 页2018年秋人教版七年级上册数学《第四章几何图形初步》单元测试题参考答案与试题解析一．选择题（共10小题）1．如图所示的四种物体中，哪种物体最接近于圆柱（）A．B．C．D．【解答】解：最接近圆柱的是生日蛋糕．故选：A．2．下列几何体的截面分别是（）A．圆、平行四边形、三角形、圆B．圆、长方形、三角形、圆C．圆、长方形、长方形、三角形D．圆、长方形、三角形、三角形【解答】解：当截面平行于圆柱底面截取圆柱时得到截面图形是圆，截面截取经过四个顶点的截面时可以截得长方形，当截面垂直圆锥的底面时，截面图形是三角形，当截面平行于圆锥的底面时，截面图形是圆．所以这几个几何体的截面分别是：圆、长方形、三角形、圆，故选：B．3．如图是我国南海地区图，图中的点分别代表三亚市，永兴岛，黄岩岛，渚碧礁，弹丸礁和曾母暗沙，该地区图上两个点之间距离最短的是（）第7 页共31 页A．三亚﹣﹣永兴岛B．永兴岛﹣﹣黄岩岛C．黄岩岛﹣﹣弹丸礁D．渚碧礁﹣﹣曾母暗山【解答】解：由图可得，三亚﹣﹣永兴岛两个点之间距离最短，故选：A．4．如图，图中共有线段（）A．7条B．8条C．9条D．10条【解答】解：线段由AD，AE，DE，AB，AC，BD，EC，BC，故选：B．5．如图，C为线段AB上一点，D为线段BC的中点，AB=20，AD=14，则AC的长为（）A．10B．8C．7D．6【解答】解：∵AB=20，AD=14，∴BD=AB﹣AD=20﹣14=6，∵D为线段BC的中点，∴BC=2BD=12，∴AC=AB﹣BC=20﹣12=8．第8 页共31 页6．如图，∠AOB是平角，∠AOC=50°，∠BOD=60°，OM平分∠BOD，ON平分∠AOC，则∠MON的度数是（）A．135°B．155°C．125°D．145°【解答】解：∵∠AOC+∠COD+∠BOD=180°，∴∠COD=180°﹣∠AOC﹣∠COD=70°，∵OM、ON分别是∠AOC、∠BOD的平分线，∴∠MOC=∠AOC=25°，∠DON=∠BOD=30°，∴∠MON=∠MOC+∠COD+∠DON=125°，故选：C．7．将长方形纸片按如图所示的方式折叠，BC、BD为折痕．若∠ABC=25°，则∠DBE的度数为（）A．50°B．65°C．45°D．60°【解答】解：∵一张长方形纸片沿BC、BD折叠，∴∠ABC=∠A′BC，∠EBD=∠E′BD，而∠ABC+∠A′BC+∠EBD+∠E′BD=180°，∴∠A′BC+∠E′BD=180°×=90°，即∠ABC+∠DBE=90°，∵∠ABC=25°，∴∠DBE=65°．第9 页共31 页8．将一块长为a米，宽为b米的矩形空地建成一个矩形花园，要求在花园中修两条入口宽均为x米的小道，其中一条小道两边分别经过矩形一组对角顶点，剩余的地方种植花草，现有从左至右三种设计方案如图所示，种植花草的面积分别为S1，S2和S3，则它们的大小关系为（）A．S3＜S1＜S2B．S1＜S2＜S3C．S2＜S1＜S3D．S1=S2=S3【解答】解：∵矩形的长为a米，宽为b米，小路的宽为x米，∴S1=ab﹣（a+b）x+S4；S2=ab﹣（a+b）x+S5；S3=ab﹣（a+b）x+S6．∵S4=x•x=x2，S5=x•sin60°•x•sin60°=x2，S6=x•sin60°•=x2，∴S2＜S1＜S3．故选：C．9．下列七个图形中是正方体的平面展开图的有（）A．1个B．2个C．3个D．4个【解答】解：由题可得，是正方体的平面展开图的有：故选：B．第10 页共31 页10．如图是一个棱长为1的正方体的展开图，点A，B，C是展开后小正方形的顶点，连接AB，BC，则∠ABC的大小是（）A．60°B．50°C．45°D．30°【解答】解：连接AC．根据勾股定理可以得到：AC=BC=，AB=，∵（）2+（）2=（）2，即AC2+BC2=AB2，∴△ABC是等腰直角三角形．∴∠ABC=45°．故选：C．二．填空题（共8小题）11．下面的几何体中，属于柱体的有4个．【解答】解：柱体分为圆柱和棱柱，所以柱体有圆柱、正方体、六棱柱，三棱柱共4个．故答案为：4．12．如图，是正方体的一个平面展开图，在这个正方体中，与“爱”字所在面相对的面上的汉字是中【解答】解：正方体的表面展开图，相对的面之间一定相隔一个正方形，第11 页共31 页“我”与“城”是相对面，“北”与“三”是相对面，“爱”与“中”是相对面．故答案为：中．13．如果线段AB=10，点C、D在直线AB上，BC=6，D是AC的中点，则A、D 两点间的距离是2或8．【解答】解：①如图1所示，∵AB=10，BC=6，∴AC=AB﹣BC=10﹣6=4，∵D是线段AC的中点，∴AD=AC=×4=2；②如图2所示，∵AB=10，BC=6，∴AC=AB+BC=10+6=16，∵D是线段AC的中点，∴AD=AC=×16=8．故答案为：2或8．14．已知线段MN=16cm，点P为任意一点，那么线段MP与NP和的最小值是16 cm．【解答】解：如图所示：所以线段MP与NP和的最小值是16cm，故答案为；1615．如图，若∠3：∠2=2：5，且∠2﹣∠1=12°，∠3等于32°．第12 页共31 页【解答】解：∵∠3：∠2=2：5，设∠3=2x，∠2=5x，∵∠1+∠2+∠3=180°，∠2﹣∠1=12°，可得：5x﹣12°+5x+2x=180°，解得：x=16，所以∠3=2×16°=32°，故答案为：32°16．如图，点B、O、D在同一直线上，且OB平分∠AOC，若∠COD=150°，则∠AOC的度数是60°．【解答】解：∵点B、O、D在同一直线上，∠COD=150°，∴∠COB=180°﹣150°=30°，∵OB平分∠AOC，∴∠AOC=2×30°=60°，故答案为：60°．17．如图，一纸片沿直线AB折成的V字形图案，已知图中∠1=62°，则∠2的度数=56°．【解答】解：由折叠可得出2∠1+∠2=180°，∵∠1=62°，第13 页共31 页∴∠2=180°﹣2×62°=56°，故答案为56°．18．如图，A、O、B在一直线上，∠1=∠2，则与∠1互补的角是∠AOD．若∠1=28°32′35″，则∠1的补角=151°27′25″．【解答】解：∵∠1=∠2，∴与∠1互补的角是∠AOD，∵∠1=28°32′35″，∴∠1的补角=151°27′25″，故答案为：∠AOD；151°27′25″三．解答题（共7小题）19．太阳可以近似地看成球体，已知太阳的半经为6.96×108m，太阳的体积大约是多少？（球的体积的计算公式是V=πr3，π取3.14）【解答】解：当r=6.96×108时，V=πr3≈×3.14×（6.96×108）3≈1.41×1027m3，答：太阳的体积大约是1.41×1027m3．20．已知一个长方体的长为1cm，宽为1cm，高为2cm，请求出：（1）长方体有12条棱，6个面；（2）长方体所有棱长的和；（3）长方体的表面积．【解答】解：（1）长方体有12条棱，6个面；第14 页共31 页故答案为：12，6；（2）（1+1+2）×4=4×4=16（cm）．故长方体所有棱长的和是16cm；（3）（1×1+1×2+1×2）×2=（1+2+2）×2=5×2=10（cm2）．故长方体的表面积是10cm2．21．如图所示，若剪下来折叠能拼成一个正方体盒子，请你想象一下，能否在空格中填上适当的数，使相对的两个面上的数互为相反数？【解答】解：依题意得：A=﹣2，B=﹣3，C=﹣4．22．如图，点B、C把线段MN分成三部分，其比是MB：BC：CN=2：3：4，P 是MN的中点，且MN=18cm，求PC的长．【解答】解：设MB=2x，则BC=3x，CN=4x，因为P是MN中点，所以MP=MN=×（2x+3x+4x）=x=9．解得x=2，∴PC=MC﹣MP=2x+3x﹣x=0.5x=1．23．如图，∠AOB是平角，∠DOE=90°，OC平分∠DOB．（1）若∠AOE=32°，求∠BOC的度数；（2）若OD是∠AOC的角平分线，求∠AOE的度数．第15 页共31 页【解答】解：（1）∠AOD=∠DOE﹣∠AOE=90°﹣32°=58°∠BOD=∠AOB﹣∠AOD=180°﹣58°=122°又OC平分∠BOD所以：∠BOC=∠BOD=×122°=61°（2）因为OC平分∠BOD，OD平分∠AOC 所以∠BOC=∠DOC=∠AOD又∠BOC+∠DOC+∠AOD=180°所以∠AOD=×180°=60°所以∠AOE=∠DOE﹣∠AOD=90°﹣60°=30°24．以直线AB上点O为端点作射线OC，使∠BOC=60°，将直角△DOE的直角顶点放在点O处．（1）如图1，若直角△DOE的边OD放在射线OB上，则∠COE=30°；（2）如图2，将直角△DOE绕点O按逆时针方向转动，使得OE平分∠AOC，说明OD所在射线是∠BOC的平分线；（3）如图3，将直角△DOE绕点O按逆时针方向转动，使得∠COD=∠AOE．求∠BOD的度数．【解答】解：（1）∵∠BOE=∠COE+∠COB=90°，又∵∠COB=60°，∴∠COE=30°，第16 页共31 页故答案为：30°；（2）∵OE平分∠AOC，∴∠COE=∠AOE=COA，∵∠EOD=90°，∴∠AOE+∠DOB=90°，∠COE+∠COD=90°，∴∠COD=∠DOB，∴OD所在射线是∠BOC的平分线；（3）设∠COD=x°，则∠AOE=5x°，∵∠DOE=90°，∠BOC=60°，∴6x=30或5x+90﹣x=120∴x=5或7.5，即∠COD=5°或7.5°∴∠BOD=65°或52.5°．25．探索性问题：已知A，B在数轴上分别表示m，n．（1）填表：（2）若A，B两点的距离为d，则d与m，n有何数量关系．（3）在数轴上整数点P到4和﹣5的距离之和为9，求出满足条件的所有这些整数的和．【解答】解：（1）5﹣2=3；0﹣（﹣4）=4；6﹣（﹣6）=12；﹣4﹣（﹣5）=1；2﹣（﹣90）=92；﹣2.5﹣（﹣4.5）=2；故答案为：3，4，12，1，92，2；（2）∵数轴上两点间的距离d等于表示两点数之差的绝对值，第17 页共31 页∴d=|m﹣n|．（3）设整数点P表示的数为x，∵点P到4和﹣5的距离之和为9，∴|x﹣4|+|x﹣（﹣5）|=9，即x﹣4+x+5=9，﹣（x﹣4）+x+5=9（﹣5和4两点间所有的整数点均成立），x ﹣4﹣（x+5）=9（舍去）或﹣（x﹣4）﹣（x+5）=9，解得x=﹣5，﹣4，﹣3，﹣2，﹣1，0，1，2，3，4；∴有这些整数的和为4+3+2+1+0﹣1﹣2﹣3﹣4﹣5=﹣5．第18 页共31 页人教版七年级上册数学第四章几何图形初步单元测试题（含答案）一、选择题1.角是指（）A. 由两条线段组成的图形B. 由两条射线组成的图形C. 由两条直线组成的图形D. 有公共端点的两条射线组成的图形2.如果一个角的补角是150°，那么这个角的余角的度数是（）A. 30°B. 60°C. 90°D. 120°3.下列说法正确的是（）A. 经过两点有且只有一条线段B. 经过两点有且只有一条直线C. 经过两点有且只有一条射线D. 经过两点有无数条直线4.如图，四条线段中，最短和最长的一条分别是（）A. acB. bdC. adD. bc5.如图，B在线段AC上，且BC=2AB，D，E分别是AB，BC的中点．则下列结论：①AB= AC；②B是AE的中点；③EC=2BD；④DE=AB．其中正确的有（）A. 1个B. 2个C. 3个D. 4个6.已知∠α=70°，则∠α的补角为（）A. 120°B. 110°C. 70°D. 20°7.下列语句中，正确的是（）．A. 比直角大的角钝角;B. 比平角小的角是钝角C. 钝角的平分线把钝角分为两个锐角;D. 钝角与锐角的差是锐角8.如图，已知AD平分∠BAE，若∠BAD=62°，则∠CAE的度数是（）第19 页共31 页A. 55°B. 56°C. 58°D. 62°9.如图，下列关系式中与图不符合的式子是（）A. AD-CD=AB+BCB. AC-BC=AD-BDC. AC-BC=AC+BDD. AD-AC=BD-BC10.如图是一个正方体的平面展开图，当把它拆成一个正方体，与空白面相对的字应该是（）A. 北B. 京C. 欢D. 迎二、填空题11.已知线段AB=8 cm，在直线AB上画线段BC，使它等于3 cm，则线段AC=________.12.若∠α=32°22′，则∠α的余角的度数为________．13.已知一个角的补角等于155°，则这个角的余角等于________14.八棱柱有________个顶点，________条棱，________个面．15.和互补，且-=50°，求和的度数． ________、 ________16.34.42°=________（用度、分、秒表示）.17.一个角的补角加上10°后，等于这个角的余角的3倍，则这个角=________ °．18.用一个平面去截长方体，截面________是平行四边形（填“可能”或“不可能”）．19.一条直线上有A、B、C三个点，AB=7cm，BC=4cm，则AC=________ ．20.已知线段AB=1996，P、Q是线段AB上的两个点，线段AQ=1200，线段BP=1050，则线段PQ=________．三、解答题21.已知∠BOC＝120°，∠AOB＝70°，求∠AOC的大小。
七年级数学几何图形初步单元测试卷附答案
一、初一数学几何模型部分解答题压轴题精选（难）1．问题情境1:如图1,AB∥CD,P是ABCD内部一点,P在BD的右侧,探究∠B,∠P,∠D之间的关系?小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠B,∠P,∠D之间满足____关系。
(直接写出结论)问题情境2如图3,AB∥CD,P是AB,CD内部一点,P在BD的左侧,可得∠B,∠P,∠D之间满足____关系。
(直接写出结论)问题迁移:请合理的利用上面的结论解决以下问题:已知AB∥CD,∠ABE与∠CDE两个角的角平分线相交于点F（1）如图4,若∠E=80°,求∠BFD的度数；（2）如图5中,∠ABM= ∠ABF,∠CDM= ∠CDF,写出∠M与∠E之间的数量关系并证明你的结论。
（3）若∠ABM= ∠ABF,∠CDM= ∠CDF,设∠E=m°,用含有n,m°的代数式直接写出∠M=________.【答案】（1）解：根据问题情境2，可得出∠BFD=∠AEF+∠CDF∵,∠ABE与∠CDE两个角的角平分线相交于点F∴∠AEF=∠FBE，∠CDF=∠FDE∴∠FBE+∠FDE=∠BFD∵∠E+∠BFD+∠FBE+∠FDE=360°∴80°+∠BFD+∠BFD=360°∴∠BFD=140°（2）结论为：6∠M+∠E=360°证明：∵∠ABM= ∠ABF,∠CDM= ∠CDF∴∠ABF=3∠ABM，∠CDF=3∠CDM∵∠ABE与∠CDE两个角的角平分线相交于点F∴∠ABE=6∠ABM，∠CDE=6∠CDM∵∠ABE+∠CDE+∠E=360°∴6（∠ABM+∠CDM）+∠E=360°∵∠M=∠ABM+∠CDM∴6∠M+∠E=360°（3）证明：根据（2）的结论可知2n∠ABM+2n∠CDM+∠E=360°2n（∠ABM+∠CDME）+∠E=360°∵∠M=∠ABM+∠CDM∴2n∠M+m°=360°∴∠M=【解析】问题情境1: 图1中∠B,∠P,∠D之间关系是：∠P+∠B+∠D=360°，问题情境2：图3中∠B,∠P,∠D之间关系是：∠P=∠B+∠D；【分析】问题情境1和2 过点P作EP∥AB，利用平行线的性质，可证得结论。
七年级数学几何图形初步单元测试卷(含答案解析)
一、初一数学几何模型部分解答题压轴题精选（难）1．数轴上A, B, C, D四点表示的有理数分别为1, 3, －5, －8（1）计算以下各点之间的距离：①A、B两点, ②B、C两点,③C、D两点,（2）若点M、N两点所表示的有理数分别为m、n，求M、N两点之间的距离．【答案】（1）AB=3-1=2；BC=3-（-5）=8；CD=-5-（-8）=-5+8=3.（2）MN=【解析】【分析】（1）数轴上两点间的距离等于数值较大的数减去数值较小的数，据此计算即可；（2）因为m、n的大小未知，则M、N两点间的距离为它们所表示的有理数之差的绝对值.2．如图，点C在∠AOB的边OA上，过点C的直线DE∥OB，CF平分∠ACD，CG⊥CF于C.（1）若∠O＝40°，求∠ECF的度数；（2）试说明CG平分∠OCD；（3）当∠O为多少度时，CD平分∠OCF？并说明理由．【答案】（1）解：∵DE//OB ，∴∠O=∠ACE，（两直线平行，同位角相等）∵∠O =40°，∴∠ACE =40°，∵∠ACD+∠ACE= (平角定义)∴∠ACD=又∵CF平分∠ACD ，∴ (角平分线定义)∴∠ECF=（2）证明：∵CG⊥CF，∴ .∴又∵）∴∵∴ (等角的余角相等）即CG平分∠OCD（3）解：结论：当∠O=60°时，CD平分∠OCF ．当∠O=60°时∵DE//OB，∴∠DCO=∠O=60°.∴∠ACD=120°.又∵CF平分∠ACD∴∠DCF=60°，∴即CD平分∠OCF【解析】【分析】（1）根据平行线“两直线平行，同位角相等”，求得∠ACE＝40°，根据平角的定义以及CF平分∠ACD ，可得到∠ACF＝70°，然后求出∠ECF的度数；（2）根据∠DCG＋∠DCF＝90°，∠GCO＋∠FCA＝90°，以及∠ACF＝∠DCF，可得到∠GCO ＝∠GCD，即可证明CG平分∠OCD；（3）根据两直线平行，内错角相等得出∠DCO＝∠O＝60°，根据角平分线可得到∠DCF＝60°，以此可得∠DCO＝∠DCF，即CD平分∠OCF．3．已知AM∥CN，点B为平面内一点，AB⊥BC于B．（1）如图1，直接写出∠A和∠C之间的数量关系________；（2）如图2，过点B作BD⊥AM于点D，求证：∠ABD=∠C；（3）如图3，在（2）问的条件下，点E、F在DM上，连接BE、BF、CF，BF平分∠DBC，BE平分∠ABD，若∠FCB+∠NCF=180°，∠BFC=3∠DBE，求∠EBC的度数．【答案】（1）∠A+∠C=90°；（2）解：如图2，过点B作BG∥DM，∵BD⊥AM，∴DB⊥BG，即∠ABD+∠ABG=90°，又∵AB⊥BC，∴∠CBG+∠ABG=90°，∴∠ABD=∠CBG，∵AM∥CN，∴∠C=∠CBG，∴∠ABD=∠C；（3）解：如图3，过点B作BG∥DM，∵BF平分∠DBC，BE平分∠ABD，∴∠DBF=∠CBF，∠DBE=∠ABE，由（2）可得∠ABD=∠CBG，∴∠ABF=∠GBF，设∠DBE=α，∠ABF=β，则∠ABE=α，∠ABD=2α=∠CBG，∠GBF=β=∠AFB，∠BFC=3∠DBE=3α，∴∠AFC=3α+β，∵∠AFC+∠NCF=180°，∠FCB+∠NCF=180°，∴∠FCB=∠AFC=3α+β，△BCF中，由∠CBF+∠BFC+∠BCF=180°，可得（2α+β）+3α+（3α+β）=180°，①由AB⊥BC，可得β+β+2α=90°，②由①②联立方程组，解得α=15°，∴∠ABE=15°，∴∠EBC=∠ABE+∠ABC=15°+90°=105°．【解析】【分析】（1）根据平行线的性质以及直角三角形的性质进行证明即可；（2）先过点B作BG∥DM，根据同角的余角相等，得出∠ABD=∠CBG，再根据平行线的性质，得出∠C=∠CBG，即可得到∠ABD=∠C；（3）先过点B作BG∥DM，根据角平分线的定义，得出∠ABF=∠GBF，再设∠DBE=α，∠ABF=β，根据∠CBF+∠BFC+∠BCF=180°，可得（2α+β）+3α+（3α+β）=180°，根据AB⊥BC，可得β+β+2α=90°，最后解方程组即可得到∠ABE=15°，进而得出∠EBC=∠ABE+∠ABC=15°+90°=105°．4．探究题学习完平行线的性质与判定之后，我们发现借助构造平行线的方法可以帮我们解决许多问题。
2018-2019学年最新人教版七年级数学上册《几何图形初步》全章综合测试题及解析-经典试题
人教版数学七年级上册“单元精品卷”（含精析）第四章几何图形初步（培优提高卷）题型选择题填空题解答题总分得分一、选择题。
（本题有10个小题，每小题3分，共30分）1．如图，几何体上半部为正三棱柱，下半部为圆柱，其俯视图是（）A． B． C． D．2．某几何体的三视图如图所示，这个几何体是（）A．圆锥 B．圆柱 C．三棱柱 D．三棱锥3．如图所示为一个无盖长方体盒子的展开图（重叠部分不计），根据图中数据，可知该无盖长方体的容积为（）A．4 B．6 C．8 D．124．如图所示，∠BAC=90°，AD⊥BC，垂足为D，则下列结论中，正确的个数为（）①AB⊥AC；②AD与AC互相垂直；③点C到AB的垂线段是线段AB；④点A到BC的距离是线段AD；⑤线段AB的长度是点B到AC的距离．A．1个 B．2个 C．3个 D．4个5．如图，平面内有公共端点的、OB、OC、OD、OE、OF，从射线OA开始按逆时针依次在射线上写出数字1、2、3、4、5、6、7…，则数字“2015”在（）A．射线OA上 B．射线OB上C．射线OD上 D．射线OE上6．下列说法中，不正确的是（）A. 若点C在线段BA的延长线上，则BA＝AC－BCB. 若点C在线段AB上，则AB＝AC+BCC. 若AC＋BC＞AB，则点C一定在线段BA外D. 若A、B、C三点不在一直线上，则AB＜AC+BC7．将量角器按如图所示的方式放置在三角形纸板上，使点C在半圆上．点A、B的读数分别为86°、30°，则∠ACB的大小为（）A、15°B、28°C、29°D、34°8．如图，直线AB，CD相交于点O，OE⊥AB于点O，OF平分∠AOE，∠1=15 °30′，则下列结论中不正确．．．的是（）A．∠2=45°B．∠1=∠3C．∠AOD与∠1互为补角D．∠1的余角等于75°30′9．如图，QQ软件里的“礼盒”图标是一个表面印有黑色实线，顶端有图示箭头的正方体．下列图形中，是该几何体的表面展开图的是（）【来源：21cnj*y.co*m】10．如图所示，把一张矩形纸片AB，在把以AB的中点O为顶点的平角∠AOB三等分，沿平角的三等分线折叠，将折叠后的图形剪出一个以O为顶点的等腰三角形，那么剪出的等腰三角形全部展开平铺后得到的平面图形一定是（）A.正三角形B.正方形C.正五边形D.正六边形二、填空题。
人教版七年级上册数学《几何图形初步》单元检测卷带答案
人教版数学七年级上学期第四章单元测试考试时间：100分钟；满分：100分第Ⅰ卷（选择题）一．选择题（共10小题，满分30分，每小题3分）1．（2018秋•密云区期末）下列四个几何体中，是三棱柱的为（）A．B．C．D．2．（2017秋•宿州期末）雨滴滴下来形成雨丝属于下列哪个选项的实际应用（）A．点动成线B．线动成面C．面动成体D．以上都不对3．（2018秋•竞秀区期末）”在山区建设公路时，时常要打通一条隧道，就能缩短路程”其中蕴含的数学道理是（）A．两点之间，线段最短B．两点确定一条直线C．过一点，有无数条直线D．连接两点之间的线段的长度是两点间的距离4．（2019春•文登区期末）下列说法正确的是（）A．延长直线ABB．延长射线ABC．反向延长射线ABD．延长线段AB到点C，使AC＝BC5．（2018秋•榆林期末）如图，右边的平面图形绕虚线l旋转一周，可以得到左边图形的是（）A．B．C．D．6．（2018秋•临沧期末）如图，下列说法中不正确的是（）A．∠1与∠AOB是同一个角B．∠AOC也可以用∠O表示C．∠β＝∠BOC D．图中有三个角7．（2019春•红河州期末）点A，B，C在同一直线上，已知AB＝3cm，BC＝1cm，则线段AC的长是（）A．2cm B．3cm C．4cm D．2cm或4cm8．（2019春•岱岳区期末）如图，点C是AB的中点，点D是BC的中点，现给出下列等式：①CD＝AC﹣DB，②CD AB，③CD＝AD﹣BC，④BD＝2AD﹣AB．其中正确的等式编号是（）A．①②③④B．①②③C．②③④D．②③9．（2019春•开福区校级期末）嘉淇乘坐一艘游船出海游玩，游船上的雷达扫描探测得到的结果如图所示，每相邻两个圆之间距离是1km（最小圆的半径是1km），下列关于小艇A，B的位置描述，正确的是（）A．小艇A在游船的北偏东60°方向上，且与游船的距离是3kmB．游船在小艇A的南偏西60°方向上，且与小艇A的距离是3kmC．小艇B在游船的北偏西30°方向上；且与游船的距离是2kmD．游船在小艇B的南偏东60°方向上，且与小艇B的距离是2km10．（2018秋•嘉祥县期末）观察下列图形，并阅读相关文字那么20条直线相交，最多交点的个数是（）A．190 B．210 C．380 D．420第Ⅱ卷（非选择题）二．填空题（共6小题，满分24分，每小题4分）11．（2018秋•番禺区期末）如图，将甲，乙两个尺子拼在一起，两端重合．若甲尺经校订是直的，那么乙尺就一定不是直的；用数学知识解释这种生活现象为．12．（2019春•莱州市期末）如图，把一条绳子折成3折，用剪刀从中剪断，得到几条绳子．13．（2019春•浦东新区期末）计算：48°59′+67°31′﹣21°12′＝．14．（2019春•浦东新区期末）在直线MN上取A、B两点，使AB＝10cm，再在线段AB上取一点C，使AC ＝2cm，P、Q分别是AB、AC的中点，则PQ＝cm．15．（2018秋•福田区校级期末）当时间为3点30分时，时钟上时针与分针所成夹角的度数是．16．（2018秋•孝义市期末）已知∠AOB＝60°，以点O为端点作射线OC，使∠BOC＝20°，再作∠AOC的平分线OD，则∠AOD的度数为．评卷人得分三．解答题（共6小题，满分46分）17．（6分）（2018秋•龙岩期末）根据语句画出图形：如图，已知A、B、C三点．①画线段AB；②画射线AC；③画直线BC；④取AB的中点P，连接PC．18．（6分）（2018秋•天心区校级期末）角度计算题：如图，已知O为AD上一点，∠AOB与∠AOC互补，ON平分∠AOB，OM平分∠AOC，若是∠MON＝42°，求∠AOB与∠AOC的度数．19．（8分）（2018秋•宁德期末）图1所示的三棱柱，高为7cm，底面是一个边长为5cm的等边三角形．（1）这个三棱柱有条棱，有个面；（2）图2方框中的图形是该三棱柱的表面展开图的一部分，请将它补全；（3）要将该三棱柱的表面沿某些棱剪开，展开成一个平面图形，需剪开条棱，需剪开棱的棱长的和的最大值为cm．20．（8分）（2018秋•龙泉驿区期末）如图，已知∠AOB内部有三条射线，其中OE平分角∠BOC，OF平分∠AOC．（1）如图1，若∠AOB＝120°，∠AOC＝50°，求∠EOF的度数；（2）如图2，若∠AOB＝α，∠AOC＝β，求∠EOF的度数．21．（8分）（2018秋•绍兴期末）如图①点C在线段AB上，点M、N分别是AC、BC的中点，且满足AC ＝a，BC＝b．（1）若a＝4 cm，b＝6 cm，求线段MN的长；（2）若点C为线段AB上任意一点，其它条件不变，你能猜想MN的长度吗?直接写出你的猜想结果；（3）若点C在线段AB的延长线上，其它条件不变，你能猜想MN的长度吗?请在图②中画出图形，写出你的猜想并说明理由．22．（10分）（2018秋•永新县期末）如图①，点O为直线AB上一点，过点O作射线OC，使∠BOC＝120°．将一直角三角板的直角顶点放在点O处，一直角边OM在射线OB上，另一直角边ON在直线AB的下方，（1）将图①中的三角板绕点O逆时针方向旋转至图②，使边OM在∠BOC的内部，且恰好平分∠BOC，求∠BON大小；（2）将图①中的三角板绕点O逆时针方向旋转至图③．①如果ON恰好是∠AOC的角平分线，则∠AOM﹣∠NOC的度数为；②如果ON始终在∠AOC的内部，∠AOM﹣∠NOC的度数不会变化，请猜测出∠AOM﹣∠NOC的度数并说明理由．参考答案一．选择题（共10小题，满分30分，每小题3分）1．（2018秋•密云区期末）下列四个几何体中，是三棱柱的为（）A．B．C．D．【解析】解：A、该几何体为四棱柱，不符合题意；B、该几何体为四棱锥，不符合题意；C、该几何体为圆柱，不符合题意；D、该几何体为三棱柱，符合题意；故选：D．【点睛】考查了认识立体图形的知识，解题的关键是能够认识各个几何体，难度不大．2．（2017秋•宿州期末）雨滴滴下来形成雨丝属于下列哪个选项的实际应用（）A．点动成线B．线动成面C．面动成体D．以上都不对【解析】解：雨滴滴下来形成雨丝属于点动成线，故选：A．【点睛】此题考查点、线、面、体，关键是根据点动成线解答．3．（2018秋•竞秀区期末）”在山区建设公路时，时常要打通一条隧道，就能缩短路程”其中蕴含的数学道理是（）A．两点之间，线段最短B．两点确定一条直线C．过一点，有无数条直线D．连接两点之间的线段的长度是两点间的距离【解析】解：由线段的性质可知，”在山区建设公路时，时常要打通一条隧道，就能缩短路程”这其中蕴含的数学道理是：两点之间，线段最短．故选：A．【点睛】本题考查的是线段的性质，即两点之间线段最短．4．（2019春•文登区期末）下列说法正确的是（）A．延长直线ABB．延长射线ABC．反向延长射线ABD．延长线段AB到点C，使AC＝BC【解析】解：A．延长直线AB，说法错误；B．延长射线AB，说法错误；C．反向延长射线AB，说法正确；D．延长线段AB到点C，则AC＞BC，故本选项错误；故选：C．【点睛】本题主要考查了直线、射线、线段的概念，注意用两个字母表示射线时，端点的字母放在前边．5．（2018秋•榆林期末）如图，右边的平面图形绕虚线l旋转一周，可以得到左边图形的是（）A．B．C．D．【解析】解：由图可知，只有D选项图形绕直线l旋转一周得到如图所示立体图形，故选：D．【点睛】本题考查了点、线、面、体，熟悉常见图形的旋转得到立体图形是解题的关键．6．（2018秋•临沧期末）如图，下列说法中不正确的是（）A．∠1与∠AOB是同一个角B．∠AOC也可以用∠O表示C．∠β＝∠BOC D．图中有三个角【解析】解：A、∠1与∠AOB是同一个角，说法正确；B、∠AOC也可用∠O来表示，说法错误；C、∠β与∠BOC是同一个角，说法正确；D、图中共有三个角：∠AOB，∠AOC，∠BOC，说法正确；故选：B．【点睛】此题主要考查了角的概念，关键是掌握角的表示方法．7．（2019春•红河州期末）点A，B，C在同一直线上，已知AB＝3cm，BC＝1cm，则线段AC的长是（）A．2cm B．3cm C．4cm D．2cm或4cm【解析】解：本题有两种情形：（1）当点C在线段AB上时，如图，AC＝AB﹣BC，又∵AB＝3cm，BC＝1cm，∴AC＝3﹣1＝2cm；（2）当点C在线段AB的延长线上时，如图，AC＝AB+BC，又∵AB＝3cm，BC＝1cm，∴AC＝3+1＝4cm．故线段AC＝2cm或4cm．故选：D．【点睛】考查了两点间的距离，在未画图类问题中，正确画图很重要，本题渗透了分类讨论的思想，体现了思维的严密性，在今后解决类似的问题时，要防止漏解．8．（2019春•岱岳区期末）如图，点C是AB的中点，点D是BC的中点，现给出下列等式：①CD＝AC﹣DB，②CD AB，③CD＝AD﹣BC，④BD＝2AD﹣AB．其中正确的等式编号是（）A．①②③④B．①②③C．②③④D．②③【解析】解：①点C是AB的中点，AC＝CB．②点C是AB的中点，∴，又∵点D是BC的中点，∴CD．故②正确；③点C是AB的中点，AC＝CB．CD＝AD﹣AC＝AD﹣BC，故③正确；④2AD﹣AB＝2AC+2CD﹣AB＝2CD＝BC，故④错误．故正确的有①②③．故选：B．【点睛】此题考查的是两点间的距离的计算，掌握线段中点的概念和性质、灵活运用数形结合思想是解题的关键．9．（2019春•开福区校级期末）嘉淇乘坐一艘游船出海游玩，游船上的雷达扫描探测得到的结果如图所示，每相邻两个圆之间距离是1km（最小圆的半径是1km），下列关于小艇A，B的位置描述，正确的是（）A．小艇A在游船的北偏东60°方向上，且与游船的距离是3kmB．游船在小艇A的南偏西60°方向上，且与小艇A的距离是3kmC．小艇B在游船的北偏西30°方向上；且与游船的距离是2kmD．游船在小艇B的南偏东60°方向上，且与小艇B的距离是2km【解析】解：A、小艇A在游船的北偏东30°，且距游船3km，故本选项不符合题意；B、游船在小艇A的南偏西30°方向上，且与小艇A的距离是3km，故本选项不符合题意；C、小艇B在游船的北偏西60°，且距游船2km，故本选项不符合题意；D、游船在小艇B的南偏东60°方向上，且与小艇B的距离是2km，故本选项符合题意．故选：D．【点睛】本题考查了方向角．熟练掌握平面内特殊位置的点的坐标特征．理解方向角的表示方法．10．（2018秋•嘉祥县期末）观察下列图形，并阅读相关文字那么20条直线相交，最多交点的个数是（）A．190 B．210 C．380 D．420【解析】解：设直线有n条，交点有m个．有以下规律：直线n条交点m个2 13 1+24 1+2+3…n m＝1+2+3+…+（n﹣1），20条直线相交有190个．故选：A．【点睛】此题主要考查了相交线，关键是找出直线条数与交点个数的计算公式．二．填空题（共6小题，满分24分，每小题4分）11．（2018秋•番禺区期末）如图，将甲，乙两个尺子拼在一起，两端重合．若甲尺经校订是直的，那么乙尺就一定不是直的；用数学知识解释这种生活现象为两点确定一条直线．【解析】解：∵甲尺是直的，两尺拼在一起两端重合，∴甲尺经校订是直的，那么乙尺就一定不是直的，用数学知识解释这种生活现象为：两点确定一条直线．故答案为：两点确定一条直线．【点睛】本题考查的是直线的性质，熟知两点确定一条直线是解答此题的关键．12．（2019春•莱州市期末）如图，把一条绳子折成3折，用剪刀从中剪断，得到几条绳子4．【解析】解：如图折成3折，有两个拐点，而不是折叠三次，故能得到4条绳子．【点睛】解题的关键是看清图中折的方式，从而作出判断．注意结合图形解题的思想．13．（2019春•浦东新区期末）计算：48°59′+67°31′﹣21°12′＝95°18′．【解析】解：48°59′+67°31′﹣21°12′＝116°30′﹣21°12′＝95°18′．故答案为：95°18′【点睛】本题主要考查了度、分、秒的四则混合运算，是角度计算中的一个难点，注意以60为进制即可，难度适中．14．（2019春•浦东新区期末）在直线MN上取A、B两点，使AB＝10cm，再在线段AB上取一点C，使AC ＝2cm，P、Q分别是AB、AC的中点，则PQ＝4cm．【解析】解：如图，∵AB＝10cm，P为AB的中点∴AP＝PB＝5cm∵AC＝2cm，∴CP＝3cm∵Q为AC的中点∴QC＝AQ＝1cm∴PQ＝QC+CP＝1+3＝4cm故答案为：4【点睛】此题主要考查两点间的距离（线段长度）计算，此类题目，通常利用图形结合进行解题．15．（2018秋•福田区校级期末）当时间为3点30分时，时钟上时针与分针所成夹角的度数是75°．【解析】解：时针从数3开始30分转了30×0.5°＝15°，分针从数字12开始30分转了30×6°＝180°，所以3点30分，时针与分针所成夹角的度数＝180°﹣90°﹣15°＝75°．故答案为：75°．【点睛】本题考查了钟面角：钟面被分成12大格，每大格30°；分针每分钟转6°，时针每分钟转0.5°．16．（2018秋•孝义市期末）已知∠AOB＝60°，以点O为端点作射线OC，使∠BOC＝20°，再作∠AOC 的平分线OD，则∠AOD的度数为20°或40°．【解析】解：（1）当OC在∠AOB的内部时，如图1所示：∵∠BOC＝20°，∠AOB＝60°，∠AOB＝∠AOC+∠BOC，∴∠AOC＝60°﹣20°＝40°，又∵OD是∠AOC的平分线，∴∠AOD＝∠COD20°；（2）当OC在∠AOB的外部时，如图2所示：∵∠AOC＝∠AOB+∠BOC，∠AOB＝60°，∠BOC＝20°，∴AOC＝80°，又∵OD是∠AOC的平分线，∴∠AOD＝∠COD40°；综合所述∠AOD的度数有两个，故答案为20°或40°．【点睛】本题综合了角平分线定义和角的和差知识，重点掌握角的计算，难点是用分类计算角的大小，易掉角的外部这一种情况．三．解答题（共6小题，满分46分）17．（6分）（2018秋•龙岩期末）根据语句画出图形：如图，已知A、B、C三点．①画线段AB；②画射线AC；③画直线BC；④取AB的中点P，连接PC．【解析】解：如图．【点睛】本题考查了直线、射线、线段，正确区分直线、线段、射线是解题关键．18．（6分）（2018秋•天心区校级期末）角度计算题：如图，已知O为AD上一点，∠AOB与∠AOC互补，ON平分∠AOB，OM平分∠AOC，若是∠MON＝42°，求∠AOB与∠AOC的度数．【解析】解：设∠AOB＝x°，因为∠AOC与∠AOB互补，则∠AOC＝180°﹣x°．由题意，得42．∴180﹣x﹣x＝84，∴﹣2x＝﹣96，解得x＝48，故∠AOB＝48°，∠AOC＝132°．【点睛】本题考查补角的定义，角平分线的定义，及角的运算．在图形中，找补角关系时，除了借助图形外，还需考虑等量关系即有没有相等的角．19．（8分）（2018秋•宁德期末）图1所示的三棱柱，高为7cm，底面是一个边长为5cm的等边三角形．（1）这个三棱柱有9条棱，有5个面；（2）图2方框中的图形是该三棱柱的表面展开图的一部分，请将它补全；（3）要将该三棱柱的表面沿某些棱剪开，展开成一个平面图形，需剪开5条棱，需剪开棱的棱长的和的最大值为31cm．【解析】解：（1）这个三棱柱有条9棱，有个5面；故答案为：9，5；（2）如图；（3）由图形可知：没有剪开的棱的条数是4条，则至少需要剪开的棱的条数是：9﹣4＝5（条）．故至少需要剪开的棱的条数是5条．需剪开棱的棱长的和的最大值为：7×3+5×2＝31（cm）．故答案为：5，31．【点睛】本题主要考查的是认识立体图形，明确n棱柱有n个侧面，2个底面，3n条棱，2n个顶点；能够数出三棱柱没有剪开的棱的条数是解答此题的关键．20．（8分）（2018秋•龙泉驿区期末）如图，已知∠AOB内部有三条射线，其中OE平分角∠BOC，OF平分∠AOC．（1）如图1，若∠AOB＝120°，∠AOC＝50°，求∠EOF的度数；（2）如图2，若∠AOB＝α，∠AOC＝β，求∠EOF的度数．【解析】解：（1）∵OF平分∠AOC，∴∠COF∠AOC30°＝15°，∵∠BOC＝∠AOB﹣∠AOC＝120°﹣30°＝90°，OE平分∠BOC，∴∠EOC∠BOC＝45°，∴∠EOF＝∠COF+∠EOC＝60°；（2）∵OF平分∠AOC，∴∠COF∠AOC，同理，∠EOC∠BOC，∴∠EOF＝∠COF+∠EOC∠AOC∠BOC（∠AOC+∠BOC）∠AOBα．【点睛】本题考查了角平分线的性质，以及角度的计算，正确理解角平分线的定义是关键．21．（8分）（2018秋•绍兴期末）如图①点C在线段AB上，点M、N分别是AC、BC的中点，且满足AC ＝a，BC＝b．（1）若a＝4 cm，b＝6 cm，求线段MN的长；（2）若点C为线段AB上任意一点，其它条件不变，你能猜想MN的长度吗?直接写出你的猜想结果；（3）若点C在线段AB的延长线上，其它条件不变，你能猜想MN的长度吗?请在图②中画出图形，写出你的猜想并说明理由．【解析】解：（1）∵M、N分别是AC、BC的中点，∴MC AC，CN BC，∴MN＝MC+CNAC BC4 6＝5cm，所以MN的长为5cm．（2）同（1），MN AC CB（AC+CB）（a+b）．（3）图如右，MN（a﹣b）．理由：由图知MN＝MC﹣NCAC BCa b（a﹣b）．【点睛】本题主要考查线段中点的定义，线段的中点把线段分成两条相等的线段．22．（10分）（2018秋•永新县期末）如图①，点O为直线AB上一点，过点O作射线OC，使∠BOC＝120°．将一直角三角板的直角顶点放在点O处，一直角边OM在射线OB上，另一直角边ON在直线AB的下方，（1）将图①中的三角板绕点O逆时针方向旋转至图②，使边OM在∠BOC的内部，且恰好平分∠BOC，求∠BON大小；（2）将图①中的三角板绕点O逆时针方向旋转至图③．①如果ON恰好是∠AOC的角平分线，则∠AOM﹣∠NOC的度数为30°；②如果ON始终在∠AOC的内部，∠AOM﹣∠NOC的度数不会变化，请猜测出∠AOM﹣∠NOC的度数并说明理由．【解析】解：（1）∵OM平分∠BOC，∠BOC＝120°，∴∠BOM＝∠MON＝60°，∵∠MON＝90°，∴∠BON＝∠MON﹣∠BOM＝90°﹣60°＝30°；（2）①∠AOM﹣∠NOC＝30°；故答案为：30°②∠AOM﹣∠NOC＝30°，理由如下：∵∠AOM＝∠MON﹣∠AON＝90°﹣∠AON，∠NOC＝∠AOC﹣∠AON＝60°﹣∠AON，∴∠AOM﹣∠NOC＝（90°﹣∠AON）﹣（60°﹣∠AON）＝30°．【点睛】本题考查了角平分线的定义，应该认真审题并仔细观察图形，找到各个量之间的关系，是解题的关键．。
(完整版)2018初一数学几何图形初步(一)几何图形练习题
几何图形初步（一）几何图形练习题一、选择题1．图1是边长为1的六个小正方形组成的图形，它可以围成图2的正方体,则图1中正方形顶点A、B在围成的正方休中的距离是( ）A．0 B．1 C． D．2．要在地球仪上确定深圳市的位置，需要知道的是（）A.高度B.经度C.纬度D.经度和纬度3．如图的几何体中，它的俯视图是( )4．如图1是一个小正方体的侧面展开图，小正方体从图2所示的位置依次翻到第1格、第2格、第3格、第4格,这时小正方体朝上一面的字是（）A．北 B．京 C．精 D．神5．（3分）如图，图案⑥是由①②③④⑤五种基本图形中的两种拼接而成的，这两种基本图形是（)A．①⑤ B．②⑤ C．③⑤ D．②④6．如图的立体图形可由哪个平面图形绕轴旋转而成（）7．如图是一个三棱柱的展开图．若AD=10，CD=2，则AB的长度可以是（）A．2 B．3 C．4 D．58．下面四个几何体中，左视图是矩形的几何体是（）9．下列几何体的主视图是三角形的是（）10．如图，从左面观察这个立体图形,能得到的平面图形是（ )A． B． C． D．11．明明用纸（如图）折成了一个正方体的盒子，里面装了一瓶墨水，与其它空盒子混放在一起，只凭观察，选出墨水在哪个盒子中( ）12．以下各图均有彼此连接的六个小正方形纸片组成，其中不能折叠成一个正方体的是( )13．用一个平面去截一个几何体，不能截得三角形截面的几何体是( ）A．圆柱 B．圆锥 C．三棱柱 D．正方体14．在下面的四个几何体中，它们各自的左视图与主视图不一样的是（）15．用4个小立方块搭成如图所示的几何体，该几何体的左视图是（ )评卷人得分一、解答题16．小强用5个大小一样的正方形制成如图所示的拼接图形（阴影部分），请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子．注意：只需添加一个符合要求的正方形,并用阴影表示．17．如图,把边长为2的正方形剪成四个完全一样的直角三角形，在下面对应的正方形网格(每个小正方形的边长均为1）中画出用这四个直角三角形按要求分别拼成的新的多边形．（要求全部用上，互不重叠，互不留隙）．（1)长方形（非正方形）；（2)平行四边形；（3）四边形（非平行四边形）．18．(本题满分10分）（1）由大小相同的小立方块搭成的几何体如左图,请在右图的方格中画出该几何体的俯视图和左视图．（2）用小立方体搭一几何体，使得它的俯视图和左视图与你在上图方格中所画的图一致，则这样的几何体最少要个小立方块，最多要个小立方块．19．(本题满分8分）一包装礼盒是底面为正方形的无盖立体图形，其展开图如所示:是由一个正方形与四个正六边形组成，已知正六边形的边长为a，甲、乙两人分别用长方形和圆形硬板纸裁剪包装纸盒．(1）问甲、乙两人谁的硬板纸利用率高,请通过计算长方形和圆的面积．．．．．．．．说明原因。
七年级几何图形初步同步单元检测(Word版 含答案)
一、初一数学几何模型部分解答题压轴题精选（难）1．已知如图，∠COD=90°，直线AB与OC交于点B，与OD交于点A，射线OE与射线AF交于点G.（1）若OE平分∠BOA，AF平分∠BAD，∠OBA=42°，则∠OGA=________；（2）若∠GOA= ∠BOA，∠GAD= ∠BAD，∠OBA=42°，则∠OGA=________；（3）将（2）中的“∠OBA=42°”改为“∠OBA= ”，其它条件不变，求∠OGA的度数.（用含的代数式表示）（4）若OE将∠BOA分成1︰2两部分，AF平分∠BAD，∠ABO= （30°< α <90°），求∠OGA的度数.（用含的代数式表示）【答案】（1）21°（2）14°（3）解：∵∠BOA=90°，∠OBA=α，∴∠BAD=∠BOA+∠ABO=90°+α，∵∠BOA=90°，∠GOA= ∠BOA,∠GAD= ∠BAD∴∠GAD=30°+ α，∠EOA=30°，∴∠OGA=∠GAD−∠EOA= α.（4）解：当∠EOD:∠COE=1:2时，∴∠EOD=30°，∵∠BAD=∠ABO+∠BOA=α+90°，∵AF平分∠BAD，∴∠FAD= ∠BAD，∵∠FAD=∠EOD+∠OGA，∴2×30°+2∠OGA=α+90°，∴∠OGA= α+15°；当∠EOD:∠COE=2:1时,则∠EOD=60°，同理得到∠OGA= α−15°，即∠OGA的度数为α+15°或α−15°.【解析】解：(1)∵∠BOA=90°,∠OBA=42°，∴∠BAD=∠BOA+∠ABO=132°，∵AF平分∠BAD,OE平分∠BOA,∠BOA=90°，∴∠GAD= ∠BAD=66°，∠EOA= ∠BOA=45°，∴∠OGA=∠GAD−∠EOA=66°−45°=21°；故答案为21°；⑵∵∠BOA=90°,∠OBA=42°，∴∠BAD=∠BOA+∠ABO=132°，∵∠BOA=90°,∠GOA= ∠BOA,∠GAD= ∠BAD,∴∠GAD=44°，∠EOA=30°，∴∠OGA=∠GAD−∠EOA=44°−30°=14°；故答案为14°；【分析】（1）根据三角形外角的性质求出∠BAD，求出∠GOA和∠GAD，根据三角形外角性质求出即可；（2）根据三角形外角的性质求出∠BAD，求出∠GOA和∠GAD，根据三角形外角性质求出即可；（3）根据三角形外角的性质求出∠BAD，求出∠GOA和∠GAD，根据三角形外角性质求出即可；（4）讨论：当∠EOD：∠COE=1：2时，利用∠BAD=∠ABO+∠BOA=α+90°，∠FAD=∠EOD+∠OGA得到2×30°+2∠OGA=α+90°，则∠OGA= α+15°；当∠EOD：∠COE=2：1时，则∠EOD=60°，同理得∠OGA= α-15°. 2．如图①，△ABC的角平分线BD，CE相交于点P.（1）如果∠A=80∘，求∠BPC= ________.（2）如图②,过点P作直线MN∥BC,分别交AB和AC于点M和N,试求∠MPB+∠NPC的度数(用含∠A的代数式表示)________.（3）将直线MN绕点P旋转。
初一上册数学(几何图形初步)练习卷(一)
初一上册数学（几何图形初步）练习卷（一）知识点1：立体图形与平面图形以及点线面体１.五棱柱有__＿_＿_＿_个顶点，_______＿条棱，____＿___个面．2．柱体包括__＿__＿__和__＿_____,锥体包括_____＿__和＿___＿___．3.圆锥的底面是__＿＿______形,侧面是_＿__＿____＿的面，侧面展开图是__＿____＿__形.４．当笔尖在纸上移动时,形成_____＿_,这说明:＿_＿__;表针旋转时,形成了一个，这说明：；长方形纸片绕它的一边旋转，形成的几何图形就是,这说明: .5.由四个大小相同的正方体组成的几何体如图所示,那么它的俯视图是( ).6.．如图是一正方体纸盒的展开图，每个面上都标注了字母或数字，则面ａ在展开前所对的面上的数字是( )．A.２B．3 C．4 D.57.按如图所示的图形中的虚线折叠可以围成一个棱柱的是( ）．8.如图所示,下列图形绕着虚线旋转一周得到圆锥体的是（)9.一个正方体的每个面都写有一个汉字，其平面展开图如图所示，那么在该正方体中,和“超”相对的字是_____＿＿＿．10.如图所示是一个几何体的三视图,则这个几何体是________．11.如图所示的一张硬纸片,它能否折成一个长方体盒子?若能,说明理由,并画出它的立体图形,计算它的体积.12.对于棱柱体而言,不同的棱柱体由不同的面构成:三棱柱由2个底面,3个侧面,共5个面构成；四棱柱由2个底面，4个侧面,共６个面构成；五棱柱由2个底面，5个侧面，共7个面构成;六棱柱由2个底面,6个侧面，共８个面构成;(1）根据以上规律判断，十二棱柱共有多少个面?（2）若某个棱柱由24个面构成,那么这个棱柱是什么棱柱?（３)棱柱底面多边形的边数为n，则侧面的个数为多少？棱柱共有多少个面?（4)底面多边形边数为n的棱柱,其顶点个数为多少个？有多少条棱?知识点2:直线、射线、线段1.在墙上钉一根木条需＿_____＿个钉子，其根据是．２.如下图(１)所示,点A在直线L＿_____,点B在直线L___＿____．３．如下图（2）所示，直线__＿＿_＿＿和直线_____＿相交于点Ｐ；直线ＡB和直线EＦ•相交于点__＿___;点R是直线_____＿＿_和直线__＿＿__＿_的交点.４.如下图(３)所示,图中共有___＿_条线段,它们是_____＿__；共有___＿＿_条射线，它们是_＿______.５.下面几种表示直线的写法中,错误的是( ）．A.直线aB.直线ＭａＣ.直线MN D．直线ＭO6.画线段AB=50ｍｍ，在线段AB上取一点C，使得5AC=2AB,在ＡB的延长线上取一点D，使得AＢ=10BD，那么ＣD=______mm．７.如右图,ＡC＝CD＝DE＝ＥB，图中和线段ＡD长度相等的线段是_____＿＿_．以D•为中点的线段是＿_＿＿_＿__.8.线段AＤ=6cｍ，线段AC＝BD=4cｍ，E、Ｆ分别是线段AＢ、CD中点，求EＦ。
新人教版七年级数学上册《几何图形初步》单元测试题
几何图形初步单元测试题一、选择题1.如图所示，一个三边相等的三角形，三边的中点用虚线连接，如果将三角形沿虚线向上折叠，得到的立体图形是（）.1题图（A）三棱柱（B）三棱锥（C）正方体（D）圆锥2.下列说法正确的是（）.（A）射线可以延长（B）射线的长度可以是5米（C）射线可以反向延长（D）射线不可以反向延长3. 把一条弯曲的河道改成直道，可以缩短航程，其中的道理可以解释为（）.（A）线段有两个端点（B）过两点可以确定一条直线（C）两点之间，线段最短（D）线段可以比较大小4. 正多面体的面数、棱数、顶点数之间存在着一个奇妙的关系，若用F、E、V分别表示正多面体的面数、棱数、顶点数，则有F＋V－E=2，现有一个正多面体共有12条棱，6个顶点，则它的面数F等于（）.（A）6 （B）8 （C）12 （D）205.如图，OC是∠AOB的平分线，OD是∠BOC的平分线，那么下列各式中正确的是（）.（A）∠COD=12∠AOB （B）∠AOD=23∠AOB （C）∠BOD=13∠AOD （D）∠BOC=23∠AOD 第6题图第6题图6. 如图所示，从O点出发的五条射线，可以组成小于平角的角的个数是（）．（A）10个（B）9个（C）8个（D）4个7. 下列说法正确的是（）.（A）一个锐角的余角比这个角大（B）一个锐角的余角比这个角小（C）一个锐角的补角比这个角大（D）一个钝角的补角比这个角大8.操场上，小明对小亮说：“你在我的北偏东30°方向上”，那么小亮可以对小明说：“你在（A）南偏西30°（B）北偏东30°（C）北偏东60°（D）南偏西60°9. 已知∠1、∠2互为补角，且∠1＞∠2，则∠2的余角是（）.（A）12（∠1＋∠2）（B）12∠1（C）12（∠1－∠2）（D）12∠210.如果线段AB=13cm,MA+MB=17 cm,那么下面说法中正确的是( ).A、M点在线段AB上．B、M点在直线AB上．C、M点在直线AB外．D、M点可能在直线AB上,也可能在直线AB外．二、填空11. 长方形绕其一边旋转一周形成的几何体是____，直角三角板绕其一直角边旋转一周形成的几何体是__________.12. 如图，已知B是AC的中点，C是BD的中点，若BC=1.5cm，则AD=________.13. 钟面上9点30分时，分针与时针所成的角的度数是___________.14. 如果79°－2x与21°＋6x互补，那么x ____________.15. 北偏西35°与南偏东65°的两条射线组成的角为_________度.16. 若线段AB=a，C是线段AB上的任意一点，M、N分别是AC和CB的中点，则MN=_____17. 水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示.如右图,是一个正方体的平面展开图,若图中的“似”表示正方体的前面, “锦”表示右面, “程”表示下面.则“祝”、“你”、“前”分别表示正方体的______________________.三、解答题18.计算：（1）40°26′＋30°30′30″÷6；（2）13°53′×3－32°5′31″.19.如图8，东西方向的海岸线上有A、B两个观测站，在A地发现它的北偏东30°方向上有一条渔船，同一时刻，在B地发现这条渔船在它的北偏西60°方向上，试画图说明这条渔船的位置．程前你祝似锦20.已知B、C、D是线段AE上的点，如果AB = BC = CE，D是CE的中点，BD = 6，求AE的长.21题图21如图9，点O是直线AB上的一点，OD是∠AOC的平分线，OE是∠COB的平分线，若∠AOD=14°，求∠DOE、∠BOE的度数．23.已知一个角的余角的补角是这个角的补角的45，求这个角的13角的余角.24.已知∠1和∠2互为补角，∠2度数的一半比∠1大45°，试求出∠1与∠2的度数．25.如图，O是直线AB上一点，OC为任一条射线，OD平分∠BOC，OE平分∠AOC. （1）指出图中∠AOD的补角，∠BOE的补角；（2）若∠BOC=68°，求∠COD和∠EOC的度数；（3）∠COD与∠EOC具有怎样的数量关系？计算线段长度的方法技巧线段是基本的几何图形，是三角形、四边形的构成元素。
七年级几何图形初步单元练习(Word版 含答案)
一、初一数学几何模型部分解答题压轴题精选（难）1．如图下图所示,已知AB//CD, ∠B=30°，∠D=120°;（1）若∠E=60°，则∠F=________;（2）请探索∠E与∠F之间满足的数量关系?说明理由.（3）如下图所示,已知EP平分∠BEF,FG平分∠EFD,反向延长FG交EP于点P,求∠P的度数;【答案】（1）90°（2）解：如图，分别过点E，F作EM∥AB，FN∥AB∴EM∥AB∥FN∴∠B=∠BEM=30°，∠MEF=∠EFN又∵AB∥CD，AB∥FN∴CD∥FN∴∠D+∠DFN=180°又∵∠D =120°∴∠DFN=60°∴∠BEF=∠MEF+30°，∠EFD=∠EFN+60°∴∠EFD=∠MEF +60°∴∠EFD=∠BEF+30°（3）解：如图，过点F作FH∥EP由（2）知，∠EFD=∠BEF+30°设∠BEF=2x°，则∠EFD=（2x+30）°∵EP平分∠BEF，GF平分∠EFD∴∠PEF= ∠BEF=x°，∠EFG= ∠EFD=（x+15）°∵FH∥EP∴∠PEF=∠EFH=x°，∠P=∠HFG ∵∠HFG=∠EFG-∠EFH=15°∴∠P=15°【解析】【解答】解：（1）分别过点E、F作EM∥AB，FN∥AB，则有AB∥EM∥FN∥CD.∴∠B=∠BEM=30°，∠MEF=∠EFN，∠DFN=180°-∠CDF=60°，∴∠BEF=∠MEF+30°，∠EFD=∠EFN+60°，∴∠EFD=∠BEF+30°=90°.【分析】（1）分别过点E、F作AB的平行线，根据平行线的性质即可求解；（2）根据平行线的性质可得∠DFN=60°，∠BEM=30°，∠MEF=∠NFE，即可得到结论；（3）过点F作FH∥EP，设∠BEF=2x°，根据（2）中结论即可表示出∠BFD，根据角平分线的定义可得∠PEF=x°，∠EFG=（x+15）°，再根据平行线的性质即可得到结论.2．在数轴上、两点分别表示有理数和，我们用表示到之间的距离；例如表示7到3之间的距离.（1）当时，的值为________.（2）如何理解表示的含义？（3）若点、在0到3（含0和3）之间运动，求的最小值和最大值.【答案】（1）5或-3（2）解：∵ = ，∴表示到-2的距离（3）解：∵点、在0到3（含0和3）之间运动，∴0≤a≤3, 0≤b≤3,当时， =0+2=2，此时值最小，故最小值为2；当时， =2+5=7，此时值最大，故最大值为7【解析】【解答】（1）∵，∴a=5或-3；故答案为：5或-3；【分析】（1）此题就是求表示数a的点与表示数1的点之间的距离是4，根据表示数a的点在表示数1的点的右边与左边两种情况考虑即可得出答案；（2）此题就是求表示数b的点与表示数-2的点之间的距离;（3）此题就是求表示数a的点与表示数2的点之间的距离及表示数b的点与表示数-2的点之间的距离和，而0≤a≤3, 0≤b≤3, 借助数轴当时，的值最小；当时，的值最大.3．如图1，点A、B分别在数轴原点O的左右两侧，且 OA+50=OB，点B对应数是90．（1）求A点对应的数；（2）如图2，动点M、N、P分别从原点O、A、B同时出发，其中M、N均向右运动，速度分别为2个单位长度/秒，7个单位长度/秒，点P向左运动，速度为8个单位长度/秒，设它们运动时间为t秒，问当t为何值时，点M、N之间的距离等于P、M之间的距离；（3）如图3，将（2）中的三动点M、N、P的运动方向改为与原来相反的方向，其余条件不变，设Q为线段MN的中点，R为线段OP的中点，求22RQ﹣28RO﹣5PN的值．【答案】（1）解：如图1，∵点B对应数是90，∴OB=90．又∵ OA+50=OB，即 OA+50=90，∴OA=120．∴点A所对应的数是﹣120（2）解：依题意得，MN=|（﹣120+7t）﹣2t|=|﹣120+5t|，PM=|2t﹣（90﹣8t）|=|10t﹣90|，又∵MN=PM，∴|﹣120+5t|=|10t﹣90|，∴﹣120+5t=10t﹣90或﹣120+5t=﹣（10t﹣90）解得t=﹣6或t=14，∵t≥0，∴t=14，点M、N之间的距离等于点P、M之间的距离（3）解：依题意得RQ=（ 45+4t）﹣（﹣60﹣4.5t）=105+8.5t，RO=45+4t，PN=（90+8t）﹣（﹣120﹣7t）=210+15t，则22RQ﹣28RO﹣5PN=22（105+8.5t）﹣28（45+4t）﹣5（210+15t）=0【解析】【分析】（1）根据点B对应的数求得OB的长度，结合已知条件和图形来求点A 所对应的数；（2）由M、N之间的距离等于P、M之间的距离列式为，列方程求出t；（3）由M、N之间的距离等于P、M之间的距离列式为，列方程求出t，并求出RQ，RO 及PN，再求出22RQ﹣28RO﹣5PN的值．4．如图（1）如图1，AB∥CD，∠AEP=40°，∠PFD=130°。
数学七年级上册 几何图形初步单元测试卷(含答案解析)
一、初一数学几何模型部分解答题压轴题精选（难）1．感知：如图①，∠ACD为△ABC的外角，易得∠ACD=∠A+∠B(不需证明) ；（1）探究：如图②,在四边形ABDC中,试探究∠BDC与∠A、∠B．、∠C之间的关系，并说明理由；（2）应用：如图③，把一块三角尺XYZ放置在△ABC上，使三角尺的两条直角边XY、XZ 恰好经过点B、C，若∠A=50°，则∠ABX+∠ACX=________度；(直接填答案，不需证明) （3）拓展：如图④，BE平分∠ABD，CE平分∠ACD，若∠BAC=100°，∠BDC=150°，则∠BEC=________度. (直接填答案，不需证明)【答案】（1）解：如图5，连接AD并延长至点F.∵∠BDF为△ABD的外角，∴∠BDF=∠BAD+∠B，同理可得∠CDF=∠CAD+∠C，∴∠BDF+∠CDF=∠BAD+∠B+∠CAD+∠C，即∠BDC=∠BAC+∠B+∠C；（2）40°（3）125°【解析】【解答】解：（2）由题意可得∠BXC=90°，由（1）中结论可得∠BXC=∠A+∠ABX+∠ACX，∵∠A=50°，∴∠ABX+∠ACX=90°-50°=40°；（3）如图6，∵∠A=100°，∠BDC=150°，∠BDC=∠A+∠ABD+∠ACD，∴∠ABD+∠ACD=150°-100°=50°，∵BE平分∠ABD，CE平分∠ACD，∴∠ABE+∠ACE= （∠ABD+∠ACD）=25°，又∵∠BEC=∠A+∠ABE+∠ACE，∴∠BEC=100°+25°=125°.【分析】（1）如图5，连接AD并延长至F，然后利用三角形外角的性质进行分析证明即可得到∠BDC=∠BAC+∠B+∠C；（2）由题意可知∠BXC=90°，结合∠A=50°和（1）中所得结论即可得到∠ABX+∠ACX=90°-50°=40°；（3）如图6，利用（1）中所得结论结合已知条件进行分析解答即可.2．如图（1），将两块直角三角板的直角顶点C叠放在一起．（1）试判断∠ACE与∠BCD的大小关系，并说明理由；（2）若∠DCE=30°，求∠ACB的度数；（3）猜想∠ACB与∠DCE的数量关系，并说明理由；（4）若改变其中一个三角板的位置，如图（2），则第（3）小题的结论还成立吗？（不需说明理由）【答案】（1）解：∠ACE=∠BCD，理由如下：∵∠ACD=∠BCE=90°，∠ACE+∠ECD=∠ECB+∠ECD=90°，∴∠ACE=∠BCD（2）解：若∠DCE=30°，∠ACD=90°，∴∠ACE=∠ACD﹣∠DCE=90°﹣30°=60°，∵∠BCE=90°且∠ACB=∠ACE+∠BCE，∠ACB=90°+60°=150°（3）解：猜想∠ACB+∠DCE=180°．理由如下：∵∠ACD=90°=∠ECB，∠ACD+∠ECB+∠ACB+∠DCE=360°，∴∠ECD+∠ACB=360°﹣（∠ACD+∠ECB）=360°﹣180°=180°（4）解：成立【解析】【分析】（1）根据同角的余角相等即可求证；（2）根据余角的定义可先求得∠ACE=∠ACD-∠DCE，再由图可得∠ACB=∠ACE+∠BCE，把∠ACE和∠BCE 的度数代入计算即可求解；（3）由图知，∠ACB=∠ACD+∠BCE-∠ECD，则∠ACB+∠ECD=∠ACD+∠BCE，把∠ACD和∠BCE的度数代入计算即可求解；（4）根据重叠的部分实质是两个角的重叠可得。
2018初一数学 几何图形初步单元测试1
2018年几何图形初步测试题一、选择题1．如图是一个正方体的表面展开图，如果相对面上所标的两个数互为相反数，那么图中x 的值是（ ）A ．8B ．3C ．2D ．-32．如图所示的几何体的俯视图是（ ）.3．下列左图是由5个相同大小的正方体搭成的几何体，则它的俯视图是（ ）4．下图中共有（ ）条线段．A ．4B ．6C ．8D ．105．下列四个图中的线段（或直线、射线）能相交的是（ ）A ．（1）B ．（2）C ．（3）D ．（4） 6．使分式2+x x有意义的x 的取值范围为（ ） A ．2≠x B ．2-≠x C ．2->x D ．2<x7．如图，C 、D 是线段AB 上两点，若CB ＝5cm ，DB=9cm ，且D 是AC 的中点，则AC 的长等于（ ）A ．6cmB ．9cmC ．8cmD ．13cm 8．点C 在线段AB 上，下列条件中不能确定．．．．点C 是线段AB 中点的是 A ． B ． C ． D ．C DB A 正面A 、 AC =BCB 、 AC +BC= AB C 、 AB =2ACD 、BC =21AB9．已知A 、B 两点之间的距离是10cm ，C 是线段AB 上的任意一点，则AC 中点与BC 中点间的距离是（ ）A ．3cmB ．4cmC ．5cmD ．不能计算10．将一副三角板如图放置，使点A 落在DE 上，若BC DE ∥，则AFC ∠的度数为（ ）A.45°B.50°C.60°D.75°11．如图，直线AB 与CD 相交于点O ，12=∠∠，若140AOE =o∠，则AOC ∠的度数为（ ）．Ａ．40oＢ．60oＣ．80oＤ．100o12．如图所示，∠AOB=156°,OD是∠AOC 的平分线，OE 是∠BOC 的平分线，那么∠DOE 等于（ ）A ．78°B ．80°C ．88°D ．90° 13．如图，直线AB 与CD 相交于点O ，∠1=∠2，若∠AOE=140°，则∠AOC 的度数为（ ）A ．40oB ．60oC ．80oD ．100o14．如图所示，已知O 是直线AB 上一点，∠1＝40°，OD 平分∠BOC ，则∠2的度数是（ ）AOCED（A）20°（B）25°（C）30°（D）70°评卷人得分一、解答题15．（本题满分7分）线段AB=4cm，延长线段AB到C，使BC = 1cm，再反向延长AB 到D，使AD=3 cm，E是AD中点，F是CD的中点，求EF的长度．16．（本题满分5分）已知：如图所示，已知线段a、b、c（a﹥c），求作：线段AB，使AB=a+b-c．17．（10分）如图，已知线段AB和CD的公共部分BD=13AB=14CD，线段AB、CD的中点E、F之间距离是10cm，求AB、CD的长．18．（6分）根据下列语句，画出图形.已知四点A、B、C、D.DCBA①画直线AB；②连接AC、BD，相交于点O；③画射线AD、BC，交于点P.[19．（满分8分）今年“五一”小长假期间，某市外来与外出旅游的总人数为226万人，分别比去年同期增长30%和20%，去年同期外来旅游比外出旅游的人数多20万人．求该市今年外来和外出旅游的人数．20．（满分5分）线段AB=14cm，C是AB上一点，且AC=9cm，O为AB中点，求线段OC 的长度··A O C BA E DB F C21．如图，如图点B 在线段AC 上，若D 是AB 的中点，E 是BC 的中点，（1）若DE=5，AE=7，求CE 的长（2）若AC=m ，试用含m 的代数式表示线段ED22．线段cm AC 6=，线段cm BC 15=，点M 是AC 的中点，在CB 上取一点N ，使2:1:=NB CN ，求MN 的长。
七年级数学几何图形初步单元达标训练题(Word版 含答案)
一、初一数学几何模型部分解答题压轴题精选（难）1．如图，EF⊥AB于F，CD⊥AB于D，点在AC边上，且∠1=∠2= ．（1）求证：EF∥CD；（2）若∠AGD=65°，试求∠DCG的度数.【答案】（1）证明：∵EF⊥AB于F，CD⊥AB于D，∴∠BFE=∠BDC=90°，∴EF∥CD.（2）解：∵EF∥CD，∴∠2=∠DCE=50°，∵∠1=∠2，∴∠1=∠DCE,∴DG∥BC，∴∠AGD=∠ACB=65°，∴∠DCG=【解析】【分析】（1）由垂直的定义，可求得∠BFE=∠CDF=90°，可证明EF∥CD；（2）利用（1）的结论，结合条件可证明DG∥BC，利用平行线的性质可得∠AGD=∠ACB= ，则∠DCG=∠ACB-∠2即可求得．2．如图1，点O是弹力墙MN上一点，魔法棒从OM的位置开始绕点O向ON的位置顺时针旋转，当转到ON位置时，则从ON位置弹回，继续向OM位置旋转；当转到OM位置时，再从OM的位置弹回，继续转向ON位置，…，如此反复．按照这种方式将魔法棒进行如下步骤的旋转：第1步，从OA0（OA0在OM上）开始旋转α至OA1；第2步，从OA1开始继续旋转2α至OA2；第3步，从OA2开始继续旋转3α至OA3，∁…．例如：当α=30°时，OA1， OA2， OA3， OA4的位置如图2所示，其中OA3恰好落在ON 上，∠A3OA4=120°；当α=20°时，OA1， OA2， OA3， OA4， OA3的位置如图3所示，其中第4步旋转到ON后弹回，即∠A3ON+∠NOA4=80°，而OA3恰好与OA2重合．解决如下问题：（1）若α=35°，在图4中借助量角器画出OA2，OA3，其中∠A3OA2的度数是________；（2）若α＜30°，且OA4所在的射线平分∠A2OA3，在如图5中画出OA1，OA2，OA3， OA4并求出α的值；（3）若α＜36°，且∠A2OA4=20°，则对应的α值是________（4）（选做题）当OA i所在的射线是∠A i OA k（i，j，k是正整数，且OA j与OA k不重合）的平分线时，旋转停止，请探究：试问对于任意角α（α的度数为正整数，且α=180°），旋转是否可以停止？写出你的探究思路．【答案】（1）45°（2）解：如图所示．∵α＜30°，∴∠A0OA3＜180°，4α＜180°．∵OA4平分∠A2OA3，∴2（180°﹣6α）+ =4α，解得：（3），，（4）解：对于角α=120°不能停止．理由如下：无论a为多少度，旋转过若干次后，一定会出现OA i是∠A i OA K是的角平分线，所以旋转会停止．但特殊的，当a为120°时，第一次旋转120°，∠MOA1=120°，第二次旋转240°时，与OM 重合，第三次旋转360°，又与OM重合，第四次旋转480°时，又与OA1重合，…依此类推，旋转的终边只会出现“与OM重合”或“与OA1重合”两种情况，不会出第三条射线，所以不会出现OA i是∠A i OA K是的角平分线这种情况，旋转不会停止【解析】【解答】解：（1）解：如图所示．aφ=45°，【分析】（1）根据题意，明确每次旋转的角度，计算即可；（2）根据各角的度数，找出等量关系式，列出方程，求出α的度数即可；（3）类比第（2）小题的算法，分三种情况讨论，求出α的度数即可；（4）无论a为多少度，旋转很多次，总会出一次OA i是∠A i OA K是的角平分线，但当a=120度时，只有两条射线，不会出现OA i是∠A i OA K是的角平分线，所以旋转会中止．3．如图1，在△ABC中，∠ABC的角平分线与∠ACB的外角∠ACD的平分线交于点A1，（1）分别计算：当∠A分别为700、800时，求∠A1的度数.（2）根据（1）中的计算结果，写出∠A与∠A1之间的数量关系________.（3）∠A1BC的角平分线与∠A1CD的角平分线交于点A2，∠A2BC的角平分线与∠A2CD的角平分线交于点A3，如此继续下去可得A4，…，∠A n，请写出∠A5与∠A的数量关系________.（4）如图2，若E为BA延长线上一动点，连EC，∠AEC与∠ACE的角平分线交于Q，当E 滑动时，有下面两个结论：①∠Q+∠A1的值为定值；②∠D-∠A1的值为定值.其中有且只有一个是正确，请写出正确结论，并求出其值.【答案】（1）解：∵A1C、A1B分别是∠ACD、∠ABC的角平分线∴∠A1BC= ∠ABC，∠A1CD= ∠ACD由三角形的外角性质知：∠A=∠ACD-∠ABC，∠A1=∠A1CD-∠A1BC，即：∠A1= （∠ACD-∠ABC）= ∠A；当∠A=70°时，∠A1=35°；当∠A=80°，∠A1=40°（2）∠A=2∠A1（3）∠A5= ∠A（4）解：△ABC中，由三角形的外角性质知：∠BAC=∠AEC+∠ACE=2（∠QEC+∠QCE）；即：2∠A1=2（180°-∠Q），化简得：∠A1+∠Q=180°故①的结论是正确，且这个定值为180°【解析】【解答】解：（2）由（1）可知∠A1== ∠A即∠A=2∠A1（3）同（1）可求得：∠A2= ∠A1= ∠A，∠A3= ∠A2= ∠A，…依此类推，∠A n= ∠A；当n=5时，∠A5= ∠A= ∠A【分析】（1）由三角形的外角性质易知：∠A=∠ACD-∠ABC，∠A1=∠A1CD-∠A1BC，而∠ABC的角平分线与∠ACB的外角∠ACD的平分线交于A1，可得∠A1= （∠ACD-∠ABC）= ∠A（2）根据（1）可得到∠A=2∠A1（3）根据（1）可得到∠A2= ∠A1=∠A，∠A3= ∠A2= ∠A，…依此类推，∠A n= ∠A，根据这个规律即可解题.（4）用三角形的外角性质求解，易知2∠A1=∠AEC+∠ACE=2（∠QEC+∠QCE），利用三角形内角和定理表示出∠QEC+∠QCE，即可得到∠A1和∠Q的关系．4．已知BE平分∠ABD，DE平分∠BDC，且∠BED =∠ABE +∠EDC.（1）如图1，求证：AB//CD；（2）如图2，若∠ABE=3∠ABF，且∠BFD=30°时，试求的值；（3）如图3，若H是直线CD上一动点（不与D重合），BI平分∠HBD，画出图形，并探究出∠EBI与∠BHD的数量关系.【答案】（1）证明：∵∠BED =∠ABE +∠EDC，∠EBD+∠BED+∠BDE=180°，∴∠ABD+∠BDC=180°，∴AB∥CD（2）解：∵BE平分∠ABD，DE平分∠BDC，∴∠ABE=∠EBD，∠EDC=∠EDB.∵∠ABD+∠BDC=180°，∴∠BED=∠ABE+∠EDC=90°.设∠ABF=α，则∠ABE=3α.如图，过F作FG∥AB，则有：∠ABF+∠CDF=∠BFD，∴∠CDF=30°-α.过E作EH∥AB，则有：∠ABE+∠CDE=∠BED，∴∠CDE=90°-3α，∴∠FDE=60°-2α，∴.（3）解：分两种情况讨论：①当H在点D的左边时，如图3.设∠HBI=∠DBI=x，∠EBH=y，则∠EBD=2x+y，∴∠ABE=∠EBD=2x+y.∵AB∥CD，∴∠BHD=∠ABH=2x+y+y=2（x+y）=2∠EBI；②当H在点D右边时，如图4.设∠HBI=∠DBI=x，∠EBD=y，则∠EBI=x+y，∴∠ABH=2x+2y.∵AB∥CD，∴∠ABH+∠BHD=180°，∴2x+2y+∠BHD=180°，∴∠BHD+2∠EBI=180°.综上所述：∠BHD=2∠EBI或∠BHD+2∠EBI=180°【解析】【分析】（1）由∠BED =∠ABE +∠EDC和三角形内角和定理即可得到∠ABD+∠BDC=180°，再由同旁内角互补，两直线平行即可得到结论；（2）由角平分线定义和∠ABD+∠BDC=180°，得到∠BED=∠ABE+∠EDC=90°.设∠ABF=α，则∠ABE=3α，过F作FG∥AB，则有∠ABF+∠CDF=∠BFD，得到∠CDF=30°-α.过E作EH∥AB，同理可得：∠CDE=90°-3α，根据角的和差得到∠FDE=60°-2α，即可得到结论；（3）分两种情况讨论：①当H在点D的左边时，②当H在点D右边时.5．以直线AB上点O为端点作射线OC，使∠BOC=60°，将直角△DOE的直角顶点放在点O 处.（1）如图1，若直角△DOE的边OD放在射线OB上，则∠COE=________；（2）如图2，将直角△DOE绕点O按逆时针方向转动，使得OE平分∠AOC，说明OD所在射线是∠BOC的平分线；（3）如图3，将直角△DOE绕点O按逆时针方向转动，使得∠COD= ∠AOE.求∠BOD的度数.【答案】（1）30（2）解：∵OE平分∠AOC，∴∠COE=∠AOE= ∠COA，∵∠EOD=90°，∴∠AOE+∠DOB=90°，∠COE+∠COD=90°，∴∠COD=∠DOB，∴OD所在射线是∠BOC的平分线（3）解：设∠COD=x°，则∠AOE=5x°，∵∠DOE=90°，∠BOC=60°，∴6x=30或5x+90﹣x=120，∴x=5或7.5，即∠COD=65°或37.5°，∴∠BOD=65°或52.5°【解析】【解答】（1）∵∠BOE=∠COE+∠COB=90°，又∵∠COB=60°，∴∠COE=∠BOE-∠COB=30°，故答案为30；【分析】（1）根据图形得出∠COE=∠BOE-∠COB，代入求出即可；（2）根据角平分线定义求出∠COE=∠AOE= ∠COA，再根据∠AOE+∠DOB=90°，∠COE+∠COD=90°，可得∠COD=∠DOB，从而问题得证；（3）设∠COD=x°，则∠AOE=5x°，根据题意则可得6x=30或5x+90﹣x=120，解方程即可得.6．（1）如图，已知C为线段AB上的一点，AC=60cm，M、N分别为AB、BC的中点.①若BC=20cm，则MN=________cm；②若BC=acm，则MN=________cm.（2）如图，射线OC在∠AOB的内部，∠AOC=60°，OM平分∠AOB，射线ON在∠BOC 内，且∠MON=30°，则ON平分∠BOC吗？并说明理由.【答案】（1）30；30（2）解：平分理由：∵OM分别平分∠AOB，∴∠BOM= ∠AOB= （∠AOC+∠BOC）=30°+ ∠BOC.又∵∠BOM=∠MON+∠BON=30°+∠BON，∴∠BON= ∠BOC.∴ON平分∠BOC.【解析】【解答】解：（1）①∵BC=20，N为BC中点，∴BN= BC=10.又∵M为AB中点，∴MB= AB=40.∴MN=MB-BN=40-10=30.故答案为30；②当BC=a时，AB=60+a，BN= a，MB= AB=30+ a，∴MN=MB-BN=30.故答案为30；【分析】（1）①由已知得到AB=80，根据线段中点求出MB和BN的值，计算MB-BN即可得结果；②分别用a表示出BN、MB，根据MN=MB-BN计算即可；（2）根据OM分别平分∠AOB，用∠BOC表示出∠BOM，再用∠BON表示出∠BOM，两个式子进行比较即可得出结论.7．如图，已知AB∥CD，CE、BE的交点为E，现作如下操作：第一次操作，分别作∠ABE和∠DCE的平分线，交点为E1，第二次操作，分别作∠ABE1和∠DCE1的平分线，交点为E2，第三次操作，分别作∠ABE2和∠DCE2的平分线，交点为E3，…，第n次操作，分别作∠ABE n﹣1和∠DCE n﹣1的平分线，交点为E n.（1）如图①，已知∠ABE=50°，∠DCE=25°，则∠BEC = ________°；（2）如图②，若∠BEC=140°，求∠BE1C的度数；（3）猜想：若∠BEC＝α度，则∠BE n C = ________ °.【答案】（1）75（2）解：如图2，∵∠ABE和∠DCE的平分线交点为E1，∴由（1）可得，∠BE1C=∠ABE1+∠DCE1= ∠ABE+ ∠DCE= ∠BEC；∵∠BEC=140°，∴∠BE1C=70°；（3）【解析】【解答】解：（1）如图①，过E作EF∥AB，∵AB∥CD，∴AB∥EF∥CD，∴∠B=∠1，∠C=∠2，∵∠BEC=∠1+∠2，∴∠BEC=∠ABE+∠DCE=75°；故答案为：75；（ 3 ）如图2，∵∠ABE1和∠DCE1的平分线交点为E2，∴由（1）可得，∠BE2C=∠ABE2+∠DCE2= ∠ABE1+ ∠DCE1= ∠CE1B= ∠BEC；∵∠ABE2和∠DCE2的平分线，交点为E3，∴∠BE3C=∠ABE3+∠DCE3= ∠ABE2+ ∠DCE2= ∠CE2B= ∠BEC；…以此类推，∠E n= ∠BEC，∴当∠BEC=α度时，∠BE n C等于 °.故答案为： .【分析】（1）先过E作EF∥AB，根据AB∥CD，得出AB∥EF∥CD，再根据平行线的性质，得出∠B=∠1，∠C=∠2，进而得到∠BEC=∠ABE+∠DCE=75°；（2）先根据∠ABE和∠DCE的平分线交点为E1，运用（1）中的结论，得出∠BE1C=∠ABE1+∠DCE1= ∠ABE+ ∠DCE= ∠BEC；（3）根据∠ABE1和∠DCE1的平分线，交点为E2，得出∠BE2C= ∠BEC；根据∠ABE2和∠DCE2的平分线，交点为E3，得出∠BE3C= ∠BEC；…据此得到规律∠E n= ∠BEC，最后求得∠BE n C的度数.8．如图，在△ABC中，点E在AC边上，连结BE，过点E作DF∥BC，交AB于点D.若BE 平分∠ABC，EC平分∠BEF.设∠ADE＝α，∠AED＝β.（1）当β＝80°时，求∠DEB的度数.（2）试用含α的代数式表示β.（3）若β＝kα（k为常数），求α的度数（用含k的代数式表示）.【答案】（1）解：∵β＝80°，∴∠CEF＝∠AED＝80°，∵BE平分∠ABC，∴∠BEC＝∠CEF＝80°，∴∠DEB＝180°﹣80°﹣80°＝20°；（2）∵DF∥BC，∴∠ADE＝∠ABC＝α，∵BE平分∠ABC，∴∠DEB＝∠EBC＝∵EC平分∠BEF，∴β＝∠CEF＝（180°﹣）＝90°﹣α；（3）∵β＝kα，∴90°﹣α＝kα，解得：α＝【解析】【分析】（1）根据对顶角的性质得到∠CEF＝∠AED＝80°，根据角平分线的定义即可得到结论；（2）根据角平分线的定义和平行线的性质即可得到结论；（3）根据题意列方程即可得到结论.9．问题情景：如图1，AB//CD，∠PAB=130°，∠PCD=120°，求∠APC的度数．小明的思路是：过点P作PE//AB，∴∠PAB+∠APE=180°．∵∠PAB=130°，∴∠APE=50°∵AB//CD，PE//AB，∴PE//CD，∴∠PCD+∠CPE=180°．∵∠PCD=120°，∴∠CPE=60°∴∠APC=∠APE+∠CPE=110°．问题迁移：如果AB与CD平行关系不变，动点P在直线AB、CD所夹区域内部运动时，∠PAB，∠PCD的度数会跟着发生变化．（1）如图3，当动点P运动到直线AC右侧时，请写出∠PAB，∠PCD和∠APC之间的数量关系？并说明理由．（2）如图4，AQ，CQ分别平分∠PAB，∠PCD，请直接写出∠AQC和∠APC的数量关系________．（3）如图5，点P在直线AC的左侧时，AQ，CQ仍然平分∠PAB，∠PCD，请直接写出∠AQC和角∠APC的数量关系________【答案】（1）∠PAB+∠PCD=∠APC理由：如图3，过点P作PF∥AB，∴∠PAB=∠APF，∵AB∥CD，PF∥AB，∴PF∥CD，∴∠PCD=∠CPF，∴∠PAB+∠PCD=∠APF+∠CPF=∠APC，即∠PAB+∠PCD=∠APC故答案为：∠PAB+∠PCD=∠APC（2）（3）2∠AQC+∠APC=360°【解析】【解答】（2）理由：如图4，∵AQ，CQ分别平分∠PAB，∠PCD，∴∠QAB= ∠PAB，∠QCD= ∠PCD，∴∠QAB+∠QCD= ∠PAB+ ∠PCD= (∠PAB+∠PCD)，由（1），可得∠PAB+∠PCD=∠APC，∠QAB+∠QCD=∠AQC∴∠AQC= ∠APC故答案为：∠AQC= ∠APC；（3）2∠AQC+∠APC=360°理由：如图5，过点P作PG∥AB ，∴∠PAB+∠APG=180°，∵AB∥CD，PG∥AB，∴PG//CD，∴∠PCD+∠CPG=180°，∴∠PAB+∠APG+∠PCD+∠CPG=360°，∴∠PAB+∠PCD+∠APC=360°，∵AQ，CQ分别平分∠PAB，∠PCD，∴∠QAB= ∠PAB，∠QCD= ∠PCD，∴∠QAB+∠QCD= ∠PAB+ ∠PCD= (∠PAB+PCD)由（1）知，∠QAB+∠QCD=∠AQC，∴∠AQC= (∠PAB+∠PCD)2∠AQC=∠PAB+∠PCD，∵∠PAB+∠PCD+∠APC=360°，∴2∠AQC+∠APC=360°．【分析】（1）过点P作PF∥AB，可得∠PAB=∠APF，根据AB∥CD，PF∥AB，可得∠PCD=∠CPF，所以∠PAB+∠PCD=∠APF+∠CPF=∠APC，即可证得∠PAB+∠PCD=∠APC；（2）已知AQ，CQ分别平分∠PAB，∠PCD，根据角平分线性质，可得∠QAB= ∠PAB，∠QCD= ∠PCD，∠QAB+∠QCD= ∠PAB+ ∠PCD= (∠PAB+∠PCD)，再根据（1）结论，即可证明∠AQC= ∠APC．（3）过点P作PG∥AB，根据平行线的性质可得∠PAB+∠APG=180°，由已知可得PG//CD，∠PCD+∠CPG=180°，证明得∠PAB+∠PCD+∠APC=360°，，再根据AQ，CQ分别平分∠PAB，∠PCD，可得∠QAB+∠QCD= ∠PAB+ ∠PCD= (∠PAB+∠PCD)，即可证明得出结论2∠AQC+∠APC=360°．10．如图，AD∥BC，∠B＝∠D＝50°，点E、F在BC上，且满足∠CAD＝∠CAE，AF平分∠BAE.（1）∠CAF＝________°；（2）若平行移动CD，那么∠ACB与∠AEB度数的比值是否随之发生变化？若变化，试说明理由；若不变，求出这个比值；（3）在平行移动CD的过程中，是否存在某种情况，使∠AFB＝∠ACD？若存在，求出∠ACD度数；若不存在，说明理由.【答案】（1）65（2）解：若平行移动CD，那么∠ACB与∠AEB度数的比值不发生变化.∵AD∥BC，∴∠DAC=∠ACB∵∠CAD＝∠CAE∴∠ACB=∠CAE∴∠AEB=∠CAE+∠ACB=2∠ACB即∠ACB：∠AEB=1:2所以，∠ACB与∠AEB度数的比值是：1:2（3）解：存在∵AD∥BC，∴∠B+∠BAD=180°,∵∠B=∠D∴∠D+∠BAD=180°∴AB∥CD∴∠AFB=∠DAF=∠DAC+∠CAF∠ACD=∠CAB=∠BAF+∠CAF∵∠AFB＝∠ACD∴∠DAC+∠CAF=∠BAF+∠CAF∴∠DAC=∠BAF∴∠DAC=∠BAF=∠CAE=∠EAF= ∠BAD= ×130°=32.5°∴∠ACD= ∠CAB=∠BAF+∠CAF =3∠DAC=3×32.5°=97.5°【解析】【解答】解：（1）∵AF平分∠BAE，∴∠BAF=∠EAF= ∠BAE，∵∠CAD＝∠CAE∴∠CAD＝∠CAE= ∠DAE∴∠CAF＝∠EAF+∠CAE= ∠BAE+ ∠DAE= ∠BAD∵AD∥BC，∠B＝∠D＝50°，∴∠BAD=180-∠B=130°,∴∠CAF＝65°【分析】（1）根据角平分线的性质可得∠CAF＝∠EAF+∠CAE= ∠BAE+ ∠DAE= ∠BAD，再根据平行线的性质得∠BAD =180-∠B，从而得出答案；（2）根据平行线的性质得∠DAC=∠ACB，再由∠CAD＝∠CAE，可知∠ACB=∠CAE，从而可得∠AEB =2∠ACB，即可得出答案；（3）根据平行线的性质得∠AFB=∠DAF=∠DAC+∠CAF，∠ACD=∠CAB=∠BAF+∠CAF，再由平行线的性质可得∠BAD=130°，即可求出答案11．如图所示，O为一个模拟钟面圆心，M、O、N 在一条直线上，指针OA、OB 分别从OM、ON 出发绕点 O 转动，OA 运动速度为每秒 30 ，OB 运动速度为每秒10 ，当一根指针与起始位置重合时，运动停止，设转动的时间为 t 秒，试解决下列问题：（1）如图①，若OA顺时针转动，OB逆时针转动， =________秒时，OA与OB第一次重合；（2）如图②，若OA、OB同时顺时针转动，①当 =3秒时，∠AOB=________ ；②当为何值时，三条射线OA、OB、ON其中一条射线是另两条射线夹角的角平分线？________【答案】（1）4.5（2）；解：由题意知，∴∠BON＝10t ，∠AON＝180－30t (0≤t≤6)，∠AON＝30t－180(6<t≤12).当ON为∠AOB的角平分线时，有180－30t ＝10t ，解得：t ＝4.5；当OA为∠BON的角平分线时，10t ＝2(30t －180)，解得：t ＝7.2；当OB为∠AON的角平分线时，30t －180＝2×10t ，解得：t ＝18（舍去）；∴经过4.5，7.2秒时，射线OA、OB、ON其中一条射线是另外两条射线夹角的平分线【解析】【解答】（1）解：若OA顺时针转动，OB逆时针转动，∴∠AOM+∠BON=180 ,∴，解得：；∴秒，OA与OB第一次重合；故答案为：4.52）解：①若OA、OB同时顺时针转动，∴，，∴；故答案为：120；【分析】（1）设t秒后第一次重合．根据题意，列出方程，解方程即可；（2）①利用180 减去OA转动的角度，加上OB转动的角度，即可得到答案；②先用t的代数式表示∠BON和∠AON，然后分为三种情况进行讨论：当ON、OA、OB为角平分线时，分别求出t的值，即可得到答案.12．已知将一副三角板(直角三角板OAB和直角三角板OCD∠AOB=90°，∠ABO=45°，∠CDO=90°，∠COD=60°)（1）如图1摆放，点O，A，C在一直线上，则∠BOD的度数是多少?（2）如图2，将直角三角板OCD绕点O逆时针方向转动，若要OB恰好平分∠COD，则∠AOC的度数是多少?（3）如图3，当三角板OCD摆放在∠AOB内部时，作射线OM平分∠AOC，射线ON平分∠BOD，如果三角板OCD在∠AOB内绕点Q任意转动，∠M0N的度数是否发生变化?如果不变，求其值；如果变化，说明理由。
七年级几何图形初步单元质量检测试卷含答案
D CB AB A第1题图会社谐和设建C BAβββααα第3题图 七年级数学单元质量检测 第四章 几何图形初步（问卷）第Ⅰ卷（选择题 共30 分）一、选择题（每小题3分，共30分）1.如图是一个小正方体的展开图，把展开图折叠成小正方体后，有“建”字一面的相对面上的字是（ ）A.和B.谐C.社D.会2.下面左边是用八块完全相同的小正方体搭成 的几何体，从上面看该几何体得到的图是（ ）3.如图，四个图形是由立体图形展开得到的，相应的立体图形顺次是（ ）A. 正方体、圆柱、三棱柱、圆锥 B. 正方体、圆锥、三棱柱、圆柱 C. 正方体、圆柱、三棱锥、圆锥 D. 正方体、圆柱、四棱柱、圆锥4.如图，对于直线AB ，线段CD ，射线EF ，其中能相交的是（ ）5.下列说法中正确的是（ ）A.画一条3厘米长的射线B.画一条3厘米长的直线C.画一条5厘米长的线段D.在线段、射线、直线中直线最长6.如图，将一副三角尺按不同位置摆放，摆放方式中∠α 与∠β 互余的是（ ）7.点E 在线段CD 上，下面四个等式①CE ＝DE ；②DE ＝21CD ；③CD ＝2CE ； ④CD ＝21DE.其中能表示E 是线段CD 中点的有（ ） A. 1个 B. 2个 C. 3个 D. 4个1乙甲N M PD C B A B ()D C AD CBA第9题图BA 第19题D C BA O 第20题CB A8. C 是线段AB 上一点，D 是BC 的中点，若AB ＝12cm ，AC ＝2cm ，则BD 的长为（ ） A. 3cm B. 4cm C. 5cm D. 6cm9.如图是一正方体的平面展开图，若AB ＝4，则该正方体A 、B 两点间的距离为（ ）A. 1B. 2C. 3D. 410.用度、分、秒表示91.34°为（ ） A. 91°20/24// B. 91°34/ C. 91°20/4// D. 91°3/4//11.下列说法中正确的是（ ）A.若∠AOB ＝2∠AOC ，则OC 平分∠AOBB.延长∠AOB 的平分线OCC.若射线OC 、OD 三等份∠AOB ，则∠AOC ＝∠DOCD.若OC 平分∠AOB ，则∠AOC ＝∠BOC12.甲、乙两人各用一张正方形的纸片ABCD 折出一个45°的角（如图）， 两人做法如下：甲：将纸片沿对角线AC 折叠，使B 点落在D 点上，则∠1＝45°； 乙：将纸片沿AM 、AN 折叠，分别使B 、D 落在对角线AC 上的一点P ，则∠MAN ＝45°对于两人的做法，下列判断正确的是（ ）A.甲乙都对B.甲对乙错C.甲错乙对D.甲乙都错 二、填空题（每小题3分，共24分）13.下列各图形中， 不是正方体的展开图（填序号）.14.已知M 、N 是线段AB 的三等分点，C 是BN 的中点，CM ＝6cm ，则AB ＝ cm.15.已知线段AB ，延长AB 到C ，使BC ＝2AB ，D 为AB 的中点，若BD ＝3cm ，则AC 的长为 cm.16.若时针由2点30分走到2点55分，则时针转过 度，分针转过 度.17.一个角的补角是这个角的余角的4倍，则这个角的度数是 .D CB A ODCBAba O DCBA18.如图，已知点O 是直线AD 上的点，∠AOB 、∠BOC 、∠COD 三个角从小到大依次相差25°，则这三个角的度数分别为.19.如图，将一副三角板叠放在一起，使直角顶点重合于O ，则∠AOC ＋∠DOB ＝ .20.如图所示，一艘船从A 点出发，沿东北方向航行至点B ，再从B 点出发沿南偏东 15°方向行至点C ，则∠ABC ＝ 度.三、解答题：（本大题共52分）21.（每小题3分，共6分）根据下列语句，画出图形. ⑴已知四点A 、B 、C 、D.① 画直线AB ；② 连接AC 、BD ，相交于点O ； ③ 画射线AD 、BC ，交于点P.⑵如图，已知线段a 、b ，画一条线段，使它等于2a －b.（不要求写画法）22.计算题：（每小题5分，共20分）⑴ （180°－91°32/24//）×3⑵ 34°25/×3＋35°42/⑶ 一个角的余角比它的补角的31还少20°，求这个角.⑷ 如图，AOB 为直线，OC 平分∠AOD ，∠BOD ＝42°，求∠AOC 的度数.23.（本大题9分）如图，是由7块正方体木块堆成的物体，请说出图⑴、图⑵、图⑶分别是从哪一个方向看得到的？⑴⑵ ⑶D CB A ba DCBA第24题图3x －2A1－2x 3第25题图E A /DC B A24.（本大题7分）如图是一个正方体的平面展开图，标注了A 字母的是正方体的正面，如果正方体的左面与右面标注的式子相等. ⑴ 求x 的值. ⑵ 求正方体的上面和底面的数字和.25.（本大题10分）探究题：如图，将书页一角斜折过去，使角的顶点A 落在A /处，BC 为折痕，BD 平分∠A /BE ，求∠CBD 的度数.三、解答题（共52分）21.（每小题3分，共6分）根据下列语句，画出图形. ⑴已知四点A 、B 、C 、D.① 画直线AB ；② 连接AC 、BD ，相交于点O ；③ 画射线AD 、BC ，交于点P 。
七年级数学几何图形初步单元测试(一)(含答案)
几何图形初步单元测试（一）一、单选题(共12道，每道8分)1.下列说法中，不正确的是( )A.圆锥和圆柱的底面都是圆B.棱锥的侧面是三角形，棱柱的侧面是四边形C.棱柱的上、下底面的形状和大小完全相同D.正方体是四棱柱，四棱柱是正方体答案：D解题思路：A选项：圆柱有上下两个底面，都是圆，圆锥有一个底面，是圆，所以A选项正确；D选项：正方体是四棱柱，并且正方体是特殊的四棱柱，六个面都是正方形，每条棱都相等．但四棱柱不一定是正方体，还有可能是长方体，故D选项错误．故选D．试题难度：三颗星知识点：几何体的底面侧面的特征2.下列说法，错误的是( )A.经过一点的直线可以有无数条B.一条直线只能用一个小写字母表示C.经过两点的直线只有一条D.线段EF和线段FE是同一条线段答案：B解题思路：一条直线可以用两个大写字母表示，也可以用一个小写字母表示，比如用直线AB，直线等来表示直线，B选项错误．故选B．试题难度：三颗星知识点：直线3.如图所示，下列说法错误的是( )A.∠1与∠AOB表示同一个角B.∠AOC可用∠O来表示C.图中共有三个角∠AOB，∠AOC，∠BOCD.∠α表示的是∠BOC答案：B解题思路：角有四种表示方法：①用一个大写字母表示（顶点处只有一个角时，才可用顶点处的一个字母来表示这个角，顶点处有多个角时，不能用顶点处的一个字母来表示这个角，例如该题中不能用∠O表示角）；②用三个大写字母表示；③用一个希腊字母表示，如∠α，∠β，∠γ，…；④用一个数字表示，如∠1，∠2，…．因此选项A和选项D正确，选项B错误．图中共有3个角，可以表示为∠AOB，∠AOC，∠BOC，所以选项C说法正确．故选B．试题难度：三颗星知识点：角的表示4.从如图所示的纸板上7个小正方形中选择1个剪去，使剩余的部分恰好能折成一个正方体，则不同的选法有( )A.3种B.4种C.5种D.6种答案：A解题思路：正方体的11种展开图：（1，4，1）型6种；（2，3，1）型3种；（2，2，2）型1种；（3，3）型1种．观察图形，该展开图类型只能为（1，4，1）型或（2，3，1）型：当为（1，4，1）型时，可剪去“数”或“学”，有2种；当为（2，3，1）型时，可剪去“生”，有1种．综上，有3种．故选A．试题难度：三颗星知识点：正方形的展开图5.已知一个不透明的正方体的六个面上分别写着1~6六个数字，如图是我们能看到的三种情况，那么数字5对面的数字是( )A.6B.4C.3D.6或4或3答案：B解题思路：由三个图可知数字1和数字2，4，5，6相邻，则数字1和数字3相对；数字2和数字1，3，4，5相邻，则数字2和数字6相对．故数字5对面的数字是4故选B．试题难度：三颗星知识点：正方体展开图——相对面、相邻面6.从三个不同方向看分别是下列三个图形的物体是( )A. B.C. D.答案：C解题思路：主视图是从正面看，可以看到列数和层数；左视图是从左面看，可以看到行数和层数；俯视图是从上面看，可以看到列数和行数．从主视图可以看出该几何体的第1列最多是2层，第2列最多是1层，第3列最多是1层；从左视图可以看出该几何体的第1行最多是2层，第2行最多是1层，如图所示，因此C选项满足条件．故选C．试题难度：三颗星知识点：几何体的三视图7.如图，点A和点B分别是棱长为20cm的正方体盒上相邻两个面的中心，一只蚂蚁在盒上由A处向B处爬行，所走的最短路程是( )A.10cmB.20cmC.30cmD.40cm答案：B解题思路：把正方体展开后点A和点B所在的面如图，根据两点之间线段最短，可知由A处向B处爬行，所走的最短路程是20cm．故选B．试题难度：三颗星知识点：两点之间线段最短8.若C是线段AB的中点，D是线段BC上一点，则下列关系错误的是( )A. B.C. D.答案：A解题思路：根据题意画图，因为D不一定是BC的中点，所以错误，A选项错误；由题意可知，，又因为C是线段AB的中点，所以，则，．所以选项B，C，D正确．故选A．试题难度：三颗星知识点：中点9.已知线段AB=60，在直线AB上画线段BC，使BC=20，点D是AC的中点，则CD的长为( )A.20B.40C.20或40D.以上都不对答案：C解题思路：根据题意，画图，应分成两种情况：①点C在线段AB的延长线上时，∵点D是AC的中点②点C在线段AB上，∵点D是AC的中点故选C．试题难度：三颗星知识点：线段的计算10.如图，OC是∠AOB的平分线，，∠BOD=15°，则∠AOD=( )A.45°B.55°C.75°D.65°答案：C解题思路：∵，∠BOD=15°∴∠COD=3∠BOD=45°∴∠BOC=45°-15°=30°∵OC平分∠AOB∴∠BOC=∠AOC=30°∴∠AOD=∠COD+∠AOC=75°故选C．试题难度：三颗星知识点：角平分线11.如图，∠AOB=90°，∠AOC=36°，∠COD:∠COB=1:2，则∠BOD的度数为( )A.18°B.36°C.27°D.31°答案：C解题思路：∵∠AOB=90°，∠AOC=36°∴∠COB=∠AOB-∠AOC=90°-36°=54°∵∠COD:∠COB=1:2∴OD平分∠BOC∴∠BOD=∠COB=×54°=27°故选C．试题难度：三颗星知识点：角的计算12.如图所示，长度为12cm的线段AB的中点为M，点C在线段MB上，且，则线段AC的长度为( )A.2cmB.4cmC.6cmD.8cm答案：D解题思路：如图，∵线段的中点为∴∵∴∵∴∴即线段AC的长度为8cm．故选D．试题难度：三颗星知识点：求线段的长。
七年级数学几何图形初步单元达标训练题(Word版 含答案)
一、初一数学几何模型部分解答题压轴题精选（难）1．如图①，△ABC的角平分线BD，CE相交于点P.（1）如果∠A=80∘，求∠BPC= ________.（2）如图②,过点P作直线MN∥BC,分别交AB和AC于点M和N,试求∠MPB+∠NPC的度数(用含∠A的代数式表示)________.（3）将直线MN绕点P旋转。
(i)当直线MN与AB，AC的交点仍分别在线段AB和AC上时，如图③，试探索∠MPB，∠NPC，∠A三者之间的数量关系，并说明你的理由。
(ii)当直线MN与AB的交点仍在线段AB上,而与AC的交点在AC的延长线上时,如图④,试问(i)中∠MPB，∠NPC，∠A三者之间的数量关系是否仍然成立?若成立，请说明你的理由；若不成立，请给出∠MPB，∠NPC，∠A三者之间的数量关系，并说明你的理由。
【答案】（1）130°（2）90°﹣∠A（3）解：(i)∠MPB+∠NPC= − ∠A.理由如下：∵∠BPC= +∠A，∴∠MPB+∠NPC= −∠BPC=180∘−( + ∠A)= −12 ∠A.(ii)不成立,有∠MPB−∠NPC= − ∠A.理由如下：由题图④可知∠MPB+∠BPC−∠NPC= ，由(1)知：∠BPC= + ∠A，∴∠MPB−∠NPC= −∠BPC= −( + ∠A)=− ∠A.【解析】【解答】(1)故答案为：( 2 )由 = 得∠MPB+∠NPC= −∠BPC= 1−( + ∠A)= − ∠A；故答案为：∠MPB+∠NPC= −∠A【分析】（1）根据角平分线的定义得出∠PBC+∠PCB=(∠ABC+∠ACB)，再根据三角形的内角和定理及∠A的度数，求出∠ABC+∠ACB的值，然后再利用三角形的内角和就可求出∠BPC的度数。
（2）根据角平分线的定义得出∠PBC+∠PCB=(∠ABC+∠ACB)，再根据三角形的内角和定理得出∠BPC=180°-（∠PBC+∠PCB），∠ABC+∠ACB=180°-∠A ，代入计算即可得出结论。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2018年几何图形初步测试题一、选择题1．如图是一个正方体的表面展开图，如果相对面上所标的两个数互为相反数，那么图中x的值是（）A．8 B．3 C．2 D．-32．如图所示的几何体的俯视图是（）.54．下图中共有（）条线段．A．4B．6C．8D．105．下列四个图中的线段（或直线、射线）能相交的是（）A．（1） B．（2） C．（3） D．（4）6．使分式2+xx有意义的x的取值范围为（）A．2≠x B．2-≠x C．2->x D．2<x7．如图，C、D是线段AB上两点，若CB＝5cm，DB=9cm，且D是AC的中点，则AC的长等于（）A．6cm B．9cm C．8cm D．13cm8．点C在线段AB上，下列条件中不能确定．．．．点C是线段AB中点的是A．B．C．D．C DBA正面A、 AC =BCB、 AC +BC= ABC、 AB =2ACD、 BC =21AB9．已知A、B两点之间的距离是10cm，C是线段AB上的任意一点，则AC中点与BC中点间的距离是（）A．3cm B．4cm C ．5cm D．不能计算10．将一副三角板如图放置，使点A落在DE上，若BC DE∥，则AFC∠的度数为（）A.45°B.50°C.60°D.75°11．如图，直线AB与CD相交于点O，12=∠∠，若140AOE=∠，则AOC∠的度数为（）．Ａ．40Ｂ．60Ｃ．80Ｄ．10012．如图所示，∠AOB=156°,OD是∠AOC的平分线，OE是∠BOC的平分线，那么∠DOE 等于（）A．78° B．80° C．88° D．90°13．如图，直线AB与CD相交于点O，∠1=∠2，若∠AOE=140°，则∠AOC的度数为（）A．40 B．60 C．80 D．10014．如图所示，已知O是直线AB上一点，∠1＝40°，OD平分∠BOC，则∠2的度数是（）AOCED（A）20°（B）25°（C）30°（D）70°评卷人得分一、解答题15．（本题满分7分）线段AB=4cm，延长线段AB到C，使BC = 1cm，再反向延长AB 到D，使AD=3 cm，E是AD中点，F是CD的中点，求EF的长度．16．（本题满分5分）已知：如图所示，已知线段a、b、c（a﹥c），求作：线段AB，使AB=a+b-c．17．（10分）如图，已知线段AB和CD的公共部分BD=13AB=14CD，线段AB、CD的中点E、F之间距离是10cm，求AB、CD的长．18．（6分）根据下列语句，画出图形.已知四点A、B、C、D.DCBA①画直线AB；②连接AC、BD，相交于点O；③画射线AD、BC，交于点P.[19．（满分8分）今年“五一”小长假期间，某市外来与外出旅游的总人数为226万人，分别比去年同期增长30%和20%，去年同期外来旅游比外出旅游的人数多20万人．求该市今年外来和外出旅游的人数．20．（满分5分）线段AB=14cm，C是AB上一点，且AC=9cm，O为AB中点，求线段OC 的长度··A O C BA E DB F C21．如图，如图点B在线段AC上，若D是AB的中点，E是BC的中点，（1）若DE=5，AE=7，求CE 的长（2）若AC=m，试用含m的代数式表示线段ED22．线段cmAC6=，线段cmBC15=，点M是AC的中点，在CB上取一点N，使2:1:=NBCN，求MN的长。
23．（本题10分）如图，点C在线段AB上，AC=8cm，CB=6cm，点M、N分别是AC、BC 的中点。
（1）求线段MN的长；（2）若C为线段AB上任意一点，满足AC+CB=a cm，其他条件不变，你能猜想MN的长度吗？并说明理由。
（3）若C在AB的延长线上，且满足AC－CB=b cm，其他条件不变， MN的长度为。
（直接写出答案）24．作图题.如图，在同一平面内有四个点A、B、C、D.①画射线BD②画直线BC③连结AC与射线BD相交于点P④延长线段AD与直线BC相交于点Q评卷人得分二、填空题25．如图，在一次数学活动课上，张明用17个边长为1的小正方体搭成了一个几何体，然后他请王亮用其他同样的小正方体在旁边再搭一个几何体，使王亮所搭几何体恰好可以和张明所搭的几何体拼成一个大长方体（不改变张明所搭几何体的形状），那么王亮至少还需要个小正方体，王亮所搭几何体表面积为________________．26．立方体木块的六个面分别标有数字1、2、3、4、5、6，下图是从不同方向观察这BCM N个立方体木块看到的数字情况，数字1和5对面的数字的和是．27．一个几何体是由若干个相同的正方体组成的，从其正面看和左面看都是三个横排的正方体，搭成这样的几何体至少需要个这样的正方体.28．如果∠A=35°，那么它的余角为．29．如图，直线AB、CD交于点O，80=∠COE，OA平分COE∠，则=∠DOB 度．30．如图所示，射线OP表示的方向是．31．已知32=∠α，则α∠的余角是度．32．若一个角的补角是150°，则这个角的余角是____________．33．已知∠1与∠2互余，∠2与∠3互补，∠1=67°，则∠3= 。
34．57.32︒= _____︒______′______"。
35．在长为48cm的线段AB上，取一点D，使AD=13AB ，C为AB的中点，则CD=______________cm．36．如图，已知点C在线段AB上，MN＝4cm,BC＝2cm,点M、N分别是AC、BC的中点，则线段AM的长度为 cm.37．如图所示，点M，N在线段AB上，且cmMB5=，cmNB14=，N是线段AM 的中点，则线段AB为cm．38．如图，若C为线段AB的中点，D在线段CB 上，6=DA，4=DB，则CD的长度是____________________．39．填空题：如图所示，点C是线段AB上的点，点D是线段BC的中点，若AB=10，AC=6，则CD=______.评卷人得分三、计算题40．（13分）已知, ∥OA，︒=∠=∠108AB，试解答下列问题：（1）如图所示，则=∠O___________°，并判断OB与AC平行吗？为什么？（2）如图，若点F、E在线段BC上，且满足AOCFOC∠=∠，并且OE平分BOF∠．则EOC∠的度数等于_____________°；（3）在第（2）题的条件下，若平行移动AC，如图．①求OCB∠:OFB∠的值；②当OCAOEB∠=∠时，求OCA∠的度数（直接写出答案，不必写出解答过程）．41．计算：48º39'+67º31'-21º17'×5；42．（本题满分6分）如图，点O在直线AB上，OC平分∠DOB．若∠COB＝36°.(1)求∠DOB的大小；(2)请你用量角器先画∠AOD的角平分线OE，再说明OE和OC的位置关系．43．如图，已知∠AOC=∠BOD=900，若∠BOC=550，求∠AOB与∠COD的度数，并比较这两BC D个角的大小.44．推理填空：（5分）如图，EF∥AD，∠1=∠2，∠BAC=70°．将求∠AGD的过程填写完整．因为EF∥AD，所以∠2=____（____________________________）又因为∠1=∠2所以∠1=∠3（______________）所以AB∥_____（_____________________________）所以∠BAC+______=180°（___________________________）因为∠BAC=70°所以∠AGD=_______．A231FGECDB45．已知，如图，DE∥BC，∠A=60°，∠B=50°；（1）求∠1的度数；（2）若FH⊥AB于点H，且∠2=∠3，试判断CD与AB的位置关系？并加以证明．46．如图所示，已知△ABC≌△FED，且BC＝ED，那么AB与EF平行吗？为什么？47．（本题5分）已知：如图所示，AB ∥CD ，AE 交CD 于点C ，DE ⊥AE ，垂足为E ，∠A ＋∠1=74º， 求：∠D 的度数．开心画一画（在原图上作图，保留作图痕迹） 48．在AD 的右侧作∠DCP ＝∠DAB ；49．在射线CP 上取一点E ，使CE ＝AB ，连接BE ．AE ． 50．画出△ABE 的BE 边上的高AF 和AB 边上的高EG ．（2分）如果已知：AB=10，BE=12，EG=6，则AF= （直接填结果）EA BD C 1参考答案1．A 【解析】 试题分析：解题的关键是熟记正方体相对面展开后间隔一个正方形；只有符号不同的两个数互为相反数.根据正方体的表面展开图的特征结合相反数的定义即可得到x 的值为8. 故选A.考点：1.正方体的表面展开图；2.相反数. 2．B. 【解析】试题分析：俯视图是从物体上面往下看到的平面图形，中间的竖线应是实线，故选B. 考点：物体的三视图识别. 3．C 【解析】试题分析：根据三视图的画法可得几何体的俯视图为C ． 考点：三视图 4．D 【解析】试题分析：同一条直线上的五个点，含有的线段数是4+3+2+1=10条. 考点：线段数量的判断. 5．A 【解析】试题分析：线段的长度是固定的，射线可以向一边无限延伸，直线可以向两边无限延伸.本题中（2）（3）（4）无法相交，只要（1）会相交. 考点：线段、射线、直线的性质. 6．B 【解析】试题分析：当20x +≠时，分式2+x x有意义，所以2-≠x ，故选：B. 考点：分式有意义的条件. 7．C 【解析】试题分析：因为CB ＝5cm ，DB=9cm ，所以CD=DB-CB=9-5=4cm ，又D 是AC 的中点，所以AC=2CD=8cm ，故选：C. 考点：线段的和差及计算. 8．B 【解析】试题分析：B 选项中不论点C 在线段AB 的什么位置都满足AC +BC= AB 所以点C 不一定是线段AB 的中点，故选B. 考点：线段的中点. 9．C ． 【解析】试题分析：∵AC+BC=AB ，∴AC 的中点与BC 的中点距离=12AB=5CM ．故选C ．考点：两点间的距离． 10．D 【解析】试题分析：根据题意可得：∠E=30°，∠ACB =45°，因为BC ∥DE ，所以∠BCE=∠E=30°，所以∠ACE=∠ACB-∠BCE=45°-30°=15°，故选：D ． 考点：1.平行线的性质；2.角的和差计算. 11．C 【解析】 试题分析：：∵∠AOE=140°，∠AOE 和∠2是邻补角， ∴∠2=180°-140°=40°，∵∠1=∠2，∴∠BOD=2∠2=80°， 又∵∠BOD 和∠AOC 是对顶角 ∴∠AOC=∠BOD=80°． 故选C ．考点：1．邻补角2．对顶角． 12．A 【解析】试题分析：因为OD 是∠AOC 的平分线，OE 是∠BOC 的平分线，所以∠DOC=12∠AOC ，∠COE=12∠BOC ，所以∠DOE=∠DOC+∠COE=12∠AOC+12∠BOC=12（∠AOC+∠BOC ）=12∠AOB=12×156°=78°,故选：A ．考点：1．角平分线；2．角的计算． 13．C 【解析】试题分析：因为∠AOE+∠2=180°，∠AOE=140°，所以∠2=40°，又因为∠1=∠2，所以∠BOD=80°，又∠AOC 和∠BOD 是对顶角，所以∠AOC=∠BOD=80°，故选：C ． 考点：1．互补；2．角的平分线；3．对顶角的性质． 14．D 【解析】试题分析：∵∠1＝40°，∴∠BOC ＝140°，∵OD 平分∠BOC ，∴∠2＝70°. 15．2.5cm 【解析】试题分析：根据条件可以求出线段DC 的长，因为E 是AD 中点，F 是CD 的中点，所以可求出线段DE,DF 的长，而EF=DF-DE ，所以EF=2.5cm. 试题解析：解：由AB=4cm ，BC=1cm ，AD=3cm得DC=4+1+3=8cm 2分 因为E 是AD 的中点， 所以DE=21AD=1.5cm 4分 因为F 是CD 的中点， 所以DF=21CD=4cm 6分 所以EF=DF-DE=2.5cm 7分考点：1.线段的中点；2.线段的和差倍分计算.16．（作图略）【解析】试题分析：先画一条射线，然后在射线上依次截取线段即可.试题解析：1、作一条射线，在射线上取一点A，以A为端点在直线上向右截取AC=a；2、再以C为端点在直线上向右截取CD=b；3、以D为端点在直线上向左截取DB=c；所得到的线段AB的长度就是：AB=a+b-c.图略考点：尺规作图.17．AB=12cm，CD=16cm【解析】试题分析：先设BD=xcm，由题意得AB=3xcm，CD=4xcm，AC=6xcm，再根据中点的定义，用含x的式子表示出AE=1.5xcm和CF=2xcm，再根据EF=AC-AE-CF=2.5xcm，且E、F之间距离是EF=10cm，所以2.5x=10，解方程求得x的值，即可求AB，CD的长．试题解析：解：设BD=xcm，则AB=3xcm，CD=4xcm，AC=6xcm．∵点E、点F分别为AB、CD的中点，∴AE=12AB=1.5xcm，CF=12CD=2xcm．∴EF=AC－AE－CF=2.5xcm．∵EF=10cm，∴2.5x=10，解得：x=4．∴AB=12cm，CD=16cm．考点：线段中点的性质18．【解析】试题分析：根据直线、线段和射线的定义作出即可．试题解析：解：如图所示．考点：直线、线段和射线的作图19．外来人数130万，外出旅游人数96万【解析】试题分析：首先设去年外来人数为x万人，则外出旅游的人数为（x﹣20）万，然后根据增长后的总人数为226万，列出方程进行求解．试题解析：设该市去年外来人数为x万人，外出旅游的人数为（x﹣20）万人，由题意得，（1+30%）x+（1+20%）（x-20）=226解得 x=100则今年外来人数为：100×（1+30%）=130（万人），今年外出旅游人数为：80×（1+20%）=96（万人）．答：该市今年外来人数为130万人，外出旅游的人数为96万人．考点：一元一次方程的应用20．2cm【解析】试题分析：根据O 为AB 的中点，求出AO 的长度，然后根据OC=AC －AO 求出长度试题解析：∵O 为AB 中点,AB=14∴OA=12AB=7cm 又∵AC=9cm ，OC=AC-AB∴OC=2 cm考点：线段中点的性质以及长度的计算21．（1）3（2）21m 【解析】欲求CE ，由E 是BC 的中点知，BE=CE,故只需求BE 即可，又BE=DE-BD=5-BD,又D 是AB 的中点可得：AD=BD=AE-DE=7-5=2(2)由D 是AB 的中点，E 是BC 的中点BD=21AB,BE=21BC 再把两者相加即可。