χ2分布临界值表
第八章习题

5.无线电厂生产一种高频管,其中一指标服从正态 无线电厂生产一种高频管, 无线电厂生产一种高频管 个管, 分布N(µ,σ2),今从一批产品中抽取 个管,测得其 ,今从一批产品中抽取8个管 分布 指标数据如下: 指标数据如下:68,43,70,65,55,56,60,72.当总体均 当总体均 未知时, 值µ未知时,能否认为该厂生产的高频管的某指标 未知时 (α = 0.05) 的标准差为σ=80? 的标准差为 ?
(α = 0.10 )
解:H 0:µ1=µ 2
H1:µ1 ≠ µ 2
X−Y 2.74 1.61 + 5 4
2 2
2 (已知σ1 , σ 2 , 两总体均值的双边U检验) 2
构造统计量 U =
N
H 0为真
~
( ,1 0 )
查表u
1- 1-
α
2
=u0.95=1.64
由样本值可得
原假设H 0的拒绝域 W = { U > 1.64} 2.14 − 1.8 U= = 2.31 2 2 2.74 1.61 + 5 4 U = 2.31 > 1.64
查表t
1-
α 2
(18)=2.拒绝域
统计量的值
T = 1.474
接受H 0,认为处理前后无差异
T = 1.474 > 2.1009
3.某厂使用 、B两种不同的原料生产同一类型产品, 某厂使用A、 两种不同的原料生产同一类型产品 两种不同的原料生产同一类型产品, 某厂使用 分别在A、 一星期的产品中取样进行测试 一星期的产品中取样进行测试, 分别在 、B一星期的产品中取样进行测试,取A种 种 原料生产的样品220件,B种原料生产的样品 件 种原料生产的样品205件, 原料生产的样品 种原料生产的样品 件 测得平均重量和重量的方差如下: 测得平均重量和重量的方差如下:
x2检验

2
A T
2
T 411.25 19.81 20.58 297.59
321 41.25
2
444 358.15
358.15
2
4.
v=(3-1)(4-1)=6, 则P<0.05,拒绝H0,认为三个地区的人群血型分布构成不同或不全相同。 查χ2界值表
服从x2分布,计算出x2值后,查表判断这么大的 x2是否为小概率事件,以判断建设检验是否成立。
χ2分布(chi-square distribution)
0.5 0.4 0.3
f ( ) 2( / 2) 2
2
1
2
( / 21)
e
2 / 2
Ý ß ×·
×Ó ¶ £ 1 Ô É È ½
0.2 0.1 0.0 0 3
3.84
×Ó ¶ £ 2 Ô É È ½ ×Ó ¶ £ 3 Ô É È ½ ×Ó ¶ £ 6 Ô É È ½
P=0.05的临界值
7.81 12.59
6
9 12 ¿ ·Ö ¨½ µ
15
18
自由度一定时,P值越小, x2值越大。 当P 值一定时,自由度越大, x2越大。 v=1时, P=0.05, x2 =3.84 P=0.01, x2 =6.63 P=0.05时, v=1, x2 =3.84 v=2, x2 =5.99
计数资料的统计推断
教师:数学统计教研室
胡冬梅
卡方检验是χ2检验(Chi-square test) 是现代统计学的创始人之一,英国人K . Pearson(1857-1936)于1900年提出的 一种具有广泛用途的统计方法,是分类 计数资料的假设检验方法,可用于两个 或多个率间或构成比之间的比较,计数 资料的关联度分析,拟合优度检验等等。
关于χ2分布的样本题怎么计算

关于χ2分布的样本题怎么计算χ2分布是概率论与数理统计中常用的一种概率分布,主要用于对样本数据的假设检验。
本文将介绍如何计算和使用χ2分布解决一个具体的样本题。
假设有一个实验,研究一个鸟种的性别比例。
调查了100只鸟的性别,并得到以下数据:雌性:35只雄性:65只现在要判断这只鸟群的性别分布是否符合已知的性别比例。
假设已知鸟群性别比例是1:1,即雌性和雄性各占一半。
我们可以使用χ2分布来检验这个假设。
首先,我们需要建立假设和备择假设:假设H0:鸟群的性别比例符合1:1备择假设H1:鸟群的性别比例不符合1:1然后,我们进行计算。
首先要计算卡方值(χ2值),计算公式为:χ2 = Σ((Oi - Ei)² / Ei)其中,Oi表示观察值,即实际测得的数量;Ei表示期望值,即按照假设得出的数量。
在这个例子中,假设雌性和雄性各占一半,则期望值分别为50只。
通过计算我们可以得到卡方值:χ2 = ((35-50)²/50) + ((65-50)²/50) = 6.5接下来,我们需要根据自由度和显著性水平确定拒绝域。
在这个例子中,自由度为1(观察数据的分类数目减1),我们选择显著性水平为0.05。
查阅χ2分布表,可以得到临界值χ2_0.05(1) ≈ 3.841。
因为计算得到的卡方值 6.5大于临界值 3.841,我们可以拒绝原假设,即鸟群的性别比例不符合1:1。
最后,我们可以计算p值来表示拒绝原假设的程度。
p值表示了在原假设成立的情况下,观察值出现的概率。
在这个例子中,p值约等于0.01。
因为p值小于0.05,我们可以得出结论:鸟群的性别比例不符合1:1,并且这种差异是显著的。
在参考内容方面,可以提供χ2分布表供读者参考。
由于不能提供链接,可以在文中直接列出一部分χ2分布表,帮助读者查找他们需要的临界值。
可以使用以下形式进行列举:卡方值自由度=1 自由度=2 自由度=3 ...0.001 0.000 0.020 0.115 ...0.010 0.004 0.051 0.216 ...0.025 0.102 0.103 0.352 ......0.975 3.841 5.991 7.815 ......通过参考内容和示例计算,读者可以更好地理解和应用χ2分布进行样本问题的分析。
8.3.2 独立性检验

拓展深化 [微判断] 1.概率值α越小,临界值xα越大. 2.独立性检验的思想类似于反证法. 3.独立性检验的结论是有多大的把握认为两个分类变量有关系.
(√ ) (√) (√)
[微训练] 1.如果根据小概率α=0.01的χ2检测试验,认为H0成立,那么具体算出的数据满
足( ) 附表:
α
0.05
xα
大学专科以上学历 大学专科以下学历
合计
积极支持教 不太赞成教育
育改革
改革
39
157
29
167
68
324
合计
196 196 392
对于教育机构的研究项目,根据上述数据能得出什么结论?
解 零假设为H0:成年人具有大学专科以上学历(包括大学专科)和对待教育改革态度 无关. 根据表中数据,计算得
χ2=392×1(963×9×19166×7-681×573×2429)2≈1.78. 因为1.78<2.706=x0.1, 根据小概率值α=0.1的χ2独立性检验,没有充分证据推断H0不成立,所以我们没有理由 说成年人具有大学专科以上学历(包括大学专科)和对待教育改革态度有关.
注:该年级在此次考试中数学成绩优秀的有 360 人,非优秀的有 880 人.
解 零假设为H0:数学成绩优秀与物理、化学、总分成绩优秀都无关系. 列出数学成绩与物理成绩的2×2列联表如下:
物理优秀
物理非优秀
合计
数学优秀
228
132360数源自非优秀143737
880
合计
371
869
1 240
将表中数据代入公式,得
下表给出了χ2独立性检验中几个常用的小概率值和相应的临界值
α
0.1
卡方分布概念及表和查表方法
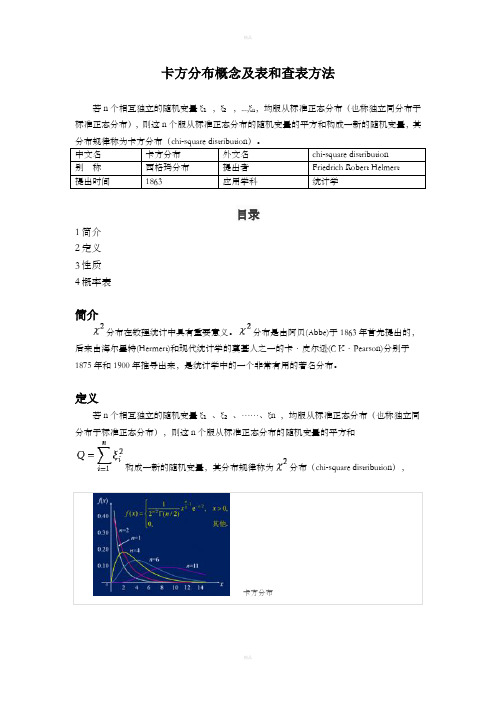
卡方分布概念及表和查表方法若n个相互独立的随机变量ξ₁,ξ₂,...,ξn,均服从标准正态分布(也称独立同分布于标准正态分布),则这n个服从标准正态分布的随机变量的平方和构成一新的随机变量,其分布规律称为卡方分布(chi-square distribution)。
中文名卡方分布外文名chi-square distribution别称西格玛分布提出者Friedrich Robert Helmert提出时间1863应用学科统计学目录1简介2定义3性质4概率表简介分布在数理统计中具有重要意义。
分布是由阿贝(Abbe)于1863年首先提出的,后来由海尔墨特(Hermert)和现代统计学的奠基人之一的卡·皮尔逊(C K·Pearson)分别于1875年和1900年推导出来,是统计学中的一个非常有用的著名分布。
定义若n个相互独立的随机变量ξ₁、ξ₂、……、ξn ,均服从标准正态分布(也称独立同分布于标准正态分布),则这n个服从标准正态分布的随机变量的平方和构成一新的随机变量,其分布规律称为分布(chi-square distribution),卡方分布其中参数称为自由度,正如正态分布中均数或方差不同就是另一个正态分布一样,自由度不同就是另一个分布。
记为或者(其中,为限制条件数)。
卡方分布是由正态分布构造而成的一个新的分布,当自由度很大时,分布近似为正态分布。
对于任意正整数x,自由度为的卡方分布是一个随机变量X的机率分布。
性质1) 分布在第一象限内,卡方值都是正值,呈正偏态(右偏态),随着参数的增大,分布趋近于正态分布;卡方分布密度曲线下的面积都是1。
2) 分布的均值与方差可以看出,随着自由度的增大,分布向正无穷方向延伸(因为均值越来越大),分布曲线也越来越低阔(因为方差越来越大)。
3)不同的自由度决定不同的卡方分布,自由度越小,分布越偏斜。
4) 若互相独立,则:服从分布,自由度为。
5) 分布的均数为自由度,记为E( ) = 。
χ2分布查表举例

χ2分布查表举例χ2分布是概率统计学中常用的一种分布,它是根据正态分布的平方和而得到的。
在实际应用中,我们经常需要查找χ2分布表来计算一些与χ2分布相关的概率或统计量。
本文将以一个具体的例子来详细介绍如何使用χ2分布表进行查表。
1. 问题描述假设有一批产品,我们想要检验其质量是否符合标准。
我们从这批产品中随机抽取了100个样本,并对每个样本进行了质量检测。
现在我们想要判断这批产品的整体质量是否符合标准,即判断总体质量是否服从某个特定的分布。
2. 假设检验为了判断总体质量是否符合某个特定的分布,我们需要进行假设检验。
假设我们已经知道总体质量服从一个特定的理论分布(比如正态分布),那么我们可以通过观察样本数据来判断这个假设是否成立。
3. 计算χ2统计量在进行假设检验时,我们需要计算一个统计量来衡量观察值与理论值之间的差异程度。
对于χ2检验而言,该统计量就是χ2统计量。
4. 计算自由度在计算χ2统计量之前,我们需要先确定自由度。
自由度是指可以独立取值的变量的个数。
对于χ2检验而言,自由度的计算方法是样本个数减去1。
5. 查找临界值根据假设检验的要求,我们需要设定一个显著性水平(一般为0.05),来判断观察值与理论值之间的差异是否显著。
为了确定是否拒绝原假设,我们需要查找χ2分布表来找到与给定显著性水平相对应的临界值。
6. 比较统计量与临界值将计算得到的χ2统计量与查找得到的临界值进行比较。
如果统计量大于临界值,则拒绝原假设;如果统计量小于等于临界值,则接受原假设。
7. 例子假设我们观察到样本数据中有60个产品符合标准,40个产品不符合标准。
我们想要判断这批产品整体质量是否符合标准。
根据样本数据,我们可以计算出χ2统计量。
根据公式:χ2 = Σ((O-E)^2 / E)其中,O表示观察到的频数,E表示期望的频数。
假设这批产品整体质量符合标准,那么我们可以根据标准来计算期望频数。
假设有100个样本,60%符合标准,40%不符合标准。
0卡方检验
总之,χ2值越小,说明实际观察与理论假设
越吻合,当根据样本算出的χ2值大于理论上 在α=0.05 水准处的 χ2 值界值时,可以认为 实际观察与理论假设不符。
假设检验的过程:
⑵ 建议χ2统计量和自由度
பைடு நூலகம்
2 i 1
9
Ai Ti
Ti
2
9.937 , k 1 s 9 1 2 6
2
检验
【教学要求】
掌握:独立样本2×2列联表资料(四格表)χ2检验;
熟悉:四格表资料的Fisher确切概率法
了解:1.连续型随机变量的χ2分布;
2.样本的拟合优度检验的基本思想。
假设检验
统计方法
描述统计 推断统计
参数估计
假设检验
定量变量
定性变量
教学内容
1. χ2分布和拟合优度检验 2.独立样本2× 2列联表资料的χ2检验 3. 2× 2列联表资料的确切概率法 4 .配对设计资料的χ2检验 5.独立样本R×C列联表资料的χ2检验
如果H0假设成立,那么Ai与Pi之差就不会很大,
故可用Ai 与Pi 之间的差异程度反映该样本的频率分
布是否与H0确定的理论分布相符。K.Pearson提出:
2
i 1
k
Ai Ti 2
Ti
可证明当H0成立时,χ2统计量近似地服从自由度v =k-1
的χ2分布。
若计算Ti时,有s个总体参数是用样本估计量替代的,
ß ×¸ Ý
× Ô Ó É ¶ È £ ½ 1
0.2 0.1 0.0 0 3
× Ô Ó É ¶ È £ ½ 2 × Ô Ó É ¶ È £ ½ 3 × Ô Ó É ¶ È £ ½ 6
