二进制工作原理
4bitalu加法器工作原理

4bitalu加法器工作原理
4位二进制加法器(4-bit binary adder)是一种电子电路,用于将两个4位二进制数相加。
最常见的4位二进制加法器是基于全加器(Full Adder)的设计。
以下是4位二进制加法器的工作原理:
输入:
4位二进制加法器有两个4位的输入,通常表示为A和B。
每一位都可以是0或1。
全加器:
4位二进制加法器由4个全加器组成,每个全加器都用于处理对应位的加法。
全加器的结构:
每个全加器包括三个输入:A的对应位(Ai)、B的对应位(Bi)和前一位的进位(Ci-1)。
输出包括两个部分:当前位的和(Si)和传递到下一位的进位(Ci)。
第一位的处理:
第一位的全加器只有两个输入,即A0和B0,因为没有前一位的进位。
输出为第一位的和(S0)和传递到第二位的进位(C1)。
中间位的处理:
对于中间的三位,每个全加器都有三个输入(Ai、Bi、Ci-1)和两个输出(Si、Ci)。
输出的和(Si)作为当前位的二进制和。
输出的进位(Ci)传递到下一位的进位输入(Ci-1)。
最后一位的处理:
最后一位的全加器输出的和(S3)和进位(C4)即为4位二进制数相加的结果。
进位检测:
如果最后一位的全加器输出的进位(C4)为1,则表示溢出。
输出:
4位二进制加法器的输出为一个4位的二进制数,其中每一位都是相应位的和。
总体而言,4位二进制加法器通过级联多个全加器,逐位相加并处理进位,实现对两个4位二进制数的加法运算。
这种结构也可以扩
展到更多位数的二进制加法器。
二进制计算机采用的主要逻辑元件

主题:二进制计算机的主要逻辑元件一、概述二进制计算机是当今世界上最广泛使用的计算机系统。
它们采用二进制系统来表示和处理数据和指令。
在二进制计算机中,存在着一些主要的逻辑元件,它们在计算机的运行中起着至关重要的作用。
二、主要逻辑元件1. 逻辑门逻辑门是构成计算机的基本逻辑元件。
它们能够执行基本的逻辑运算,如与、或、非等。
常见的逻辑门有与门、或门、非门等。
在计算机中,逻辑门被组合成各种复杂的逻辑电路,用来实现各种功能。
2. 寄存器寄存器是一种用来存储数据的元件。
在计算机中,寄存器通常用来存储临时数据、位置区域或指令。
寄存器的大小通常是以位(bit)来表示的,如8位寄存器、16位寄存器等。
3. 存储器存储器是计算机中用来存储数据和指令的元件。
存储器分为内存和外存,内存通常指的是随机存取存储器(RAM),它用来存储正在运行的程序和数据;外存通常指的是磁盘或固态硬盘,它用来存储长期的数据和程序。
4. ALU(算术逻辑单元)ALU是计算机中用来执行算术和逻辑运算的部件。
它能够执行加、减、乘、除等算术运算,也能够执行与、或、非等逻辑运算。
5. 控制单元控制单元是计算机中用来控制指令执行顺序的部件。
它能够从存储器中取出指令,解码指令,并且控制各个部件的工作。
6. 时钟时钟是计算机中用来同步各个部件工作的部件。
它能够在一个固定的时间间隔内发出脉冲信号,使得各个部件按照统一的节拍工作。
7. 数据总线数据总线是计算机中用来传输数据的通道。
它能够同时传输多位数据,如8位、16位、32位等。
8. 位置区域总线位置区域总线是计算机中用来传输位置区域信息的通道。
它能够指示存储器中的特定位置。
9. 控制总线控制总线是计算机中用来传输控制信号的通道。
它能够传输各种控制信号,如读写信号、中断信号等。
三、总结二进制计算机中的主要逻辑元件包括逻辑门、寄存器、存储器、ALU、控制单元、时钟、数据总线、位置区域总线和控制总线。
它们共同构成了计算机的基本操作和功能。
二进制码转BCD码原理

⼆进制码转BCD码原理有时候没有采⽤BCD计数器,⼜需要⽤⼗进制形式显⽰⼆进制数据,最常⽤的⽅法是编码转换:将⼆进制码转换成BCD码(8421)。
8421码:8421码⼜称⼗进制码,它只选⽤了四位⼆进制码中前10组代码,4个码表达10个数,即⽤0000~1001分别代表它所对应的⼗进制数,余下的六组代码不⽤。
如果要我将⼆进制码转成BCD码,我会看看他们何时分道扬镳,以此观察⼆者的区别。
对于BCD计数器,当计数到1001时,下⼀次计数要进位,得到0001_0000。
对于⼆进制计数器,下⼀次计数得到的是1010。
不可能重新计⼀次数来得到BCD码,太浪费时间了,但是直接让我转我也束⼿⽆策。
我们很快发现按位重建的话,消耗的时钟周期数是⼆进制位数,还可以接受。
深⼊思考⼀下,发现是可⾏的。
就像标准LSB乘法⼀样,从⼆进制⾼位开始重建,⽤⼀个寄存器每个周期进⾏shift-add操作。
如果不⼲其他的,花费n个周期即可重建出n-bit⼆进制数。
这个⼯作量已经是⼀个⽐特串⾏乘法器了,结果肯定是原来的⼆进制数不会错。
每4个bit分为⼀组BCD码,对于任意⼀组在任意⼀个周期状态下,只要数据≥5,那么下⼀次移位就会超出BCD码范围,对于BCD 计数器来说需要进位。
为使4位⼆进制码进位,要满⾜逢16进⼀。
由于BCD码是逢10进⼀,直接给当前组4bit数据补上差距3即可。
下⼀次移位的时候,差距扩⼤为6,如果BCD码应该进位,那么⼆进制码也会进位,同步进位,⽬的达成。
寄存器中的编码已经是BCD码了,但是这个BCD码代表的值和⼆进制代表的值是⼀样的。
⼆进制重建可以进⾏shift-add操作,BCD码重建同样可以进⾏shift-add操作,只不过BCD码有⾃⼰的规则,在shift-add的时候要进⾏⼀点修正罢了。
在任意周期,重建出来的⼆进制码和BCD码表⽰的值都是⼀样的。
所以最终重建出来的BCD码是正确的。
二进制计数器工作原理

二进制计数器工作原理
二进制计数器是一种电子数字电路,用于计数二进制数字。
它通常由
多个触发器组成,每个触发器都有两个稳定状态:置位和复位。
当计
数器接收到时钟信号时,它会根据当前状态向下计数或向上计数。
在
向下计数模式下,计数器会从最大值开始减少,直到达到最小值为止。
在向上计数模式下,计数器会从最小值开始增加,直到达到最大值为止。
二进制计数器的工作原理可以分为以下几个步骤:
1. 初始化:在使用计数器之前,需要将其初始化为一个特定的值。
这
可以通过将所有触发器的状态设置为相应的二进制值来完成。
2. 计数:当计数器接收到时钟信号时,它会根据当前状态进行计数。
如果处于向上模式,则将当前状态加1;如果处于向下模式,则将当前状态减1。
3. 溢出检测:当计数器达到其最大或最小值时,它会发出一个溢出信号。
这可以通过检测所有触发器是否都处于其稳定状态来实现。
4. 重置:如果需要重新开始计数,则可以使用重置信号将所有触发器
的状态设置为初始值。
总之,二进制计数器是一种非常重要的电子数字电路,它可以用于各种应用,如时序控制、频率分频和计时器等。
理解其工作原理对于设计和使用计数器至关重要。
二进制数字调制原理
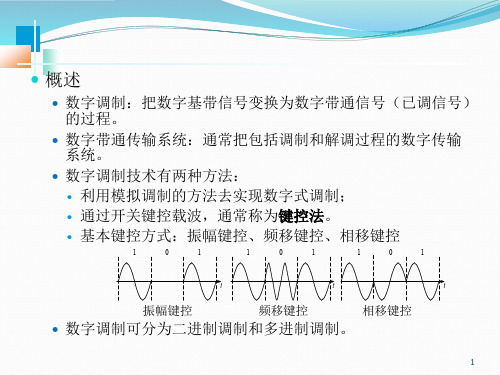
其中,fs = 1/Ts为基带信号的带宽。图中的fc为两个载频的中心频率。
21
6.1.3 二进制相移键控(2PSK)
2PSK信号的表达式: 在2PSK中,通常用初始相位0和分别表示二进制“1”和“0”。因 此,2PSK信号的时域表达式为
e2PSK (t) A cos(ct n )
G(0) TS
P2PSK (
f
)
Ts 4
sin ( ( f
f fc )Ts fc )Ts
2
sin ( ( f
f fc )Ts fc )Ts
2
29
功率谱密度曲线
P2PSK f
fc
fc fs fc fc fs
f
从以上分析可见,二进制相移键控信号的频谱特性与2ASK的十分 相似,带宽也是基带信号带宽的两倍。区别仅在于当P=1/2时,其 谱中无离散谱(即载波分量),此时2PSK信号实际上相当于抑制 载波的双边带信号。因此,它可以看作是双极性基带信号作用下的
23
典型波形
1
0
0
1
1
t Ts
24
2PSK信号的调制器原理方框图
模拟调制的方法
双极性
s(t)
不归零
码型变换
乘法器
e2PSK (t)
键控法
cosct
c os ct
开关电路
0
e2PSK (t)
1800 移相
s(t)
25
2PSK信号的解调器原理方框图和波形图:
e2PSK (t)
带通 滤波器
2ASK信号的带宽是基带信号带宽的两倍,若只计谱的主瓣(第一 个谱零点位置),则有
式中 fs = 1/Ts
二进制数序列-概述说明以及解释

二进制数序列-概述说明以及解释1.引言1.1 概述概述部分的内容:在计算机科学和信息技术领域中,二进制数是一种重要而基础的数学表示方法。
它由两个数码0和1组成,是一种仅用两个不同数码表示数字的系统,被广泛应用于数字通信、计算机编程和数据处理等领域。
二进制数的序列由一串0和1的数字组成,通过这种表示方法,我们能够更好地理解和运算任意复杂的数据。
二进制数的表示方法和其他进制不同,它采用了基数为2的系统。
每个数位上的数字只能是0或者1,这与我们常见的十进制数不同,十进制数中可以使用0到9的数字表示。
从二进制数的基本概念到具体的表示方法,我们将在接下来的章节中一一展开。
二进制数在计算机科学中的重要性不可忽视。
计算机的内部数据处理和存储都是以二进制数的形式进行的,因此理解二进制数非常关键。
同时,二进制数也是计算机编程中的重要基础,了解二进制数的表示和运算方法能够帮助我们更好地处理数据和编写高效的程序。
本文将以简明扼要的方式介绍二进制数的基本概念和表示方法,并探讨二进制数在计算机领域中的应用。
通过阅读本文,读者将能够对二进制数有一个清晰的认识,并进一步了解二进制数的重要性和用途。
接下来的章节将详细介绍二进制数的概念、表示和应用,以帮助读者更好地理解和运用二进制数。
1.2文章结构文章结构部分的内容可以是以下内容:文章结构是指文章的整体组织架构,包括引言、正文和结论三个主要部分。
在本篇文章中,我们将介绍二进制数序列的相关概念和表示方法,并探讨二进制数在计算机中的重要性和应用。
引言部分是文章的开端,它主要包括对二进制数序列主题的概述、文章结构的介绍以及写作目的的阐述。
在本篇文章中,我们将首先概述二进制数的基本概念,然后详细介绍二进制数的表示方法。
最后,我们将探讨二进制数在计算机中的重要性和应用。
正文部分是文章的主体部分,主要围绕二进制数的基本概念和表示方法展开。
在2.1节中,我们将详细解释二进制数的基本概念,包括二进制数的定义、特点和基本运算。
74ls390工作原理(一)

74ls390工作原理(一)74LS390工作原理什么是74LS39074LS390是一种二进制分频器/计数器芯片,常用于数字逻辑系统中。
它由两个带有异步清零功能的Ripple type的BCD计数器串联而成。
74LS390的结构74LS390由两个独立的4位二进制计数器组成,每个计数器的输入和输出都可以独立地进行控制。
74LS390既可以作为计数器使用,也可以作为分频器使用。
74LS390的工作原理74LS390的计数是通过四个JK触发器和一个与门实现的。
JK触发器的时钟信号由输入的晶体时钟分频得到,分频系数由上面的控制引脚控制。
通过对计数器的控制,可以实现数值的增加或减少。
74LS390的应用74LS390常用于计数器、分频器、频率测量和脉冲生成等数字逻辑设计中。
在数字电子钟、电视机中也经常会用到它。
总结74LS390是一种十分常见的数字逻辑IC芯片,可以实现计数和分频等功能,应用广泛。
深入理解74LS390的工作原理对于数字逻辑系统的设计有着重要的意义。
74LS390的引脚功能以下是74LS390的引脚功能及其描述:引脚描述引脚描述CP1 第一个计数器的时钟输入CP0 第二个计数器的时钟输入MR 异步清零输入,清零后计数器输出为0QA-QD 第一个计数器的四个二进制输出QB-QG 第二个计数器的四个二进制输出CET 两个计数器的使能输入,使能为高电平有效TC 整个74LS390的借位输出,当计数器输出为0时为高电平Q/Q̅A̅-第一个计数器的四个输出和其反相输出Q/Q̅D̅Q/Q̅B̅-第二个计数器的四个输出和其反相输出Q/Q̅G̅74LS390的工作模式74LS390有两种工作模式:计数模式和分频模式。
在计数模式下,74LS390会对传入的时钟信号进行计数。
当计数器计数到最大值时,会通过TC引脚的高电平输出一个借位信号,并将计数器清零,重新开始计数。
在分频模式下,通过对CP1和CP0控制,可以设置计数器的分频系数,使得输出信号的频率等于输入信号的频率除以分频系数。
rs触发器工作原理表达式

rs触发器工作原理表达式
触发器(RS Flip-flop)是一种二进制存储元件,可以将输入的数据进行存储并输出。
其工作原理如下:
1. 起始状态:置入S(Set)和R(Reset)输入为0,RS触发器处于复位状态,输出为Q=0和Q=1。
2. 当R=0、S=1时,触发器进入置位状态(Set):Q=1和
Q=0。
3. 当R=1、S=0时,触发器进入复位状态(Reset):Q=0和Q=1。
4. 当R=0、S=0时,触发器保持前一状态不变。
5. 当R=1、S=1时,触发器处于禁止状态,输出结果不确定。
触发器的工作原理可以用逻辑表达式表示为:
Q(t+1) = S + Q(t) = S + RQ(t)
Q(t+1) = R + Q(t)
其中,Q(t)和Q(t)分别表示触发器当前的输出状态,Q(t+1)和Q(t+1)表示下一个时刻的输出状态,S和R分别表示触发器的设置(Set)和复位(Reset)输入。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
